If we are to use geodesics and covariant derivatives as tools for studying Riemannian geometry, it is evident that we need a way to single out a particular connection on a Riemannian manifold that reflects the properties of the metric. In this chapter, guided by the example of the tangential connection on a submanifold of  , we describe two properties that determine a unique connection on every Riemannian manifold. The first property, compatibility with the metric, is easy to motivate and understand. The second, symmetry, is a bit more mysterious; but it is motivated by the fact that it is invariantly defined, and is always satisfied by the tangential connection. It turns out that these two conditions are enough to determine a unique connection associated with any Riemannian or pseudo-Riemannian metric, called the Levi-Civita connection after the early twentieth-century Italian differential geometer Tullio Levi-Civita.
, we describe two properties that determine a unique connection on every Riemannian manifold. The first property, compatibility with the metric, is easy to motivate and understand. The second, symmetry, is a bit more mysterious; but it is motivated by the fact that it is invariantly defined, and is always satisfied by the tangential connection. It turns out that these two conditions are enough to determine a unique connection associated with any Riemannian or pseudo-Riemannian metric, called the Levi-Civita connection after the early twentieth-century Italian differential geometer Tullio Levi-Civita.
After defining the Levi-Civita connection, we investigate the exponential map, which conveniently encodes the collective behavior of geodesics and allows us to study how they change as the initial point and initial velocity vary. Having established the properties of this map, we introduce normal neighborhoods and normal coordinates, which are essential computational and theoretical tools for studying local geometric properties near a point. Then we introduce the analogous notion for studying properties near a submanifold: tubular neighborhoods and Fermi coordinates. Finally, we return to our three main model Riemannian manifolds and determine their geodesics.
Except where noted otherwise, the results and proofs of this chapter do not use positivity of the metric, so they apply equally well to Riemannian and pseudo-Riemannian manifolds.
The Tangential Connection Revisited
We are eventually going to show that on each Riemannian manifold there is a natural connection that is particularly well suited to computations in Riemannian geometry. Since we get most of our intuition about Riemannian manifolds from studying submanifolds of  with the induced metric, let us start by examining that case.
with the induced metric, let us start by examining that case.
Let  be an embedded submanifold. As a guiding principle, consider the idea mentioned at the beginning of Chapter 4: a geodesic in M should be “as straight as possible.” A reasonable way to make this rigorous is to require that the geodesic have no acceleration in directions tangent to the manifold, or in other words that its acceleration vector have zero orthogonal projection onto TM.
be an embedded submanifold. As a guiding principle, consider the idea mentioned at the beginning of Chapter 4: a geodesic in M should be “as straight as possible.” A reasonable way to make this rigorous is to require that the geodesic have no acceleration in directions tangent to the manifold, or in other words that its acceleration vector have zero orthogonal projection onto TM.
The tangential connection defined in Example 4.9 is perfectly suited to this task, because it computes covariant derivatives on M by taking ordinary derivatives in  and projecting them orthogonally to TM.
and projecting them orthogonally to TM.
It is easy to compute covariant derivatives along curves in M with respect to the tangential connection. Suppose  is a smooth curve. Then
is a smooth curve. Then  can be regarded as either a smooth curve in M or a smooth curve in
can be regarded as either a smooth curve in M or a smooth curve in  , and a smooth vector field V along
, and a smooth vector field V along  that takes its values in TM can be regarded as either a vector field along
that takes its values in TM can be regarded as either a vector field along  in M or a vector field along
in M or a vector field along  in
in  . Let
. Let  denote the covariant derivative of V along
denote the covariant derivative of V along  (as a curve in
(as a curve in  ) with respect to the Euclidean connection
) with respect to the Euclidean connection  , and let
, and let  denote its covariant derivative along
denote its covariant derivative along  (as a curve in M) with respect to the tangential connection
(as a curve in M) with respect to the tangential connection  . The next proposition shows that the two covariant derivatives along
. The next proposition shows that the two covariant derivatives along  have a simple relationship to each other.
have a simple relationship to each other.
Proposition 5.1.
 be an embedded submanifold,
be an embedded submanifold,  a smooth curve in M, and V a smooth vector field along
a smooth curve in M, and V a smooth vector field along  that takes its values in TM. Then for each
that takes its values in TM. Then for each  ,
,
Proof.
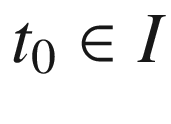 be arbitrary. By Proposition 2.14, on some neighborhood U of
be arbitrary. By Proposition 2.14, on some neighborhood U of  in
in 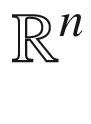 there is an adapted orthonormal frame for TM, that is, a local orthonormal frame
there is an adapted orthonormal frame for TM, that is, a local orthonormal frame 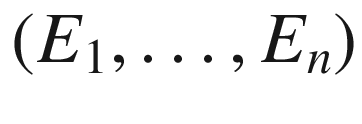 for
for  such that
such that  restricts to an orthonormal frame for TM at points of
restricts to an orthonormal frame for TM at points of  (where
(where 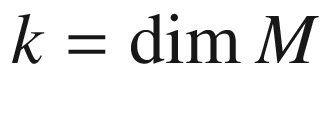 ). If
). If  is small enough that
is small enough that  , then for
, then for  we can write
we can write
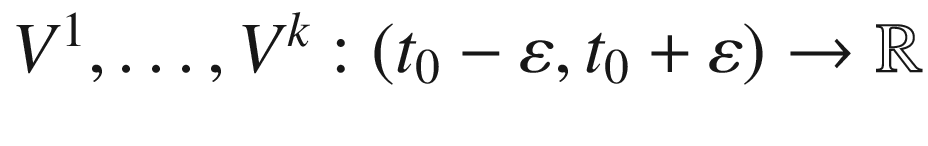 . Formula (4.15) yields
. Formula (4.15) yields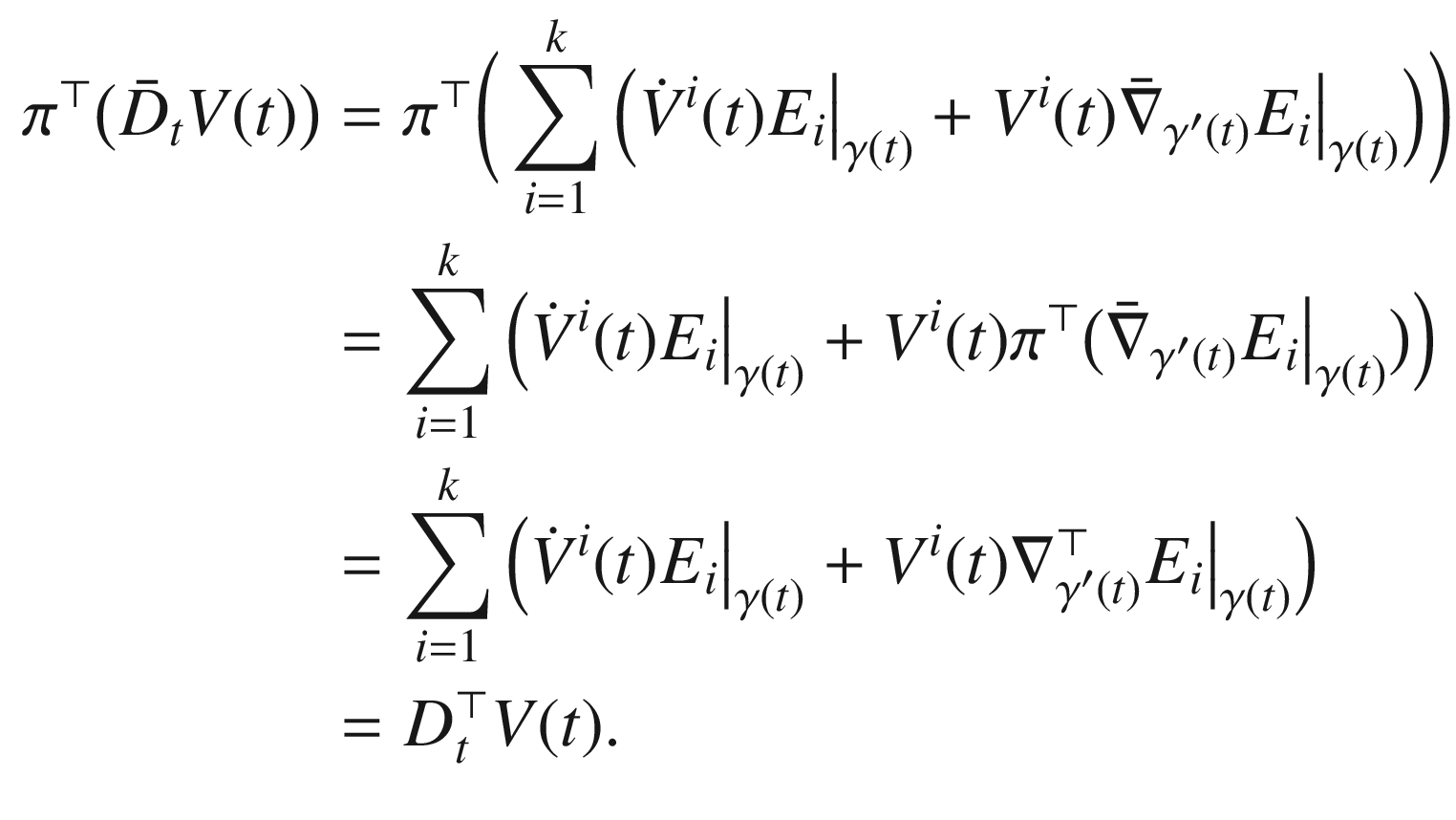

Corollary 5.2.
Suppose  is an embedded submanifold. A smooth curve
is an embedded submanifold. A smooth curve  is a geodesic with respect to the tangential connection on M if and only if its ordinary acceleration
is a geodesic with respect to the tangential connection on M if and only if its ordinary acceleration  is orthogonal to
is orthogonal to  for all
for all  .
.
Proof.
As noted in Example 4.8, the connection coefficients of the Euclidean connection on  are all zero. Thus it follows from (4.15) that the Euclidean covariant derivative of
are all zero. Thus it follows from (4.15) that the Euclidean covariant derivative of  along
along  is just its ordinary acceleration:
is just its ordinary acceleration:  . The corollary then follows from Proposition 5.1.
. The corollary then follows from Proposition 5.1. 
 be the pseudo-Euclidean space of signature (r, s). If
be the pseudo-Euclidean space of signature (r, s). If  is an embedded Riemannian or pseudo-Riemannian submanifold, then for each
is an embedded Riemannian or pseudo-Riemannian submanifold, then for each  , the tangent space
, the tangent space 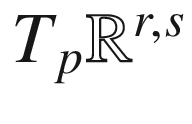 decomposes as a direct sum
decomposes as a direct sum  , where
, where 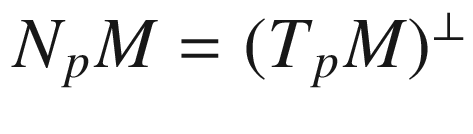 is the orthogonal complement of
is the orthogonal complement of  with respect to
with respect to 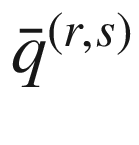 . We let
. We let 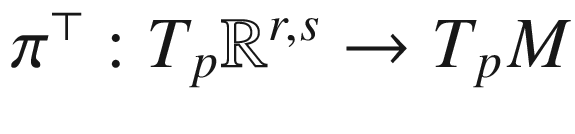 be the
be the  -orthogonal projection, and define the tangential connection
-orthogonal projection, and define the tangential connection  on M by
on M by
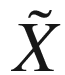 and
and  are smooth extensions of X and Y to a neighborhood of M, and
are smooth extensions of X and Y to a neighborhood of M, and  is the ordinary Euclidean connection on
is the ordinary Euclidean connection on 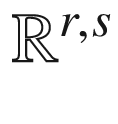 . This is a well-defined connection on M by the same argument as in the Euclidean case, and the next proposition is proved in exactly the same way as Corollary 5.2.
. This is a well-defined connection on M by the same argument as in the Euclidean case, and the next proposition is proved in exactly the same way as Corollary 5.2.Proposition 5.3.
Suppose M is an embedded Riemannian or pseudo-Riemannian submanifold of the pseudo-Euclidean space  . A smooth curve
. A smooth curve  is a geodesic with respect to
is a geodesic with respect to  if and only if
if and only if  is
is  -orthogonal to
-orthogonal to  for all
for all  .
.
 Exercise 5.4. Prove the preceding proposition.
Exercise 5.4. Prove the preceding proposition.
Connections on Abstract Riemannian Manifolds
There is a celebrated (and hard) theorem of John Nash [Nas56] that says that every Riemannian metric on a smooth manifold can be realized as the induced metric of some embedding in a Euclidean space. That theorem was later generalized independently by Robert Greene [Gre70] and Chris J. S. Clarke [Cla70] to pseudo-Riemannian metrics. Thus, in a certain sense, we would lose no generality by studying only submanifolds of Euclidean and pseudo-Euclidean spaces with their induced metrics, for which the tangential connection would suffice. However, when we are trying to understand intrinsic properties of a Riemannian manifold, an embedding introduces a great deal of extraneous information, and in some cases actually makes it harder to discern which geometric properties depend only on the metric. Our task in this chapter is to distinguish some important properties of the tangential connection that make sense for connections on an abstract Riemannian or pseudo-Riemannian manifold, and to use them to single out a unique connection in the abstract case.
Metric Connections
 has one very nice property with respect to the Euclidean metric: it satisfies the product rule
has one very nice property with respect to the Euclidean metric: it satisfies the product rule
 regarded as a (0, 0)-tensor field, which is really just
regarded as a (0, 0)-tensor field, which is really just  by virtue of property (ii) of Prop. 4.15.) The Euclidean connection has the same property with respect to the pseudo-Euclidean metric on
by virtue of property (ii) of Prop. 4.15.) The Euclidean connection has the same property with respect to the pseudo-Euclidean metric on  . It is almost immediate that the tangential connection on a Riemannian or pseudo-Riemannian submanifold satisfies the same product rule, if we now interpret all the vector fields as being tangent to M and interpret the inner products as being taken with respect to the induced metric on M (see Prop. 5.8 below).
. It is almost immediate that the tangential connection on a Riemannian or pseudo-Riemannian submanifold satisfies the same product rule, if we now interpret all the vector fields as being tangent to M and interpret the inner products as being taken with respect to the induced metric on M (see Prop. 5.8 below). on TM is said to be compatible with
on TM is said to be compatible with  , or to be a metric connection, if it satisfies the following product rule for all
, or to be a metric connection, if it satisfies the following product rule for all 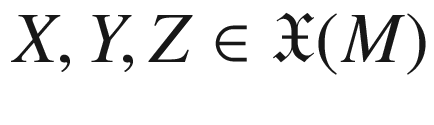 :
:
Proposition 5.5
 be a connection on TM. The following conditions are equivalent:
be a connection on TM. The following conditions are equivalent:- (a)
 is compatible with g:
is compatible with g:  .
. - (b)
g is parallel with respect to
 :
:  .
. - (c)In terms of any smooth local frame
 , the connection coefficients of
, the connection coefficients of  satisfy
satisfy  (5.2)
(5.2) - (d)If V, W are smooth vector fields along any smooth curve
 , then
, then  (5.3)
(5.3) - (e)
If V, W are parallel vector fields along a smooth curve
 in M, then
in M, then  is constant along
is constant along  .
. - (f)
Given any smooth curve
 in M, every parallel transport map along
in M, every parallel transport map along  is a linear isometry.
is a linear isometry. - (g)
Given any smooth curve
 in M, every orthonormal basis at a point of
in M, every orthonormal basis at a point of  can be extended to a parallel orthonormal frame along
can be extended to a parallel orthonormal frame along  (Fig. 5.1).
(Fig. 5.1).

A parallel orthonormal frame
Proof.
 (b). By (4.14) and (4.12), the total covariant derivative of the symmetric 2-tensor g is given by
(b). By (4.14) and (4.12), the total covariant derivative of the symmetric 2-tensor g is given by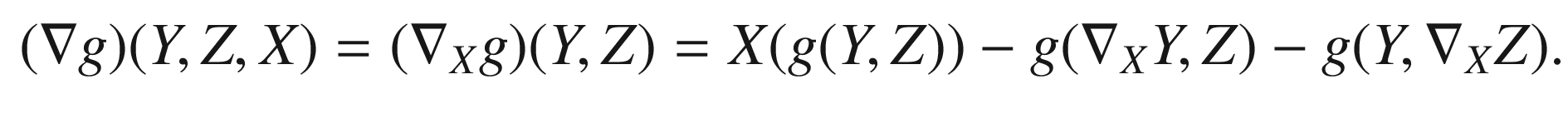
 (c), note that Proposition 4.18 shows that the components of
(c), note that Proposition 4.18 shows that the components of  in terms of a smooth local frame
in terms of a smooth local frame 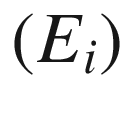 are
are
 (d). Assume (a), and let V, W be smooth vector fields along a smooth curve
(d). Assume (a), and let V, W be smooth vector fields along a smooth curve  . Given
. Given 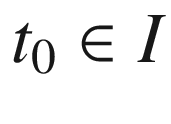 , in a neighborhood of
, in a neighborhood of  we may choose coordinates
we may choose coordinates  and write
and write  and
and  for some smooth functions
for some smooth functions  . Applying (5.1) to the extendible vector fields
. Applying (5.1) to the extendible vector fields 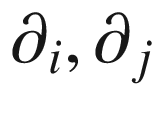 , we obtain
, we obtain
 , and then (a) follows from part (iii) of Theorem 4.24.
, and then (a) follows from part (iii) of Theorem 4.24.Now we will prove (d)  (e)
(e)  (f)
(f)  (g)
(g)  (d). Assume first that (d) holds. If V and W are parallel along
(d). Assume first that (d) holds. If V and W are parallel along  , then (5.3) shows that
, then (5.3) shows that  has zero derivative with respect to t, so it is constant along
has zero derivative with respect to t, so it is constant along  .
.
Now assume (e). Let  be arbitrary vectors in
be arbitrary vectors in  , and let V, W be their parallel transports along
, and let V, W be their parallel transports along  , so that
, so that  ,
,  ,
,  , and
, and  . Because
. Because  is constant along
is constant along  , it follows that
, it follows that  , so
, so  is a linear isometry.
is a linear isometry.
Next, assuming (f), we suppose  is a smooth curve and
is a smooth curve and  is an orthonormal basis for
is an orthonormal basis for  , for some
, for some  . We can extend each
. We can extend each  by parallel transport to obtain a smooth parallel vector field
by parallel transport to obtain a smooth parallel vector field  along
along  , and the assumption that parallel transport is a linear isometry guarantees that the resulting n-tuple
, and the assumption that parallel transport is a linear isometry guarantees that the resulting n-tuple  is an orthonormal frame at all points of
is an orthonormal frame at all points of  .
.
 be a parallel orthonormal frame along
be a parallel orthonormal frame along  . Given smooth vector fields V and W along
. Given smooth vector fields V and W along 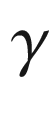 , we can express them in terms of this frame as
, we can express them in terms of this frame as  and
and 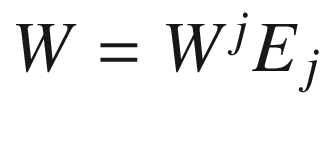 . The fact that the frame is orthonormal means that the metric coefficients
. The fact that the frame is orthonormal means that the metric coefficients  are constants along
are constants along  (
( or 0), and the fact that it is parallel means that
or 0), and the fact that it is parallel means that  and
and  . Thus both sides of (5.3) reduce to the following expression:
. Thus both sides of (5.3) reduce to the following expression:

Corollary 5.6.
Suppose (M, g) is a Riemannian or pseudo-Riemannian manifold with or without boundary,  is a metric connection on M, and
is a metric connection on M, and  is a smooth curve.
is a smooth curve.
- (a)
 is constant if and only if
is constant if and only if  is orthogonal to
is orthogonal to  for all
for all  .
. - (b)
If
 is a geodesic, then
is a geodesic, then  is constant.
is constant.
 Exercise 5.7. Prove the preceding corollary.
Exercise 5.7. Prove the preceding corollary.
Proposition 5.8.
If M is an embedded Riemannian or pseudo-Riemannian submanifold of  or
or  , the tangential connection on M is compatible with the induced Riemannian or pseudo-Riemannian metric.
, the tangential connection on M is compatible with the induced Riemannian or pseudo-Riemannian metric.
Proof.
 satisfies (5.1). Suppose
satisfies (5.1). Suppose  , and let
, and let  be smooth extensions of them to an open subset of
be smooth extensions of them to an open subset of 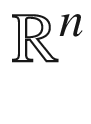 or
or  . At points of M, we have
. At points of M, we have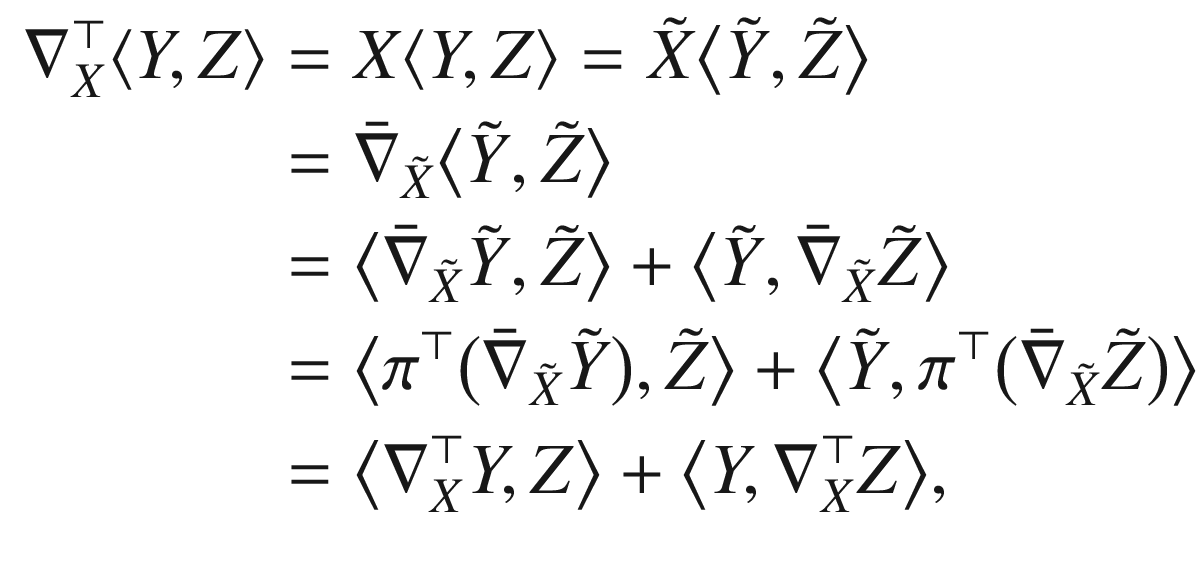
 and
and  are tangent to M.
are tangent to M. 
Symmetric Connections
![$$\begin{aligned}{}[X, Y] = X\big (Y^i\big )\frac{\partial }{\partial x^i}- Y\big (X^i\big )\frac{\partial }{\partial x^i}. \end{aligned}$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_Equ38.png)
 and
and  . Therefore, the Euclidean connection satisfies the following identity for all smooth vector fields X, Y:
. Therefore, the Euclidean connection satisfies the following identity for all smooth vector fields X, Y:![$$\begin{aligned} \bar{\nabla }_X Y - \bar{\nabla }_Y X = [X, Y]. \end{aligned}$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_Equ39.png)
 on the tangent bundle of a smooth manifold M is symmetric if
on the tangent bundle of a smooth manifold M is symmetric if![$$\begin{aligned} \nabla _X Y - \nabla _Y X \equiv [X,Y] \text { for all } X, Y\in \mathfrak X(M). \end{aligned}$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_Equ40.png)
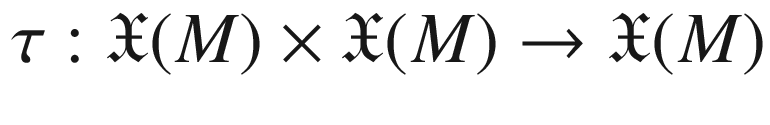 defined by
defined by![$$\begin{aligned} \tau (X,Y)= \nabla _X Y - \nabla _Y X - [X, Y]. \end{aligned}$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_Equ41.png)
 is symmetric if and only if its torsion vanishes identically. It follows from the result of Problem 4-6 that a connection is symmetric if and only if its connection coefficients in every coordinate frame satisfy
is symmetric if and only if its torsion vanishes identically. It follows from the result of Problem 4-6 that a connection is symmetric if and only if its connection coefficients in every coordinate frame satisfy  ; this is the origin of the term “symmetric."
; this is the origin of the term “symmetric."Proposition 5.9.
If M is an embedded (pseudo-)Riemannian submanifold of a (pseudo-)Euclidean space, then the tangential connection on M is symmetric.
Proof.
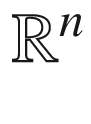 , where
, where 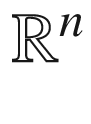 is endowed either with the Euclidean metric or with a pseudo-Euclidean metric
is endowed either with the Euclidean metric or with a pseudo-Euclidean metric  ,
,  . Let
. Let 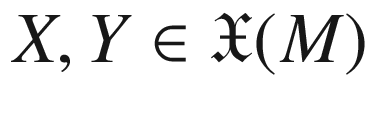 , and let
, and let  be smooth extensions of them to an open subset of the ambient space. If
be smooth extensions of them to an open subset of the ambient space. If  represents the inclusion map, it follows that X and Y are
represents the inclusion map, it follows that X and Y are  -related to
-related to 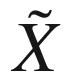 and
and  , respectively, and thus by the naturality of the Lie bracket (Prop. A.39), [X, Y] is
, respectively, and thus by the naturality of the Lie bracket (Prop. A.39), [X, Y] is  -related to
-related to ![$$\big [\tilde{X},\tilde{Y}\big ]$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_IEq182.png) . In particular,
. In particular, ![$$\big [\tilde{X},\tilde{Y}\big ]$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_IEq183.png) is tangent to M, and its restriction to M is equal to [X, Y]. Therefore,
is tangent to M, and its restriction to M is equal to [X, Y]. Therefore,![$$\begin{aligned} \nabla ^\top _X Y - \nabla ^\top _Y X&= \pi ^\top \big (\bar{\nabla }_{\tilde{X}}\tilde{Y}\big |_M - \bar{\nabla }_{\tilde{Y}}\tilde{X}\big |_M\big )\\&= \pi ^\top \big ( \bigl [ \tilde{X},\tilde{Y}\bigr ]\big |_M\big )\\&= \bigl [ \tilde{X},\tilde{Y}\bigr ]\big |_M\\&=[X, Y]. \end{aligned}$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_Equ42.png)

The last two propositions show that if we wish to single out a connection on each Riemannian or pseudo-Riemannian manifold in such a way that it matches the tangential connection when the manifold is presented as an embedded submanifold of  or
or  with the induced metric, then we must require at least that the connection be compatible with the metric and symmetric. It is a pleasant fact that these two conditions are enough to determine a unique connection.
with the induced metric, then we must require at least that the connection be compatible with the metric and symmetric. It is a pleasant fact that these two conditions are enough to determine a unique connection.
Theorem 5.10
(Fundamental Theorem of Riemannian Geometry). Let (M, g) be a Riemannian or pseudo-Riemannian manifold (with or without boundary). There exists a unique connection  on TM that is compatible with g and symmetric. It is called the Levi-Civita connection of
on TM that is compatible with g and symmetric. It is called the Levi-Civita connection of  (or also, when g is positive definite, the
Riemannian connection
).
(or also, when g is positive definite, the
Riemannian connection
).
Proof.
 . Suppose, therefore, that
. Suppose, therefore, that  is such a connection, and let
is such a connection, and let  . Writing the compatibility equation three times with X, Y, Z cyclically permuted, we obtain
. Writing the compatibility equation three times with X, Y, Z cyclically permuted, we obtain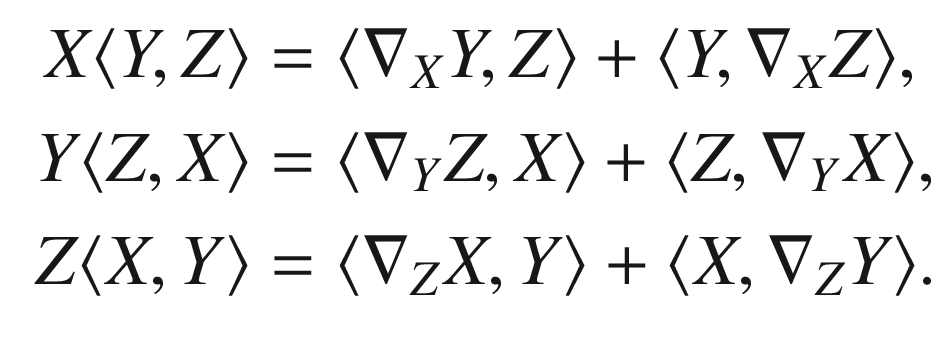
![$$\begin{aligned} \begin{aligned} X\langle Y,Z \rangle&= \langle \nabla _XY,Z \rangle +\langle Y,\nabla _ZX \rangle +\langle Y,[X,Z] \rangle ,\\ Y\langle Z,X \rangle&= \langle \nabla _YZ,X \rangle +\langle Z,\nabla _XY \rangle +\langle Z,[Y,X] \rangle ,\\ Z\langle X,Y \rangle&= \langle \nabla _ZX,Y \rangle +\langle X,\nabla _YZ \rangle +\langle X,[Z, Y] \rangle . \end{aligned} \end{aligned}$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_Equ44.png)
![$$\begin{aligned} \begin{aligned} X\langle Y,Z \rangle +Y\langle Z,X \rangle -&Z\langle X, Y \rangle =\\&2\langle \nabla _XY,Z \rangle +\langle Y,[X,Z] \rangle +\langle Z,[Y,X] \rangle -\langle X,[Z, Y] \rangle . \end{aligned} \end{aligned}$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_Equ45.png)
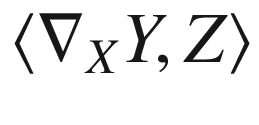 , we get
, we get
![$$\begin{aligned} \langle \nabla _XY, Z \rangle = \tfrac{1}{2}\big ( X\langle Y,Z \rangle&+Y\langle Z,X \rangle -Z\langle X,Y \rangle \nonumber \\&\qquad -\langle Y,[X,Z] \rangle -\langle Z,[Y,X] \rangle +\langle X,[Z, Y] \rangle \big ). \end{aligned}$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_Equ5.png)
 and
and  are two connections on TM that are symmetric and compatible with g. Since the right-hand side of (5.5) does not depend on the connection, it follows that
are two connections on TM that are symmetric and compatible with g. Since the right-hand side of (5.5) does not depend on the connection, it follows that  for all X, Y, Z. This can happen only if
for all X, Y, Z. This can happen only if 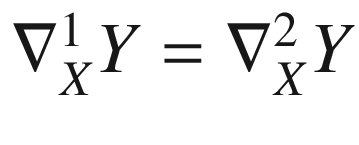 for all X and Y, so
for all X and Y, so 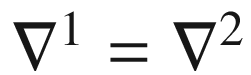 .
.To prove existence, we use (5.5), or rather a coordinate version of it. It suffices to prove that such a connection exists in each coordinate chart, for then uniqueness ensures that the connections in different charts agree where they overlap.
 be any smooth local coordinate chart. Applying (5.5) to the coordinate vector fields, whose Lie brackets are zero, we obtain
be any smooth local coordinate chart. Applying (5.5) to the coordinate vector fields, whose Lie brackets are zero, we obtain


 and noting that
and noting that  , we get
, we get

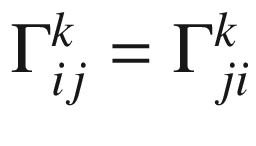 , so the connection is symmetric by Problem 4-6(b). Thus only compatibility with the metric needs to be checked. Using (5.7) twice, we get
, so the connection is symmetric by Problem 4-6(b). Thus only compatibility with the metric needs to be checked. Using (5.7) twice, we get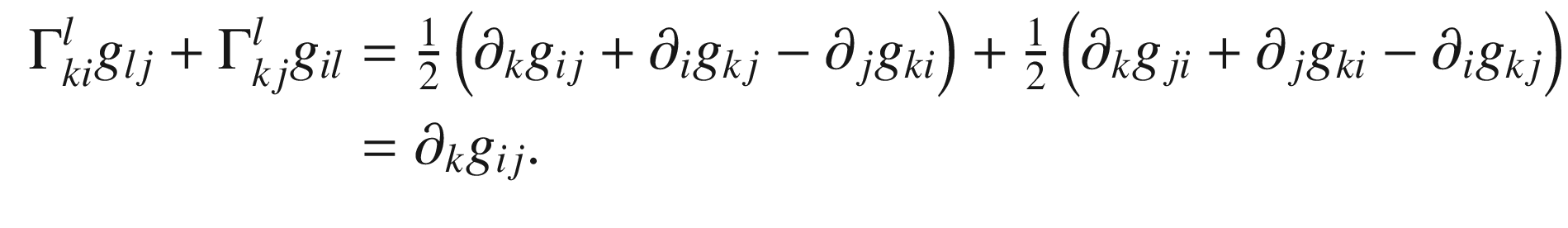
 is compatible with g.
is compatible with g. 
A bonus of this proof is that it gives us explicit formulas that can be used for computing the Levi-Civita connection in various circumstances.
Corollary 5.11
(Formulas for the Levi-Civita Connection). Let (M, g) be a Riemannian or pseudo-Riemannian manifold (with or without boundary), and let  be its Levi-Civita connection.
be its Levi-Civita connection.
- (a)In terms of vector fields: If X, Y, Z are smooth vector fields on M, then(This is known as Koszul’s formula.)
![$$\begin{aligned} \langle \nabla _XY, Z \rangle = \tfrac{1}{2}&\big ( X\langle Y,Z \rangle +Y\langle Z,X \rangle -Z\langle X,Y \rangle \nonumber \\&\qquad \qquad -\langle Y,[X,Z] \rangle -\langle Z,[Y,X] \rangle +\langle X,[Z, Y] \rangle \big ). \end{aligned}$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_Equ9.png) (5.9)
(5.9) - (b)In coordinates: In any smooth coordinate chart for M, the coefficients of the Levi-Civita connection are given by
 (5.10)
(5.10) - (c)In a local frame: Let
 be a smooth local frame on an open subset
be a smooth local frame on an open subset  , and let
, and let  be the
be the  smooth functions defined by Then the coefficients of the Levi-Civita connection in this frame are
smooth functions defined by Then the coefficients of the Levi-Civita connection in this frame are![$$\begin{aligned}{}[E_i, E_j] = c_{ij}^k E_k. \end{aligned}$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_Equ11.png) (5.11)
(5.11) (5.12)
(5.12) - (d)In a local orthonormal frame: If g is Riemannian,
 is a smooth local orthonormal frame, and the functions
is a smooth local orthonormal frame, and the functions  are defined by (5.11), then
are defined by (5.11), then  (5.13)
(5.13)
Proof.
 ,
,  , and
, and  , to obtain
, to obtain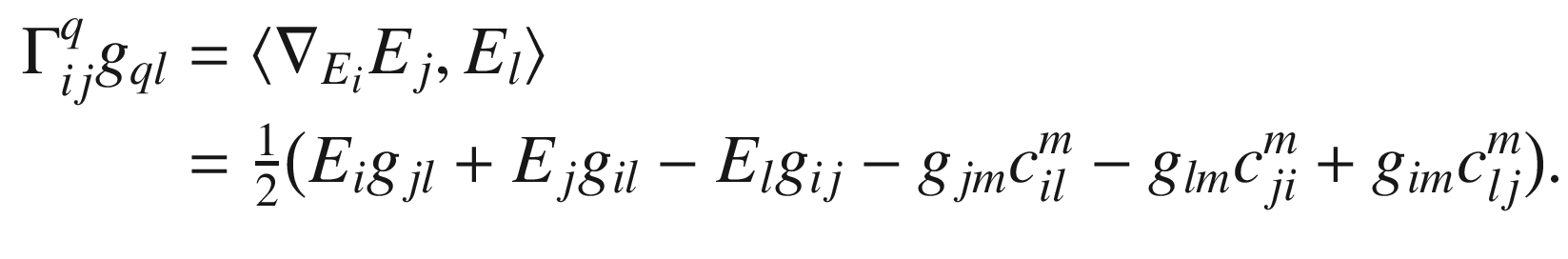
 and simplifying yields (5.12). Finally, under the hypotheses of (d), we have
and simplifying yields (5.12). Finally, under the hypotheses of (d), we have  , so (5.12) reduces to (5.13) after rearranging and using the fact that
, so (5.12) reduces to (5.13) after rearranging and using the fact that  is antisymmetric in i, j.
is antisymmetric in i, j. 
On every Riemannian or pseudo-Riemannian manifold, we will always use the Levi-Civita connection from now on without further comment. Geodesics with respect to this connection are called
Riemannian
(or
pseudo-Riemannian
) geodesics, or simply “geodesics” as long as there is no risk of confusion. The connection coefficients  of the Levi-Civita connection in coordinates, given by (5.10), are called the Christoffel symbols of g.
of the Levi-Civita connection in coordinates, given by (5.10), are called the Christoffel symbols of g.
The next proposition shows that these connections are familiar ones in the case of embedded submanifolds of Euclidean or pseudo-Euclidean spaces.
Proposition 5.12.
- (a)
The Levi-Civita connection on a (pseudo-)Euclidean space is equal to the Euclidean connection.
- (b)
Suppose M is an embedded (pseudo-)Riemannian submanifold of a (pseudo-)Euclidean space. Then the Levi-Civita connection on M is equal to the tangential connection
 .
.
Proof.
We observed earlier in this chapter that the Euclidean connection is symmetric and compatible with both the Euclidean metric  and the pseudo-Euclidean metrics
and the pseudo-Euclidean metrics  , which implies (a). Part (b) then follows from Propositions 5.8 and 5.9.
, which implies (a). Part (b) then follows from Propositions 5.8 and 5.9. 
An important consequence of the definition is that because Levi-Civita connections are defined in coordinate-independent terms, they behave well with respect to isometries. Recall the definition of the pullback of a connection (see Lemma 4.37).
Proposition 5.13
(Naturality of the Levi-Civita Connection). Suppose (M, g) and  are
Riemannian or pseudo-Riemannian manifolds with or without boundary, and let
are
Riemannian or pseudo-Riemannian manifolds with or without boundary, and let  denote the Levi-Civita connection of g and
denote the Levi-Civita connection of g and  that of
that of  . If
. If  is an isometry, then
is an isometry, then  .
.
Proof.
 is symmetric and compatible with g. The fact that
is symmetric and compatible with g. The fact that  is an isometry means that for any
is an isometry means that for any  and
and  ,
,
 . Therefore,
. Therefore,
![$$\begin{aligned} \bigl (\varphi ^*{\tilde{\nabla }}\bigr )_X Y - \bigl (\varphi ^*{\tilde{\nabla }}\bigr )_Y X&= \big (\varphi ^{-1}\big )_* \big ( {\tilde{\nabla }}_{\varphi _*X} (\varphi _*Y) - {\tilde{\nabla }}_{\varphi _*Y} (\varphi _*X)\big )\\&= \big (\varphi ^{-1}\big )_* \bigl [ \varphi _*X,\varphi _*Y\bigr ]\\&= [X, Y]. \end{aligned}$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_Equ51.png)

Corollary 5.14
(Naturality of Geodesics). Suppose (M, g) and  are
Riemannian or pseudo-Riemannian manifolds with or without boundary, and
are
Riemannian or pseudo-Riemannian manifolds with or without boundary, and  is a local isometry. If
is a local isometry. If  is a geodesic in M, then
is a geodesic in M, then  is a geodesic in
is a geodesic in  .
.
Proof.
This is an immediate consequence of Proposition 4.38, together with the fact that being a geodesic is a local property. 
Like every connection on the tangent bundle, the Levi-Civita connection induces connections on all tensor bundles.
Proposition 5.15.
Suppose (M, g) is a Riemannian or pseudo-Riemannian manifold. The connection induced on each tensor bundle by the Levi-Civita connection is compatible with the induced inner product on tensors, in the sense that  for every vector field X and every pair of smooth tensor fields
for every vector field X and every pair of smooth tensor fields  .
.
Proof.
Since every tensor field can be written as a sum of tensor products of vector and/or covector fields, it suffices to consider the case in which  and
and  , where
, where  and
and  are covariant or contravariant 1-tensor fields, as appropriate. In this case, the formula follows from (2.15) by a routine computation.
are covariant or contravariant 1-tensor fields, as appropriate. In this case, the formula follows from (2.15) by a routine computation. 
Proposition 5.16.
Let (M, g) be an oriented Riemannian manifold. The Riemannian volume form of g is parallel with respect to the Levi-Civita connection.
Proof.
Let  and
and  be arbitrary, and let
be arbitrary, and let  be a smooth curve satisfying
be a smooth curve satisfying  and
and  . Let
. Let  be a parallel oriented orthonormal frame along
be a parallel oriented orthonormal frame along  . Since
. Since  and
and  along
along  , formula (4.12) shows that
, formula (4.12) shows that  .
. 
Proposition 5.17.
 represents the operation of lowering the ith index, then
represents the operation of lowering the ith index, then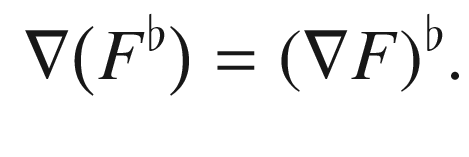
 denotes raising the ith index, then
denotes raising the ith index, then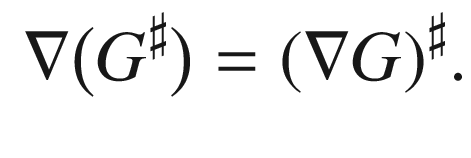
Proof.
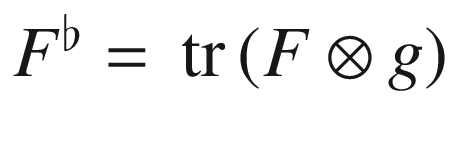 , where the trace is taken on the ith and last indices of
, where the trace is taken on the ith and last indices of  . Because g is parallel, for every vector field X we have
. Because g is parallel, for every vector field X we have  . Because
. Because  commutes with traces, therefore,
commutes with traces, therefore,
Because the sharp and flat operators are inverses of each other when applied to the same index position, (5.15) follows by substituting  into (5.14) and applying
into (5.14) and applying  to both sides.
to both sides. 
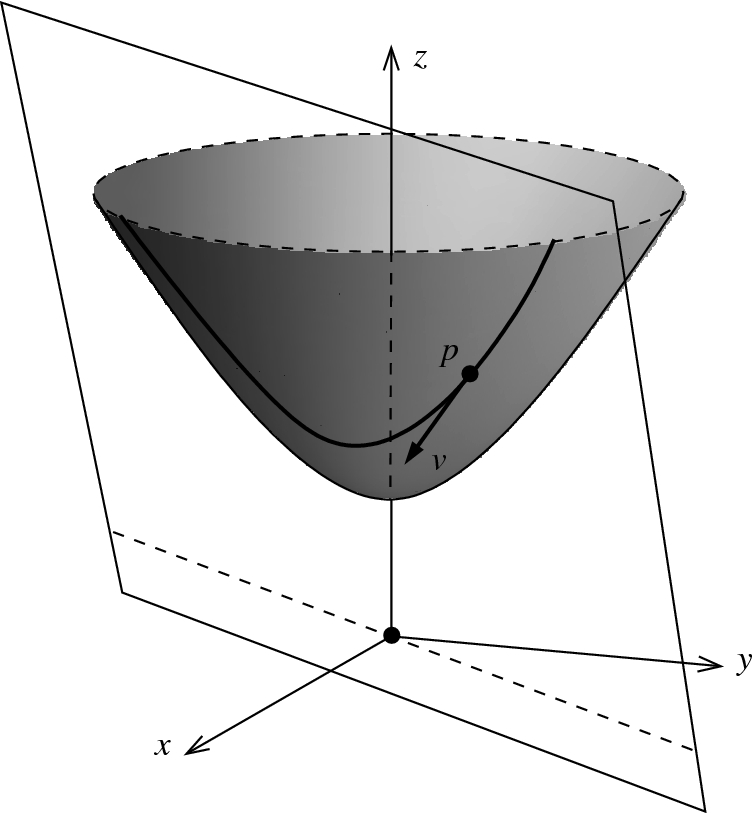
The Exponential Map
Throughout this section, we let (M, g) be a Riemannian or pseudo-Riemannian n-manifold, endowed with its Levi-Civita connection. Corollary 4.28 showed that each initial point  and each initial velocity vector
and each initial velocity vector  determine a unique maximal geodesic
determine a unique maximal geodesic  . To deepen our understanding of geodesics, we need to study their collective behavior, and in particular, to address the following question: How do geodesics change if we vary the initial point or the initial velocity? The dependence of geodesics on the initial data is encoded in a map from the tangent bundle into the manifold, called the exponential map, whose properties are fundamental to the further study of Riemannian geometry.
. To deepen our understanding of geodesics, we need to study their collective behavior, and in particular, to address the following question: How do geodesics change if we vary the initial point or the initial velocity? The dependence of geodesics on the initial data is encoded in a map from the tangent bundle into the manifold, called the exponential map, whose properties are fundamental to the further study of Riemannian geometry.
(It is worth noting that the existence of the exponential map and the basic properties expressed in Proposition 5.19 below hold for every connection in TM, not just for the Levi-Civita connection. For simplicity, we restrict attention here to the latter case, because that is all we need. We also restrict to manifolds without boundary, in order to avoid complications with geodesics running into a boundary.)
The next lemma shows that geodesics with proportional initial velocities are related in a simple way.
Lemma 5.18
 ,
, 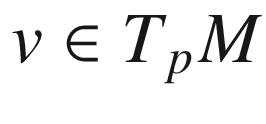 , and
, and  ,
,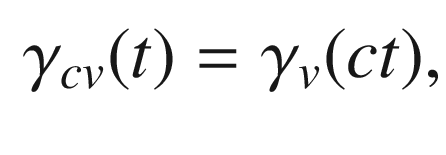
Proof.
If  , then both sides of (5.16) are equal to p for all
, then both sides of (5.16) are equal to p for all  , so we may assume that
, so we may assume that  . It suffices to show that
. It suffices to show that  exists and (5.16) holds whenever the right-hand side is defined. (The same argument with the substitutions
exists and (5.16) holds whenever the right-hand side is defined. (The same argument with the substitutions  ,
,  , and
, and  then implies that the conclusion holds when only the left-hand side is known to be defined.)
then implies that the conclusion holds when only the left-hand side is known to be defined.)
Suppose the maximal domain of  is the open interval
is the open interval  . For simplicity, write
. For simplicity, write  , and define a new curve
, and define a new curve  by
by  , where
, where  . We will show that
. We will show that  is a geodesic with initial point p and initial velocity cv; it then follows by uniqueness and maximality that it must be equal to
is a geodesic with initial point p and initial velocity cv; it then follows by uniqueness and maximality that it must be equal to  .
.
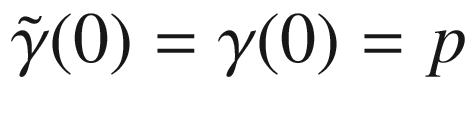 . Choose any smooth local coordinates on M and write the coordinate representation of
. Choose any smooth local coordinates on M and write the coordinate representation of  as
as  ; then the chain rule gives
; then the chain rule gives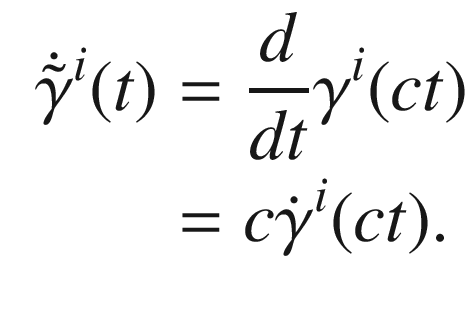
 .
.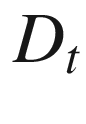 and
and  denote the covariant differentiation operators along
denote the covariant differentiation operators along 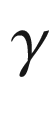 and
and 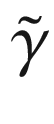 , respectively. Using the chain rule again in coordinates yields
, respectively. Using the chain rule again in coordinates yields
 is a geodesic, so
is a geodesic, so  , as claimed.
, as claimed. 
The assignment  defines a map from TM to the set of geodesics in M. More importantly, by virtue of the rescaling lemma, it allows us to define a map from (a subset of) the tangent bundle to M itself, which sends each line through the origin in
defines a map from TM to the set of geodesics in M. More importantly, by virtue of the rescaling lemma, it allows us to define a map from (a subset of) the tangent bundle to M itself, which sends each line through the origin in  to a geodesic.
to a geodesic.
 , the
domain of the exponential map
, by
, the
domain of the exponential map
, by![$$\begin{aligned} \mathscr {E} = \{ v\in TM: \gamma _v \text { is defined on an interval containing}\,\, [0,1]\}, \end{aligned}$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_Equ55.png)
 by
by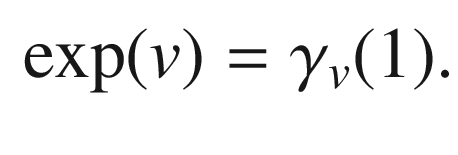
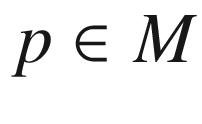 , the restricted exponential map at p, denoted by
, the restricted exponential map at p, denoted by  , is the restriction of
, is the restriction of 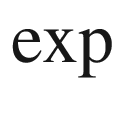 to the set
to the set  .
.The exponential map of a Riemannian manifold should not be confused with the exponential map of a Lie group. The two are closely related for bi-invariant metrics (see Problem 5-8), but in general they need not be. To avoid confusion, we always designate the exponential map of a Lie group G by  , and reserve the undecorated notation
, and reserve the undecorated notation  for the Riemannian exponential map.
for the Riemannian exponential map.
The next proposition describes some essential features of the exponential map. Recall that a subset of a vector space V is said to be star-shaped with respect to a point  if for every
if for every  , the line segment from x to y is contained in S.
, the line segment from x to y is contained in S.
Proposition 5.19
(Properties of the Exponential Map). Let (M, g) be a Riemannian or pseudo-Riemannian manifold, and let  be its exponential map.
be its exponential map.
- (a)
 is an open subset of TM containing the image of the zero section, and each set
is an open subset of TM containing the image of the zero section, and each set  is star-shaped with respect to 0.
is star-shaped with respect to 0. - (b)For each
 , the geodesic
, the geodesic  is given by for all t such that either side is defined.
is given by for all t such that either side is defined. (5.17)
(5.17) - (c)
The exponential map is smooth.
- (d)
Foreach point
 , the differential
, the differential  is the identity map of
is the identity map of  , under the usual identification of
, under the usual identification of  with
with  .
.
Proof.
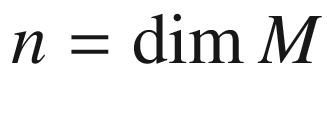 . The rescaling lemma with
. The rescaling lemma with  says precisely that
says precisely that  whenever either side is defined; this is (b). Moreover, if
whenever either side is defined; this is (b). Moreover, if 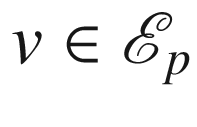 , then by definition
, then by definition 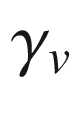 is defined at least on [0, 1]. Thus for
is defined at least on [0, 1]. Thus for  , the rescaling lemma says that
, the rescaling lemma says that
 is star-shaped with respect to 0.
is star-shaped with respect to 0.Next we will show that  is open and
is open and  is smooth. To do so, we revisit the proof of the existence and uniqueness theorem for geodesics (Theorem 4.27) and reformulate it in a more invariant way. Let
is smooth. To do so, we revisit the proof of the existence and uniqueness theorem for geodesics (Theorem 4.27) and reformulate it in a more invariant way. Let  be any smooth local coordinates on an open set
be any smooth local coordinates on an open set  , let
, let  be the projection, and let
be the projection, and let  denote the associated natural coordinates for
denote the associated natural coordinates for  (see p. 384). In terms of these coordinates, formula (4.18) defines a smooth vector field G on
(see p. 384). In terms of these coordinates, formula (4.18) defines a smooth vector field G on  . The integral curves of G are the curves
. The integral curves of G are the curves  that satisfy the system of ODEs given by (4.17), which is equivalent to the geodesic equation under the substitution
that satisfy the system of ODEs given by (4.17), which is equivalent to the geodesic equation under the substitution  , as we observed in the proof of Theorem 4.27. Stated somewhat more invariantly, every integral curve of G on
, as we observed in the proof of Theorem 4.27. Stated somewhat more invariantly, every integral curve of G on  projects to a geodesic under
projects to a geodesic under  (which in these coordinates is just
(which in these coordinates is just  ); conversely, every geodesic
); conversely, every geodesic  in U lifts to an integral curve of G in
in U lifts to an integral curve of G in  by setting
by setting  .
.
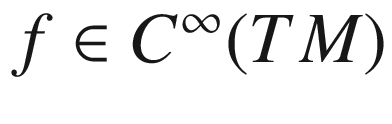 by
by
 , depending on whether we wish to emphasize the point at which v is tangent.) Since this formula is independent of coordinates, it shows that the various definitions of G given by (4.18) in different coordinate systems agree.
, depending on whether we wish to emphasize the point at which v is tangent.) Since this formula is independent of coordinates, it shows that the various definitions of G given by (4.18) in different coordinate systems agree. as
as  and those of its velocity as
and those of its velocity as  . Using the chain rule and the geodesic equation in the form (4.17), we can write the right-hand side of (5.18) as
. Using the chain rule and the geodesic equation in the form (4.17), we can write the right-hand side of (5.18) as
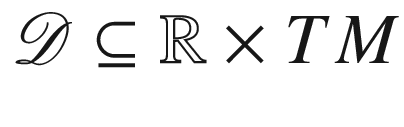 containing
containing 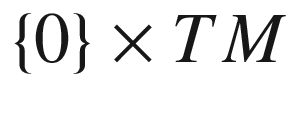 and a smooth map
and a smooth map  , such that each curve
, such that each curve  is the unique maximal integral curve of G starting at (p, v), defined on an open interval containing 0.
is the unique maximal integral curve of G starting at (p, v), defined on an open interval containing 0.Now suppose  . This means that the geodesic
. This means that the geodesic  is defined at least on the interval [0, 1], and therefore so is the integral curve of G starting at
is defined at least on the interval [0, 1], and therefore so is the integral curve of G starting at  . Since
. Since  , there is a neighborhood of (1, (p, v)) in
, there is a neighborhood of (1, (p, v)) in  on which the flow of G is defined (Fig. 5.2). In particular, this means that there is a neighborhood of (p, v) on which the flow exists for
on which the flow of G is defined (Fig. 5.2). In particular, this means that there is a neighborhood of (p, v) on which the flow exists for ![$$t\in [0,1]$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_IEq365.png) , and therefore on which the exponential map is defined. This shows that
, and therefore on which the exponential map is defined. This shows that  is open.
is open.
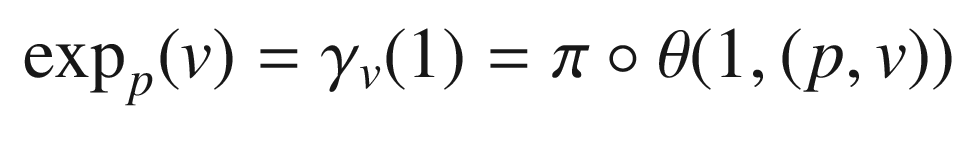
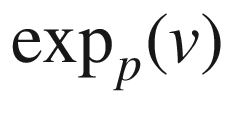 is a smooth function of (p, v).
is a smooth function of (p, v). for an arbitrary vector
for an arbitrary vector  , we just need to choose a curve
, we just need to choose a curve 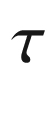 in
in 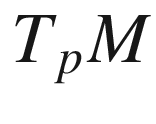 starting at 0 whose initial velocity is v, and compute the initial velocity of
starting at 0 whose initial velocity is v, and compute the initial velocity of 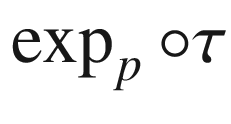 . A convenient curve is
. A convenient curve is 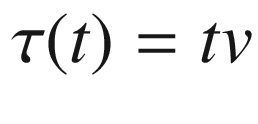 , which yields
, which yields
 is the identity map.
is the identity map. 

 is open
is open
Corollary 5.14 on the naturality of geodesics translates into the following important property of the exponential map.
Proposition 5.20
 are
Riemannian or pseudo-Riemannian manifolds and
are
Riemannian or pseudo-Riemannian manifolds and  is a local isometry. Then for every
is a local isometry. Then for every  , the following diagram commutes:
, the following diagram commutes:
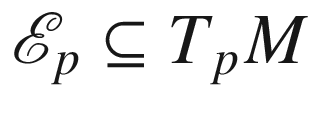 and
and 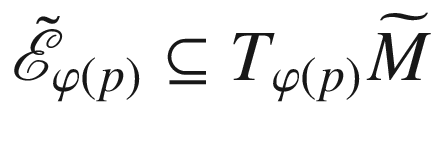 are the domains of the restricted exponential maps
are the domains of the restricted exponential maps  (with respect to g) and
(with respect to g) and  (with respect to
(with respect to  ), respectively.
), respectively. Exercise 5.21. Prove Proposition 5.20.
Exercise 5.21. Prove Proposition 5.20.
An important consequence of the naturality of the exponential map is the following proposition, which says that local isometries of connected manifolds are completely determined by their values and differentials at a single point.
Proposition 5.22.
Let (M, g) and  be Riemannian or pseudo-Riemannian manifolds, with M connected. Suppose
be Riemannian or pseudo-Riemannian manifolds, with M connected. Suppose  are local isometries such that for some point
are local isometries such that for some point  , we have
, we have  and
and  . Then
. Then  .
.
Proof.
Problem 5-10. 
A Riemannian or pseudo-Riemannian manifold (M, g) is said to be
geodesically complete
if every maximal geodesic is defined for all  , or equivalently if the domain of the exponential map is all of TM. It is easy to construct examples of manifolds that are not geodesically complete; for example, in every proper open subset of
, or equivalently if the domain of the exponential map is all of TM. It is easy to construct examples of manifolds that are not geodesically complete; for example, in every proper open subset of  with its Euclidean metric or with a pseudo-Euclidean metric, there are geodesics that reach the boundary in finite time. Similarly, on
with its Euclidean metric or with a pseudo-Euclidean metric, there are geodesics that reach the boundary in finite time. Similarly, on  with the metric
with the metric  obtained from the sphere by stereographic projection, there are geodesics that escape to infinity in finite time. Geodesically complete manifolds are the natural setting for global questions in Riemannian or pseudo-Riemannian geometry; beginning with Chapter 6, most of our attention will be focused on them.
obtained from the sphere by stereographic projection, there are geodesics that escape to infinity in finite time. Geodesically complete manifolds are the natural setting for global questions in Riemannian or pseudo-Riemannian geometry; beginning with Chapter 6, most of our attention will be focused on them.
Normal Neighborhoods and Normal Coordinates
We continue to let (M, g) be a Riemannian or pseudo-Riemannian manifold of dimension n (without boundary). Recall that for every  , the restricted exponential map
, the restricted exponential map  maps the open subset
maps the open subset  smoothly into M. Because
smoothly into M. Because  is invertible, the inverse function theorem guarantees that there exist a neighborhood V of the origin in
is invertible, the inverse function theorem guarantees that there exist a neighborhood V of the origin in  and a neighborhood U of p in M such that
and a neighborhood U of p in M such that  is a diffeomorphism. A neighborhood U of
is a diffeomorphism. A neighborhood U of  that is the diffeomorphic image under
that is the diffeomorphic image under  of a star-shaped neighborhood of
of a star-shaped neighborhood of  is called a normal neighborhood of
is called a normal neighborhood of  .
.
 for
for  determines a basis isomorphism
determines a basis isomorphism 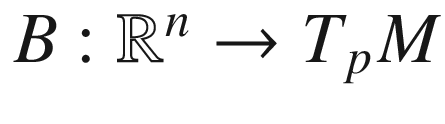 by
by  . If
. If  is a normal neighborhood of p, we can combine this isomorphism with the exponential map to get a smooth coordinate map
is a normal neighborhood of p, we can combine this isomorphism with the exponential map to get a smooth coordinate map  :
:
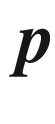 .
.Proposition 5.23
 for
for  , there is a unique normal coordinate chart
, there is a unique normal coordinate chart  on U such that
on U such that  for
for 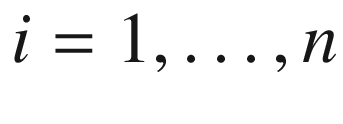 . In the Riemannian case, any two normal coordinate charts
. In the Riemannian case, any two normal coordinate charts 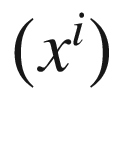 and
and  are related by
are related by
 .
.Proof.
Let  be a normal coordinate chart on U centered at p, with coordinate functions
be a normal coordinate chart on U centered at p, with coordinate functions  . By definition, this means that
. By definition, this means that  , where
, where  is the basis isomorphism determined by some orthonormal basis
is the basis isomorphism determined by some orthonormal basis  for
for  . Note that
. Note that  because
because  is the identity and B is linear. Thus
is the identity and B is linear. Thus  , which shows that the coordinate basis is orthonormal at p. Conversely, every orthonormal basis
, which shows that the coordinate basis is orthonormal at p. Conversely, every orthonormal basis  for
for  yields a basis isomorphism B and thus a normal coordinate chart
yields a basis isomorphism B and thus a normal coordinate chart  , which satisfies
, which satisfies  by the computation above.
by the computation above.
 is another such chart, then
is another such chart, then
 and therefore has the form (5.19) in terms of standard coordinates on
and therefore has the form (5.19) in terms of standard coordinates on  . Since
. Since  and
and  are the same coordinates if and only if
are the same coordinates if and only if  is the identity matrix, this shows that the normal coordinate chart associated with a given orthonormal basis is unique.
is the identity matrix, this shows that the normal coordinate chart associated with a given orthonormal basis is unique. 
Proposition 5.24
(Properties of Normal Coordinates). Let (M, g) be a Riemannian or pseudo-Riemannian n-manifold, and let  be any normal coordinate chart centered at
be any normal coordinate chart centered at  .
.
- (a)
The coordinates of p are
 .
. - (b)
The components of the metric at p are
 if g is Riemannian, and
if g is Riemannian, and  otherwise.
otherwise. - (c)For every
 , the geodesic
, the geodesic  starting at p with initial velocity v is represented in normal coordinates by the line as long as t is in some interval I containing 0 such that
starting at p with initial velocity v is represented in normal coordinates by the line as long as t is in some interval I containing 0 such that (5.20)
(5.20) .
. - (d)
The Christoffel symbols in these coordinates vanish at p.
- (e)
All of the first partial derivatives of
 in these coordinates vanish at p.
in these coordinates vanish at p.
Proof.
Part (a) follows directly from the definition of normal coordinates, and parts (b) and (c) follow from Propositions 5.23 and 5.19(b), respectively.
 be arbitrary. The geodesic equation (4.16) for
be arbitrary. The geodesic equation (4.16) for  simplifies to
simplifies to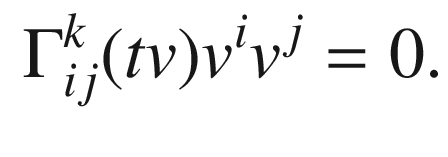
 shows that
shows that 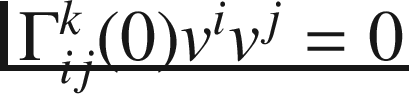 for every index k and every vector v. In particular, with
for every index k and every vector v. In particular, with 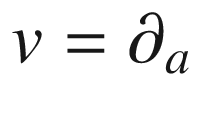 for some fixed a, this shows that
for some fixed a, this shows that  for each a and k (no summation). Substituting
for each a and k (no summation). Substituting  and
and  for any fixed pair of indices a and b and subtracting, we conclude also that
for any fixed pair of indices a and b and subtracting, we conclude also that 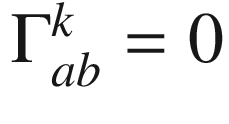 at p for all a, b, k. Finally, (e) follows from (d) together with (5.2) in the case
at p for all a, b, k. Finally, (e) follows from (d) together with (5.2) in the case 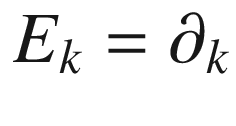 .
. 
Because they are given by the simple formula (5.20), the geodesics starting at p and lying in a normal neighborhood of p are called radial geodesics . (But be warned that geodesics that do not pass through p do not in general have a simple form in normal coordinates.)
Tubular Neighborhoods and Fermi Coordinates
The exponential map and normal coordinates give us a good understanding of the behavior of geodesics starting a point. In this section, we generalize those constructions to geodesics starting on any embedded submanifold. We restrict attention to the Riemannian case, because we will be using the Riemannian distance function.
Suppose (M, g) is a Riemannian manifold,  is an embedded submanifold, and
is an embedded submanifold, and  is the normal bundle of P in M. Let
is the normal bundle of P in M. Let  denote the domain of the exponential map of M, and let
denote the domain of the exponential map of M, and let  . Let
. Let  denote the restriction of
denote the restriction of  (the exponential map of M) to
(the exponential map of M) to  . We call E the
normal exponential map of P in M
.
. We call E the
normal exponential map of P in M
.
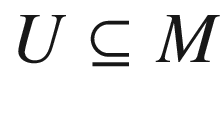 that is the diffeomorphic image under E of an open subset
that is the diffeomorphic image under E of an open subset 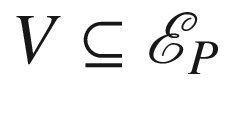 whose intersection with each fiber
whose intersection with each fiber 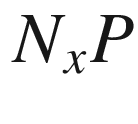 is star-shaped with respect to 0. We will be primarily interested in normal neighborhoods of the following type: a normal neighborhood of P in M is called a tubular neighborhood if it is the diffeomorphic image under E of a subset
is star-shaped with respect to 0. We will be primarily interested in normal neighborhoods of the following type: a normal neighborhood of P in M is called a tubular neighborhood if it is the diffeomorphic image under E of a subset 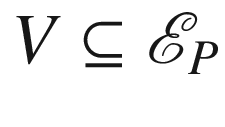 of the form
of the form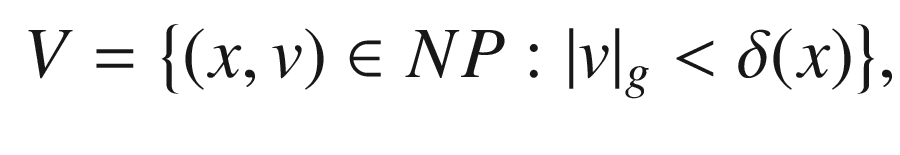
 (Fig. 5.3). If U is the diffeomorphic image of such a set V for a constant function
(Fig. 5.3). If U is the diffeomorphic image of such a set V for a constant function  , then it is called a uniform tubular neighborhood of radius
, then it is called a uniform tubular neighborhood of radius 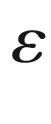 , or an
, or an 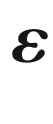 -tubular neighborhood.
-tubular neighborhood.
A tubular neighborhood

Injectivity of E
Theorem 5.25
(Tubular Neighborhood Theorem). Let (M, g) be a Riemannian manifold. Every embedded submanifold of M has a tubular neighborhood in M, and every compact submanifold has a uniform tubular neighborhood.
Proof.
 be an embedded submanifold, and let
be an embedded submanifold, and let  be the subset
be the subset 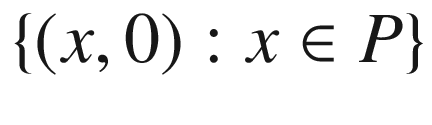 (the image of the zero section of NP). We begin by showing that the normal exponential map E is a local diffeomorphism on a neighborhood of
(the image of the zero section of NP). We begin by showing that the normal exponential map E is a local diffeomorphism on a neighborhood of  . By the inverse function theorem, it suffices to show that the differential
. By the inverse function theorem, it suffices to show that the differential 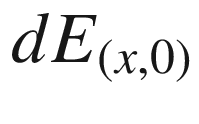 is bijective at each point
is bijective at each point  . The restriction of E to
. The restriction of E to 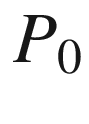 is just the diffeomorphism
is just the diffeomorphism  followed by the embedding
followed by the embedding  , so
, so  maps the subspace
maps the subspace 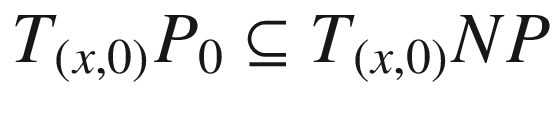 isomorphically onto
isomorphically onto 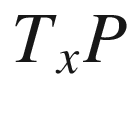 . On the other hand, on the fiber
. On the other hand, on the fiber  , E agrees with the restricted exponential map
, E agrees with the restricted exponential map  , which is a diffeomorphism near 0, so
, which is a diffeomorphism near 0, so 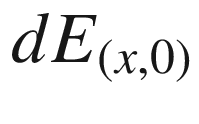 maps
maps 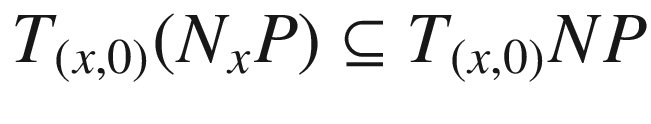 isomorphically onto
isomorphically onto  . Since
. Since  , this shows that
, this shows that  is surjective, and hence it is bijective for dimensional reasons. Thus E is a diffeomorphism on a neighborhood of (x, 0) in NP, which we can take to be of the form
is surjective, and hence it is bijective for dimensional reasons. Thus E is a diffeomorphism on a neighborhood of (x, 0) in NP, which we can take to be of the form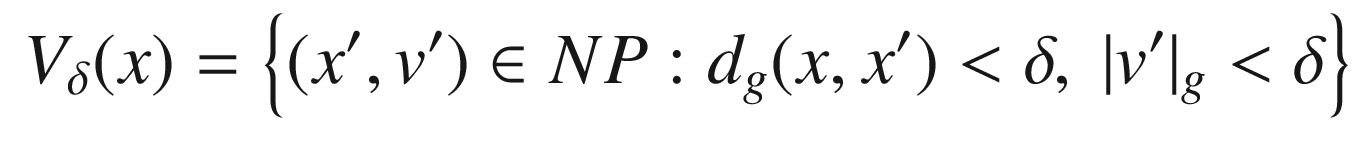
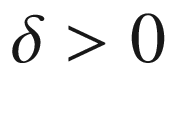 . (Here we are using the fact that P is embedded in M, so it has the subspace topology.)
. (Here we are using the fact that P is embedded in M, so it has the subspace topology.) of the form (5.21) on which E is a diffeomorphism onto its image. For each point
of the form (5.21) on which E is a diffeomorphism onto its image. For each point  , define
, define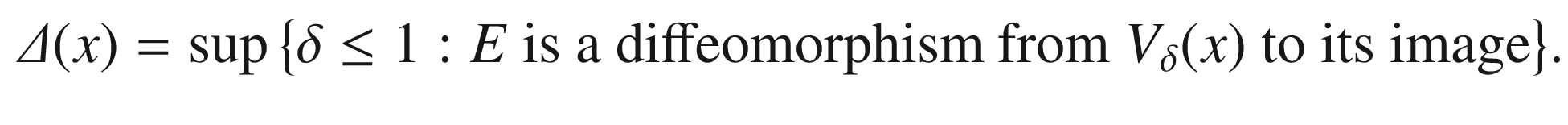
 is positive for each x. Note that E is injective on the entire set
is positive for each x. Note that E is injective on the entire set 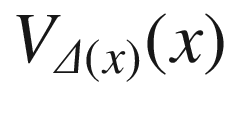 , because any two points
, because any two points  in this set are in
in this set are in 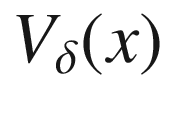 for some
for some 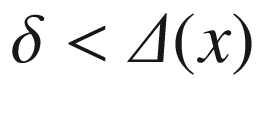 . Because it is an injective local diffeomorphism, E is actually a diffeomorphism from
. Because it is an injective local diffeomorphism, E is actually a diffeomorphism from 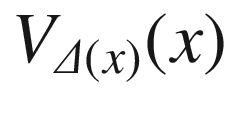 onto its image.
onto its image. is continuous. For any
is continuous. For any  , if
, if  , then the triangle inequality shows that
, then the triangle inequality shows that 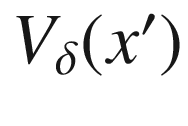 is contained in
is contained in  for
for  , which implies that
, which implies that  , or
, or
 , then (5.24) holds for trivial reasons. Reversing the roles of x and
, then (5.24) holds for trivial reasons. Reversing the roles of x and  yields an analogous inequality, which shows that
yields an analogous inequality, which shows that  , so
, so  is continuous.
is continuous. , which is an open subset of NP containing
, which is an open subset of NP containing 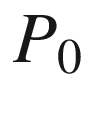 . We show that E is injective on V. Suppose (x, v) and
. We show that E is injective on V. Suppose (x, v) and 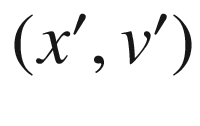 are points in V such that
are points in V such that  (Fig. 5.4). Assume without loss of generality that
(Fig. 5.4). Assume without loss of generality that  . Because
. Because  , there is an admissible curve from x to
, there is an admissible curve from x to  of length
of length  , and thus
, and thus
 are in
are in  . Since E is injective on this set, this implies
. Since E is injective on this set, this implies  .
.The set  is open in M because
is open in M because  is a local diffeomorphism and thus an open map, and
is a local diffeomorphism and thus an open map, and  is a diffeomorphism. Therefore, U is a tubular neighborhood of P.
is a diffeomorphism. Therefore, U is a tubular neighborhood of P.
Finally, if P is compact, then the continuous function  achieves a minimum value
achieves a minimum value  on P, so U contains a uniform tubular neighborhood of radius
on P, so U contains a uniform tubular neighborhood of radius  .
. 
Fermi Coordinates
Now we will construct coordinates on a tubular neighborhood that are analogous to Riemannian normal coordinates around a point. Let P be an embedded p-dimensional submanifold of a Riemannian n-manifold (M, g), and let  be a normal neighborhood of P, with
be a normal neighborhood of P, with  for some appropriate open subset
for some appropriate open subset  .
.
 be a smooth coordinate chart for P, and let
be a smooth coordinate chart for P, and let  be a local orthonormal frame for the normal bundle NP; by shrinking
be a local orthonormal frame for the normal bundle NP; by shrinking 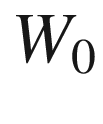 if necessary, we can assume that the coordinates and the local frame are defined on the same open subset
if necessary, we can assume that the coordinates and the local frame are defined on the same open subset  . Let
. Let 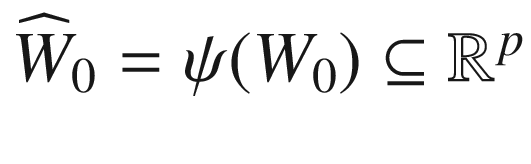 , and let
, and let 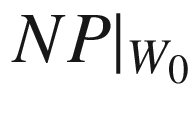 be the portion of the normal bundle over
be the portion of the normal bundle over 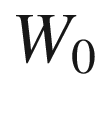 . The coordinate map
. The coordinate map  and frame
and frame  yield a diffeomorphism
yield a diffeomorphism  defined by
defined by
 . Let
. Let  and
and 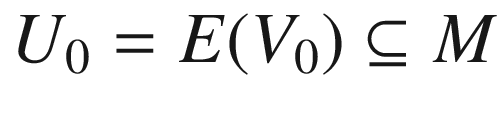 , and define a smooth coordinate map
, and define a smooth coordinate map  by
by  :
:

Here is the analogue of Proposition 5.24 for Fermi coordinates.
Proposition 5.26
(Properties of Fermi Coordinates). Let P be an embedded p-dimensional submanifold of a Riemannian n-manifold (M, g), let U be a normal neighborhood of P in M, and let  be Fermi coordinates on an open subset
be Fermi coordinates on an open subset  . For convenience, we also write
. For convenience, we also write  for
for  .
.
- (a)
 is the set of points where
is the set of points where  .
. - (b)At each point
 , the metric components satisfy the following:
, the metric components satisfy the following: 
- (c)
For every
 and
and  , the geodesic
, the geodesic  starting at q with initial velocity v is the curve with coordinate expression
starting at q with initial velocity v is the curve with coordinate expression  .
. - (d)
At each
 , the Christoffel symbols in these coordinates satisfy
, the Christoffel symbols in these coordinates satisfy  , provided
, provided  .
. - (e)
At each
 , the partial derivatives
, the partial derivatives  vanish for
vanish for  .
.
Proof.
Problem 5-18. 
Geodesics of the Model Spaces
In this section we determine the geodesics of the three types of frame-homogeneous Riemannian manifolds defined in Chapter 3. We could, of course, compute the Christoffel symbols of these metrics in suitable coordinates, and try to find the geodesics by solving the appropriate differential equations; but for these spaces, much easier methods are available based on symmetry and other geometric considerations.
Euclidean Space
On  with the Euclidean metric, Proposition 5.12 shows that the Levi-Civita connection is the Euclidean connection. Therefore, as one would expect, constant-coefficient vector fields are parallel, and the
Euclidean geodesics are straight lines with constant-speed parametrizations (Exercises 4.29 and 4.30). Every Euclidean space is geodesically complete.
with the Euclidean metric, Proposition 5.12 shows that the Levi-Civita connection is the Euclidean connection. Therefore, as one would expect, constant-coefficient vector fields are parallel, and the
Euclidean geodesics are straight lines with constant-speed parametrizations (Exercises 4.29 and 4.30). Every Euclidean space is geodesically complete.
Spheres
Because the round metric on the sphere  is induced by the Euclidean metric on
is induced by the Euclidean metric on  , it is easy to determine the geodesics on a sphere using Corollary 5.2. Define a great circle on
, it is easy to determine the geodesics on a sphere using Corollary 5.2. Define a great circle on  to be any subset of the form
to be any subset of the form  , where
, where  is a 2-dimensional linear subspace.
is a 2-dimensional linear subspace.
Proposition 5.27.
A nonconstant curve on  is a maximal geodesic if and only if it is a periodic constant-speed curve whose image is a great circle. Thus every sphere is geodesically complete.
is a maximal geodesic if and only if it is a periodic constant-speed curve whose image is a great circle. Thus every sphere is geodesically complete.
Proof.
Let  be arbitrary. Because
be arbitrary. Because  is a defining function for
is a defining function for  , a vector
, a vector  is tangent to
is tangent to  if and only if
if and only if  , where we think of p as a vector by means of the usual identification of
, where we think of p as a vector by means of the usual identification of  with
with  . Thus
. Thus  is exactly the set of vectors orthogonal to p.
is exactly the set of vectors orthogonal to p.
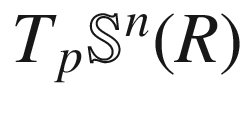 . Let
. Let 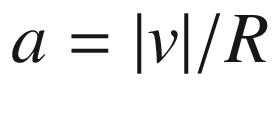 and
and 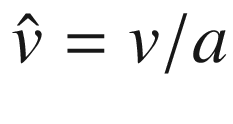 (so
(so  ), and consider the smooth curve
), and consider the smooth curve  given by
given by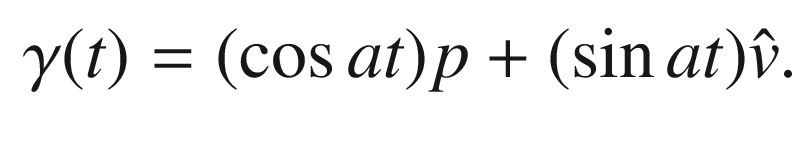
 , so
, so  for all t. Moreover,
for all t. Moreover,
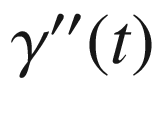 is proportional to
is proportional to  (thinking of both as vectors in
(thinking of both as vectors in  ), it follows that
), it follows that  is
is  -orthogonal to
-orthogonal to 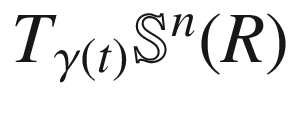 , so
, so 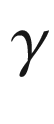 is a geodesic in
is a geodesic in  by Corollary 5.2. Since
by Corollary 5.2. Since  and
and  , it follows that
, it follows that 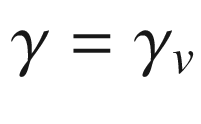 .
.Each  is periodic of period
is periodic of period  , and has constant speed by Corollary 5.6 (or by direct computation). The image of
, and has constant speed by Corollary 5.6 (or by direct computation). The image of  is the great circle formed by the intersection of
is the great circle formed by the intersection of  with the linear subspace spanned by
with the linear subspace spanned by  , as you can check.
, as you can check.
Conversely, suppose C is a great circle formed by intersecting  with a 2-dimensional subspace
with a 2-dimensional subspace  , and let
, and let  be an orthonormal basis for
be an orthonormal basis for  . Then C is the image of the geodesic with initial point
. Then C is the image of the geodesic with initial point  and initial velocity v.
and initial velocity v. 
Hyperbolic Spaces
A great hyperbola

Geodesics of 

Geodesics of 
Proposition 5.28.
 whose image is one of the following:
whose image is one of the following:- (a)
Hyperboloid model: The intersection of
 with a 2-dimensional linear subspace of
with a 2-dimensional linear subspace of  , called a great hyperbola (Fig. 5.5).
, called a great hyperbola (Fig. 5.5). - (b)
Beltrami–Klein model: The interior of a line segment whose endpoints both lie on
 (Fig. 5.6).
(Fig. 5.6). - (c)
Ball model: The interior of a diameter of
 , or the intersection of
, or the intersection of  with a Euclidean circle that intersects
with a Euclidean circle that intersects  orthogonally (Fig. 5.7).
orthogonally (Fig. 5.7). - (d)
Half-space model: The intersection of
 with one of the following: a line parallel to the y-axis or a Euclidean circle with center on
with one of the following: a line parallel to the y-axis or a Euclidean circle with center on  (Fig. 5.8).
(Fig. 5.8).
Every hyperbolic space is geodesically complete.

Geodesics of 
Proof.
We begin with the hyperboloid model, for which the proof is formally quite similar to what we just did for the sphere. Since the Riemannian connection on  is equal to the tangential connection by Proposition 5.12, it follows from Corollary 5.2 that a smooth curve
is equal to the tangential connection by Proposition 5.12, it follows from Corollary 5.2 that a smooth curve  is a geodesic if and only if its acceleration
is a geodesic if and only if its acceleration  is everywhere
is everywhere  -orthogonal to
-orthogonal to  (where
(where  is the Minkowski metric).
is the Minkowski metric).
 be arbitrary. Note that
be arbitrary. Note that  is a defining function for
is a defining function for  , and (3.10) shows that the gradient of f at p is equal to 2p (where we regard p as a vector in
, and (3.10) shows that the gradient of f at p is equal to 2p (where we regard p as a vector in  as before). It follows that a vector
as before). It follows that a vector  is tangent to
is tangent to  if and only if
if and only if  . Let
. Let 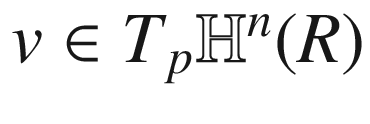 be an arbitrary nonzero vector. Put
be an arbitrary nonzero vector. Put  and
and  , and define
, and define  by
by
 takes its values in
takes its values in  and that its acceleration vector is everywhere proportional to
and that its acceleration vector is everywhere proportional to  . Thus
. Thus 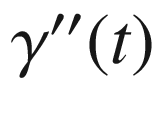 is
is  -orthogonal to
-orthogonal to  , so
, so  is a geodesic in
is a geodesic in  and therefore has constant speed. Because it satisfies the initial conditions
and therefore has constant speed. Because it satisfies the initial conditions  and
and  , it is equal to
, it is equal to  . Note that
. Note that 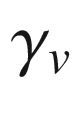 is a smooth embedding of
is a smooth embedding of 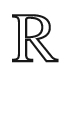 into
into  whose image is the great hyperbola formed by the intersection between
whose image is the great hyperbola formed by the intersection between 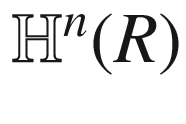 and the plane spanned by
and the plane spanned by  .
.Conversely, suppose  is any 2-dimensional linear subspace of
is any 2-dimensional linear subspace of  that has nontrivial intersection with
that has nontrivial intersection with  . Choose
. Choose  , and let v be another nonzero vector in
, and let v be another nonzero vector in  that is
that is  -orthogonal to p, which implies
-orthogonal to p, which implies  . Using the computation above, we see that the image of the geodesic
. Using the computation above, we see that the image of the geodesic  is the great hyperbola formed by the intersection of
is the great hyperbola formed by the intersection of  with
with  .
.
Before considering the other three models, note that since maximal geodesics in  are constant-speed embeddings of
are constant-speed embeddings of  , it follows from naturality that maximal geodesics in each of the other models are also constant-speed embeddings of
, it follows from naturality that maximal geodesics in each of the other models are also constant-speed embeddings of  . Thus each model is geodesically complete, and to determine the geodesics in the other models we need only determine their images.
. Thus each model is geodesically complete, and to determine the geodesics in the other models we need only determine their images.
Consider the Beltrami–Klein model. Recall the isometry  given by
given by  (see (3.11)). The image of a maximal geodesic in
(see (3.11)). The image of a maximal geodesic in  is a great hyperbola, which is the set of points
is a great hyperbola, which is the set of points  that solve a system of
that solve a system of  independent linear equations. Simple algebra shows that
independent linear equations. Simple algebra shows that  satisfies a linear equation
satisfies a linear equation  if and only if
if and only if  satisfies the affine equation
satisfies the affine equation  . Thus c maps each great hyperbola onto the intersection of
. Thus c maps each great hyperbola onto the intersection of  with an affine subspace of
with an affine subspace of  , and since it is the image of a smooth curve, it must be the intersection of
, and since it is the image of a smooth curve, it must be the intersection of  with a straight line.
with a straight line.
 constructed in Chapter 3:
constructed in Chapter 3: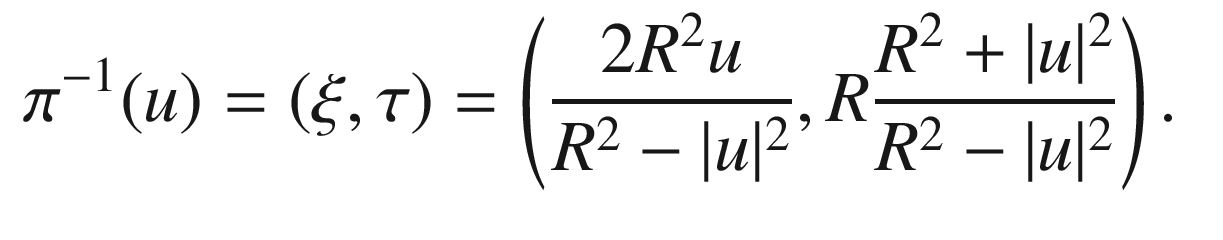
 that satisfy a single linear equation
that satisfy a single linear equation  . In the special case
. In the special case  , this hyperbola is mapped by
, this hyperbola is mapped by  to a straight line segment through the origin, as can easily be seen from the geometric definition of
to a straight line segment through the origin, as can easily be seen from the geometric definition of  . If
. If  , we can assume (after multiplying through by a constant if necessary) that
, we can assume (after multiplying through by a constant if necessary) that  , and write the linear equation as
, and write the linear equation as 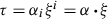 (where the dot represents the Euclidean dot product between elements of
(where the dot represents the Euclidean dot product between elements of  ). Under
). Under  , this pulls back to the equation
, this pulls back to the equation
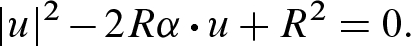

 , this locus is either empty or a point on
, this locus is either empty or a point on  , so it contains no points in
, so it contains no points in 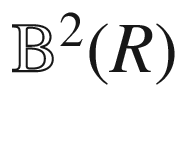 . Since we are assuming that it is the image of a maximal geodesic, we must therefore have
. Since we are assuming that it is the image of a maximal geodesic, we must therefore have  . In that case, (5.26) is the equation of a circle with center
. In that case, (5.26) is the equation of a circle with center 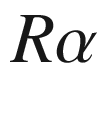 and radius
and radius  . At a point
. At a point  where the circle intersects
where the circle intersects 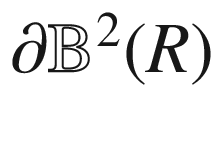 , the three points 0,
, the three points 0, 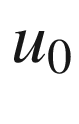 , and
, and 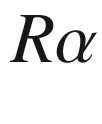 form a triangle with sides
form a triangle with sides  ,
, 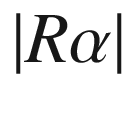 , and
, and 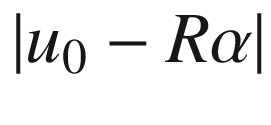 (Fig. 5.9), which satisfy the Pythagorean identity by (5.26); therefore the circle meets
(Fig. 5.9), which satisfy the Pythagorean identity by (5.26); therefore the circle meets  in a right angle.
in a right angle.In the higher-dimensional case, a geodesic on  is determined by a 2-plane. If the 2-plane contains the point
is determined by a 2-plane. If the 2-plane contains the point  , then the corresponding geodesic on
, then the corresponding geodesic on  is a line through the origin as before. Otherwise, we can use an orthogonal transformation in the
is a line through the origin as before. Otherwise, we can use an orthogonal transformation in the  variables (which preserves
variables (which preserves  ) to move this 2-plane so that it lies in the
) to move this 2-plane so that it lies in the  subspace, and then we are in the same situation as in the 2-dimensional case.
subspace, and then we are in the same situation as in the 2-dimensional case.
 given in Chapter 3:
given in Chapter 3:
 and
and  in place of
in place of 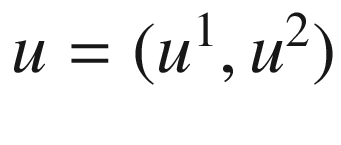 ,
, 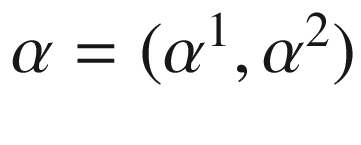 , we get
, we get
 and simplifying yields
and simplifying yields
 , in which case the condition
, in which case the condition 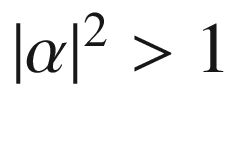 forces
forces  , and then it is a straight line
, and then it is a straight line  . The other class of geodesics on the ball, line segments through the origin, can be handled similarly.
. The other class of geodesics on the ball, line segments through the origin, can be handled similarly.In the higher-dimensional case, suppose first that  is a maximal geodesic such that
is a maximal geodesic such that  lies on the y-axis and
lies on the y-axis and  is in the span of
is in the span of  . From the explicit formula (3.15) for
. From the explicit formula (3.15) for  , it follows that
, it follows that  lies on the v-axis in the ball, and
lies on the v-axis in the ball, and  is in the span of
is in the span of  . The image of the geodesic
. The image of the geodesic  is either part of a line through the origin or an arc of a circle perpendicular to
is either part of a line through the origin or an arc of a circle perpendicular to  , both of which are contained in the
, both of which are contained in the  -plane. By the argument in the preceding paragraph, it then follows that the image of
-plane. By the argument in the preceding paragraph, it then follows that the image of  is contained in the
is contained in the  -plane and is either a vertical half-line or a semicircle centered on the
-plane and is either a vertical half-line or a semicircle centered on the  hyperplane. For the general case, note that translations and orthogonal transformations in the x-variables preserve vertical half-lines and circles centered on the
hyperplane. For the general case, note that translations and orthogonal transformations in the x-variables preserve vertical half-lines and circles centered on the  hyperplane in
hyperplane in  , and they also preserve the metric
, and they also preserve the metric  . Given an arbitrary maximal geodesic
. Given an arbitrary maximal geodesic  , after applying an x-translation we may assume that
, after applying an x-translation we may assume that  lies on the y-axis, and after an orthogonal transformation in the x variables, we may assume that
lies on the y-axis, and after an orthogonal transformation in the x variables, we may assume that  is in the span of
is in the span of  ; then the argument above shows that the image of
; then the argument above shows that the image of  is either a vertical half-line or a semicircle centered on the
is either a vertical half-line or a semicircle centered on the  hyperplane.
hyperplane. 

Geodesics are arcs of circles orthogonal to the boundary of 
Euclidean and Non-Euclidean Geometries
In two dimensions, our model spaces can be interpreted as models of classical Euclidean and non-Euclidean plane geometries.
Euclidean Plane Geometry
Euclid’s axioms for plane and spatial geometry, written around 300 BCE, became a model for axiomatic treatments of geometry, and indeed for all of mathematics. As standards of rigor evolved, mathematicians revised and added to Euclid’s axioms in various ways. One axiom system that meets modern standards of rigor was created by David Hilbert [Hil71]. Here (in somewhat simplified form) are his axioms for plane geometry. (See [Hil71, Gan73, Gre93] for more complete treatments of Hilbert’s axioms, and see [LeeAG] for a different axiomatic approach based on the real number system.)
Given a line l and a point P, we say that
 contains
contains  if P lies on l.
if P lies on l.A set of points is said to be collinear if there is a line that contains them all.
Given two distinct points A, B, the segment
 is the set consisting of A, B, and all points C such that C is between A and B.
is the set consisting of A, B, and all points C such that C is between A and B.The notation
 means that
means that  is congruent to
is congruent to  .
.Given two distinct points A, B, the ray
 is the set consisting of A, B, and all points C such that either C is between A and B or B is between A and C.
is the set consisting of A, B, and all points C such that either C is between A and B or B is between A and C.An interior point of the ray
 is a point that lies on
is a point that lies on  and is not equal to A.
and is not equal to A.Given three noncollinear points A, O, B, the angle
 is the union of the rays
is the union of the rays  and
and  .
.The notation
 means that
means that  is congruent to
is congruent to  .
.Given a line l and two points A, B that do not lie on l, we say that
 and
and  are on the same side of
are on the same side of  if no point of
if no point of  lies on l.
lies on l.Two lines are said to be parallel if there is no point that lies on both of them.
- Incidence Postulates:
- (a)
For any two distinct points A, B, there exists a unique line that contains both of them.
- (b)
There exist at least two points on each line, and there exist at least three noncollinear points.
- (a)
- Order Postulates:
- (a)
If a point B lies between a point A and a point C, then A, B, C are three distinct points of a line, and B also lies between C and A.
- (b)
Given two distinct points A and C, there always exists at least one point B such that C lies between A and B.
- (c)
Given three distinct points on a line, no more than one of them lies between the other two.
- (d)
Let A, B, C be three noncollinear points, and let l be a line that does not contain any of them. If l contains a point of
 , then it also contains a point of
, then it also contains a point of  or
or  .
.
- (a)
- Congruence Postulates:
- (a)
If A, B are two points on a line l, and
 is a point on a line
is a point on a line  , then it is always possible to find a point
, then it is always possible to find a point  on a given ray of
on a given ray of  starting at
starting at  such that
such that  .
. - (b)
If segments
 and
and  are congruent to the same segment
are congruent to the same segment  , then
, then  and
and  are congruent to each other.
are congruent to each other. - (c)
On a line l, let
 and
and  be two segments that, except for B, have no points in common. Furthermore, on the same or another line
be two segments that, except for B, have no points in common. Furthermore, on the same or another line  , let
, let  and
and  be two segments that, except for
be two segments that, except for  , have no points in common. In that case, if
, have no points in common. In that case, if  and
and  , then
, then  .
. - (d)
Let
 be an angle and
be an angle and  a line, and let a definite side of
a line, and let a definite side of  be given. Let
be given. Let  be a ray on
be a ray on  starting at a point
starting at a point  . Then there exists one and only one ray
. Then there exists one and only one ray  such that
such that  and at the same time all the interior points of
and at the same time all the interior points of  lie on the given side of
lie on the given side of  .
. - (e)
If for two triangles
 and
and  the congruences
the congruences  ,
,  , and
, and  hold, then
hold, then  and
and  as well.
as well.
- (a)
Euclidean Parallel Postulate: Given a line l and a point A that does not lie on l, there exists a unique line that contains A and is parallel to l.
Given an axiomatic system such as this one, an interpretation of the system is simply an assignment of a definition for each of the primitive terms. An interpretation is called a model of the axiomatic system provided that each of the axioms becomes a theorem when the primitive terms are given the assigned meanings.
A point is an element of
 .
.A line is the image of a maximal geodesic with respect to the Euclidean metric.
Given a point A and a line l, we say that
 lies on
lies on  if
if  .
.Given three distinct points A, B, C, we say that
 is between
is between  and
and  if B is on the geodesic segment joining A to C.
if B is on the geodesic segment joining A to C.Given two sets of points S and
 , we say that
, we say that  is congruent to
is congruent to  if there is a Euclidean isometry
if there is a Euclidean isometry  such that
such that  .
.
With this interpretation, it will come as no surprise that Hilbert’s postulates are all theorems; proving them is just a standard exercise in plane analytic geometry.
 Exercise 5.29. Verify that all of Hilbert’s axioms are theorems when the primitive terms are given the interpretations listed above.
Exercise 5.29. Verify that all of Hilbert’s axioms are theorems when the primitive terms are given the interpretations listed above.
Hyperbolic Parallel Postulate: Given a line l and a point A that does not lie on l, there exist at least two distinct lines that contain A and are parallel to l.
We obtain an interpretation of this new axiomatic system by giving definitions to the primitive terms just as we did above, but now with  replaced by
replaced by  and
and  replaced by any hyperbolic metric
replaced by any hyperbolic metric  . (The axioms we have listed here do not distinguish among hyperbolic metrics of different radii.) In Problem 5-19, you will be asked to prove that some of Hilbert’s axioms are theorems under this interpretation.
. (The axioms we have listed here do not distinguish among hyperbolic metrics of different radii.) In Problem 5-19, you will be asked to prove that some of Hilbert’s axioms are theorems under this interpretation.
Elliptic Parallel Postulate: No two lines are parallel.
Unfortunately, we cannot simply replace the Euclidean parallel postulate with this one and leave the other axioms alone, because it already follows from Hilbert’s other axioms that for every line l and every point  there exists at least one line through A that is parallel to l (for a proof, see [Gre93], for example). Nonetheless, we already know of an interesting geometry that satisfies the elliptic parallel postulate—the sphere
there exists at least one line through A that is parallel to l (for a proof, see [Gre93], for example). Nonetheless, we already know of an interesting geometry that satisfies the elliptic parallel postulate—the sphere  with the round metric
with the round metric  . To construct a consistent axiomatic system including the elliptic parallel postulate, some of the other axioms need to be modified.
. To construct a consistent axiomatic system including the elliptic parallel postulate, some of the other axioms need to be modified.
If we take the sphere as a guide, with images of maximal geodesics as lines, then we can see already that the first incidence postulate needs to be abandoned, because if  are antipodal points (meaning that
are antipodal points (meaning that  ), then there are infinitely many lines containing A and B. Any axiomatic system for which
), then there are infinitely many lines containing A and B. Any axiomatic system for which  is a model is called double elliptic geometry, because every pair of distinct lines intersects in exactly two points.
is a model is called double elliptic geometry, because every pair of distinct lines intersects in exactly two points.
It is also possible to construct an elliptic geometry in which the incidence postulates hold, as in the following example.
Example 5.30.
The real projective plane  has a frame-homogeneous Riemannian metric g that is locally isometric to a round metric on
has a frame-homogeneous Riemannian metric g that is locally isometric to a round metric on  (see Example 2.34 and Problem 3-2). As Problem 5-20 shows, single elliptic geometry satisfies Hilbert’s incidence postulates as well as the elliptic parallel postulate. This interpretation is called single elliptic geometry. //
(see Example 2.34 and Problem 3-2). As Problem 5-20 shows, single elliptic geometry satisfies Hilbert’s incidence postulates as well as the elliptic parallel postulate. This interpretation is called single elliptic geometry. //
- 5-1.
Let (M, g) be a Riemannian or pseudo-Riemannian manifold, and let
 be its Levi-Civita connection. Suppose
be its Levi-Civita connection. Suppose  is another connection on TM, and D is the difference tensor between
is another connection on TM, and D is the difference tensor between  and
and  (Prop. 4.13). Let
(Prop. 4.13). Let  denote the covariant 3-tensor field defined by
denote the covariant 3-tensor field defined by  . Show that
. Show that  is compatible with g if and only if
is compatible with g if and only if  is antisymmetric in its last two arguments:
is antisymmetric in its last two arguments:  for all
for all  . Conclude that on every Riemannian or pseudo-Riemannian manifold of dimension at least 2, the space of metric connections is an infinite-dimensional affine space. (Used on p. 121.)
. Conclude that on every Riemannian or pseudo-Riemannian manifold of dimension at least 2, the space of metric connections is an infinite-dimensional affine space. (Used on p. 121.) - 5-2.Let
 be a connection on the tangent bundle of a Riemannian manifold (M, g). Show that
be a connection on the tangent bundle of a Riemannian manifold (M, g). Show that  is compatible with g if and only if the connection 1-forms
is compatible with g if and only if the connection 1-forms  (Problem 4-14) with respect to each local frame
(Problem 4-14) with respect to each local frame  satisfy Show that this implies that with respect to every local orthonormal frame, the matrix
satisfy Show that this implies that with respect to every local orthonormal frame, the matrix
 is skew-symmetric.
is skew-symmetric. - 5-3.Define a connection on
 by setting (in standard coordinates) with all other connection coefficients equal to zero. Show that this connection is compatible with the Euclidean metric and has the same geodesics as the Euclidean connection, but is not symmetric. (See Problem 4-9.)
by setting (in standard coordinates) with all other connection coefficients equal to zero. Show that this connection is compatible with the Euclidean metric and has the same geodesics as the Euclidean connection, but is not symmetric. (See Problem 4-9.)
- 5-4.
Let C be an embedded smooth curve in the half-plane
 , and let
, and let  be the surface of revolution determined by C as in Example 2.20. Let
be the surface of revolution determined by C as in Example 2.20. Let  be a unit-speed local parametrization of C, and let X be the parametrization of
be a unit-speed local parametrization of C, and let X be the parametrization of  given by (2.11).
given by (2.11).- (a)
Compute the Christoffel symbols of the induced metric on
 in
in  coordinates.
coordinates. - (b)
Show that each meridian is the image of a geodesic on
 .
. - (c)
Determine necessary and sufficient conditions for a latitude circle to be the image of a geodesic.
- (a)
- 5-5.
Recall that a vector field Y defined on (an open subset of) a Riemannian manifold is said to be parallel if
 .
.- (a)
Let
 and
and  . Show that there is a unique parallel vector field Y on
. Show that there is a unique parallel vector field Y on  such that
such that  .
. - (b)
Let
 be the spherical coordinate parametrization of an open subset U of the unit sphere
be the spherical coordinate parametrization of an open subset U of the unit sphere  (see Example 2.20 and Problem 5-4), and let
(see Example 2.20 and Problem 5-4), and let  ,
,  denote the coordinate vector fields associated with this parametrization. Compute
denote the coordinate vector fields associated with this parametrization. Compute  and
and  , and conclude that
, and conclude that  is parallel along the equator and along each meridian
is parallel along the equator and along each meridian  .
. - (c)
Let
 . Show that there is no parallel vector field W on any neighborhood of p in
. Show that there is no parallel vector field W on any neighborhood of p in  such that
such that  .
. - (d)
Use (a) and (c) to show that no neighborhood of p in
 is isometric to an open subset of
is isometric to an open subset of  .
.(Used on p. 194.)
- (a)
- 5-6.
Suppose
 is a
Riemannian submersion. If Z is any vector field on M, we let
is a
Riemannian submersion. If Z is any vector field on M, we let  denote its horizontal lift to
denote its horizontal lift to  (see Prop. 2.25).
(see Prop. 2.25).- (a)Show that for every pair of vector fields
 , we have
, we have ![$$\begin{aligned}&\big \langle {{\tilde{X}}},{{\tilde{Y}}}\big \rangle = \langle X,Y \rangle \circ \pi ;\\&\big [{{\tilde{X}}},{{\tilde{Y}}}\big ]^H = \widetilde{[X,Y]};\\&\big [{{\tilde{X}}}, W\big ]\text { is vertical if } W\in \mathfrak X\big ({{\widetilde{M}}}\big ) \text { is vertical.} \end{aligned}$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_Equ75.png)
- (b)Let
 and
and  denote the Levi-Civita connections of
denote the Levi-Civita connections of  and g, respectively. Show that for every pair of vector fields
and g, respectively. Show that for every pair of vector fields  , we have [Hint: Let
, we have [Hint: Let![$$\begin{aligned} {\tilde{\nabla }}_{{{\tilde{X}}}}{{\tilde{Y}}}= \widetilde{\nabla _XY} + \tfrac{1}{2} \big [{{\tilde{X}}},{{\tilde{Y}}}\big ]^V. \end{aligned}$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_Equ27.png) (5.27)
(5.27) be a horizontal lift and W a vertical vector field on
be a horizontal lift and W a vertical vector field on  , and compute
, and compute  and
and  using (5.9).]
using (5.9).](Used on p. 224.)
- (a)
- 5-7.
Suppose
 and
and  are Riemannian manifolds.
are Riemannian manifolds.- (a)
Prove that if
 is endowed with the product metric, then a curve
is endowed with the product metric, then a curve  of the form
of the form  is a geodesic if and only if
is a geodesic if and only if  is a geodesic in
is a geodesic in  for
for  .
. - (b)
Now suppose
 is a strictly positive smooth function, and
is a strictly positive smooth function, and  is the resulting
warped product (see Example 2.24). Let
is the resulting
warped product (see Example 2.24). Let  be a smooth curve and
be a smooth curve and  a point in
a point in  , and define
, and define  by
by  . Prove that
. Prove that  is a geodesic with respect to the warped product metric if and only if
is a geodesic with respect to the warped product metric if and only if  is a geodesic with respect to
is a geodesic with respect to  .
.(Used on p. 316.)
- (a)
- 5-8.
Let G be a Lie group and
 its Lie algebra. Suppose g is a
bi-invariant Riemannian metric on G, and
its Lie algebra. Suppose g is a
bi-invariant Riemannian metric on G, and  is the corresponding inner product on
is the corresponding inner product on  (see Prop. 3.12). Let
(see Prop. 3.12). Let  denote the adjoint representation of
denote the adjoint representation of  (see Appendix C).
(see Appendix C).- (a)Show that
 is a skew-adjoint endomorphism of
is a skew-adjoint endomorphism of  for every
for every  : [Hint: Take the derivative of
: [Hint: Take the derivative of
 with respect to t at
with respect to t at  , where
, where  is the Lie group exponential map of G, and use the fact that
is the Lie group exponential map of G, and use the fact that  .]
.] - (b)
Show that
![$$\nabla _X Y = \tfrac{1}{2}[X, Y]$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_IEq920.png) whenever X and Y are left-invariant vector fields on G.
whenever X and Y are left-invariant vector fields on G. - (c)
Show that the geodesics of g starting at the identity are exactly the one-parameter subgroups. Conclude that under the canonical isomorphism of
 described in Proposition C.3, the restricted Riemannian exponential map at the identity coincides with the
Lie group exponential map
described in Proposition C.3, the restricted Riemannian exponential map at the identity coincides with the
Lie group exponential map  . (See Prop. C.7.)
. (See Prop. C.7.) - (d)
Let
 be the set of positive real numbers, regarded as a Lie group under multiplication. Show that
be the set of positive real numbers, regarded as a Lie group under multiplication. Show that  is a bi-invariant metric on
is a bi-invariant metric on  , and the restricted Riemannian exponential map at 1 is given by
, and the restricted Riemannian exponential map at 1 is given by  .
.(Used on pp. 128, 224.)
- (a)
- 5-9.Suppose (M, g) is a Riemannian manifold and
 is a smooth coordinate chart on a neighborhood of
is a smooth coordinate chart on a neighborhood of  such that
such that  and
and  is star-shaped with respect to 0. Prove that this chart is a normal coordinate chart for g if and only if
is star-shaped with respect to 0. Prove that this chart is a normal coordinate chart for g if and only if  and the following identity is satisfied on U:
and the following identity is satisfied on U: 
- 5-10.
Prove Proposition 5.22 (a local isometry is determined by its value and differential at one point).
- 5-11.
Recall the groups
 ,
,  , and
, and  defined in Chapter 3, which act isometrically on the model Riemannian manifolds
defined in Chapter 3, which act isometrically on the model Riemannian manifolds  ,
,  , and
, and  , respectively.
, respectively.- (a)Show that

- (b)
Show that in each case, for each point p in
 ,
,  , or
, or  , the isotropy group at p is a subgroup isomorphic to
, the isotropy group at p is a subgroup isomorphic to  .
. - (c)
Strengthen the result above by showing that if (M, g) is one of the Riemannian manifolds
 ,
,  , or
, or  , U is a connected open subset of M, and
, U is a connected open subset of M, and  is a local isometry, then
is a local isometry, then  is the restriction to U of an element of
is the restriction to U of an element of  .
.(Used on pp. 57, 58, 67, 348, 349.)
- (a)
- 5-12.
Suppose M is a connected n-dimensional Riemannian manifold, and G is a Lie group acting isometrically and effectively on M. Show that
 . (Used on p. 261.)
. (Used on p. 261.) - 5-13.
Let (M, g) be a Riemannian manifold.
- (a)Show that the following formula holds for every smooth 1-form
 :
: 
- (b)Generalize this to an arbitrary k-form
 as follows: where
as follows: where
 denotes the alternation operator defined in (B.9). [Hint: For each
denotes the alternation operator defined in (B.9). [Hint: For each  , do the computation in normal coordinates centered at p, and note that both sides of the equation are well defined, independently of the choice of coordinates.]
, do the computation in normal coordinates centered at p, and note that both sides of the equation are well defined, independently of the choice of coordinates.](Used on p. 209.)
- (a)
- 5-14.
Suppose (M, g) is a Riemannian manifold, and let
 and
and  be the divergence and Laplace operators defined on pages 32–33.
be the divergence and Laplace operators defined on pages 32–33.- (a)
Show that for every vector field
 ,
,
 can be written in terms of the total covariant derivative as
can be written in terms of the total covariant derivative as  , and that if
, and that if  in terms of some local frame, then
in terms of some local frame, then  . [Hint: Show that it suffices to prove the formulas at the origin in normal coordinates.]
. [Hint: Show that it suffices to prove the formulas at the origin in normal coordinates.] - (b)Show that the Laplace operator acting on a smooth function u can be expressed asand in terms of any local frame,
 (5.28)(Used on pp. 218, 256, 333.)
(5.28)(Used on pp. 218, 256, 333.) (5.29)
(5.29)
- (a)
- 5-15.
- 5-16.By analogy with the formula
 developed in Problem 5-14, we can define a divergence operator on tensor fields of any rank on a Riemannian manifold. If F is any smooth k-tensor field (covariant, contravariant, or mixed), we define the divergence of F by where the trace is taken on the last two indices of the
developed in Problem 5-14, we can define a divergence operator on tensor fields of any rank on a Riemannian manifold. If F is any smooth k-tensor field (covariant, contravariant, or mixed), we define the divergence of F by where the trace is taken on the last two indices of the
 -tensor field
-tensor field  . (If F is purely contravariant, then
. (If F is purely contravariant, then  can be replaced with
can be replaced with  , because the next-to-last index of
, because the next-to-last index of  is already an upper index.) Extend the integration by parts formula of Problem 2-22 as follows: if F is a smooth covariant k-tensor field and G is a smooth covariant
is already an upper index.) Extend the integration by parts formula of Problem 2-22 as follows: if F is a smooth covariant k-tensor field and G is a smooth covariant  -tensor field on a compact smooth Riemannian manifold (M, g) with boundary, then where
-tensor field on a compact smooth Riemannian manifold (M, g) with boundary, then where
 is the induced metric on
is the induced metric on  . This is often written more suggestively as
. This is often written more suggestively as 
- 5-17.
Suppose (M, g) is a Riemannian manifold and
 is an embedded submanifold. Show that P has a tubular neighborhood that is diffeomorphic to the total space of the normal bundle NP, by a diffeomorphism that sends the zero section of NP to P. [Hint: First show that the function
is an embedded submanifold. Show that P has a tubular neighborhood that is diffeomorphic to the total space of the normal bundle NP, by a diffeomorphism that sends the zero section of NP to P. [Hint: First show that the function  in (5.21) can be chosen to be smooth.]
in (5.21) can be chosen to be smooth.] - 5-18.
Prove Proposition 5.26 (properties of Fermi coordinates).
- 5-19.
Use
 with the metric
with the metric  to construct an interpretation of Hilbert’s axioms with the hyperbolic parallel postulate substituted for the Euclidean one, and prove that the incidence postulates, congruence postulate (e), and the hyperbolic parallel postulate are theorems in this geometry. (Used on p. 144.)
to construct an interpretation of Hilbert’s axioms with the hyperbolic parallel postulate substituted for the Euclidean one, and prove that the incidence postulates, congruence postulate (e), and the hyperbolic parallel postulate are theorems in this geometry. (Used on p. 144.) - 5-20.
Show that single elliptic geometry (Example 5.30) satisfies Hilbert’s incidence postulates and the elliptic parallel postulate if points are defined as elements of
 and lines are defined as images of maximal geodesics.
and lines are defined as images of maximal geodesics. - 5-21.
Let (M, g) be a Riemannian or pseudo-Riemannian manifold and
 . Show that for every orthonormal basis
. Show that for every orthonormal basis  for
for  there is a smooth orthonormal frame
there is a smooth orthonormal frame  on a neighborhood of p such that
on a neighborhood of p such that  and
and  for each i.
for each i. - 5-22.
A smooth vector field X on a Riemannian manifold is called a Killing vector field if the Lie derivative of the metric with respect to X vanishes. By Proposition B.10, this is equivalent to the requirement that the metric be invariant under the flow of X. Prove that X is a Killing vector field if and only if the covariant 2-tensor field
 is antisymmetric. [Hint: Use Prop. B.9.] (Used on pp. 190, 315.)
is antisymmetric. [Hint: Use Prop. B.9.] (Used on pp. 190, 315.) - 5-23.Let (M, g) be a connected Riemannian manifold and
 . An admissible loop based at p is an admissible curve
. An admissible loop based at p is an admissible curve ![$$\gamma :[a, b]\mathrel {\rightarrow }M$$](../images/56724_2_En_5_Chapter/56724_2_En_5_Chapter_TeX_IEq986.png) such that
such that  . For each such loop
. For each such loop  , let
, let  denote the parallel transport operator
denote the parallel transport operator  along
along  , and let
, and let  denote the set of all automorphisms of
denote the set of all automorphisms of  obtained in this way:
obtained in this way: 
- (a)
Show that
 is a subgroup of
is a subgroup of  (the set of all linear isometries of
(the set of all linear isometries of  ), called the holonomy group at p.
), called the holonomy group at p. - (b)
Let
 denote the subset obtained by restricting to loops
denote the subset obtained by restricting to loops  that are path-homotopic to the constant loop. Show that
that are path-homotopic to the constant loop. Show that  is a normal subgroup of
is a normal subgroup of  , called the
restricted holonomy group at p
.
, called the
restricted holonomy group at p
. - (c)
Given
 , show that there is an isomorphism of
, show that there is an isomorphism of  with
with  that takes
that takes  to
to  .
. - (d)
Show that M is orientable if and only if
 (the set of linear isometries with determinant
(the set of linear isometries with determinant  ) for some
) for some  .
. - (e)
Show that g is flat if and only if
 is the trivial group for some
is the trivial group for some  .
.
- (a)




