Before we delve into the general theory of Riemannian manifolds, we pause to give it some substance by introducing a variety of “model Riemannian manifolds” that should help to motivate the general theory. These manifolds are distinguished by having a high degree of symmetry.
We begin by describing the most symmetric model spaces of all—Euclidean spaces, spheres, and hyperbolic spaces. We analyze these in detail, and prove that each one has a very large isometry group: not only is there an isometry taking anypoint to any other point, but in fact one can find an isometry taking anyorthonormal basis at one point to any orthonormal basis at any other point. As we will see in Chapter 8, this has strong consequences for the curvatures of these manifolds.
After introducing these very special models, we explore some more general classes of Riemannian manifolds with symmetry—the invariant metrics on Lie groups, homogeneous spaces, and symmetric spaces.
At the end of the chapter, we give a brief introduction to some analogous models in the pseudo-Riemannian case. For the particular case of Lorentz manifolds, these are the Minkowski spaces, de Sitter spaces, and anti-de Sitter spaces, which are important model spaces in general relativity.
Symmetries of Riemannian Manifolds
The main feature of the Riemannian manifolds we are going to introduce in this chapter is that they are all highly symmetric, meaning that they have large groups of isometries.
Let (M, g) be a Riemannian manifold. Recall that  denotes the set of all isometries from M to itself, which is a group under composition. We say that (M, g) is a homogeneous Riemannian manifold if
denotes the set of all isometries from M to itself, which is a group under composition. We say that (M, g) is a homogeneous Riemannian manifold if  acts transitively on M, which is to say that for each pair of points
acts transitively on M, which is to say that for each pair of points  , there is an isometry
, there is an isometry  such that
such that  .
.
The isometry group does more than just act on M itself. For every  , the global differential
, the global differential  maps TM to itself and restricts to a linear isometry
maps TM to itself and restricts to a linear isometry  for each
for each  .
.
Given a point  , let
, let  denote the isotropy subgroup at p, that is, the subgroup of
denote the isotropy subgroup at p, that is, the subgroup of  consisting of isometries that fix p. For each
consisting of isometries that fix p. For each  , the linear map
, the linear map  takes
takes  to itself, and the map
to itself, and the map  given by
given by  is a representation of
is a representation of  , called the isotropy representation. We say that M is isotropic at
, called the isotropy representation. We say that M is isotropic at  if the isotropy representation of
if the isotropy representation of  acts transitively on the set of unit vectors in
acts transitively on the set of unit vectors in  . If M is isotropic at every point, we say simply that M is isotropic.
. If M is isotropic at every point, we say simply that M is isotropic.
 denote the set of all orthonormal bases for all tangent spaces of M:
denote the set of all orthonormal bases for all tangent spaces of M:
 on
on  , defined by using the differential of an isometry
, defined by using the differential of an isometry  to push an orthonormal basis at p forward to an orthonormal basis at
to push an orthonormal basis at p forward to an orthonormal basis at  :
:
 , or in other words, if for all
, or in other words, if for all 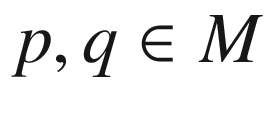 and choices of orthonormal bases at p and q, there is an isometry taking p to q and the chosen basis at p to the one at q. (Warning: Some authors, such as
[Boo86, dC92, Spi79], use the term isotropic to refer to the property we have called frame-homogeneous.)
and choices of orthonormal bases at p and q, there is an isometry taking p to q and the chosen basis at p to the one at q. (Warning: Some authors, such as
[Boo86, dC92, Spi79], use the term isotropic to refer to the property we have called frame-homogeneous.)Proposition 3.1.
Let (M, g) be a Riemannian manifold.
- (a)
If M is isotropic at one point and it is homogeneous, then it is isotropic.
- (b)
If M is frame-homogeneous, then it is homogeneous and isotropic.
Proof.
Problem 3-3. 
A homogeneous Riemannian manifold looks geometrically the same at every point, while an isotropic one looks the same in every direction. It turns out that an isotropic Riemannian manifold is automatically homogeneous; however, a Riemannian manifold can be isotropic at one point without being isotropic (for example, the paraboloid  in
in  with the induced metric); homogeneous without being isotropic anywhere (for example, the Berger metrics on
with the induced metric); homogeneous without being isotropic anywhere (for example, the Berger metrics on  discussed in Problem 3-10 below); or homogeneous and isotropic without being frame-homogeneous (for example, the Fubini–Study metrics on complex projective spaces discussed in Example 2.30). The proofs of these claims will have to wait until we have developed the theories of geodesics and curvature (see Problems 6-18, 8-5, 8-16, and 8-13).
discussed in Problem 3-10 below); or homogeneous and isotropic without being frame-homogeneous (for example, the Fubini–Study metrics on complex projective spaces discussed in Example 2.30). The proofs of these claims will have to wait until we have developed the theories of geodesics and curvature (see Problems 6-18, 8-5, 8-16, and 8-13).
As mentioned in Chapter 1, the Myers–Steenrod theorem shows that  is always a Lie group acting smoothly on M. Although we will not use that result, in many cases we can identify a smooth Lie group action that accounts for at least some of the isometry group, and in certain cases we will be able to prove that it is the entire isometry group.
is always a Lie group acting smoothly on M. Although we will not use that result, in many cases we can identify a smooth Lie group action that accounts for at least some of the isometry group, and in certain cases we will be able to prove that it is the entire isometry group.
Euclidean Spaces
The simplest and most important model Riemannian manifold is of course  -dimensional Euclidean space, which is just
-dimensional Euclidean space, which is just  with the Euclidean metric
with the Euclidean metric  given by (2.8).
given by (2.8).
Somewhat more generally, if V is any n-dimensional real vector space endowed with an inner product, we can set  for any
for any  and any
and any  . Choosing an orthonormal basis
. Choosing an orthonormal basis  for V defines a basis isomorphism from
for V defines a basis isomorphism from  to V that sends
to V that sends  to
to  ; this is easily seen to be an isometry of (V, g) with
; this is easily seen to be an isometry of (V, g) with  , so all n-dimensional inner product spaces are isometric to each other as Riemannian manifolds.
, so all n-dimensional inner product spaces are isometric to each other as Riemannian manifolds.
It is easy to construct isometries of the Riemannian manifold  : for example, every orthogonal linear transformation
: for example, every orthogonal linear transformation  preserves the Euclidean metric, as does every translation
preserves the Euclidean metric, as does every translation  . It follows that every map of the form
. It follows that every map of the form  , formed by first applying the orthogonal map A and then translating by b, is an isometry.
, formed by first applying the orthogonal map A and then translating by b, is an isometry.
 . Regard
. Regard  as a Lie group under addition, and let
as a Lie group under addition, and let  be the natural action of
be the natural action of  on
on  . Define the Euclidean group
. Define the Euclidean group
 to be the semidirect product
to be the semidirect product  determined by this action: this is the Lie group whose underlying manifold is the product space
determined by this action: this is the Lie group whose underlying manifold is the product space  , with multiplication given by
, with multiplication given by  (see Example C.12). It has a faithful representation given by the map
(see Example C.12). It has a faithful representation given by the map  defined in block form by
defined in block form by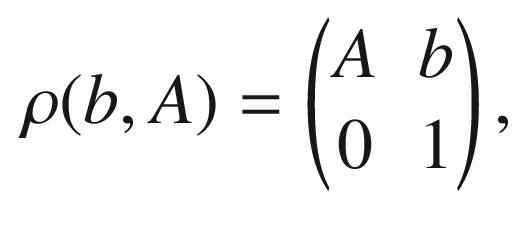
 column matrix.
column matrix. via
via
 is endowed with the Euclidean metric, this action is isometric and the induced action on
is endowed with the Euclidean metric, this action is isometric and the induced action on  is transitive.
(Later, we will see that this is in fact the full isometry group of
is transitive.
(Later, we will see that this is in fact the full isometry group of  —see Problem 5-11—but we do not need that fact now.) Thus each Euclidean space is frame-homogeneous.
—see Problem 5-11—but we do not need that fact now.) Thus each Euclidean space is frame-homogeneous.
Transitivity of  on
on 
Spheres
Our second class of model Riemannian manifolds comes in a family, with one for each positive real number. Given  , let
, let  denote the sphere of radius R centered at the origin in
denote the sphere of radius R centered at the origin in  , endowed with the metric
, endowed with the metric  (called the round metric of radius
(called the round metric of radius  ) induced from the Euclidean metric on
) induced from the Euclidean metric on  . When
. When  , it is the round metric on
, it is the round metric on  introduced in Example 2.13, and we use the notation
introduced in Example 2.13, and we use the notation  .
.
One of the first things one notices about the spheres is that like Euclidean spaces, they are highly symmetric.We can immediately write down a large group of isometries of  by observing that the linear action of the orthogonal group
by observing that the linear action of the orthogonal group  on
on  preserves
preserves  and the Euclidean metric, so its restriction to
and the Euclidean metric, so its restriction to  acts isometrically on the sphere. (Problem 5-11 will show that this is the full isometry group.)
acts isometrically on the sphere. (Problem 5-11 will show that this is the full isometry group.)
Proposition 3.2.
The group  acts transitively on
acts transitively on  , and thus each round sphere is frame-homogeneous.
, and thus each round sphere is frame-homogeneous.
Proof.
It suffices to show that given any  and any orthonormal basis
and any orthonormal basis  for
for  , there is an orthogonal map that takes the “north pole”
, there is an orthogonal map that takes the “north pole”  to p and the basis
to p and the basis  for
for  to
to  .
.
To do so, think of p as a vector of length R in  , and let
, and let  denote the unit vector in the same direction (Fig. 3.1). Since the basis vectors
denote the unit vector in the same direction (Fig. 3.1). Since the basis vectors  are tangent to the sphere, they are orthogonal to
are tangent to the sphere, they are orthogonal to  , so
, so  is an orthonormal basis for
is an orthonormal basis for  . Let
. Let  be the matrix whose columns are these basis vectors. Then
be the matrix whose columns are these basis vectors. Then  , and by elementary linear algebra,
, and by elementary linear algebra,  takes the standard basis vectors
takes the standard basis vectors  to
to  . It follows that
. It follows that  . Moreover, since
. Moreover, since  acts linearly on
acts linearly on  , its differential
, its differential  is represented in standard coordinates by the same matrix as
is represented in standard coordinates by the same matrix as  itself, so
itself, so  for
for  , and
, and  is the desired orthogonal map.
is the desired orthogonal map. 
 and
and  on a manifold M are said to be conformally related (or pointwise conformal or just conformal) to each other if there is a positive function
on a manifold M are said to be conformally related (or pointwise conformal or just conformal) to each other if there is a positive function  such that
such that  . Given two Riemannian manifolds (M, g) and
. Given two Riemannian manifolds (M, g) and 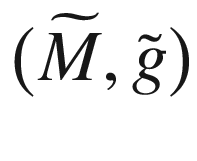 , a diffeomorphism
, a diffeomorphism  is called a conformal diffeomorphism (or a conformal transformation) if it pulls
is called a conformal diffeomorphism (or a conformal transformation) if it pulls  back to a metric that is conformal to g:
back to a metric that is conformal to g: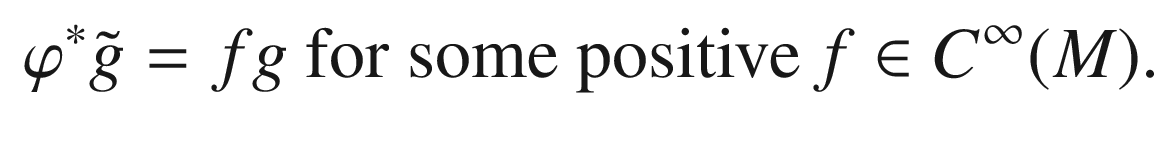
A Riemannian manifold (M, g) is said to be locally conformally flat if every point of M has a neighborhood that is conformally equivalent to an open set in  .
.
 Exercise 3.3.
Exercise 3.3.
- (a)
Show that for every smooth manifold M, conformality is an equivalence relation on the set of all Riemannian metrics on M.
- (b)
Show that conformal equivalence is an equivalence relation on the class of all Riemannian manifolds.
 Exercise 3.4. Suppose
Exercise 3.4. Suppose  and
and  are conformally related metrics on an oriented n-manifold. Show that their volume forms are related by
are conformally related metrics on an oriented n-manifold. Show that their volume forms are related by  .
.
 and
and  minus a point is provided by stereographic projection from the north pole. This is the map
minus a point is provided by stereographic projection from the north pole. This is the map  that sends a point
that sends a point  , written
, written  , to
, to 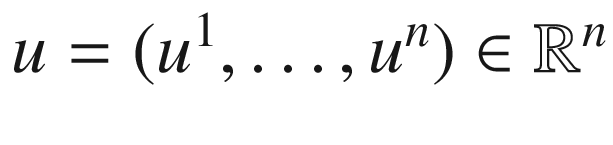 , where
, where 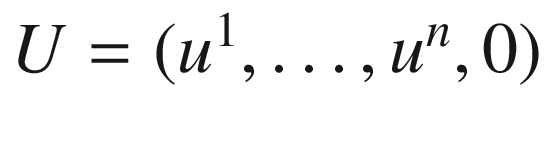 is the point where the line through N and P intersects the hyperplane
is the point where the line through N and P intersects the hyperplane  in
in 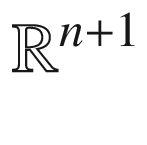 (Fig. 3.2). Thus U is characterized by the fact that
(Fig. 3.2). Thus U is characterized by the fact that 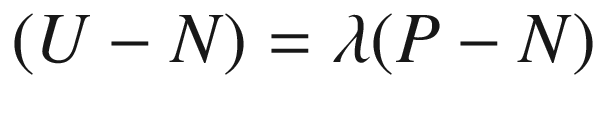 for some nonzero scalar
for some nonzero scalar  . Writing
. Writing  ,
,  , and
, and  , we obtain the system of equations
, we obtain the system of equations

Stereographic projection
 and plugging it into the first equation, we get the following formula for stereographic projection from the north pole of the sphere of radius R:
and plugging it into the first equation, we get the following formula for stereographic projection from the north pole of the sphere of radius R: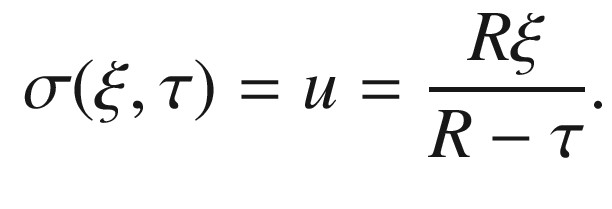
 is defined and smooth on all of
is defined and smooth on all of  . The easiest way to see that it is a diffeomorphism is to compute its inverse. Solving the two equations of (3.3) for
. The easiest way to see that it is a diffeomorphism is to compute its inverse. Solving the two equations of (3.3) for  and
and  gives
gives
 is characterized by these equations and the fact that P is on the sphere. Thus, substituting (3.5) into
is characterized by these equations and the fact that P is on the sphere. Thus, substituting (3.5) into  gives
gives

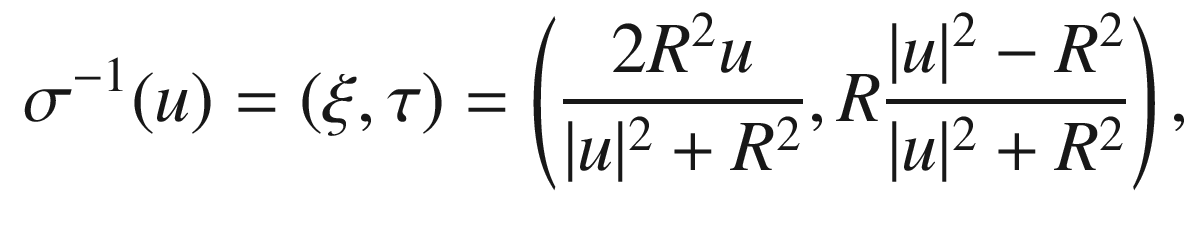
 back to
back to  and shows that
and shows that  is a diffeomorphism.
is a diffeomorphism.Proposition 3.5.
Stereographic projection is a conformal diffeomorphism between  and
and  .
.
Proof.
 is a smooth parametrization of
is a smooth parametrization of  , so we can use it to compute the pullback metric. Using the usual technique of substitution to compute pullbacks, we obtain the following coordinate representation of
, so we can use it to compute the pullback metric. Using the usual technique of substitution to compute pullbacks, we obtain the following coordinate representation of  in stereographic coordinates:
in stereographic coordinates:
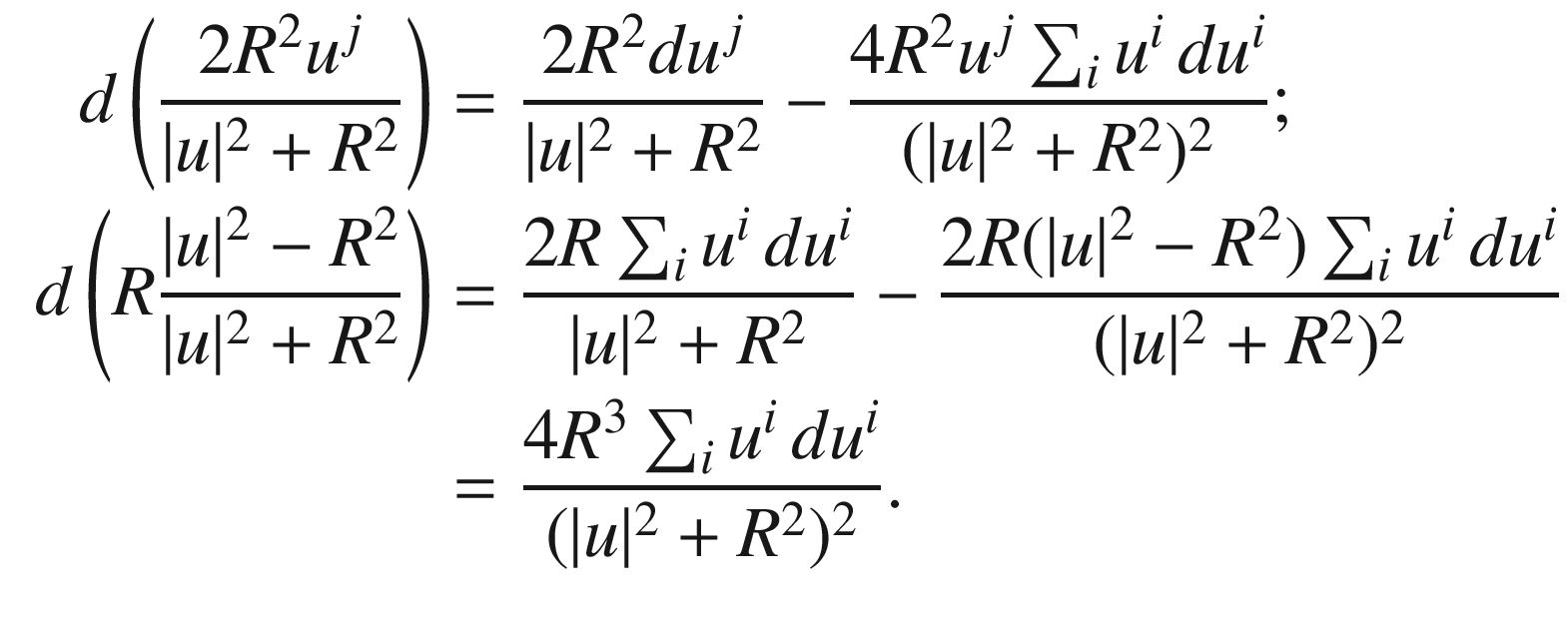
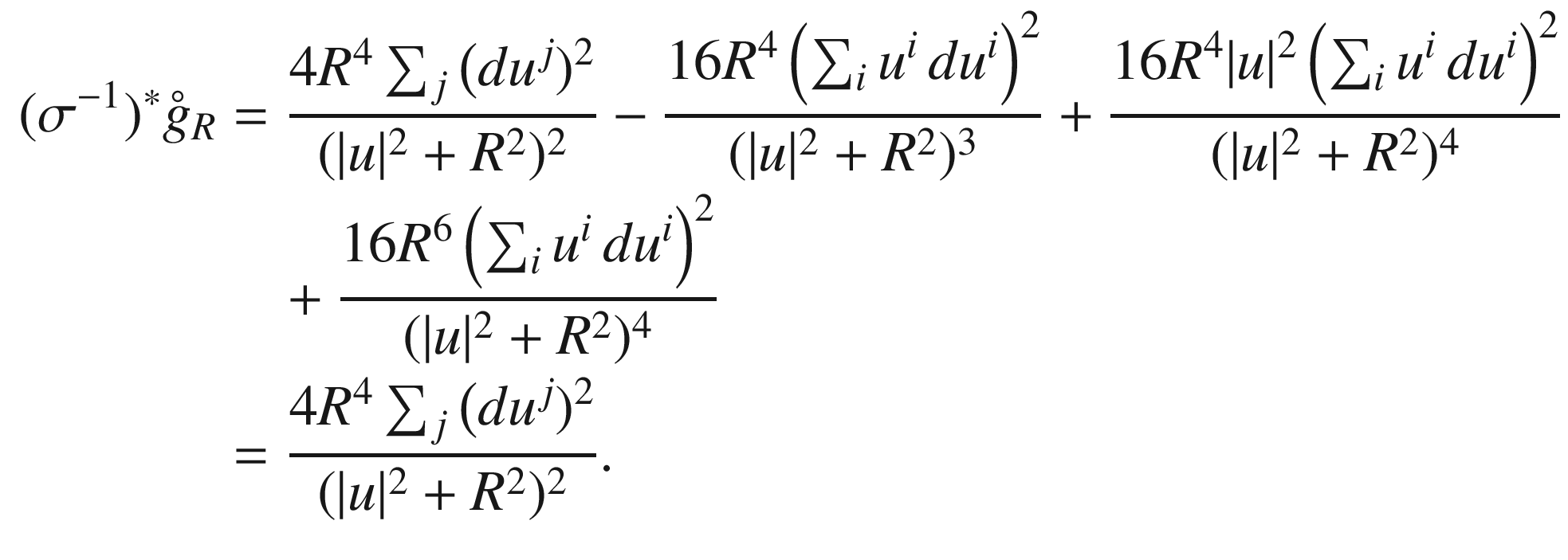
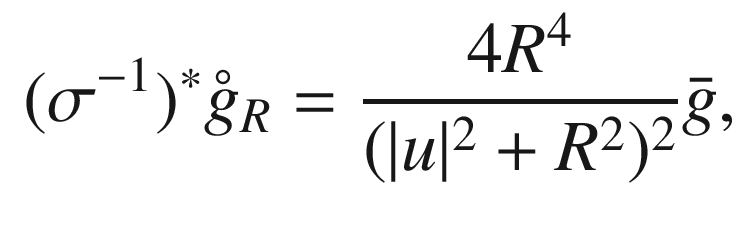
 now represents the Euclidean metric on
now represents the Euclidean metric on  , and so
, and so  is a conformal diffeomorphism.
is a conformal diffeomorphism. 
Corollary 3.6.
Each sphere with a round metric is locally conformally flat.
Proof.
Stereographic projection gives a conformal equivalence between a neighborhood of any point except the north pole and Euclidean space; applying a suitable rotation and then stereographic projection (or stereographic projection from the south pole), we get such an equivalence for a neighborhood of the north pole as well. 
Hyperbolic Spaces
Our third class of model Riemannian manifolds is perhaps less familiar than the other two. For each  and each
and each  we will define a frame-homogeneous Riemannian manifold
we will define a frame-homogeneous Riemannian manifold  , called hyperbolic space of radius
, called hyperbolic space of radius  . There are four equivalent models of the hyperbolic spaces, each of which is useful in certain contexts. In the next theorem, we introduce all of them and show that they are isometric.
. There are four equivalent models of the hyperbolic spaces, each of which is useful in certain contexts. In the next theorem, we introduce all of them and show that they are isometric.
Theorem 3.7.
Let n be an integer greater than 1. For each fixed  , the following Riemannian manifolds are all mutually isometric.
, the following Riemannian manifolds are all mutually isometric.
- (a)(Hyperboloid model)
 is the submanifold of Minkowski space
is the submanifold of Minkowski space  defined in standard coordinates
defined in standard coordinates  as the “upper sheet”
as the “upper sheet”  of the two-sheeted hyperboloid
of the two-sheeted hyperboloid  , with the induced metric where
, with the induced metric where
 is inclusion, and
is inclusion, and  is the Minkowski metric:
is the Minkowski metric:  (3.8)
(3.8) - (b)(Beltrami–Klein model)
 is the ball of radius R centered at the origin in
is the ball of radius R centered at the origin in  , with the metric given in coordinates
, with the metric given in coordinates  by
by  (3.9)
(3.9) - (c)(Poincaré ball model)
 is the ball of radius R centered at the origin in
is the ball of radius R centered at the origin in  , with the metric given in coordinates
, with the metric given in coordinates  by
by 
- (d)(Poincaré half-space model)
 is theupper half-space in
is theupper half-space in  defined in coordinates
defined in coordinates  by
by  , endowed with the metric
, endowed with the metric 
Proof.
Let  be given. We need to verify that
be given. We need to verify that  is actually a Riemannian submanifold of
is actually a Riemannian submanifold of  , or in other words that
, or in other words that  is positive definite. One way to do this is to show, as we will below, that it is the pullback of
is positive definite. One way to do this is to show, as we will below, that it is the pullback of  or
or  (both of which are manifestly positive definite) by a diffeomorphism. Alternatively, here is a direct proof using some of the theory of submanifolds of pseudo-Riemannian manifolds developed in Chapter 1.
(both of which are manifestly positive definite) by a diffeomorphism. Alternatively, here is a direct proof using some of the theory of submanifolds of pseudo-Riemannian manifolds developed in Chapter 1.
 is an open subset of a level set of the smooth function
is an open subset of a level set of the smooth function  given by
given by  . We have
. We have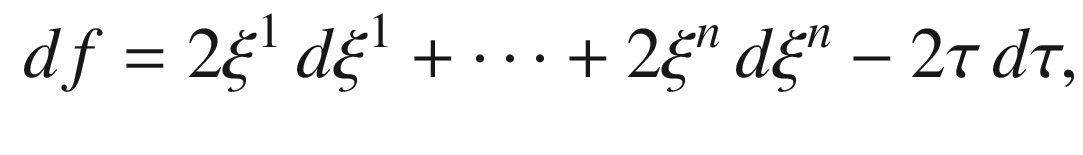
 is given by
is given by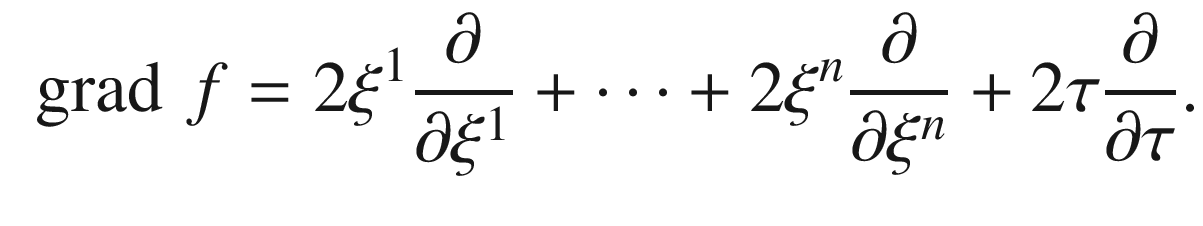

 at points of
at points of  . Thus it follows from Corollary 2.71 that
. Thus it follows from Corollary 2.71 that  is a pseudo-Riemannian submanifold of signature (n, 0), which is to say it is Riemannian.
is a pseudo-Riemannian submanifold of signature (n, 0), which is to say it is Riemannian. ,
, 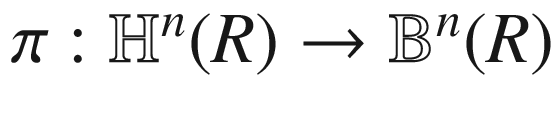 , and
, and  (shown schematically in Fig. 3.3).
(shown schematically in Fig. 3.3).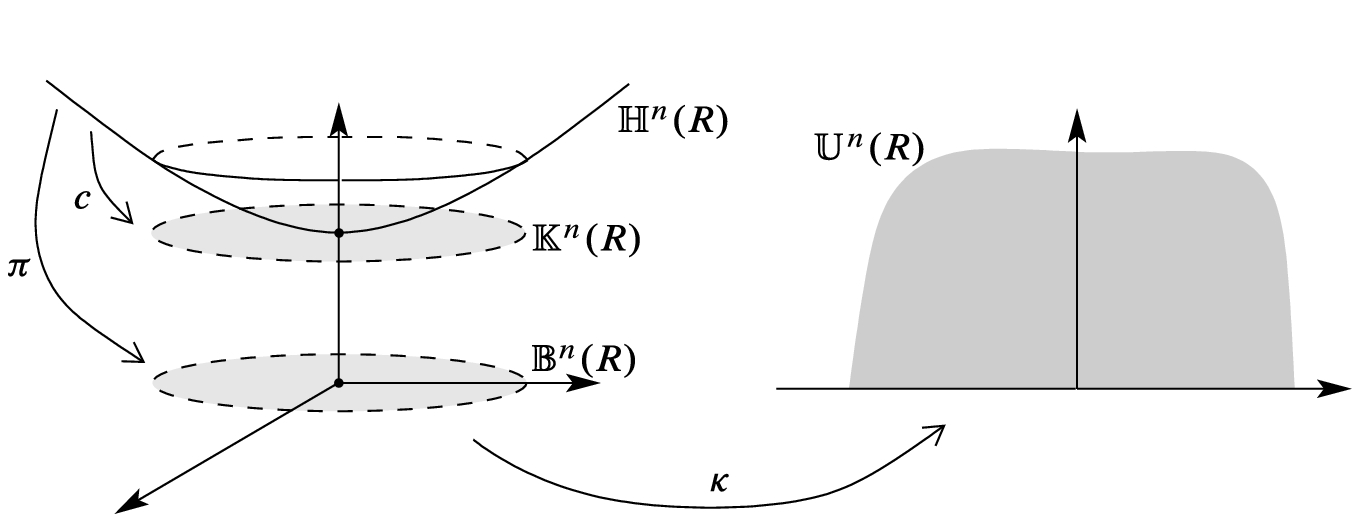
Isometries among the hyperbolic models
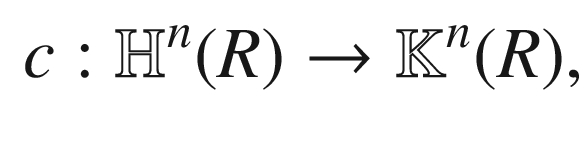
 , set
, set  , where
, where  is the point where the line from the origin to P intersects the hyperplane
is the point where the line from the origin to P intersects the hyperplane  (Fig. 3.4). Because W is characterized as the unique scalar multiple of P whose last coordinate is R, we have
(Fig. 3.4). Because W is characterized as the unique scalar multiple of P whose last coordinate is R, we have  , and therefore c is given by the formula
, and therefore c is given by the formula
Central projection from the hyperboloid to the Beltrami–Klein model
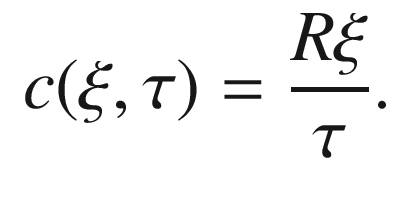
 guarantees that
guarantees that  , so c maps
, so c maps  into
into  . To show that c is a diffeomorphism, we determine its inverse map. Let
. To show that c is a diffeomorphism, we determine its inverse map. Let  be arbitrary. The unique positive scalar
be arbitrary. The unique positive scalar  such that the point
such that the point 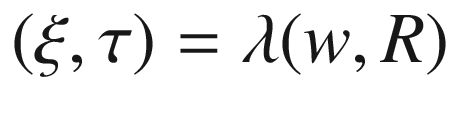 lies on
lies on  is characterized by
is characterized by  , and therefore
, and therefore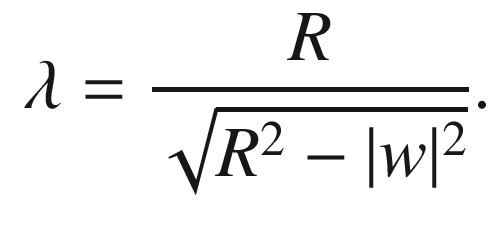

 and
and  , we use the fact that
, we use the fact that  is the metric induced from
is the metric induced from  , analogously to the computation we did for stereographic projection above. With
, analogously to the computation we did for stereographic projection above. With  defined by (3.12), we have
defined by (3.12), we have
 .
.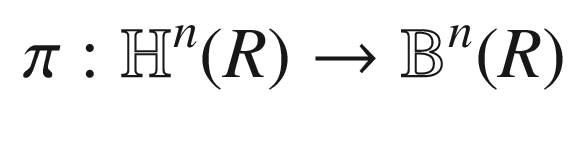
 denote the point
denote the point  . For any
. For any  , set
, set  , where
, where 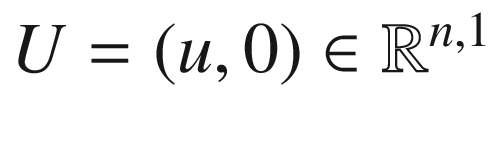 is the point where the line through S and P intersects the hyperplane
is the point where the line through S and P intersects the hyperplane  (Fig. 3.5). The point U is characterized by
(Fig. 3.5). The point U is characterized by  for some nonzero scalar
for some nonzero scalar 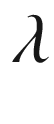 , or
, or
Hyperbolic stereographic projection
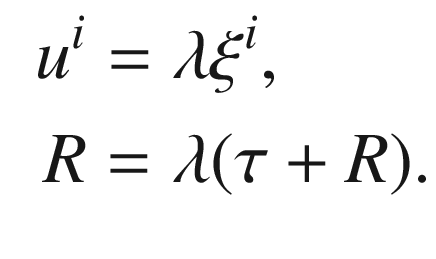
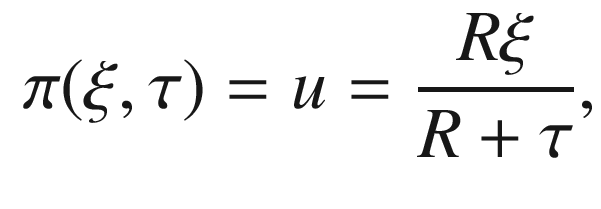
 because
because  . A computation similar to the ones before shows that the inverse map is
. A computation similar to the ones before shows that the inverse map is
 . The computation proceeds just as in the spherical case, so we skip over most of the details:
. The computation proceeds just as in the spherical case, so we skip over most of the details: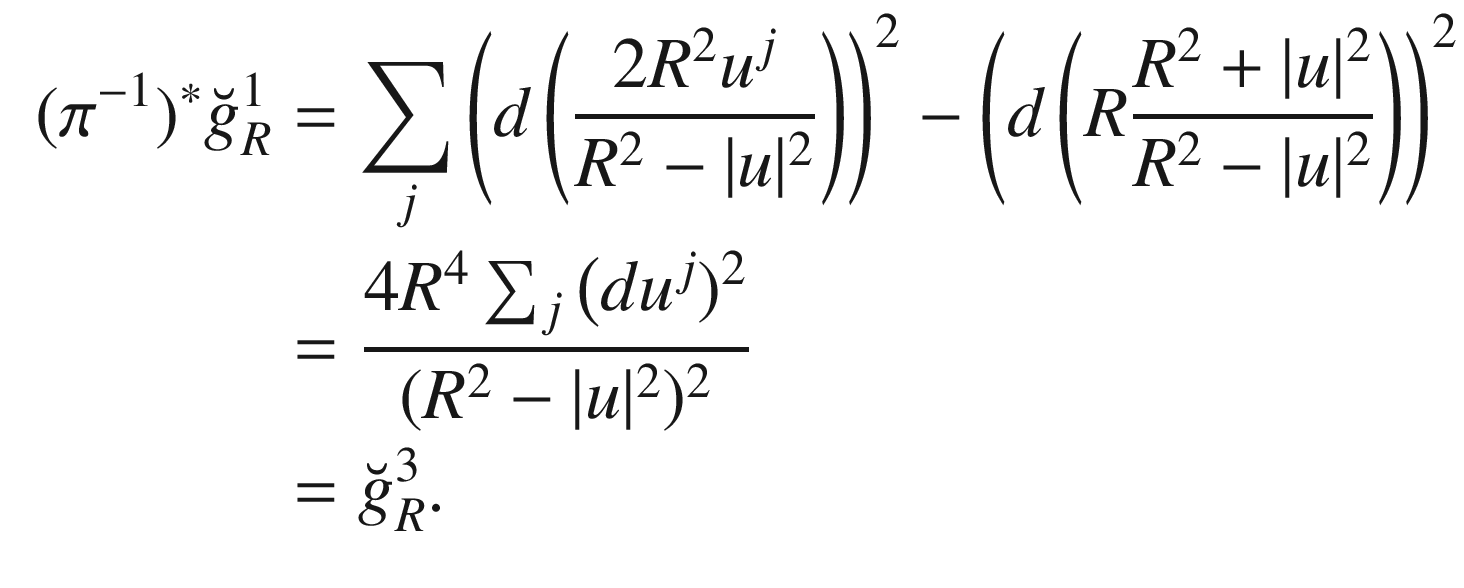

 . In the 2-dimensional case,
. In the 2-dimensional case,  is easy to write down in complex notation
is easy to write down in complex notation  and
and  . It is a variant of the classical Cayley transform:
. It is a variant of the classical Cayley transform: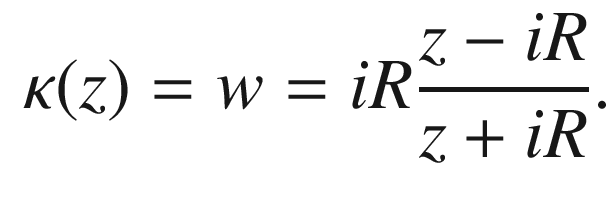
 onto
onto  . Separating z into real and imaginary parts, we can also write this in real terms as
. Separating z into real and imaginary parts, we can also write this in real terms as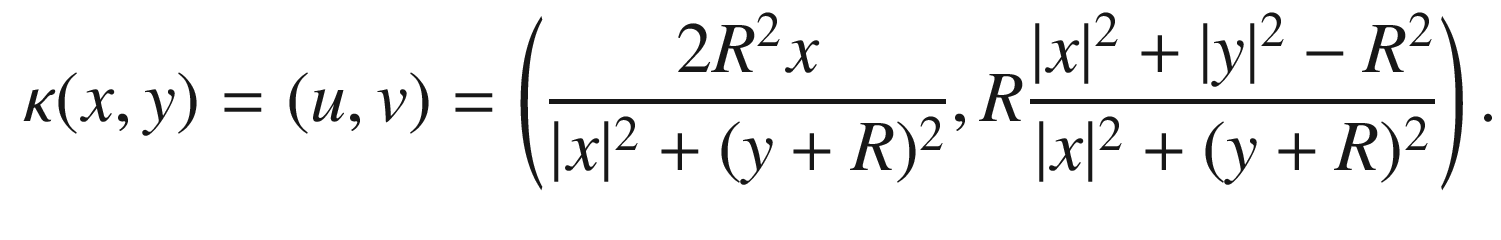
 , and it is easy to check that it maps the upper half-space
, and it is easy to check that it maps the upper half-space  into the ball of radius R. A direct computation shows that its inverse is
into the ball of radius R. A direct computation shows that its inverse is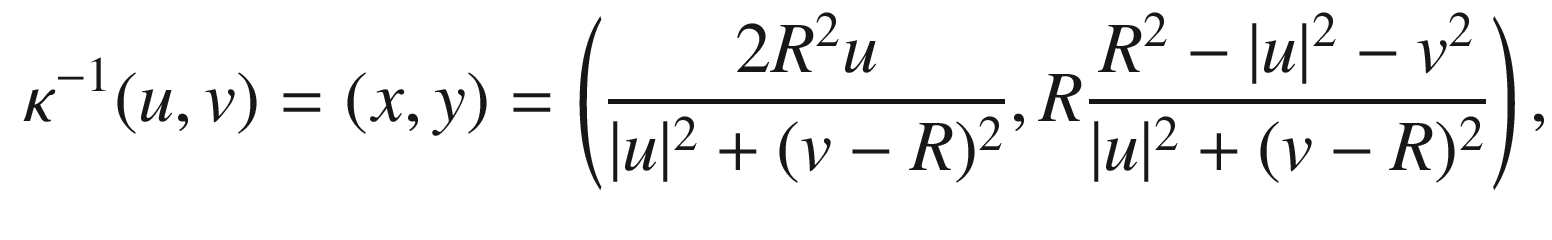
 is a diffeomorphism, called the generalized Cayley transform. The verification that
is a diffeomorphism, called the generalized Cayley transform. The verification that  is basically a long calculation, and is left to Problem 3-4.
is basically a long calculation, and is left to Problem 3-4. 
We often use the generic notation
 to refer to any one of the Riemannian manifolds of Theorem 3.7, and
to refer to any one of the Riemannian manifolds of Theorem 3.7, and  to refer to the corresponding metric; the special case
to refer to the corresponding metric; the special case  is denoted by
is denoted by
 and is called simply hyperbolic space, or in the 2-dimensional case, the hyperbolic plane.
and is called simply hyperbolic space, or in the 2-dimensional case, the hyperbolic plane.
Because all of the models for a given value of R are isometric to each other, when analyzing them geometrically we can use whichever model is most convenient for the application we have in mind. The next corollary is an example in which the Poincaré ball and half-space models serve best.
Corollary 3.8.
Each hyperbolic space is locally conformally flat.
Proof.
In either the Poincaré ball model or the half-space model, the identity map gives a global conformal equivalence with an open subset of Euclidean space. 
The examples presented so far might give the impression that most Riemannian manifolds are locally conformally flat. This is far from the truth, but we do not yet have the tools to prove it. See Problem 8-25 for some explicit examples of Riemannian manifolds that are not locally conformally flat.
The symmetries of  are most easily seen in the hyperboloid model. Let
are most easily seen in the hyperboloid model. Let  denote the group of linear maps from
denote the group of linear maps from  to itself that preserve the Minkowski metric, called the
to itself that preserve the Minkowski metric, called the  -dimensional Lorentz group. Note that each element of
-dimensional Lorentz group. Note that each element of  preserves the hyperboloid
preserves the hyperboloid  , which has two components determined by
, which has two components determined by  and
and  . We let
. We let  denote the subgroup of
denote the subgroup of  consisting of maps that take the
consisting of maps that take the  component of the hyperboloid to itself. (This is called the orthochronous Lorentz group, because physically it represents coordinate changes that preserve the forward time direction.) Then
component of the hyperboloid to itself. (This is called the orthochronous Lorentz group, because physically it represents coordinate changes that preserve the forward time direction.) Then  preserves
preserves  , and because it preserves
, and because it preserves  it acts isometrically on
it acts isometrically on  . (Problem 5-11 will show that this is the full isometry group.) Recall that
. (Problem 5-11 will show that this is the full isometry group.) Recall that  denotes the set of all orthonormal bases for all tangent spaces of
denotes the set of all orthonormal bases for all tangent spaces of  .
.
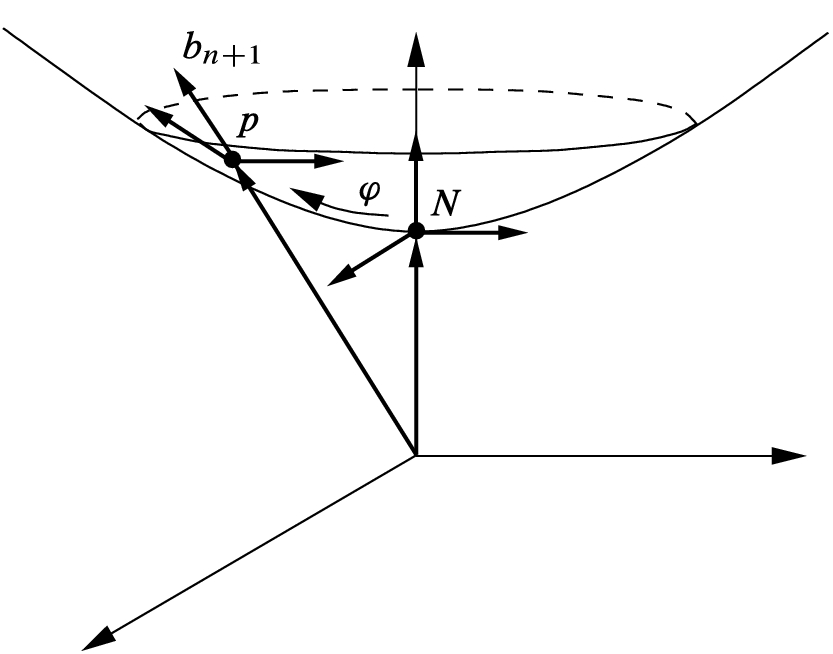
Proposition 3.9.
The group  acts transitively on
acts transitively on  , and therefore
, and therefore  is frame-homogeneous.
is frame-homogeneous.
Proof.
 and
and  is an orthonormal basis for
is an orthonormal basis for  . Identifying
. Identifying  with an element of
with an element of  in the usual way, we can regard
in the usual way, we can regard  as a
as a  -unit vector in
-unit vector in  , and (3.10) shows that it is a scalar multiple of the
, and (3.10) shows that it is a scalar multiple of the  -gradient of the defining function f and thus is orthogonal to
-gradient of the defining function f and thus is orthogonal to  with respect to
with respect to  . Thus
. Thus  is a
is a  -orthonormal basis for
-orthonormal basis for  , and
, and  has the following expression in terms of the dual basis
has the following expression in terms of the dual basis  :
: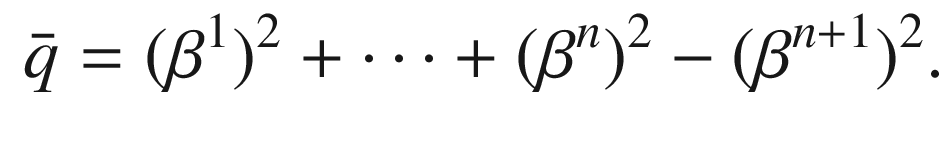
 is an element of
is an element of  sending
sending  to p and
to p and  to
to  (Fig. 3.6).
(Fig. 3.6). 
Frame homogeneity of 
Invariant Metrics on Lie Groups
Lie groups provide us with another large class of homogeneous Riemannian manifolds. (See Appendix C for a review of the basic facts about Lie groups that we will use.)
Let G be a Lie group. A Riemannian metric g on G is said to be left-invariant if it is invariant under all left translations:  for all
for all  . Similarly, g is right-invariant if it is invariant under all right translations, and bi-invariant if it is both left- and right-invariant. The next lemma shows that left-invariant metrics are easy to come by.
. Similarly, g is right-invariant if it is invariant under all right translations, and bi-invariant if it is both left- and right-invariant. The next lemma shows that left-invariant metrics are easy to come by.
Lemma 3.10.
Let G be a Lie group and let  be its Lie algebra of left-invariant vector fields.
be its Lie algebra of left-invariant vector fields.
- (a)
A Riemannian metric g on G is left-invariant if and only if for all
 , the function g(X, Y) is constant on G.
, the function g(X, Y) is constant on G. - (b)
The restriction map
 together with the natural identification
together with the natural identification  gives a bijection between left-invariant Riemannian metrics on G and inner products on
gives a bijection between left-invariant Riemannian metrics on G and inner products on  .
.
 Exercise 3.11. Prove the preceding lemma.
Exercise 3.11. Prove the preceding lemma.
Thus all we need to do to construct a left-invariant metric is choose any inner product on  , and define a metric on G by applying that inner product to left-invariant vector fields. Right-invariant metrics can be constructed in a similar way using right-invariant vector fields. Since a Lie group acts transitively on itself by either left or right translation, every left-invariant or right-invariant metric is homogeneous.
, and define a metric on G by applying that inner product to left-invariant vector fields. Right-invariant metrics can be constructed in a similar way using right-invariant vector fields. Since a Lie group acts transitively on itself by either left or right translation, every left-invariant or right-invariant metric is homogeneous.
Much more interesting are the bi-invariant metrics, because, as you will be able to prove later (Problems 7-13 and 8-17), their curvatures are intimately related to the structure of the Lie algebra of the group. But bi-invariant metrics are generally much rarer than left-invariant or right-invariant ones; in fact, some Lie groups have no bi-invariant metrics at all (see Problems 3-12 and 3-13). Fortunately, there is a complete answer to the question of which Lie groups admit bi-invariant metrics, which we present in this section.
We begin with a proposition that shows how to determine whether a given left-invariant metric is bi-invariant, based on properties of the adjoint representation of the group. Recall that this is the representation  given by
given by  , where
, where  is the automorphism defined by conjugation:
is the automorphism defined by conjugation:  . See Appendix C for more details.
. See Appendix C for more details.
Proposition 3.12.
Let G be a Lie group and  its Lie algebra. Suppose g is a left-invariant Riemannian metric on G, and let
its Lie algebra. Suppose g is a left-invariant Riemannian metric on G, and let  denote the corresponding inner product on
denote the corresponding inner product on  as in Lemma 3.10. Then g is bi-invariant if and only if
as in Lemma 3.10. Then g is bi-invariant if and only if  is invariant under the action of
is invariant under the action of  , in the sense that
, in the sense that  for all
for all  and
and  .
.
Proof.
 is the associated inner product on
is the associated inner product on  . Let
. Let  be arbitrary, and note that
be arbitrary, and note that  is the composition of left multiplication by
is the composition of left multiplication by  followed by right multiplication by
followed by right multiplication by 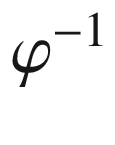 . Thus for every
. Thus for every  , left-invariance implies
, left-invariance implies  . Therefore, for all
. Therefore, for all 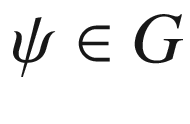 and
and  , we have
, we have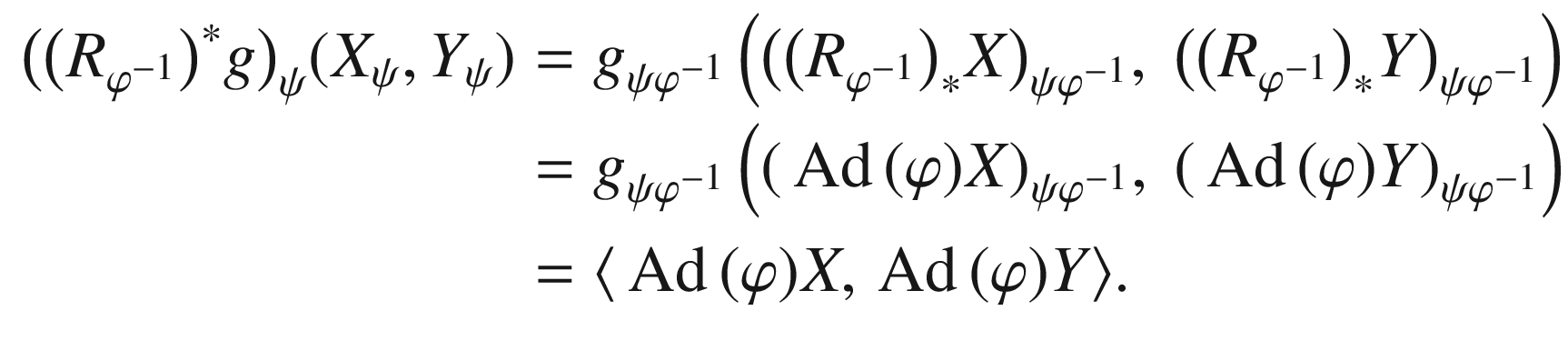
 is invariant under
is invariant under  . Then the expression on the last line above is equal to
. Then the expression on the last line above is equal to  , which shows that
, which shows that  . Since this is true for all
. Since this is true for all  , it follows that g is bi-invariant.
, it follows that g is bi-invariant. for each
for each  , so the above computation yields
, so the above computation yields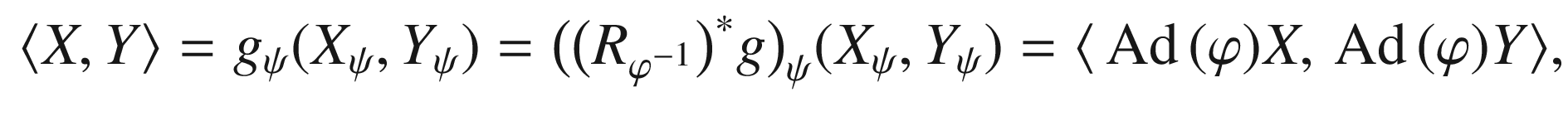
 is
is  -invariant.
-invariant. 
In order to apply the preceding proposition, we need a lemma about finding invariant inner products on vector spaces. Recall from Appendix C that for every finite-dimensional real vector space V,  denotes the Lie group of all invertible linear maps from V to itself. If H is a subgroup of
denotes the Lie group of all invertible linear maps from V to itself. If H is a subgroup of  , an inner product
, an inner product  on V is said to be
on V is said to be  -invariant if
-invariant if  for all
for all  and
and  .
.
Lemma 3.13.
Suppose V is a finite-dimensional real vector space and H is a subgroup of  . There exists an H-invariant inner product on V if and only if H has compact closure in
. There exists an H-invariant inner product on V if and only if H has compact closure in  .
.
Proof.
Assume first that there exists an H-invariant inner product  on V. This implies that H is contained in the subgroup
on V. This implies that H is contained in the subgroup  consisting of linear isomorphisms of V that are orthogonal with respect to this inner product. Choosing an orthonormal basis of V yields a Lie group isomorphism between
consisting of linear isomorphisms of V that are orthogonal with respect to this inner product. Choosing an orthonormal basis of V yields a Lie group isomorphism between  and
and  (where
(where  ), so
), so  is compact; and the closure of H is a closed subset of this compact group, and thus is itself compact.
is compact; and the closure of H is a closed subset of this compact group, and thus is itself compact.
 , and let K denote the closure. A simple limiting argument shows that K is itself a subgroup, and thus it is a Lie group by the closed subgroup theorem (Thm. C.8). Let
, and let K denote the closure. A simple limiting argument shows that K is itself a subgroup, and thus it is a Lie group by the closed subgroup theorem (Thm. C.8). Let  be an arbitrary inner product on V, and let
be an arbitrary inner product on V, and let 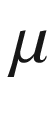 be a right-invariant volume form on K (for example, the volume form of some right-invariant metric on K). For fixed
be a right-invariant volume form on K (for example, the volume form of some right-invariant metric on K). For fixed  , define a smooth function
, define a smooth function  by
by  . Then define a new inner product
. Then define a new inner product  on V by
on V by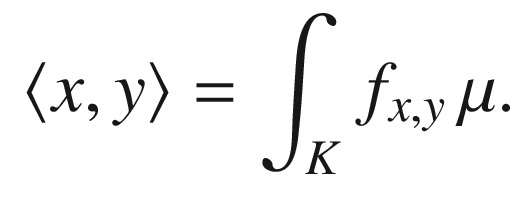
 is symmetric and bilinear over
is symmetric and bilinear over  . For each nonzero
. For each nonzero  , we have
, we have  everywhere on K, so
everywhere on K, so  , showing that
, showing that  is indeed an inner product.
is indeed an inner product. be arbitrary. Then for all
be arbitrary. Then for all  and
and  , we have
, we have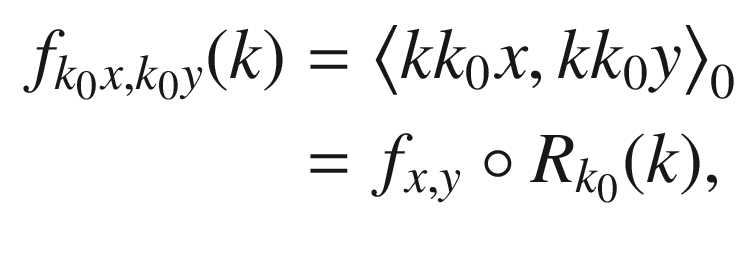
 is right translation by
is right translation by  . Because
. Because  is right-invariant, it follows from diffeomorphism invariance of the integral that
is right-invariant, it follows from diffeomorphism invariance of the integral that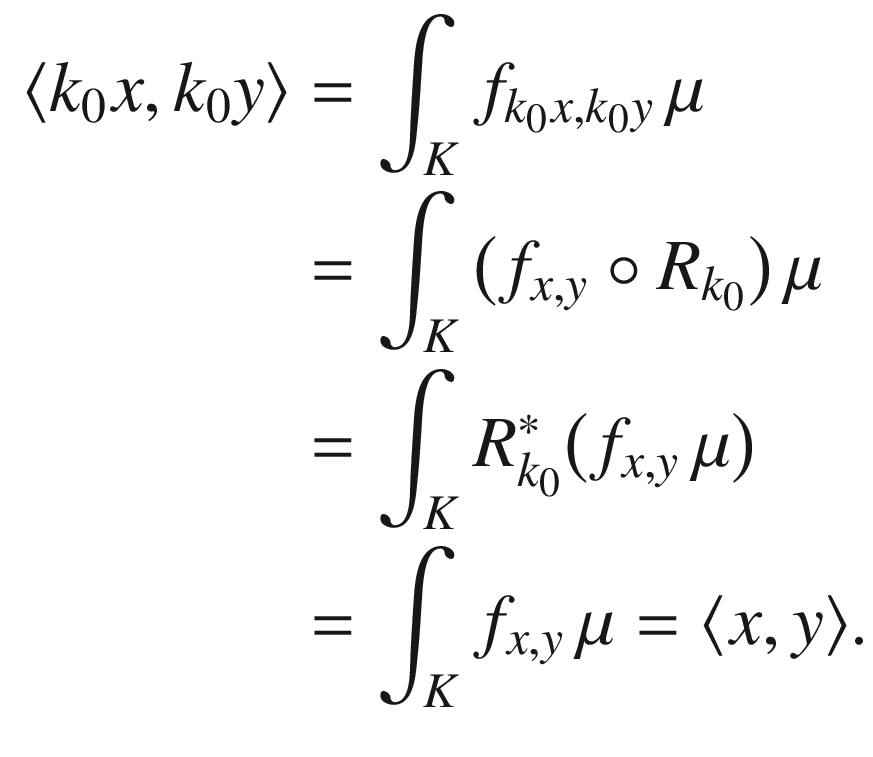
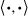 is K-invariant, and it is also H-invariant because
is K-invariant, and it is also H-invariant because  .
. 
Theorem 3.14
(Existence of Bi-invariant Metrics). Let G be a Lie group and  its Lie algebra. Then G admits a bi-invariant metric if and only if
its Lie algebra. Then G admits a bi-invariant metric if and only if  has compact closure in
has compact closure in  .
.
Proof.
Proposition 3.12 shows that there is a bi-invariant metric on G if and only if there is an  -invariant inner product on
-invariant inner product on  , and Lemma 3.13 in turn shows that the latter is true if and only if
, and Lemma 3.13 in turn shows that the latter is true if and only if  has compact closure in
has compact closure in  .
. 
The most important application of the preceding theorem is to compact groups.
Corollary 3.15.
Every compact Lie group admits a bi-invariant Riemannian metric.
Proof.
If G is compact, then  is a compact subgroup of
is a compact subgroup of  because
because  is continuous.
is continuous. 
Another important application is to prove that certain Lie groups do not admit bi-invariant metrics. One way to do this is to note that if  has compact closure in
has compact closure in  , then every orbit of
, then every orbit of  must be a bounded subset of
must be a bounded subset of  with respect to any choice of norm, because it is contained in the image of the compact set
with respect to any choice of norm, because it is contained in the image of the compact set  under a continuous map of the form
under a continuous map of the form  from
from  to
to  . Thus if one can find an element
. Thus if one can find an element  and a subset
and a subset  such that the elements of the form
such that the elements of the form  are unbounded in
are unbounded in  for
for  , then there is no bi-invariant metric.
, then there is no bi-invariant metric.
Here are some examples.
Example 3.16
- (a)
Every left-invariant metric on an abelian Lie group is bi-invariant, because the adjoint representation is trivial. Thus the Euclidean metric on
 and the flat metric on
and the flat metric on  of Example 2.21 are both bi-invariant.
of Example 2.21 are both bi-invariant. - (b)
If a metric g on a Lie group G is left-invariant, then the induced metric on every Lie subgroup
 is easily seen to be left-invariant. Similarly, if g is bi-invariant, then the induced metric on H is bi-invariant.
is easily seen to be left-invariant. Similarly, if g is bi-invariant, then the induced metric on H is bi-invariant. - (c)
The Lie group
 (the group of
(the group of  real matrices of determinant 1) admits many left-invariant metrics (as does every positive-dimensional Lie group), but no bi-invariant ones. To see this, recall that the Lie algebra of
real matrices of determinant 1) admits many left-invariant metrics (as does every positive-dimensional Lie group), but no bi-invariant ones. To see this, recall that the Lie algebra of  is isomorphic to the algebra
is isomorphic to the algebra  of trace-free
of trace-free  matrices, and the adjoint representation is given by
matrices, and the adjoint representation is given by  (see Example C.10). If we let
(see Example C.10). If we let  and
and  for
for  , then
, then  , which is unbounded as
, which is unbounded as  . Thus the orbit of
. Thus the orbit of  is not contained in any compact subset, which implies that there is no bi-invariant metric on
is not contained in any compact subset, which implies that there is no bi-invariant metric on  . A similar argument shows that
. A similar argument shows that  admits no bi-invariant metric for any
admits no bi-invariant metric for any  . In view of (b) above, this shows also that
. In view of (b) above, this shows also that  admits no bi-invariant metric for
admits no bi-invariant metric for  . (Of course,
. (Of course,  does admit bi-invariant metrics because it is abelian.)
does admit bi-invariant metrics because it is abelian.) - (e)With
 regarded as a submanifold of
regarded as a submanifold of  , the map gives a diffeomorphism from
, the map gives a diffeomorphism from (3.16)
(3.16) to
to  . Under the inverse of this map, the round metric on
. Under the inverse of this map, the round metric on  pulls back to a bi-invariant metric on
pulls back to a bi-invariant metric on  , as Problem 3-10 shows.
, as Problem 3-10 shows. - (e)Let
 denote the Lie algebra of
denote the Lie algebra of  , identified with the algebra of skew-symmetric
, identified with the algebra of skew-symmetric  matrices, and define a bilinear form on
matrices, and define a bilinear form on  by This is an
by This is an
 -invariant inner product, and thus determines a bi-invariant Riemannian metric on
-invariant inner product, and thus determines a bi-invariant Riemannian metric on  (see Problem 3-11).
(see Problem 3-11). - (f)
- (g)For
 , the
, the  -dimensional Heisenberg group is the Lie subgroup
-dimensional Heisenberg group is the Lie subgroup  defined by where x and y are treated as column matrices. These are the simplest examples of nilpotent Lie groups, meaning that the series of subgroups
defined by where x and y are treated as column matrices. These are the simplest examples of nilpotent Lie groups, meaning that the series of subgroups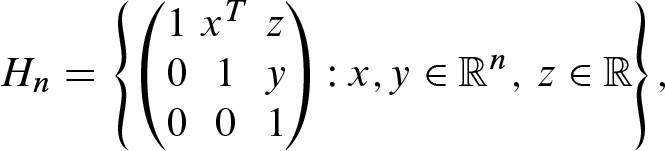
![$$G\supseteq [G,G] \supseteq [G,[G, G]] \supseteq \cdots $$](../images/56724_2_En_3_Chapter/56724_2_En_3_Chapter_TeX_IEq453.png) eventually reaches the trivial subgroup (where for any subgroups
eventually reaches the trivial subgroup (where for any subgroups  , the notation
, the notation ![$$[G_1,G_2]$$](../images/56724_2_En_3_Chapter/56724_2_En_3_Chapter_TeX_IEq456.png) means the subgroup of G generated by all elements of the form
means the subgroup of G generated by all elements of the form  for
for  ). There are many left-invariant metrics on
). There are many left-invariant metrics on  , but no bi-invariant ones, as Problem 3-13 shows.
, but no bi-invariant ones, as Problem 3-13 shows. - (h)Our last example is a group that plays an important role in the classification of 3-manifolds. Let
 denote the following 3-dimensional Lie subgroup of
denote the following 3-dimensional Lie subgroup of  : This group is the simplest nonnilpotent example of a solvable Lie group, meaning that the series of subgroups
: This group is the simplest nonnilpotent example of a solvable Lie group, meaning that the series of subgroups
![$$G\supseteq [G,G] \supseteq [[G,G],[G, G]] \supseteq \cdots $$](../images/56724_2_En_3_Chapter/56724_2_En_3_Chapter_TeX_IEq463.png) eventually reaches the trivial subgroup. Like the Heisenberg groups,
eventually reaches the trivial subgroup. Like the Heisenberg groups,  admits left-invariant metrics but not bi-invariant ones (Problem 3-14). //
admits left-invariant metrics but not bi-invariant ones (Problem 3-14). //
In fact, John Milnor showed in 1976 [Mil76] that the only Lie groups that admit bi-invariant metrics are those that are isomorphic to direct products of compact groups and abelian groups.
Other Homogeneous Riemannian Manifolds
There are many homogeneous Riemannian manifolds besides the frame-homogeneous ones and the Lie groups with invariant metrics. To identify other examples, it is natural to ask the following question: If M is a smooth manifold endowed with a smooth, transitive action by a Lie group G (called a homogeneous G-space or just a homogeneous space), is there a Riemannian metric on M that is invariant under the group action?
The next theorem gives a necessary and sufficient condition for existence of an invariant Riemannian metric that is usually easy to check.
Theorem 3.17
(Existence of Invariant Metrics on Homogeneous Spaces). Suppose G is a Lie group and M is a homogeneous G-space. Let  be a point in M, and let
be a point in M, and let  denote the isotropy representation at
denote the isotropy representation at  . There exists a G-invariant Riemannian metric on M if and only if
. There exists a G-invariant Riemannian metric on M if and only if  has compact closure in
has compact closure in  .
.
Proof.
Assume first that g is a G-invariant metric on M. Then the inner product  on
on  is invariant under the isotropy representation, so it follows from Lemma 3.13 that
is invariant under the isotropy representation, so it follows from Lemma 3.13 that  has compact closure in
has compact closure in  .
.
 has compact closure in
has compact closure in  . Lemma 3.13 shows that there is an inner product
. Lemma 3.13 shows that there is an inner product  on
on  that is invariant under the isotropy representation. For arbitrary
that is invariant under the isotropy representation. For arbitrary  , we define an inner product
, we define an inner product  on
on  by choosing an element
by choosing an element  such that
such that  and setting
and setting
 are any two such elements of G, then
are any two such elements of G, then  with
with  , so
, so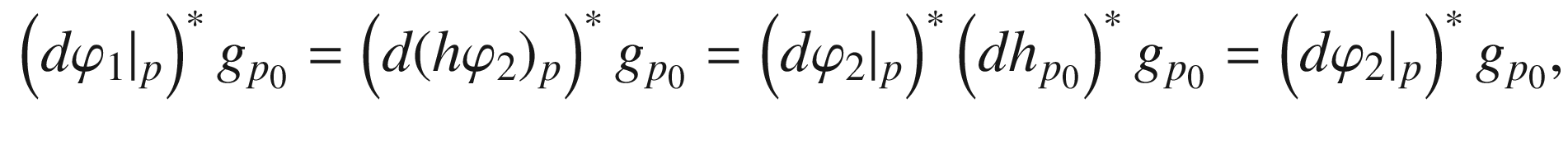
 given by
given by  is a smooth surjection because the action is smooth and transitive. Given
is a smooth surjection because the action is smooth and transitive. Given  , if we let
, if we let  denote the map
denote the map  and
and  the left translation by
the left translation by  , then the map
, then the map  satisfies
satisfies
 on G by
on G by  . (It will typically not be positive definite, because
. (It will typically not be positive definite, because 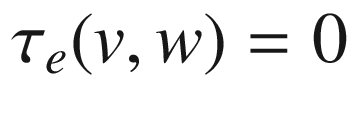 if either v or w is tangent to the isotropy group
if either v or w is tangent to the isotropy group  and thus in the kernel of
and thus in the kernel of  .) For all
.) For all  , (3.17) implies
, (3.17) implies
 is a left-invariant tensor field on G. Every basis
is a left-invariant tensor field on G. Every basis  for the Lie algebra of G forms a smooth global left-invariant frame for G, and with respect to such a frame the components
for the Lie algebra of G forms a smooth global left-invariant frame for G, and with respect to such a frame the components 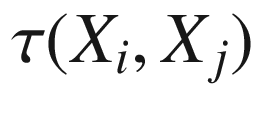 are constant; thus
are constant; thus  is a smooth tensor field on G.
is a smooth tensor field on G. , the fact that
, the fact that  is a surjective smooth submersion implies that there exist a neighborhood U of p and a smooth local section
is a surjective smooth submersion implies that there exist a neighborhood U of p and a smooth local section  (Thm. A.17). Then
(Thm. A.17). Then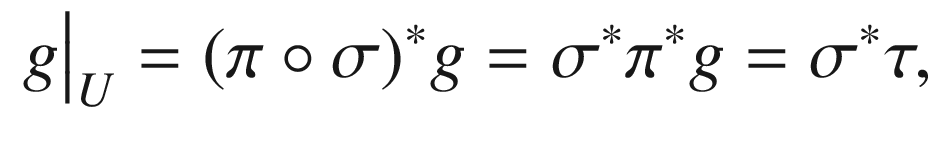

The next corollary, which follows immediately from Theorem 3.17, addresses the most commonly encountered case. (Other necessary and sufficient conditions for the existence of invariant metrics are given in [Poo81, 6.58–6.59].)
Corollary 3.18.
If a Lie group G acts smoothly and transitively on a smooth manifold M with compact isotropy groups, then there exists a G-invariant Riemannian metric on M. 
 Exercise 3.19. Suppose G is a Lie group and M is a homogeneous G-space that admits at least one g-invariant metric. Show that for each
Exercise 3.19. Suppose G is a Lie group and M is a homogeneous G-space that admits at least one g-invariant metric. Show that for each  , the map
, the map  gives a bijection between G-invariant metrics on M and
gives a bijection between G-invariant metrics on M and  -invariant inner products on
-invariant inner products on  .
.
Locally Homogeneous Riemannian Manifolds
A Riemannian manifold (M, g) is said to be locally homogeneous if for every pair of points  there is a Riemannian isometry from a neighborhood of p to a neighborhood of q that takes p to q. Similarly, we say that (M, g) is locally frame-homogeneous if for every
there is a Riemannian isometry from a neighborhood of p to a neighborhood of q that takes p to q. Similarly, we say that (M, g) is locally frame-homogeneous if for every  and every pair of orthonormal bases
and every pair of orthonormal bases  for
for  and
and  for
for  , there is an isometry from a neighborhood of p to a neighborhood of q that takes p to q, and whose differential takes
, there is an isometry from a neighborhood of p to a neighborhood of q that takes p to q, and whose differential takes  to
to  for each i.
for each i.
Every homogeneous Riemannian manifold is locally homogeneous, and every frame-homogeneous one is locally frame-homogeneous. Every proper open subset of a homogeneous or frame-homogeneous Riemannian manifold is locally homogeneous or locally frame-homogeneous, respectively. More interesting examples arise in the following way.
Proposition 3.20.
Suppose  is a homogeneous Riemannian manifold, (M, g) is a Riemannian manifold, and
is a homogeneous Riemannian manifold, (M, g) is a Riemannian manifold, and  is a Riemannian covering. Then (M, g) is locally homogeneous. If
is a Riemannian covering. Then (M, g) is locally homogeneous. If  is frame-homogeneous, then (M, g) is locally frame-homogeneous.
is frame-homogeneous, then (M, g) is locally frame-homogeneous.
 Exercise 3.21. Prove this proposition.
Exercise 3.21. Prove this proposition.
Locally homogeneous Riemannian metrics play an important role in classification theorems for manifolds, especially in low dimensions. The most fundamental case is that of compact 2-manifolds, for which we have the following important theorem.
Theorem 3.22
(Uniformization of Compact Surfaces). Every compact, connected, smooth 2-manifold admits a locally frame-homogeneous Riemannian metric, and a Riemannian covering by the Euclidean plane, hyperbolic plane, or round unit sphere.
Sketch of proof. The proof relies on the topological classification of compact surfaces (see, for example, [LeeTM, Thms. 6.15 and 10.22]), which says that every connected compact surface is homeomorphic to a sphere, a connected sum of one or more tori, or a connected sum of one or more projective planes. The crux of the proof is showing that each of the model surfaces on this list has a metric that admits a Riemannian covering by one of the model frame-homogeneous manifolds, and therefore is locally frame-homogeneous by Proposition 3.20. We consider each model surface in turn.
The 2-sphere:  , of course, has its round metric, and the identity map is a Riemannian covering.
, of course, has its round metric, and the identity map is a Riemannian covering.
The 2-torus: Exercise 2.36 shows that the flat metric on  described in Example 2.21 admits a Riemannian covering by
described in Example 2.21 admits a Riemannian covering by  .
.
 copies of
copies of  : It is shown in [LeeTM, Example 6.13] that such a surface is homeomorphic to a quotient of a regular 4n-sided polygonal region by side identifications indicated schematically by the sequence of labels
: It is shown in [LeeTM, Example 6.13] that such a surface is homeomorphic to a quotient of a regular 4n-sided polygonal region by side identifications indicated schematically by the sequence of labels  (Fig. 3.7 illustrates the case
(Fig. 3.7 illustrates the case  ). Let
). Let 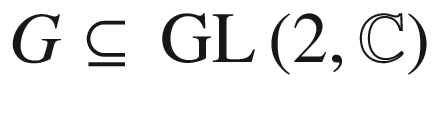 be the following subgroup:
be the following subgroup:
A connected sum of tori

Constructing a Riemannian covering

 , there is a discrete subgroup
, there is a discrete subgroup  such that the quotient map
such that the quotient map  is a covering map, and
is a covering map, and  is homeomorphic to a connected sum of n tori. The group is found by first identifying a compact region
is homeomorphic to a connected sum of n tori. The group is found by first identifying a compact region  bounded by a “regular geodesic polygon," which is a union of 4n congruent circular arcs making interior angles that all measure exactly
bounded by a “regular geodesic polygon," which is a union of 4n congruent circular arcs making interior angles that all measure exactly  , so that 4n of them fit together locally to fill out a neighborhood of a point (see Fig. 3.8). (The name “geodesic polygon" reflects the fact that these circular arcs are segments of geodesics with respect to the hyperbolic metric, as we will see in Chapter 5.) Then
, so that 4n of them fit together locally to fill out a neighborhood of a point (see Fig. 3.8). (The name “geodesic polygon" reflects the fact that these circular arcs are segments of geodesics with respect to the hyperbolic metric, as we will see in Chapter 5.) Then  is the group generated by certain elements of G that take an edge with a label
is the group generated by certain elements of G that take an edge with a label  or
or  to the other edge with the same label. Because
to the other edge with the same label. Because  acts isometrically, it follows that such a connected sum admits a locally frame-homogeneous metric and a Riemannian covering by the Poincaré disk. For details, see the proofs of Theorems 12.29 and 12.30 of [LeeTM].
acts isometrically, it follows that such a connected sum admits a locally frame-homogeneous metric and a Riemannian covering by the Poincaré disk. For details, see the proofs of Theorems 12.29 and 12.30 of [LeeTM].The projective plane: Example 2.34 shows that  has a metric that admits a 2-sheeted Riemannian covering by
has a metric that admits a 2-sheeted Riemannian covering by  .
.
 : It is shown in [LeeTM, Lemma 6.16] that
: It is shown in [LeeTM, Lemma 6.16] that  is homeomorphic to the Klein bottle, which is the quotient space of the unit square
is homeomorphic to the Klein bottle, which is the quotient space of the unit square ![$$[0,1]\times [0,1]$$](../images/56724_2_En_3_Chapter/56724_2_En_3_Chapter_TeX_IEq548.png) by the equivalence relation generated by the following relations (see Fig. 3.9):
by the equivalence relation generated by the following relations (see Fig. 3.9):
The Klein bottle

Connected sum of three projective planes

 be the Euclidean group in two dimensions as defined earlier in this chapter, and let
be the Euclidean group in two dimensions as defined earlier in this chapter, and let  be the subgroup defined by
be the subgroup defined by
 acts freely and properly on
acts freely and properly on  , and every
, and every  -orbit has a representative in the unit square such that two points in the square are in the same orbit if and only if they satisfy the equivalence relation generated by the relations in (3.19). Thus the orbit space
-orbit has a representative in the unit square such that two points in the square are in the same orbit if and only if they satisfy the equivalence relation generated by the relations in (3.19). Thus the orbit space  is homeomorphic to the Klein bottle, and since the group action is isometric, it follows that the Klein bottle inherits a flat, locally frame-homogeneous metric and the quotient map is a Riemannian covering. Problem 3-18 asks you to work out the details.
is homeomorphic to the Klein bottle, and since the group action is isometric, it follows that the Klein bottle inherits a flat, locally frame-homogeneous metric and the quotient map is a Riemannian covering. Problem 3-18 asks you to work out the details.A connected sum of  copies of
copies of  : Such a surface is homeomorphic to a quotient of a regular 2n-sided polygonal region by side identifications according to
: Such a surface is homeomorphic to a quotient of a regular 2n-sided polygonal region by side identifications according to  [LeeTM, Example 6.13]. As in the case of a connected sum of tori, there is a compact region
[LeeTM, Example 6.13]. As in the case of a connected sum of tori, there is a compact region  bounded by a 2n-sided regular geodesic polygon whose interior angles are all
bounded by a 2n-sided regular geodesic polygon whose interior angles are all  (see Fig. 3.10), and there is a discrete group of isometries that realizes the appropriate side identifications and yields a quotient homeomorphic to the connected sum. The new ingredient here is that because such a connected sum is not orientable, we must work with the full group of isometries of
(see Fig. 3.10), and there is a discrete group of isometries that realizes the appropriate side identifications and yields a quotient homeomorphic to the connected sum. The new ingredient here is that because such a connected sum is not orientable, we must work with the full group of isometries of  , not just the (orientation-preserving) ones determined by elements of G; but otherwise the argument is essentially the same as the one for connected sums of tori. The details can be found in [Ive92, Section VII.1].
, not just the (orientation-preserving) ones determined by elements of G; but otherwise the argument is essentially the same as the one for connected sums of tori. The details can be found in [Ive92, Section VII.1].
There is one remaining step. The arguments above show that each compact topological 2-manifold possesses a smooth structure and a locally frame-homogeneous Riemannian metric, which admits a Riemannian covering by one of the three frame-homogeneous model spaces. However, we started with a smooth compact 2-manifold, and we are looking for a Riemannian metric that is smooth with respect to the given smooth structure. To complete the proof, we appeal to a result by James Munkres [Mun56], which shows that any two smooth structures on a 2-manifold are related by a diffeomorphism; thus after pulling back the metric by this diffeomorphism, we obtain a locally frame-homogeneous metric on M with its originally given smooth structure. 
 with the Euclidean metric
with the Euclidean metric with a round metric
with a round metric with a hyperbolic metric
with a hyperbolic metric with a product of a round metric and the Euclidean metric
with a product of a round metric and the Euclidean metric with a product of a hyperbolic metric and the Euclidean metric
with a product of a hyperbolic metric and the Euclidean metricThe Heisenberg group
 of Example 3.16(g) with a left-invariant metric
of Example 3.16(g) with a left-invariant metricThe group
 of Example 3.16(h) with a left-invariant metric
of Example 3.16(h) with a left-invariant metricThe universal covering group of
 with a left-invariant metric
with a left-invariant metric
The Thurston geometrization conjecture was proved in 2003 by Grigori Perelman. The proof is described in several books [BBBMP, KL08, MF10, MT14].
Symmetric Spaces
We end this section with a brief introduction to another class of Riemannian manifolds with abundant symmetry, called symmetric spaces. They turn out to be intermediate between frame-homogeneous and homogeneous Riemannian manifolds.
Here is the definition. If (M, g) is a Riemannian manifold and  , a point reflection at p is an isometry
, a point reflection at p is an isometry  that fixes p and satisfies
that fixes p and satisfies  . A Riemannian manifold (M, g) is called a (Riemannian) symmetric space if it is connected and for each
. A Riemannian manifold (M, g) is called a (Riemannian) symmetric space if it is connected and for each  there exists a point reflection at p. (The modifier “Riemannian" is included to distinguish such spaces from other kinds of symmetric spaces that can be defined, such as pseudo-Riemannian symmetric spaces and affine symmetric spaces; since we will be concerned only with Riemannian symmetric spaces, we will sometimes refer to them simply as “symmetric spaces" for brevity.)
there exists a point reflection at p. (The modifier “Riemannian" is included to distinguish such spaces from other kinds of symmetric spaces that can be defined, such as pseudo-Riemannian symmetric spaces and affine symmetric spaces; since we will be concerned only with Riemannian symmetric spaces, we will sometimes refer to them simply as “symmetric spaces" for brevity.)
Although we do not yet have the tools to prove it, we will see later that every Riemannian symmetric space is homogeneous (see Problem 6-19). More generally, (M, g) is called a ( Riemannian) locally symmetric space if each  has a neighborhood U on which there exists an isometry
has a neighborhood U on which there exists an isometry  that is a point reflection at p. Clearly every Riemannian symmetric space is locally symmetric.
that is a point reflection at p. Clearly every Riemannian symmetric space is locally symmetric.
The next lemma can be used to facilitate the verification that a given Riemannian manifold is symmetric.
Lemma 3.23.
If (M, g) is a connected homogeneous Riemannian manifold that possesses a point reflection at one point, then it is symmetric.
Proof.
 be a point reflection at
be a point reflection at  . Given any other point
. Given any other point  , by homogeneity there is an isometry
, by homogeneity there is an isometry  satisfying
satisfying  . Then
. Then  is an isometry that fixes q. Because
is an isometry that fixes q. Because  is linear, it commutes with multiplication by
is linear, it commutes with multiplication by  , so
, so
 is a point reflection at q.
is a point reflection at q. 
Example 3.24
- (a)
Suppose (M, g) is any connected frame-homogeneous Riemannian manifold. Then for each
 , we can choose an orthonormal basis
, we can choose an orthonormal basis  for
for  , and frame homogeneity guarantees that there is an isometry
, and frame homogeneity guarantees that there is an isometry  that fixes p and sends
that fixes p and sends  to
to  , which implies that
, which implies that  . Thus every frame-homogeneous Riemannian manifold is a symmetric space. In particular, all Euclidean spaces, spheres, and hyperbolic spaces are symmetric.
. Thus every frame-homogeneous Riemannian manifold is a symmetric space. In particular, all Euclidean spaces, spheres, and hyperbolic spaces are symmetric. - (b)Suppose G is a connected Lie group with a bi-invariant Riemannian metric g. If we define
 by
by  , then it is straightforward to check that
, then it is straightforward to check that  for every
for every  , from which it follows that
, from which it follows that  . To see that
. To see that  is an isometry, let
is an isometry, let  be arbitrary. The identity
be arbitrary. The identity  for all
for all  implies that
implies that  , and therefore it follows from bi-invariance of g that Therefore
, and therefore it follows from bi-invariance of g that Therefore
 is an isometry of g and hence a point reflection at e. Lemma 3.23 then implies that (G, g) is a symmetric space.
is an isometry of g and hence a point reflection at e. Lemma 3.23 then implies that (G, g) is a symmetric space. - (c)
The complex projective spaces introduced in Example 2.30 and the Grassmann manifolds introduced in Problem 2-7 are all Riemannian symmetric spaces (see Problems 3-19 and 3-20).
- (d)
Every product of Riemannian symmetric spaces is easily seen to be a symmetric space when endowed with the product metric. A symmetric space is said to be irreducible if it is not isometric to a product of positive-dimensional symmetric spaces. //
Model Pseudo-Riemannian Manifolds
The definitions of the Euclidean, spherical, and hyperbolic metrics can easily be adapted to give analogous classes of frame-homogeneous pseudo-Riemannian manifolds.
The first example is one we have already seen: the pseudo-Euclidean space of signature  is the pseudo-Riemannian manifold
is the pseudo-Riemannian manifold
 , where
, where  is the pseudo-Riemannian metric defined by (2.24).
is the pseudo-Riemannian metric defined by (2.24).
 and the pseudohyperbolic space
and the pseudohyperbolic space  as follows. As manifolds,
as follows. As manifolds,
 and
and  are defined by
are defined by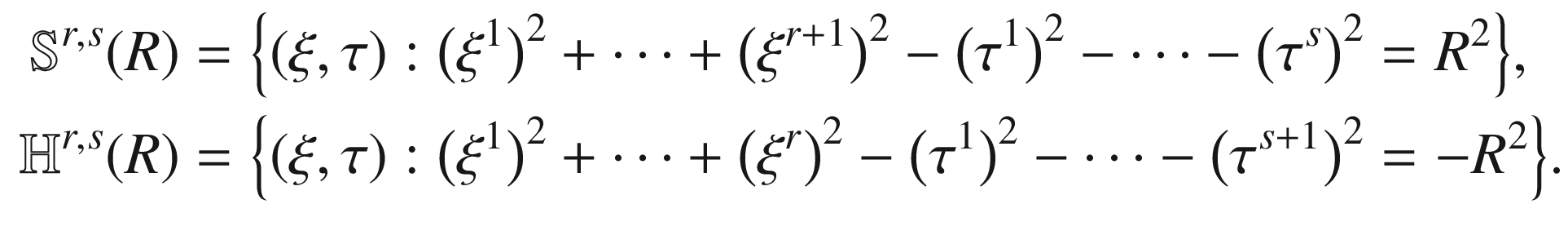
 on
on  , and
, and  on
on 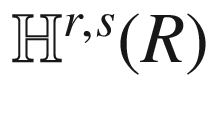 .
.Theorem 3.25.
For all r, s, and R as above,  and
and  are pseudo-Riemannian manifolds of signature (r, s).
are pseudo-Riemannian manifolds of signature (r, s).
Proof.
Problem 3-22. 
It turns out that these pseudo-Riemannian manifolds all have the same degree of symmetry as the three classes of model Riemannian manifolds introduced earlier. For pseudo-Riemannian manifolds, though, it is necessary to modify the definition of frame homogeneity slightly. If (M, g) is a pseudo-Riemannian manifold of signature (r, s), let us say that an orthonormal basis for some tangent space  is in standard order if the expression for
is in standard order if the expression for  in terms of the dual basis
in terms of the dual basis  is
is  , with all positive terms coming before the negative terms. With this understanding, we define
, with all positive terms coming before the negative terms. With this understanding, we define  to be the set of all standard-ordered orthonormal bases for all tangent spaces to M, and we say that (M, g) is frame-homogeneous if the isometry group acts transitively on
to be the set of all standard-ordered orthonormal bases for all tangent spaces to M, and we say that (M, g) is frame-homogeneous if the isometry group acts transitively on  .
.
Theorem 3.26.
All pseudo-Euclidean spaces, pseudospheres, and pseudohyperbolic spaces are frame-homogeneous.
Proof.
Problem 3-23. 
In the particular case of signature (n, 1), the Lorentz manifolds  and
and  are called de Sitter space of radius
are called de Sitter space of radius  and anti-de Sitter space of radius
and anti-de Sitter space of radius  , respectively.
, respectively.
Problems
- 3-1.
Show that (3.2) defines a smooth isometric action of
 on
on  , and the induced action on
, and the induced action on  is transitive. (Used on p. 57.)
is transitive. (Used on p. 57.) - 3-2.
Prove that the metric on
 described in Example 2.34 is frame-homogeneous. (Used on p. 145)
described in Example 2.34 is frame-homogeneous. (Used on p. 145) - 3-3.
Prove Proposition 3.1 (about homogeneous and isotropic Riemannian manifolds).
- 3-4.
Complete the proof of Theorem 3.7 by showing that
 .
. - 3-5.
- (a)
Prove that
 is isometric to
is isometric to  for each
for each  .
. - (b)
Prove that
 is isometric to
is isometric to  for each
for each  .
. - (c)
We could also have defined a family of metrics on
 by
by  . Why did we not bother?
. Why did we not bother?(Used on p. 185.)
- (a)
- 3-6.
Show that two Riemannian metrics
 and
and  are conformal if and only if they define the same angles but not necessarily the same lengths, and that a diffeomorphism is a conformal equivalence if and only if it preserves angles. [Hint: Let
are conformal if and only if they define the same angles but not necessarily the same lengths, and that a diffeomorphism is a conformal equivalence if and only if it preserves angles. [Hint: Let  be a local orthonormal frame for
be a local orthonormal frame for  , and consider the
, and consider the  -angle between
-angle between  and
and  .] (Used on p. 59.)
.] (Used on p. 59.) - 3-7.Let
 denote the upper half-plane model of the hyperbolic plane (of radius 1), with the metric
denote the upper half-plane model of the hyperbolic plane (of radius 1), with the metric  . Let
. Let  denote the group of
denote the group of  real matrices of determinant 1. Regard
real matrices of determinant 1. Regard  as a subset of the complex plane with coordinate
as a subset of the complex plane with coordinate  , and let Show that this defines a smooth, transitive, orientation-preserving, and isometric action of
, and let Show that this defines a smooth, transitive, orientation-preserving, and isometric action of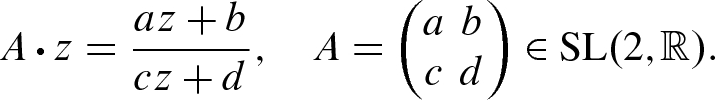
 on
on  . Is the induced action transitive on
. Is the induced action transitive on  ?
? - 3-8.Let
 denote the Poincaré disk model of the hyperbolic plane (of radius 1), with the metric
denote the Poincaré disk model of the hyperbolic plane (of radius 1), with the metric  , and let
, and let  be the subgroup defined by (3.18). Regarding
be the subgroup defined by (3.18). Regarding  as a subset of the complex plane with coordinate
as a subset of the complex plane with coordinate  , let G act on
, let G act on  by Show that this defines a smooth, transitive, orientation-preserving, and isometric action of G on
by Show that this defines a smooth, transitive, orientation-preserving, and isometric action of G on
 . [Hint: One way to proceed is to define an action of G on the upper half-plane by
. [Hint: One way to proceed is to define an action of G on the upper half-plane by 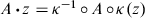 , where
, where  is the Cayley transform defined by (3.14) in the case
is the Cayley transform defined by (3.14) in the case  , and use the result of Problem 3-7.] (Used on pp. 73, 185.)
, and use the result of Problem 3-7.] (Used on pp. 73, 185.) - 3-9.
Suppose G is a compact Lie group with a left-invariant metric g and a left-invariant orientation. Show that the Riemannian volume form
 is bi-invariant. [Hint: Show that
is bi-invariant. [Hint: Show that  is equal to the Riemannian volume form for a bi-invariant metric.]
is equal to the Riemannian volume form for a bi-invariant metric.] - 3-10.Consider the basisfor the Lie algebra

 . For each positive real number a, define a left-invariant metric
. For each positive real number a, define a left-invariant metric  on the group
on the group  by declaring X, Y, aZ to be an orthonormal frame.
by declaring X, Y, aZ to be an orthonormal frame.- (a)
Show that
 is bi-invariant if and only if
is bi-invariant if and only if  .
. - (b)
Show that the map defined by (3.16) is an isometry between
 and
and  . [Remark:
. [Remark:  with any of these metrics is called a Berger sphere, named after Marcel Berger.]
with any of these metrics is called a Berger sphere, named after Marcel Berger.](Used on pp. 56, 71, 259.)
- (a)
- 3-11.
Prove that the formula
 defines a bi-invariant Riemannian metric on
defines a bi-invariant Riemannian metric on  . (See Example 3.16(e).)
. (See Example 3.16(e).) - 3-12.
Regard the upper half-space
 as a Lie group as described in Example 3.16(f).
as a Lie group as described in Example 3.16(f).- (a)
Show that for each
 , the hyperbolic metric
, the hyperbolic metric  on
on  is left-invariant.
is left-invariant. - (b)
Show that
 does not admit any bi-invariant metrics.
does not admit any bi-invariant metrics.(Used on pp. 68, 72.)
- (a)
- 3-13.
Write down an explicit formula for an arbitrary left-invariant metric on the Heisenberg group
 of Example 3.16(g) in terms of global coordinates
of Example 3.16(g) in terms of global coordinates  , and show that the group has no bi-invariant metrics. (Used on pp. 68, 72.)
, and show that the group has no bi-invariant metrics. (Used on pp. 68, 72.) - 3-14.
- 3-15.Let
 be the
be the  -dimensional Minkowski space with coordinates
-dimensional Minkowski space with coordinates  and with the Minkowski metric
and with the Minkowski metric  . Let
. Let  be the set
be the set 
- (a)
Prove that S is a smooth submanifold diffeomorphic to
 , and with the induced metric
, and with the induced metric  it is isometric to the round unit
it is isometric to the round unit  -sphere.
-sphere. - (b)
Define an action of the orthochronous Lorentz group
 on S as follows: For every
on S as follows: For every  , let
, let  denote the 1-dimensional subspace of
denote the 1-dimensional subspace of  spanned by p. Given
spanned by p. Given  , show that the image set
, show that the image set  is a 1-dimensional subspace that intersects S in exactly one point, so we can define
is a 1-dimensional subspace that intersects S in exactly one point, so we can define 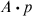 to be the unique point in
to be the unique point in  . Prove that this is a smooth transitive action on S.
. Prove that this is a smooth transitive action on S. - (c)
Prove that
 acts by conformal diffeomorphisms of (S, g).
acts by conformal diffeomorphisms of (S, g).
- (a)
- 3-16.
Prove that there is no Riemannian metric on the sphere that is invariant under the group action described in Problem 3-15.
- 3-17.Given a Lie group G, define an action of the product group
 on G by
on G by  . Show that this action is transitive, and that the isotropy group of the identity is the diagonal subgroup
. Show that this action is transitive, and that the isotropy group of the identity is the diagonal subgroup  . Then show that the following diagram commutes: where
. Then show that the following diagram commutes: where
 is the isotropy representation of
is the isotropy representation of  and
and  is the Lie algebra of G, and use this to give an alternative proof of Theorem 3.14.
is the Lie algebra of G, and use this to give an alternative proof of Theorem 3.14. - 3-18.
Let
 be the subgroup defined by (3.20). Prove that
be the subgroup defined by (3.20). Prove that  acts freely and properly on
acts freely and properly on  and the orbit space is homeomorphic to the Klein bottle, and conclude that the Klein bottle has a flat metric and a Riemannian covering by the Euclidean plane.
and the orbit space is homeomorphic to the Klein bottle, and conclude that the Klein bottle has a flat metric and a Riemannian covering by the Euclidean plane. - 3-19.
Show that the Fubini–Study metric on
 (Example 2.30) is homogeneous, isotropic, and symmetric. (Used on p. 78.)
(Example 2.30) is homogeneous, isotropic, and symmetric. (Used on p. 78.) - 3-20.
Show that the metric on the Grassmannian
 defined in Problem 2-7 is homogeneous, isotropic, and symmetric. (Used on p. 78.)
defined in Problem 2-7 is homogeneous, isotropic, and symmetric. (Used on p. 78.) - 3-21.
Let
 be a simply connected Riemannian manifold, and suppose
be a simply connected Riemannian manifold, and suppose  and
and  are countable subgroups of
are countable subgroups of  acting smoothly, freely, and properly on M (when endowed with the discrete topology). For
acting smoothly, freely, and properly on M (when endowed with the discrete topology). For  , let
, let  , and let
, and let  be the Riemannian metric on
be the Riemannian metric on  that makes the quotient map
that makes the quotient map  a Riemannian covering (see Prop. 2.32). Prove that the Riemannian manifolds
a Riemannian covering (see Prop. 2.32). Prove that the Riemannian manifolds  and
and  are isometric if and only if
are isometric if and only if  and
and  are conjugate subgroups of
are conjugate subgroups of  .
. - 3-22.
Prove Theorem 3.25 (showing that pseudospheres and pseudohyperbolic spaces are pseudo-Riemannian manifolds). [Hint: Mimic the argument in the proof of Theorem 3.7 that
 is Riemannian.]
is Riemannian.] - 3-23.
Prove Theorem 3.26 (pseudo-Euclidean spaces, pseudospheres, and pseudohyperbolic spaces are frame-homogeneous).
- 3-24.Prove that for all positive integers r and s and every real number
 , both the pseudohyperbolic space
, both the pseudohyperbolic space  and the pseudosphere
and the pseudosphere  are diffeomorphic to
are diffeomorphic to  . [Hint: Consider the maps
. [Hint: Consider the maps  given by
given by ![$$\begin{aligned} \varphi (x, y) = \left( Rx, \big ( \sqrt{1+|x|^2}\big )Ry\right) , \quad \psi (x, y) = \left( \big ( \sqrt{1+|x|^2}\big )Ry, Rx\right) .] \end{aligned}$$](../images/56724_2_En_3_Chapter/56724_2_En_3_Chapter_TeX_Equ58.png)
- 3-25.Let
 be the r-dimensional ball of radius R with the Beltrami–Klein metric (3.9), and let
be the r-dimensional ball of radius R with the Beltrami–Klein metric (3.9), and let  be the product manifold
be the product manifold  with the pseudo-Riemannian warped product metric
with the pseudo-Riemannian warped product metric  , where
, where  is given by Define
is given by Define
 by Prove that the image of F is the anti-de Sitter space
by Prove that the image of F is the anti-de Sitter space
 , and F defines a pseudo-Riemannian covering of
, and F defines a pseudo-Riemannian covering of  by
by  . [Remark: We are tacitly extending the notions of warped product metric and Riemannian coverings to the pseudo-Riemannian case in the obvious ways. It follows from the result of Problem 3-24 that
. [Remark: We are tacitly extending the notions of warped product metric and Riemannian coverings to the pseudo-Riemannian case in the obvious ways. It follows from the result of Problem 3-24 that  is simply connected when
is simply connected when  but
but  is not. This shows that
is not. This shows that  , called universal anti-de Sitter space of radius R, is the universal pseudo-Riemannian covering manifold of
, called universal anti-de Sitter space of radius R, is the universal pseudo-Riemannian covering manifold of  .]
.]









