This chapter has a dual purpose: first to apply the theory of curvature to Riemannian submanifolds, and then to use these concepts to derive a precise quantitative interpretation of the curvature tensor.
After introducing some basic definitions and terminology concerning Riemannian submanifolds, we define a vector-valued bilinear form called the second fundamental form, which measures the way a submanifold curves within the ambient manifold. We then prove the fundamental relationships between the intrinsic and extrinsic geometries of a submanifold, including the Gauss formula, which relates the Riemannian connection on the submanifold to that of the ambient manifold, and the Gauss equation, which relates their curvatures. We then show how the second fundamental form measures the extrinsic curvature of submanifold geodesics.
Using these tools, we focus on the special case of hypersurfaces, and use the second fundamental form to define some real-valued curvature quantities called the principal curvatures, mean curvature, and Gaussian curvature. Specializing even more to hypersurfaces in Euclidean space, we describe various concrete geometric interpretations of these quantities. Then we prove Gauss’s Theorema Egregium, which shows that the Gaussian curvature of a surface in  can be computed intrinsically from the curvature tensor of the induced metric.
can be computed intrinsically from the curvature tensor of the induced metric.
In the last section, we introduce the promised quantitative geometric interpretation of the curvature tensor. It allows us to compute sectional curvatures, which are just the Gaussian curvatures of 2-dimensional submanifolds swept out by geodesics tangent to 2-planes in the tangent space. Finally, we compute the sectional curvatures of our frame-homogeneous model Riemannian manifolds—Euclidean spaces, spheres, and hyperbolic spaces.
The Second Fundamental Form
Suppose (M, g) is a Riemannian submanifold of a Riemannian manifold  . Recall that this means that M is a submanifold of
. Recall that this means that M is a submanifold of  endowed with the induced metric
endowed with the induced metric  (where
(where  is the inclusion map). Our goal in this chapter is to study the relationship between the geometry of M and that of
is the inclusion map). Our goal in this chapter is to study the relationship between the geometry of M and that of  .
.
Although we focus our attention in this chapter on embedded submanifolds for simplicity, the results we present are all local, so they apply in much greater generality. In particular, if  is an immersed submanifold, then every point of M has a neighborhood in M that is embedded in
is an immersed submanifold, then every point of M has a neighborhood in M that is embedded in  , so the results of this chapter can be applied by restricting to such a neighborhood. Even more generally, if (M, g) is any Riemannian manifold and
, so the results of this chapter can be applied by restricting to such a neighborhood. Even more generally, if (M, g) is any Riemannian manifold and  is an isometric immersion (meaning that
is an isometric immersion (meaning that  ), then again every point
), then again every point  has a neighborhood
has a neighborhood  such that
such that  is an embedding, so the results apply to
is an embedding, so the results apply to  . We leave it to the reader to sort out the minor modifications in notation and terminology needed to handle these more general situations.
. We leave it to the reader to sort out the minor modifications in notation and terminology needed to handle these more general situations.
The results in the first section of this chapter apply virtually without modification to Riemannian submanifolds of pseudo-Riemannian manifolds (ones on which the induced metric is positive definite), so we state most of our theorems in that case. Recall that when the ambient metric  is indefinite, this includes the assumption that the induced metric
is indefinite, this includes the assumption that the induced metric  is positive definite. Some of the results can also be extended to pseudo-Riemannian submanifolds of mixed signature, but there are various pitfalls to watch out for in that case; so for simplicity we restrict to the case of Riemannian submanifolds. See [dC92] for a thorough treatment of pseudo-Riemannian submanifolds.
is positive definite. Some of the results can also be extended to pseudo-Riemannian submanifolds of mixed signature, but there are various pitfalls to watch out for in that case; so for simplicity we restrict to the case of Riemannian submanifolds. See [dC92] for a thorough treatment of pseudo-Riemannian submanifolds.
Also, most of these results can be adapted to manifolds and submanifolds with boundary, simply by embedding everything in slightly larger manifolds without boundary, but one might need to be careful about the statements of some of the results when the submanifold intersects the boundary. Since the interaction of submanifolds with boundaries is not our primary concern here, for simplicity we state all of these results in the case of empty boundary only.
Throughout this chapter, therefore, we assume that  is a Riemannian or pseudo-Riemannian manifold of dimension m, and (M, g) is an embedded n-dimensional Riemannian submanifold of
is a Riemannian or pseudo-Riemannian manifold of dimension m, and (M, g) is an embedded n-dimensional Riemannian submanifold of  . We call
. We call  the ambient manifold. We will denote covariant derivatives and curvatures associated with (M, g) in the usual way (
the ambient manifold. We will denote covariant derivatives and curvatures associated with (M, g) in the usual way ( , R,
, R,  , etc.), and write those associated with
, etc.), and write those associated with  with tildes (
with tildes ( ,
,  ,
,  , etc.). We can unambiguously use the inner product notation
, etc.). We can unambiguously use the inner product notation  to refer either to g or to
to refer either to g or to  , since g is just the restriction of
, since g is just the restriction of  to pairs of vectors in TM.
to pairs of vectors in TM.
 . The starting point for doing so is the orthogonal decomposition of sections of the ambient tangent bundle
. The starting point for doing so is the orthogonal decomposition of sections of the ambient tangent bundle 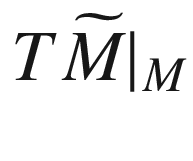 into tangential and orthogonal components. Just as we did for submanifolds of
into tangential and orthogonal components. Just as we did for submanifolds of  in Chapter 4, we define orthogonal projection maps called
tangential
and
normal projections
:
in Chapter 4, we define orthogonal projection maps called
tangential
and
normal projections
:
 for M in
for M in  , these are just the usual projections onto
, these are just the usual projections onto  and
and  respectively, so both projections are smooth bundle homomorphisms (i.e., they are linear on fibers and map smooth sections to smooth sections). If X is a section of
respectively, so both projections are smooth bundle homomorphisms (i.e., they are linear on fibers and map smooth sections to smooth sections). If X is a section of  , we often use the shorthand notations
, we often use the shorthand notations  and
and  for its tangential and normal projections.
for its tangential and normal projections. , we can extend them to vector fields on an open subset of
, we can extend them to vector fields on an open subset of 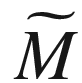 (still denoted by X and Y), apply the ambient covariant derivative operator
(still denoted by X and Y), apply the ambient covariant derivative operator  , and then decompose at points of M to get
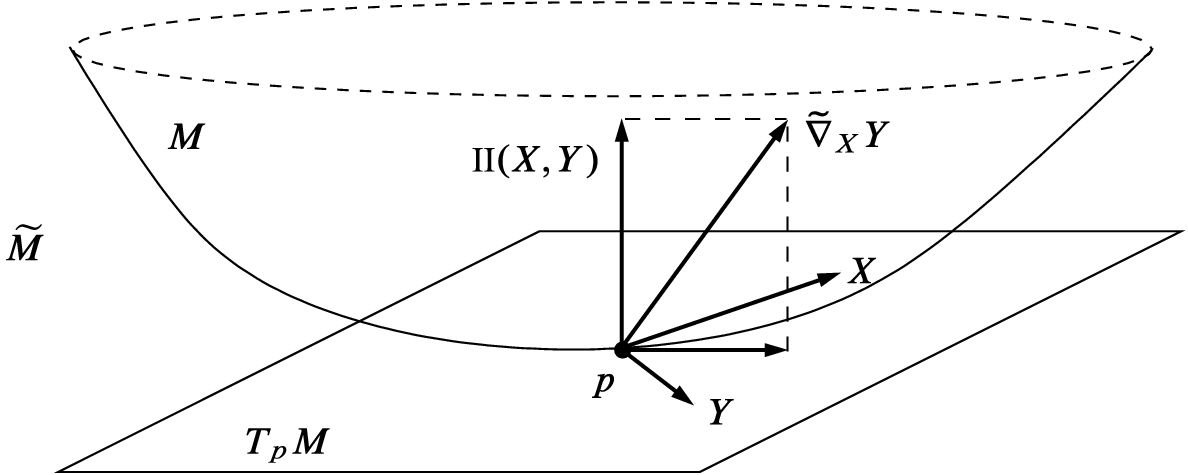
, and then decompose at points of M to get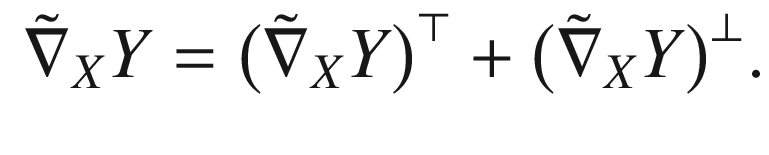
 to be the map
to be the map  (read “two”) given by
(read “two”) given by
 (Fig. 8.1). Since
(Fig. 8.1). Since  maps smooth sections to smooth sections,
maps smooth sections to smooth sections,  is a smooth section of
is a smooth section of  .
.
The second fundamental form
The term first fundamental form , by the way, was originally used to refer to the induced metric g on M. Although that usage has mostly been replaced by more descriptive terminology, we seem unfortunately to be stuck with the name “second fundamental form.” The word “form” in both cases refers to bilinear form, not differential form.
Proposition 8.1
(Properties of the Second Fundamental Form). Suppose (M, g) is an embedded Riemannian submanifold of a Riemannian or pseudo-Riemannian manifold  , and let
, and let  .
.
- (a)
 is independent of the extensions of X and Y to an open subset of
is independent of the extensions of X and Y to an open subset of  .
. - (b)
 is bilinear over
is bilinear over  in X and Y.
in X and Y. - (c)
 is symmetric in X and Y.
is symmetric in X and Y. - (d)
The value of
 at a point
at a point  depends only on
depends only on  and
and  .
.
Proof.
 , and for simplicity denote the extended vector fields also by X and Y. We begin by proving that
, and for simplicity denote the extended vector fields also by X and Y. We begin by proving that  is symmetric in X and Y when defined in terms of these extensions. The symmetry of the connection
is symmetric in X and Y when defined in terms of these extensions. The symmetry of the connection  implies
implies![$$\begin{aligned} \mathrm {II}(X,Y) - \mathrm {II}(Y,X) = \big ({\tilde{\nabla }}_XY - {\tilde{\nabla }}_YX\big )^\perp =[X, Y]^\perp . \end{aligned}$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_Equ33.png)
![$$[X, Y]^\perp =0$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_IEq67.png) , so
, so  is symmetric.
is symmetric.Because  depends only on
depends only on  , it follows that the value of
, it follows that the value of  at p depends only on
at p depends only on  , and in particular is independent of the extension chosen for X. Because
, and in particular is independent of the extension chosen for X. Because  is linear over
is linear over  in X, and every
in X, and every  can be extended to a smooth function on a neighborhood of M in
can be extended to a smooth function on a neighborhood of M in  , it follows that
, it follows that  is linear over
is linear over  in X. By symmetry, the same claims hold for Y.
in X. By symmetry, the same claims hold for Y. 
As a consequence of the preceding proposition, for every  and all vectors
and all vectors  , it makes sense to interpret
, it makes sense to interpret  as the value of
as the value of  at p, where V and W are any vector fields on M such that
at p, where V and W are any vector fields on M such that  and
and  , and we will do so from now on without further comment.
, and we will do so from now on without further comment.
We have not yet identified the tangential term in the decomposition of  . Proposition 5.12(b) showed that in the special case of a submanifold of a Euclidean or pseudo-Euclidean space, it is none other than the covariant derivative with respect to the Levi-Civita connection of the induced metric on M. The following theorem shows that the same is true in the general case. Therefore, we can interpret the second fundamental form as a measure of the difference between the intrinsic Levi-Civita connection on M and the ambient Levi-Civita connection on
. Proposition 5.12(b) showed that in the special case of a submanifold of a Euclidean or pseudo-Euclidean space, it is none other than the covariant derivative with respect to the Levi-Civita connection of the induced metric on M. The following theorem shows that the same is true in the general case. Therefore, we can interpret the second fundamental form as a measure of the difference between the intrinsic Levi-Civita connection on M and the ambient Levi-Civita connection on  .
.
Theorem 8.2
 . If
. If  are extended arbitrarily to smooth vector fields on a neighborhood of M in
are extended arbitrarily to smooth vector fields on a neighborhood of M in  , the following formula holds along M:
, the following formula holds along M:
Proof.
Because of the decomposition (8.1) and the definition of the second fundamental form, it suffices to show that  at all points of M.
at all points of M.
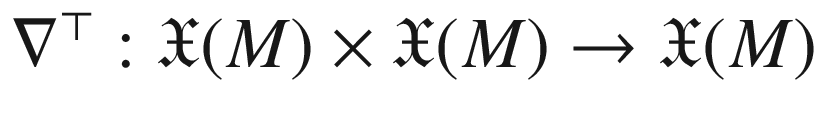 by
by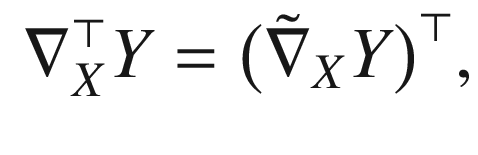
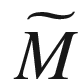 . We examined a special case of this construction, in which
. We examined a special case of this construction, in which  is a Euclidean or pseudo-Euclidean metric, in Example 4.9. It follows exactly as in that example that
is a Euclidean or pseudo-Euclidean metric, in Example 4.9. It follows exactly as in that example that  is a connection on M, and exactly as in the proofs of Propositions 5.8 and 5.9 that it is symmetric and compatible with g. The uniqueness of the Riemannian connection on M then shows that
is a connection on M, and exactly as in the proofs of Propositions 5.8 and 5.9 that it is symmetric and compatible with g. The uniqueness of the Riemannian connection on M then shows that 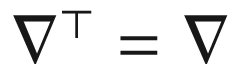 .
. 
The Gauss formula can also be used to compare intrinsic and extrinsic covariant derivatives along curves. If  is a smooth curve and X is a vector field along
is a smooth curve and X is a vector field along  that is everywhere tangent to M, then we can regard X as either a vector field along
that is everywhere tangent to M, then we can regard X as either a vector field along  in
in  or a vector field along
or a vector field along  in M. We let
in M. We let  and
and  denote its covariant derivatives along
denote its covariant derivatives along  as a curve in
as a curve in  and as a curve in M, respectively. The next corollary shows how the two covariant derivatives are related.
and as a curve in M, respectively. The next corollary shows how the two covariant derivatives are related.
Corollary 8.3
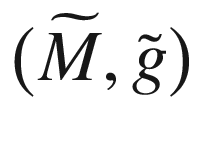 , and
, and  is a smooth curve. If X is a smooth vector field along
is a smooth curve. If X is a smooth vector field along  that is everywhere tangent to M, then
that is everywhere tangent to M, then
Proof.
 , we can find an adapted orthonormal frame
, we can find an adapted orthonormal frame  in a neighborhood of
in a neighborhood of 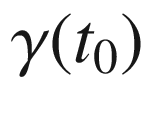 . (Recall that our default assumption is that
. (Recall that our default assumption is that  and
and  .) In terms of this frame, X can be written
.) In terms of this frame, X can be written  . Applying the product rule and the Gauss formula, and using the fact that each vector field
. Applying the product rule and the Gauss formula, and using the fact that each vector field  is extendible, we get
is extendible, we get
 , we obtain a scalar-valued symmetric bilinear form
, we obtain a scalar-valued symmetric bilinear form  by
by
 denote the self-adjoint linear map associated with this bilinear form, characterized by
denote the self-adjoint linear map associated with this bilinear form, characterized by
 is called the Weingarten map in the direction of
is called the Weingarten map in the direction of  . Because the second fundamental form is bilinear over
. Because the second fundamental form is bilinear over  , it follows that
, it follows that  is linear over
is linear over  and thus defines a smooth bundle homomorphism from TM to itself.
and thus defines a smooth bundle homomorphism from TM to itself.Proposition 8.4
 . For every
. For every  and
and  , the following equation holds:
, the following equation holds:
 .
.Proof.
 is independent of the choice of extensions of X and N by Proposition 4.26. Let
is independent of the choice of extensions of X and N by Proposition 4.26. Let  be arbitrary, extended to a vector field on an open subset of
be arbitrary, extended to a vector field on an open subset of 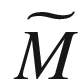 . Since
. Since  vanishes identically along M and X is tangent to M, the following holds at points of M:
vanishes identically along M and X is tangent to M, the following holds at points of M:


In addition to describing the difference between the intrinsic and extrinsic connections, the second fundamental form plays an even more important role in describing the difference between the curvature tensors of  and M. The explicit formula, also due to Gauss, is given in the following theorem.
and M. The explicit formula, also due to Gauss, is given in the following theorem.
Theorem 8.5
 . For all
. For all  , the following equation holds:
, the following equation holds:
Proof.
 . At points of M, using the definition of the curvature and the Gauss formula, we get
. At points of M, using the definition of the curvature and the Gauss formula, we get![$$\begin{aligned} \begin{aligned} \widetilde{ Rm }(W,X,Y,Z)&= \langle {\tilde{\nabla }}_W{\tilde{\nabla }}_X Y - {\tilde{\nabla }}_X{\tilde{\nabla }}_W Y - {\tilde{\nabla }}_{[W,X]}Y,\ Z\rangle \\&= \langle {\tilde{\nabla }}_W(\nabla _X Y+\mathrm {II}(X,Y)) - {\tilde{\nabla }}_X(\nabla _W Y+\mathrm {II}(W,Y)) \\&\qquad - {\tilde{\nabla }}_{[W, X]}Y,\ Z\rangle . \end{aligned} \end{aligned}$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_Equ39.png)
 (with
(with  or
or  playing the role of N) to get
playing the role of N) to get![$$\begin{aligned} \begin{aligned} \widetilde{ Rm }(W,X,Y,Z)&= \big \langle {\tilde{\nabla }}_W\nabla _X Y,Z\big \rangle -\big \langle \mathrm {II}(X,Y),\mathrm {II}(W,Z)\big \rangle \\&\quad -\big \langle {\tilde{\nabla }}_X\nabla _W Y,Z\big \rangle +\big \langle \mathrm {II}(W,Y),\mathrm {II}(X,Z)\big \rangle - \big \langle {\tilde{\nabla }}_{[W,X]}Y, Z\big \rangle . \end{aligned} \end{aligned}$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_Equ40.png)
 into its tangential and normal components, we see that only the tangential component survives, because Z is tangent to M. The Gauss formula allows each such term to be rewritten in terms of
into its tangential and normal components, we see that only the tangential component survives, because Z is tangent to M. The Gauss formula allows each such term to be rewritten in terms of  , giving
, giving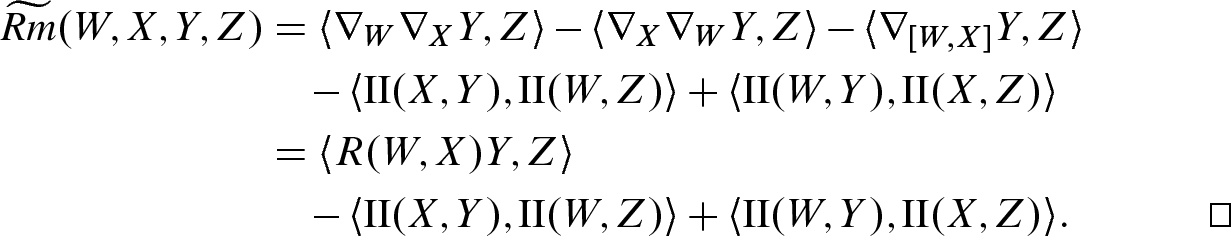
There is one other fundamental submanifold equation, which relates the normal part of the ambient curvature endomorphism to derivatives of the second fundamental form. We will not have need for it, but we include it here for completeness. To state it, we need to introduce a connection on the normal bundle of a Riemannian submanifold.
 , the
normal connection
, the
normal connection
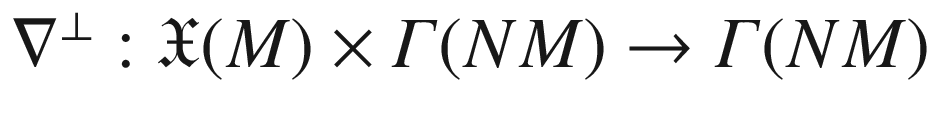 is defined by
is defined by
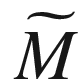 .
.Proposition 8.6.
 , then
, then  is a well-defined connection in NM, which is compatible with
is a well-defined connection in NM, which is compatible with  in the sense that for any two sections
in the sense that for any two sections  of NM and every
of NM and every  , we have
, we have
 Exercise 8.7. Prove the preceding proposition.
Exercise 8.7. Prove the preceding proposition.
 denote the bundle whose fiber at each point
denote the bundle whose fiber at each point  is the set of bilinear maps
is the set of bilinear maps  . It is easy to check that F is a smooth vector bundle over M, and that smooth sections of F correspond to smooth maps
. It is easy to check that F is a smooth vector bundle over M, and that smooth sections of F correspond to smooth maps  that are bilinear over
that are bilinear over  , such as the second fundamental form. Define a connection
, such as the second fundamental form. Define a connection  in F as follows: if B is any smooth section of F, let
in F as follows: if B is any smooth section of F, let  be the smooth section of F defined by
be the smooth section of F defined by
 Exercise 8.8. Prove that
Exercise 8.8. Prove that  is a connection in F.
is a connection in F.
Now we are ready to state the last of the fundamental equations for submanifolds. This equation was independently discovered (in the special case of surfaces in  ) by Karl M. Peterson (1853), Gaspare Mainardi (1856), and Delfino Codazzi (1868–1869), and is sometimes designated by various combinations of these three names. For the sake of simplicity we use the traditional but historically inaccurate name Codazzi equation.
) by Karl M. Peterson (1853), Gaspare Mainardi (1856), and Delfino Codazzi (1868–1869), and is sometimes designated by various combinations of these three names. For the sake of simplicity we use the traditional but historically inaccurate name Codazzi equation.
Theorem 8.9
 . For all
. For all  , the following equation holds:
, the following equation holds:
Proof.

![$$\begin{aligned} \widetilde{ Rm }(W,X,Y,N)&= \big <{\tilde{\nabla }}_W\big (\nabla _X Y+\mathrm {II}(X,Y)\big ) - {\tilde{\nabla }}_X\big (\nabla _W Y+\mathrm {II}(W,Y)\big ) \\&\qquad - {\tilde{\nabla }}_{[W, X]}Y,\ N\big \rangle . \end{aligned}$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_Equ44.png)
![$$\begin{aligned} \widetilde{ Rm }&\left( W,X,Y,N\right) \\&= \big \langle \mathrm {II}\left( W,\nabla _X Y\right) +\left( \nabla ^F_W\mathrm {II}\right) \left( X,Y\right) + \mathrm {II}\left( \nabla _WX,Y\right) + \mathrm {II}\left( X,\nabla _W Y\right) ,\ N\big \rangle \\&\quad - \big \langle \mathrm {II}\left( X,\nabla _W Y\right) +\left( \nabla ^F_X\mathrm {II}\right) \left( W,Y\right) + \mathrm {II}\left( \nabla _XW,Y\right) + \mathrm {II}\left( W,\nabla _X Y\right) ,\ N\big \rangle \\&\quad -\big \langle \mathrm {II}\left( [W,X], Y\right) ,\ N\big \rangle . \end{aligned}$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_Equ45.png)
 and
and  cancel each other in pairs, and three other terms sum to zero because
cancel each other in pairs, and three other terms sum to zero because ![$$\nabla _WX - \nabla _XW -[W, X]=0$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_IEq170.png) . What remains is (8.7).
. What remains is (8.7). 
Curvature of a Curve
 is a smooth unit-speed curve in M. We define the
(geodesic) curvature of
is a smooth unit-speed curve in M. We define the
(geodesic) curvature of  as the length of the acceleration vector field, which is the function
as the length of the acceleration vector field, which is the function  given by
given by
 is an arbitrary regular curve in a Riemannian manifold (not necessarily of unit speed), we first find a unit-speed reparametrization
is an arbitrary regular curve in a Riemannian manifold (not necessarily of unit speed), we first find a unit-speed reparametrization  , and then define the curvature of
, and then define the curvature of  at t to be the curvature of
at t to be the curvature of  at
at  . In a pseudo-Riemannian manifold, the same approach works, but we have to restrict the definition to curves
. In a pseudo-Riemannian manifold, the same approach works, but we have to restrict the definition to curves 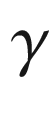 such that
such that  is everywhere nonzero. Problem 8-6 gives a formula that can be used in the Riemannian case to compute the geodesic curvature directly without explicitly finding a unit-speed reparametrization.
is everywhere nonzero. Problem 8-6 gives a formula that can be used in the Riemannian case to compute the geodesic curvature directly without explicitly finding a unit-speed reparametrization.From the definition, it follows that a smooth unit-speed curve has vanishing geodesic curvature if and only if it is a geodesic, so the geodesic curvature of a curve can be regarded as a quantitative measure of how far it deviates from being a geodesic. If  with the Euclidean metric, the geodesic curvature agrees with the notion of curvature introduced in advanced calculus courses.
with the Euclidean metric, the geodesic curvature agrees with the notion of curvature introduced in advanced calculus courses.
Now suppose  is a Riemannian or pseudo-Riemannian manifold and (M, g) is a Riemannian submanifold. Every regular curve
is a Riemannian or pseudo-Riemannian manifold and (M, g) is a Riemannian submanifold. Every regular curve  has two distinct geodesic curvatures: its
intrinsic curvature
has two distinct geodesic curvatures: its
intrinsic curvature
 as a curve in M, and its
extrinsic curvature
as a curve in M, and its
extrinsic curvature
 as a curve in
as a curve in  . The second fundamental form can be used to compute the relationship between the two.
. The second fundamental form can be used to compute the relationship between the two.
Proposition 8.10
(Geometric Interpretation of  ). Suppose (M, g) is an embedded Riemannian submanifold of a Riemannian or pseudo-Riemannian manifold
). Suppose (M, g) is an embedded Riemannian submanifold of a Riemannian or pseudo-Riemannian manifold  ,
,  , and
, and  .
.
- (a)
 is the
is the  -acceleration at p of the g-geodesic
-acceleration at p of the g-geodesic  .
. - (b)
If v is a unit vector, then
 is the
is the  -curvature of
-curvature of  at p.
at p.
Proof.
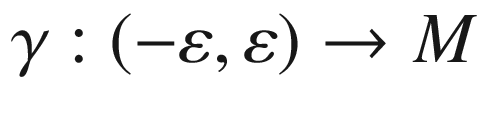 is any regular curve with
is any regular curve with  and
and  . Applying the Gauss formula (Corollary 8.3) to the vector field
. Applying the Gauss formula (Corollary 8.3) to the vector field  along
along  , we obtain
, we obtain
 is a g-geodesic in M, this formula simplifies to
is a g-geodesic in M, this formula simplifies to

Note that the second fundamental form is completely determined by its values of the form  for unit vectors v, by the following lemma.
for unit vectors v, by the following lemma.
Lemma 8.11.
Suppose V is an inner product space, W is a vector space, and  are symmetric and bilinear. If
are symmetric and bilinear. If  for every unit vector
for every unit vector  , then
, then  .
.
Proof.
 can be written
can be written 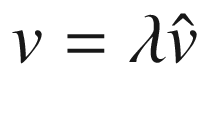 for some unit vector
for some unit vector  , so the bilinearity of B and
, so the bilinearity of B and  implies
implies  for every v, not just unit vectors. The result then follows from the following polarization identity, which is proved in exactly the same way as its counterpart (2.2) for inner products:
for every v, not just unit vectors. The result then follows from the following polarization identity, which is proved in exactly the same way as its counterpart (2.2) for inner products: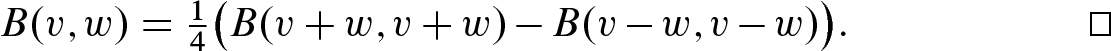
Because the intrinsic and extrinsic accelerations of a curve are usually different, it is generally not the case that a  -geodesic that starts tangent to M stays in M; just think of a sphere in Euclidean space, for example. A Riemannian submanifold (M, g) of
-geodesic that starts tangent to M stays in M; just think of a sphere in Euclidean space, for example. A Riemannian submanifold (M, g) of  is said to be totally geodesic if every
is said to be totally geodesic if every  -geodesic that is tangent to M at some time
-geodesic that is tangent to M at some time  stays in M for all t in some interval
stays in M for all t in some interval  .
.
Proposition 8.12.
 , The following are equivalent:
, The following are equivalent:- (a)
M is totally geodesic in
 .
. - (b)
Every g-geodesic in M is also a
 -geodesic in
-geodesic in  .
. - (c)
The second fundamental form of M vanishes identically.
Proof.
 (b)
(b)  (c)
(c)  (a). First assume that M is totally geodesic. Let
(a). First assume that M is totally geodesic. Let  be a g-geodesic. For each
be a g-geodesic. For each 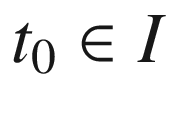 , let
, let  be the
be the  -geodesic with
-geodesic with  and
and  . The hypothesis implies that there is some open interval
. The hypothesis implies that there is some open interval  containing
containing 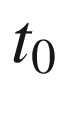 such that
such that  for
for  . On
. On  , the Gauss formula (8.2) for
, the Gauss formula (8.2) for  reads
reads
 on
on  , which means that
, which means that  is also a g-geodesic there. By uniqueness of geodesics, therefore,
is also a g-geodesic there. By uniqueness of geodesics, therefore,  on
on  , so it follows in turn that
, so it follows in turn that 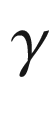 is a
is a  -geodesic there. Since the same is true in a neighborhood of every
-geodesic there. Since the same is true in a neighborhood of every  , it follows that
, it follows that  is a
is a  -geodesic on its whole domain.
-geodesic on its whole domain.Next assume that every g-geodesic is a  -geodesic. Let
-geodesic. Let  and
and  be arbitrary, and let
be arbitrary, and let  be the g-geodesic with
be the g-geodesic with  and
and  . The hypothesis implies that
. The hypothesis implies that  is also a
is also a  -geodesic. Thus
-geodesic. Thus  , so the Gauss formula yields
, so the Gauss formula yields  along
along  . In particular,
. In particular,  . By Lemma 8.11, this implies that
. By Lemma 8.11, this implies that  is identically zero.
is identically zero.
Finally, assume that  , and let
, and let  be a
be a  -geodesic such that
-geodesic such that  and
and  for some
for some  . Let
. Let  be the g-geodesic with the same initial conditions:
be the g-geodesic with the same initial conditions:  and
and  . The Gauss formula together with the hypothesis
. The Gauss formula together with the hypothesis  implies that
implies that  , so
, so  is also a
is also a  -geodesic. By uniqueness of geodesics, therefore,
-geodesic. By uniqueness of geodesics, therefore,  on the intersection of their domains, which implies that
on the intersection of their domains, which implies that  lies in M for t in some open interval around
lies in M for t in some open interval around  .
. 
Hypersurfaces
Now we specialize the preceding considerations to the case in which M is a hypersurface (i.e., a submanifold of codimension 1) in  . Throughout this section, our default assumption is that (M, g) is an embedded n-dimensional Riemannian submanifold of an
. Throughout this section, our default assumption is that (M, g) is an embedded n-dimensional Riemannian submanifold of an  -dimensional Riemannian manifold
-dimensional Riemannian manifold  . (The analogous formulas in the pseudo-Riemannian case are a little different; see Problem 8-19.)
. (The analogous formulas in the pseudo-Riemannian case are a little different; see Problem 8-19.)
In this situation, at each point of M there are exactly two unit normal vectors. In terms of any local adapted orthonormal frame  , the two choices are
, the two choices are  . In a small enough neighborhood of each point of M, therefore, we can always choose a smooth unit normal vector field along M.
. In a small enough neighborhood of each point of M, therefore, we can always choose a smooth unit normal vector field along M.
If both M and  are orientable, we can use an orientation to pick out a global smooth unit normal vector field along all of M. In general, though, this might or might not be possible. Since all of our computations in this chapter are local, we will always assume that we are working in a small enough neighborhood that a smooth unit normal field exists. We will address as we go along the question of how various quantities depend on the choice of normal vector field.
are orientable, we can use an orientation to pick out a global smooth unit normal vector field along all of M. In general, though, this might or might not be possible. Since all of our computations in this chapter are local, we will always assume that we are working in a small enough neighborhood that a smooth unit normal field exists. We will address as we go along the question of how various quantities depend on the choice of normal vector field.
The Scalar Second Fundamental Form and the Shape Operator
 , we can replace the vector-valued second fundamental form
, we can replace the vector-valued second fundamental form  by a simpler
scalar-valued form. The scalar second fundamental form of
by a simpler
scalar-valued form. The scalar second fundamental form of  is the symmetric covariant 2-tensor field
is the symmetric covariant 2-tensor field  defined by
defined by  (see (8.3)); in other words,
(see (8.3)); in other words,
 and noting that
and noting that  is orthogonal to N, we can rewrite the definition as
is orthogonal to N, we can rewrite the definition as
 at each point, the definition of h is equivalent to
at each point, the definition of h is equivalent to
 multiplies h by
multiplies h by 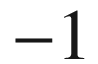 , so the sign of h depends on which unit normal is chosen; but h is otherwise independent of the choices.
, so the sign of h depends on which unit normal is chosen; but h is otherwise independent of the choices. by (8.4); in the case of a hypersurface, we use the notation
by (8.4); in the case of a hypersurface, we use the notation  and call it the shape operator of
and call it the shape operator of  . Alternatively, we can think of s as the (1, 1)-tensor field on M obtained from h by raising an index. It is characterized by
. Alternatively, we can think of s as the (1, 1)-tensor field on M obtained from h by raising an index. It is characterized by
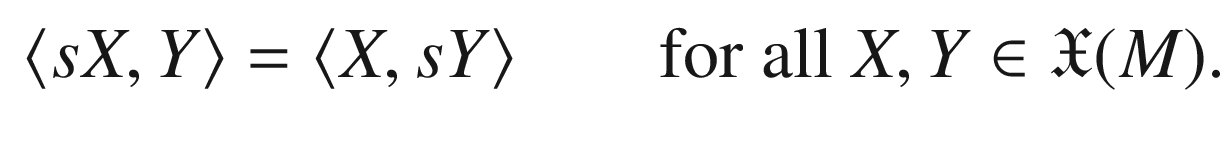


Theorem 8.13
(Fundamental Equations for a Hypersurface). Suppose (M, g) is a Riemannian hypersurface in a Riemannian manifold  , and N is a smooth unit normal vector field along M.
, and N is a smooth unit normal vector field along M.
- (a)The Gauss Formula for a Hypersurface: If
 are extended to an open subset of
are extended to an open subset of  , then
, then 
- (b)The Gauss Formula for a Curve in a Hypersurface: If
 is a smooth curve and
is a smooth curve and  is a smooth vector field along
is a smooth vector field along  , then
, then 
- (c)The Weingarten Equation for a Hypersurface: For every
 ,
,  (8.11)
(8.11) - (d)The Gauss Equation for a Hypersurface: For all
 ,
, 
- (e)The Codazzi Equation for a Hypersurface: For all
 ,
, 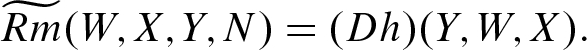 (8.12)
(8.12)
Proof.
Parts (a), (b), and (d) follow immediately from substituting (8.10) into the general versions of the Gauss formula and Gauss equation. To prove (c), note first that the general version of the Weingarten equation can be written  . Since
. Since  , it follows that
, it follows that  is tangent to M, so (c) follows.
is tangent to M, so (c) follows.


 is symmetric in its first two indices yields
is symmetric in its first two indices yields

Principal Curvatures
At
every point  , we have seen that the shape operator s is a self-adjoint linear endomorphism of the tangent space
, we have seen that the shape operator s is a self-adjoint linear endomorphism of the tangent space  . To analyze such an operator, we recall some linear-algebraic facts about self-adjoint endomorphisms.
. To analyze such an operator, we recall some linear-algebraic facts about self-adjoint endomorphisms.
Lemma 8.14.
Suppose V is a finite-dimensional inner product space and  is a self-adjoint linear endomorphism. Let C denote the set of unit vectors in V. There is a vector
is a self-adjoint linear endomorphism. Let C denote the set of unit vectors in V. There is a vector  where the function
where the function  achieves its maximum among elements of C, and every such vector is an eigenvector of s with eigenvalue
achieves its maximum among elements of C, and every such vector is an eigenvector of s with eigenvalue  .
.
 Exercise 8.15. Use the Lagrange multiplier rule (Prop. A.29) to prove this lemma.
Exercise 8.15. Use the Lagrange multiplier rule (Prop. A.29) to prove this lemma.
Proposition 8.16
(Finite-Dimensional Spectral Theorem). Suppose V is a finite-dimensional inner product space and  is a self-adjoint linear endomorphism. Then V has an orthonormal basis of s-eigenvectors, and all of the eigenvalues are real.
is a self-adjoint linear endomorphism. Then V has an orthonormal basis of s-eigenvectors, and all of the eigenvalues are real.
Proof.
The proof is by induction on  . The
. The  result is easy, so assume that the theorem holds for some
result is easy, so assume that the theorem holds for some  and suppose
and suppose  . Lemma 8.14 shows that s has a unit eigenvector
. Lemma 8.14 shows that s has a unit eigenvector  with a real eigenvalue
with a real eigenvalue  . Let
. Let  be the span of
be the span of  . Since
. Since  , self-adjointness of s implies
, self-adjointness of s implies  . The inductive hypothesis applied to
. The inductive hypothesis applied to  implies that
implies that  has an orthonormal basis
has an orthonormal basis  of s-eigenvectors with real eigenvalues, and then
of s-eigenvectors with real eigenvalues, and then  is the desired basis of V.
is the desired basis of V. 
 , we see that s has real eigenvalues
, we see that s has real eigenvalues  , and there is an orthonormal basis
, and there is an orthonormal basis  for
for  consisting of s-eigenvectors, with
consisting of s-eigenvectors, with  for each i (no summation). In this basis, both h and s are represented by diagonal matrices, and h has the expression
for each i (no summation). In this basis, both h and s are represented by diagonal matrices, and h has the expression
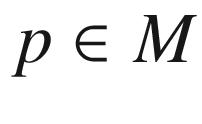 are called the principal curvatures of
are called the principal curvatures of  at
at  , and the corresponding eigenspaces are called the principal directions. The principal curvatures all change sign if we reverse the normal vector, but the principal directions and principal curvatures are otherwise independent of the choice of coordinates or bases.
, and the corresponding eigenspaces are called the principal directions. The principal curvatures all change sign if we reverse the normal vector, but the principal directions and principal curvatures are otherwise independent of the choice of coordinates or bases. , and the
mean curvature
as
, and the
mean curvature
as  . Since the determinant and trace of a linear endomorphism are basis-independent, these are well defined once a unit normal is chosen. In terms of the principal curvatures, they are
. Since the determinant and trace of a linear endomorphism are basis-independent, these are well defined once a unit normal is chosen. In terms of the principal curvatures, they are
 , then H changes sign, while K is multiplied by
, then H changes sign, while K is multiplied by  .
.Computations in Semigeodesic Coordinates
Semigeodesic coordinates (Prop. 6.41) provide an extremely convenient tool for computing the invariants of hypersurfaces.
 be an
be an 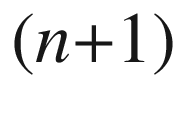 -dimensional Riemannian manifold, and let
-dimensional Riemannian manifold, and let  be semigeodesic coordinates on an open subset
be semigeodesic coordinates on an open subset 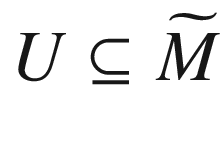 . (For example, they might be Fermi coordinates for the hypersurface
. (For example, they might be Fermi coordinates for the hypersurface  ; see Example 6.43.) For each real number a such that
; see Example 6.43.) For each real number a such that  , the level set
, the level set  is a properly embedded hypersurface in U. Let
is a properly embedded hypersurface in U. Let  denote the induced metric on
denote the induced metric on 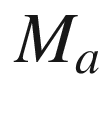 . Corollary 6.42 shows that
. Corollary 6.42 shows that  is given by
is given by
 give smooth coordinates for each hypersurface
give smooth coordinates for each hypersurface  , and in those coordinates the induced metric
, and in those coordinates the induced metric  is given by
is given by  . (Here we use the summation convention with Greek indices running from 1 to n.) The vector field
. (Here we use the summation convention with Greek indices running from 1 to n.) The vector field  restricts to a unit normal vector field along each hypersurface
restricts to a unit normal vector field along each hypersurface  .
.As the next proposition shows, semigeodesic coordinates give us a simple formula for the second fundamental forms of all of the submanifolds  at once.
at once.
Proposition 8.17.
 -coordinates of the scalar second fundamental form, the shape operator, and the mean curvature of
-coordinates of the scalar second fundamental form, the shape operator, and the mean curvature of 
 with respect to the normal
with respect to the normal  are given by
are given by
Proof.
 is
is  , which Corollary 6.42 shows is equal to
, which Corollary 6.42 shows is equal to  (noting that the roles of g and
(noting that the roles of g and  in that corollary are being played here by
in that corollary are being played here by  and
and  , respectively). Equation (8.9) evaluated at points of
, respectively). Equation (8.9) evaluated at points of  gives
gives
 and
and  follow by using
follow by using  (the inverse matrix of
(the inverse matrix of  ) to raise an index and then taking the trace.
) to raise an index and then taking the trace. 
Minimal Hypersurfaces
A natural question that has received a great deal of attention over the past century is this: Given a simple closed curve C in  , is there an embedded or immersed surface M with
, is there an embedded or immersed surface M with  that has least area among all surfaces with the same boundary? If so, what is it? Such surfaces are models of the soap films that are produced when a closed loop of wire is dipped in soapy water.
that has least area among all surfaces with the same boundary? If so, what is it? Such surfaces are models of the soap films that are produced when a closed loop of wire is dipped in soapy water.
More generally, we can consider the analogous question for hypersurfaces in Riemannian manifolds. Suppose M is a compact codimension-1 submanifold with nonempty boundary in an  -dimensional Riemannian manifold
-dimensional Riemannian manifold  . By analogy with the case of surfaces in
. By analogy with the case of surfaces in  , it is traditional to use the term area to refer to the n-dimensional volume of M with its induced Riemannian metric, and to say that M is area-minimizing if it has the smallest area among all compact embedded hypersurfaces in
, it is traditional to use the term area to refer to the n-dimensional volume of M with its induced Riemannian metric, and to say that M is area-minimizing if it has the smallest area among all compact embedded hypersurfaces in  with the same boundary. One key observation is the following theorem, which is an analogue for hypersurfaces of Theorem 6.4 about length-minimizing curves.
with the same boundary. One key observation is the following theorem, which is an analogue for hypersurfaces of Theorem 6.4 about length-minimizing curves.
Theorem 8.18.
Let M be a compact codimension-1 submanifold with nonempty boundary in an  -dimensional Riemannian manifold
-dimensional Riemannian manifold  . If M is area-minimizing, then its mean curvature is identically zero.
. If M is area-minimizing, then its mean curvature is identically zero.
Proof.
Let g denote the induced metric on M. The fact that M minimizes area among hypersurfaces with the same boundary means, in particular, that it minimizes area among small perturbations of M in a neighborhood of a single point. We will exploit this idea to prove that M must have zero mean curvature everywhere.
 be arbitrary, let
be arbitrary, let  be Fermi coordinates for M on an open set
be Fermi coordinates for M on an open set ![$${\smash [t]{\tilde{U}}}\subseteq {{\widetilde{M}}}$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_IEq391.png) containing p (see Example 6.43), and let
containing p (see Example 6.43), and let ![$$U = {\smash [t]{\tilde{U}}}\cap M$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_IEq392.png) . By taking
. By taking ![$${\smash [t]{\tilde{U}}}$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_IEq393.png) sufficiently small, we can arrange that U is a regular coordinate ball in M (see p. 374) and
sufficiently small, we can arrange that U is a regular coordinate ball in M (see p. 374) and ![$${\smash [t]{\tilde{U}}}\cap \partial M=\varnothing $$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_IEq394.png) . We use
. We use  as coordinates on M, and observe the summation convention with Greek indices running from 1 to n.
as coordinates on M, and observe the summation convention with Greek indices running from 1 to n.
The hypersurface 
 be an arbitrary smooth real-valued function on M with compact support in U. For sufficiently small t, define a set
be an arbitrary smooth real-valued function on M with compact support in U. For sufficiently small t, define a set  by
by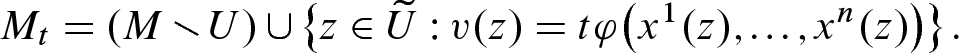
 is an embedded smooth hypersurface in
is an embedded smooth hypersurface in  , which agrees with M outside of U and which coincides with the graph of
, which agrees with M outside of U and which coincides with the graph of  in
in ![$${\smash [t]{\tilde{U}}}$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_IEq402.png) . Let
. Let ![$$f_t:U\mathrel {\rightarrow }{\smash [t]{\tilde{U}}}$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_IEq403.png) be the graph parametrization of
be the graph parametrization of ![$$M_t\cap {\smash [t]{\tilde{U}}}$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_IEq404.png) , given in Fermi coordinates by
, given in Fermi coordinates by
 by
by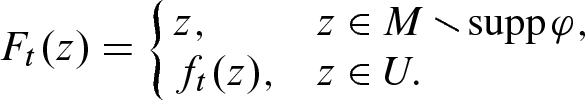
 denote the induced Riemannian metric on
denote the induced Riemannian metric on  , and let
, and let  denote the pulled-back metric on M. When
denote the pulled-back metric on M. When  , we have
, we have  , and both
, and both  and
and  are equal to the induced metric g on M. Since
are equal to the induced metric g on M. Since  is given by (8.13) in Fermi coordinates, a simple computation shows that in U,
is given by (8.13) in Fermi coordinates, a simple computation shows that in U,  has the coordinate expression
has the coordinate expression  , where
, where
 ,
,  is equal to g and thus is independent of t.
is equal to g and thus is independent of t. is a smooth hypersurface with the same boundary as M, our hypothesis guarantees that
is a smooth hypersurface with the same boundary as M, our hypothesis guarantees that 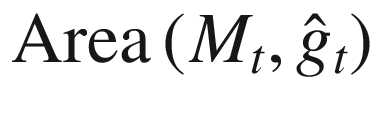 achieves a minimum at
achieves a minimum at  . Because
. Because  is an isometry from
is an isometry from  to
to  , we can express this area as follows:
, we can express this area as follows: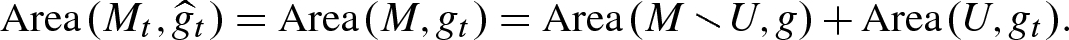
 on U:
on U:
 denotes the determinant of the matrix
denotes the determinant of the matrix 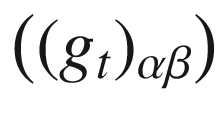 defined by (8.15). The integrand above is a smooth function of t and
defined by (8.15). The integrand above is a smooth function of t and  , so the area is a smooth function of t. We have
, so the area is a smooth function of t. We have
 shows that the partial derivative of
shows that the partial derivative of  with respect to the matrix entry in position
with respect to the matrix entry in position  is equal to the cofactor
is equal to the cofactor 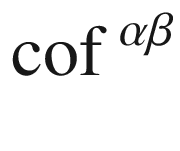 , and thus by the chain rule,
, and thus by the chain rule,
 component of the inverse matrix is given by
component of the inverse matrix is given by  . Thus from (8.17) and (8.15) we obtain
. Thus from (8.17) and (8.15) we obtain

 attains a minimum at
attains a minimum at  , we conclude that
, we conclude that  for every such
for every such  .
.Now suppose for the sake of contradiction that  . If
. If  , we can let
, we can let  be a smooth nonnegative bump function that is positive at p and supported in a small neighborhood of p on which
be a smooth nonnegative bump function that is positive at p and supported in a small neighborhood of p on which  . The argument above shows that
. The argument above shows that  , which is impossible because the integrand is nonnegative on U and positive on an open set. A similar argument rules out
, which is impossible because the integrand is nonnegative on U and positive on an open set. A similar argument rules out  . Since p was an arbitrary point in
. Since p was an arbitrary point in  , we conclude that
, we conclude that  on
on  , and then by continuity on all of M.
, and then by continuity on all of M. 
Because of the result of Theorem 8.18, a hypersurface (immersed or embedded, with or without boundary) that has mean curvature identically equal to zero is called a minimal hypersurface (or a minimal surface when it has dimension 2). It is an unfortunate historical accident that the term “minimal hypersurface” is defined in this way, because in fact, a minimal hypersurface is just a critical point for the area, not necessarily area-minimizing. It can be shown that as in the case of geodesics, a small enough piece of every minimal hypersurface is area-minimizing.
As a complement to the above theorem about hypersurfaces that minimize area with fixed boundary, we have the following result about hypersurfaces that minimize area while enclosing a fixed volume.
Theorem 8.19.
Suppose  is a Riemannian
is a Riemannian  -manifold,
-manifold,  is a compact regular domain, and
is a compact regular domain, and  . If M has the smallest surface area among boundaries of compact regular domains with the same volume as D, then M has constant mean curvature (computed with respect to the outward unit normal).
. If M has the smallest surface area among boundaries of compact regular domains with the same volume as D, then M has constant mean curvature (computed with respect to the outward unit normal).
Proof.
Let g denote the induced metric on M. Assume for the sake of contradiction that the mean curvature H of M is not constant, and let  be points such that
be points such that  .
.
Since M is compact, it has an  -tubular neighborhood for some
-tubular neighborhood for some  by Theorem 5.25. As in the previous proof, let
by Theorem 5.25. As in the previous proof, let  be Fermi coordinates for M on an open set
be Fermi coordinates for M on an open set ![$${\smash [t]{\tilde{U}}}\subseteq {{\widetilde{M}}}$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_IEq457.png) containing p, and let
containing p, and let ![$$U = {\smash [t]{\tilde{U}}}\cap M$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_IEq458.png) . We may assume that U is a regular coordinate ball in M and the image of the chart is a set of the form
. We may assume that U is a regular coordinate ball in M and the image of the chart is a set of the form  for some open subset
for some open subset  . Similarly, let
. Similarly, let  be Fermi coordinates for M on an open set
be Fermi coordinates for M on an open set ![$${\smash [t]{\widetilde{W}}}\subseteq {{\widetilde{M}}}$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_IEq462.png) containing q and satisfying the analogous conditions, and let
containing q and satisfying the analogous conditions, and let ![$$W = {\smash [t]{\widetilde{W}}}\cap M$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_IEq463.png) . By replacing v with its negative if necessary, we can arrange that
. By replacing v with its negative if necessary, we can arrange that ![$$D\cap {\smash [t]{\tilde{U}}}$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_IEq464.png) is the set where
is the set where  , and similarly for w. Also, by shrinking both domains, we can assume that the mean curvature of M satisfies
, and similarly for w. Also, by shrinking both domains, we can assume that the mean curvature of M satisfies  on U and
on U and  on W, where
on W, where  are constants such that
are constants such that  .
.
 and
and  be smooth real-valued functions on M, with
be smooth real-valued functions on M, with  compactly supported in U and
compactly supported in U and  compactly supported in W, and satisfying
compactly supported in W, and satisfying  . For sufficiently small
. For sufficiently small  , define a subset
, define a subset 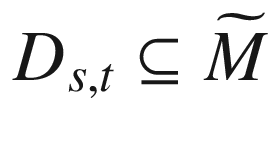 as follows:
as follows:
 , so
, so  and
and  (see Fig. 8.3). For sufficiently small s and t, the set
(see Fig. 8.3). For sufficiently small s and t, the set  is a regular domain and
is a regular domain and  is a compact smooth hypersurface, and
is a compact smooth hypersurface, and  and
and  are both smooth functions of (s, t). For convenience, write
are both smooth functions of (s, t). For convenience, write  and
and  .
.
The domain 

 fixed and let s vary, the only change in volume occurs in the part of
fixed and let s vary, the only change in volume occurs in the part of  contained in
contained in ![$${\smash [t]{\tilde{U}}}$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_IEq489.png) , so the fundamental theorem of calculus gives
, so the fundamental theorem of calculus gives![$$\begin{aligned} \frac{\partial V}{\partial s}(0,0)&= \left. \frac{d}{d s}\right| _{s=0}\mathrm{Vol}\big (D_{s, 0}\cap {\smash [t]{\tilde{U}}}\big )\\&= \left. \frac{d}{d s}\right| _{s=0}\int _{U}\left( \int _{-\varepsilon }^{s\varphi (x)}\sqrt{\det {\tilde{g}}(x,v)}\, dv\right) dx^1\cdots dx^n\\&= \int _{U}\left( \left. \frac{d}{d s}\right| _{s=0}\int _{-\varepsilon }^{s\varphi (x)}\sqrt{\det {\tilde{g}}(x,v)}\, dv\right) dx^1\cdots dx^n\\&= \int _{U} \varphi (x) \sqrt{\det {\tilde{g}}(x, 0)}\, dx^1\cdots dx^n = \int _U \varphi \, dV_g =1, \end{aligned}$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_Equ65.png)
 in these coordinates. Similarly,
in these coordinates. Similarly,  .
. and
and  , the implicit function theorem guarantees that there is a smooth function
, the implicit function theorem guarantees that there is a smooth function  for some
for some  such that
such that  . The chain rule then implies
. The chain rule then implies
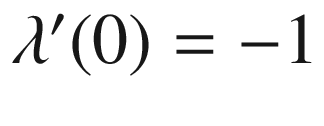 .
.
 . But our choice of U and V together with the fact that
. But our choice of U and V together with the fact that  guarantees that
guarantees that  , which is a contradiction.
, which is a contradiction. 
We do not pursue minimal or constant-mean-curvature hypersurfaces any further in this book, but you can find a good introductory treatment in [CM11].
Hypersurfaces in Euclidean Space
Now we specialize even further, to hypersurfaces in Euclidean space. In this section, we assume that  is an embedded n-dimensional submanifold with the induced Riemannian metric. The Euclidean metric will be denoted as usual by
is an embedded n-dimensional submanifold with the induced Riemannian metric. The Euclidean metric will be denoted as usual by  , and covariant derivatives and curvatures associated with
, and covariant derivatives and curvatures associated with  will be indicated by a bar. The induced metric on M will be denoted by g.
will be indicated by a bar. The induced metric on M will be denoted by g.
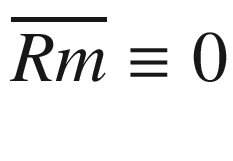 , the Gauss and Codazzi equations take even simpler forms:
, the Gauss and Codazzi equations take even simpler forms:



 is completely determined by the second fundamental form. A symmetric 2-tensor field that satisfies
is completely determined by the second fundamental form. A symmetric 2-tensor field that satisfies  is called a Codazzi tensor, so (8.20) can be expressed succinctly by saying that h is a Codazzi tensor.
is called a Codazzi tensor, so (8.20) can be expressed succinctly by saying that h is a Codazzi tensor. Exercise 8.20. Show that a smooth 2-tensor field h on a Riemannian manifold is a Codazzi tensor if and only if both h and
Exercise 8.20. Show that a smooth 2-tensor field h on a Riemannian manifold is a Codazzi tensor if and only if both h and  are symmetric.
are symmetric.
 for which h is the scalar second fundamental form. (Note that an immersion is locally an embedding, so the theorem applies in a neighborhood of each point.) It is a remarkable fact that the Gauss and Codazzi equations are actually sufficient, at least locally. A sketch of a proof of this fact, called the fundamental theorem of hypersurface theory, can be found in [Pet16, pp. 108–109].
for which h is the scalar second fundamental form. (Note that an immersion is locally an embedding, so the theorem applies in a neighborhood of each point.) It is a remarkable fact that the Gauss and Codazzi equations are actually sufficient, at least locally. A sketch of a proof of this fact, called the fundamental theorem of hypersurface theory, can be found in [Pet16, pp. 108–109].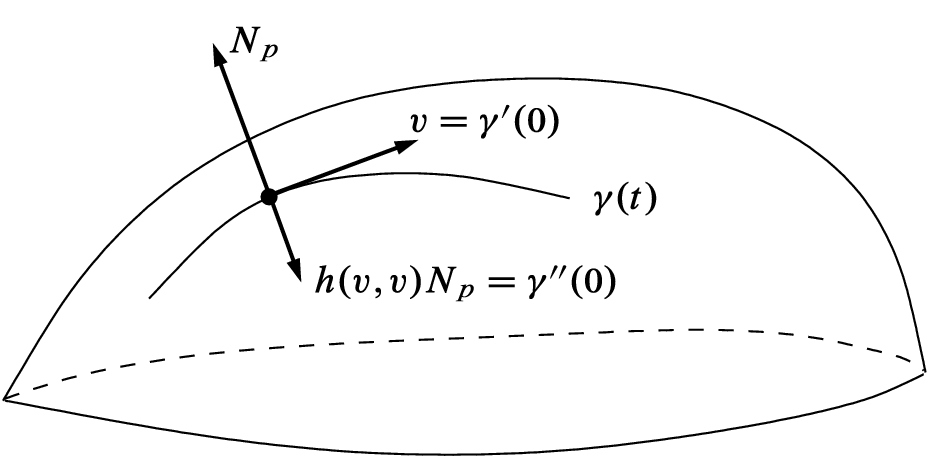
Geometric interpretation of h(v, v)
In the setting of a hypersurface  , we can give some very concrete geometric interpretations of the quantities we have defined so far. We begin with curves. For every unit vector
, we can give some very concrete geometric interpretations of the quantities we have defined so far. We begin with curves. For every unit vector  , let
, let  be the g-geodesic in M with initial velocity v. Then the Gauss formula shows that the ordinary Euclidean acceleration of
be the g-geodesic in M with initial velocity v. Then the Gauss formula shows that the ordinary Euclidean acceleration of  at 0 is
at 0 is  (Fig. 8.4). Thus |h(v, v)| is the Euclidean curvature of
(Fig. 8.4). Thus |h(v, v)| is the Euclidean curvature of  at 0, and
at 0, and  if and only if
if and only if  points in the same direction as
points in the same direction as  . In other words, h(v, v) is positive if
. In other words, h(v, v) is positive if  is curving in the direction of
is curving in the direction of  , and negative if it is curving away from
, and negative if it is curving away from  .
.
The next proposition shows that this Euclidean curvature can be interpreted in terms of the radius of the “best circular approximation,” as mentioned in Chapter 1.
Proposition 8.21.
Suppose  is a unit-speed curve,
is a unit-speed curve,  , and
, and  .
.
- (a)
There is a unique unit-speed parametrized circle
 , called the osculating circle at
, called the osculating circle at  , with the property that c and
, with the property that c and  have the same position, velocity, and acceleration at
have the same position, velocity, and acceleration at  .
. - (b)
The Euclidean curvature of
 at
at  is
is  , where R is the radius of the osculating circle.
, where R is the radius of the osculating circle.
Proof.
 with center q and radius R has a unit-speed parametrization of the form
with center q and radius R has a unit-speed parametrization of the form
 . By direct computation, such a parametrization satisfies
. By direct computation, such a parametrization satisfies

 by construction. Uniqueness is left as an exercise.
by construction. Uniqueness is left as an exercise. 
 Exercise 8.22. Complete the proof of the preceding proposition by proving uniqueness of the osculating circle.
Exercise 8.22. Complete the proof of the preceding proposition by proving uniqueness of the osculating circle.
Computations in Euclidean Space
When we wish to compute the invariants of a Euclidean hypersurface  , it is usually unnecessary to go to all the trouble of computing Christoffel symbols. Instead, it is usually more effective to use either a defining function or a parametrization to compute the scalar second fundamental form, and then use (8.21) to compute the curvature. Here we describe several contexts in which this computation is not too hard.
, it is usually unnecessary to go to all the trouble of computing Christoffel symbols. Instead, it is usually more effective to use either a defining function or a parametrization to compute the scalar second fundamental form, and then use (8.21) to compute the curvature. Here we describe several contexts in which this computation is not too hard.
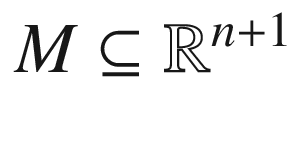 is a smooth embedded hypersurface, and let
is a smooth embedded hypersurface, and let  be a smooth local parametrization of M. The coordinates
be a smooth local parametrization of M. The coordinates  on
on  thus give local coordinates for M. The coordinate vector fields
thus give local coordinates for M. The coordinate vector fields  push forward to vector fields
push forward to vector fields  on M, which we can view as sections of the restricted tangent bundle
on M, which we can view as sections of the restricted tangent bundle  , or equivalently as
, or equivalently as 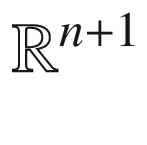 -valued functions. If we think of
-valued functions. If we think of  as a vector-valued function of u, these vectors can be written as
as a vector-valued function of u, these vectors can be written as
 .
.Once these vector fields are computed, a unit normal field can be computed as follows: Choose any coordinate vector field  that is not contained in
that is not contained in  (there will always be one, at least in a neighborhood of each point). Then apply the Gram–Schmidt algorithm to the local frame
(there will always be one, at least in a neighborhood of each point). Then apply the Gram–Schmidt algorithm to the local frame  along M to obtain an adapted orthonormal frame
along M to obtain an adapted orthonormal frame  . The two choices of unit normal are
. The two choices of unit normal are  .
.
The next proposition gives a formula for the second fundamental form that is often easy to use for computation.
Proposition 8.23.
 is an embedded hypersurface,
is an embedded hypersurface,  is a smooth local parametrization of M,
is a smooth local parametrization of M,  is the local frame for TM determined by X, and N is a unit normal field on M. Then the scalar second fundamental form is given by
is the local frame for TM determined by X, and N is a unit normal field on M. Then the scalar second fundamental form is given by
Proof.
 be an arbitrary point of U and let
be an arbitrary point of U and let  . For each
. For each  , the curve
, the curve  is a smooth curve in M whose initial velocity is
is a smooth curve in M whose initial velocity is  . Regarding the normal field N as a smooth map from M to
. Regarding the normal field N as a smooth map from M to 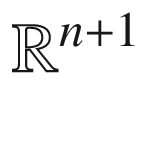 , we have
, we have
 is tangent to M and N is normal, the following expression is zero for all
is tangent to M and N is normal, the following expression is zero for all  :
:
 and using the product rule for ordinary inner products in
and using the product rule for ordinary inner products in  yields
yields


Here is an application of this formula: it shows how the principal curvatures give a concise description of the local shape of an embedded hypersurface by approximating the surface with the graph of a quadratic function.
Proposition 8.24.
 is a Riemannian hypersurface. Let
is a Riemannian hypersurface. Let  , and let
, and let  denote the principal curvatures of M at p with respect to some choice of unit normal. Then there is an isometry
denote the principal curvatures of M at p with respect to some choice of unit normal. Then there is an isometry  that takes p to the origin and takes a neighborhood of p in M to a graph of the form
that takes p to the origin and takes a neighborhood of p in M to a graph of the form  , where
, where
Proof.
Replacing M by its image under a translation and a rotation (which are Euclidean isometries), we may assume that p is the origin and  is equal to the span of
is equal to the span of  . Then after reflecting in the
. Then after reflecting in the  -hyperplane if necessary, we may assume that the chosen unit normal is
-hyperplane if necessary, we may assume that the chosen unit normal is  . By an orthogonal transformation in the first n variables, we can also arrange that the scalar second fundamental form at 0 is diagonal with respect to the basis
. By an orthogonal transformation in the first n variables, we can also arrange that the scalar second fundamental form at 0 is diagonal with respect to the basis  , with diagonal entries
, with diagonal entries  .
.
 is the graph of a smooth function of the form
is the graph of a smooth function of the form  with
with  . A smooth local parametrization of M is then given by
. A smooth local parametrization of M is then given by  , and the fact that
, and the fact that  is spanned by
is spanned by  guarantees that
guarantees that 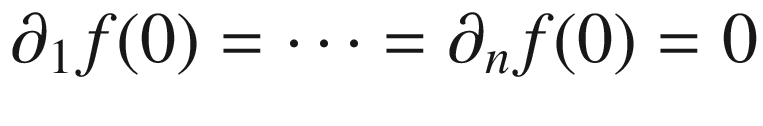 . Because
. Because  at 0, Proposition 8.23 then yields
at 0, Proposition 8.23 then yields

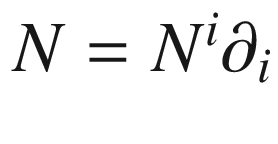 on an open subset of
on an open subset of  that restricts to a unit normal vector field along M, then the shape operator can be computed straightforwardly using the Weingarten equation and observing that the Euclidean covariant derivatives of N are just ordinary directional derivatives in Euclidean space. Thus for every vector
that restricts to a unit normal vector field along M, then the shape operator can be computed straightforwardly using the Weingarten equation and observing that the Euclidean covariant derivatives of N are just ordinary directional derivatives in Euclidean space. Thus for every vector  tangent to M, we have
tangent to M, we have
 such that
such that  is a regular level set of F (see Prop. A.27). The definition ensures that
is a regular level set of F (see Prop. A.27). The definition ensures that 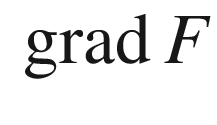 (the gradient of F with respect to
(the gradient of F with respect to  ) is nonzero on some neighborhood of
) is nonzero on some neighborhood of  , so a convenient choice for a unit normal vector field along M is
, so a convenient choice for a unit normal vector field along M is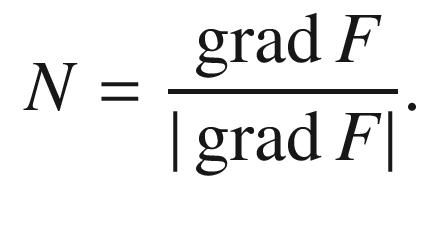
Example 8.25
 defined by
defined by  is a smooth defining function for each sphere
is a smooth defining function for each sphere  . The gradient of this function is
. The gradient of this function is  , which has length 2R along
, which has length 2R along  . The smooth vector field
. The smooth vector field
 . (It is the outward pointing normal.) The shape operator is now easy to compute:
. (It is the outward pointing normal.) The shape operator is now easy to compute:
 . The principal curvatures, therefore, are all equal to
. The principal curvatures, therefore, are all equal to  , and it follows that the mean curvature is
, and it follows that the mean curvature is 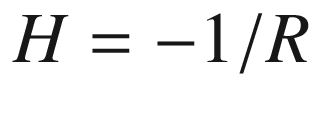 and the Gaussian curvature is
and the Gaussian curvature is  . //
. // , either of the above methods can be used. When a parametrization X is given, the normal vector field is particularly easy to compute: because
, either of the above methods can be used. When a parametrization X is given, the normal vector field is particularly easy to compute: because  and
and  span the tangent space to M at each point, their cross product is a nonzero normal vector, so one choice of unit normal is
span the tangent space to M at each point, their cross product is a nonzero normal vector, so one choice of unit normal is
The Gaussian Curvature of a Surface Is Intrinsic
Because the Gaussian and mean curvatures are defined in terms of a particular embedding of M into  , there is little reason to suspect that they have much to do with the intrinsic Riemannian geometry of (M, g). The next exercise illustrates the fact that the mean curvature has no intrinsic meaning.
, there is little reason to suspect that they have much to do with the intrinsic Riemannian geometry of (M, g). The next exercise illustrates the fact that the mean curvature has no intrinsic meaning.
 Exercise 8.26. Let
Exercise 8.26. Let  be the plane
be the plane  , and let
, and let  be the cylinder
be the cylinder  . Show that
. Show that  and
and  are locally isometric, but the former has mean curvature zero, while the latter has mean curvature
are locally isometric, but the former has mean curvature zero, while the latter has mean curvature  , depending on which normal is chosen.
, depending on which normal is chosen.
The amazing discovery made by Gauss was that the Gaussian curvature of a surface in  is actually an intrinsic invariant of the Riemannian manifold (M, g). He was so impressed with this discovery that he called it Theorema Egregium, Latin for “excellent theorem."
is actually an intrinsic invariant of the Riemannian manifold (M, g). He was so impressed with this discovery that he called it Theorema Egregium, Latin for “excellent theorem."
Theorem 8.27
(Gauss’s Theorema Egregium). Suppose (M, g) is an embedded 2-dimensional Riemannian submanifold of  . For every
. For every  , the Gaussian curvature of M at p is equal to one-half the scalar curvature of g at p, and thus the Gaussian curvature is a local isometry invariant of (M, g).
, the Gaussian curvature of M at p is equal to one-half the scalar curvature of g at p, and thus the Gaussian curvature is a local isometry invariant of (M, g).
Proof.
 be arbitrary, and choose an orthonormal basis
be arbitrary, and choose an orthonormal basis  for
for  . In this basis g is represented by the identity matrix, and the shape operator has the same matrix as the scalar second fundamental form. Thus
. In this basis g is represented by the identity matrix, and the shape operator has the same matrix as the scalar second fundamental form. Thus  , and the Gauss equation (8.21) reads
, and the Gauss equation (8.21) reads
 , and thus by the definition of the Kulkarni–Nomizu product we have
, and thus by the definition of the Kulkarni–Nomizu product we have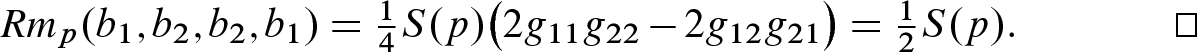
Motivated by the Theorema Egregium, for an abstract Riemannian 2-manifold (M, g), not necessarily embedded in  , we define the Gaussian curvature to be
, we define the Gaussian curvature to be  , where S is the scalar curvature. If M is a Riemannian submanifold of
, where S is the scalar curvature. If M is a Riemannian submanifold of  , then the Theorema Egregium shows that this new definition agrees with the original definition of K as the determinant of the shape operator. The following result is a restatement of Corollary 7.27 using this new definition.
, then the Theorema Egregium shows that this new definition agrees with the original definition of K as the determinant of the shape operator. The following result is a restatement of Corollary 7.27 using this new definition.
Corollary 8.28.
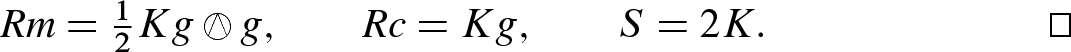
Sectional Curvatures
 ), p is a point of M, and
), p is a point of M, and  is a star-shaped neighborhood of zero on which
is a star-shaped neighborhood of zero on which  is a diffeomorphism onto an open set
is a diffeomorphism onto an open set  . Let
. Let  be any 2-dimensional linear subspace of
be any 2-dimensional linear subspace of  . Since
. Since  is an embedded 2-dimensional submanifold of V, it follows that
is an embedded 2-dimensional submanifold of V, it follows that  is an embedded 2-dimensional submanifold of
is an embedded 2-dimensional submanifold of  containing p (Fig. 8.5), called the plane section determined by
containing p (Fig. 8.5), called the plane section determined by  . Note that
. Note that  is just the set swept out by geodesics whose initial velocities lie in
is just the set swept out by geodesics whose initial velocities lie in  , and
, and  is exactly
is exactly  .
.
A plane section
We define the
sectional curvature of
 , denoted by
, denoted by  , to be the intrinsic Gaussian curvature at p of the surface
, to be the intrinsic Gaussian curvature at p of the surface  with the metric induced from the embedding
with the metric induced from the embedding  . If (v, w) is any basis for
. If (v, w) is any basis for  , we also use the notation
, we also use the notation  for
for  .
.

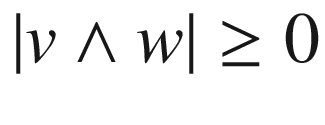 , with equality if and only if v and w are linearly dependent, and
, with equality if and only if v and w are linearly dependent, and  when v and w are orthonormal. (One can define an inner product on the space
when v and w are orthonormal. (One can define an inner product on the space  of contravariant alternating 2-tensors, analogous to the inner product on forms defined in Problem 2-16, and this is the associated norm; see Problem 8-33(a).)
of contravariant alternating 2-tensors, analogous to the inner product on forms defined in Problem 2-16, and this is the associated norm; see Problem 8-33(a).)Proposition 8.29
 . If v, w are linearly independent vectors in
. If v, w are linearly independent vectors in  , then the sectional curvature of the plane spanned by v and w is given by
, then the sectional curvature of the plane spanned by v and w is given by
Proof.
Let  be the subspace spanned by (v, w). For this proof, we denote the induced metric on
be the subspace spanned by (v, w). For this proof, we denote the induced metric on  by
by  , and its associated curvature tensor by
, and its associated curvature tensor by  . By definition,
. By definition,  is equal to
is equal to  , the Gaussian curvature of
, the Gaussian curvature of  at p.
at p.
 in M vanishes at p. To see why, let
in M vanishes at p. To see why, let  be arbitrary, and let
be arbitrary, and let  be the g-geodesic with initial velocity z, whose image lies in
be the g-geodesic with initial velocity z, whose image lies in  for t sufficiently near 0. By the Gauss formula for vector fields along curves,
for t sufficiently near 0. By the Gauss formula for vector fields along curves,
 gives
gives  . Since z was an arbitrary element of
. Since z was an arbitrary element of  and
and  is symmetric, polarization shows that
is symmetric, polarization shows that  at p. (We cannot in general expect
at p. (We cannot in general expect  to vanish at other points of
to vanish at other points of  —it is only at p that all g-geodesics starting tangent to
—it is only at p that all g-geodesics starting tangent to  remain in
remain in  .) The Gauss equation then tells us that the curvature tensors of M and
.) The Gauss equation then tells us that the curvature tensors of M and  are related at p by
are related at p by
 .
. for
for  . Based on the observations above, we see that the sectional curvature of
. Based on the observations above, we see that the sectional curvature of  is
is
 . The Gram–Schmidt algorithm yields an orthonormal basis as follows:
. The Gram–Schmidt algorithm yields an orthonormal basis as follows:

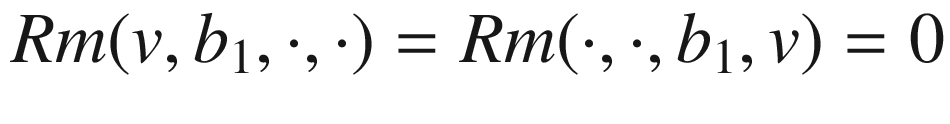 because
because  is a multiple of v. To simplify the denominator of this last expression, we substitute
is a multiple of v. To simplify the denominator of this last expression, we substitute  to obtain
to obtain

 Exercise 8.30. Suppose (M, g) is a Riemannian manifold and
Exercise 8.30. Suppose (M, g) is a Riemannian manifold and  for some positive constant
for some positive constant  . Use Theorem 7.30 to prove that for every
. Use Theorem 7.30 to prove that for every  and plane
and plane  , the sectional curvatures of
, the sectional curvatures of  with respect to
with respect to  and g are related by
and g are related by  .
.
Proposition 8.29 shows that one important piece of quantitative information provided by the curvature tensor is that it encodes the sectional curvatures of all plane sections. It turns out, in fact, that this is all of the information contained in the curvature tensor: as the following proposition shows, the sectional curvatures completely determine the curvature tensor.
Proposition 8.31.
 and
and 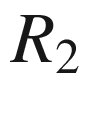 are
algebraic curvature tensors on a finite-dimensional inner product space V. If for every pair of linearly independent vectors
are
algebraic curvature tensors on a finite-dimensional inner product space V. If for every pair of linearly independent vectors  ,
,
 .
.Proof.
Let  and
and  be tensors satisfying the hypotheses, and set
be tensors satisfying the hypotheses, and set  . Then D is an algebraic curvature tensor, and
. Then D is an algebraic curvature tensor, and  for all
for all  . (This is true by hypothesis when v and w are linearly independent, and it is true by the symmetries of D when they are not.) We need to show that
. (This is true by hypothesis when v and w are linearly independent, and it is true by the symmetries of D when they are not.) We need to show that  .
.



We can also give a geometric interpretation of the Ricci and scalar curvatures on a Riemannian manifold. Since the Ricci tensor is symmetric and bilinear, Lemma 8.11 shows that it is completely determined by its values of the form  for unit vectors v.
for unit vectors v.
Proposition 8.32
(Geometric Interpretation of Ricci and Scalar Curvatures). Let (M, g) be a Riemannian n-manifold and  .
.
- (a)
For every unit vector
 ,
,  is the sum of the sectional curvatures of the 2-planes spanned by
is the sum of the sectional curvatures of the 2-planes spanned by  , where
, where  is any orthonormal basis for
is any orthonormal basis for  with
with  .
. - (b)
The scalar curvature at p is the sum of all sectional curvatures of the 2-planes spanned by ordered pairs of distinct basis vectors in any orthonormal basis.
Proof.
 , let
, let  be as in the hypothesis. Then
be as in the hypothesis. Then  is given by
is given by
 be any orthonormal basis for
be any orthonormal basis for  , and compute
, and compute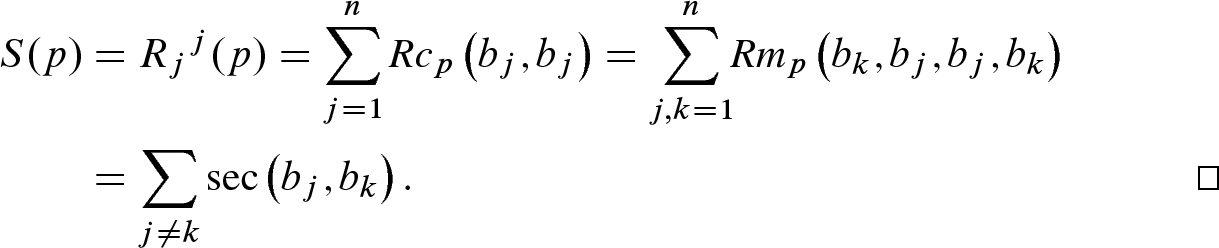
One consequence of this proposition is that if (M, g) is a Riemannian manifold in which all sectional curvatures are positive, then the Ricci and scalar curvatures are both positive as well. The analogous statement holds if “positive" is replaced by “negative," “nonpositive," or “nonnegative."
If the opposite sign convention is chosen for the curvature tensor, then the right-hand side of formula (8.28) has to be adjusted accordingly, with  taking the place of
taking the place of  . This is so that whatever sign convention is chosen for the curvature tensor, the notion of positive or negative sectional, Ricci, or scalar curvature has the same meaning for everyone.
. This is so that whatever sign convention is chosen for the curvature tensor, the notion of positive or negative sectional, Ricci, or scalar curvature has the same meaning for everyone.
Sectional Curvatures of the Model Spaces
We can now compute the sectional curvatures of our three families of frame-homogeneous model spaces. A Riemannian metric or Riemannian manifold is said to have constant sectional curvature if the sectional curvatures are the same for all planes at all points.
Lemma 8.33.
If a Riemannian manifold (M, g) is frame-homogeneous, then it has constant sectional curvature.
Proof.
Frame homogeneity implies, in particular, that given two 2-planes at the same or different points, there is an isometry taking one to the other. The result follows from the isometry invariance of the curvature tensor. 
Thus to compute the sectional curvature of one of our model spaces, it suffices to compute the sectional curvature for one plane at one point in each space.
Theorem 8.34
- (a)
 has constant sectional curvature 0.
has constant sectional curvature 0. - (b)
 has constant sectional curvature
has constant sectional curvature  .
. - (c)
 has constant sectional curvature
has constant sectional curvature  .
.
Proof.
First we consider the simplest case: Euclidean
space. Since the curvature tensor of  is identically zero, clearly all sectional curvatures are zero. This is also easy to see geometrically, since each plane section is actually a plane, which has zero Gaussian curvature.
is identically zero, clearly all sectional curvatures are zero. This is also easy to see geometrically, since each plane section is actually a plane, which has zero Gaussian curvature.
Next consider the
sphere  . We need only compute the sectional curvature of the plane
. We need only compute the sectional curvature of the plane  spanned by
spanned by  at the point
at the point  . The geodesics with initial velocities in
. The geodesics with initial velocities in  are great circles in the
are great circles in the  subspace. Therefore
subspace. Therefore  is isometric to the round 2-sphere of radius R embedded in
is isometric to the round 2-sphere of radius R embedded in  . As Example 8.25 showed,
. As Example 8.25 showed,  has Gaussian curvature
has Gaussian curvature  . Therefore
. Therefore  has constant sectional curvature equal to
has constant sectional curvature equal to  .
.
Finally, the proof for
hyperbolic spaces is left to Problem 8-28. 
Note that for every real number c, exactly one of the model spaces listed above has constant sectional curvature c. These spaces will play vital roles in our comparison and local-to-global theorems in the last two chapters of the book.
 Exercise 8.35. Show that the metric on
real projective space
Exercise 8.35. Show that the metric on
real projective space  defined in Example 2.34 has constant positive sectional curvature.
defined in Example 2.34 has constant positive sectional curvature.
Since the sectional curvatures determine the curvature tensor, one would expect to have an explicit formula for the full curvature tensor when the sectional curvature is constant. Such a formula is provided in the following proposition.
Proposition 8.36.
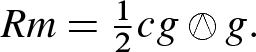



Proof.
Problem 8-29. 
The basic concepts of Riemannian metrics and sectional curvatures in arbitrary dimensions were introduced by Bernhard Riemann in a famous 1854 lecture at Göttingen University [Spi97, Vol. II, Chap. 4]. These were just a few of the seminal accomplishments in his tragically short life.
Problems
- 8-1.
Suppose U is an open set in
 and
and  is a smooth function. Let
is a smooth function. Let  be the graph of f, endowed with the induced Riemannian metric and upward unit normal (see Example 2.19).
be the graph of f, endowed with the induced Riemannian metric and upward unit normal (see Example 2.19).- (a)
Compute the components of the shape operator in graph coordinates, in terms of f and its partial derivatives.
- (b)
Let
 be the n-dimensional paraboloid defined as the graph of
be the n-dimensional paraboloid defined as the graph of  . Compute the principal curvatures of M.
. Compute the principal curvatures of M.(Used on p. 361.)
- (a)
- 8-2.
Let (M, g) be an embedded Riemannian hypersurface in a Riemannian manifold
 , let F be a local defining function for M, and let
, let F be a local defining function for M, and let  .
.- (a)Show that the scalar second fundamental form of M with respect to the unit normal N is given byfor all

 .
. - (b)Show that the mean curvature of M is given bywhere

 and
and  is the divergence operator of
is the divergence operator of  (see Problem 5-14). [Hint: First prove the following linear-algebra lemma: If V is a finite-dimensional inner product space,
(see Problem 5-14). [Hint: First prove the following linear-algebra lemma: If V is a finite-dimensional inner product space,  is a unit vector, and
is a unit vector, and  is a linear map that takes
is a linear map that takes  to
to  , then
, then  , where
, where  is defined by
is defined by  .]
.]
- (a)
- 8-3.
Let C be an embedded smooth curve in the half-plane
 , and let
, and let  be the surface of revolution determined by C as in Example 2.20. Let
be the surface of revolution determined by C as in Example 2.20. Let  be a unit-speed local parametrization of C, and let X be the local parametrization of
be a unit-speed local parametrization of C, and let X be the local parametrization of  given by (2.11).
given by (2.11).- (a)
Compute the shape operator and principal curvatures of
 in terms of a and b, and show that the principal directions at each point are tangent to the meridians and latitude circles.
in terms of a and b, and show that the principal directions at each point are tangent to the meridians and latitude circles. - (b)
Show that the Gaussian curvature of
 at a point
at a point  is equal to
is equal to  .
.
- (a)
- 8-4.
Show that there is a surface of revolution in
 that has constant Gaussian curvature equal to 1 but does not have constant principal curvatures. [Remark: We will see in Chapter 10 that this surface is locally isometric to
that has constant Gaussian curvature equal to 1 but does not have constant principal curvatures. [Remark: We will see in Chapter 10 that this surface is locally isometric to  (see Cor. 10.15), so this gives an example of two nonflat hypersurfaces in
(see Cor. 10.15), so this gives an example of two nonflat hypersurfaces in  that are locally isometric but have different principal curvatures.]
that are locally isometric but have different principal curvatures.] - 8-5.
Let
 be the paraboloid given by
be the paraboloid given by  , with the induced metric. Prove that S is isotropic at only one point. (Used on p. 56.)
, with the induced metric. Prove that S is isotropic at only one point. (Used on p. 56.) - 8-6.Suppose (M, g) is a Riemannian manifold, and
 is a regular (but not necessarily unit-speed) curve in M. Show that the geodesic curvature of
is a regular (but not necessarily unit-speed) curve in M. Show that the geodesic curvature of  at
at  is where the norm in the numerator is the one defined by (8.27). Show also that in
is where the norm in the numerator is the one defined by (8.27). Show also that in
 with the Euclidean metric, the formula can be written
with the Euclidean metric, the formula can be written 
- 8-7.
For
 , let
, let  be the surface of revolution obtained by revolving the curve
be the surface of revolution obtained by revolving the curve  around the z-axis, called a catenoid. Show that
around the z-axis, called a catenoid. Show that  is a minimal surface for each w.
is a minimal surface for each w. - 8-8.
For
 , let
, let  be the one-dimensional submanifold
be the one-dimensional submanifold  ; it is the union of two unit circles lying in the
; it is the union of two unit circles lying in the  planes. Let
planes. Let  , where c is the unique positive solution to the equation
, where c is the unique positive solution to the equation  . Prove that if
. Prove that if  , then there are two distinct positive values
, then there are two distinct positive values  such that the portions of the catenoids
such that the portions of the catenoids  and
and  lying in the region
lying in the region  are minimal surfaces with boundary
are minimal surfaces with boundary  (using the notation of Problem 8-7), while if
(using the notation of Problem 8-7), while if  , there is exactly one such value, and if
, there is exactly one such value, and if  , there are none. [Remark: This phenomenon can be observed experimentally. If you dip two parallel wire circles into soapy water, as long as they are close together they will form an area-minimizing soap film in the shape of a portion of a catenoid (the one with the larger “waist,”
, there are none. [Remark: This phenomenon can be observed experimentally. If you dip two parallel wire circles into soapy water, as long as they are close together they will form an area-minimizing soap film in the shape of a portion of a catenoid (the one with the larger “waist,”  in the notation above). As you pull the circles apart, the “waist" of the catenoid gets smaller, until the ratio of the distance between the circles to their diameter reaches
in the notation above). As you pull the circles apart, the “waist" of the catenoid gets smaller, until the ratio of the distance between the circles to their diameter reaches  , at which point the film will burst and the only soap film that can be formed is two disjoint flat disks.]
, at which point the film will burst and the only soap film that can be formed is two disjoint flat disks.] - 8-9.
Let
 be a Riemannian hypersurface, and let N be a smooth unit normal vector field along M. At each point
be a Riemannian hypersurface, and let N be a smooth unit normal vector field along M. At each point  ,
,  can be thought of as a unit vector in
can be thought of as a unit vector in  and therefore as a point in
and therefore as a point in  . Thus each choice of unit normal vector field defines a smooth map
. Thus each choice of unit normal vector field defines a smooth map  , called the Gauss map of
, called the Gauss map of  . Show that
. Show that  , where K is the Gaussian curvature of M.
, where K is the Gaussian curvature of M. - 8-10.Suppose
 is a product metric on
is a product metric on  as in (2.12). (See also Problem 7-6.)
as in (2.12). (See also Problem 7-6.)- (a)
Show that for each point
 , the submanifolds
, the submanifolds  and
and  are totally geodesic.
are totally geodesic. - (b)
Show that
 for every 2-plane
for every 2-plane  spanned by
spanned by  and
and  .
. - (c)
Show that if
 and
and  both have nonnegative sectional curvature, then
both have nonnegative sectional curvature, then  does too; and if
does too; and if  and
and  both have nonpositive sectional curvature, then
both have nonpositive sectional curvature, then  does too.
does too. - (d)
Now suppose
 has constant sectional curvature
has constant sectional curvature  for
for  ; let
; let  . Show that (M, g) is Einstein if and only if
. Show that (M, g) is Einstein if and only if  ; and (M, g) has constant sectional curvature if and only if
; and (M, g) has constant sectional curvature if and only if  or
or  .
.(Used on p. 366.)
- (a)
- 8-11.
Suppose
 is a smooth surface,
is a smooth surface,  , and
, and  is a normal vector to M at p. Show that if
is a normal vector to M at p. Show that if  is any affine plane containing p and parallel to
is any affine plane containing p and parallel to  , then there is a neighborhood U of p in
, then there is a neighborhood U of p in  such that
such that  is a smooth embedded curve in
is a smooth embedded curve in  , and the principal curvatures of M at p are equal to the minimum and maximum signed Euclidean curvatures of these curves as
, and the principal curvatures of M at p are equal to the minimum and maximum signed Euclidean curvatures of these curves as  varies. [Remark: This justifies the informal recipe for computing principal curvatures given in Chapter 1.]
varies. [Remark: This justifies the informal recipe for computing principal curvatures given in Chapter 1.] - 8-12.
Suppose
 is a
Riemannian submersion, and
is a
Riemannian submersion, and  has all sectional curvatures bounded below by a constant c. Use O’Neill’s formula (Problem 7-14) to show that the sectional curvatures of (M, g) are bounded below by the same constant.
has all sectional curvatures bounded below by a constant c. Use O’Neill’s formula (Problem 7-14) to show that the sectional curvatures of (M, g) are bounded below by the same constant. - 8-13.
Let
 be the
Riemannian submersion described in Example 2.30. In this problem, we identify
be the
Riemannian submersion described in Example 2.30. In this problem, we identify  with
with  by means of coordinates
by means of coordinates  defined by
defined by  .
.- (a)Show that the vector fieldon

 is tangent to
is tangent to  and spans the vertical space
and spans the vertical space  at each point
at each point  . (The implicit summation here is from 1 to
. (The implicit summation here is from 1 to  .)
.) - (b)Show that for all horizontal vector fields W, Z on
 , where
, where![$$\begin{aligned}{}[W,Z]^V = -d\omega (W, Z) S = 2\langle W, JZ\rangle S, \end{aligned}$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_Equ97.png)
 is the 1-form on
is the 1-form on  given by and
given by and
 is the real-linear orthogonal map given by (This is just multiplication by
is the real-linear orthogonal map given by (This is just multiplication by
 in complex coordinates. Notice that
in complex coordinates. Notice that  .)
.) - (c)Using O’Neill’s formula (Problem 7-14), show that the curvature tensor of
 satisfies for every
satisfies for every
 and
and  , where
, where  are horizontal lifts of w, x, y, z to an arbitrary point
are horizontal lifts of w, x, y, z to an arbitrary point  .
. - (d)Using the notation of part (c), show that for orthonormal vectors
 , the sectional curvature of the plane spanned by
, the sectional curvature of the plane spanned by  is
is 
- (e)
Show that for
 , the sectional curvatures at each point of
, the sectional curvatures at each point of  take on all values between 1 and 4, inclusive, and conclude that
take on all values between 1 and 4, inclusive, and conclude that  is not frame-homogeneous.
is not frame-homogeneous. - (f)
Compute the Gaussian curvature of
 .
.(Used on pp. 56, 262, 367.)
- (a)
- 8-14.
Show that a Riemannian 3-manifold is Einstein if and only if it has constant sectional curvature.
- 8-15.
Suppose (M, g) is a 3-dimensional Riemannian manifold that is homogeneous and isotropic. Show that g has constant sectional curvature. Show that the analogous result in dimension 4 is not true. [Hint: See Problem 8-13.]
- 8-16.
For each
 , let
, let  be the
Berger metric on
be the
Berger metric on  defined in Problem 3-10. Compute the sectional curvatures with respect to
defined in Problem 3-10. Compute the sectional curvatures with respect to  of the planes spanned by (X, Y), (Y, Z), and (Z, X). Prove that if
of the planes spanned by (X, Y), (Y, Z), and (Z, X). Prove that if  , then
, then  is homogeneous but not isotropic anywhere. (Used on p. 56.)
is homogeneous but not isotropic anywhere. (Used on p. 56.) - 8-17.
Let G be a Lie group with a bi-invariant metric g (see Problem 7-13).
- (a)
Suppose X and Y are orthonormal elements of
 . Show that
. Show that ![$$\sec (X_p, Y_p) = \tfrac{1}{4}\big |[X, Y]\big |^2$$](../images/56724_2_En_8_Chapter/56724_2_En_8_Chapter_TeX_IEq874.png) for each
for each  , and conclude that the sectional curvatures of (G, g) are all nonnegative.
, and conclude that the sectional curvatures of (G, g) are all nonnegative. - (b)
Show that every Lie subgroup of G is totally geodesic in G.
- (c)
Now suppose G is connected. Show that G is flat if and only if it is abelian.
(Used on p. 282.)
- (a)
- 8-18.
Suppose (M, g) is a Riemannian hypersurface in a Riemannian manifold
 , and N is a unit normal vector field along M. We say that M is convex (with respect to N) if its scalar second fundamental form satisfies
, and N is a unit normal vector field along M. We say that M is convex (with respect to N) if its scalar second fundamental form satisfies  for all
for all  . Show that if M is convex and
. Show that if M is convex and  has sectional curvatures bounded below by a constant c, then all sectional curvatures of M are bounded below by c.
has sectional curvatures bounded below by a constant c, then all sectional curvatures of M are bounded below by c. - 8-19.Suppose (M, g) is a Riemannian hypersurface in an
 -dimensional Lorentz manifold
-dimensional Lorentz manifold  , and N is a smooth unit normal vector field along M. Define the
scalar second fundamental form
h and the shape operator s by requiring that
, and N is a smooth unit normal vector field along M. Define the
scalar second fundamental form
h and the shape operator s by requiring that  and
and  for all
for all  . Prove the
following Lorentz analogues of the formulas of Theorem 8.13 (with notation as in that theorem):
. Prove the
following Lorentz analogues of the formulas of Theorem 8.13 (with notation as in that theorem):- (a)
Gauss Formula:
 .
. - (b)
Gauss Formula for a Curve:
 .
. - (c)
Weingarten Equation:
 .
. - (d)
Gauss Equation:
 .
. - (e)
Codazzi Equation:
 .
.
- (a)
- 8-20.Suppose
 is an
is an  -dimensional Lorentz manifold, and assume that
-dimensional Lorentz manifold, and assume that  satisfies the Einstein field equation with a cosmological constant:
satisfies the Einstein field equation with a cosmological constant:  , where
, where  is a constant and T is a smooth symmetric 2-tensor field (see p. 211). Let (M, g) be a Riemannian hypersurface in
is a constant and T is a smooth symmetric 2-tensor field (see p. 211). Let (M, g) be a Riemannian hypersurface in  , and let h be its scalar second fundamental form as defined in Problem 8-19. Use the results of Problem 8-19 to show that g and h satisfy the following
Einstein constraint equations
on M: where S is the scalar curvature of g,
, and let h be its scalar second fundamental form as defined in Problem 8-19. Use the results of Problem 8-19 to show that g and h satisfy the following
Einstein constraint equations
on M: where S is the scalar curvature of g,
 the divergence of h with respect to g as defined in Problem 5-16,
the divergence of h with respect to g as defined in Problem 5-16,  is the function
is the function  , and J is the 1-form
, and J is the 1-form  . [Remark: When J and
. [Remark: When J and  are both zero, these equations, known as the vacuum Einstein constraint equations, are necessary conditions for g and h to be the metric and second fundamental form of a Riemannian hypersurface in an
are both zero, these equations, known as the vacuum Einstein constraint equations, are necessary conditions for g and h to be the metric and second fundamental form of a Riemannian hypersurface in an  -dimensional Lorentz manifold satisfying the vacuum Einstein field equation with cosmological constant
-dimensional Lorentz manifold satisfying the vacuum Einstein field equation with cosmological constant  . It was proved in 1950 by Yvonne Choquet-Bruhat that these conditions are also sufficient; for a proof, see [CB09, pp. 166–168].]
. It was proved in 1950 by Yvonne Choquet-Bruhat that these conditions are also sufficient; for a proof, see [CB09, pp. 166–168].] - 8-21.For every linear endomorphism
 , the associated quadratic form is the function
, the associated quadratic form is the function  defined by
defined by  . Prove that [Hint: Show that
. Prove that [Hint: Show that
 when
when  by examining the effect of the isometry and compute
by examining the effect of the isometry and compute
 using the fact that
using the fact that  on the sphere.] [Remark: It is a standard fact of linear algebra that the trace of A is independent of the choice of basis. This gives a geometric interpretation to the trace as n times the average value of the associated quadratic form Q.]
on the sphere.] [Remark: It is a standard fact of linear algebra that the trace of A is independent of the choice of basis. This gives a geometric interpretation to the trace as n times the average value of the associated quadratic form Q.](Used on p. 313.)
- 8-22.Let (M, g) be a Riemannian n-manifold and
 . Proposition 8.32 gave a geometric interpretation of the Ricci curvature at p based on a choice of orthonormal basis. This problem describes an interpretation that does not refer to a basis. For each unit vector
. Proposition 8.32 gave a geometric interpretation of the Ricci curvature at p based on a choice of orthonormal basis. This problem describes an interpretation that does not refer to a basis. For each unit vector  , prove that where
, prove that where
 denotes the set of unit vectors in
denotes the set of unit vectors in  that are orthogonal to v and
that are orthogonal to v and  denotes the Riemannian metric on
denotes the Riemannian metric on  induced from the flat metric
induced from the flat metric  on
on  . [Hint: Use Problem 8-21.]
. [Hint: Use Problem 8-21.] - 8-23.
Suppose (M, g) is a connected n-dimensional Riemannian manifold, and a Lie group G acts isometrically and effectively on M. Problem 5-12 showed that
 . Prove that if equality holds, then g has constant sectional curvature.
. Prove that if equality holds, then g has constant sectional curvature. - 8-24.Let (M, g) be a connected Riemannian manifold. Recall the definition of k-point homogeneous from Problem 6-18. Prove the following:
- (a)
If (M, g) is homogeneous, then it has constant scalar curvature.
- (b)
If (M, g) is 2-point homogeneous, then it is Einstein.
- (c)
If (M, g) is 3-point homogeneous, then it has constant sectional curvature.
- (a)
- 8-25.For
 , suppose
, suppose  is a Riemannian manifold of dimension
is a Riemannian manifold of dimension  with constant sectional curvature
with constant sectional curvature  ; and let
; and let  be the product metric on
be the product metric on  . Show that the Weyl tensor of g is given by where
. Show that the Weyl tensor of g is given by where
 and
and  for
for  . Conclude that (M, g) is locally conformally flat if and only if
. Conclude that (M, g) is locally conformally flat if and only if  . (See also Problem 7-6.)
. (See also Problem 7-6.)(Used on p. 67.)
- 8-26.Let (M, g) be a 4-dimensional Riemannian manifold. Given
 and an orthonormal basis
and an orthonormal basis  for
for  , prove that the Weyl tensor at p satisfies where
, prove that the Weyl tensor at p satisfies where
 is the sectional curvature of the plane spanned by
is the sectional curvature of the plane spanned by  .
. - 8-27.
Prove that the Fubini–Study metric on
 is not locally conformally flat. [Hint: Use Problems 8-13 and 8-26.]
is not locally conformally flat. [Hint: Use Problems 8-13 and 8-26.] - 8-28.
Complete the proof of Theorem 8.34 by showing in two ways that the hyperbolic space of radius R has constant sectional curvature equal to
 .
.- (a)
In the hyperboloid model, compute the second fundamental form of
 at the point
at the point  , and use either the general form of the Gauss equation (Thm. 8.5) or the formulas of Problem 8-19.
, and use either the general form of the Gauss equation (Thm. 8.5) or the formulas of Problem 8-19. - (b)
In the Poincaré ball model, use formula (7.44) for the conformal transformation of the curvature to compute the Riemann curvature tensor at the origin.
- (a)
- 8-29.
Prove Proposition 8.36 (curvature tensors on constant-curvature spaces).
- 8-30.Suppose
 is a hypersurface with the induced Riemannian metric. Show that the Ricci tensor of M satisfies where H and s are the mean curvature and shape operator of M, respectively, and
is a hypersurface with the induced Riemannian metric. Show that the Ricci tensor of M satisfies where H and s are the mean curvature and shape operator of M, respectively, and
 .
. - 8-31.
For
 , show that any k points in the hyperbolic space
, show that any k points in the hyperbolic space  lie in a totally geodesic
lie in a totally geodesic  -dimensional submanifold, which is isometric to
-dimensional submanifold, which is isometric to  .
. - 8-32.
Suppose (M, g) is a Riemannian manifold and G is a Lie group acting smoothly and isometrically on M. Let
 be the fixed point set of G, that is, the set of points
be the fixed point set of G, that is, the set of points  such that
such that  for all
for all  . Show that each connected component of S is a smoothly embedded totally geodesic submanifold of M. (The reason for restricting to a single connected component is that different components may have different dimensions.)
. Show that each connected component of S is a smoothly embedded totally geodesic submanifold of M. (The reason for restricting to a single connected component is that different components may have different dimensions.) - 8-33.
Suppose (M, g) is a Riemannian manifold. Let
 denote the bundle of 2-vectors (alternating contravariant 2-tensors) on M.
denote the bundle of 2-vectors (alternating contravariant 2-tensors) on M.- (a)Show that there is a unique fiber metric on
 whose associated norm satisfies for all tangent vectors w, x at every point
whose associated norm satisfies for all tangent vectors w, x at every point
 .
. - (b)Show that there is a unique bundle endomorphism
 , called the curvature operator of g, that satisfies for all tangent vectors w, x, y, z at a point of M, where the inner product on the left-hand side is the one described in part (a).
, called the curvature operator of g, that satisfies for all tangent vectors w, x, y, z at a point of M, where the inner product on the left-hand side is the one described in part (a). (8.30)
(8.30) - (c)
A Riemannian metric is said to have positive curvature operator if
 is positive definite, and negative curvature operator if
is positive definite, and negative curvature operator if  is negative definite. Show that positive curvature operator implies positive sectional curvature, and negative curvature operator implies negative sectional curvature. [Remark: This is the reason for the negative sign in (8.30). If the Riemann curvature tensor is defined as the negative of ours, the negative sign should be omitted.]
is negative definite. Show that positive curvature operator implies positive sectional curvature, and negative curvature operator implies negative sectional curvature. [Remark: This is the reason for the negative sign in (8.30). If the Riemann curvature tensor is defined as the negative of ours, the negative sign should be omitted.] - (d)Show that the converse need not be true, by using the results of Problem 8-13 to compute the following expression on
 with the Fubini–Study metric: where w, x, y, z are orthonormal vectors at an arbitrary point of
with the Fubini–Study metric: where w, x, y, z are orthonormal vectors at an arbitrary point of
 , chosen so that their horizontal lifts satisfy
, chosen so that their horizontal lifts satisfy  and
and  .
.
- (a)