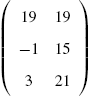
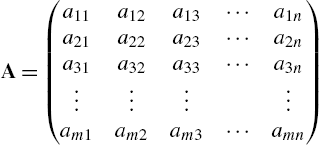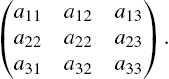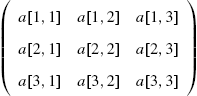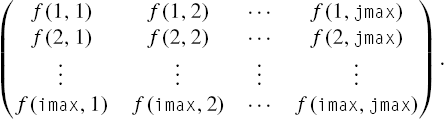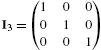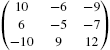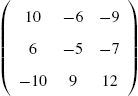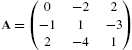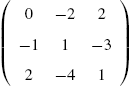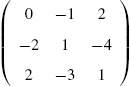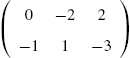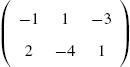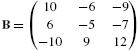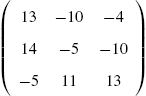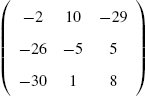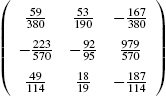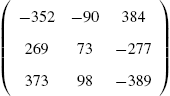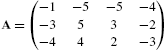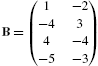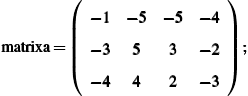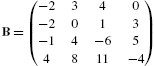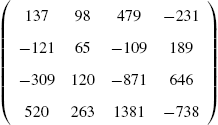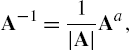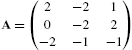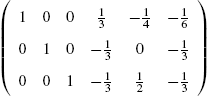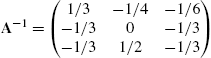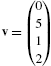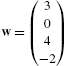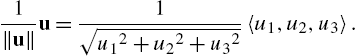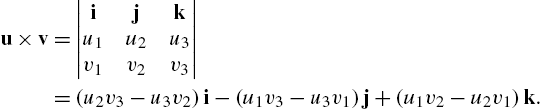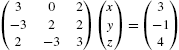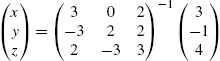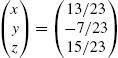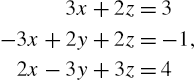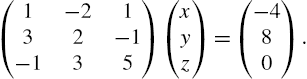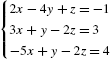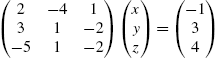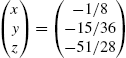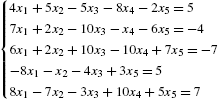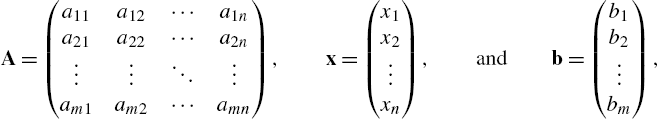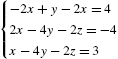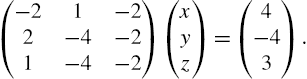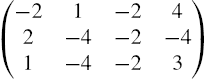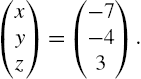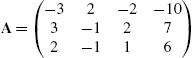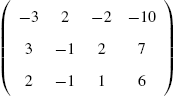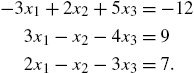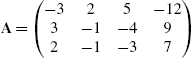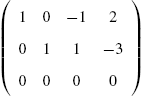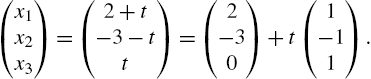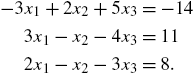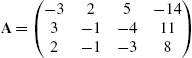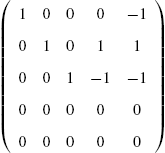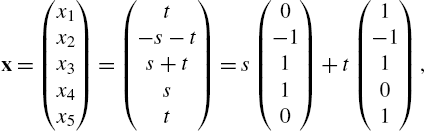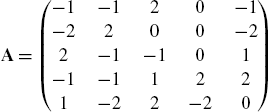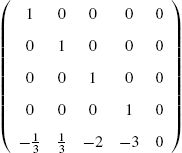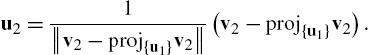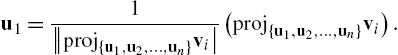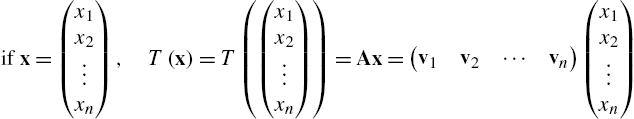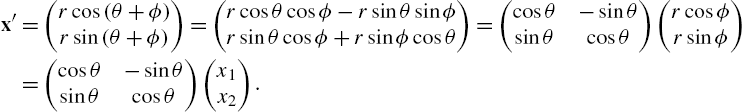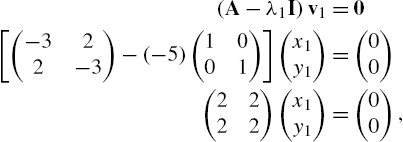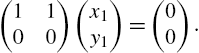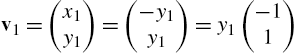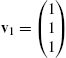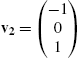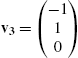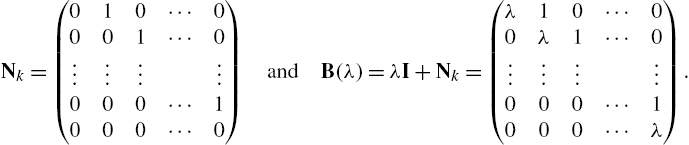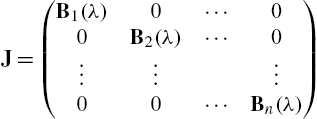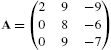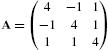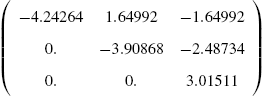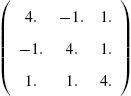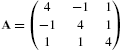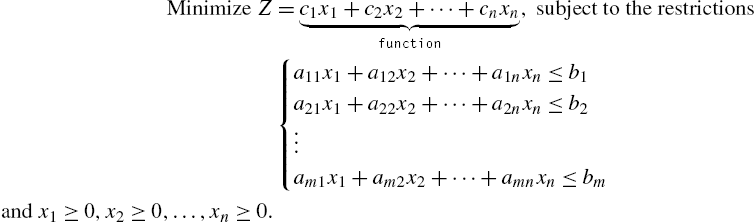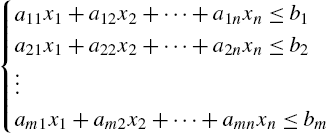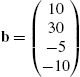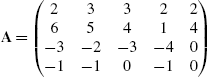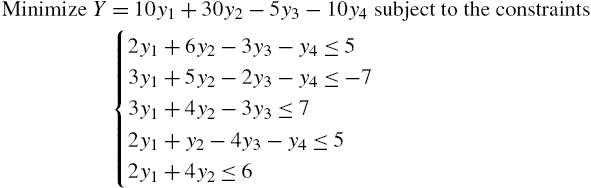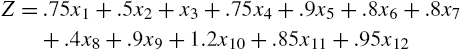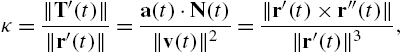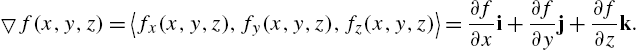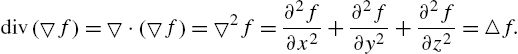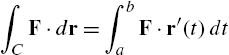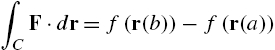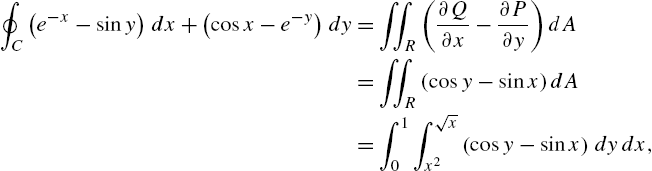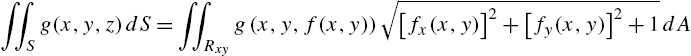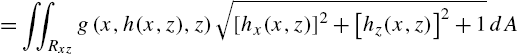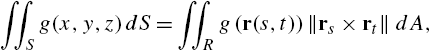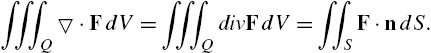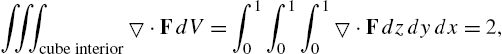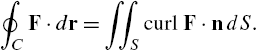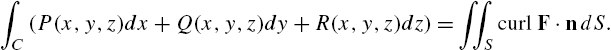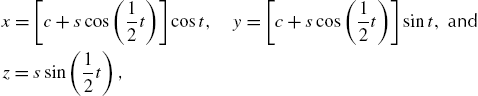Matrices and Vectors: Topics from Linear Algebra and Vector Calculus
Keywords
Linear algebra; Eigenvalues; Eigenvectors; Vector calculus; Engineering applications; Linear programming; Photo special effects; Applying effects to photos and figures
5.1 Nested Lists: Introduction to Matrices, Vectors, and Matrix Operations
5.1.1 Defining Nested Lists, Matrices, and Vectors
In Mathematica, a matrix is a list of lists where each list represents a row of the matrix. Therefore, the ![]() matrix
matrix
is entered with
A={{a11,a12,...,a1n},{a21,a22,...,a2n},...,{am1,am2,...amn}}.
For example, to use Mathematica to define m to be the matrix ![]() enter the command
enter the command
m={{a11,a12},{a21,a22}}.
The command m=Array[a,{2,2}] produces a result equivalent to this. Once a matrix A has been entered, it can be viewed in the traditional row-and-column form using the command MatrixForm[A]. You can quickly construct ![]() matrices by clicking on the
matrices by clicking on the ![]() button from the BasicMathInput palette, which is accessed by going to Palettes followed by BasicMathInput.
button from the BasicMathInput palette, which is accessed by going to Palettes followed by BasicMathInput.
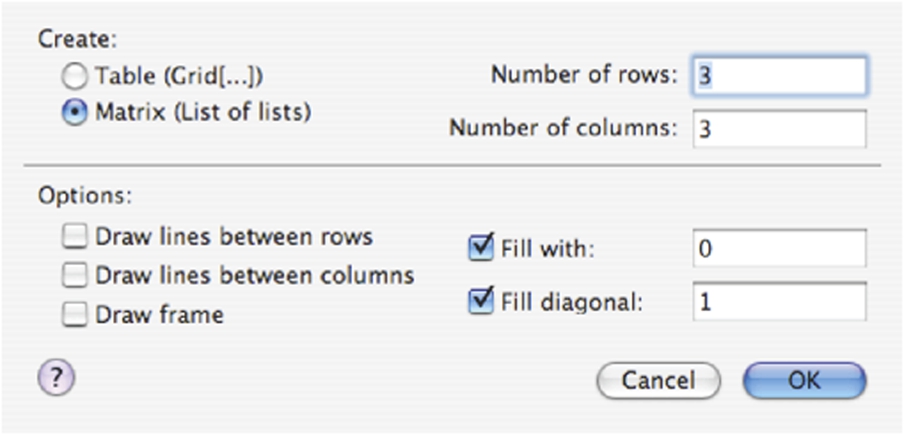
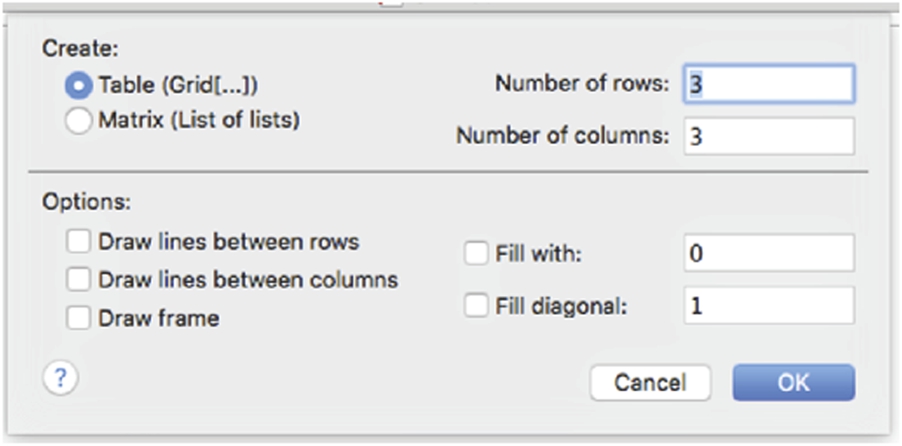
Alternatively, you can construct matrices of any dimension by going to the Mathematica menu under Insert and selecting Create Table/Matrix/Palette...
Use Part, ([[...]]) to select elements of lists. Because of the construct of the matrix, m[[i]] returns the ith row of M. The transpose of M, ![]() , is the matrix obtained by interchanging the rows and columns of matrix M. Thus, to extract the ith column of M, use the commands mt=Transpose[m] followed by mt[[i]].
, is the matrix obtained by interchanging the rows and columns of matrix M. Thus, to extract the ith column of M, use the commands mt=Transpose[m] followed by mt[[i]].
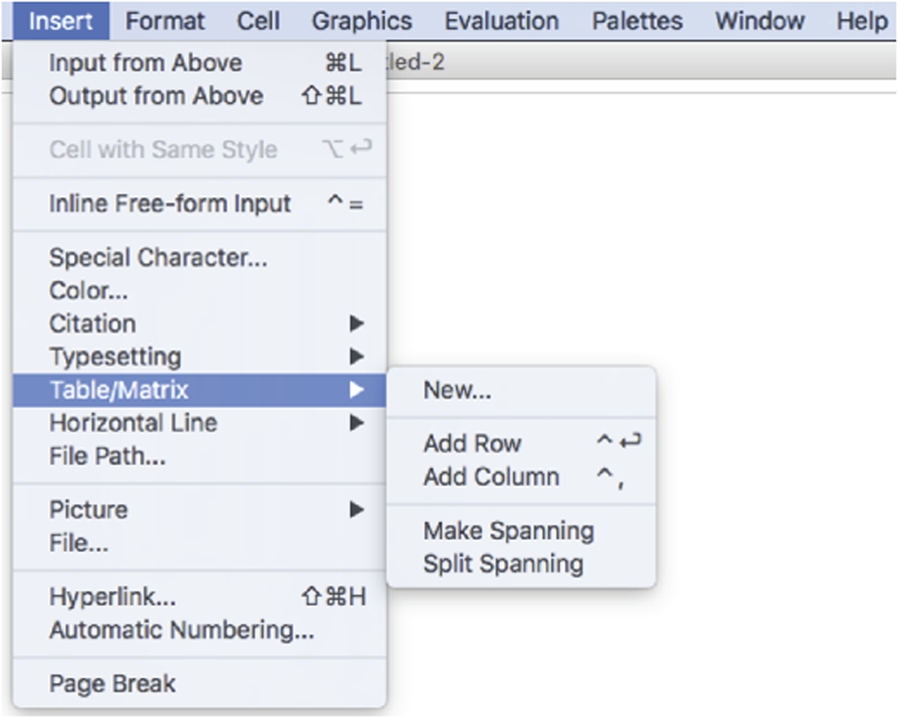
The resulting pop-up window allows you to create tables, matrices, and palettes. To create a matrix, select Matrix, enter the number of rows and columns of the matrix, and select any other options. Pressing the OK button places the desired matrix at the position of the cursor in the Mathematica notebook.
More generally the commands Table[f[i,j],{i,imax},{j,jmax}] and Array[f,{imax,jmax}] yield nested lists corresponding to the ![]() matrix
matrix
Table[f[i,j],{i,imin,imax,istep},{j,jmin,jmax,jstep}] returns the list of lists
{{f[imin,jmin],f[imin,jmin+jstep],...,f[imin,jmax]},
{f[imin+istep,jmin],...,f[imin+istep,jmax]},
...,{f[imax,jmin],...,f[imax,jmax]}}
and the command
Table[f[i,j,k,...],{i,imin,imax,istep},{j,jmin,jmax,jstep},
{k,kmin,kmax,kstep},...]
calculates a nested list; the list associated with i is outermost. If istep is omitted, the stepsize is one.
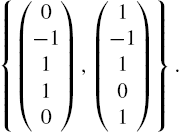
In Mathematica, a vector is a list of numbers and, thus, is entered in the same manner as lists. For example, to use Mathematica to define the row vector vectorv to be ![]() enter vectorv={v1,v2,v3}. Similarly, to define the column vector vectorv to be
enter vectorv={v1,v2,v3}. Similarly, to define the column vector vectorv to be ![]() enter vectorv={v1,v2,v3} or vectorv={{v1},{v2},{v3}}.
enter vectorv={v1,v2,v3} or vectorv={{v1},{v2},{v3}}.
Generally, with Mathematica you do not need to distinguish between row and column vectors: Mathematica usually performs computations with vectors and matrices correctly as long as the computations are well-defined.
5.1.2 Extracting Elements of Matrices
For the ![]() matrix
matrix ![]() defined earlier, m[[1]] yields the first element of matrix m which is the list
defined earlier, m[[1]] yields the first element of matrix m which is the list ![]() or the first row of m; m[[2,1]] yields the first element of the second element of matrix m which is
or the first row of m; m[[2,1]] yields the first element of the second element of matrix m which is ![]() . In general, if m is an
. In general, if m is an ![]() matrix, m[[i,j]] or Part[m,i,j] returns the unique element in the ith row and jth column of m. More specifically, m[[i,j]] yields the jth part of the ith part of m; list[[i]] or Part[list,i] yields the ith part of list; list[[i,j]] or Part[list,i,j] yields the jth part of the ith part of list, and so on.
matrix, m[[i,j]] or Part[m,i,j] returns the unique element in the ith row and jth column of m. More specifically, m[[i,j]] yields the jth part of the ith part of m; list[[i]] or Part[list,i] yields the ith part of list; list[[i,j]] or Part[list,i,j] yields the jth part of the ith part of list, and so on.
If m is a matrix, the ith row of m is extracted with m[[i]]. The command Transpose[m] yields the transpose of the matrix m, the matrix obtained by interchanging the rows and columns of m. We extract columns of m by computing Transpose[m] and then using Part to extract rows from the transpose. Namely, if m is a matrix, Transpose[m][[i]] extracts the ith row from the transpose of m which is the same as the ith column of m.
Alternatively, if A is ![]() (rows × columns) the ith column of A is the vector that consists of the ith part of each row of the matrix so given an i-value Table[A[[j,i]],{j,1,n}] returns the ith column of A.
(rows × columns) the ith column of A is the vector that consists of the ith part of each row of the matrix so given an i-value Table[A[[j,i]],{j,1,n}] returns the ith column of A.
The example illustrates that Take[list,n] returns the first n elements of list; Take[list,{n}] returns the nth element of list; Take[list,{n1,n2,...}] returns the ![]() st,
st, ![]() nd, ... elements of list, and so on.
nd, ... elements of list, and so on.
5.1.3 Basic Computations with Matrices
Mathematica performs all of the usual operations on matrices. Matrix addition (![]() ), scalar multiplication (
), scalar multiplication (![]() ), matrix multiplication (when defined) (AB), and combinations of these operations are all possible. The transpose of A,
), matrix multiplication (when defined) (AB), and combinations of these operations are all possible. The transpose of A, ![]() , is obtained by interchanging the rows and columns of A and is computed with the command Transpose[A]. If A is a square matrix, the determinant of A is obtained with Det[A].
, is obtained by interchanging the rows and columns of A and is computed with the command Transpose[A]. If A is a square matrix, the determinant of A is obtained with Det[A].
If A and B are ![]() matrices satisfying
matrices satisfying ![]() , where I is the
, where I is the ![]() matrix with 1's on the diagonal and 0's elsewhere (the
matrix with 1's on the diagonal and 0's elsewhere (the ![]() identity matrix), B is called the inverse of A and is denoted by
identity matrix), B is called the inverse of A and is denoted by ![]() . If the inverse of a matrix A exists, the inverse is found with Inverse[A]. Thus, assuming that
. If the inverse of a matrix A exists, the inverse is found with Inverse[A]. Thus, assuming that ![]() has an inverse (
has an inverse (![]() ), the inverse is
), the inverse is ![]() .
.
![]()
![]()
Special attention must be given to the notation that must be used in taking the product of a square matrix with itself. The following example illustrates how Mathematica interprets the expression (matrixb)^n. The command (matrixb)^n raises each element of the matrix matrixb to the nth power. The command MatrixPower is used to compute powers of matrices.
If ![]() , the inverse of A can be computed using the formula
, the inverse of A can be computed using the formula
where ![]() is the transpose of the cofactor matrix.
is the transpose of the cofactor matrix.
If A has an inverse, reducing the matrix ![]() to reduced row echelon form results in
to reduced row echelon form results in ![]() . This method is often easier to implement than (5.1).
. This method is often easier to implement than (5.1).
5.1.4 Basic Computations with Vectors
5.1.4.1 Basic Operations on Vectors
Computations with vectors are performed in the same way as computations with matrices.
5.1.4.2 Basic Operations on Vectors in 3-Space
We review the elementary properties of vectors in 3-space. Let
and
be vectors in space.
1. u and v are equal if and only if their components are equal:
2. The length (or norm) of u is
3. If c is a scalar (number),
4. The sum of u and v is defined to be the vector
5. If ![]() , a unit vector with the same direction as u is
, a unit vector with the same direction as u is
6. u and v are parallel if there is a scalar c so that ![]() .
.
7. The dot product of u and v is
If θ is the angle between u and v,
Consequently, u and v are orthogonal if ![]() .
.
8. The cross product of u and v is
You should verify that ![]() and
and ![]() . Hence,
. Hence, ![]() is orthogonal to both u and v.
is orthogonal to both u and v.
Topics from linear algebra (including determinants, which were mentioned previously) are discussed in more detail in the next sections. For now, we illustrate several of the basic operations listed above: u.v and Dot[u,v] compute ![]() ; Cross[u,v] computes
; Cross[u,v] computes ![]() .
.
With the exception of the cross product, the calculations described above can also be performed on vectors in the plane.
If you only need to display a two-dimensional array in row-and-column form, it is easier to use Grid rather than Table together with TableForm or MatrixForm.

For a list of all the options associated with Grid, enter Options[Grid].

Thus,
![]()
creates a basic grid. The first row consists of the entries a, b, and c; the second row d and e; and the third row f. See Fig. 5.5. Note that elements of grids can be any Mathematica object, including other grids.

You can create quite complex arrays with Grid. For example, elements of grids can be any Mathematica object, including grids.
In the following, we use ExampleData to generate several typical Mathematica objects.
![]()
![]()
![]()
![]()
Using our first grid, the above, and a few more strings we create a more sophisticated grid in Fig. 5.6.

![]()
5.2 Linear Systems of Equations
5.2.1 Calculating Solutions of Linear Systems of Equations
To solve the system of linear equations ![]() , where A is the coefficient matrix, b is the known vector and x is the unknown vector, we often proceed as follows: if
, where A is the coefficient matrix, b is the known vector and x is the unknown vector, we often proceed as follows: if ![]() exists, then
exists, then ![]() so
so ![]() .
.
Mathematica offers several commands for solving systems of linear equations, however, that do not depend on the computation of the inverse of A. The command
Solve[{eqn1,eqn2,...,eqnm},{var1,var2,...,varn}]
solves an ![]() system of linear equations (m equations and n unknown variables). Note that both the equations as well as the variables are entered as lists. If one wishes to solve for all variables that appear in a system, the command Solve[{eqn1,eqn2,...eqnn}] attempts to solve eqn1, eqn2, ..., eqnn for all variables that appear in them. (Remember that a double equals sign (==) must be placed between the left and right-hand sides of each equation.)
system of linear equations (m equations and n unknown variables). Note that both the equations as well as the variables are entered as lists. If one wishes to solve for all variables that appear in a system, the command Solve[{eqn1,eqn2,...eqnn}] attempts to solve eqn1, eqn2, ..., eqnn for all variables that appear in them. (Remember that a double equals sign (==) must be placed between the left and right-hand sides of each equation.)
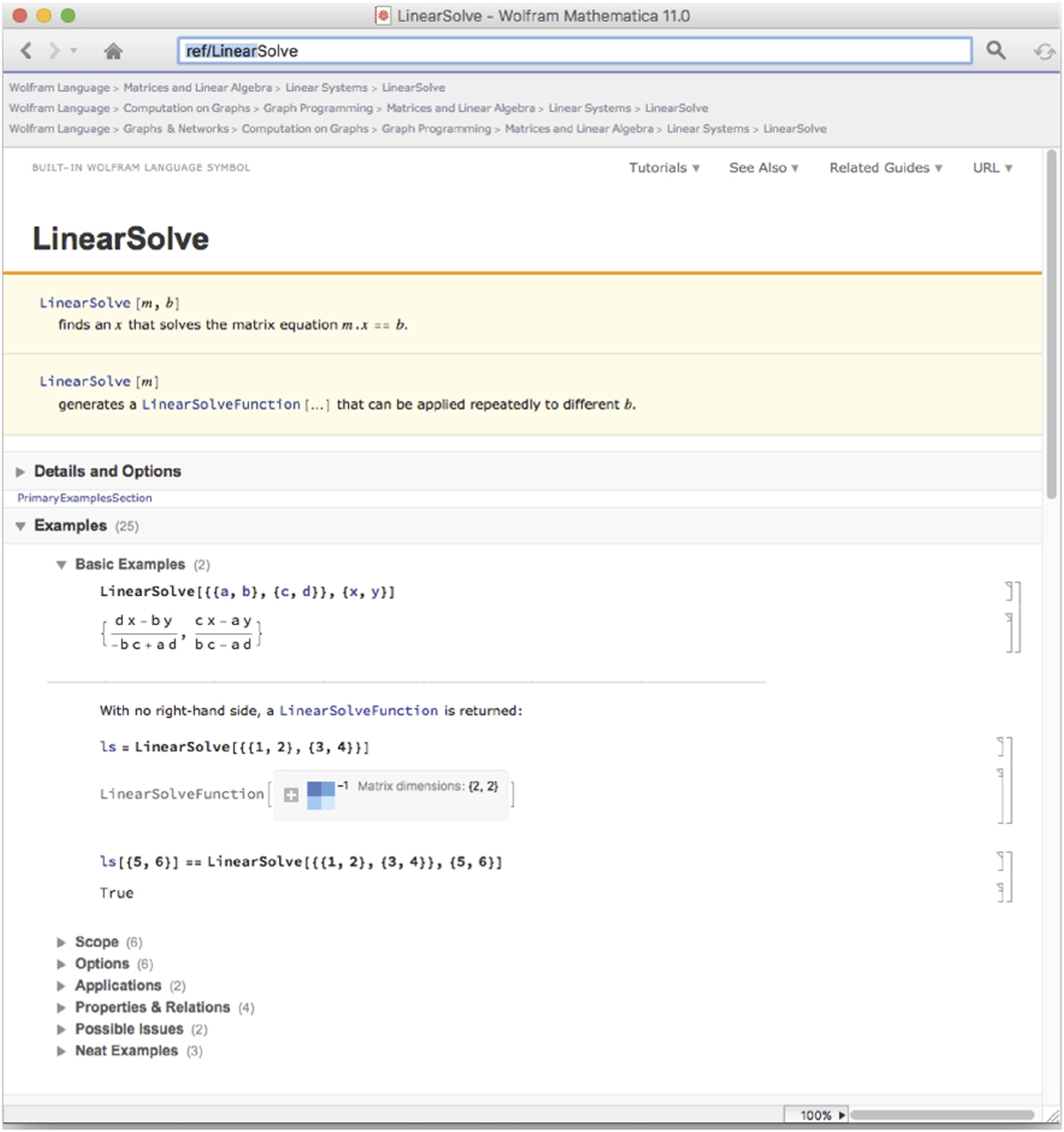
In addition to using Solve to solve a system of linear equations, the command
LinearSolve[A,b]
calculates the solution vector x of the system ![]() . LinearSolve generally solves a system more quickly than does Solve as we see from the comments in the Documentation Center.
. LinearSolve generally solves a system more quickly than does Solve as we see from the comments in the Documentation Center.
Enter indexed variables such ![]() ,
, ![]() , …,
, …, ![]() as x[1], x[2], …, x[n]. If you need to include the entire list, Table[x[i],{i,1,n}] usually produces the desired result(s).
as x[1], x[2], …, x[n]. If you need to include the entire list, Table[x[i],{i,1,n}] usually produces the desired result(s).
5.2.2 Gauss–Jordan Elimination
Given the matrix equation ![]() , where
, where
the ![]() matrix A is called the coefficient matrix for the matrix equation
matrix A is called the coefficient matrix for the matrix equation ![]() and the
and the ![]() matrix
matrix
is called the augmented (or associated) matrix for the matrix equation. We may enter the augmented matrix associated with a linear system of equations directly or we can use commands like Join to help us construct the augmented matrix. For example, if A and B are rectangular matrices that have the same number of columns, Join[A,B] returns ![]() . On the other hand, if A and B are rectangular matrices that have the same number of rows, Join[A,B,2] returns the concatenated matrix
. On the other hand, if A and B are rectangular matrices that have the same number of rows, Join[A,B,2] returns the concatenated matrix ![]() .
.
In the following example, we carry out the steps of the row reduction process.
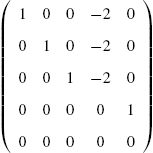
It is important to remember that if you reduce the augmented matrix to reduced-row-echelon form, the results show you the solution to the problem. RowReduce[A] row reduces A to reduced-row-echelon form.
5.3 Selected Topics from Linear Algebra
5.3.1 Fundamental Subspaces Associated with Matrices
Let ![]() be an
be an ![]() matrix with entry
matrix with entry ![]() in the ith row and jth column. The row space of A,
in the ith row and jth column. The row space of A, ![]() , is the spanning set of the rows of A; the column space of A,
, is the spanning set of the rows of A; the column space of A, ![]() , is the spanning set of the columns of A. If A is any matrix, then the dimension of the column space of A is equal to the dimension of the row space of A. The dimension of the row space (column space) of a matrix A is called the rank of A. The nullspace of A is the set of solutions to the system of equations
, is the spanning set of the columns of A. If A is any matrix, then the dimension of the column space of A is equal to the dimension of the row space of A. The dimension of the row space (column space) of a matrix A is called the rank of A. The nullspace of A is the set of solutions to the system of equations ![]() . The nullspace of A is a subspace and its dimension is called the nullity of A. The rank of A is equal to the number of nonzero rows in the row echelon form of A, the nullity of A is equal to the number of zero rows in the row echelon form of A. Thus, if A is a square matrix, the sum of the rank of A and the nullity of A is equal to the number of rows (columns) of A.
. The nullspace of A is a subspace and its dimension is called the nullity of A. The rank of A is equal to the number of nonzero rows in the row echelon form of A, the nullity of A is equal to the number of zero rows in the row echelon form of A. Thus, if A is a square matrix, the sum of the rank of A and the nullity of A is equal to the number of rows (columns) of A.
1. NullSpace[A] returns a list of vectors which form a basis for the nullspace (or kernel) of the matrix A.
2. RowReduce[A] yields the reduced row echelon form of the matrix A.
5.3.2 The Gram–Schmidt Process
A set of vectors ![]() is orthonormal means that
is orthonormal means that ![]() for all values of i and
for all values of i and ![]() for
for ![]() . Given a set of linearly independent vectors
. Given a set of linearly independent vectors ![]() , the set of all linear combinations of the elements of S,
, the set of all linear combinations of the elements of S, ![]() , is a vector space. Note that if S is an orthonormal set and
, is a vector space. Note that if S is an orthonormal set and ![]() , then
, then ![]() . Thus, we may easily express u as a linear combination of the vectors in S. Consequently, if we are given any vector space, V, it is frequently convenient to be able to find an orthonormal basis of V. We may use the Gram–Schmidt process to find an orthonormal basis of the vector space
. Thus, we may easily express u as a linear combination of the vectors in S. Consequently, if we are given any vector space, V, it is frequently convenient to be able to find an orthonormal basis of V. We may use the Gram–Schmidt process to find an orthonormal basis of the vector space ![]() .
.
We summarize the algorithm of the Gram–Schmidt process so that given a set of n linearly independent vectors ![]() , where
, where ![]() , we can construct a set of orthonormal vectors
, we can construct a set of orthonormal vectors ![]() so that
so that ![]() .
.
1. Let ![]() ;
;
2. Compute ![]() ,
, ![]() , and let
, and let
Then, ![]() and
and ![]() ;
;
3. Generally, for ![]() , compute
, compute
![]() , and let
, and let
Then, ![]() and
and
and
4. Because ![]() and
and ![]() is an orthonormal set,
is an orthonormal set, ![]() is an orthonormal basis of V.
is an orthonormal basis of V.
The Gram–Schmidt procedure is well-suited to computer arithmetic. The following code performs each step of the Gram–Schmidt process on a set of n linearly independent vectors ![]() . At the completion of each step of the procedure, gramschmidt[vecs] prints the list of vectors corresponding to
. At the completion of each step of the procedure, gramschmidt[vecs] prints the list of vectors corresponding to ![]() and returns the list of vectors
and returns the list of vectors ![]() . Note how comments are inserted into the code using (*...*).
. Note how comments are inserted into the code using (*...*).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Mathematica contains functions that perform most of the operations discussed here.
1. Orthogonalize[{v1,v2,...},Method->GramSchmidt] returns an orthonormal set of vectors given the set of vectors ![]() . Note that this command does not illustrate each step of the Gram–Schmidt procedure as the gramschmidt function defined above.
. Note that this command does not illustrate each step of the Gram–Schmidt procedure as the gramschmidt function defined above.
2. Normalize[v] returns ![]() given the nonzero vector v.
given the nonzero vector v.
3. Projection[v1,v2] returns the projection of ![]() onto
onto ![]() :
: ![]() .
.
Thus,
![]()
![]()
returns an orthonormal basis for the subspace of ![]() spanned by the vectors
spanned by the vectors ![]() ,
, ![]() , and
, and ![]() . The command
. The command
![]()
![]()
finds a unit vector with the same direction as the vector 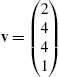 . Entering
. Entering
![]()
![]()
finds the projection of 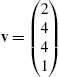 onto
onto 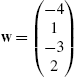 .
.
5.3.3 Linear Transformations
A function ![]() is a linear transformation means that T satisfies the properties
is a linear transformation means that T satisfies the properties ![]() and
and ![]() for all vectors u and v in
for all vectors u and v in ![]() and all real numbers c. Let
and all real numbers c. Let ![]() be a linear transformation and suppose
be a linear transformation and suppose ![]() ,
, ![]() , …,
, …, ![]() where
where ![]() represents the standard basis of
represents the standard basis of ![]() and
and ![]() ,
, ![]() , …,
, …, ![]() are (column) vectors in
are (column) vectors in ![]() . The associated matrix of T is the
. The associated matrix of T is the ![]() matrix
matrix ![]() :
:
Moreover, if A is any ![]() matrix, then A is the associated matrix of the linear transformation defined by
matrix, then A is the associated matrix of the linear transformation defined by ![]() . In fact, a linear transformation T is completely determined by its action on any basis.
. In fact, a linear transformation T is completely determined by its action on any basis.
The kernel of the linear transformation T, ![]() , is the set of all vectors x in
, is the set of all vectors x in ![]() such that
such that ![]() :
: ![]() . The kernel of T is a subspace of
. The kernel of T is a subspace of ![]() . Because
. Because ![]() for all x in
for all x in ![]() ,
, ![]() so the kernel of T is the same as the nullspace of A.
so the kernel of T is the same as the nullspace of A.
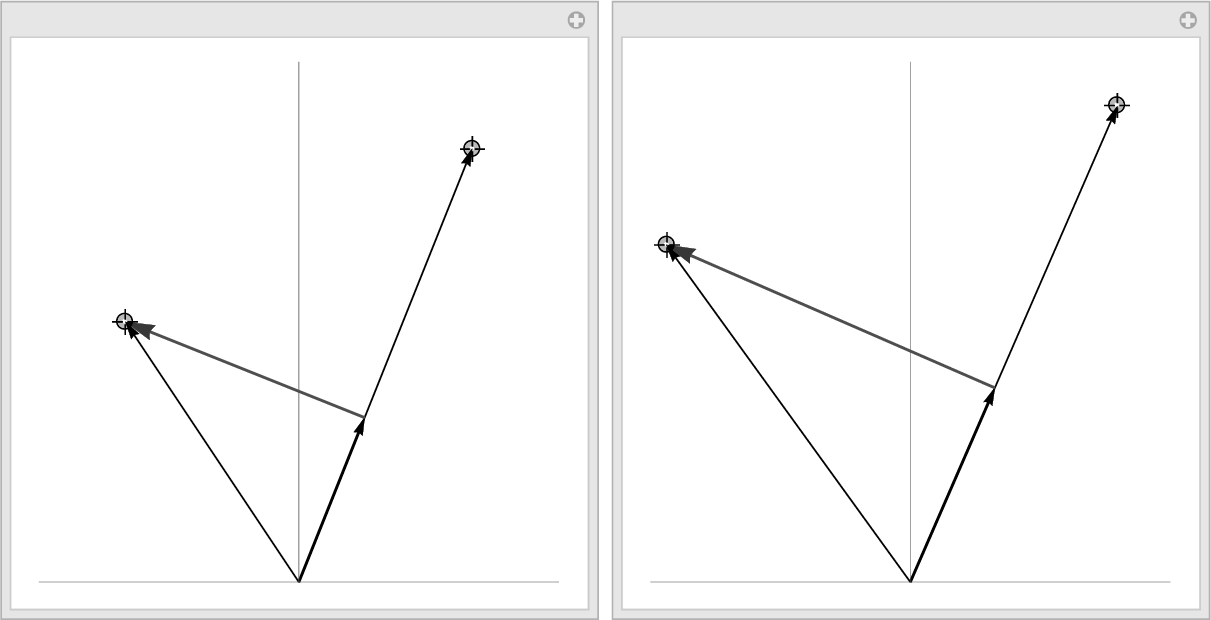
Application: Rotations
Let ![]() be a vector in
be a vector in ![]() and θ an angle. Then, there are numbers r and ϕ given by
and θ an angle. Then, there are numbers r and ϕ given by ![]() and
and ![]() so that
so that ![]() and
and ![]() . When we rotate
. When we rotate ![]() through the angle θ, we obtain the vector
through the angle θ, we obtain the vector ![]() . Using the trigonometric identities
. Using the trigonometric identities ![]() and
and ![]() we rewrite
we rewrite
Thus, the vector ![]() is obtained from x by computing
is obtained from x by computing ![]() . Generally, if θ represents an angle, the linear transformation
. Generally, if θ represents an angle, the linear transformation ![]() defined by
defined by ![]() is called the rotation of
is called the rotation of ![]() through the angle θ. We write code to rotate a polygon through an angle θ. The procedure rotate uses a list of n points and the rotation matrix defined in r to produce a new list of points that are joined using the Line graphics directive. Entering
through the angle θ. We write code to rotate a polygon through an angle θ. The procedure rotate uses a list of n points and the rotation matrix defined in r to produce a new list of points that are joined using the Line graphics directive. Entering
Line[{{x1,y1},{x2,y2},...,{xn,yn}}]
represents the graphics primitive for a line in two dimensions that connects the points listed in {{x1,y1},{x2,y2},...,{xn,yn}}. Entering
Show[Graphics[Line[{{x1,y1},{x2,y2},...,{xn,yn}}]]]
displays the line. This rotation can be determined for one value of θ. However, a more interesting result is obtained by creating a list of rotations for a sequence of angles and then displaying the graphics objects. This is done for ![]() to
to ![]() using increments of
using increments of ![]() . Hence, a list of nine graphs is given for the square with vertices
. Hence, a list of nine graphs is given for the square with vertices ![]() ,
, ![]() ,
, ![]() , and
, and ![]() and displayed in Fig. 5.7.
and displayed in Fig. 5.7.

![]()
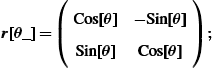
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5.3.4 Eigenvalues and Eigenvectors
Let A be an ![]() matrix. λ is an eigenvalue of A if there is a nonzero vector, v, called an eigenvector, satisfying
matrix. λ is an eigenvalue of A if there is a nonzero vector, v, called an eigenvector, satisfying ![]() . Because
. Because ![]() has a unique solution of
has a unique solution of ![]() if
if ![]() , to find non-zero solutions, v, of
, to find non-zero solutions, v, of ![]() , we begin by solving
, we begin by solving ![]() . That is, we find the eigenvalues of A by solving the characteristic polynomial
. That is, we find the eigenvalues of A by solving the characteristic polynomial ![]() for λ. Once we find the eigenvalues, the corresponding eigenvectors are found by solving
for λ. Once we find the eigenvalues, the corresponding eigenvectors are found by solving ![]() for v.
for v.
If A is ![]() , Eigenvalues[A] finds the eigenvalues of A, Eigenvectors[A] finds the eigenvectors, and Eigensystem[A] finds the eigenvalues and corresponding eigenvectors. CharacteristicPolynomial[A,lambda] finds the characteristic polynomial of A as a function of λ.
, Eigenvalues[A] finds the eigenvalues of A, Eigenvectors[A] finds the eigenvectors, and Eigensystem[A] finds the eigenvalues and corresponding eigenvectors. CharacteristicPolynomial[A,lambda] finds the characteristic polynomial of A as a function of λ.
5.3.5 Jordan Canonical Form
Let ![]() represent a
represent a ![]() matrix with the indicated elements. The
matrix with the indicated elements. The ![]() Jordan block matrix is given by
Jordan block matrix is given by ![]() where λ is a constant:
where λ is a constant:
Hence, ![]() can be defined as
can be defined as 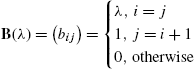 . A Jordan matrix has the form
. A Jordan matrix has the form
where the entries ![]() ,
, ![]() , 2, …, n represent Jordan block matrices.
, 2, …, n represent Jordan block matrices.
Suppose that A is an ![]() matrix. Then there is an invertible
matrix. Then there is an invertible ![]() matrix C such that
matrix C such that ![]() where J is a Jordan matrix with the eigenvalues of A as diagonal elements. The matrix J is called the Jordan canonical form of A. The command
where J is a Jordan matrix with the eigenvalues of A as diagonal elements. The matrix J is called the Jordan canonical form of A. The command
JordanDecomposition[m]
yields a list of matrices {s,j} such that m=s.j.Inverse[s] and j is the Jordan canonical form of the matrix m.
For a given matrix A, the unique monic polynomial q of least degree satisfying ![]() is called the minimal polynomial of A. Let p denote the characteristic polynomial of A. Because
is called the minimal polynomial of A. Let p denote the characteristic polynomial of A. Because ![]() , it follows that q divides p. We can use the Jordan canonical form of a matrix to determine its minimal polynomial.
, it follows that q divides p. We can use the Jordan canonical form of a matrix to determine its minimal polynomial.
5.3.6 The QR Method
The conjugate transpose (or Hermitian adjoint matrix) of the ![]() complex matrix A which is denoted by
complex matrix A which is denoted by ![]() is the transpose of the complex conjugate of A. Symbolically, we have
is the transpose of the complex conjugate of A. Symbolically, we have ![]() . A complex matrix A is unitary if
. A complex matrix A is unitary if ![]() . Given a matrix A, there is a unitary matrix Q and an upper triangular matrix R such that
. Given a matrix A, there is a unitary matrix Q and an upper triangular matrix R such that ![]() . The product matrix QR is called the QR factorization of A. The command
. The product matrix QR is called the QR factorization of A. The command
QRDecomposition[N[m]]
determines the QR decomposition of the matrix m by returning the list {q,r}, where q is an orthogonal matrix, r is an upper triangular matrix and m=Transpose[q].r.
One of the most efficient and most widely used methods for numerically calculating the eigenvalues of a matrix is the QR Method. Given a matrix A, then there is a Hermitian matrix Q and an upper triangular matrix R such that ![]() . If we define a sequence of matrices
. If we define a sequence of matrices ![]() , factored as
, factored as ![]() ;
; ![]() , factored as
, factored as ![]() ;
; ![]() , factored as
, factored as ![]() ; and in general,
; and in general, ![]() ,
, ![]() , 2, … then the sequence
, 2, … then the sequence ![]() converges to a triangular matrix with the eigenvalues of A along the diagonal or to a nearly triangular matrix from which the eigenvalues of A can be calculated rather easily.
converges to a triangular matrix with the eigenvalues of A along the diagonal or to a nearly triangular matrix from which the eigenvalues of A can be calculated rather easily.
5.4 Maxima and Minima Using Linear Programming
5.4.1 The Standard Form of a Linear Programming Problem
We call the linear programming problem of the following form the standard form of the linear programming problem:
The command
Minimize[{function,inequalities},{variables}]
solves the standard form of the linear programming problem. Similarly, the command
Maximize[{function,inequalities},{variables}]
solves the linear programming problem: Maximize ![]() , subject to the restrictions
, subject to the restrictions
and ![]() ,
, ![]() , …,
, …, ![]() .
.
We demonstrate the use of Minimize in the following example.
5.4.2 The Dual Problem
Given the standard form of the linear programming problem in equations (5.2), the dual problem is as follows: “Maximize ![]() subject to the constraints
subject to the constraints ![]() for
for ![]() , 2, …, n and
, 2, …, n and ![]() for
for ![]() , 2, …, m.” Similarly, for the problem: “Maximize
, 2, …, m.” Similarly, for the problem: “Maximize ![]() subject to the constraints
subject to the constraints ![]() for
for ![]() , 2, …, m and
, 2, …, m and ![]() for
for ![]() , 2, …, n,” the dual problem is as follows: “Minimize
, 2, …, n,” the dual problem is as follows: “Minimize ![]() subject to the constraints
subject to the constraints ![]() for
for ![]() , 2, …, n and
, 2, …, n and ![]() for
for ![]() , 2, …, m.”
, 2, …, m.”
Of course, linear programming models can involve numerous variables. Consider the following: given the standard form linear programming problem in equations (5.2), let 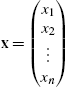 ,
, 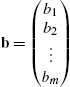 ,
, ![]() , and A denote the
, and A denote the ![]() matrix
matrix 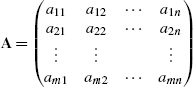 . Then the standard form of the linear programming problem is equivalent to finding the vector x that maximizes
. Then the standard form of the linear programming problem is equivalent to finding the vector x that maximizes ![]() subject to the restrictions
subject to the restrictions ![]() and
and ![]() ,
, ![]() , …,
, …, ![]() . The dual problem is: “Minimize
. The dual problem is: “Minimize ![]() where
where ![]() subject to the restrictions
subject to the restrictions ![]() (componentwise) and
(componentwise) and ![]() ,
, ![]() , …,
, …, ![]() .”
.”
The command
LinearProgramming[c,A,b]
finds the vector x that minimizes the quantity Z=c.x subject to the restrictions A.x>=b and x>=0. LinearProgramming does not yield the minimum value of Z as did Minimize and Maximize and the value must be determined from the resulting vector.
Application: A Transportation Problem
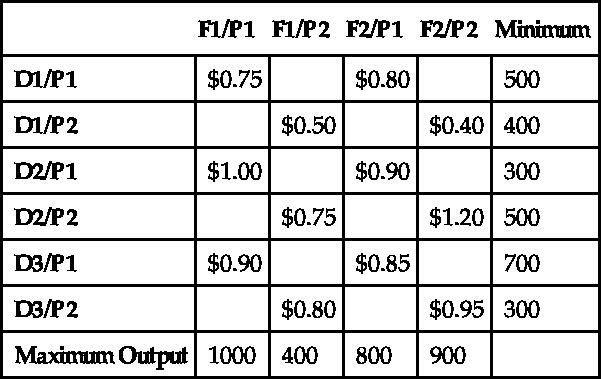
A certain company has two factories, F1 and F2, each producing two products, P1 and P2, that are to be shipped to three distribution centers, D1, D2, and D3. The following table illustrates the cost associated with shipping each product from the factory to the distribution center, the minimum number of each product each distribution center needs, and the maximum output of each factory. How much of each product should be shipped from each plant to each distribution center to minimize the total shipping costs?
| F1/P1 | F1/P2 | F2/P1 | F2/P2 | Minimum | |
| D1/P1 | $0.75 | $0.80 | 500 | ||
| D1/P2 | $0.50 | $0.40 | 400 | ||
| D2/P1 | $1.00 | $0.90 | 300 | ||
| D2/P2 | $0.75 | $1.20 | 500 | ||
| D3/P1 | $0.90 | $0.85 | 700 | ||
| D3/P2 | $0.80 | $0.95 | 300 | ||
| Maximum Output | 1000 | 400 | 800 | 900 |
5.5 Selected Topics from Vector Calculus
5.5.1 Vector-Valued Functions
We now turn our attention to vector-valued functions. In particular, we consider vector-valued functions of the following forms.
For the vector-valued functions (5.3) and (5.4), differentiation and integration are carried out term-by-term, provided that all the terms are differentiable and integrable. Suppose that C is a smooth curve defined by ![]() ,
, ![]() .
.
1. If ![]() , the unit tangent vector,
, the unit tangent vector, ![]() , is
, is ![]() .
.
2. If ![]() , the principal unit normal vector,
, the principal unit normal vector, ![]() , is
, is ![]() .
.
3. The arc length function, ![]() , is
, is ![]() . In particular, the length of C on the interval
. In particular, the length of C on the interval ![]() is
is ![]() .
.
4. The curvature, κ, of C is
where ![]() and
and ![]() .
.
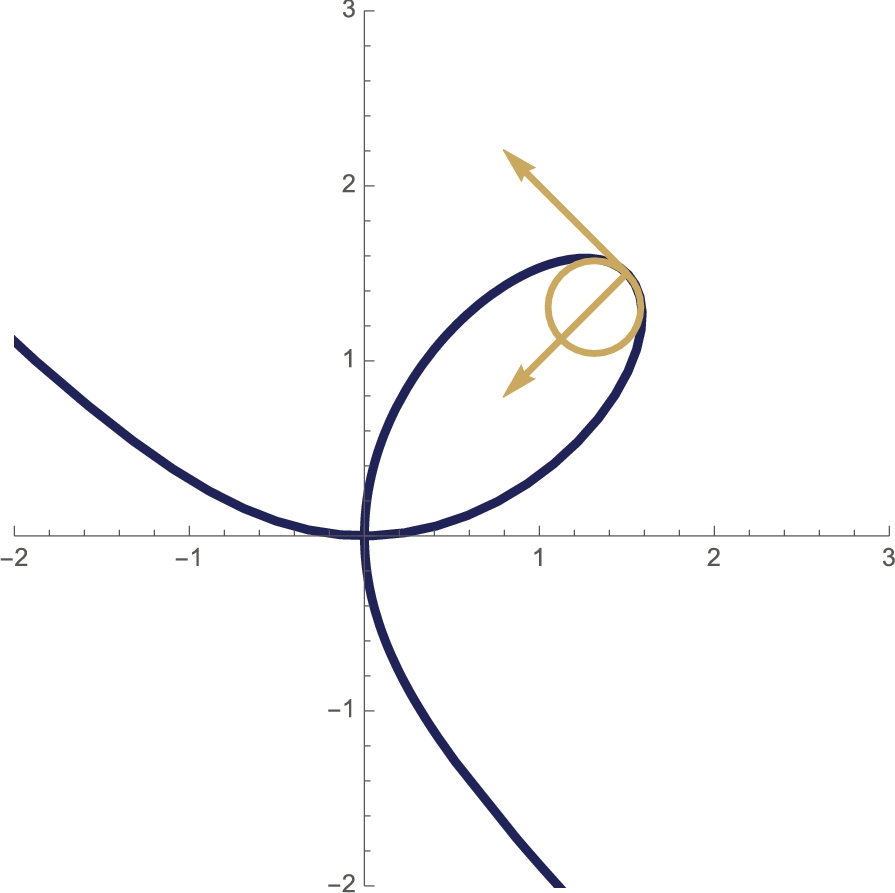
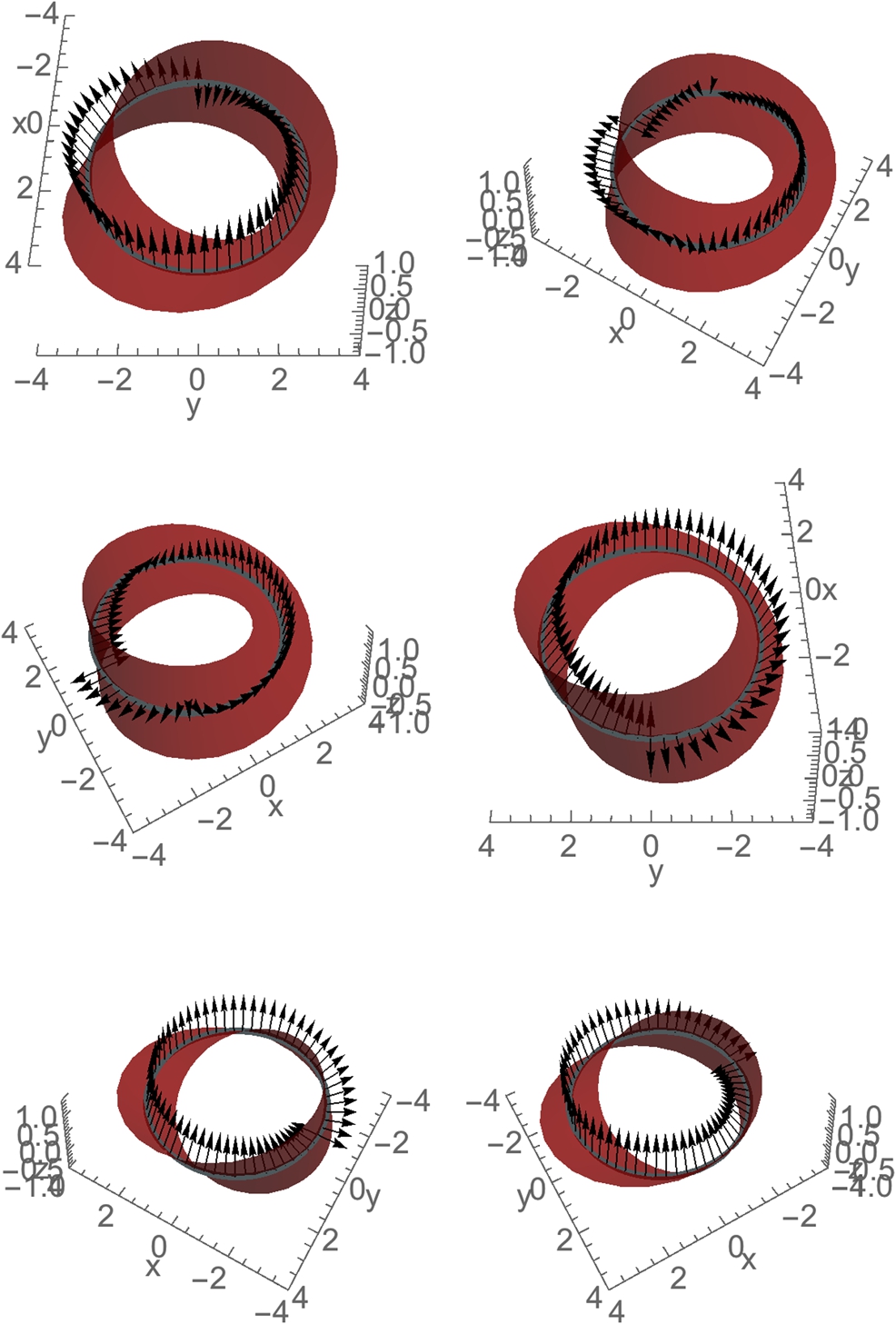
In the example, we computed the curvature at ![]() . Of course, we could choose other t values. With Manipulate,
. Of course, we could choose other t values. With Manipulate,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
we can see the osculating circle at various values of ![]() . See Fig. 5.9.
. See Fig. 5.9.
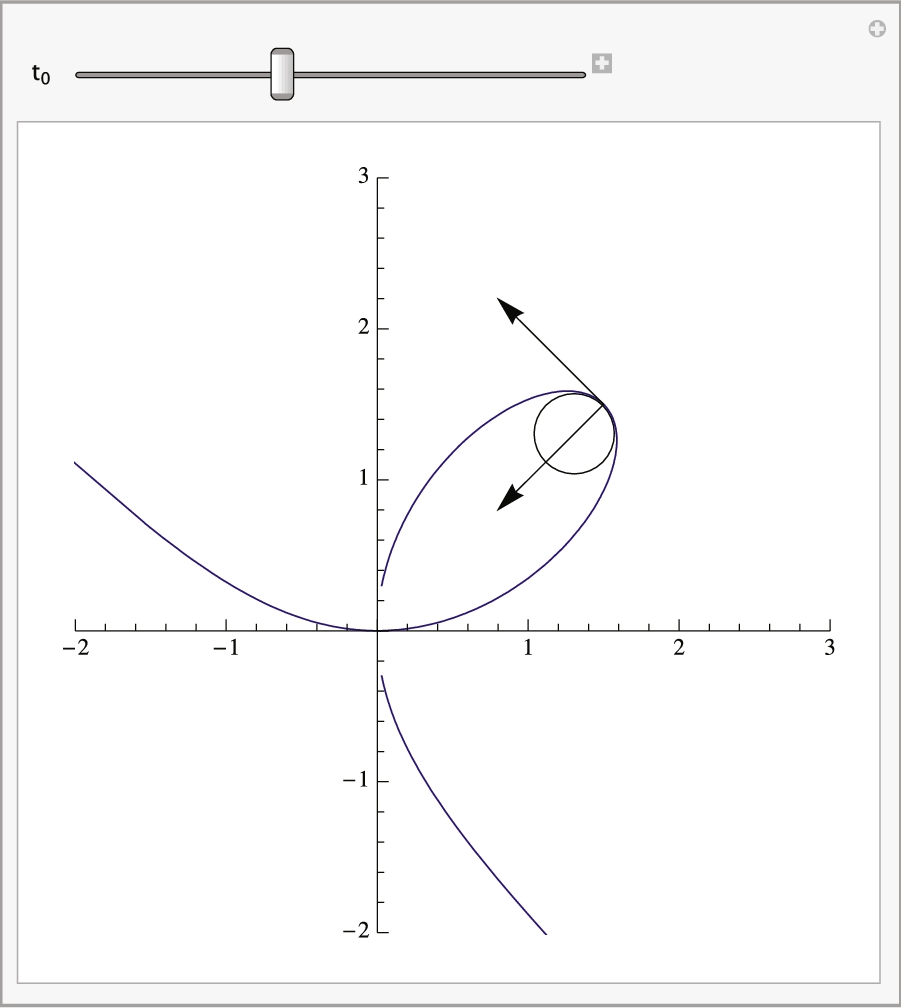
Of course, this particular choice of using the folium to illustrate the procedure could be modified as well. With
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
we not only allow ![]() to vary but also
to vary but also ![]() . Note that the resulting Manipulate object is quite slow on all except the fastest computers. See Fig. 5.10 (b).
. Note that the resulting Manipulate object is quite slow on all except the fastest computers. See Fig. 5.10 (b).

Recall that the gradient of ![]() is the vector-valued function
is the vector-valued function ![]() . Similarly, we define the gradient of
. Similarly, we define the gradient of ![]() to be
to be
A vector field F is conservative if there is a function f, called a potential function, satisfying ![]() . In the special case that
. In the special case that ![]() , F is conservative if and only if
, F is conservative if and only if
The divergence of the vector field ![]() is the scalar field
is the scalar field
The Div command can be used to find the divergence of a vector field:
Div[{P(x,y,z),Q(x,y,z),R(x,y,z)},"Cartesian"]
computes the divergence of ![]() in the Cartesian coordinate system. If you omit “Cartesian,” the default coordinates are the Cartesian coordinate system. However, if you are using a non-Cartesian coordinates system such as cylindrical or spherical coordinates, be sure to replace “Cartesian” with “Cylindrical,” “Spherical” or the name of the coordinate system you are using. Note that Mathematica supports nearly all coordinate systems used by scientists.
in the Cartesian coordinate system. If you omit “Cartesian,” the default coordinates are the Cartesian coordinate system. However, if you are using a non-Cartesian coordinates system such as cylindrical or spherical coordinates, be sure to replace “Cartesian” with “Cylindrical,” “Spherical” or the name of the coordinate system you are using. Note that Mathematica supports nearly all coordinate systems used by scientists.
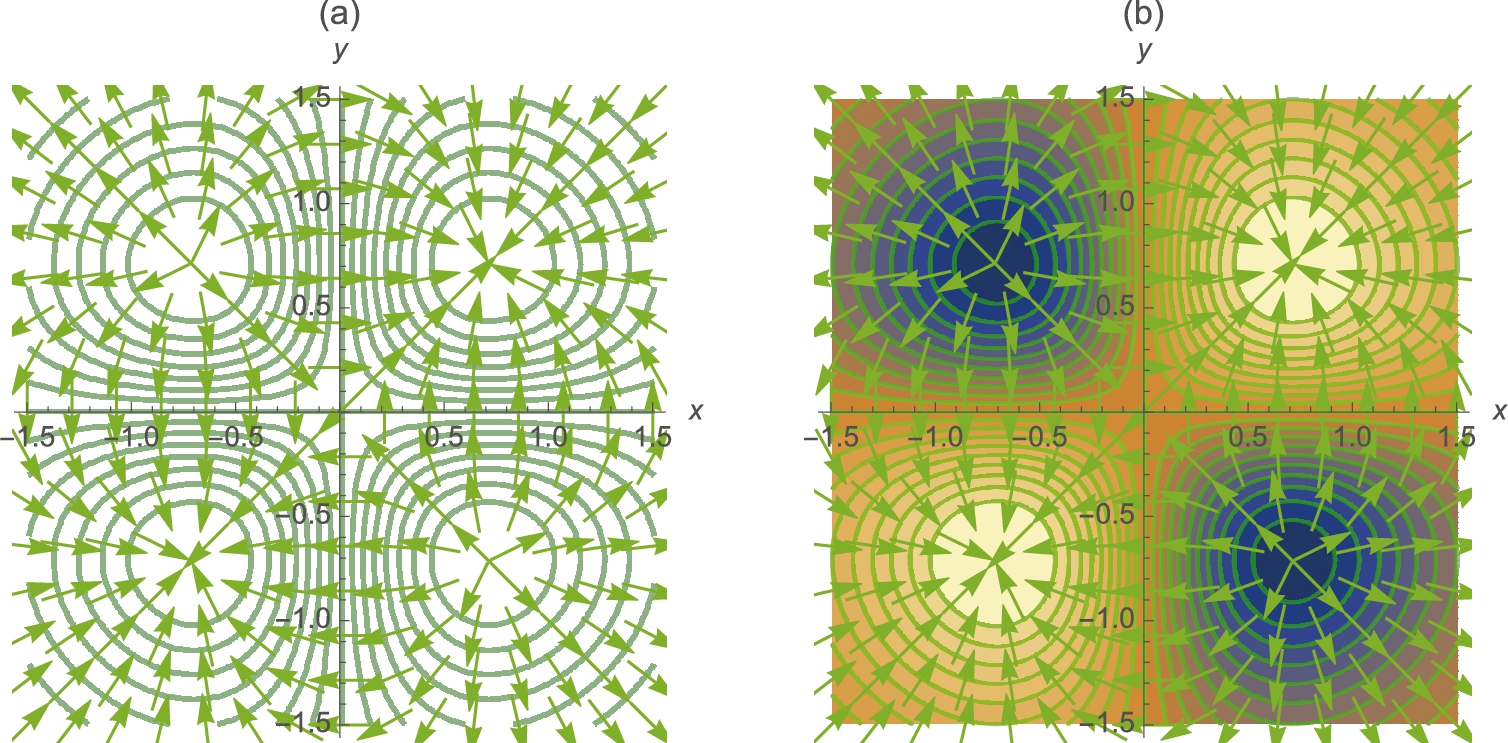
The Laplacian of the scalar field ![]() is defined to be
is defined to be
In the same way that Div computes the divergence of a vector field Laplacian computes the Laplacian of a scalar field.
The curl of the vector field ![]() is
is
If ![]() , F is conservative if and only if
, F is conservative if and only if ![]() , in which case F is said to be irrotational.
, in which case F is said to be irrotational.
5.5.2 Line Integrals
If F is continuous on the smooth curve C with parametrization ![]() ,
, ![]() , the line integral of F on C is
, the line integral of F on C is
If F is conservative and C is piecewise smooth, line integrals can be evaluated using the Fundamental Theorem of Line Integrals.
If C is a piecewise smooth simple closed curve and ![]() and
and ![]() have continuous partial derivatives, Green's Theorem relates the line integral
have continuous partial derivatives, Green's Theorem relates the line integral ![]() to a double integral.
to a double integral.
5.5.3 Surface Integrals
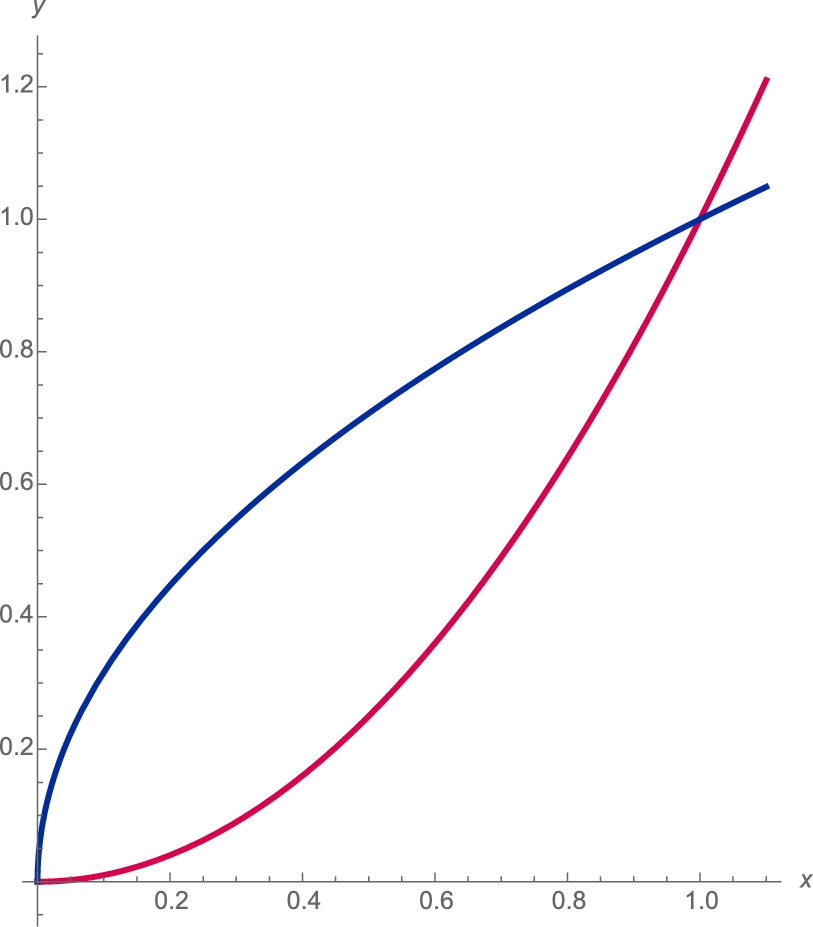
Let S be the graph of ![]() (
(![]() ,
, ![]() ) and let
) and let ![]() (
(![]() ,
, ![]() ) be the projection of S onto the xy (xz, yz) plane. Then,
) be the projection of S onto the xy (xz, yz) plane. Then,
If S is defined parametrically by
the formula
where
is also useful.
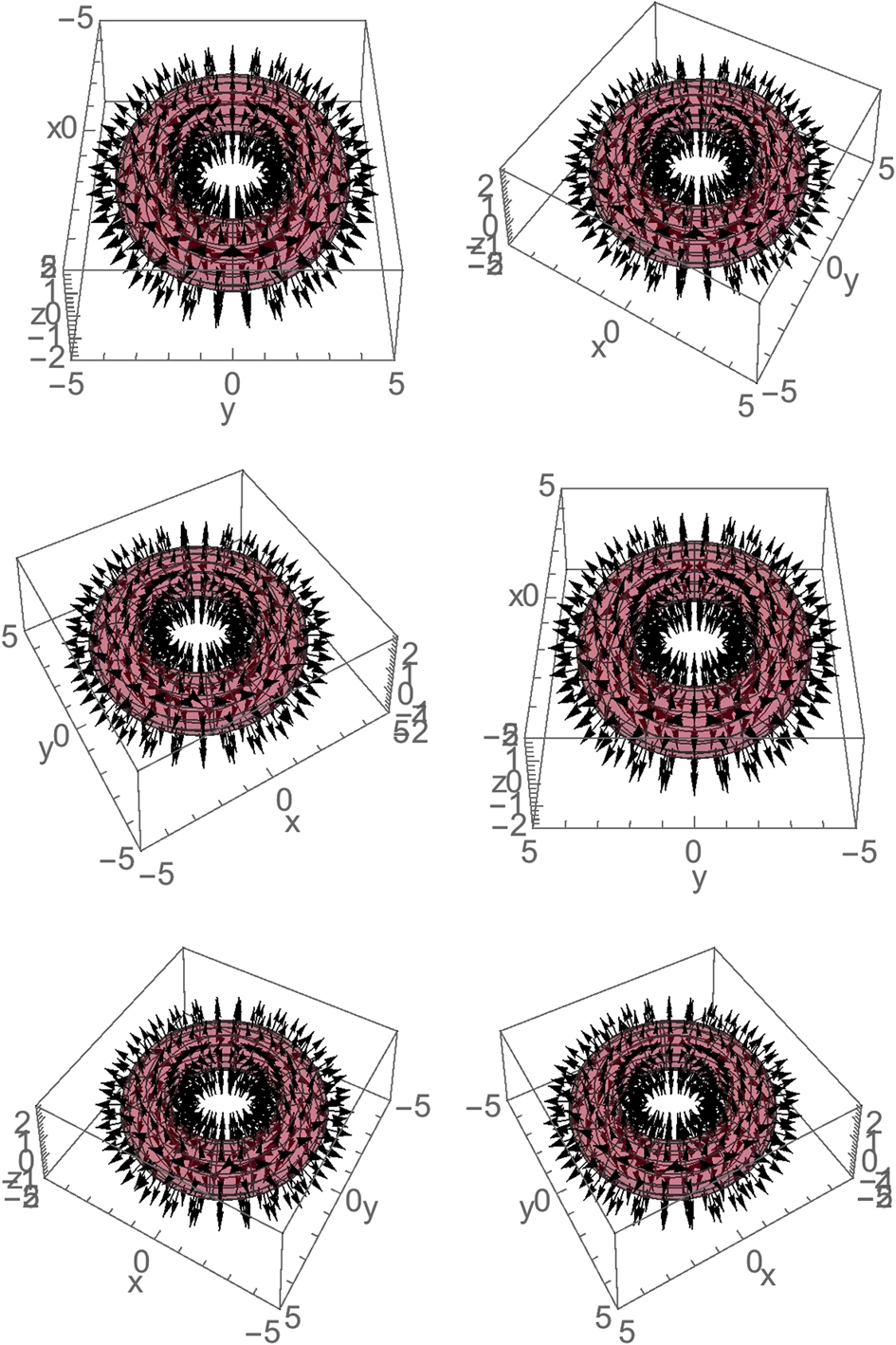
In (5.19), ![]() is called the outward flux of the vector field F across the surface S. If S is a portion of the level curve
is called the outward flux of the vector field F across the surface S. If S is a portion of the level curve ![]() for some g, then a unit normal vector n may be taken to be either
for some g, then a unit normal vector n may be taken to be either
If S is defined parametrically by
a unit normal vector to the surface is ![]() and (5.19) becomes
and (5.19) becomes ![]() .
.
In other words, the surface integral of the normal component of the curl of F taken over S equals the line integral of the tangential component of the field taken over C. In particular, if ![]() , then
, then
5.5.4 A Note on Nonorientability
Suppose that S is the surface determined by
and let
where
if ![]() . If n is defined, n is orthogonal (or perpendicular) to S. We state three familiar definitions of orientable.
. If n is defined, n is orthogonal (or perpendicular) to S. We state three familiar definitions of orientable.
• S is orientable if S has a unit normal vector field, n, that varies continuously between any two points ![]() and
and ![]() on S. (See [5].)
on S. (See [5].)
• S is orientable if S has a continuous unit normal vector field, n. (See [5] and [16].)
• S is orientable if a unit vector n can be defined at every nonboundary point of S in such a way that the normal vectors vary continuously over the surface S. (See [11].)
A path is order preserving if our chosen orientation is preserved as we move along the path.
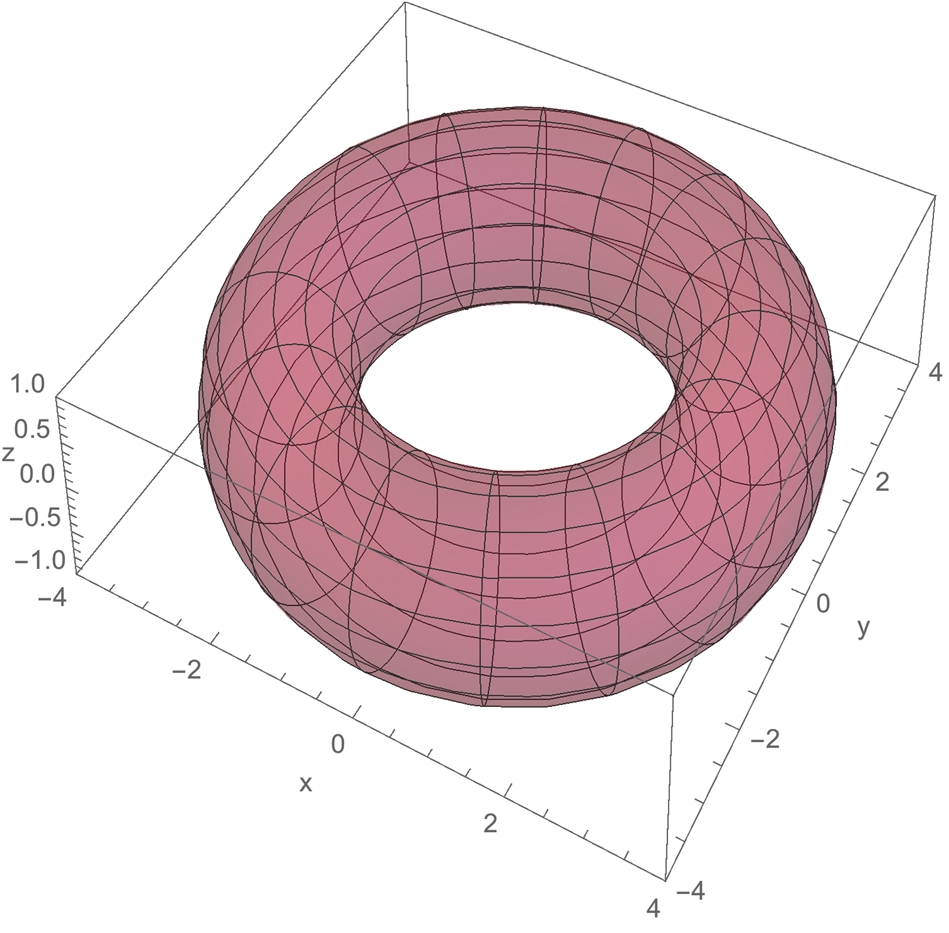
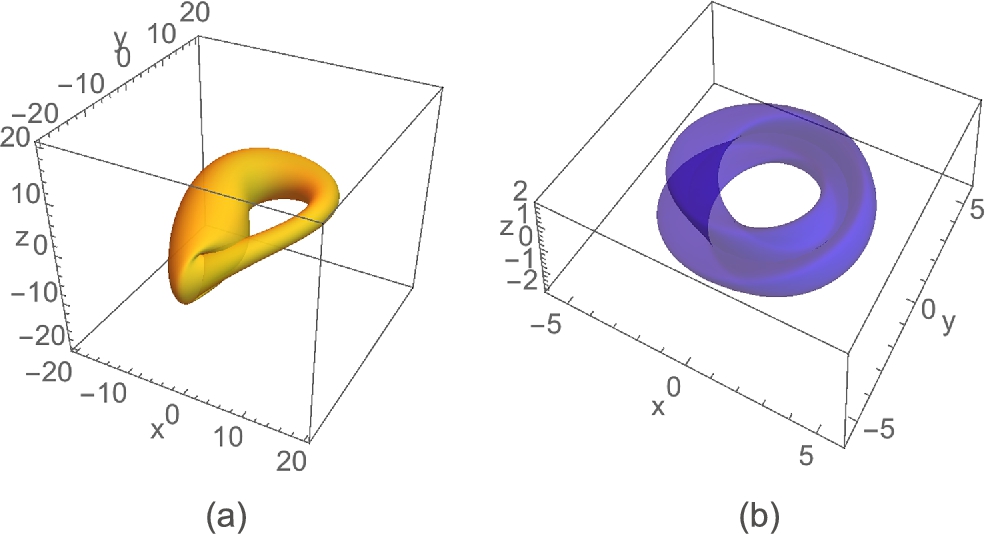
Thus, a surface like a torus is orientable.
If a 2-manifold, S, has an order reversing path (or not order preserving path), S is nonorientable (or not orientable).
Determining whether a given surface S is orientable or not may be a difficult problem.
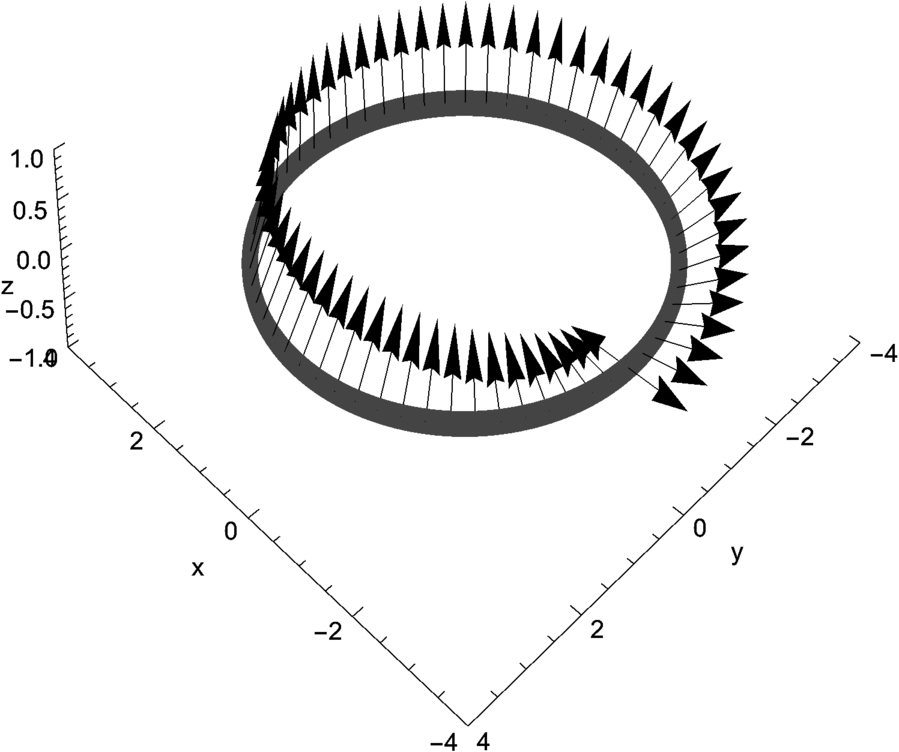
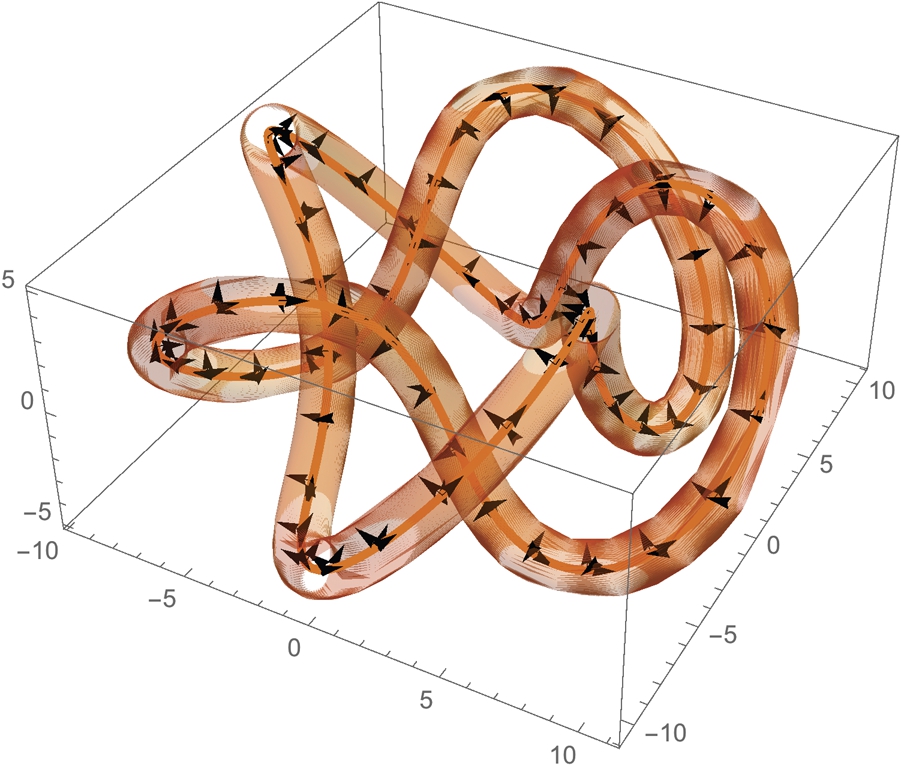
5.5.5 More on Tangents, Normals, and Curvature in R 3 
Earlier, we discussed the unit tangent and normal vectors and curvature for a vector-valued function ![]() . These concepts can be extended to curves and surfaces in space.
. These concepts can be extended to curves and surfaces in space.
For ![]() , the Frenet frame field is the ordered triple
, the Frenet frame field is the ordered triple ![]() , where T is the unit tangent vector field, N is the unit normal vector field, and B is the unit binormal vector field. Each of these vectors has norm 1 and each is orthogonal to the other (the dot product of one with another is 0) and the Frenet formulas are satisfied:
, where T is the unit tangent vector field, N is the unit normal vector field, and B is the unit binormal vector field. Each of these vectors has norm 1 and each is orthogonal to the other (the dot product of one with another is 0) and the Frenet formulas are satisfied: ![]() ,
, ![]() ,
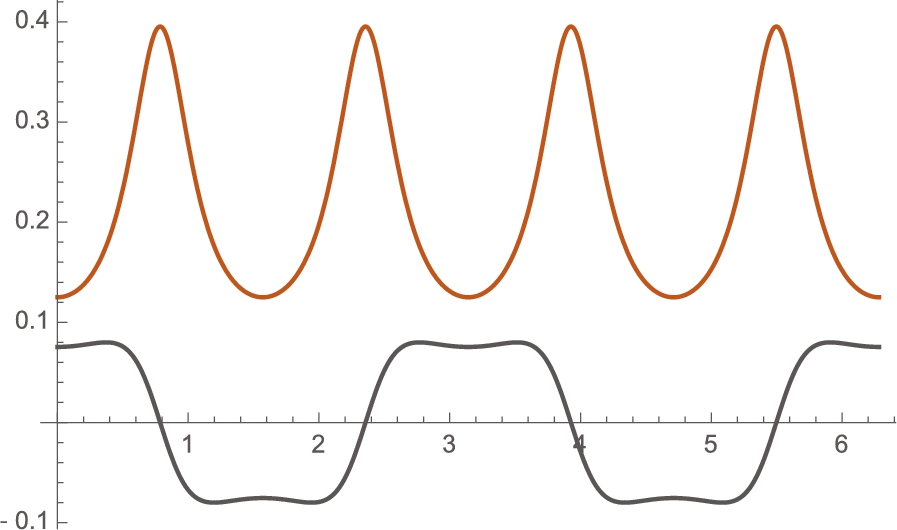
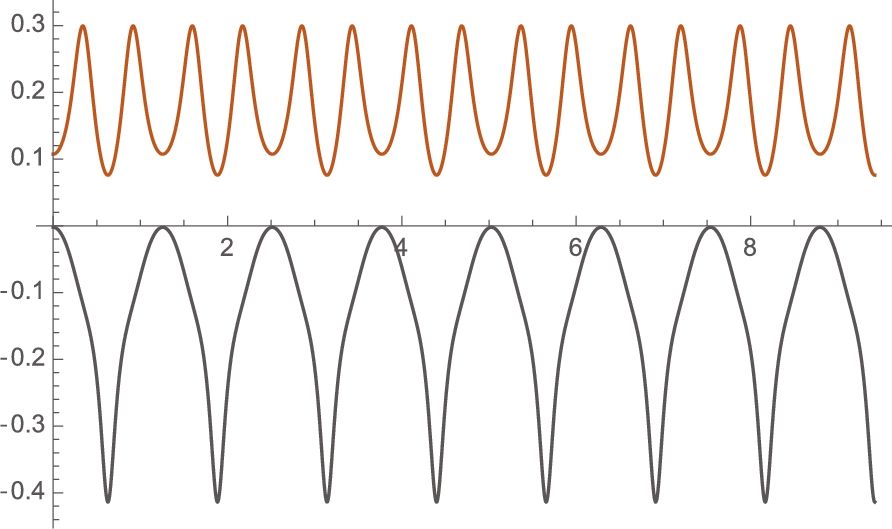
, ![]() . τ is the torsion of the curve γ; κ is the curvature. For the curve
. τ is the torsion of the curve γ; κ is the curvature. For the curve ![]() , formulas for these quantities are given by:
, formulas for these quantities are given by:
We adjust Gray's routines slightly for Mathematica 11. Here is the unit tangent vector,
![]()
![]()
Similarly, the binormal is defined with
![]()
![]()
![]()
![]()
so the unit normal is defined with
![]()
Notice how we use Assumptions to instruct Mathematica to assume that the domain of γ consists of real numbers. In the same manner, we define the curvature and torsion.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
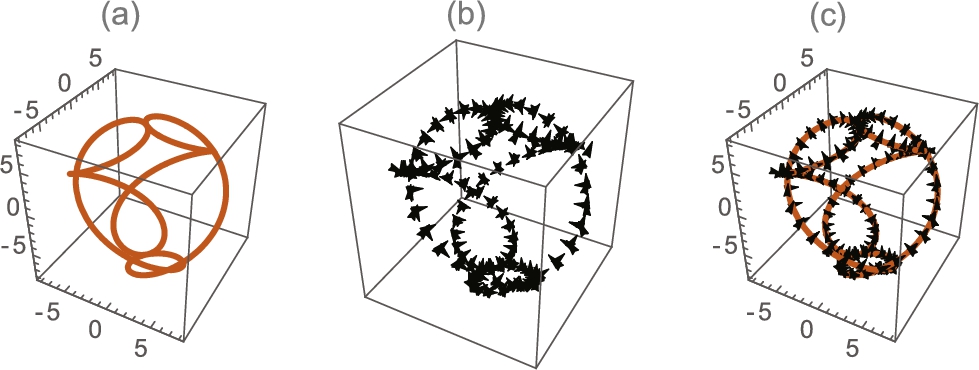
In even the simplest situations, these calculations are quite complicated. Graphically seeing the results may be more meaningful that the explicit formulas.
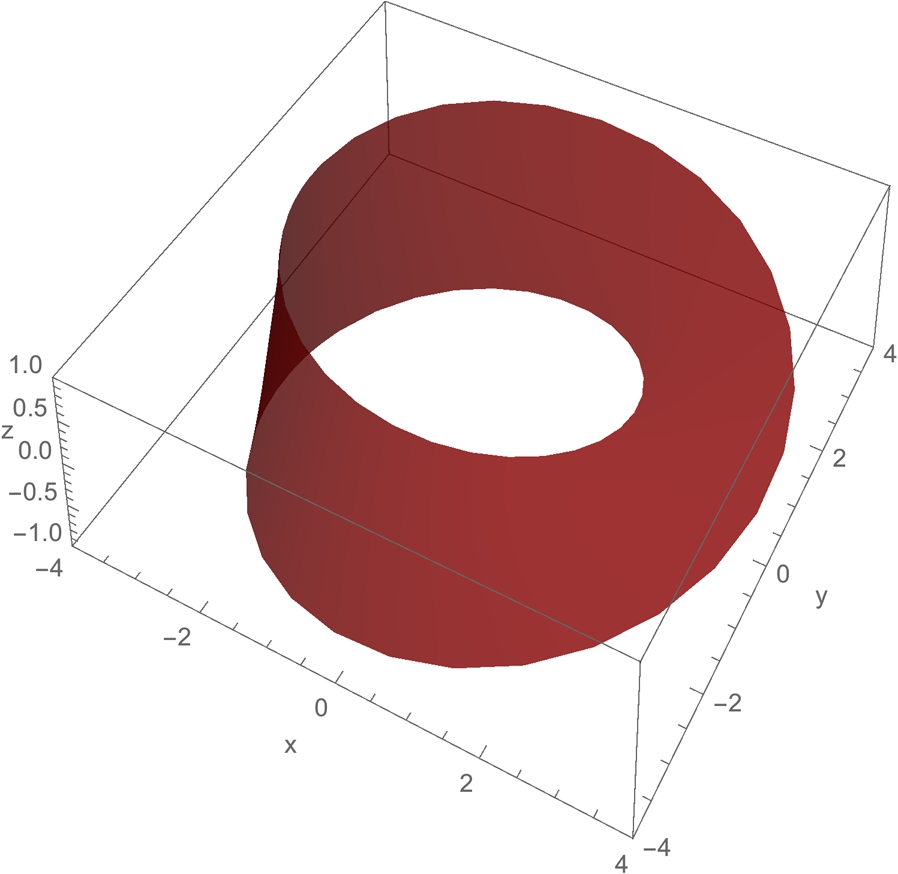
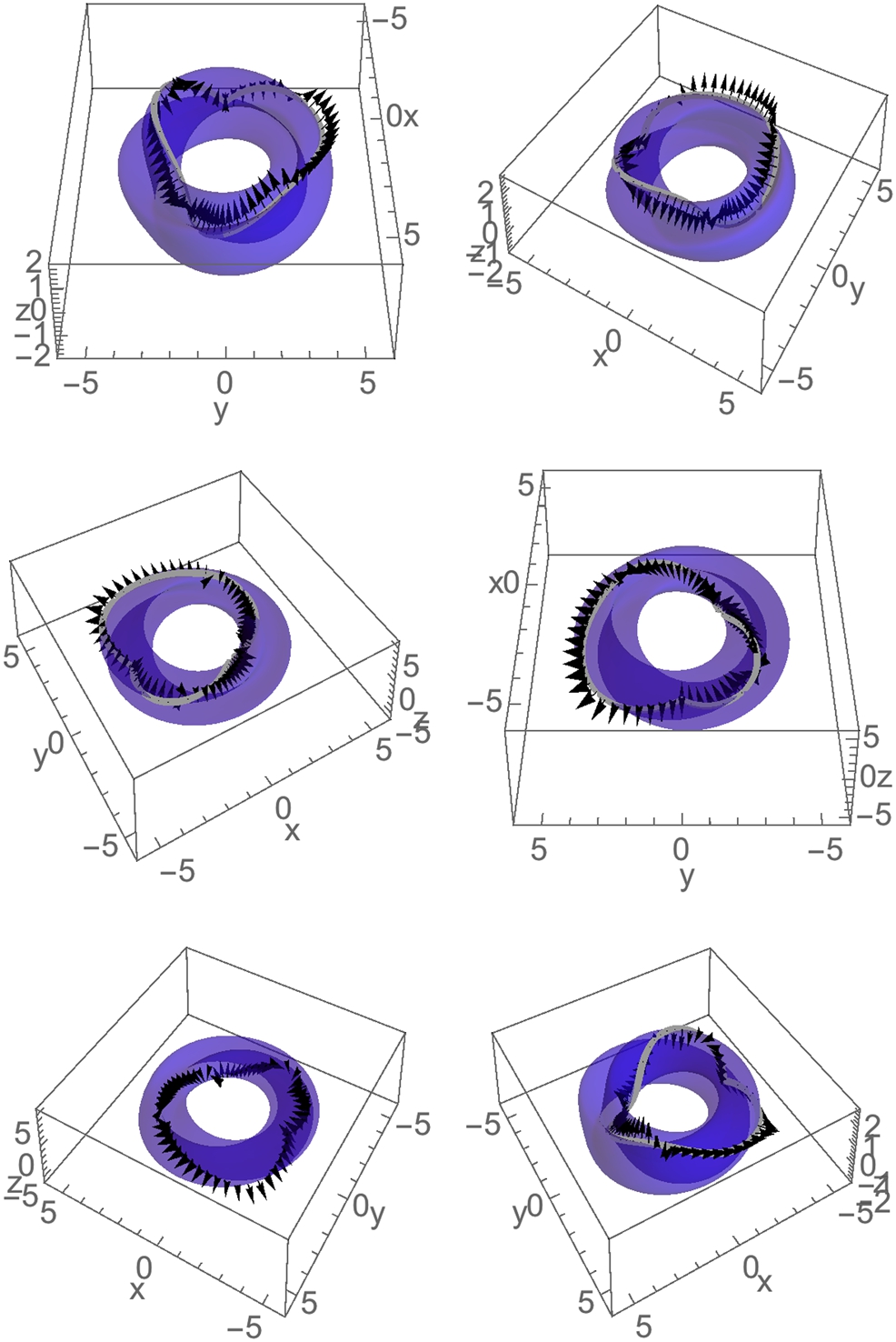
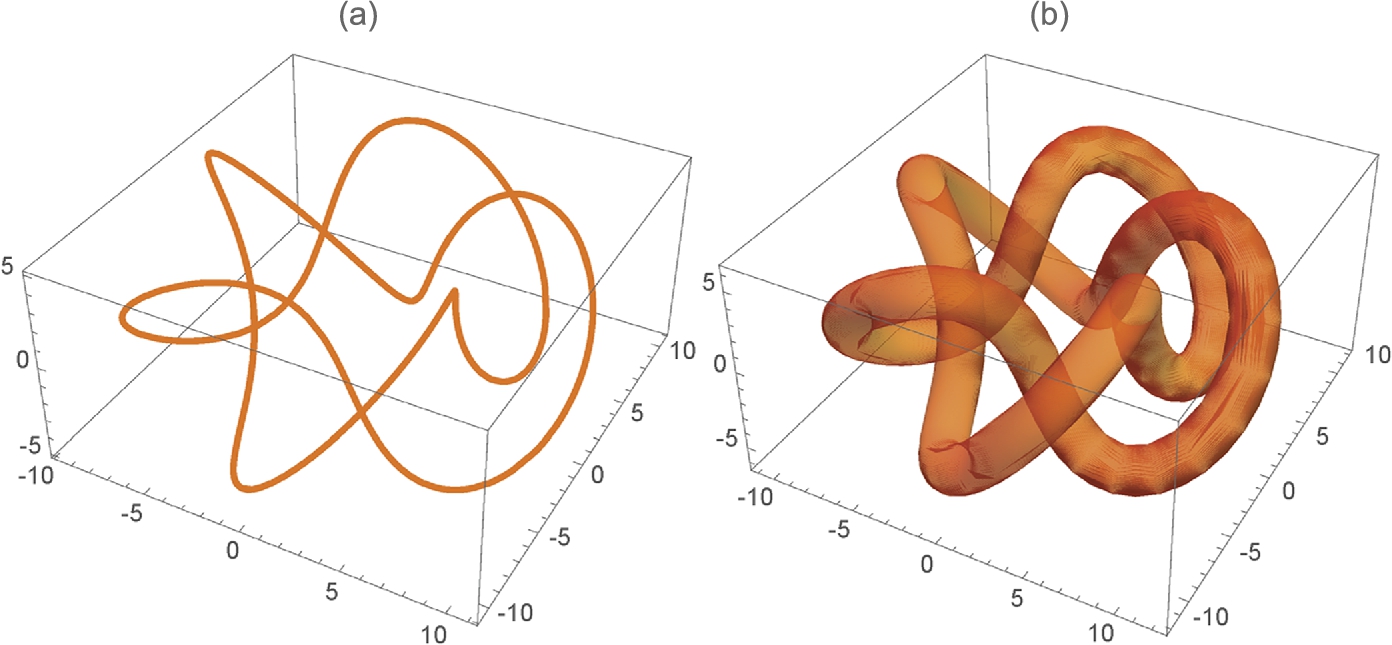
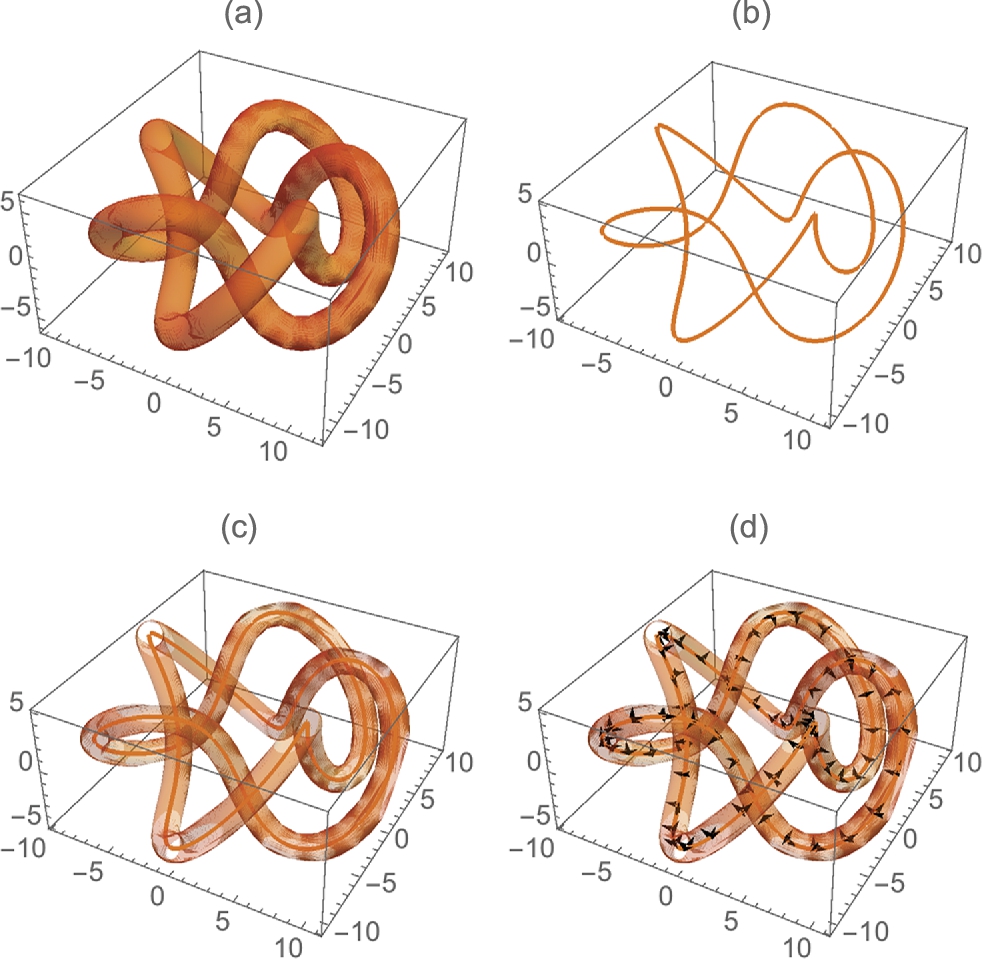
The previous example illustrates that capturing the depth of three-dimensional curves by projections into two dimensions can be difficult. Sometimes taking advantage of three-dimensional surface plots can help. For a basic space curve, tubecurve places a “tube” of radius r around the space curve.
![]()
![]()
![]()
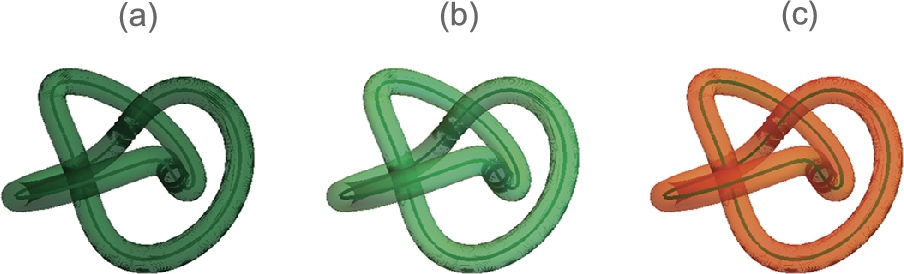
To illustrate the utility, we redefine torusknot that was presented in Chapter 2.
![]()
![]()
![]()
For surfaces in ![]() , extending and stating these definitions precisely becomes even more complicated. First, define the vector triple product (xyz), where
, extending and stating these definitions precisely becomes even more complicated. First, define the vector triple product (xyz), where 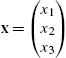 ,
, 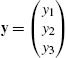 , and
, and  , by
, by  . We assume that
. We assume that ![]() is a vector-valued function with domain contained in a “nice” region
is a vector-valued function with domain contained in a “nice” region ![]() and range in
and range in ![]() . The Gaussian curvature,
. The Gaussian curvature, ![]() , and the mean curvature,
, and the mean curvature, ![]() , under reasonable conditions, are given by the formulas
, under reasonable conditions, are given by the formulas
For the parametrically defined surface ![]() , the unit normal field, U, is
, the unit normal field, U, is ![]() . Observe that the expressions that result from explicitly computing U,
. Observe that the expressions that result from explicitly computing U, ![]() , and
, and ![]() are almost always so complicated that they are impossible to understand.
are almost always so complicated that they are impossible to understand.
After defining vtp to return the vector triple product of three vectors, we define gaussianc and meanc to compute ![]() and
and ![]() for a parametrically defined surface
for a parametrically defined surface ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
]
5.6 Matrices and Graphics
5.6.1 Manipulating Photographs with Built-In Functions
As introduced in Chapter 2, Mathematica contains a wide range of functions that allow you to manipulate images such as photographs quickly to achieve a variety of photographic effects.
To import a photograph or other image into Mathematica, use Import. Generally, the object that is to be imported should be in your root directory. However, Mathematica supports clicking and dragging: you can simply click on the file and drag it to the desired location in your Mathematica notebook.
For “standard” effects and manipulation of photographs, try using ImageEffect first. ImageEffect is fast and has a wide range of options. We illustrate just a few here. First, we import a graphic,
![]()
![]()

Next, we use ImageEffect to apply a variety of commonly used enhancements to the image, p1. The results are shown in Fig. 5.31.

![]()
![]()
![]()
![]()
![]()
Once you have imported an image either using Import or by selecting and dragging the image into the desired location in your Mathematica notebook, Mathematica gives you a wide range of functions to obtain information about the image.
![]()
![]()

To determine the size of your image, number of pixel columns by number of pixel rows, use ImageDimensions.
![]()
![]()
Here, we illustrate ImageAdjust with a few of its options (see Fig. 5.32).

![]()
![]()
![]()
![]()
ColorQuantize[image,n] approximates image with n colors. To see the resulting colors, use DominantColors. Observe that the colors are displayed in small squares.
![]()

To see the RGB code, click on the color or use InputForm to see the actual color codes displayed as a list.
![]()
![]()
ImageApply may give the most flexibility for dealing with a graphic as it allows you to manipulate the graphic pixel-by-pixel. Closely related commands to those discussed include ImageFilter, ImageConvolve, and ImageCorrelate. Use ?<command> to obtain detailed help regarding the capabilities of each (see Fig. 5.33).

![]()
![]()
![]()
![]()
![]()
![]()
5.6.2 Manipulating Photographs by Viewing Them as a Matrix or Array
With Mathematica, virtually every object is a list or list of lists, including images. In situations where you want to manipulate your image or photograph with more detail than that provided by the built-in Mathematica functions for manipulating Image objects, you may want to manipulate the data that determines the image directly. To do so, it is important to understand that the underlying data of an Image object is generally a matrix. Typically, the entries of the matrix for the image are single digits for black-and-white images or ordered triples of the form {r,g,b} for color jpegs. The easiest way to determine the size of the image is to use ImageDimensions[image]. The resulting list {n,m} indicates that the dimensions of image are n pixels of rows by m pixels of columns.
Mathematica contains several functions that allow you to represent matrices graphically. These commands are analogous to the corresponding ones for dealing with lists (like ListPlot) or functions (such as Plot, Plot3D, and ContourPlot).
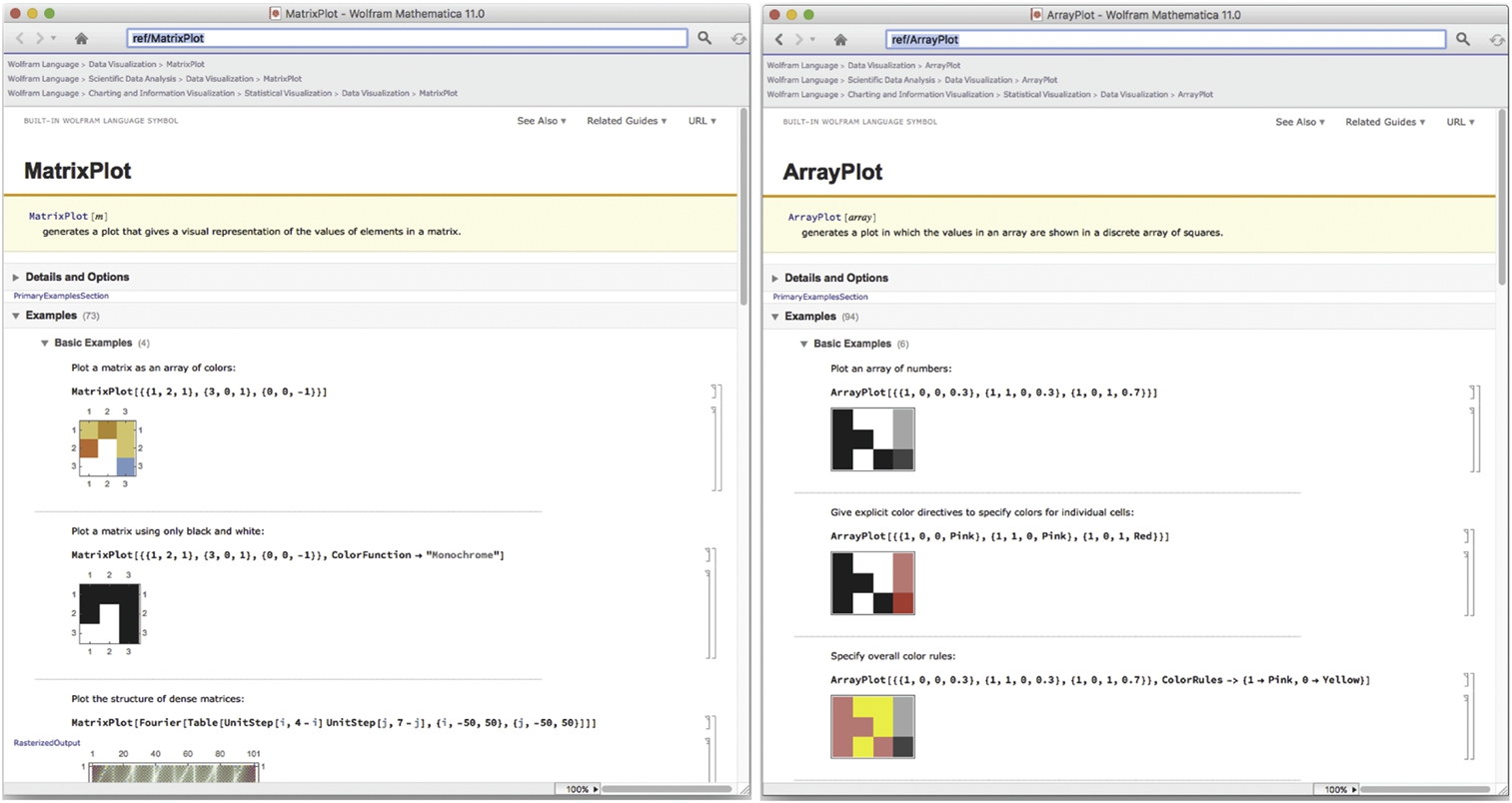
1. MatrixPlot[A] generates a grid with the same dimensions as A. The cells are shaded according to the entries of A. The default is in color.
2. ArrayPlot[A] generates a grid with the same dimensions as A. The cells are shaded according to the entries of A. The default is in black and white.
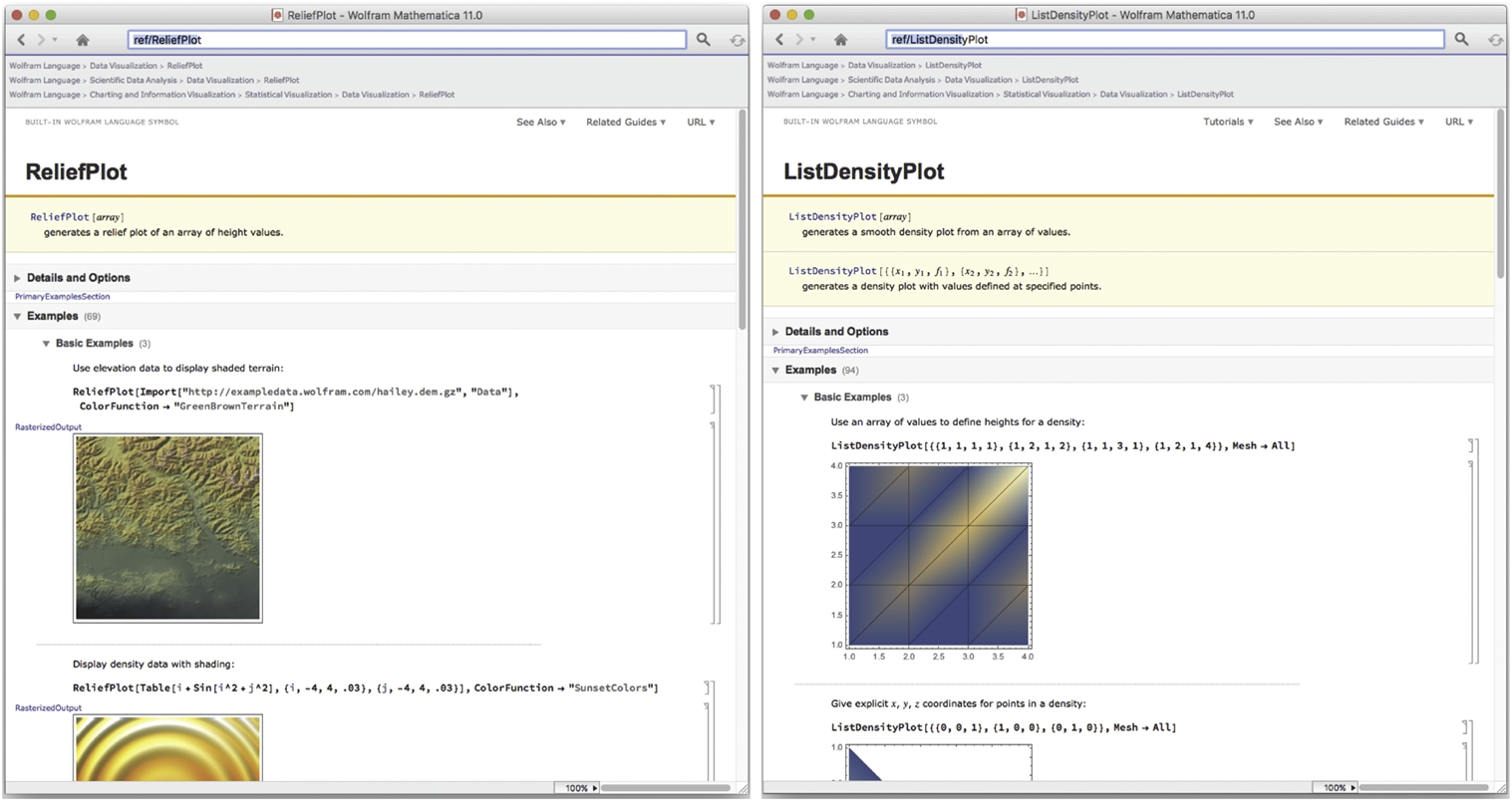
3. ListContourPlot[A] generates a contour plot using the entries of A as the height values.
4. ReliefPlot[A] generates a relief plot using the entries of A as the height values.
Observe that ArrayPlot and MatrixPlot are virtually interchangeable. However, the entries of ArrayPlot need not be numbers. If Mathematica cannot determine how to shade a cell, the default is to shade it in a dark maroon color. Although these functions generate graphics that depend on the entries of the matrix, loosely speaking we will use phrases like “we use MatrixPlot to plot A” and “we use ArrayPlot to graph A” to describe the graphic that results from applying one of these functions to an array.
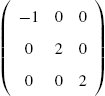
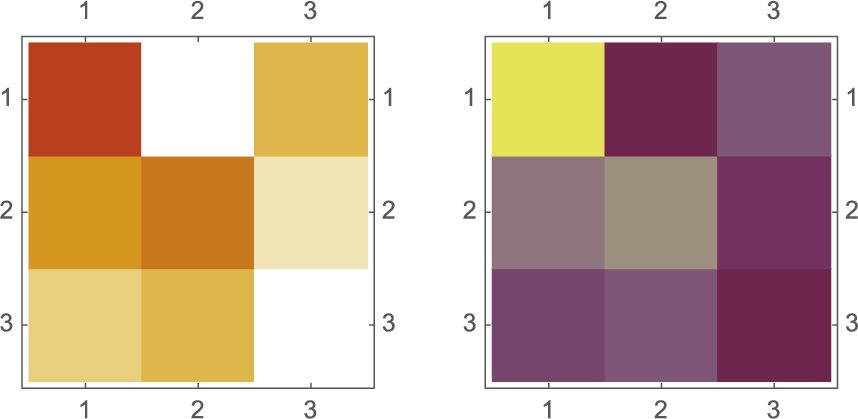
For example, consider the arrays  ,
, 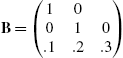 , and
, and ![]() .
.
In the first command, Mathematica shades all the cells according to its GrayLevel value. However, in the second and third commands, Mathematica cannot shade the cells in the second row and all the cells, respectively, because ordered triples cannot be evaluated by GrayLevel. However, RGBColor evaluates ordered triples so Mathematica shades the cells in Fig. 5.34 (c) according to their RGBColor value. See Fig. 5.34.

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
MatrixPlot is unable to graphically represent B or C. However, coloring is automatic with MatrixPlot. See Fig. 5.35.
![]()
![]()
![]()
![]()
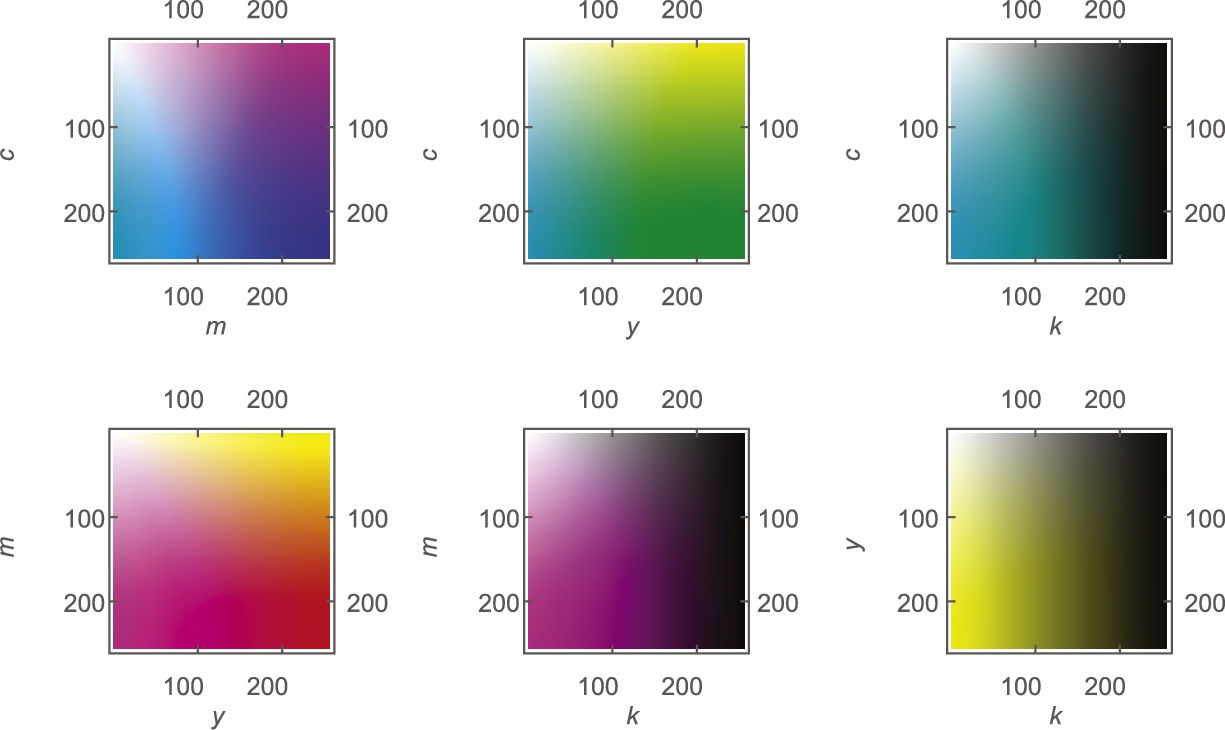
If you need to adjust the color of a graphic, usually you can use the ColorSchemes palette to select an appropriate gradient or color function. In other situations, you might wish to create your own using Blend. To use Blend, you might need to know how various RGBColors or CMYKColors vary as the variables affecting the color change.
ArrayPlot can help us see the variability in the colors. With the following, we see how RGBColor[r,g,b] affects color for ![]() ,
, ![]() , and then
, and then ![]() . The results are shown together in Fig. 5.36. The figure can help us select appropriate values to generate our own color blending function using Blend rather than relying on Mathematica's built-in color schemes and gradients.
. The results are shown together in Fig. 5.36. The figure can help us select appropriate values to generate our own color blending function using Blend rather than relying on Mathematica's built-in color schemes and gradients.

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
We modify the calculation slightly to see how CMYKColor varies as we adjust two parameters. Keep in mind that each t2 is a ![]() array. Each entry of t2 is an ordered quadruple, which is illustrated in the first calculation where we use Part to take the 5th element of the 8th part of t2 (see Fig. 5.37).
array. Each entry of t2 is an ordered quadruple, which is illustrated in the first calculation where we use Part to take the 5th element of the 8th part of t2 (see Fig. 5.37).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Keep in mind that you can load files into Mathematica with Import or by clicking and dragging the image to the desired location in your Mathematica notebook. Generally, the underlying structure of the loaded file is relatively easy to understand. Be careful when you import data into Mathematica. We recommend that you use ExampleData to investigate your routines before finalizing them. Although importing external files into Mathematica is easy, understanding the underlying structure of the imported data may take some time but be necessary to produce the results you desire.
We illustrate a few of the subtle differences that can be encountered with several images.
Using Import, we import a graphic into Mathematica. The result is shown in Fig. 5.38 (a).

![]()
![]()

We use ImageDimensions to determine the size of the image.
![]()
![]()
Alternatively, using Length we see that p2 has 439 rows (pixels)
![]()
439
and then counting the number of entries in the first row of p2, we see that p2 has 640 columns (pixels).
![]()
640
To convert the image to an array (matrix) that we can manipulate, we use ImageData.
![]()
After we have obtained the image data from p1 in p2, we see that it is a matrix where each entry is a list of the form ![]() , corresponding to the RGB color code for that pixel.
, corresponding to the RGB color code for that pixel.
![]()
![]()
ArrayPlot produces the negative of an image. See Fig. 5.38 (a).
![]()
To manipulate p2, it is important to understand that p2 is a ![]() array where each entry is a
array where each entry is a ![]() list, corresponding to the RGB color codes for that particular pixel.
list, corresponding to the RGB color codes for that particular pixel.
![]()
![]()
![]()
640
To convert the image to a different color, we first convert the matrix to a list of ordered triples, p3, define ![]() , apply f to p3, and then apply a color function to the result. In this example, we chose to use the Rainbow color function.
, apply f to p3, and then apply a color function to the result. In this example, we chose to use the Rainbow color function.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
We show the results in Fig. 5.38. On a color printer, the results are amazing.
![]()
![]()
The results are shown side-by-side in Fig. 5.38. Printed on a color printer, the results are amazing.
![]()
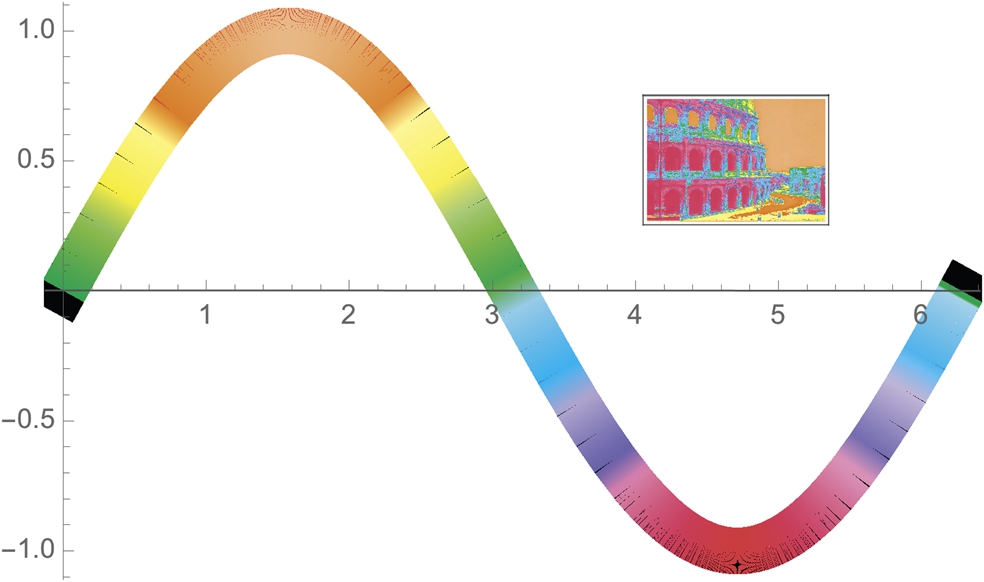
Now that we understand how to manipulate an image, we can be creative. In the following, the image is scaled so that the width of the image is 70 pixels (because of ImageSize->70). We then display the small image with another graphic. Using Inset, we put the Colliseum next to a sine graph that is plotted using the same coloring gradient. See Fig. 5.39.
![]()
![]()
![]()
An alternative way to visualize the data is to use ListContourPlot. To assure that the aspect ratio of the original image is preserved, include the AspectRatio->Automatic option in the ListContourPlot command (see Fig. 5.40).

![]()
![]()
![]()
![]()
![]()
![]()
The structure of a black and white jpeg differs from that of a color one. To see so, we import a very old picture of the second author of this text,
![]()
![]()

and name the result p1. With ImageDimensions, we see that p1 is 428 pixels wide by 600 pixels tall.
![]()
![]()
We obtain the data for the image with ImageData. With Length, we see that the resulting array has 600 rows and 428 columns, confirming the result obtained with ImageDimensions. Using Short, we see the form of each entry. For the black-and-white image, each entry is a number that corresponds to a GrayLevel.
![]()
![]()
600
![]()
428
![]()
![]()
In Fig. 5.41, we illustrate the use of ListContourPlot and ReliefPlot along with various options.

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
ReliefPlot can help add insight to images, especially when they have geographical or biological meaning. For example, this jpeg
![]()
![]()
shows the beginning of a biological process of a cell.
With ImageDimensions, we see that p1 is a 400 pixels wide by 500 pixels tall. After obtaining the image data with ImageData, these calculations are confirmed with length.
![]()
![]()
![]()
![]()
500
![]()
500
![]()
400
Viewing p2 as a ![]() array, each entry is
array, each entry is ![]() array/vector. To easily apply a function, f, that assigns a number to each ordered triple, we use Flatten to convert the nested list/array p2 to a list of ordered triples in p3.
array/vector. To easily apply a function, f, that assigns a number to each ordered triple, we use Flatten to convert the nested list/array p2 to a list of ordered triples in p3.
![]()
![]()
![]()
200000
![]()
To apply our own color function to this data set, we convert the ordered triples to some other form. For illustrative purposes, we convert each ordered triple ![]() in p3 to the number
in p3 to the number ![]() . The result is converted back to a
. The result is converted back to a ![]() array, with Partition in p4.
array, with Partition in p4.
![]()
![]()
![]()
500
We then use ReliefPlot, ListContourPlot, and ListDensityPlot along with various options to graph the result in Fig. 5.42.
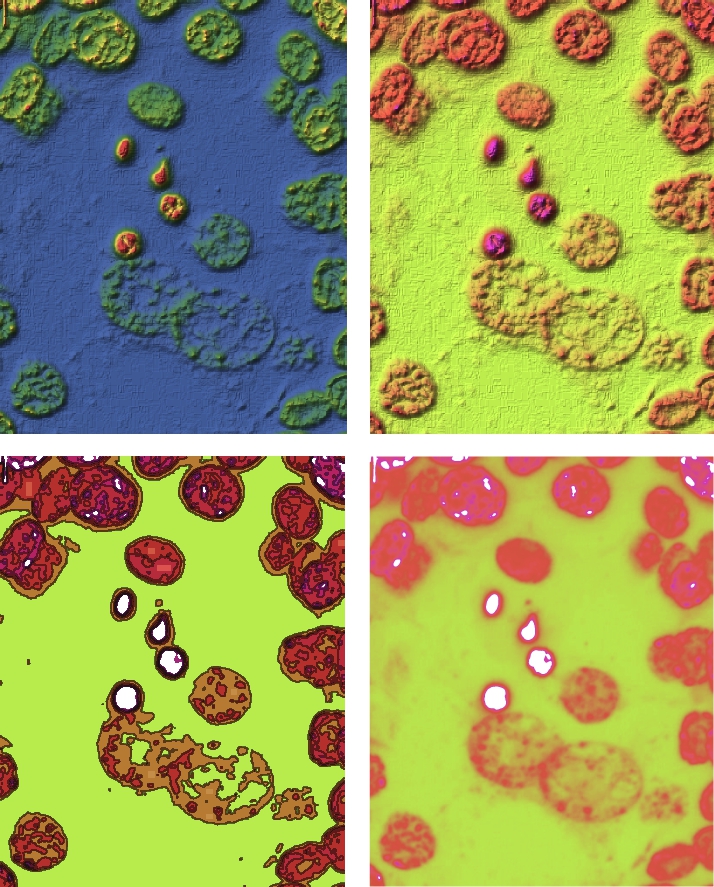
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()