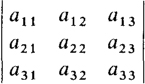
A knowledge of determinants is necessary for using Cramer’s rule, which is a popular method for solving the simultaneous equations that occur in the analysis of a circuit. A determinant is a square arrangement of numbers between two vertical lines, as follows:
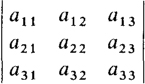
in which each a is a number. The first and second subscripts indicate the row and column, respectively, that each number is in.
A determinant with two rows and columns is a second-order determinant. One with three rows and columns is a third-order determinant, and so on.
Determinants have values. The value of the second-order determinant
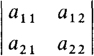
is a11a22 – a21a12, which is the product of the numbers on the principal diagonal minus the product of the numbers on the other diagonal:
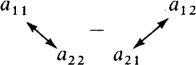
For example, the value of
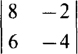
is 8(–4) –6(–2) = –32 + 12 = –20.
A convenient method for evaluating a third-order determinant is to repeat the first two columns to the right of the third column and then take the sum of the products of the numbers on the diagonals indicated by downward arrows, as follows, and subtract from this the sum of the products of the numbers on the diagonals indicated by upward arrows. The result is
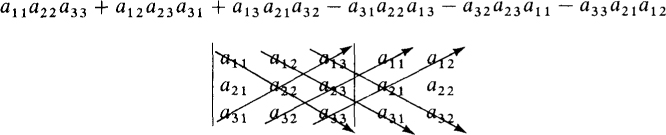
For example, the value of
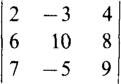
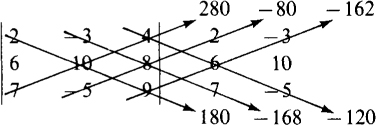
is 180 – 168 – 120 – (280 – 80 – 162) = –146.
Evaluations of higher-order determinants require other methods that will not be considered here.
Before Cramer’s rule can be applied to solve for the unknowns in a set of equations, the equations must be arranged with the unknowns on one side, say the left, of the equal signs and the knowns on the right-hand side. The unknowns should have the same order in each equation. For example, I1 may be the first unknown in each equation, I2 the second, and so on. Then, by Cramer’s rule, each unknown is the ratio of two determinants. The denominator determinants are the same, being formed from the coefficients of the unknowns. Each numerator determinant differs from the denominator determinant in only one column. For the first unknown, the numerator determinant has a first column that is the right-hand side of the equations. For the second unknown, the numerator determinant has a second column that is the right-hand side of the equations, and so on. As an illustration, for
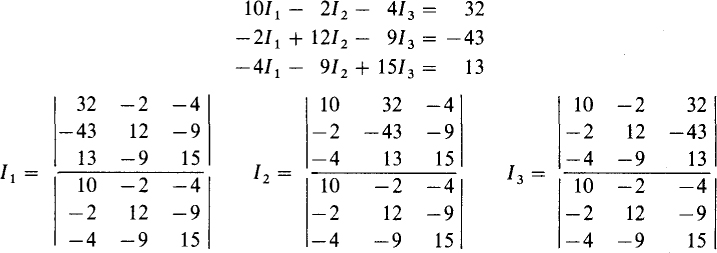
Although using Cramer’s rule is popular, a much better way to solve the simultaneous equations of interest here is to use an advanced scientific calculator. No programming is required, the equations are easy to enter, and solutions can be obtained just by pressing a single key. Typically the equations must be first placed in matrix form. But no knowledge of matrix algebra is required.
To be placed in matrix form, the equations must be arranged in exactly the same form as for using Cramer’s rule, with the unknowns being in the same order in each equation. Then, three matrices are formed from these equations. As an illustration, for the following previously considered equations,
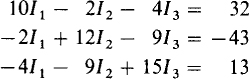
the corresponding matrix equation is
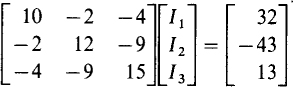
Incidentally, a matrix comprising a single column is usually referred to as a vector.
The elements of the three-by-three matrix are just the coefficients of the unknowns and are identical to the elements in the denominator determinant of Cramer’s rule. The adjacent vector has elements that are the unknowns being solved for, and the vector on the right-hand side has elements that consist of the right-hand sides of the original equations.
The elements of the vector on the right-hand side and the elements of the coefficient matrix are then entered into a calculator. The exact method of entering the elements depends on the calculator used but should be simple to do. Typically, the solutions are returned in a vector,.and they appear in the same order as the corresponding quantity symbols in the vector of unknowns.
The calculator method cannot be too strongly recommended. The decrease in errors and the time saved will quickly compensate the user for the little additional cost that was required to purchase such a calculator. The calculator should also be capable of solving simultaneous equations that have complex, instead of just real, coefficients, as will be required later for the analysis of sinusoidally excited circuits.
Depending on the type of analysis, a circuit with either no voltage sources or no current sources may be preferable. Because a circuit may have an undesired type of source, it is convenient to be able to transform voltage sources to equivalent current sources, and current sources to equivalent voltage sources. For a transformation, each voltage source should have a series internal resistance, and each current source a parallel internal resistance.
Figure 4-la shows the transformation from a voltage source to an equivalent current source, and Fig. 4-1b the transformation from a current source to an equivalent voltage source. This equivalence applies only to the external circuit connected to these sources. The voltages and currents of this external circuit will be the same with either source. Internally, the sources are usually not equivalent.
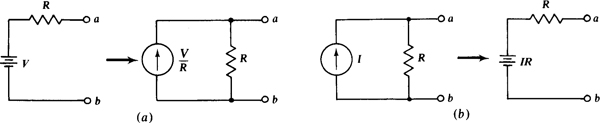
Fig. 4-1
As shown, in the transformation of a voltage source to an equivalent current source, the same resistor is in parallel with the current source, and the source current equals the original source voltage divided by the resistance of this resistor. The current source arrow is directed toward the terminal nearest the positive terminal of the voltage source. In the transformation from a current source to an equivalent voltage source, the same resistor is in series with the voltage source, and the source voltage equals the original source current times the resistance of this resistor. The positive terminal of the voltage source is nearest the terminal toward which the arrow of the current source is directed. This same procedure applies to the transformations of dependent sources.
In mesh analysis, KVL is applied with mesh currents, which are currents assigned to meshes, and preferably referenced to flow clockwise, as shown in Fig. 4-2a.
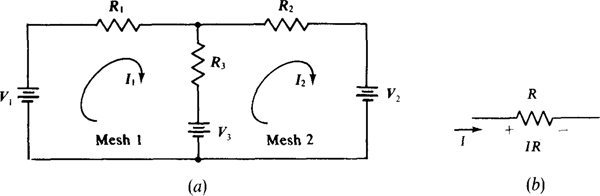
Fig. 4-2
KVL is applied to each mesh, one at a time, using the fact that in the direction of a current I, the voltage drop across a resistor is IR, as shown in Fig. 4-2b. The voltage drops across the resistors taken in the direction of the mesh currents are set equal to the voltage rises across the voltage sources. As an illustration, in the circuit shown in Fig. 4-2a, around mesh 1 the drops across resistors R1 and R3 are I1R1 and (I1 – I2)R3, respectively, the latter because the current through R3 in the direction of I1 is I1 – I2, The total voltage rise from voltage sources is V1 – V3, in which V3 has a negative sign because it is a voltage drop. So, the mesh equation for mesh 1 is
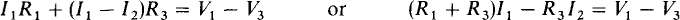
Notice that R1 + R3, the coefficient of I1, is the sum of the resistances of the resistors in mesh 1. This sum is called the self-resistance of mesh 1. Also, –R3, the coefficient of I2, is the negative of the resistance of the resistor that is common to or mutual to meshes 1 and 2. R3 is called the mutual resistance. In mesh equations, mutual resistance terms always have negative signs because the other mesh currents always flow through the mutual resistors in directions opposite to those of the principal mesh currents.
It is easier to write mesh equations using self-resistances and mutual resistances than it is to directly apply KVL. Doing this for mesh 2 results in
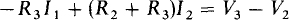
In a mesh equation, the voltage for a voltage source has a positive sign if the voltage source aids the flow of the principal mesh current—that is, if this current flows out of the positive terminal—because this aiding is equivalent to a voltage rise. Otherwise, a source voltage has a negative sign.
For mesh analysis, the transformation of all current sources to voltage sources is usually preferable because there is no formula for the voltages across current sources. If, however, a current source is positioned at the exterior of a circuit such that only one mesh current flows through it, that current source can remain because the mesh current through it is known—it is the source current or the negative of it, depending on direction. KVL is not applied to this mesh.
The number of mesh equations equals the number of meshes minus the number of current sources, if there are any.
Loop analysis is similar to mesh analysis, the principal difference being that the current paths selected are loops that are not necessarily meshes. Also, there is no convention on the direction of loop currents; they can be clockwise or counterclockwise. As a result, mutual terms can be positive when KVL is applied to the loops.
For loop analysis, no current source need be transformed to a voltage source. But each current source should have only one loop current flowing through it so that the loop current is known. Also, then KVL is not applied to this loop because the current source voltage is unknown.
Obviously, the loops for the loop currents must be selected such that every component has at least one loop current flowing through it. The number of these loops equals the number of meshes if the circuit is planar —that is, if the circuit can be drawn on a flat surface with no wires crossing. In general, the number of loop currents required is B – N + 1, where B is the number of branches and N is the number of nodes.
If the current through only one component is desired, the loops should be selected such that only one loop current flows through this component. Then, only one current has to be solved for. In contrast, for mesh analysis, finding the current through an interior component requires solving for two mesh currents.
For nodal analysis, preferably all voltage sources are transformed to current sources and all resistances are converted to conductances. KCL is applied to all nodes but the ground node, which is often indicated by a ground symbol at the bottom node of the circuit, as shown in Fig. 4-3a. As mentioned in Chap. 3, almost always the bottom node is selected as the ground node even though any node can be. Conventionally, voltages on all other nodes are referenced positive with respect to the ground node. As a consequence, showing node voltage polarity signs is not necessary.
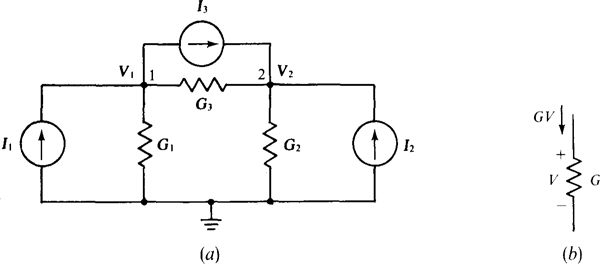
Fig. 4-3
In nodal analysis, KCL is applied to each nongrounded node, one at a time, using the fact that in the direction of a voltage drop V, the current in a resistor is GV, as shown in Fig. 4-3b. The currents leaving a node through resistors are set equal to the currents entering the node from current sources. As an illustration, in the circuit shown in Fig. 4-3a, the current flowing down through the resistor with conductance G1, is G1 V1. The current to the right through the resistor with conductance G3 is G3(V1 – V2). This current is equal to the conductance times the voltage at the node at which the current enters the resistor minus the voltage at the node at which the current leaves the resistor. The quantity (V1, – V2) is, of course, just the resistor voltage referenced positive at the node at which the current enters the resistor and negative at the node at which the current leaves the resistor, as is required for associated references. The current entering node 1 from current sources is I1 – I3, in which I3 has a negative sign because it is actually leaving node 1. So, the nodal equation for node 1 is
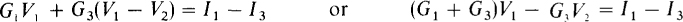
Notice that the V1 coefficient of G1 + G3 is the sum of the conductances of the resistors connected to node 1. This sum is called the self-conductance of node 1. The coefficient of V2 is – G3, the negative of the conductance of the resistor connected between nodes 1 and 2. G3 is called the mutual conductance of nodes 1 and 2. Mutual conductance terms always have negative signs because all nongrounded node voltages have the same reference polarity—all are positive.
It is easier to write nodal equations using self-conductances and mutual conductances than it is to directly apply KCL. Doing this for node 2 results in
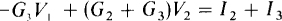
The transformation of all voltage sources to current sources is not absolutely essential for nodal analysis, but is usually preferable for the shortcut approach with self-conductances and mutual conductances. The problem with voltage sources is that there is no formula for the currents flowing through them. Nodal analysis, though, is fairly easy to use with circuits having grounded voltage sources, each of which has a terminal connected to ground. Such voltage sources give known voltages at their nongrounded terminal nodes, making it unnecessary to apply KCL at these nodes. Other voltage sources—floating voltage sources—can be transformed to current sources.
The number of nodal equations equals the number of nongrounded nodes minus the number of grounded voltage sources.
Mesh, loop, and nodal analyses are about the same for circuits having dependent sources as for circuits having only independent sources. Usually, though, there are a few more equations. Also, positive terms may appear in the circuit equations where only negative mutual resistance or conductance terms appear for circuits having no dependent sources. Almost always, a good first step in the analysis of a circuit containing dependent sources is to solve for the dependent source controlling quantities in terms of the mesh or loop currents or node voltages being solved for.
4.1 Evaluate the following determinants:
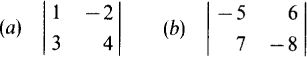
(a) The product of the numbers on the principal diagonal is 1 × 4 = 4, and for the numbers on the other diagonal is – 2 × 3 = – 6. The value of the determinant is the first product minus the second product: 4 –(–6) = 10.
(b) Similarly, the value of the second determinant is – 5(– 8) – 7(6) = 40 – 42 = –2.
4.2 Evaluate the following determinant:
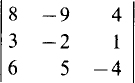
One method of evaluation is to repeat the first two columns to the right of the third column and then find the products of the numbers on the diagonals, as indicated:
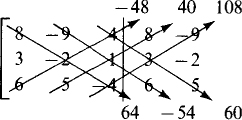
The value of the determinant is the sum of the products for the downward-pointing arrows minus the sum of the products for the upward-pointing arrows:
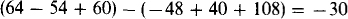
4.3 Use Cramer’s rule to solve for the unknowns in
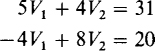
The first unknown V1 equals the ratio of two determinants. The denominator determinant has elements that are the coefficients of V1 and V2. The numerator determinant differs only in having the first column replaced by the right-hand sides of the equations:
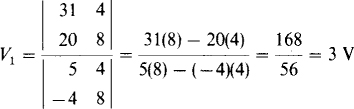
The denominator determinant for V2 has the same value of 56. In the numerator determinant the second column, instead of the first, is replaced by the right-hand sides of the equations:
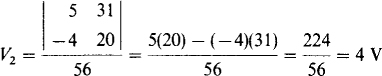
4.4 Use Cramer’s rule to solve for the unknowns in
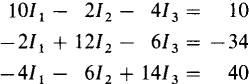
All three unknowns have the same denominator determinant of coefficients, which evaluates to
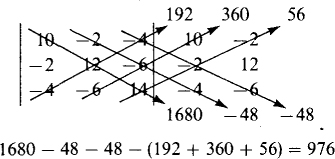
In the numerator determinants, the right-hand sides of the equations replace the first column for I1, the second column for I2, and the third column for I3:
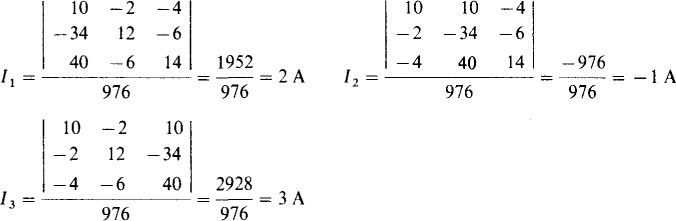
4.5 Transform the voltage sources shown in Fig. 4-4 to current sources.
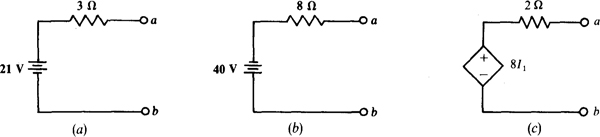
Fig. 4-4
(a) The current of the equivalent current source equals the voltage of the original voltage source divided by the resistance: 21/3 = 7 A. The current direction is toward node a because the positive terminal of the voltage source is toward that node. The parallel resistor is the same 3-Ω resistor of the original voltage source. The equivalent current source is shown in Fig. 4-5a.
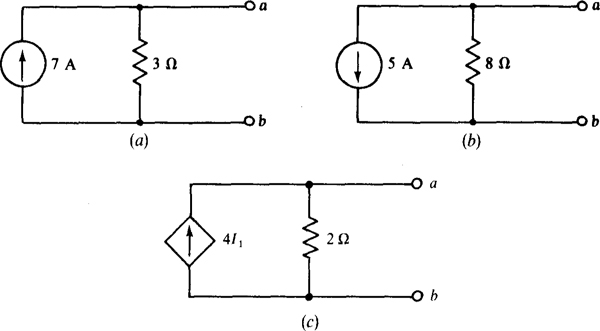
Fig. 4-5
(b) The current of the current source is 40/8 = 5 A. It is directed toward node b because the positive terminal of the voltage source is toward that node. The parallel resistor is the same 8-Ω resistor of the voltage source. Figure 4-5b shows the equivalent current source.
(c) The current of the current source is 8I1/2 = 4I1, with a direction toward node a because the positive terminal of the voltage source is toward that node. The parallel resistor is the same 2-Ω resistor of the voltage source. Figure 4-5c shows the equivalent current source.
4.6 Transform the current sources shown in Fig. 4-6 to voltage sources.
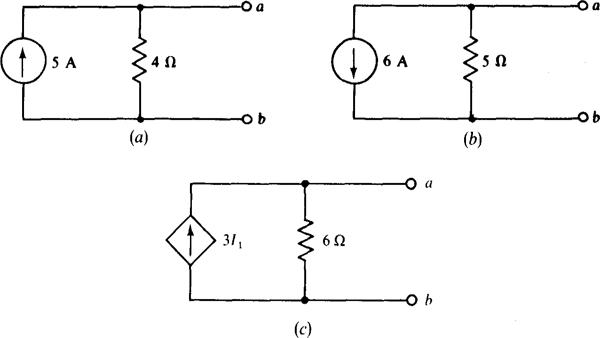
Fig. 4-6
(a) The voltage of the equivalent voltage source equals the current of the original current source times the resistance: 5 × 4 = 20 V. The positive terminal is toward node a because the direction of the current of the original current source is toward that node. Of course, the source resistance remains 4 Ω, but is in series instead of in parallel. Figure 4-7a shows the equivalent voltage source.

Fig. 4-7
(b) The voltage is 6 × 5 = 30 V, positive toward node b because the direction of the current of the original current source is toward that node. The source resistance is the same 5 Ω, but is in series. The equivalent voltage source is shown in Fig. 4-7b.
(c) The voltage is 3I1, × 6 = 18I1, positive toward node a because the direction of the current of the current source is toward that node. The source resistance is the same 6 Ω but is in series. The equivalent voltage source is shown in Fig. 4-7c.
4.7 Find the currents down through the resistors in the circuit shown in Fig. 4-8. Then transform the current source and 2-Ω resistor to an equivalent voltage source and again find the resistor currents. Compare results.
Fig. 4-8
By current division, the current down through the 2-Ω resistor is
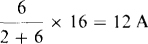
The remainder of the source current (16 – 12 = 4 A) flows down through the 6-Ω resistor.
Transformation of the current source produces a voltage source of 16 × 2 = 32 V in series with a 2-Ω resistor, all in series with the 6-Ω resistor, as shown in the circuit of Fig. 4-9. In this circuit, the same current 32/(2 + 6) = 4 A flows through both resistors. The 6-Ω resistor current is the same as for the original circuit, but the 2-Ω resistor current is different. This result illustrates the fact that although a transformed source produces the same voltages and currents in the circuit exterior to the source, the voltages and currents inside the source usually change.
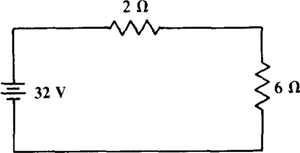
Fig. 4-9
4.8 For the circuit of Fig. 4-10, use repeated source transformations to obtain a single mesh circuit, and then find the current I.
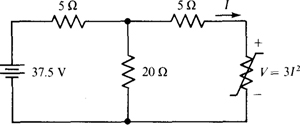
Fig. 4-10
The first step is to transform the voltage source and series resistor into a current source and parallel resistor. The resistance does not change, but the source current is 37.5/5 = 7.5 A directed upward. The 5-Ω resistor from the source transformation is in parallel with the 20-Ω resistor. Consequently, the combined resistance is (5 × 20)/(5 + 20) = 4 Ω. The next step is to transform the 7.5-A current source and the parallel 4-Ω resistor into a series voltage source and resistor. The resistance remains the same, and the voltage of the voltage source is 4(7.5) = 30 V, positive upward, as shown in the circuit of Fig. 4-11, which is a single mesh circuit.
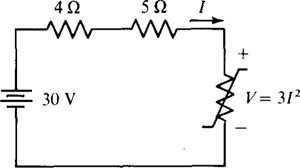
Fig. 4-11
The KVL equation for this circuit is 3I2 + 9I – 30 = 0, from which the current I can be obtained by applying the quadratic formula:
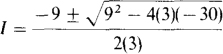
The solutions are I = 2 A and I = –5 A. Only the I = 2A is physically possible. The current must be positive since in the circuit of Fig. 4-11 there is only one source, and current must flow out of the positive terminal of this source.
4.9 Find the mesh currents in the circuit shown in Fig. 4-12.
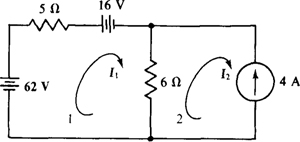
Fig. 4-12
The self-resistance of mesh 1 is 5 + 6 = 11 Ω, and the resistance mutual with mesh 2 is 6 Ω. The sum of the source voltage rises in the direction of I1 is 62 – 16 = 46 V. So, the mesh 1 KVL equation is 11I1 – 6I2 = 46.
No KVL equation is needed for mesh 2 because I2 is the only current flowing through the 4-A current source, with the result that I2 = –4 A. The current I2 is negative because its reference direction is down through the current source, but the 4-A source current actually flows up. Incidentally, a KVL equation cannot be written for mesh 2 without introducing a variable for the voltage across the current source because this voltage is unknown.
The substitution of I2 = – 4 A into the mesh 1 equation results in
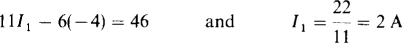
4.10 Determine the mesh currents in the circuit shown in Fig. 4-13.
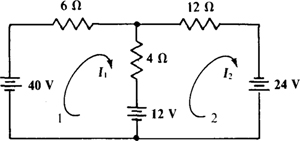
Fig. 4-13
The self-resistance of mesh 1 is 6 + 4 = 10 Ω, the mutual resistance with mesh 2 is 4 Ω, and the sum of the source voltage rises in the direction of I1 is 40 – 12 = 28 V. So, the mesh 1 KVL equation is 10I1, – 4I2 = 28.
Similarly, for mesh 2 the self-resistance is 4 + 12 = 16 Ω, the mutual resistance is 4Ω, and the sum of the voltage rises from voltage sources is 24 + 12 = 36 V. These give a mesh 2 KVL equation of –4I1 + 16I2 = 36.
Placing the two mesh equations together shows the symmetry of coefficients (here –4) about the principal diagonal as a result of the common mutual resistance:
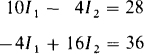
A good way to solve these two equations is to add four times the first equation to the second equation to eliminate I2. The result is
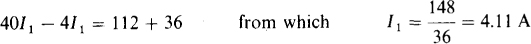
This substituted into the second equation gives
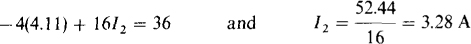
4.11 Obtain the mesh currents in the circuit of Fig. 4-14.
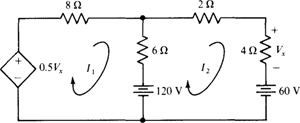
Fig. 4-14
A good first step is to solve for the controlling quantity Vx in terms of the mesh current I2. Clearly, Vx = 4I2, and consequently the voltage of the dependent source is 0.5 Vx = 0.5(4I2) = 2I2. Then, the application of KVL to the meshes gives
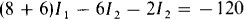
and
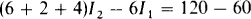
In matrix form, these simplify to

In the matrix of coefficients, the lack of symmetry about the principal diagonal is the result of the action of the dependent source. The solutions can be obtained by using Cramer’s rule or, preferably, by using a calculator. The mesh currents are I1 = –8 A and I2 = 1 A.
4.12 Find the mesh currents in the circuit shown in Fig. 4-15.
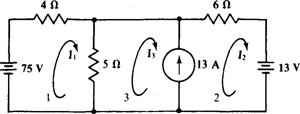
Fig. 4-15
One analysis approach is to transform the 13-A current source and parallel 5-Ω resistor into a voltage source, as shown in the circuit of Fig. 4-16.
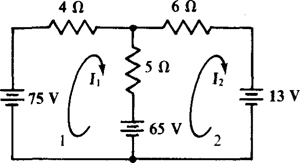
Fig. 4-16
The self-resistance of mesh 1 is 4 + 5 = 9 Ω, and that of mesh 2 is 6 + 5 = 11 Ω. The mutual resistance is 5 Ω. The voltage rises from sources are 75 – 65 = 10 V for mesh 1 and 65 – 13 = 52 V for mesh 2. The corresponding mesh equations are
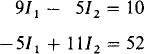
Multiplying the first equation by 5 and the second by 9 and then adding them eliminates I1:
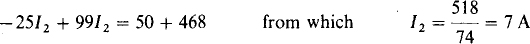
This substituted into the first equation produces
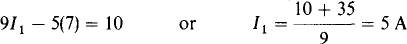
From the original circuit shown in Fig. 4-15, the current through the current source is I2–I3 = 13 A, and so
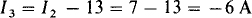
Another approach is to use the so-called supermesh method, which is applicable when a circuit contains internal current sources. Mesh currents are used, but for each internal current source, KVL is applied to the loop that would be a mesh if the current source were removed. For the circuit of Fig. 4-15, this loop (supermesh) comprises the 5-Ω and 6-Ω resistors and the 13-V source. The KVL equation is 5(I3 – I1) + 6I2 = –13. This, with the mesh 1 equation of 9I1 – 5I3 = 75, comprises two equations with three unknowns. The required third equation can be obtained by applying KCL to either node of the current source, or, more simply, by noting that the current up through the current source in terms of mesh currents is I2 – I3. This current must, of course, be equal to the 13 A of the source. So, the two KVL equations are augmented with the single KCL equation I2 – I3 = 13. In matrix form these equations are
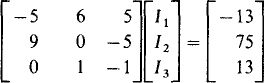
The solutions are the same as obtained before: I1 = 5 A, I2 = 7 A, and I3 = –6 A.
In general, for the supermesh approach, the K.VL equations must be augmented with KCL equations, the number of which is equal to the number of internal current sources.
4.13 Find the mesh currents in the circuit shown in Fig. 4-17.
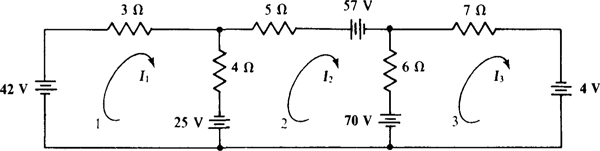
Fig. 4-17
The self-resistances are 3 + 4 = 7 Ω. for mesh 1, 4 + 5 + 6 = 15 Ω for mesh 2, and 6 + 7 = 13 Ω for mesh 3. The mutual resistances are 4 Ω for meshes 1 and 2, 6 Ω for meshes 2 and 3, and 0 Ω for meshes 1 and 3. The aiding source voltages are 42 + 25 = 67 V for mesh 1, –25 – 57 – 70 = –152 V for mesh 2, and 70 + 4 = 74 V for mesh 3. So, the mesh equations are
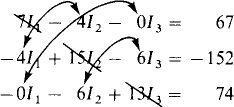
Notice the indicated symmetry of the mutual coefficients about the principal diagonal, shown as a dashed line. Because of the common mutual resistances, this symmetry always occurs—unless a circuit has dependent sources. Also, notice for each mesh that the self-resistance is equal to or greater than the sum of the mutual resistances because the self-resistance includes the mutual resistances.
By Cramer’s rule,
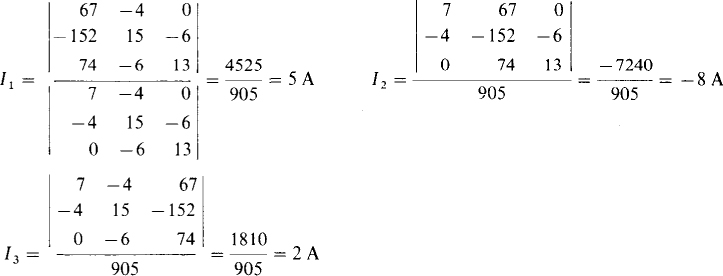
4.14 Find the mesh currents in the circuit shown in Fig. 4-18.
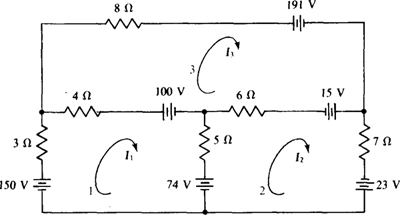
Fig. 4-18
The self-resistances are 3 + 4 + 5 = 12 Ω for mesh 1, 5 + 6 + 7 = 18 Ω for mesh 2, and 6 + 4 + 8 = 18 Ω for mesh 3. The mutual resistances are 5 Ω for meshes 1 and 2, 6 Ω for meshes 2 and 3, and 4 Ω for meshes 1 and 3. The aiding source voltages are 150 – 100 – 74 = –24 V for mesh 1, 74 + 15 + 23 = 112 V for mesh 2, and 100 – 191 – 15 = –106 V for mesh 3. So, the mesh equations are
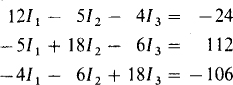
For a check, notice the symmetry of the coefficients about the principal diagonal.

4.15 Use mesh analysis in determining the power absorbed by the dependent voltage source in the circuit of Fig. 4-19.
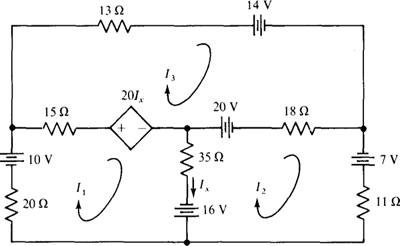
Fig. 4-19
In terms of mesh currents, the dependent source controlling quantity Ix is Ix = I1 – I2. So, the dependent source provides a voltage of 20Ix – 20(I1 – I2). In writing mesh equations for a circuit that has dependent sources, a good approach is to temporarily ignore the dependent sources, write the mesh equations using the self- and mutual-resistance approach, and then add the dependent source expressions to the pertinent equations. The result of doing that here is
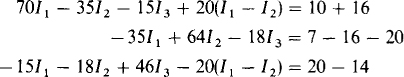
which simplify to

The solutions are I1 = 0.148 A, I2 = –0.3 A, and I3 = 0.256 A. Finally, the power absorbed by the dependent source is equal to the source voltage times the current flow into the positive-referenced terminal:
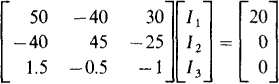
4.16 Use mesh analysis in finding V0 in the circuit of Fig. 4.20.
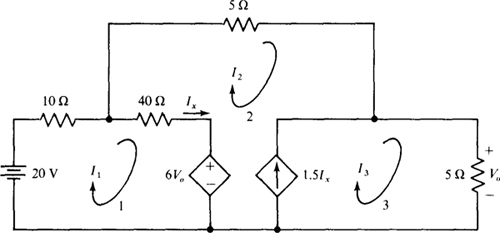
Fig. 4-20
As always for a circuit containing dependent sources, a good first step is to solve for the dependent source controlling quantities in terms of the quantities being solved for, which are mesh currents here. Obviously, Ix = I1 – I2 and V0 = 5I3. So, the dependent current source provides a current of 1.5Ix = 1.5(I1 – I2) and the dependent voltage source provides a voltage of 6V0 = 6(5I3) = 30I3.
The KVL equation for mesh 1 is (10 + 40)I1 – 40I2 + 30I3 = 20. Preferably, KVL should not be applied to meshes 2 and 3 because of the dependent current source that is in these meshes. But a good approach to use is the supermesh method presented in Prob. 4.12. Applying KVL to the mesh obtained by deleting this current source gives the equation –30I3 + 40(I2 – I1) + 5I2 + 5I3 = 0. The necessary third independent equation, 1.5(I1 – I2) = I3 – I2, is obtained by applying KCL at a terminal of the dependent current source. These three equations simplify to, in matrix form,
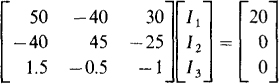
Then Cramer’s rule or, preferably, a calculator can be used to obtain the current I3 = 0.792 A. Finally, V0 = 5I3 = 5(0.792) = 3.96 V.
4.17 Use loop analysis to find the current flowing to the right through the 5-kΩ resistor in the circuit shown in Fig. 4-21.
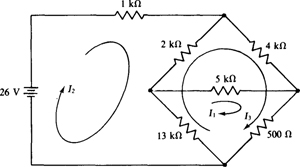
Fig. 4-21
Three loop currents are required because the circuit has three meshes. Only one loop current should flow through the 5-kΩ resistor so that only one current needs to be solved for. The paths for the two other loop currents can be selected as shown, but there are other suitable paths.
As has been mentioned, since working with kilohms is inconvenient, a common practice is to drop those units—to divide each resistance by 1000. But then the current answers will be in milliamperes. With this approach, and from self-resistances, mutual resistances, and aiding source voltages, the loop equations are
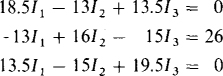
Notice the symmetry of the I coefficients about the principal diagonal, just as for mesh equations. But there is the difference that some of these coefficients are positive. This is the result of two loop currents flowing through a mutual resistor in the same direction—something that cannot happen in mesh analysis if all mesh currents are selected in the clockwise direction, as is conventional.
From Cramer’s rule,
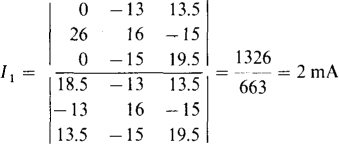
4.18 Use loop analysis to find the current down through the 8-Ω resistor in the circuit shown in Fig. 4-22.
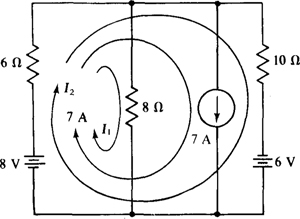
Fig. 4-22
Because the circuit has three meshes, the analysis requires three loop currents. The loops can be selected as shown, with only one current I1 flowing through the 8-Ω resistor so that only one current needs to be solved for. Also, only one loop current should flow through the 7-A source so that this loop current is known, making it unnecessary to apply KVL to the corresponding loop. There are other ways of selecting the loop current paths to satisfy these conditions.
The self-resistance of the first loop is 6 + 8 = 14 Ω, and the resistance mutual with the second loop is 6 Ω. The 7-A current flowing through the 6-Ω resistor produces a 42-V drop in the first loop. The resulting loop equation is
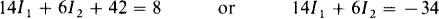
The 6 coefficient of I2 is positive because I2 flows through the 6-Ω resistor in the same direction as I1.
For the second loop, the self-resistance is 6 + 10 = 16 Ω, of which 6 Ω is mutual with the first loop.
The second loop equation is

The two loop equations together are
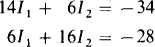
Multiplying the first equation by 8 and the second by –3 and then adding them eliminates I2:
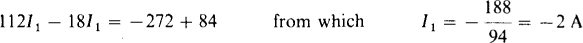
4.19 Two 12-V batteries are being charged from a 16-V generator. The internal resistances are 0.5 and 0.8 Ω for the batteries and 2 Ω for the generator. Find the currents flowing into the positive battery terminals.
The arrangement is basically parallel, with just two nodes. If the voltage at the positive node with respect to the negative node is called V, the current flowing away from the positive node through the sources is
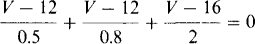
Multiplying by 4 produces

Consequently, the current into the 12-V battery with 0.5-Ω internal resistance is (12.533 – 12)/0.5 = 1.07 A, and the current into the other 12-V battery is (12.533 – 12)/0.8 = 0.667 A.
4.20 Determine the node voltages in the circuit shown in Fig. 4-23,
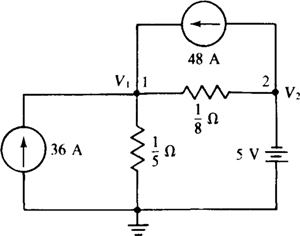
Fig. 4-23
Using self-conductances and mutual conductances is almost always best for getting the nodal equations. The self-conductance of node 1 is 5 + 8 = 13 S, and the mutual conductance is 8 S. The sum of the currents from current sources into this node is 36 + 48 = 84 A. So, the node 1 KCL equation is 13V1 – 8V2 = 84.
No KCL equation is needed for node 2 because a grounded voltage source is connected to it, making V2 = –5 V. Anyway, a KCL equation cannot be written for this node without introducing a variable for the current through the 5-V source because this current is unknown.
The substitution of V2 = – 5 V into the node 1 equation results in
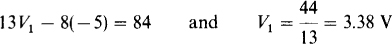
4.21 Find the node voltages in the circuit shown in Fig. 4-24.
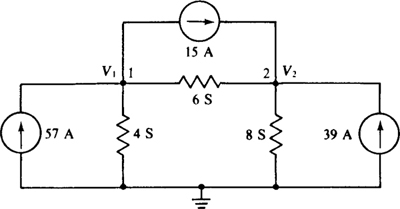
Fig. 4-24
The self-conductance of node 1 is 6 + 4 = 10 S. The conductance mutual with node 2 is 6 S, and the sum of the currents into node 1 from current sources is 57 – 15 = 42 A. So, the node 1 KCL equation is 10V1 – 6V2 = 42.
Similarly, for node 2 the self-conductance is 6 + 8 = 14 S, the mutual conductance is 6 S, and the sum of the input currents from current sources is 39 + 15 = 54 A. These give a node 2 KCL equation of –6V1 + 14V2 = 54.
Placing the two nodal equations together shows the symmetry of the coefficients (– 6 here) about the principal diagonal as a result of the same mutual conductance coefficient in both equations:
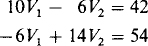
Three times the first equation added to five times the second eliminates V1. The result is
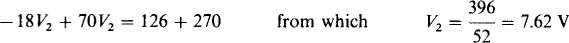
This substituted into the first equation gives
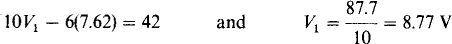
4.22 Use nodal analysis in finding I in the circuit of Fig. 4-25.
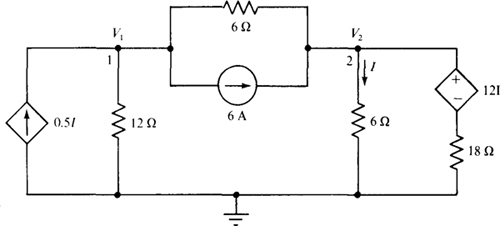
Fig. 4-25
The controlling quantity I in terms of node voltages is I = V2/6. Consequently, the dependent current source provides a current of 0.5I = 0.5(V2/6) = V2/12, and the dependent voltage source provides a voltage of 12I = 12(V2/6) = 2V2.
Because of the presence of the dependent sources, it may be best to apply KCL at nodes 1 and 2 on a branch-to-branch basis instead of attempting to use a shortcut method. Doing this gives
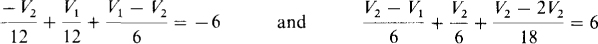
These simplify to
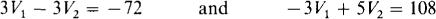
Adding these equations eliminates V1 and results in 2V2 = 36 or V2 = 18 V. Finally,
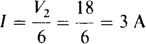
4.23 Find the node voltages in the circuit shown in Fig. 4-26.
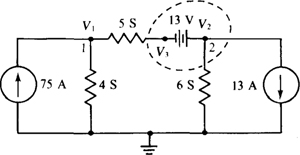
Fig. 4-26
One analysis approach is to transform the voltage source and series resistor to a current source and parallel resistor, as shown in the circuit of Fig. 4-27.
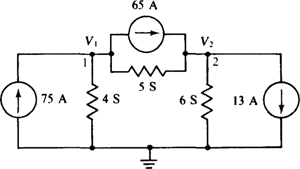
Fig. 4-27
The self-conductance of node 1 is 4 + 5 = 9 S, and that of node 2 is 5 + 6 = 11 S. The mutual conductance is 5 S. The sum of the currents into node 1 from current sources is 75 – 65 = 10 A, and that into node 2 is 65 – 13 = 52 A. Thus, the corresponding nodal equations are
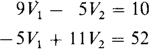
Except for V’s instead of I’s, these are the same equations as for Prob. 4.12. Consequently, the answers are the same: V1 = 5 V and V2 = 7 V. Circuits having such similar equations are called duals.
From the original circuit shown in Fig. 4-26, the 13-V source makes V3 13 V more negative than V2: V3 = V2 – 13 = 7 – 13 = –6V.
Another approach is to apply the so-called supernode method, which is applicable for the nodal analyses of circuits that contain floating voltage sources. (A voltage source is floating if neither terminal is connected to ground.) For this method, each floating voltage source is enclosed in a separate loop, or closed surface, as shown in Fig. 4-26 for the 13-V source. Then KCL is applied to each closed surface as well as to the nongrounded nodes to which no other voltage sources are connected.
For the circuit of Fig. 4-26, KCL can be applied to node 1 in the usual fashion. The result is 9V1 – 5V3 = 75. For a supernode, it is best not to use any shortcuts but instead to consider each branch current. For the supernode shown this gives 6V2 + 5(V3 – V1) = –13. Another independent equation is needed. It can be obtained from the voltage drop across the floating voltage source: V2 – V3 = 13. So, the two KCL equations are augmented with a single KVL equation. In matrix form these equations are
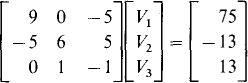
The solutions are, of course, the same: V1 = 5 V, V2 = 7 V, and V3 = –6 V.
In general, for the supernode approach, the KCL equations must be augmented with KVL equations, the number of which is equal to the number of floating voltage sources.
4.24 Use nodal analysis to obtain the node voltages V1 and V2 in the circuit of Fig. 4-28.
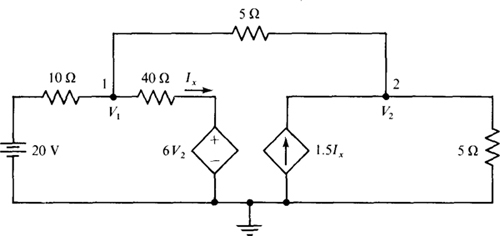
Fig. 4-28
The controlling current Ix expressed in terms of node voltages is Ix = (V1 – 6V2)/40. So, the dependent current source provides a current of 1.5Ix = 1.5(V1 – 6V2)/40. Applying KCL to nodes 1 and 2 produces
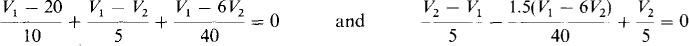
These simplify to
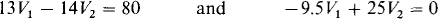
which have solutions of V1 = 10.4 V and V2 = 3.96 V, as can easily be obtained.
The circuit of Fig. 4-28 is the same as that of Fig. 4-20 of Prob. 4.16 in which mesh analysis was used. Observe that nodal analysis is easier to apply than mesh analysis since there is one less equation and the equations are easier to obtain. Often, but not always, one analysis method is best. The ability to select the best analysis method comes mostly from experience. The first step should always be to check the number of required equations for the various analysis methods: mesh, loop, and nodal.
4.25 Obtain the nodal equations for the circuit shown in Fig. 4-29.
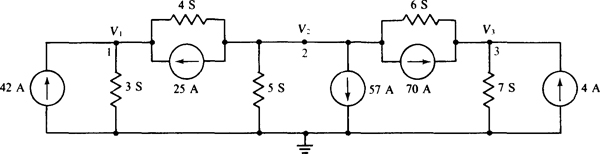
Fig. 4-29
The self-conductances are 3 + 4 = 7 S for node 1, 4 + 5 + 6 = 13 S for node 3. The mutual conductances are 4S for nodes 1 and 2, = 15S for node 2, and 6 + 7 = 6S for nodes 2 and 3, and 0 S for nodes 1 and 3. The currents flowing into the nodes from current sources are 42 + 25 = 67 A for node 1, – 25 – 57 – 70 = –152 A for node 2, and 70 + 4 = 74 A for node 3. So, the nodal equations are
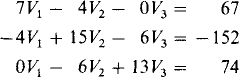
Notice the symmetry of coefficients about the principal diagonal. This symmetry always occurs for circuits that do not have dependent sources.
Since this set of equations is the same as that for Prob. 4.13, except for having V’s instead of I’s, the answers are the same: V1 = 5 V, V2 = –8 V, and V3 = 2 V.
4.26 Obtain the nodal equations for the circuit shown in Fig. 4-30.
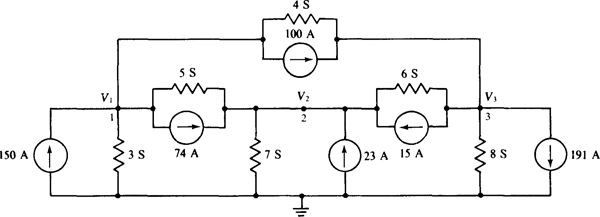
Fig. 4-30
The self-conductances are 3 + 4 + 5 = 12 S for node 1, 5 + 6 + 7= 18 S for node 2, and 6 + 4 + 8 = 18 S for node 3. The mutual conductances are 5 S for nodes 1 and 2, 6 S for nodes 2 and 3, and 4 S for nodes 1 and 3. The currents into the nodes from current sources are 150 – 100 – 74 = –24 A for node 1, 74 + 15 + 23 = 112 A for node 2, and 100 – 191 – 15 = –106 A for node 3. So, the nodal equations are
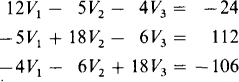
As a check, notice the symmetry of the coefficients about the principal diagonal.
Since these equations are basically the same as those in Prob. 4.14, the answers are the same: V1 = –2 V, V2 = 4 V, and V3 = –5 V.
4.27 Figure 4-31 shows a transistor with a bias circuit. If Ic = 50IB and if VBE = 0.7 V, find VCE.
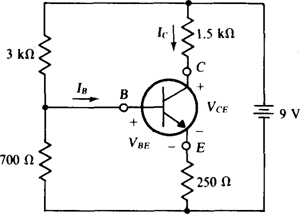
Fig. 4-31
Perhaps the best way to find VCE is to first find IB and Ic, and from them the voltage drops across the 1.5-kΩ and 250-Ω resistors. Then, use KVL on the right-hand mesh and obtain VCE from 9 V minus these two drops.
IB can be found from the two left-hand meshes. The current through the 250-Ω resistor is Ic + IB = 50IB + IB = 51IB, giving a voltage drop of (51IB)(250). This drop added to VBE is the drop across the 700-Ω resistor. Thus, the current through this resistor is [0.7 + (51IB)(250)]/700. From KCL applied at the left-hand node, this current plus IB is the total current flowing through the 3-kΩ resistor. The voltage drop across this resistor added to the drop across the 700-Ω resistor equals 9 V, as is evident from the outside loop:
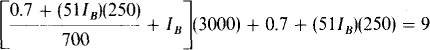
From this, IB = 75.3 μA. So, Ic = 50IB = 3.76 mA and
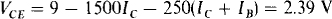
4.28 Evaluate the following determinants:
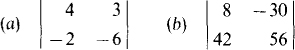
Ans. (a) –18, (b) 1708
4.29 Evaluate the following determinants:

Ans, (a) 23 739, (b) –26 022
4.30 Use Cramer’s rule to solve for the unknowns in
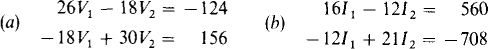
Ans. (a) V1 = –2V, V2 = 4V; (b) I1 = 17 A, I2 = –24 A
4.31 Without using Cramer’s rule or the matrix-calculator approach, solve for the unknowns in
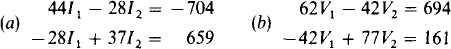
Ans. (a) I1 = –9 A, I2 = 11 A; (b) V1 = 20 V, V2 = 13 V
4.32 Use Cramer’s rule to solve for the unknowns in
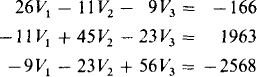
Ans. V1 – 11 V, V2 = 21 V, V3 = –39 V
4.33 What is the current-source equivalent of a 12-V battery with a 0.5-Ω internal resistance?
Ans. I = 24 A, R = 0.5 Ω
4.34 What is the voltage-source equivalent of a 3-A current source in parallel with a 2-kΩ resistor?
Ans. V = 6kV, R = 2 kΩ
4.35 Use repeated source transformations in obtaining I in the circuit of Fig. 4-32.
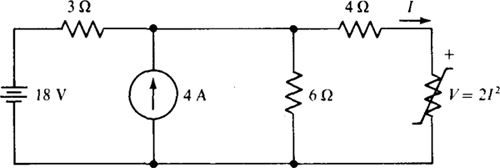
Fig. 4-32
Ans. 2 A
4.36 Find the mesh currents in the circuit shown in Fig. 4-33.
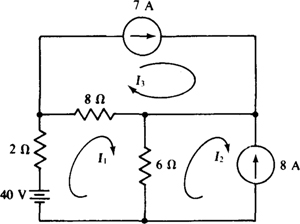
Fig. 4-33
Ans. I1 = 3 A, I2 = –8A, I3 = 7 A
4.37 Solve for the mesh currents in the circuit shown in Fig. 4-34.
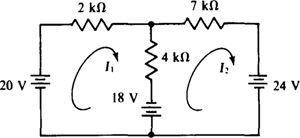
Fig. 4-34
Ans. I1 = 5 mA, I2 = –2 mA
4.38 Repeat Prob. 4.37 with the 24-V source changed to – 1 V.
Ans. I1 = 7 mA, I2 = 1 mA
4.39 Two 12-V batteries in parallel provide current to a light bulb that has a hot resistance of 0.5 Ω. If the battery internal resistances are 0.1 and 0.2 Ω, find the power consumed by the light bulb.
Ans. 224 W
4.40 Determine Ix in the circuit of Fig. 4-35.

Fig. 4-35
Ans. –4.86 mA
4.41 Calculate the mesh currents in the circuit of Fig. 4-36.
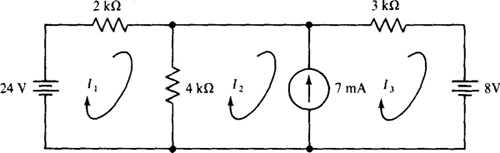
Fig. 4-36
Ans. I1 = 2 mA, I2 = –3 mA, I3 = 4 mA
4.42 Find the mesh currents in the circuit shown in Fig. 4-37.
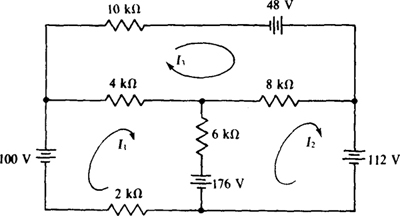
Fig. 4-37
Ans. I1 = –2mA, I2 = 6mA, I3 = 4 mA
4.43 Double the voltages of the voltage sources in the circuit shown in Fig. 4-37 and redetermine the mesh currents. Compare them with the original mesh currents.
Ans. I1 = –4 mA, I2 = 12mA, I3 = 8 mA, double
4.44 Double the resistances of the resistors in the circuit shown in Fig. 4-37 and redetermine the mesh currents. Compare them with the original mesh currents.
Ans. I1 = –1mA, I2 = 3 mA, I3 = 2 mA, half
4.45 Repeat Prob. 4.42 with the three voltage-source changes of 176 to 108 V, 112 to 110 V, and 48 to 66 V.
Ans. I1 = 3 mA, I2 = 4 mA, I3 = 5 mA
4.46 For a certain three-mesh circuit, the self-resistances are 20, 25, and 32 Ω for meshes 1, 2, and 3, respectively. The mutual resistances are 10 Ω for meshes 1 and 2, 12 Ω for meshes 2 and 3, and 6 Ω for meshes 1 and 3. The aiding voltages from voltage sources are –74, 227, and –234 V for meshes 1, 2, and 3, respectively. Find the mesh currents.
Ans. I1 = –3A, I2 = 5A, I3 = –6A
4.47 Repeat Prob. 4.46 for the same self-resistances and mutual resistances, but for aiding source voltages of 146, –273, and 182 V for meshes 1, 2, and 3, respectively.
Ans. I1 = 5A, I2 = –7A, I3 = 4A
4.48 Obtain the mesh currents in the circuit of Fig. 4-38.
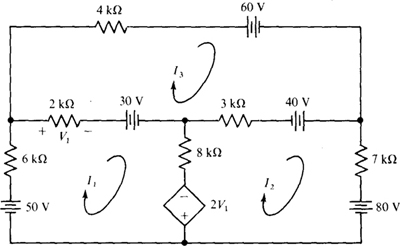
Fig. 4-38
Ans. I1 = –0.879 mA, I2 = –6.34 mA, I3 = –10.1mA
4.49 Determine the mesh currents in the circuit of Fig. 4-39.
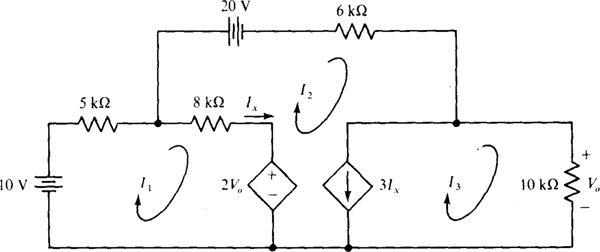
Fig. 4-39
Ans. I1 = –3.26 mA, I2 = –1.99 mA, I3 = 1.82 mA
4.50 Use loop analysis to find the current flowing down through the 6-Ω resistor in the circuit shown in Fig. 4-33.
Ans. 11 A
4.51 Use loop analysis to find the current flowing to the right through the 8-kΩ resistor in the circuit shown in Fig. 4-37.
Ans. 2 mA
4.52 Use loop analysis to find the current I in the circuit shown in Fig. 4-40.
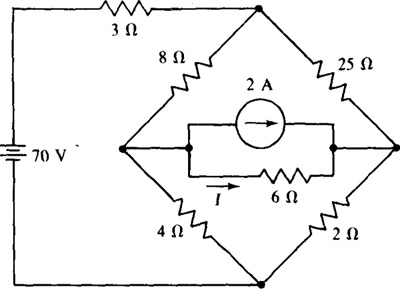
Fig. 4-40
Ans. 0.375 A
4.53 Obtain the node voltages in the circuit shown in Fig. 4-41.
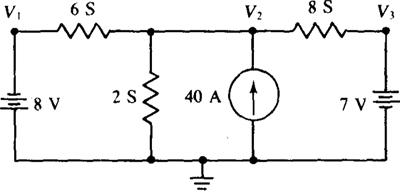
Fig. 4-41
Ans. V1 = –8V, V2 = 3V, V3 = 7 V
4.54 Find the node voltages in the circuit shown in Fig. 4-42.
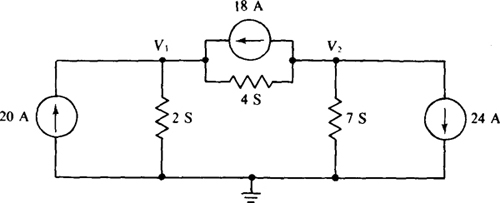
Fig. 4-42
Ans. V1 = 5V, V2 = – 2 V
4.55 Double the currents from the current sources in the circuit shown in Fig. 4-42 and redetermine the node voltages. Compare them with the original node voltages.
Ans. V1 = 10V, V2 = –4V, double
4.56 Double the conductances of the resistors in the circuit shown in Fig. 4-42 and redetermine the node voltages. Compare them with the original node voltages.
Ans. V1 = 2.5 V, V2 = – 1 V, half
4.57 Repeat Prob. 4.54 with the 24-A source changed to – 1 A.
Ans. V1 = 7 V, V2 = 1 V
4.58 Find V0 for the circuit shown in Fig. 4-43.
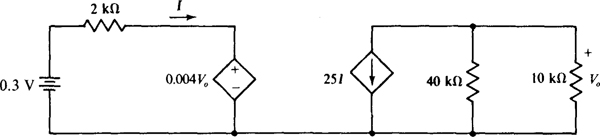
Fig. 4-43
Ans. –50 V
4.59 Find V in the circuit shown in Fig. 4-44.
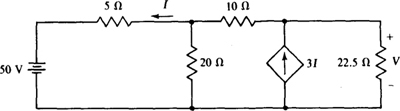
Fig. 4-44
Ans. 180V
4.60 Calculate the node voltages in the circuit of Fig. 4-45.
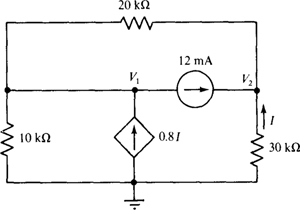
Fig. 4-45
Ans. V1 = –63.5 V, V2 = 105.9 V
4.61 Find the voltages V1, V2, and V3 in the circuit shown in Fig. 4-46.
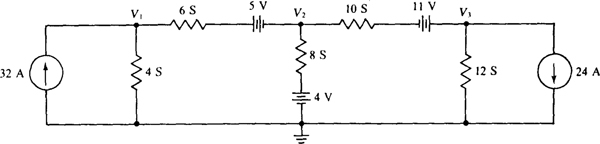
Fig. 4-46
Ans. V1 = 5V, V2 = –2V, V3 = 3 V
4.62 Find the node voltages in the circuit shown in Fig. 4-47.
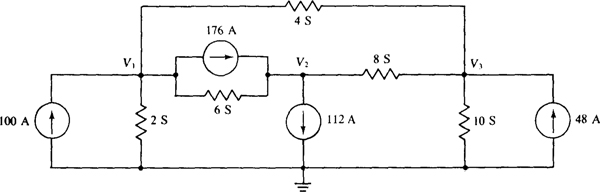
Fig. 4-47
Ans. V1 = –2 V, V2 = 6 V, V3 = 4 V
4.63 Repeat Prob. 4.62 with the three current-source changes of 176 to 108 A, 112 to 110 A, and 48 to 66 A.
Ans. V1= 3V, V2 = 4 V, V3 = 5 V
4.64 For a certain four-node circuit, including a ground node, the self-conductances are 40, 50, and 64 S for nodes 1, 2, and 3, respectively. The mutual conductances are 20 S for nodes 1 and 2, 24 S for nodes 2 and 3, and 12 S for nodes 1 and 3. Currents flowing in current sources connected to these nodes are 74 A away from node 1, 227 A into node 2, and 234 A away from node 3. Find the node voltages.
Ans. V1 = –1.5 V, V2 = 2.5 V, V3 = –3 V
4.65 Repeat Prob. 4.64 for the same self-conductances and mutual conductances, but for source currents of 292 A into node 1, 546 A away from node 2, and 364 A into node 3.
Ans. V1 = 5V, V2 = –7 V, V3 = 4 V
4.66 In the circuit shown in Fig. 4-48, find VCE if Ic = 30IB and VBE = 0.7 V.
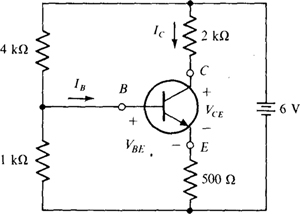
Fig. 4-48
Ans. 3.68 V
4.67 Repeat Prob. 4.66 with the dc voltage source changed to 9 V and the collector resistor changed from 2 kΩ to 2.5 kΩ.
Ans. 2.89 V