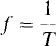
In the circuits considered so far, the independent sources have all been dc. From this point on, the circuits have alternating-current (ac) sources.
An ac voltage (or ac current) varies sinusoidally with time, as shown in Fig. 10-la. This is a periodic voltage since it varies with time such that it continually repeats. The smallest nonrepeatable portion of a periodic waveform is a cycle, and the duration of a cycle is the period T of the wave. The reciprocal of the period, and the number of cycles in a period, is the frequency, which has a quantity symbol f:
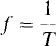
Fig. 10-1
The SI unit of frequency is the hertz, with unit symbol Hz.
In these definitions, notice the terms wave and waveform. They do not refer to the same thing. A wave is a varying voltage or current, but a waveform is a graph of such a voltage or current. Often, however, these terms are used interchangeably..
Although the sine wave of Fig. 10-1a is by far the most common periodic wave, there are other common ones: Figure 10-1b shows a square wave, Fig. 10-1c a sawtooth wave, and Fig. 10-1d a triangular wave. The dashed lines at both ends indicate that the waves have no beginnings and no ends, as is strictly required for periodic waves. But, of course, all practical voltages and currents have beginnings and ends. When a wave is obviously periodic, these dashed lines are often omitted.
The voltage waveforms shown in Fig. 10-1a and b are negative or below the time axis for part of each period. During these times, the corresponding voltages have polarities opposite the reference polarities. Of course, when the waveforms are above the time axis, these voltages have the same polarities as the references. For similar graphs of currents, the currents flow in the current reference directions when the waveforms are above the time axis, and in opposite directions when the waveforms are below that axis.
Figure 10-2 shows the basics of an ac generator or alternator for generating a sinusoidal voltage. The conductor, which in practice is a coil of wire, is rotated by a steam turbine or by some other source of mechanical energy. This rotation causes a continuous change of magnetic flux linking the conductor, thereby inducing a sine wave voltage in the conductor. This change of flux, and so the induced voltage, varies from zero when the conductor is horizontal to a maximum when the conductor is vertical. If t = 0 s corresponds to a time when the conductor is horizontal and the induced voltage is increasing, the induced voltage is v = Vm sin ωt, where Vm is the peak value or amplitude, sin is the operation designator for a sine wave, ωt is the argument, and ω is the quantity symbol for the radian frequency of the voltage. (Some authors use the terms “angular velocity” or “angular frequency” instead of radian frequency.) The SI unit of radian frequency is radian per second, and the unit symbol is rad/s. The frequency f and the radian frequency ω are related by
ω = 2πf
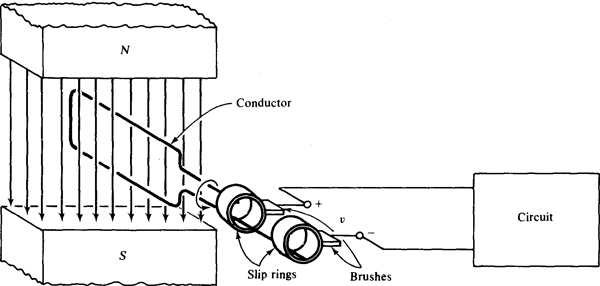
Fig. 10-2
The radian in radian per second is an SI angular unit, with symbol rad, and it is an alternative to degrees. A radian is the angle subtended by an arc on the circumference of a circle if the arc has a length equal to the radius. Since the circumference of a circle equals 2πr, where r is the radius, it follows that 2π rad equals 360° or
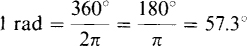
This relation is useful for converting from degrees to radians and from radians to degrees. Specifically,
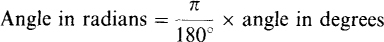
and
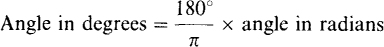
But, of course, a scientific calculator will perform either conversion at the press of a key. The waveform of sin cot has the shape shown in Fig. 10-la. In each cycle it varies from 0 to a positive peak or maximum of 1, back to 0, then to a negative peak or minimum of –1, and back to 0 again. For any value of the argument cot, sin wt can be evaluated with a calculator operated in the radians mode. Alternatively, the argument can be converted to degrees and the calculator operated in the more popular decimal degrees mode. For example, sin (π/6) = sin 30° = 0.5.
The abscissa of a graph of a sine wave can be expressed in radians, degrees, or time. Sometimes, when time is used, it is in fractions of the period T, as in Fig. 10-1a. Usually, determining what the fractions should be is obvious from the corresponding proportions of a cycle.
Consider the graphing of one cycle of a specific ac voltage: vx =20 sin 377f V. The peak value or amplitude is 20 V because sin 377t has a maximum value of 1. The radian frequency is ω = 377 rad/s, which corresponds to I = w/2π = 60 Hz, the frequency of the electrical power systems in the United States. The period is T= 1/60 = 16.7 ms. A cycle of this voltage can be plotted by substituting, into 20 sin 377t, different times for t from the time interval of f = 0s to t = 16.7 ms. Figure 10-3a shows the results of evaluating this sine wave at 21 different times and drawing a smooth curve through the plotted points. For comparison purposes, all three abscissa units—seconds, radians, and degrees—are shown.
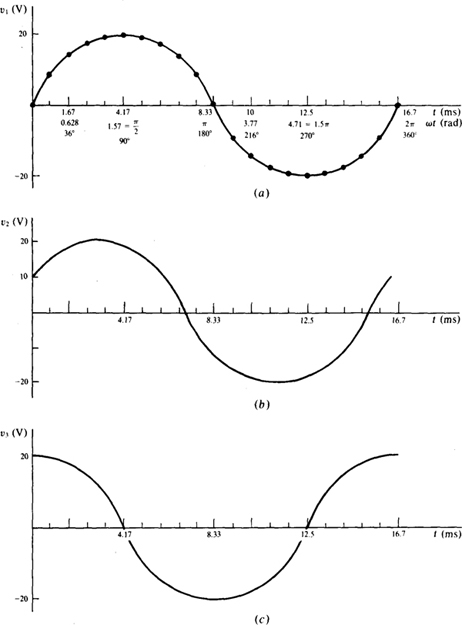
Fig. 10-3
Figure 10-3b shows a graph of one cycle of v2 = 20 sin (377t + 30°) V. Notice that the argument 377t + 30° is the sum of two terms, the first of which is in radians and the second of which is in degrees. Showing such an addition is common despite the fact that before the terms can be added, either the first term must be converted to degrees or the second term must be converted to radians. The 30° in the argument is called the phase angle.
The cosine wave, with designator cos, is as important as the sine wave. Its waveform has the same shape as the sine waveform, but is shifted 90°—a fourth of a period—ahead of it. Sine and cosine waves are so similar that the same term “sinusoid” is applied to both as well as to phase-shifted sine and cosine waves. Figure 10-3c is a graph of v3 = 20 sin (377i + 90°) = 20 cos 377f V. Notice that the values of the cosine wave v3 occur one-fourth period earlier than corresponding ones for the sine wave v1.
Some sine and cosine identities are important in the study of ac circuit analysis:
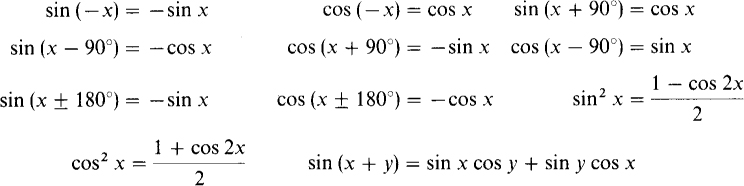
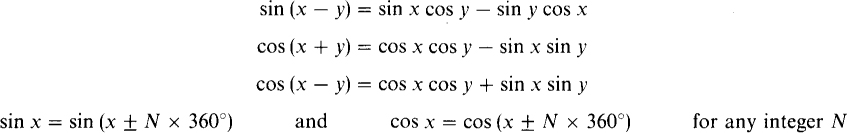
Sinusoids of the same frequency have phase relations that have to do with the angular difference of the sinusoidal arguments. For example, because of the added 30° in its argument, v2 = 20 sin (377t + 30°) V of the last section leads v1, = 20 sin 377f V by 30°. Alternatively, v1 lags v2 by 30°. This means that the peaks, zeros, and other values of v2 occur earlier than those of vl by a time corresponding to 30°. Another but less specific way of expressing this phase relation is to say that v2 and v2 have a 30° phase difference or that they are 30° out of phase. Similarly, the cosine wave v3 leads the sine wavev3 by 90° or v1 lags v3 by 90°. They have a phase difference of 90°; they are 90° out of phase. Sinusoids that have a 0° phase difference are said to be in phase. Figure 10-4a shows sinusoids that are in phase, and Fig. 10-4b shows sinusoids that are 180° out of phase.
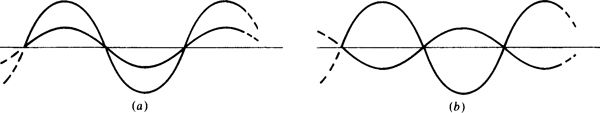
Fig. 10-4
The phase difference between two sinusoids can be found by subtracting the phase angle of one from that of the other, provided that both sinusoids have either the sine form or the cosine form, and that the amplitudes have the same sign—both positive or both negative. Additionally, of course, the two sinusoids must have the same frequency.
The average value of a periodic wave is a quotient of area and time—the area being that between the corresponding waveform and the time axis for one period, and the time being one period. Areas above the time axis are positive, and areas below are negative. The areas must be algebraically added (signs must be included) to obtain the total area between the waveform and time axis for one period. (The average value of a periodic wave is always assumed to be calculated over a period unless otherwise specified.)
The average value of a sinusoid is zero because over one period the positive and negative areas cancel in the sum of the two areas. For some purposes, though, a nonzero “average” is used. By definition, it is the average of a positive half-cycle. From calculus, this average is 2/π = 0.637 times the peak value.
If a resistor of R ohms has a voltage v = Vm sin (ωt + ϑ) across it, the current is, by Ohm’s law, i = v/R = (VmR) sin (ωt + ϑ). The multiplier VJR is the current peak Im. Im= VmR. Notice that the current is in phase with the voltage. To repeat, a resistor current and voltage are in phase. (The references are, of course, assumed to be associated.)
Instantaneous resistor power dissipation varies with time because the instantaneous voltage and current vary with time, and the power is the product of the two. Specifically,
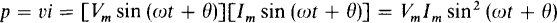
which shows that the peak power is Pm = VmIm, and it occurs each time that sin (ω + 0) = +1. From the identity sin2 x = (1 – cos 2x)/2,
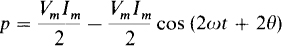
which is a constant plus a sinusoid of twice the frequency of the voltage and current. This instantaneous power is zero each time that the voltage and current are zero, but it is never negative because the positive first term is always equal to or greater than the second term, which is negative half the time. The fact that the power is never negative means that a resistor never delivers power to a circuit. Rather, it dissipates as heat all the energy it receives.
The average power supplied to a resistor is just the first term: Pm = VmIm/2, because the average value of the second term is zero. From Vm = ImR,
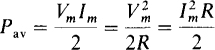
These formulas differ from the corresponding dc formulas by a factor of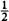 
Although periodic voltages and currents vary with time, it is convenient to associate with them specific values called effective values. Effective voltages are used, for example, in the rating of electrical appliances. The 120-V rating of an electric hair dryer and the 240-V rating of an electric clothes dryer are effective values. Also, most ac ammeters and voltmeters give readings in effective values.
By definition, the effective value of a periodic voltage or current (veff or Ieff) is the positive dc voltage or current that produces the same average power loss in a resistor: Pav = V2eff/R and Pav = I2eff/R. Since for a sinusoidal voltage the average power loss is Pav = V2m/2R,
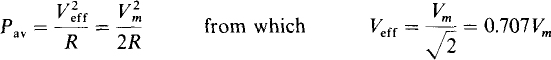
Similarly, leff = Im/
= 0.707lm. So, the effective value of a sinusoidal voltage or current equals the peak value divided by .
Another name for effective value is root mean square (rms). The corresponding voltage and current notations are Vrms and Irms, which are the same as Veff and Ieff. This name stems from a procedure for finding the effective or rms value of any periodic voltage or current—not just sinusoids. As can be derived using calculus, this procedure is to
1. Square the periodic voltage or current.
2. Find the average of this squared wave over one period. Another name for this average is the mean.
3. Find the positive square root of this average.
Unfortunately, except for square-type waves, finding the area in step 2 requires calculus. Incidentally, if this procedure is applied to a sawtooth and a triangular wave, the result is the same effective value—the peak value divided by 
.
If an inductor of L henries has a current i = lm sin (ωt +θ) flowing through it, the voltage across the inductor is
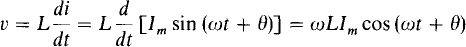
The multiplier ωLlm is the peak voltage Vm: Vm = ωLIm and Im = Vm/ωL. From a comparison of Im – Vm/ωL and Im = VR, clearly ωL has a current-limiting action similar to that of R.
The quantity ωL is called the inductive reactance of the inductor. Its quantity symbol is XL:
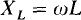
It has the same ohm unit as resistance. Unlike resistance, though, inductive reactance depends on frequency—the greater the frequency the greater its value and so the greater its current-limiting action. For sinusoids of very low frequency, approaching 0 Hz or dc, an inductive reactance is almost zero, which means that an inductor is almost a short circuit to such sinusoids, in agreement with dc results. At the other frequency extreme, for sinusoids of very high frequencies, approaching infinity, an inductive reactance approaches infinity, which means that an inductor is almost an open circuit to such sinusoids.
From a comparison of the inductor current and voltage sinusoids, it can be seen that the inductor voltage leads the inductor current by 90° or the inductor current lags the inductor voltage by 90°.
The instantaneous power absorbed by an inductor is
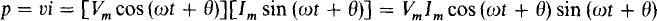
which from sine and cosine identities reduces to
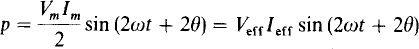
This power is sinusoidal at twice the voltage and current frequency. Being sinusoidal, its average value is zero—a sinusoidally excited inductor absorbs zero average power. In terms of energy, at the times when p is positive, an inductor absorbs energy. And at the times when p is negative, an inductor returns energy to the circuit and acts as a source. Over a period, it delivers just as much energy as it receives.
If a capacitor of C farads has a voltage v = Vm sin (ωt + ϑ) across it, the capacitor current is
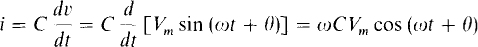
The multiplier ωCVm is the peak current lm: I,m = ωCVm and Vm/Im = 1/ωC. So, a capacitor has a current-limiting action similar to that of a resistor, with 1/ ωC corresponding to R. Because of this, some electric circuits books define capacitive reactance as 1/ωC. However, almost all electrical engineering circuits books include a negative sign and define capacitive reactance as
The negative sign relates to phase shift, as will be explained in Chap. 12. Of course, the quantity symbol for capacitive reactance is Xc and the unit is the ohm.
Because 1/ωC is inversely proportional to frequency, the greater the frequency the greater the current for the same voltage peak. For high-frequency sinusoids, a capacitor is almost a short circuit, and for low-frequency sinusoids approaching 0 Hz or dc, a capacitor is almost an open circuit.
From a comparison of the capacitor voltage and current sinusoids, it can be seen that the capacitor current leads the capacitor voltage by 90°, or the capacitor voltage lags the capacitor current by 90’. This is the opposite of the inductor voltage and current phase relation.
The instantaneous power absorbed by a capacitor is
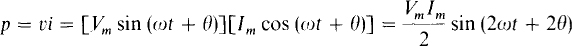
the same as for an inductor. The instantaneous power absorbed is sinusoidal at twice the voltage and current frequency and has a zero average value. So, a capacitor absorbs zero average power. Over a period a capacitor delivers just as much energy as it absorbs.
10.1 Find the periods of periodic voltages that have frequencies of (a) 0.2 Hz, (b) 12 kHz, and (c) 4.2 MHz.
(a) From T = 1/f’, T= 1/0.2 = 5 s
(b) Similarly, T = 1/(12 × 103) s = 83.3 μs
(c) r = 1/(4.2 × 106)s = 238 ns
10.2 Find the frequencies of periodic currents that have periods of (a) 50 μs, (b) 42 ms, and (c) 1 h.
(a) From f = 1/T, f = 1/(50 μ 1(T6) Hz = 20 kHz
(b) Similarly, f = 1/(42 × 10’ 3) = 23.8 Hz
(c)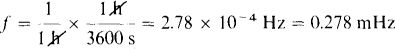 
10.3 What are the period and frequency of a periodic voltage that has 12 cycles in 46 ms?
The period is the time taken for one cycle, which can be found by dividing the 12 cycles into the time that it takes for them to occur (46 ms): T = 46/12 = 3.83 ms. Of course, the frequency is the reciprocal of the period: f = 1/(3.83 × 10–3) = 261 Hz. Alternatively, but what amounts to the same thing, the frequency is the number of cycles that occur in 1 s: f = 12/(46 × 10–3) = 261 Hz.
10.4 Find the period, the frequency, and the number of cycles shown for the periodic wave illustrated in Fig. 10-5.
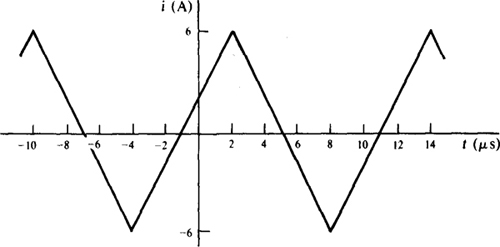
Fig. 10-5
The wave has one positive peak at 2 μs and another positive peak at 14 μs, between which times there is one cycle. So, the period is T = 14 – 2 = 12 μs, and the frequency is f = 1/T = 1/(12 × 1CT6) Hz = 83.3 kHz. There is one other cycle shown—from – 10 to 2 μs.
10.5 Convert the following angles in degrees to angles in radians: (a) 49°, (b) – 130°, and (c) 435°.
(a)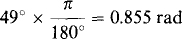
(b)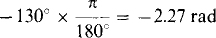
(c)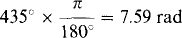 
10.6 Convert the following angles in radians to angles in degrees: (a) ω/18 rad, (b) —0.562 rad, and (c) 4 rad.
(a)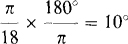 
(b)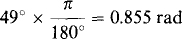
(c)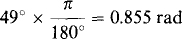
10.7 Find the periods and frequencies of sinusoidal currents that have radian frequencies of (a) 9ω rad/s, (b) 0.042 rad/s, and (c) 13 M rad/s.
From f = ω/2n and T =1/f,
(a) f = 9ω/2ω = 4.5 Hz, T = 1/4.5 = 0.222 s
(b) f = 0.042/2ω: Hz = 6.68 mHz, T= 1/(6.68 × 10”3) = 150 s
(c) f = 13 × 106/2ti Hz = 2.07 MHz, T = 1/(2.07 × 106) s = 0.483 μs
10.8 Find the radian frequencies of sinusoidal voltages that have periods of (a) 4 s, (b) 6.3 ms, and (c) 7.9 μ(S.
From ω = 2ωf = 2ω/T.
(a) ω = 2ω/4 = 1.57 rad/s
(b) ω = 2ω/(6.3 × 10–3) = 997 rad/s
(c) ω = 2ω/(7.9 × 10–6) = rad/s = 0.795 Mrad/s
10.9 Find the amplitudes and frequencies of (a) 42.1 sin(377t + 30°) and (b) -6.39 cos(105t -20°).
(a) The amplitude is the magnitude of the multiplier: |42.1| = 42.1. Note the vertical lines about 42.1 for designating the magnitude operation, which removes a negative sign, if there is one. The radian frequency is the multiplier of t: 377 rad/s. From it, and f = ω/2Ą, the frequency is f = 377/2ω = 60 Hz.
(b) Similarly, the amplitude is | —6.39| = 6.39. The radian frequency is 105 rad/s, from which f= ω/2ω = 105/2ttHz = 15.9 kHz.
10.10 Find the instantaneous value of v = 70 sin 400ωt V at t = 3 ms.
Substituting for t: υ(3 ms) = 70 sin (40071 × 3 × 10–3) = 70 sin 1.2ω V. Since the 1.2ω sinusoidal argument is in radians, a calculator must be operated in the radians mode for this evaluation. The result is —41.1 V. Alternatively, the angle can be converted to degrees, 1.2ω × 180°/ω = 216° and a calculator operated in the more popular decimal degrees mode: v (3 ms) = 70 sin 216’ = —41.1 V.
10.11 A current sine wave has a peak of 58 mA and a radian frequency of 90 rad/s. Find the instantaneous current at t = 23 ms.
From the specified peak current and frequency, the expression for the current is i = 58 sin 90t mA. For t = 23 ms, this evaluates to
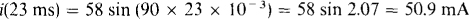
Of course, the 2.07 in radians could have been converted to degrees; 2.07 × 180°/ω = 118.6, and then 58 sin 118.6° evaluated.
10.12 Evaluate (a) v = 200 sin (3393t + ω/7) V and (b) i = 67 cos (3016t – 42c) mA at t= 1.1ms.
From substituting 1.1 × 10–3 for t,
(a)v (l.l ms) = 200 sin (3393 × 1.1 × 10–3 + ω/7) = 200 sin 4.18 = -172 V
Operating a calculator in the radians mode is convenient for this calculation because both parts of the sinusoidal argument are in radians.
(b)i (l.l ms) = 67cos(3016 × 1.1 × 10–3 – 42°) = 67 cos (190° – 42°) = -56.9 mA
Note that the first term was converted from radians to degrees so that it could be added to the second term. Alternatively, the second term could have been converted to radians.
10.13 Find expressions for the sinusoids shown in Fig. 10-6.
Fig. 10-6
The sinusoid shown in Fig. 10-6a can be considered to be either a phase-shifted sine wave or a phase-shifted cosine wave—it does not make any difference. For the selection of a phase-shifted sine wave, the general expression is ω’= 12 sin (ω + 0), since the peak value is shown as 12. The radian frequency ω can be found from the period. One-fourth of a period occurs in the 15-ms time interval from —5 to 10 ms, which means that T = 4 × 15 = 60 ms, and so ω= ω/T = 2ω/(60 × 10 –3) = 104.7 rad/s. From the zero value at t — – 5 ms and the fact that the waveform is going from negative to positive then, just as a sine wave does for a zero argument, the argument can be zero at this time: 104.7(—5 × 10–3) + φ = 0, from which 9 = 0.524 rad = 30°. The result is v = 12 sin (104.7t + 0.524) = 12 sin (104.7t + 30°) V.
Now consider the equation for the current shown in Fig. 10-6b. From ω = 2ωf = 2ω(60) = 377 rad/s and the peak value of 10 mA, i = 10 cos (37ω + 9) mA, with the arbitrary selection of a phase-shifted cosine wave. The angle φ can be determined from the zero value at ωt = O 7ω. For this value of ωt, the phase-shifted cosine argument can be 1.5ω rad because at 1.5ω rad = 270° a cosine waveform is zero and going from negative to positive, as can be seen from Fig. 10-3c. So, for ωt = 0.7ω, the argument can be ωt + ω =.7φ + ρ= 1.571, from which φ = O.8φ rad = 144°. The result is i = 10 cos (377t + 0.8φ) = 10cos(377t + 144°) mA.
10.14 Sketch a cycle of ν = 30 sin (754t + 60°) V for the period beginning at t = 0 s. Have all three abscissa units of time, radians, and degrees.
A fairly accurate sketch can be made from the initial value, the peaks of 30 and —30 V, and the times at which the waveform is zero and at its peaks. Also needed is the period, which is T = 2ω/ω = 27i/754 = 8.33 ms. The initial value can be found by substituting 0 for t in the argument. The result is v = 30 sin 60° = 26 V. The waveform is zero for the first time when the argument is π radians since sin π = 0. This time can be found from the argument with the 60° converted to π/3 radians: 754t + ω/3 = ω, from which t = 2.78 ms. The next zero is half a period later: 2.78 + 8.33/2 = 6.94 ms. The positive peak for this cycle occurs at a time when the sinusoidal argument is n/2: 754t + ω/3 = ω/2, from which t = 0.694 ms. The negative peak is half a period later: t = 0.694 + 8.33/2 = 4.86 ms. The radian units for these times can be found from ωt = 754t = 2407πt. Of course, the corresponding degree units can be found by converting from radians to degrees. Figure 10-7 shows the sinusoid.
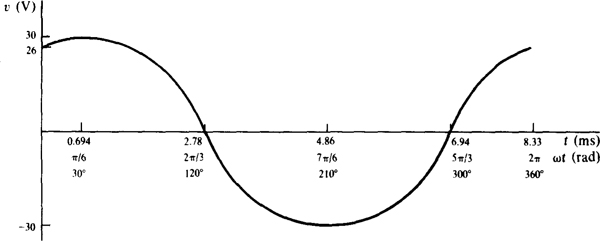
Fig. 10-7
10.15 What is the shortest time required for a 2.1 krad/s sinusoid to increase from zero to four-fifths of its peak value?
For convenience, the expression for the sinusoid can be considered to be Vm sin (2.1 × 103t). The time required for this wave to equal 0.8 Vm can be found from Vm sin (2.1 × 103t) = 0.8 Vm, which simplifies to sin (2.1 × 103t) = 0.8. This can be evaluated for t by taking the inverse sine, called the arcsine, of both sides. This operation causes the sin operation to be canceled, leaving the argument. On a calculator, the arcsine may be designated by “sin–1” or “asin.” Taking the arcsine of both sides produces
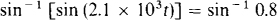
which simplifies to 2.1 × 103t = sin – 0.8, from which
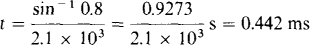
The 0.9273 is, of course, in radians.
10.16 If 50 V is the peak voltage induced in the conductor of the alternator shown in Fig. 10-2, find the voltage induced after the conductor has rotated through an angle of 35° from its vertical position.
When the conductor is in a vertical position, the induced voltage is a maximum in magnitude, but can be either positive or negative. The vertical position can, for convenience, be considered to correspond to 0°. Then, since the induced voltage is sinusoidal, and since the cosine wave has a peak at 0°, the voltage can be considered to be ν = ± 50 cos 0, in which ϑ is the angle of the conductor from the vertical. So, with the conductor at 35° from the vertical, the induced voltage is v = ±50 cos 35° = ±V.
10.17 If the conductor in the alternator shown in Fig. 10-2 is rotating at 60 Hz, and if the induced voltage has a peak of 20 V, find the induced voltage 20 ms after the conductor passes through a horizontal position if the voltage is increasing then.
The simplest expression for the induced voltage is v = 20 sin 377t V if t = 0 s corresponds to the time at which the conductor is in the specified horizontal position. This is the voltage expression because the induced voltage is sinusoidal, 20 V is specified as the peak, 377 rad/s corresponds to 60 Hz, and sin ω is zero at t = 0 s and is increasing. So,
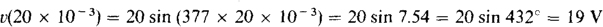
10.18 Find the periods of (a) 7 – 4 cos (400t + 30°), (b) 3 sin2 4t, and (c) 4 cos 3t sin 3t.
(a) The expression 7 – 4 cos (400t + 30°) is a sinusoid of – 4 cos (400t + 30°) “riding” on a constant 7. Since only the sinusoid contributes to the variations of the wave, only it determines the period: T = 2ω/ω = 2ω/400 s = 15.7 ms.
(b) Because of the square, it is not immediately obvious what the period is. The identity sin2 × = (1 – cos 2x)/2 can be used to eliminate the square:
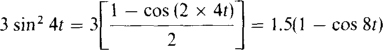
From the cosine wave portion, the period is T = 2ω/ω = 2ω:/8 = 0.785 s.
(c) Because of the product of the sinusoids in 4 cos 3t sin 3t, some simplification must be done before the period can be determined. The identity sin (x + y) = sin × cos y + sin y cos x can be used for this by setting y = x. The result is
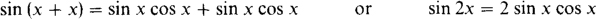
from which sin × cos × = (sin 2x)/2. Here, × = 3t, and so
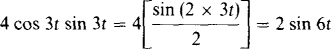
From this, the period is T = 2ω/aω = 2ω/6 = 1.05 s.
10.19 Find the phase relations for the following pairs of sinusoids:
(a) v = 60 sin (377t + 50°) V, i= 3 sin (754t – 10°) A
(b) v1 =6.4 sin (7.1πt + 30°) V, v2 = 7.3 sin (7.1 πt – 10°) V
(c) v = 42.3 sin (400t + 60°) V, i = -4.1 sin (400t – 50°) A
(a) There is no phase relation because the sinusoids have different frequencies.
(b) The angle by which v1 leads v2 is the phase angle of vi minus the phase angle of v2: ang v1 — ang v2 = 30° – (-10°) = 40°. Alternatively, v2 lags v1 by 40°.
(c) The amplitudes must have the same sign before a phase comparison can be made. The negative sign of i can be eliminated by using the identity – sin × = sin (x ± 180°). The positive sign in + is more convenient because, as will be seen, it leads to a phase difference of the smallest angle, as is generally preferable. The result is
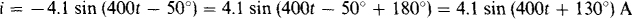
The angle by which v leads i is the phase angle of v minus the phase angle of i: ang v – ang í = 60° – 130° = —70°. The negative sign indicates that v lags, instead of leads, i by 70°. Alternatively, i leads v by 70°. If the negative sign in ± had been used, the result would have been that v leads i by 290°, which is equivalent to – 70° because 360° can be subtracted from (or added to) a sinusoidal angle without affecting the value of the sinusoid.
10.20 Find the angle by which i1 = 3.1 sin (754t – 20°) mA leads i2 = - 2.4 cos (754t + 30°) mA.
Before a phase comparison can be made, both amplitudes must have the same sign, and both sinusoids must be of the same form: either phase-shifted sine waves or phase shifted cosine waves. The negative sign of i2 can be eliminated by using the identity —cos × = cos (x + 180°). At this point it is not clear whether the positive or negative sign is preferable, and so both will be kept:
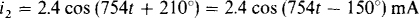
Both of these phase-shifted cosine waves can be converted to phase-shifted sine waves by using the identity cos × = sin (x + 90°):
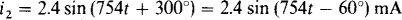
Now a phase angle comparison can be made: i, leads i2 by —20° – 300° = —320° from the first i2 expression, or by —20° – (– 60°) = 40° from the second i2 expression. Being smaller in magnitude, the 40° lead is preferable to a – 320° lead. But both are equivalent.
10.21 Find the average values of the periodic waveforms shown in Fig. 10-8.
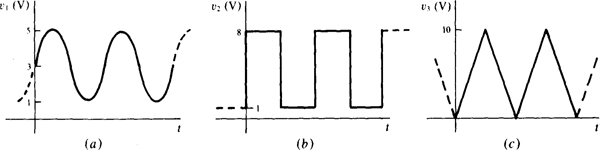
Fig. 10-8
The waveform shown in Fig. 10-8a is a sinusoid “riding” on top of a constant 3 V. Since the average value of the sinusoid is zero, the average value of the waveform equals the constant 3 V.
The average value of the waveform shown in Fig. 10-86, and of any waveform, is the area under the waveform for one period, divided by the period. Since for the cycle beginning at t = 0 s, the waveform is at 8 V for half a period and is at 1 V for the other half-period, the area underneath the curve for this one cycle is, from the height-times-base formula for a rectangular area, 8 × T/2 + 1 × T/2 = 4.5T. So, the average value is 4.5T/T=4.5V. Note that the average value does not depend on the period. This is generally true.
The cycle of the waveform shown in Fig. 10-8c beginning at f = 0 s is a triangle with a height of 10 and a base of T. The area under the curve for this one cycle is, from the triangular area formula of one-half the height times the base, 0.5 × 10 × T= 57. And so the average value is 5T/T= 5 V.
10.22 What are the average values of the periodic waveforms shown in Fig. 10-9?
Fig. 10-9
For the cycle starting at f = 0 s, the i1, waveform shown in Fig. 10-9« is at 8 A for half a period and is at —3 A for the next half-period. So, the area for this cycle is 8(T/2) + (– 3)(7,’2) = 2.57, and the average value is 2.5T/T= 2.5 A.
The i2 waveform shown in Fig. 10-9b has a complete cycle from r = 0 s to t = 5 s. For the first 2 s the area under the curve is 6x2 = 12. For the next second it is -2x1 = -2. And for the last 2 s it is -4x2= -8. The algebraic sum of these areas is 12 – 2 – 8 = 2, which divided by the period of 5 results in an average value of 2/5 = 0.4 A.
10.23 What is the average power absorbed by a circuit component that has a voltage v = 6sin(377t + 10°) V across it when a current; = 0.3 sin (377f – 20e) A flows through it? Assume associated references since there is no statement to the contrary.
The average power is, of course, the average value of the instantaneous power p:
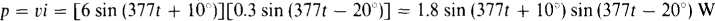
This can be simplified using a sine-cosine identity derived by subtracting cos (x + y) = cos x cos y – sin x sin y from cos (x – y) = cos x cos y + sin.v sin y. The result is the identity sin x sin y = 0.5[cos (x-y)- cos (x + y)]. Here, x = 311t + 10° and y = 377f – 20°. So,
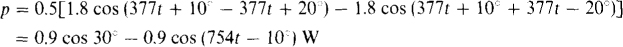
Since the second term is a sinusoid, and so has an average value of zero, the average power equals the first term:
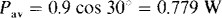
Note in particular that the average power is not equal to the product of the average voltage (0 V) and the average current (0 A), nor is it equal to the product of the effective value of voltage (6/) and the effective value of current (0.3/).
10.24 If the voltage across a single circuit component is i; = 40 sin (400f + 10°) V for a current through it of i = 34.1 sin (400t + 10°) mA, and if the references are associated, as should be assumed, what is the component?
Since the voltage and current are in phase, the component is a resistor. The resistance is R = Vm/ = 40/(34.1 × 10-3) Ω = 1.17 kΩ.
10.25 The voltage across a 62-Ω resistor is v = 30 sin (200πt + 30°) V. Find the resistor current and plot one cycle of the voltage and current waveforms on the same graph.
From i = v/R, i = [30 sin (200tií + 30c)]/62 = 0.484 sin (200ωf + 30°) A. Of course, the period is T = 2n/co = 2ω/200ω s = 10 ms. For both waves, the curves will be plotted from the initial, peak, and zero values and the times at which they occur. At í = 0 s, v = 30 sin 30° = 15 V and i = 0.484 sin 30° = 0.242 A. The positive peaks of 30 V and 0.484 A occur at a time tp corresponding to 60° since the sinusoidal arguments are 90° then. From the proportionality tp/T = 60°/360°, the peak time is tp = 10/6 = 1.67 ms. Of course, the negative peaks occur at a half-period later, at 1.67 + 5 = 6.67 ms. The first zero values occur at a time corresponding to 150° because the sinusoidal arguments are 180° then. Using a proportionality again, this time is (150/360)(10) = 4.17 ms. The next zeros occur one half-period later, at 4.17 + 5 = 9.17 ms. The voltage and current waveforms are shown in Fig. 10-10. The relative heights of the voltage and current peaks should not be of concern, because they are in different units.
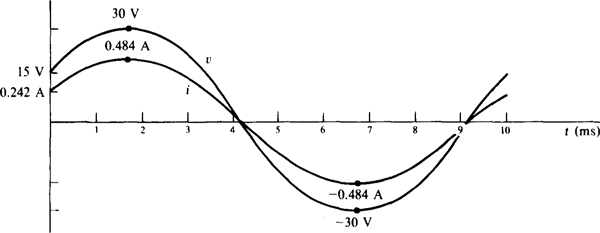
Fig. 10-10
10.26 A 30-Ω. resistor has a voltage of dissipation of the resistor?
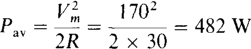
10.27 Find the average power absorbed by a 2.7-Ω resistor when the current i= 1.2 sin (377t + 30°) A flows through it.
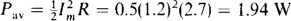
10.28 What is the peak voltage at a 120-V electric outlet?
The 120 V is the effective value of the sinusoidal voltage at the outlet. Since for a sinusoid the peak is times the effective value, the peak voltage at the outlet is × 120 = 170 V.
10.29 What is the reading of an ac voltmeter connected across a 680-Ω resistor that has a current of i = 6.2 cos (377f – 20°) mA flowing through it?
The voltmeter reads the effective value of the resistor voltage, which can be found from leff and R. Since Vm = ImR, then Vm/ = (Vm/(R) or Veff = IeffR. So,
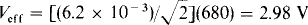
10.30 What is the reading of an ac voltmeter connected across a 10-Ω resistor that has a peak power dissipation of 40 W?
The peak voltage Vm can be found from the peak power: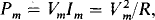 
from which 
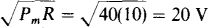. The effective or rms voltage, which is the voltmeter reading, is Vm/ = 20/= 14.1V.
10.31 What is the expression for a 240-Hz sine wave of voltage that has an rms value of 120 V?
Since the peak voltage is 120 × = 170 V and the radian frequency is 2ω × 240 = 1508 rad/s, the sine wave is v = 170 sin 1508t V.
10.32 Find the effective value of a periodic voltage that has a value of 20 V for one half-period and —10 V for the other half-period.
The first step is to square the wave. The result is 400 for the first half-period and (—10)2 = 100 for the second half-period. The next step is to find the average of the squares from the area divided by the period: (400 × T/2 + 100 × T/2)/T = 250. The last step is to find the square root of this average: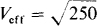 
= 15.8V.
10.33 Find the effective value of the periodic current shown in Fig. 10-11a.
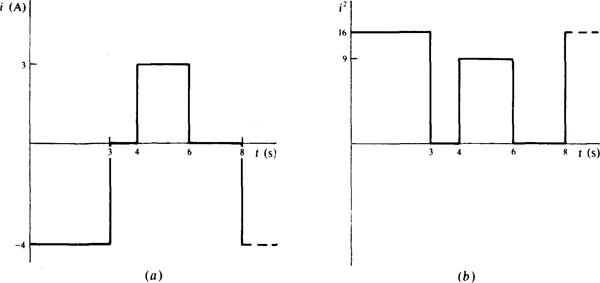
Fig. 10-11
The first step is to square the wave, which has a period of 8 s. The squared wave is shown in Fig. 10-1 b. The next step is to find the average of the squared wave, which can be found by dividing the area by the period: [16(3) + 9(6 – 4)]/8 = 8.25. The last step is to find the square root of this average: Ieff =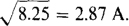 
10.34 Find the reactances of a 120-mH inductor at (a) 0 Hz (dc), (b) 40 rad/s, (c) 60 Hz, and (d) 30 kHz.
From XL = ωL = 2ωL,
(a) XL = 2ω(0)(120 × 10”3) = 0Ω
(b) XL = 40(120 × 10–3) = 4.8Ω
(c) XL = 2ω(60)(120 × 10”3) = 45.2 Ω
(d) XL = 2ω(30 × 103)(120 × 10–3) Ω = 22.6 kΩ
10.35 Find the inductances of the inductors that have reactances of (a) 5 Ω at 377 rad/s, (b) 1.2 kΏ at 30 kHz, and (c) 1.6 MΩ at 22.5 Mhz.
Solving for L in XL = ωL results in L – Xl/ω = Xl/2ωf. So,
(a) L = 5/377 H = 13.3 mH
(b) L = (1.2 × 103)/(2ω × 30 × 103) H = 6.37 mH
(c) L = (1.6 × 106)/(2ω × 22.5 × 106) H = 11.3 mH
10.36 Find the frequencies at which a 250-mH inductor has reactances of 30 Ω and 50 kΩ
from XL= ωL, = the frequency is f= XL/2ωL, and so
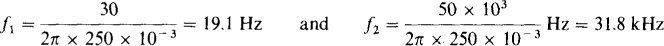
10.37 What is the voltage across a 30-mH inductor that has a 40-mA, 60-Hz current flowing through it?
The specified current is, of course, the effective value, and the desired voltage is the effective value of voltage, although not specifically stated. In general, the ac current and voltage values given are effective values unless otherwise specified. Because XL = Vm/Lm, it follows that XL = (Vm/)/(Im/) = Veff/Ieff. So, here, Veff = IeffXL=(40 × 10 -1)(2ω × 60)(30 × 10-3=0.452 V
10.38 The voltage v = 30 sin (200ωt + 30°) V is across an inductor that has a reactance of 62 Ω. Find the inductor current and plot one cycle of the voltage and current on the same graph.
The current peak equals the voltage peak divided by the reactance: m = 30/62 = 0.484 A. And, since the current lags the voltage by 90°,
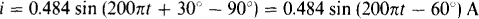
The voltage graph is the same as that shown in Fig. 10-10. The current graph for these values, though, differs from that in Fig. 10-10 by a shift right by a time corresponding to 90°, which time is one-fourth of a period: 10/4 = 2.5 ms. The waveforms are shown in Fig. 10-12.
Fig. 10-12
10.39 Find the voltages across a 2-H inductor for the following currents:
(a) 10 A, (b) 10 sin (377t + 10°) A, and (c) 10 cos (104£ – 20°) A. As always, assume associated references because there is no statement to the contrary.
(a) The inductor voltage is zero because the current is a constant and the time derivative of a constant is zero: v = 2 d(l0)/dt = 0 V. From another point of view, the reactance is 0 Ω because the frequency is 0 Hz, and so Vm = ImXL = 10(0) = 0 V.
(b) The voltage peak equals the current peak times the reactance of 377 × 2 = 754 Ω:
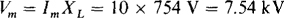
Since the voltage leads the current by 90° and since sin (x + 90°) = cos x,
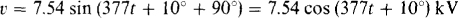
(c) Similarly, Vm = ImXL = 10(104 × 2) V = 0.2 MV, and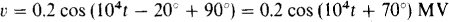 
10.40 Find the reactances of a 0.1 -/F capacitor at (a) 0 Hz (dc), (b) 377 rad/s, (c) 30 kHz, and (d) 100 MHz.
From Xc= - 1/coC = – l/2ω/C,
(a) 
(b)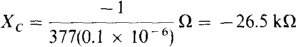 
(c)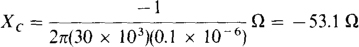 
(d)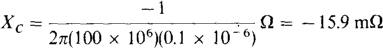 
10.41 Find the capacitances of capacitors that have a reactance of – 500 Ω at (a) 377 rad/s, (b) 10 kHz, and (c) 22.5 MHz.
Solving for C in Xc = – 1/ωC results in C = – 1/ωXc = – 1/(2ωf × Xc). So,
(a)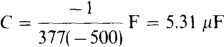 
(c)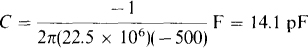 
10.42 Find the frequencies at which a 2-μF capacitor has reactances of —0.1 and – 2500 Ω.
From Xc = – 1/ωC = —1/2ωfC, the frequency is f = —1/(Xc × 2ωC). So,
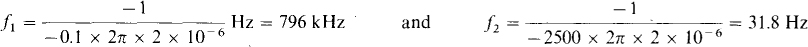
10.43 What current flows through a 0.1-/μF capacitor that has 200 V at 400 Hz across it?
Although not specifically stated, it should be understood that the effective capacitor voltage is specified and the effective capacitor current is to be found. If both sides of Im, = ωCVm are divided by the result is Im/ =ωCVm/ or Ieff = ωCVeff so,
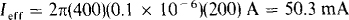
10.44 What is the voltage across a capacitor that carries a 120-mA current if the capacitive reactance is -230 Ω?
From the solution to Prob. 10.43, Ieff = ωCVff or Veff – Iff(1/ωC). Since 1/ωC is the magnitude of capacitive reactance, the effective voltage and current of a capacitor have a relation of Veff = leff|Xc|. Consequently, here, Veff = (120 × 10-3)|- 230| - 27.6 V.
10.45 The voltage v = 30 sin (200ωt + 30°) V is across a capacitor that has a reactance of —62 Ω. Find the capacitor current and plot one cycle of the voltage and current on the same graph.
From Vm/Im = 1ωC = |Xc|, the current peak equals the voltage peak divided by the magnitude of capacitive reactance: Im = 30/1 – 62| = 0.484 A. And, since the current leads the voltage by 90°,
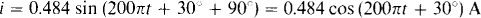
Notice that the current sinusoid has the same phase angle as the voltage sinusoid, but, because of the 90° lead, is a phase-shifted cosine wave instead of the phase-shifted sine wave of the voltage.
The voltage graph is the same as that in Fig. 10-10. The current graph differs from that in Fig. 10-10 by a shift left by a time corresponding to 90°, which time is one-fourth of a period: 10/4 = 2.5 ms. The waveforms are shown in Fig. 10-13.
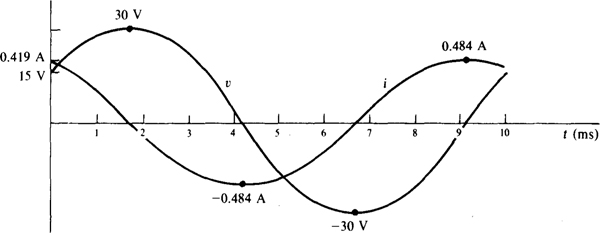
Fig. 10-13
10.46 What currents flow through a 2μ capacitor for voltages of (a) v = 5 sin (317t + 10°) V and (b)v= 12 cos(104t-20°)V?
(a) The current peak equals ωC times the voltage peak:
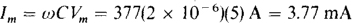
Also, because the capacitor current leads the capacitor voltage by 90° and the voltage is a phase-shifted sine wave, the current can be expressed as a phase-shifted cosine wave with the same phase angle: i = 3.77 cos (377f + 10”) mA.
(b)The current peak is
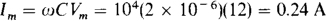
Also, the current leads the voltage by 90°. As a result,
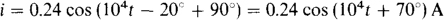
10.47 Find the periods of periodic currents that have frequencies of (a) 1.2 mHz, (b) 2.31kHz, and (c) 16.7 MHz.
Ans. (a) 833 s, (b) 433 μs, (c) 59.9 ns
10.48 What are the frequencies of periodic voltages that have periods of (a) 18.3 ps, (b) 42.3 s, and (c) 1 d?
Ans. (a) 546 GHz (gigahertz—i.e., 109 Hz), (b) 23.6 mHz, (c) 11.6/(Hz
10.49 What are the period and frequency of a periodic current for which 423 cycles occur in 6.19 ms?
Ans. 14.6 μs, 68.3 kHz
10.50 Convert the following angles in degrees to angles in radians: (a) —40°, (b) —1123°, and (c) 78°.
Ans, (a) -0.698 rad, (b) - 19.6 rad, (c) 1.36 rad
10.51 Convert the following angles in radians to angles in degrees: (a) 13.4 rad, (b) 0.675 rad, and (c) -11.7 rad.
Ans. (a) 768°, (b) 38.7°, (c) -670°
10.52 Find the periods of sinusoidal voltages that have radian frequencies of (a) 120ωrad/s, (b) 0.625 rad/s, and (c) 62.1 krad/s.
Ans. (a) 16.7 ms, (b) 10.1 s, (c) 101, μ
10.53 Find the radian frequencies of sinusoidal currents that have periods of (a) 17.6 μs, (b) 4.12 ms, and (c) 1 d.
Ans. (a) 357 krad/s, (b) 1.53 krad/s, (c) 72.7 μrad/s
10.54 What are the amplitudes and frequencies of (a) -63.7 cos (754t – 50°) and (b) 429 sin (4000t + 15°)?
Ans. (a) 63.7, 120 Hz; (b) 429, 637 Hz
10.55 Find the instantaneous value of i = 80 sin 500t mA at (a)l = 4ms and (b)t = 2.1s.
Ans. (a) 72.7 mA, (b) 52 mA
10.56 What is the frequency of a sine wave of voltage which has a 45-V peak and which continuously increases from 0 V at t = 0 s to 24 V at f = 46.2 ms?
Ans. 1.94 Hz
10.57 If a voltage cosine wave has a peak value of 20 V at t = 0 s, and if it takes a minimum of 0.123 s for this voltage to decrease from 20 to 17 V, find the voltage at t = 4.12 s.
Ans. 19.3 V.
10.58 What is the instantaneous value of; i = 13.2 cos (377 t + 50°) mA at (a) t= -42.1ms and (b) f = 6.3 s?
Ans. (a) -10 mA, (b) 7.91 mA
10.59 Find an expression for a 400-Hz sinusoidal current that has a 2.3-A positive peak at t = —0.45 ms.
Ans. i = 2.3 cos (800πt + 64.8°) A
10.60 Find an expression for a sinusoidal voltage that is 0 V at t = —8.13 ms, after which it increases to a peak of 15 V at t = 6.78 ms.
Ans. v= 15 sin (105r + 49.1C) V
10.61 What is the shortest time required for a 4.3-krad/s sinusoid to increase from two-fifths to four-fifths of its peak value?
Ans. 120 us
10.62 If 43.7 V is the peak voltage induced in the conductor of the alternator shown in Fig. 10-2, find the voltage induced after the conductor has rotated through an angle of 43’ from its horizontal position.
Ans. ±29.8 V
10.63 If the conductor of the alternator in Fig. 10-2 is rotating at 400 Hz, and if the induced voltage has a 23-V peak, find the induced voltage 0.23 ms after the conductor passes through its vertical position.
Ans. ± 19.3 V
10.64 Find the periods of (a) 4 + 3 sin (800πt - 15°), (b) 8.1 cos2 9πt, and (c) 8 sin 16t cos 16t.
Ans. (a) 2.5 ms, (ft) 111 ms, (c) 196 ms
10.65 Find the phase relations for the following pairs of sinusoids:
(a) v = 6 sin (30t – 40 ‘) V, i = 10 sin (30t – tî/3) mA
(b) Vl = -8sin(40t-80”) V, v2 = - 10 sin (40t – 50) V
(c) i1 = 4 cos (70t – 40’) mA, i2 = - 6 cos (70t + 80”) mA
(d) v= -4sin(45t + 5’)V, i = 7 cos (45t + 80’) mA
Ans. (a) c leads i by 20°, (b) v1 lags v2 by 30°, (c) ii leads i2 by 60°, (d) v leads i by 15°
10.66 Find the average value of a half-wave rectified sinusoidal voltage that has a peak of 12 V. This wave consists only of the positive half-cycles of the sinusoidal voltage. It is zero during the times that the sinusoidal is negative.
Ans. 3.82 V
10.67 Find the average values of the periodic waveforms shown in Fig. 10-14.
Ans. (a) 3.5, (b) 4, (c)
Fig. 10-14
10.68 What is the average power absorbed by a circuit component that has a voltage v = 10 V across it when a current i = 5 + 6 cos 33t A flows through it?
Ans. 50 W
10.69 Find the average power absorbed by a circuit component that has a voltage v = 20.3 cos (754t – 10) V across it when a current i = 15.6 cos (754t – 30°) mA flows through it.
Ans. 149 mW
10.70 What is the conductance of a resistor that has a voltage v = 50.1 sin (200πt + 30°) V across it when a current i = 6.78 sin (2007rf + 30°) mA flows through it?
Ans. 135 μS
10.71 If the voltage v = 150 cos (377t + 45°) V is across a 33-kΩ resistor, what is the resistor current?
Ans. i = 4.55 cos (377t + 45°) mA
10.72 Find the average power absorbed by an 82-Ω resistor that has a voltage v = 311 cos (377t – 45°) V across it.
Ans. 590 W
10.73 What is the average power absorbed by a 910-Ω resistor that has a current i = 9.76 sin (754r – 36”) mA flowing through it?
Ans. 43.3 mW
10.74 Find the average power absorbed by a resistor having a voltage v = 87.7 cos (400ωt – 15°) V across it and a current i = 2.72 cos (400ωt – 15°) mA flowing through it.
Ans. 119 mW
10.75 What is the reading of an ac ammeter that is in series with a 470-fl resistor that has a voltage i; = 150 cos (377t + 30c) V across it?
Ans. 226 mA
10.76 What is the reading of an ac ammeter that is in series with a 270-Ω resistor that has a peak power dissipation of 10 W?
Ans. 136 mA
10.77 What is the expression for a 400-Hz current cosine wave that has an effective value of 13.2 mA?
Ans. i = 18.7 cos 800ωt mA
10.78 Find the effective value of v = 3 + 2 sin 4t V. (Hint: Use a sinusoidal identity in finding the average value of the squared voltage.)
Ans. 3.32 V
10.79 Find the effective value of a periodic current that has a value of 40 mA for two-thirds of a period and 25 mA for the remaining one-third of the period. Would the effective value be different if the current were – 25 mA instead of 25 mA for the one-third period?
Ans. 35.7 mA, no
10.80 Find the effective value of a periodic current that in a 20-ms period has a value of 0.761 A for 4 ms, 0 A for 2 ms, —0.925 A for 8 ms, and 1.23 A for the remaining 6 ms. Would the effective value be different if the time segments were in seconds instead of in milliseconds?
Ans. 0.955 A, no
10.81 Find the reactances of a 180-mH inductor at (a) 754 rad/s, (b) 400 Hz, and (c) 250 kHz.
Ans. (a) 136 Ω, (b) 452 Ω, (c) 283 kΩ
10.82 Find the inductances of the inductors that have reactances of (a) 72.1 Ω at 754 rad/s, (b) 11.9 Ω at 12 kHz, and (c) 42.1 kΩ at 2.1 MHz.
Ans. (a)95.6mH, (b)158βH, (c)3.19mH
10.83 What are the frequencies at which a 120-mH inductor has reactances of (a) 45 Ω and (b) 97.1 kΩ?
Ans. (a) 59.7 Hz, (b) 129 kHz
10.84 What current flows through an 80-mH inductor that has 120 V at 60 Hz across it?
Ans. 3.98 A
10.85 What is the inductance of the inductor that will draw a current of 250 mA when connected to a 120-V, 60-Hz voltage source?
Ans. 1.27 H
10.86 What are the currents that flow in a 500-mH inductor for voltages of (a) v = 170 sin (400t + ω/6) V and (b)v= 156cos(1000it + 10°) V?
Ans. (a) i = 0.85 sin (400t – 60°) A, (b) i = 0.312 sin (l000t + 10°) A
10.87 Find the reactances of a 0.25-βf capacitor at (a) 754 rad/s, (b) 400 Hz, and (c) 2 MHz.
Ans. (a) -5.31 kΩ, (b)-1.59 kΩ, (c)-0.318Ω
10.88 Find the capacitances of the capacitors that have reactances of (a) —700 ω at 377 rad/s, (b) —450 φ at 400 Hz, and (c) -1.23 kΩ at 25 kHz.
Ans. (a) 3.79μF, (b) 0.884 μF, (c)5.18nF
10.89 Find the frequency at which a 0.1 -/μF capacitor and a 120-m H inductor have the same magnitude of reactance.
Ans. 1.45 kHz
10.90 What is the capacitance of a capacitor that draws 150 mA when connected to a 100-V, 400-Hz voltage source?
Ans. 0.597 μF
10.91 What are the currents that flow in a 0.5-μF capacitor for capacitor voltages of (a) v = 190 sin (377t + 15°) V and (b) v = 200 cos (1000t – 40°) V?
Ans. (a) i = 35.8 cos (377t + 15°) mA, (b) i = 0.1 cos (l000t + 50°) A
10.92 What are the voltages across a 2-μF capacitor for currents of (a) i = 7 sin (754t + 15°) mA and (b) i = 250cos(103i-30°)mA?
Ans. (a) v = 4.64 sin (754t – 75°) V, (b) v = 125 sin (103t – 30°) V
