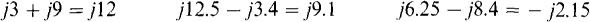
The best way to analyze almost all ac circuits is by using complex algebra. Complex algebra is an extension of the algebra of real numbers—the common algebra. In complex algebra, though, complex numbers are included along with their own special rules for addition, multiplication, subtraction, and division. As is explained in Chaps. 12 and 13, in ac circuit analysis, sinusoidal voltages and currents are transformed into complex numbers called phasors; resistances, inductances, and capacitances are transformed into complex numbers called impedances; and then complex algebra is applied in much the same way that ordinary algebra is applied in dc circuit analysis.
A scientific calculator will operate on complex numbers as readily as on real numbers. But still it is important to know how to perform the various operations on complex numbers without the use of a calculator.
The common numbers that everyone uses are real numbers. But these are not the only kind of numbers. There are also imaginary numbers. The name “imaginary” is misleading because it suggests that these numbers are only in the imagination, when actually they are just as much numbers as the common real numbers. Imaginary numbers were invented when it became necessary to have numbers that are square roots of negative numbers (no real numbers are). This inventing of numbers was not new since it had been preceded by the inventions of noninteger real numbers and negative real numbers.
Imaginary numbers need to be distinguished from real numbers because different rules must be applied in the mathematical operations involving them. There is no one universally accepted way of representing imaginary numbers. In the electrical field, however, it is standard to use the letter j, as in j2, j0.01, and –j5.6.
The rules for adding and subtracting imaginary numbers are the same as those for adding and subtracting real numbers except that the sums and differences are imaginary. To illustrate,
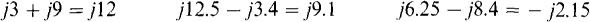
The multiplication rule, though, is different. The product of two imaginary numbers is a real number that is the negative of the product that would be found if the numbers were real numbers instead. For example,
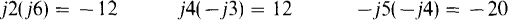
Also, j1(j1) = – 1, from which 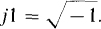 Likewise,
Likewise, 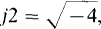 and so forth.
and so forth.
Sometimes powers of j1 appear in calculations. These can have values of 1, –1, j1, and –j1, as can be shown by starting with (j1)2 = j1(j1) = – 1 and then progressively multiplying by j1 and evaluating. As an illustration, (j1)3 = j1(j1)2 = j1(–1) = –j1 and (j1)4 = j1(j1)3 = j1(–j1)= 1.
The product of a real number and an imaginary number is an imaginary number that, except for being imaginary, is the same as if the numbers were both real. For example, 3(j5) = j15 and –j5.1(4) = –j20.4.
In the division of two imaginary numbers, the quotient is real and the same as if the numbers were real. As an illustration,
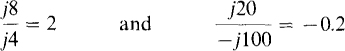
A convenient memory aid for division is to treat the j’s as if they are numbers and to divide them out as in
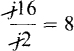
This should be viewed as a memory aid only, because j just designates a number as being imaginary and is not a number itself. However, treating) as a number in division, as well as in the other mathematical operations, is often done because of convenience and the fact that it does give correct answers.
If an imaginary number is divided by a real number, the quotient is imaginary but otherwise the same as for real numbers. For example,
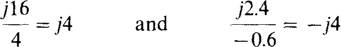
The only difference if the denominator is imaginary and the numerator is real is that the quotient is the negative of the above. To illustrate,
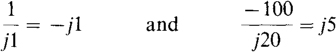
The basis for this rule can be shown by multiplying a numerator and denominator by j1, as in
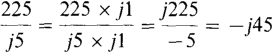
Multiplying to make the denominator real, as here, is called rationalizing.
If a real number and an imaginary number are added, as in 3 + j4, or subtracted, as in 6 – j8 the result is considered to be a single complex number in rectangular form. Other forms of complex numbers are introduced in the next section.
A complex number can be represented by a point on the complex plane shown in Fig. 11.1. The horizontal axis, called the real axis, and the vertical axis, called the imaginary axis, divide the complex plane into four quadrants, as labeled. Both axes have the same scale. The points for real numbers are on the real axis because a real number can be considered to be a complex number with a zero imaginary part. Figure 11-1 has four of these points: —5, —1, 2, and 4. The points for imaginary numbers are on the imaginary axis because an imaginary number can be considered to be a complex number with a zero real part. Figure 11-1 has four of these points: j3, j1, —j2, and —j4. Other complex numbers have nonzero real and imaginary parts, and so correspond to points off the axes. The real part of each number gives the position to the right or to the left of the vertical axis, and the imaginary part gives the position above or below the horizontal axis. Figure 11-1 has four of these numbers, one in each quadrant.
Fig. 11-1
In Fig. 11-1 the complex numbers 4 + j2 and 4 — j2 have the same real part, and they also have the same imaginary part—except for sign. A pair of complex numbers having this relation are said to be conjugates: 4 + j2 is the conjugate of 4 — j2, and also 4 — j2 is the conjugate of 4 + j2. Points for conjugate numbers have the same horizontal position but opposite vertical positions, being equidistant on opposite sides of the real axis. If lines are drawn from the origin to these points, both lines will have the same length, and, except for sign, the same angle from the positive real axis. (Angles are positive if measured in a counterclockwise direction from this axis, and negative if measured in a clockwise direction.) These graphical relations of conjugates are important for the polar form of complex numbers presented in the next section.
The rectangular form is the only practical form for addition and subtraction. These operations are applied separately to the real and imaginary parts. As an illustration, (3 + j4) + (2 + j6) = 5 + j10 and (6 — j7) — (4 — j2) = 2 — j5.
In the multiplication of complex numbers in the rectangular form, the ordinary rules of algebra are used along with the rules for imaginary numbers. For example,
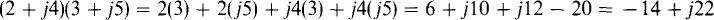
It follows from this multiplication rule that if a complex number is multiplied by its conjugate, the product is real and is the sum of the real part squared and the imaginary part squared. To illustrate,
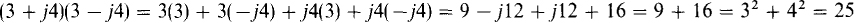
In the division of complex numbers in rectangular form, the numerator and denominator are first multiplied by the conjugate of the denominator to make the denominator real, or rationalized, so that the division will be straightforward. As an example of this operation, consider
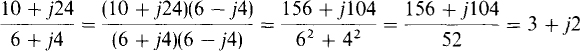
The polar form of a complex number is a shorthand for the exponential form. Polar or exponential forms are usually the best forms for multiplying and dividing, but are not useful for adding and subtracting unless done graphically, which is rarely done. Typically, though, a scientific calculator can add and subtract complex numbers in polar form as well as in rectangular form. The exponential form is Aejθ, where A is the magnitude and θ is the angle of the complex number. Also, e = 2.718 … is the base of the natural logarithm. The polar shorthand for Aejθ is 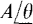 as in 4ej45° =
as in 4ej45° = 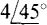 and in —8ej60° =
and in —8ej60° = 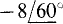 Although both forms are equivalent, the polar form is much more popular because it is easier to write.
Although both forms are equivalent, the polar form is much more popular because it is easier to write.
That a number such as 5ej60 is a complex number is evident from Euler’s identity: ejθ = cos θ + j sin θ. As an illustration, 7ej30° = 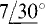 = 7 cos 30° + j7 sin 30° = 6.06 + j3.5. This use of Euler’s identity not only shows that a number such as Aejθ =
= 7 cos 30° + j7 sin 30° = 6.06 + j3.5. This use of Euler’s identity not only shows that a number such as Aejθ = 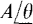 is a complex number, but also gives a method for converting a number from exponential or polar form to rectangular form.
is a complex number, but also gives a method for converting a number from exponential or polar form to rectangular form.
Another use of Euler’s identity is for deriving formulas for converting a complex number from rectangular form to the exponential and polar forms. Suppose that x and y are known in x + jy, and that A and θ are to be found such that x + jy = Aejθ = 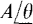 By Euler’s identity, x + jy = A cos θ + jA sin θ. Since two complex numbers are equal only if the real parts are equal and if the imaginary parts are equal, it follows that x = A cos θ and y = A sin θ. Taking the ratio of these equations eliminates A:
By Euler’s identity, x + jy = A cos θ + jA sin θ. Since two complex numbers are equal only if the real parts are equal and if the imaginary parts are equal, it follows that x = A cos θ and y = A sin θ. Taking the ratio of these equations eliminates A:
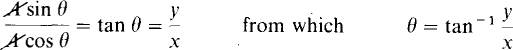
(Note that if x is negative, 180° must be either added to or subtracted from θ.) So, θ can be found from the arctangent of the ratio of the imaginary part to the real part. With θ known, A can be found by substituting θ into either x = A cos θ or into y = A sin θ.
Another popular way of finding A is from a formula based on squaring both sides of A cos θ = x and of A sin θ = y and adding:
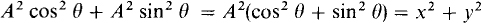
But since, from trigonometry, cos2θ + sin2 θ = 1, it follows that A2 = x2 + y2 and 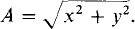 So, the magnitude of a complex number equals the square root of the sum of the squares of the real and imaginary parts. Most scientific calculators have a built-in feature for converting between rectangular and polar forms.
So, the magnitude of a complex number equals the square root of the sum of the squares of the real and imaginary parts. Most scientific calculators have a built-in feature for converting between rectangular and polar forms.
This conversion can also be understood from a graphical consideration. Figure 11-2a shows a directed line from the origin to the point for the complex number x + jy. As shown in Fig. 11-2b, this line forms a right triangle with its horizontal and vertical projections. From elementary trigonometry, x = A cos θ, y = A sin θ, and 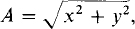 in agreement with the results from Euler’s identity. Often this line, instead of the point, is considered to correspond to a complex number because its length and angle are the amplitude and angle of the complex number in polar form.
in agreement with the results from Euler’s identity. Often this line, instead of the point, is considered to correspond to a complex number because its length and angle are the amplitude and angle of the complex number in polar form.
Fig. 11-2
As has been mentioned, the conjugate of a complex number in rectangular form differs only in the sign of the imaginary part. In polar form this difference appears as a difference in sign of the angle, as can be shown by converting any two conjugates to polar form. For example, 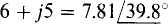 and its conjugate is
and its conjugate is 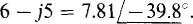
As stated, the rectangular form is best for adding and subtracting, and the polar form is often best for multiplying and dividing. The multiplication and division formulas for complex numbers in polar form are easy to derive from the corresponding exponential numbers and the law of exponents. The product of the complex numbers Aejθ and Bejφ is (Aejθ)(Bejφ) = ABej (θ + φ), which has a magnitude AB that is the product of the individual magnitudes and an angle θ + φ that, by the law of exponents, is the sum of the individual angles. In polar form this is 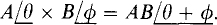
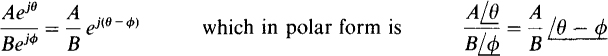
So, the magnitude of the quotient is the quotient A/B of the magnitudes, and the angle of the quotient is, by the law of exponents, the difference θ — φ of the numerator angle minus the denominator angle.
By definition, a phasor is a complex number associated with a phase-shifted sine wave such that, if the phasor is in polar form, its magnitude is the effective (rms) value of the voltage or current and its angle is the phase angle of the phase-shifted sine wave. For example, 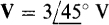 is the phasor for
is the phasor for  and
and 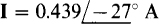 is the phasor for i = 0.621 sin (754t – 27°) A. Of course, 0.621 =
is the phasor for i = 0.621 sin (754t – 27°) A. Of course, 0.621 =  (0.439).
(0.439).
Note the use of the boldface letters V and I for the phasor voltage and current quantity symbols. It is conventional to use boldface letter symbols for all complex quantities. Also, a superscript asterisk is used to designate a conjugate. As an illustration, if V = 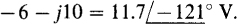 V* =
V* = 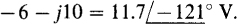 The magnitude of a phasor variable is indicated by using lightface, and the magnitude of a complex number is indicated by using parallel lines. For example, if I = 3 + j4 =
The magnitude of a phasor variable is indicated by using lightface, and the magnitude of a complex number is indicated by using parallel lines. For example, if I = 3 + j4 = 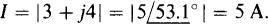 , then I = |3 + j4| = |
, then I = |3 + j4| = |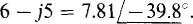 | = 5A.
| = 5A.
A common error is to equate a phasor and its corresponding sinusoid. They cannot be equal because the phasor is a complex constant, but the sinusoid is a real function of time. In short, it is wrong to write something like 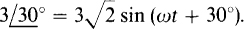
Phasors are usually shown in the polar form for convenience. But the rectangular form is just as correct because, being a complex number, a phasor can be expressed in any of the complex number forms. Not all complex numbers, though, are phasors—just those corresponding to sinusoids.
There is not complete agreement on the definition of a phasor. Many electrical engineers use the sinusoidal peak value instead of the effective value. Also, they use the angle from the phase-shifted cosine wave instead of the sine wave.
One use of phasors is for summing sinusoids of the same frequency. If each sinusoid is transformed into a phasor and the phasors added and then reduced to a single complex number, this number is the phasor for the sum sinusoid. As an illustration, the single sinusoid corresponding to v = 3 sin (2t + 30°) + 2 sin (2t – 15°) V can be found by adding the corresponding phasors,
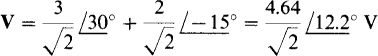
and then transforming the sum phasor to a sinusoid. The result is v = 4.64 sin (2t + 12.2°) V. This procedure works for any number of sinusoids being added and subtracted, provided that all have the same frequency.
Notice that using  did not contribute anything to the final result. The
did not contribute anything to the final result. The  was introduced in finding the phasors, and then deleted in transforming the sum phasor to a sinusoid. When the problem statement is in sinusoids and the answer is to be a sinusoid, it is easier to neglect the
was introduced in finding the phasors, and then deleted in transforming the sum phasor to a sinusoid. When the problem statement is in sinusoids and the answer is to be a sinusoid, it is easier to neglect the  and use phasors that are based on peak values instead of rms values.
and use phasors that are based on peak values instead of rms values.
Phasors are sometimes shown on a complex plane in a diagram called a phasor diagram. The phasors are shown as arrows directed out from the origin with lengths corresponding to the phasor magnitudes, and arranged at angles that are the corresponding phasor angles. Such diagrams are convenient for showing the angular relations among voltages and currents of the same frequency. Sometimes they are also used for adding and subtracting, but not if accuracy is important.
Another diagram, called a funicular diagram, is more convenient for graphical addition and subtraction. In this type of diagram the adding and subtracting are the same as for vectors. For adding, the arrows of the phasors are placed end to end and the sum phasor is found by drawing an arrow from the tail of the first arrow to the tip of the last. If a phasor is to be subtracted, its arrow is rotated 180 (reversed) and then added.
11.1 Perform the following operations:
(a) j2 + j3 – j6 – j8 (b) j2(–j3)(j4)(–j6) (c) 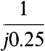 (d)
(d) 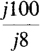
(a) The rules for adding and subtracting imaginary numbers are the same as for adding and subtracting real numbers, except that the result is imaginary. So,
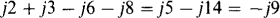
(b) The numbers can be multiplied two at a time, with the result
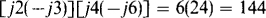
Alternatively, j1 can be factored from each factor and a power of j1 found times a product of real numbers:
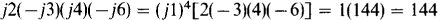
(c) The denominator can be made real by multiplying the numerator and denominator by j1, and then division performed as if the numbers were real—except that the quotient is imaginary:
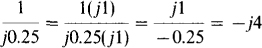
Alternatively, since 1/j1 = –j1,
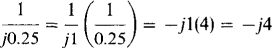
(d) For convenience, the j’s can be considered to be numbers and divided out:
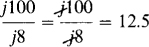
11.2 Add or subtract as indicated, and express the results in rectangular form:
(a) (6.21 + j3.24) + (4.13 – j9.47)
(b) (7.34 – j1.29) – (5.62 + j8.92)
(c) (– 24 + j12) – (– 36 – j16) – (17 – j24)
The real and imaginary parts are separately added or subtracted:
(a) (6.21 + j3.24) + (4.13 – j9.47) = (6.21 + 4.13) + j (3.24 – 9.47) = 10.34 – j6.23
(b) (7.34 – j1.29) – (5.62 + j8.92) = (7.34 – 5.62) – j (1.29 + 8.92) = 1.72 – j10.21
(c) (– 24 + j12) – (– 36 – j16) – (17 – j24) = (– 24 + 36 – 17) + j (12 + 16 + 24)= – 5 + j52
11.3 Find the following products and express them in rectangular form:
(a) (4 + j2)(3 + j4) (b) (6 + j2)(3 – j5)(2 – j3)
In the multiplication of complex numbers in rectangular form, the ordinary rules of algebra are used along with the rules for imaginary numbers:
(a) (4 + j2)(3 + j4) = 4(3) + 4(j4) + j2(3) + j2(j4) = 12 + j16 + j6 – 8 = 4 + j22
(b) It is best to multiply two numbers at a time:
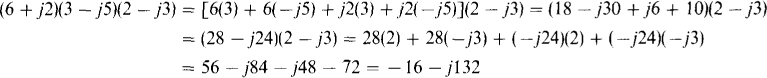
Multiplying three or more complex numbers in rectangular form usually requires more work than does converting them to polar form and multiplying.
11.4 Evaluate
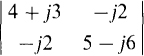
The value of this second-order determinant equals the product of the elements on the principal diagonal minus the product of the elements on the other diagonal, the same as for one with real elements:
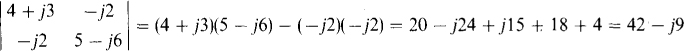
11.5 Evaluate
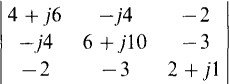
The evaluation of a third-order determinant with complex elements is the same as for one with real elements:
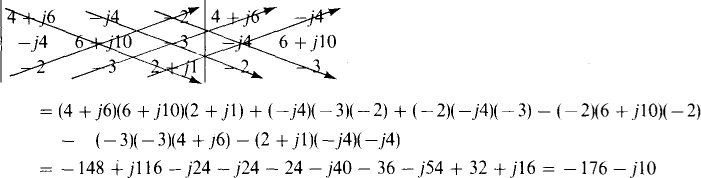
Although this procedure is straightforward, it is difficult to do without making errors. Using a calculator is much better.
11.6 Find the following quotients in rectangular form:
(a) 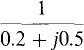 (b)
(b) 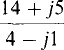
For division in the rectangular form, the numerator and denominator should be multiplied by the conjugate of the denominator to make the denominator real. Then the division is straightforward. Doing this results in
(a) 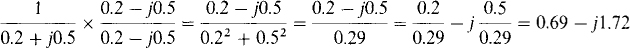
(b) 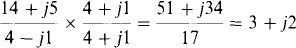
11.7 Convert the following numbers to polar form:
(a) 6 + j9 (b) –21.4 + j33.3 (c) –0.521 – j1.42 (d) 4.23 + j4.23
If a calculator is used that does not have a rectangular-to-polar conversion feature, then a complex number x + jy can be converted to its equivalent 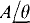 with the formulas
with the formulas 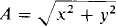 and θ = tan–1 (y/x). With this approach
and θ = tan–1 (y/x). With this approach
(a) 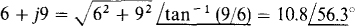
(b) 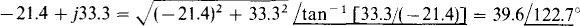
Typically, a calculator will give tan–1 (–33.3/21.4) = –57.3°, which differs from the correct angle by 180°. For such a calculator, this error of 180° always occurs in a rectangular-to-polar form conversion whenever the real part of the complex number is negative. The solution, of course, is to change the calculator angle by either positive or negative 180°, whichever is more convenient.
(c) 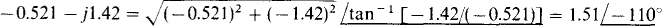
Again, because the real part is negative, a calculator may not give an angle of —110°, but tan–1 (1.42/0.521) = 70°, instead,
(d) 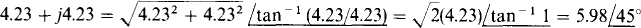
As can be generalized from this result, when the magnitudes of the real and imaginary parts are equal, the polar magnitude is  times this magnitude. Also, the angle is 45° if the number is in the first quadrant of the complex plane, 135 if it is in the second, — 135° if it is in the third, and —45° if it is in the fourth.
times this magnitude. Also, the angle is 45° if the number is in the first quadrant of the complex plane, 135 if it is in the second, — 135° if it is in the third, and —45° if it is in the fourth.
11.8 Convert the following numbers to rectangular form:
(a) 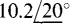 (b)
(b) 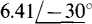 (c)
(c) 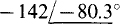 (d)
(d) 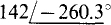 (e)
(e) 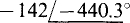
If a calculator is used that does not have a polar-to-rectangular conversion feature, then Euler’s identity can be used: 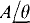 = A cos θ +j A sin θ. With this approach
= A cos θ +j A sin θ. With this approach
(a) 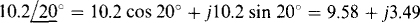
(b) 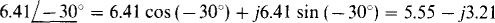
(c) 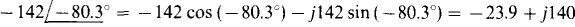
(d) 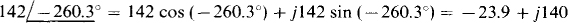
(e) 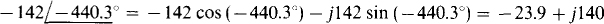
Parts (c) and (d) show that an angular difference of 180° corresponds to multiplying by — 1. And parts (c) and (e) show that an angular difference of 360° has no effect. So, in general, 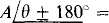
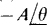 and
and 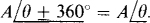
11.9 Find the following products in polar form:
(a) 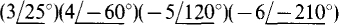 (b)
(b) 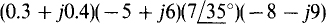
(a) When all the factors are in polar form, the magnitude of the product is the product of the individual magnitudes along with negative signs, if any, and the angle of the product is the sum of the individual angles. So,
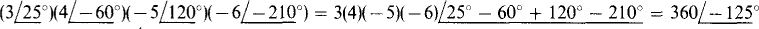
(b) The numbers in rectangular form must be converted to polar form before being multiplied:
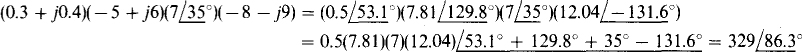
11.10 Find the quotients in polar form for (a) 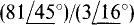 and (b)
and (b) 
(a) When the numerator and denominator are in polar form, the magnitude of the quotient is the quotient of the magnitudes, and the angle of the quotient is the angle of the numerator minus the angle of the denominator. So,
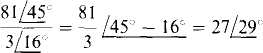
(b) The denominator should be converted to polar form as a first step:
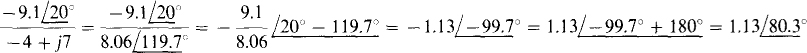
11.11 Find the following quotient:
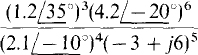
Since each exponent of a number indicates how many times the number is to be multiplied by itself, the effect of an exponent is to raise the number magnitude to this exponent and to multiply the number angle by this exponent. Thus,
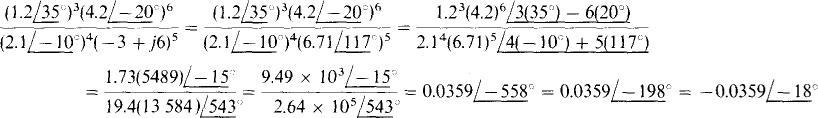
11.12 Find the corresponding phasor voltages and currents for the following:
(a) v =  (50) sin (377t – 35°) V
(50) sin (377t – 35°) V
(b) i =  (90.4) sin (754t + 48°) mA
(90.4) sin (754t + 48°) mA
(c) v = 83.6 cos (400t – 15°) V
(d) i = 3.46 cos (815t + 30°) A
A phasor in polar form has a magnitude that is the effective value of the corresponding sinusoidal voltage or current, and an angle that is the phase angle of the sinusoid if it is in phase-shifted sine-wave form. So,
(a) 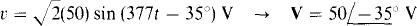
(b) 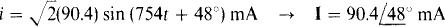
(c) 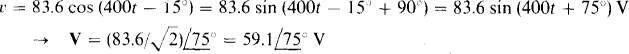
(d) 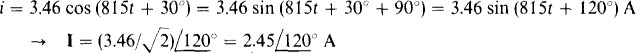
11.13 Find the voltages and currents corresponding to the following phasor voltages and currents (each sinusoid has a radian frequency of 377 rad/s):
(a) 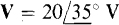 (b)
(b) 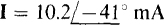 (c) V = 4 – j6 V (d) I = – 3 + j1 A
(c) V = 4 – j6 V (d) I = – 3 + j1 A
If a phasor is in polar form, the corresponding voltage or current is a phase-shifted sine wave that has a phase angle that is the phasor angle, and a peak value that is the  times the phasor magnitude. Thus,
times the phasor magnitude. Thus,
(a) 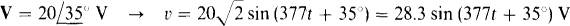
(b) 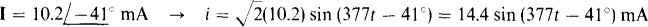
(c) 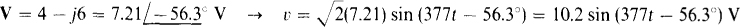
(d) 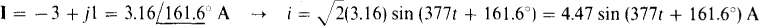
11.14 Find a single sinusoid that is the equivalent of each of the following:
(a) 6.23 sin ωt + 9.34 cos ωt
(b) 5 sin (4t – 20°) + 6 sin (4t + 45°) – 7 cos (4t – 60°) + 8 cos (4t + 30°)
(c) 5 sin 377t + 6 cos 754t
A phasor approach can be used since the terms are sinusoids. The procedure is to find the phasor corresponding to each sinusoid, add the phasors to obtain a single complex number, and then find the sinusoid corresponding to this number. Preferably the phasors are based on peak values because there is no advantage in introducing a factor of  since the problems statements are in sinusoids and the answers are to be in sinusoids. Thus,
since the problems statements are in sinusoids and the answers are to be in sinusoids. Thus,
(a) 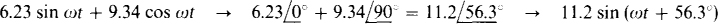
(b) 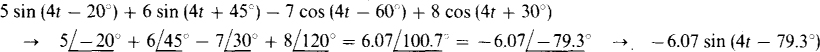
(c) The sinusoids cannot be combined because they have different frequencies.
11.15 For the circuit shown in Fig. 11-3, find vs if v1 = 10.2 sin (754t + 30°) V, v2 = 14.9 sin (754t – 10°) V, and v3 = cos (754t – 25°) V.
Fig. 11-3
By KVL, vs = v1 – v2 + v3 = 10.2 sin (754t + 30°) – 14.9 sin (754t – 10°) + 16.1 cos (754t – 25°) V The sum sinusoid can be found by using phasors:
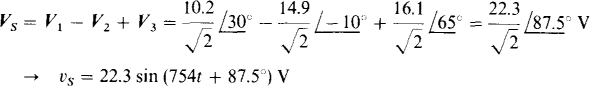
Since the problem statement is in sinusoids and the final result is a sinusoid, finding the solution would have been slightly easier using phasors based on peak rather than rms values.
11.16 In the circuit shown in Fig. 11-4, voltmeters VM1 and VM2 have readings of 40 and 30 V, respectively. Find the reading of voltmeter VM3.
Fig. 11-4
It is tempting to conclude that, by KVL, the reading of voltmeter VM3 is the sum of the readings of voltmeters VM1 and VM2. But this is wrong because KVL applies to phasor voltages and not to the rms voltages of the voltmeter readings. The rms voltages, being positive real constants, do not have the angles that the phasor voltages have.
For the phasors required for KVL, angles must be associated with the given rms voltages. One angle can be arbitrarily selected because only the magnitude of the sum is desired. If 0° is selected for the resistor voltage phasor, this phasor is 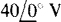 and then that for the inductor voltage must be
and then that for the inductor voltage must be 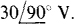 The inductor voltage phasor has a 90° greater angle because this voltage leads the current by 90°, but the resistor voltage is in phase with the current. By KVL, the phasor voltage for the source is
The inductor voltage phasor has a 90° greater angle because this voltage leads the current by 90°, but the resistor voltage is in phase with the current. By KVL, the phasor voltage for the source is 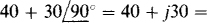
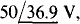 which has an rms value of 50 V. So, the reading of voltmeter VM3 is 50 V, and not the 30 + 40 = 70 V that might at first be supposed.
which has an rms value of 50 V. So, the reading of voltmeter VM3 is 50 V, and not the 30 + 40 = 70 V that might at first be supposed.
11.17 Find vs for the circuit shown in Fig. 11-5.
Fig. 11-5
The voltage vs can be determined from vS = vR + vL + vc after these component voltages are found. By Ohm’s law,
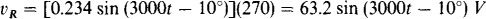
The inductor voltage vL leads the current by 90° and has a peak value of ωL = 3000(120 × 10–3) = 360 times the peak value of the current:
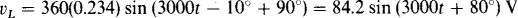
The capacitor voltage vc lags the current by 90° and has a peak value that is 1/ωC = 1/(3000 × 6 × 10–6) = 55.6 times the peak value of the current:
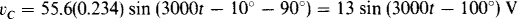
Phasors, which are conveniently based on peak values, can be used to find the sum sinusoid:
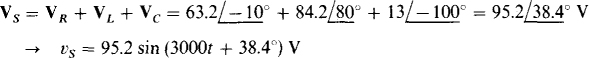
11.18 Find is for the circuit shown in Fig. 11-6.
Fig. 11-6
The current is can be determined from iS = iR + iL + iC after these component currents are found. By Ohm’s law,
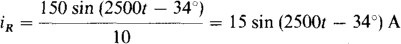
The inductor current iL lags the voltage by 90° and has a peak value that is 1/ωL = 1/(2500 × 6 × 10–3) = 1/15 times the peak value of the voltage:
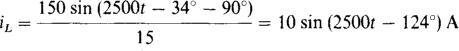
The capacitor current ic leads the voltage by 90° and has a peak value that is ωC = 2500(20 × 10–6) = 0.05 times the peak value of the voltage:
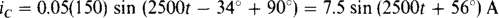
Phasors, which are conveniently based on peak values, can be used to find the sum sinusoid:
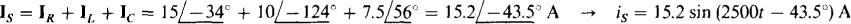
11.19 If two currents have phasors of 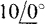 and
and 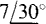 mA, what is the angle and rms value of the current that is the sum of these currents? Solve by using a funicular diagram. Check the answer by using complex algebra.
mA, what is the angle and rms value of the current that is the sum of these currents? Solve by using a funicular diagram. Check the answer by using complex algebra.
Figure 11-7 shows the tail of the 7-mA phasor at the tip of the 10-mA phasor, as required for vector addition. The sum phasor, extending from the tail of the 10-mA phasor to the tip of the 7-mA phasor, has a length corresponding to approximately 16.5 mA and an angle of approximately 13°. In comparison, the result from complex algebra is
Fig. 11-7
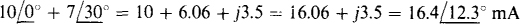
which is, of course, considerably more accurate than the graphical result.
11.20 A synchronous motor draws a 9-A current from a 240-V, 60-Hz source. A parallel induction motor draws 8 A. If the synchronous motor current leads the applied voltage by 20°, and if the induction motor current lags this voltage by 30°, what is the total current drawn from the source? Find this current graphically and algebraically.
The choice of the reference phasor—the one arranged horizontally at 0”—is somewhat arbitrary. The voltage phasor or either current phasor could be used. In fact, no phasor has to be at 0°, but it is usually convenient to have one at this angle. In Fig. 11-8 the synchronous motor current phasor is arbitrarily positioned horizontally, and the induction motor current phasor at its tip is positioned at an angle of -50° with it since there is a 20° — (— 30°) = 50° phase angle difference between the two currents. Also shown is the sum phasor, which has a measured length corresponding to 15.4 A. In comparison, from complex algebra,
Fig. 11-8
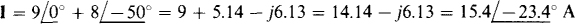
and
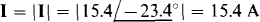
in agreement with the graphical result to three significant digits. Usually, agreement to only two significant digits should be expected because of the comparative lack of accuracy with the graphical approach.
11.21 Perform the following operations:
(a) j6 — j7 + j4 — j8 + j9 (b) (j2)2(—j3)(j7)(—j8)(j0.9) (c) 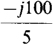 (d)
(d) 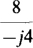
Ans. (a) j4, (b) —604.8, (c) —j20, (d) j2
11.22 Perform the following operations and express the results in rectangular form:
(a) (4.59 + j6.28) + (5.21 — j4.63)
(b) (8.21 + j4.31) — (4.92 — j6.23) — (—5.16 + j7.21)
(c) 3 + j4 — 5 + j6 — 7 + j8 — 9 + j10 — 11
Ans. (a) 9.8 + j1.65, (b) 8.45 + j3.33, (c) —29 + j28
11.23 Find the following products and express them in rectangular form:
(a) (6 — j7)(4 + j2)
(b) (5 + j1)(—7 — j4)(—6 + j9)
(c) (—2 + j6)(—4 — j4)(—6 + j8)(7 + j3)
Ans. (a) 38 — j16, (b) 429 — j117, (c) — 1504 + j2272
11.24 Find the following products and express them in rectangular form:
(a) (4 + j3)2(4 – j3)2 (b) (0.6 — j0.3)2(—2 + j4)3
Ans. (a) 625, (b) 18 — j36
11.25 Evaluate 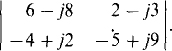
Ans. 44 + j78
11.26 Evaluate 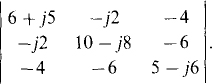
Ans. 156 — j762
11.27 Evaluate 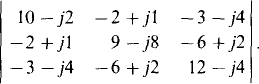
Ans. —65 — j1400
11.28 Find the following quotients in rectangular form:
(a) 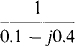 (b)
(b) 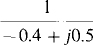 (c)
(c) 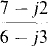
Ans. (a) 0.588 + j2.35, (b) —0.976 — j1.22, (c) 1.07 + j0.2
11.29 Convert each of the following to polar form:
(a) 8.1 + j11
(b) 16.3 — j12.2
(c) —33.4 + j14.7
(d) —12.7 — j17.3
(e) 16.2 + j16.2
(f) —19.1 + j19.1
Ans. (a) 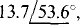
(b) 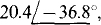
(c) 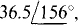
(d) 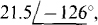
(e) 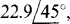
(f) 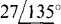
11.30 Convert each of the following to rectangular form:
(a) 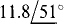
(b) 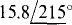
(c) 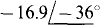
(d) 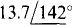
(e) 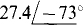
(f) 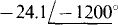
Ans. (a) 7.43 + j9.17, (b) —10.8 + j8.43, (c) —12.9 — j9.06, (d) 8.01 — j26.2, (e) —13.7 + j9.93, (f) 12.1 + j20.9
11.31 Perform the following operations and express the results in polar form:
(a) 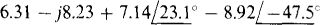
(b) 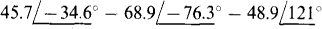
(c) 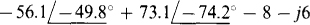
Ans (a) 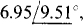 (b)
(b) 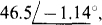 (c)
(c) 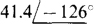
11.32 Find the following products in polar form:
(a) 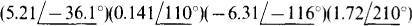
(b) 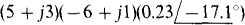
(c) 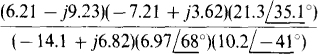
Ans (a) 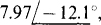 (b)
(b) 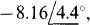 (c)
(c) 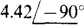
11.33 Find the following quotients in polar form:
(a) 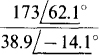 (b)
(b) 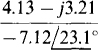 (c)
(c) 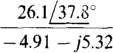
Ans. (a) 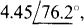 (b)
(b) 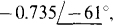 (c)
(c) 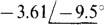
11.34 Find the following quotients in polar form:
(a) 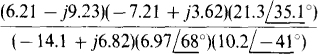
(b) 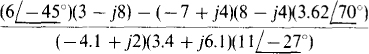
Ans. (a) 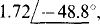 (b)
(b) 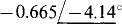
11.35 Find the following quotient in polar form:
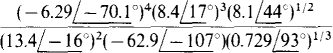
Ans. 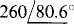
11.36 Find the corresponding phasor voltages and currents of the following in polar form:
(a) v =  (42.1) sin (400t — 30°)V
(42.1) sin (400t — 30°)V
(b)i =  (36.9) sin (6000t + 72°) A
(36.9) sin (6000t + 72°) A
(c) v = —64.3 sin (377t — 34°) V
(d) i = —38.1 cos (754t — 72°) A
(e) v = —86.4 cos (672t + 34°) V
Ans.(a) 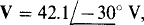 (b)
(b)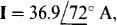 c)
c) 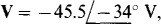 d)
d) 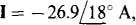 e) V =
e) V = 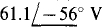
11.37 Find the voltages and currents corresponding to the following phasor voltages and currents (each sinusoid has a radian frequency of 754 rad/s):
(a) 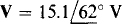
(b) 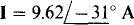
(c) 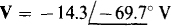
(d) I = 4 — j6 A
(e) V = —7 — j8 V
(f) I = —8.96 + j7.61 A
Ans. (a) v = 21.4 sin (754t + 62°) V
(b) i = 13.6 sin (754t — 31°)A
(c) v = —20.2 sin (754t — 69.7°) V
(d) i = 10.2 sin (754t — 56.3°) A
(e) v = —15 sin (754t + 48.8°) V
(f) i = —16.6 sin (754t — 40.3°) A
11.38 Find a single sinusoid that is the equivalent of each of the following:
(a) 7.21 sin ωt + 11.2 cos ωt
(b) —8.63 sin 377t — 4.19 cos 377t
(c) 4.12 sin (64t — 10°) — 6.23 sin (64t — 35°) + 7.26 cos (6t — 35°) — 8.92 cos (64t + 17°)
Ans. (a) 13.3 sin (ωt + 57.2°), (b) —9.59 sin (377t + 25.9°), (c) 5.73 sin (64t + 2.75°)
11.39 In Fig. 11-9, find i1, if i2 = 14.6 sin (377t — 15°) mA, i3 = 21.3 sin(377t + 30°) mA, and i4 = 13.7 cos (377t + 15°) mA.
Fig. 11-9
Ans. i1 = —27.7 cos (377t + 88.3°) mA
11.40 In the circuit shown in Fig. 11-10, ammeters A1 and A2 have readings of 4 and 3 A, respectively. What is the reading of ammeter A3?
Fig. 11-10
Ans. 2.65 A
11.41 A current i = 0.621 sin (400t + 30°) mA flows through a 3.3-kΩ resistor in series with a 0.5-μF capacitor. Find the voltage across the series combination. Of course, as always, assume associated references when, as here, there is no statement to the contrary.
Ans. v = 3.72 sin (400t — 26.6°) V
11.42 A voltage v = 240 sin (400t + 10°) V is across a 680-Ω resistor in parallel with a 1-H inductor. Find the current flowing into this parallel combination.
Ans. i = 0.696 sin (400t — 49.5°) A
11.43 A current i = 0.248 cos (377t — 15°) A flows through the series combination of a 91-Ω resistor, a 120-mH inductor, and a 20-μF capacitor. Find the voltage across the series combination.
Ans. v = 31.3 sin (377t + 31.2°) V
11.44 The voltage v = 120 sin (1000t + 20°) V is across the parallel combination of a 10-kΩ resistor, a 100-mH inductor, and a 10-μF capacitor. Find the total current iT flowing into the parallel combination. Also, find the inductor current iL and compare peak values of iL and iT.
Ans. iT = 0.012 sin (1000t + 20°) A and iL = 1.2 sin (1000t — 70°) A. The inductor current peak is 100 times the input current peak.