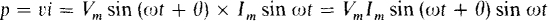
The major topic of this chapter is the average power absorbed over a period by ac components and circuits. Consequently, it will not be necessary to always use the adjective “average” with power to avoid misunderstanding. Also, it is not necessary to use the subscript notation “av” with the symbol P. Similarly, since the popular power formulas have only effective or rms values of voltage and current, the subscript notation “eff” can be deleted from Veff and Ieff (or “rms” from Vrms and Irms) and just the lightface V and I used to designate effective or rms values.
As a final introductory point, in the following text material and problems the specified voltages and currents always have associated references unless there are statements or designations to the contrary.
The average power absorbed by a two-terminal ac circuit can be derived from the instantaneous power absorbed. If the circuit has an applied voltage v = Vm sin (ωt + 0) and an input current i = Im sin ωt, the instantaneous power absorbed by the circuit is
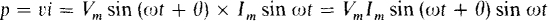
This can be simplified by using the trigonometric identity
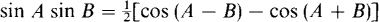
and the substitutions A = ωt + θ and B = ωt. The result is
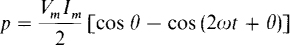
Since
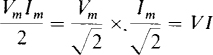
the instantaneous power can be expressed as
The average value of this power is the sum of the average values of the two terms. The second term, being sinusoidal, has a zero average value over a period. The first term, though, is a constant, and so must be the average power absorbed by the circuit over a period. So,
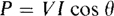
It is important to remember that in this formula the angle θ is the angle by which the input voltage leads the input current. For a circuit that does not contain any independent sources, this is the impedance angle.
For a purely resistive circuit, θ = 0° and cos 0° = 1 and so P = VI cos θ = VI. For a purely inductive circuit, θ = 90° and cos θ = cos 90° = 0, and so P = 0 W, which means that a purely inductive circuit absorbs zero average power. The same is true for a purely capacitive circuit since, for it, 0 = –90° and cos(–90°) = 0.
The term “cos 0” is called the power factor. It is often symbolized as PF, as in P = VI × PF. The angle 0 is called the power factor angle. As mentioned, it is often also the impedance angle.
The power factor angle has different signs for inductive and capacitive circuits, but since cos θ = cos (— θ), the sign of the power factor angle has no effect on the power factor. Because the power factors of inductive and capacitive circuits cannot be distinguished mathematically, they are distinguished by name. The power factor of an inductive circuit is called a lagging power factor and that of a capacitive circuit is called a leading power factor. These names can be remembered from the fact that for an inductive circuit the current lags the voltage, and for a capacitive circuit the current leads the voltage.
Another power formula can be obtained by substituting V = IZ into P = VI cos θ
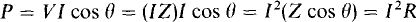
Of course, R = Z cos θ is the input resistance, the same as the real part of the input impedance. The formula P = I2R may seem obvious from dc considerations, but remember that R is usually not the resistance of a physical resistor. Rather, it is the real part of the input impedance and is usually dependent on inductive and capacitive reactances as well as on resistances.
Similarly, with the substitution of I = YV,
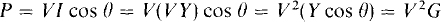
in which G = Y cos θ is the input conductance. In using this formula P = V2G, remember that, except for a purely resistive circuit, the input conductance G is not the inverse of the input resistance R. If, however, V is the voltage across a resistor of R ohms, then P = V2G = V2/R.
Average power can be measured by an instrument called a wattmeter, as shown in Fig. 15-1. It has two pairs of terminals: a pair of voltage terminals on the left-hand side and a pair of current terminals on the right-hand side. The bottom terminal of each pair has a ± designation for aiding in connecting up the wattmeter, as will be explained.
Fig. 15-1
For a measurement of power absorbed by a load, the voltage terminals are connected in parallel with the load and the current terminals are connected in series with the load. Because the voltage circuit inside the wattmeter has a very high resistance and the current circuit has a very low resistance, the voltage circuit can be considered an open circuit and the current circuit a short circuit for the power measurements of almost all loads. As a result, inserting a wattmeter in a circuit seldom has a significant effect on the power absorbed. For convenience, in circuit diagrams the voltage circuit will be shown as a coil labeled “pc” (for potential coil) and the current circuit will be shown as a coil labeled “cc” (for current coil), as shown in Fig. 15-2. One type of wattmeter, the electrodynamometer wattmeter, actually has such coils.
Fig. 15-2
The ± designations help in making wattmeter connections so that the wattmeter reads upscale, to the right in Fig. 15-1, for positive absorbed power. A wattmeter will read upscale with the connection in Fig. 15-2 if the load absorbs average power. Notice that, for the associated voltage and current references, the reference current enters the ± current terminal and the positive reference of the voltage is at the ± voltage terminal. The effect is the same, though, if both coils are reversed. If a load is active—a source of average power—then one coil connection, but not both, should be reversed for an upscale reading. Then, the wattmeter reading is considered to be negative for this connection. Incidentally, in the circuit shown in Fig. 15-2, the wattmeter reads essentially the same with the potential coil connected on the source side of the current coil instead of on the load side.
For industrial power considerations, a quantity called reactive power is often useful. It has the quantity symbol Q and the unit of voltampere reactive, the symbol for which is VAR. Reactive power, which is often referred to as vars, is defined as
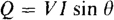
for a two-terminal circuit with an input rms voltage V and an input rms current I. This Q is absorbed reactive power. The θ is the angle by which the input voltage leads the input current—the power factor angle. The quantity “sin θ” is called the reactive factor of the load and has the symbol RF. Notice that it is negative for capacitive loads and is positive for inductive loads. A load that absorbs negative vars is considered to be producing vars—that is, it is a source of reactive power.
As was done for real power P, other formulas for Q can be found by substituting from V = IZ and I = YV into Q = VI sin θ. These formulas are
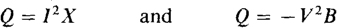
where X is the reactance or imaginary part of the input impedance and B is the susceptance or imaginary part of the input admittance. (Remember that B is not the inverse of X.) Additionally, if V is the voltage across an inductor or capacitor with reactance X, then Q = V2/X. So, Q = V2ωL for an inductor and Q = —ωCV2 for a capacitor.
There is a relation among the real power of a load, the reactive power, and another power called the complex power. For the derivation of this relation, consider the load impedance triangle shown in Fig. 15-3a. If each side is multiplied by the square of the rms current I to the load, the result is the triangle shown in Fig. 15-3b. Notice that this multiplication does not affect the impedance angle θ since each side is multiplied by the same quantity. The horizontal side is the real power P = I2R, the vertical side is j1 times the reactive power, jI2X = jQ, and the hypotenuse I2Z is the complex power of the load. Complex power has the quantity symbol S and the unit of Voltampere with symbol VA. These power quantities are shown in Fig. 15-3c, which is known as the power triangle. From this triangle, clearly S = P + jQ.
Fig. 15-3
The length of the hypotenuse |S| = S, is called the apparent power. Its name comes from the fact that it is equal to the product of the input rms voltage and current:
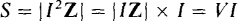
and from the fact that in dc circuits this product VI is the power absorbed. The substitution of V = IZ and I = V/Z into S = VI produces two other formulas: S = I2Z and S = V2/Z.
The VI formula for apparent power leads to another popular formula for complex power. Since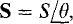 
, and S = VI, then 
.
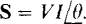A third formula for complex power is S = VI*, where I* is the conjugate of the input current I. This is a valid formula since the magnitude of VI* is the product of the applied rms voltage and current, and, consequently, is the apparent power. Also, the angle of this product is the angle of the voltage phasor minus the angle of the current phasor, with the subtraction occurring because of the use of the conjugate of the current phasor. This difference in angles is, of course, the complex power angle 0—the angle by which the input voltage leads the input current—and also the power factor angle.
One use of complex power is for obtaining the total complex power of several loads energized by the same source, usually in parallel. It can be shown that the total complex power is the sum of the individual complex powers, regardless of how the loads are connected. It follows that the total real power is the sum of the individual real powers, and that the total reactive power is the sum of the individual reactive powers. To repeat for emphasis: Complex powers, real powers, and reactive powers can be added to obtain the total complex power, real power, and reactive power, respectively. The same is not true for apparent powers. In general, apparent powers cannot be added to obtain a total apparent power any more than rms voltages or currents can be added to obtain a total rms voltage or current.
The total complex power can be used to find the total input current, as should be apparent from the fact that the magnitude of the total complex power, the apparent power, is the product of the input voltage and current. Another use for complex power is in power factor correction, which is the subject of the next section.
In the consumption of a large amount of power, a large power factor is desirable—the larger the better. The reason is that the current required to deliver a given amount of power to a load is inversely proportional to the load power factor, as is evident from rearranging P = VI cos θ to
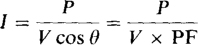
So, for a given power P absorbed and applied voltage V, the smaller the power factor the greater the current I to the load. Larger than necessary currents are undesirable because of the accompanying larger voltage losses and I2R power losses in power lines and other power distribution equipment.
As a practical matter, low power factors are always the result of inductive loads because almost all loads are inductive. From a power triangle viewpoint, the vars that such loads consume make the power triangle have a large vertical side and so a large angle θ. The result is a small cos θ, which is the power factor. Improving the power factor of a load requires adding capacitors across the power line at the load to provide the vars consumed by the inductive load. From another point of view, these capacitors supply current to the load inductors, which current, without the capacitors, would have to come over the power line. More accurately, there is a current interchange between these capacitors and the load inductors.
Although adding sufficient capacitance to increase the power factor to unity is possible, it may not be economical. For finding the minimum capacitance required to improve the power factor to the amount desired, the general procedure is to first calculate the initial number of vars Qi being consumed by the load. This can be calculated from Qi = P tan θi, which formula should be apparent from the power triangle shown in Fig. 15-3c. Of course, θiis the load impedance angle. The next step is to determine the final impedance angle θf from the final desired power factor: θf = cos–1 PFf. This angle is used in Qf = P tan θf to find the total number of vars Qf for the combined load. This formula is valid since adding the parallel capacitor or capacitors does not change P. The next step is to find the vars that the added capacitors must provide: ΔQ = Qf = Qi. Finally, ΔQ is used to find the required amount of capacitance:
If ΔQ is defined as Qi = Qf, the negative sign can be eliminated in the formula for C; then, C = ΔQ/ωV2. All this procedure can be done in one step with
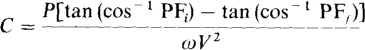
Although calculating the capacitance required for power factor correction may be a good academic exercise, it is not necessary on the job. Manufacturers specify their power factor correction capacitors by operating voltages and the kilovars the capacitors produce. So, for power factor correction, it is only necessary to know the voltages of the lines across which the capacitors will be placed and the kilovars required.
15.1 The instantaneous power absorbed by a circuit is p = 10 + 8 sin (377t + 40°) W. Find the maximum, minimum, and average absorbed powers.
The maximum value occurs at those times when the sinusoidal term is a maximum. Since this term has a maximum value of 8, pmax = 10 + 8 = 18 W. The minimum value occurs when the sinusoidal term is at its minimum value of –8: pmin = 10 – 8 = 2 W. Because the sinusoidal term has a zero average value, the average power absorbed is P = 10 + 0 = 10 W.
15.2 With v = 300 cos(20t + 30°) V applied, a circuit draws I = 15 cos (20t – 25°) A. Find the power factor and also the average, maximum, and minimum absorbed powers.
The power factor of the circuit is the cosine of the power factor angle, which is the angle by which the voltage leads the current:
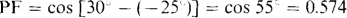
It is lagging because the current lags the voltage.
The average power absorbed is the product of the rms voltage and current and the power factor:
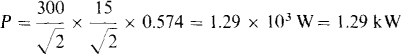
The maximum and minimum absorbed powers can be found from the instantaneous power, which is
This can be simplified by using the trigonometric identity
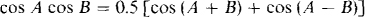
and the substitutions A = 20t + 30° and B = 20t – 25. The result is
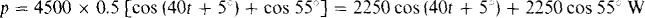
Clearly, the maximum value occurs when the first cosine term is 1 and the minimum value when this term is –1:
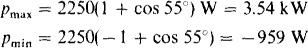
The negative minimum absorbed power indicates that the circuit is delivering power instead of absorbing it.
15.3 For each following load voltage and current pair find the corresponding power factor and average power absorbed:
(a) v = 277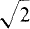
sin (377t + 30°) V, i = 5.1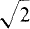sin(377t – 10°) A
(b) v = 679 sin (377t + 50°) V, I = 13 cos (377t + 10°) A
(c) v = –170 sin(377t – 30°)V, i = 8.1 cos (377t + 30°) A
(a) Since the angle by which the voltage leads the current is θ = 30° – (–10°) = 40°, the power factor is PF = cos 40° = 0.766. It is lagging because the current lags the voltage, or, in other words, because the power factor angle θ is positive. The average power absorbed is the product of the rms voltage and current and the power factor:
(b) The power factor angle θ can be found by phase angle subtraction only if v and i have the same sinusoidal form, which they do not have here. The cosine term of i can be converted to the sine form of v by using the identity cos x = sin (x + 90°):
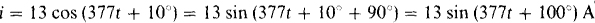
So, the power factor angle is θ = 50° – 100° = –50°, and the power factor is PF = cos (– 50°) = 0.643. It is a leading power factor because the current leads the voltage, and also because θ is negative, which is equivalent. The average power absorbed is
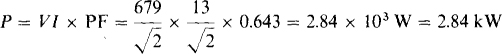
(c) The voltage sinusoid will be put in the same sinusoidal form as the current sinusoid as an aid in finding θ. The negative sign can be eliminated by using –sin x = sin (x ± 180°):
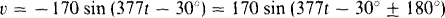
Then the identity sin x = cos (x – 90°) can be used:
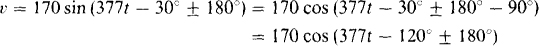
The positive sign of ±180° should be selected to make the voltage and current phase angles as close together as possible:
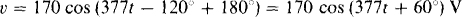
So, θ = 60° – 30° = 30°, and the power factor is PF = cos 30° = 0.866. It is lagging because θ is positive. Finally, the average power absorbed is
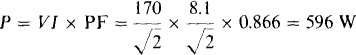
15.4 Find the power factor of a circuit that absorbs 1.5 kW for a 120-V input voltage and a 16-A current.
From P = VI × PF, the power factor is
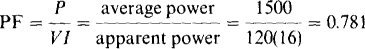
There is not enough information given to determine whether this power factor is leading or lagging.
Note that the power factor is equal to the average power divided by the apparent power. Some authors of circuit analysis books use this for the definition of power factor because it is more general than PF = cos θ.
15.5 What is the power factor of a fully loaded 10-hp induction motor that operates at 80 percent efficiency while drawing 28 A from a 480-V line?
The motor power factor is equal to the power input divided by the apparent power input. And, the power input is the power output divided by the efficiency of operation:
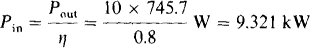
in which 1 hp = 745.7 W is used. So,
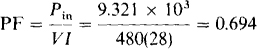
This power factor is lagging because induction motors are inductive loads.
15.6 Find the power absorbed by a load of 6∠30° Ω when 42 V is applied.
The rms current needed for the power formulas is equal to the rms voltage divided by the magnitude of the impedance: I = 42/6 = 7 A. Of course, the power factor is the cosine of the impedance angle: PF = cos 30° = 0.866. Thus,
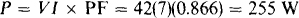
The absorbed power can also be obtained from P = I2R, in which R = Z cos θ = 6 cos 30° = 5.2 Ω:
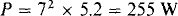
The power cannot be found from P = V2/R, as is evident from the fact that V2/R = 422/5.2 = 339 W, which is incorrect. The reason for the incorrect result is that the 42 V is across the entire impedance and not just the resistance part. For P = V2/R to be valid, the V used must be that across R.
15.7 What power is absorbed by a circuit that has an input admittance of 0.4 + j0.5 S and an input current of 30 A?
The formula P = V2G can be used after the input voltage V is found. It is equal to the current divided by the magnitude of the admittance:
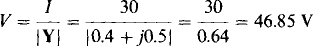
So P = V2G = (46.85)20.4 = 878 W
Alternatively, the power formula P = VI cos θ can be used. The power factor angle θ is the negative of the admittance angle: θ = –tan–1 (0.5/0.4) = – 51.34°. So,
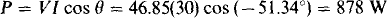
15.8 A resistor in parallel with a capacitor absorbs 20 W when the combination is connected to a 240-V, 60-Hz source. If the power factor is 0.7 leading, what are the resistance and capacitance?
The resistance can be found by solving for R in P = V2/R:
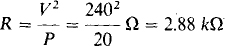
One way to find the capacitance is from the susceptance B, which can be found from B = G tan φ after the conductance G and admittance angle φ are known. The conductance is
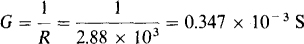
For this capacitive circuit, the admittance angle is the negative of the power factor angle: φ = –(–cos–1 0.7) = 45.6°. So,
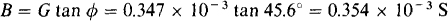
Finally, since B = wC,
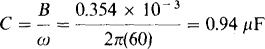
15.9 A resistor in series with a capacitor absorbs 10 W when the combination is connected to a 120-V, 400-Hz source. If the power factor is 0.6 leading, what are the resistance and capacitance?
Because this is a series circuit, impedance should be used to find the resistance and capacitance. The impedance can be found by using the input current, which from P = VI × PF is
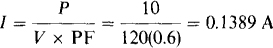
The magnitude of the impedance is equal to the voltage divided by the current, and the impedance angle is, for this capacitive circuit, the negative of the arccosine of the power factor:
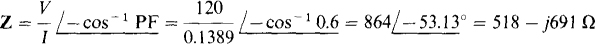
From the real part the resistance is R = 518 Ω, and from the imaginary part and X = –1/ωC, the capacitance is
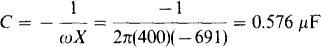
15.10 If a coil draws 0.5 A from a 120-V, 60-Hz source at a 0.7 lagging power factor, what are the coil resistance and inductance?
The resistance and inductance can be obtained from the impedance. The impedance magnitude is Z = V/I = 120/0.5 = 240 Q, and the impedance angle is the power factor angle: θ = cos–1 0.7 = 45.57°. So, the coil impedance is Z = 240∠45.57° = 168 + j171.4 Ω. From the real part, the coil resistance is R = 168 Ω, and from the imaginary part the coil reactance is 171.4 Ω. The inductance can be found from X = ωL. It is L = X/ω = 171.4/2π(60) = 0.455 H.
15.11 A resistor and parallel capacitor draw 0.2 A from a 24-V, 400-Hz source at a 0.8 leading power factor. Find the resistance and capacitance.
Since the components are in parallel, admittance should be used to find the resistance and capacitance. The admittance magnitude is Y = I/V = 0.2/24 = 8.33 mS, and the admittance angle is, for this capacitive circuit, the arccosine of the power factor: cos –1 0.8 = 36.9°. Thus, the admittance is
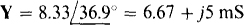
From the real part, the conductance of the resistor is 6.67 mS, and so the resistance is R = 1/(6.67 × 10–3) = 150 Ω. From the imaginary part the capacitive susceptance is 5 mS, and so the capacitance is
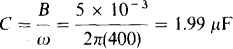
15.12 Operating at maximum capacity, a 12 470-V alternator supplies 35 MW at a 0.7 lagging power factor. What is the maximum real power that the alternator can deliver?
The limitation on the alternator capacity is the maximum voltamperes—the apparent power, which is the real power divided by the power factor. For this alternator, the maximum apparent power is P/PF = 35/0.7 = 50 MVA. At unity power factor all of this would be real power, which means that the maximum real power that this alternator can supply is 50 MW.
15.13 An induction motor delivers 50 hp while operating at 80 percent efficiency from 480-V lines. If the power factor is 0.6, what current does the motor draw? If the power factor is 0.9, instead, what current does this motor draw?
The current can be found from P = VI × PF, where P is the motor input power of 50 × 745.7/0.8 = 46.6 kW. For a power factor of 0.6, the current to the motor is
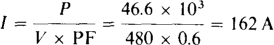
And, for a power factor of 0.9, it is
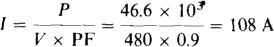
This 54-A decrease in current for the same output power shows why a large power factor is desirable.
15.14 For the circuit shown in Fig. 15-4, find the wattmeter reading when the ± terminal of the potential coil is connected to node a, and also when it is connected to node b.
Fig. 15-4
The wattmeter reading is equal to VI cos θ, where V is the rms voltage across the potential coil, 7 is the rms current flowing through the current coil, and θ is the phase angle difference of the corresponding voltage and current phasors when they are referenced as shown with respect to the ± markings of the wattmeter coils. These three quantities must be found to determine the wattmeter reading.
The phasor current I is
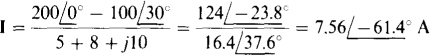
With the ± terminal of the potential coil at node a, the phasor voltage drop V across this coil is the 200∠0° -V source voltage minus the drop across the 5-Ω resistor:
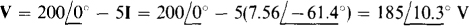
The wattmeter reading is
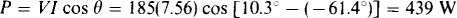
With the ± terminal of the potential coil at node b, V is equal to the voltage drop across the j10-Ω impedance and the 100∠30°-V source:
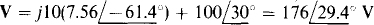
And so the wattmeter reading is
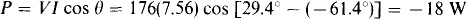
Probably the wattmeter cannot directly give a negative reading. If not, then the connections to one wattmeter coil should be reversed so that the wattmeter reads upscale. And, the reading should be interpreted as being negative.
15.15 In the circuit shown in Fig. 15-5, find the total power absorbed by the three resistors. Then find the sum of the readings of the two wattmeters. Compare results.
Fig. 15-5
The powers absorbed by the resistors can be found by using P = I2R. The current through the resistors
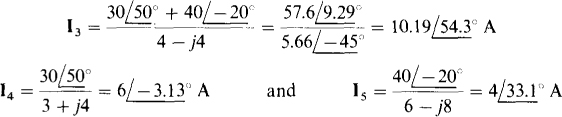
Of course, only the rms values of these currents are used in P = I2R:
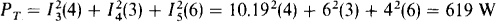
The currents I1 and I2 are needed in finding the wattmeter readings since these are the currents that flow through the current coils:
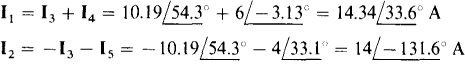
Obviously, the potential coil voltages are V1 = 30∠50° V and V2 = –40∠–20 = 40∠160 V. These potential coil voltages and current coil currents produce wattmeter readings that have a sum of
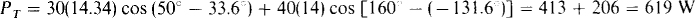
Observe that this sum of the two wattmeter readings is equal to the total power absorbed. This should not be expected, since each wattmeter reading cannot be associated with powers absorbed by certain resistors. It can be shown, though, that this result is completely general for loads with three wires and for the connections shown. This use of wattmeters is the famous two-wattmeter method that is popular for measuring power to three-phase loads, as will be considered in Chap. 17.
15.16 What is the reactive factor of an inductive load that has an apparent power input of 50 kVA while absorbing 30 kW?
The reactive factor is the sine of the power factor angle θ, which is
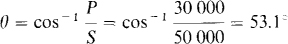
So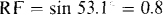 
15.17 With v = 200 sin (377t + 30°) V applied, a circuit draws i = 25 sin (377t – 20°) A. What is the reactive factor and what is the reactive power absorbed?
The reactive factor is the sine of the power factor angle θ, which is the phase angle of the voltage minus the phase angle of the current: θ = 30 – (– 20°) = 50°. So, RF = sin 50° = 0.766. The reactive power absorbed can be found from Q = VI × RF, where V and I are the rms values of the voltage and current:
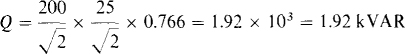
15.18 What is the reactive factor of a circuit that has an input impedance of 40∠50° Ω? Also, what reactive power does the circuit absorb when the input current is 5 A?
The reactive factor is the sine of the impedance angle: RF = sin 50° = 0.766. An easy way to find the reactive power is with the formula Q = I2X, where X, the reactance, is equal to 40 sin 50° = 30.64 Ω:
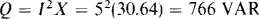
15.19 What is the reactive factor of a circuit that has an input impedance of 20∠–40° Q? What is the reactive power absorbed with 240 V applied?
The reactive factor is the sine of the impedance angle: RF = sin (– 40) = –0.643. Perhaps the easiest way to find the reactive power absorbed is from Q = VI × RF. The only unknown in this formula is the rms current, which is equal to the rms voltage divided by the magnitude of impedance: I = VIZ = 240/20= 12 A. Then,
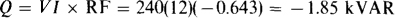
The negative sign indicates that the circuit delivers vars, as should be expected from this capacitive circuit.
As a check, the formula Q = I2X can be used, in which X, the imaginary part of the impedance, is X = 20 sin (–40°)= –12.86 Ω: Q = 122(–12.86) = – 1.85 kVAR, the same.
15.20 When 3 A flows through a circuit with an input admittance of 0.4 +/0.5 S, what reactive power does the circuit consume?
The reactive power consumed can be found from Q = I2X after X is found from the admittance. Of course X is the imaginary part of the input impedance Z. Solving for Z,
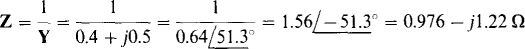
So, x = –1.22 Ω and
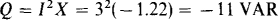
The negative sign indicates that the circuit delivers reactive power.
A check can be made by using Q = – V2B, where V = IZ = 3(1.56) = 4.68 V. (Of course, B = 0.5 S from the input admittance.) So,
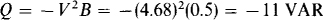
15.21 Two circuit elements in series consume 60 VAR when connected to a 120-V, 60-Hz source. If the reactive factor is 0.6, what are the two components and what are their values?
The two components can be found from the input impedance. The angle of this impedance is the arcsine of the reactive factor: θ = sin–1 0.6 = 36.9°. The magnitude of the impedance can be found by substituting I = V/Z into Q = VI × RF:
So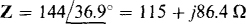 
From this impedance, the two elements must be a resistor with a resistance of R = 115 Ω and an inductor with a reactance of 86.4 Ω. The inductance is
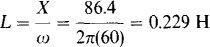
15.22 What resistor and capacitor in parallel present the same load to a 480-V, 60-Hz source as a fully loaded 20-hp synchronous motor that operates at a 75 percent efficiency and a 0.8 leading power factor?
The resistance can be found from the motor input power, which is
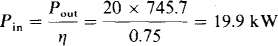
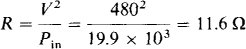
From Pin = v2/R,
The corresponding conductance and the admittance angle, which is the negative of the power factor angle, can be used to find the capacitive susceptance. And then the capacitance can be found from this susceptance. The conductance is G = 1/11.6 = 0.0863 S, and the admittance angle is φ = cos–1 0.8 = 36.9°. So, the susceptance is
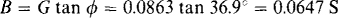
Finally, the capacitance is this susceptance divided by the radian frequency:
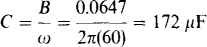
15.23 A 120-mH inductor is energized by 120 V at 60 Hz. Find the average, peak, and reactive powers absorbed.
Since the power factor is zero (PF = cos 90° = 0), the inductor absorbs zero average power: P = 0 W. The peak power can be obtained from the instantaneous power. As derived in this chapter, the general expression for instantaneous power is
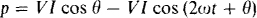
For an inductor, θ = 90°, which means that the first term is zero. Consequently, the peak power is the peak value of the second term, which is VI: pmax = VI. The voltage V is given: V = 120 V. The current I can be found from this voltage divided by the inductive reactance:
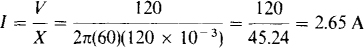
So pmax = VI = 120(2.65) = 318 W
The reactive power absorbed is
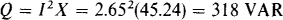
which has the same numerical value as the peak power absorbed by the inductor. This is generally true because Q = I2X = (IX)I = VI, and VI is the peak power absorbed by the inductor.
15.24 What are the power components resulting from a 4-A current flowing into a load of 30∠40° Ω? In other words, what are the complex, real, reactive, and apparent powers of the load?
From Fig. 15-3b, the complex power S is
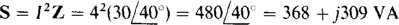
The real power is the real part, P = 368 W, the reactive power is the imaginary part, Q = 309 VAR, and the apparent power is the magnitude, S = 480 VA.
15.25 Find the power components of an induction motor that delivers 5 hp while operating at an 85 percent efficiency and a 0.8 lagging power factor.
The input power is
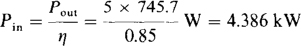
The apparent power, which is the magnitude of the complex power, is the real power divided by the power factor: S = 4.386/0.8 = 5.48 kVA. The angle of the complex power is the power factor angle: θ = cos–1 0.8 = 36.9°. So, the complex power is
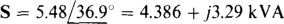
The reactive power is, of course, the imaginary part: Q = 3.29 kVAR.
15.26 Find the power components of a load that draws 20∠–30° A with 240∠20° V applied.
The complex power can be found from S = VI*. Since I = 20∠– 30° A, its conjugate is I* = 20∠30° A, and the complex power is
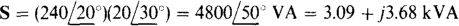
From the magnitude and real and imaginary parts, the apparent, real, and reactive powers are S = 4.8 kVA, P = 3.09 kW, and Q = 3.68 kVAR.
15.27 A load, connected across a 12 470-V line, draws 20 A at a 0.75 lagging power factor. Find the load impedance and the power components.
Since the impedance magnitude is equal to the voltage divided by the current, and the impedance angle is the power factor angle, the load impedance is
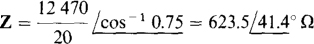
From S = I2Z, the complex power is
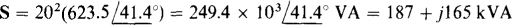
From the magnitude and the real and imaginary parts, S = 249.4 kVA, P = 187kW, and Q = 165kVAR.
15.28 A 20-μF capacitor and a parallel 200-Ω resistor draw 4 A at 60 Hz. Find the power components.
Once the impedance is found, the complex power can be obtained from S = I2Z. The capacitive reactance is
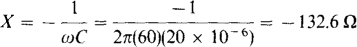
and the impedance of the parallel combination is
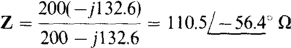
Substitution into S = I2Z results in a complex power of
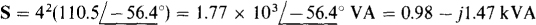
So, S = 1.77kVA, P = 0.98kW, and Q = –1.47kVAR.
15.29 A fully loaded 10-hp induction motor operates from a 480-V, 60-Hz line at an efficiency of 85 percent and a 0.8 lagging power factor. Find the overall power factor when a 33.3-μF capacitor is placed in parallel with the motor.
The power factor can be determined from the power factor angle, which is θ = tan–1 (QT/Pin). For this, the input power Pin and the total reactive power QT are needed. The capacitor does not change the real power absorbed, which is
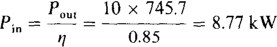
The total reactive power is the sum of the motor and capacitive reactive powers. As is evident from power triangle considerations, the reactive power QM of the motor is equal to the power times the tangent of the motor power factor angle, which is the arccosine of the motor power factor:
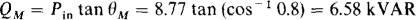
The reactive power absorbed by the capacitor is
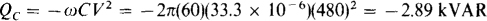
And the total reactive power is
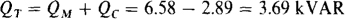
With QT and Pin known, the power factor angle θ can be determined:
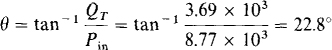
And the overall power factor is PF = cos 22.8° = 0.922. It is lagging because the power factor angle is positive.
15.30 A 240-V source energizes the parallel combination of a purely resistive 6-kW heater and an induction motor that draws 7 kVA at a 0.8 lagging power factor. Find the overall load power factor and also the current from the source.
The power factor and current can be determined from the total complex power ST, which is the sum of the complex powers of the heater and motor:
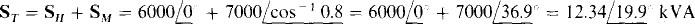
The overall power factor is the cosine of the angle of the total complex power: PF = cos 19.9° = 0.94. It is lagging, of course, because the power factor angle is positive. The source current is equal to the total apparent power divided by the voltage:
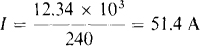
Notice that the total apparent power of 12.34 kVA is not the sum of the load apparent powers of 6 and 7 kVA. This is generally true except in the unusual situation in which all complex powers have the same angle.
15.31 A 480-V source energizes two loads in parallel, supplying 2 kVA at a 0.5 lagging power factor to one load and 4 kVA at a 0.6 leading power factor to the other load. Find the source current and also the total impedance of the combination.
The current can be found from the total apparent power, which is the magnitude of the total complex power:
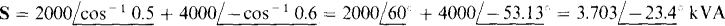
The power factor angle for the 4-kVA load is negative because the power factor is leading, which means that the current leads the voltage.
The current is equal to the apparent power divided by the voltage:
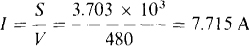
From S = I2Z, the impedance is equal to the complex power divided by the square of the current:
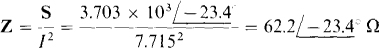
15.32 Three loads are connected across a 277-V line. One is a fully loaded 5-hp induction motor operating at a 75 percent efficiency and a 0.7 lagging power factor. Another is a fully loaded 7-hp synchronous motor operating at an 80 percent efficiency and a 0.4 leading power factor. The third is a 5-kW resistive heater. Find the total line current and the overall power factor.
The line current and power factor can be determined from the total complex power, which is the sum of the individual complex powers. The complex power of the induction motor has a magnitude that is equal to the input power divided by the power factor, and an angle that is the power factor angle. The same is true for the synchronous motor. The complex power for the heater is, of course, the same as the real power. So,
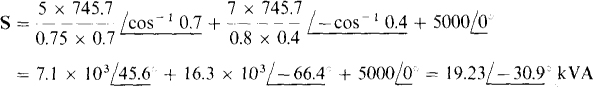
The total line current is equal to the apparent power divided by the line voltage: I = (19.23 × 103)/277 = 69.4 A. And, the overall power factor is the cosine of the angle of the total complex power: PF = cos (– 30.9°) = 0.858. It is leading because the power factor angle is negative.
15.33 In the circuit shown in Fig. 15-6, load 1 absorbs 2.4 kW and 1.8 kVAR, load 2 absorbs 1.3 kW and 2.6 kVAR, and load 3 absorbs 1 kW and generates 1.2kVAR. Find the total power components, the source current I1, and the impedance of each load.
Fig. 15-6
The total complex power is the sum of the individual complex powers:
From the total complex power, the total apparent power is ST = 5.69 kVA, the total real power is PT = 4.7 kW, and the total reactive power is QT = 3.2 kVAR. The source current magnitude I1 is equal to the apparent power divided by the source voltage: I1 = (5.69 × 103)/600 = 9.48 A. And the angle of I1 is the angle of the voltage minus the power factor angle: 20° – 34.2° = –14.2°. So, I1 = 9.48∠–14.2° A.
The angle of the load 1 impedance Zt is the load power factor angle, which is also the angle of the complex power S1. Since S1 = 2400 + j1800 = 3000∠36.9° VA, this impedance angle is θ = 36.9°. Because the load 1 voltage is known, the magnitude Z, can be found from S1 = V2/Z1:
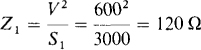
So, Z1 = Z1∠θ = 120∠36.9° Ω. The impedances Z2 and Z3 of loads 2 and 3 cannot be found in a similar manner because the load voltages are not known. But the rms current I2 can be found from the sum of the complex powers of loads 2 and 3, and used in S = I2Z to find the impedances. This sum is
The apparent power S23 can be used to obtain I2 from S23 = VI2:
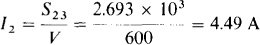
Since S2 = 1300 + j2600 VA = 2.91∠63.4° kVA, the impedance of load 2 is
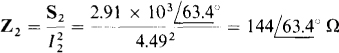
Similarly, S3 = 1000 – j1200 VA = 1.562∠–50.2° kVA, and
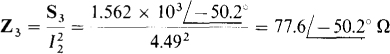
15.34 A load that absorbs 100-kW at a 0.7 lagging power factor has capacitors placed across it to produce an overall power factor of 0.9 lagging. The line voltage is 480 V. How much reactive power must the capacitors produce, and what is the resulting decrease in line current?
The initial reactive power is Qip tan θi where θi is the initial power factor angle: θi = cos–1 0.7 = 45.6°. Therefore
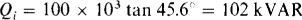
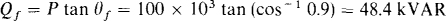
Consequently, the capacitors must supply 102 — 48.4 = 53.6 kVAR.
The initial and final currents can be obtained from P = VI × PF:
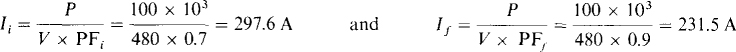
The resulting decrease in line current is 297.6 – 231.5 = 66.1 A.
15.35 A synchronous motor that draws 20 kW is in parallel with an induction motor that draws 50 kW at a lagging power factor of 0.7. If the synchronous motor is operated at a leading power factor, how much reactive power must it provide to cause the overall power factor to be 0.9 lagging, and what is its power factor?
Since the total power input is PT = 20 + 50 = 70 kW, the total reactive power is
Because the reactive power absorbed by the induction motor is
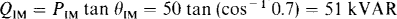
the synchronous motor must supply Qm – QT = 51 – 33.9 = 17.1 kVAR. Thus, QSM = – 17.1 kVAR.
The resulting power factor of the synchronous motor is cos θSM in which θSM, the synchronous motor power factor angle, is
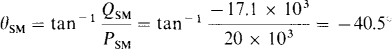
So, PFSM = cos (–40.5°) = 0.76 leading.
15.36 A factory draws 100 A at a 0.7 lagging power factor from a 12 470-V, 60-Hz line. What capacitor placed across the line at the input to the factory increases the overall power factor to unity? Also, what are the final currents for the factory, capacitor, and line?
The capacitance can be determined from the reactive power that the capacitor must provide to cause the power factor to be unity. The reactive power absorbed by the factory is the apparent power times the reactive factor, which is the sine of the arccosine of the power factor: RF = sin (cos–1 0.7) = 0.714. Thus
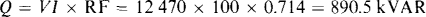
For a unity power factor, the capacitor must supply all this reactive power. Since the formula for generated capacitor reactive power is Q = ωCV2, the required capacitance is
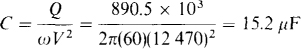
Adding the capacitor in parallel does not change the current input to the factory since there is no change in the factory load. This current remains at 100 A. The current to the capacitor can be found from Q = VIC × RF with RF = – 1 since the power factor angle is –90° for the capacitor. The result is
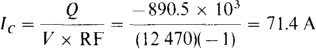
The total final line current IfL can be found from the input power, which is
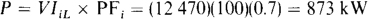
Adding the capacitor does not change this power, but it does change the power factor to 1. So, from P = VIfL × PFf
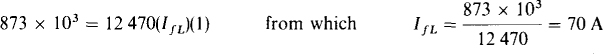
Notice that the 70-A rms final line current is not equal to the sum of the capacitor 71.4-A rms current and the factory 100-A rms current. This should not be surprising because, in general, rms quantities cannot be validly added since the phasor angles are not included.
15.37 A 240-V, 60-Hz source energizes a load of 30∠50° Ω. What capacitor in parallel with this load produces an overall power factor of 0.95 lagging?
Although powers could be used in the solution, it is often easier to use admittance when a circuit or its impedance is specified. The initial admittance is
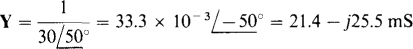
Adding the capacitor changes only the susceptance, which becomes
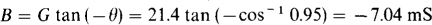
This formula B – G tan (– θ) should be evident from admittance triangle considerations and the fact that the admittance angle is the negative of the power factor angle. From ΔB = wC,
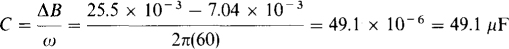
15.38 At 60 Hz, what is the power factor of the circuit shown in Fig. 15-7? What capacitor connected across the input terminals causes the overall power factor to be 1 (unity)? What capacitor causes the overall power factor to be 0.85 lagging?
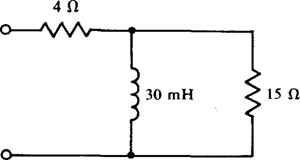
Fig. 15-7
Because a circuit is specified, the power factor and capacitor are probably easier to find using impedance and admittance instead of powers. The power factor is the cosine of the impedance angle. Since the reactance of the inductor is 2π(60)(0.03) = 11.3 Ω, the impedance of the circuit is
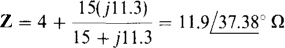
And the power factor is PF = cos 37.38° = 0.795 lagging.
Because the capacitor is to be connected in parallel, the circuit admittance should be used to determine the capacitance. Before the capacitor is added, this admittance is
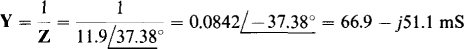
For unity power factor, the imaginary part of the admittance must be zero, which means that the added capacitor must have a susceptance of 51.1 mS. Consequently, its capacitance is
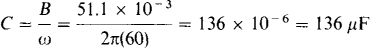
A different capacitor is required for a power factor of 0.85 lagging. The new susceptance can be found from B = G tan (–θ) where G is the conductance, which does not change by adding a parallel capacitor, and θ is the new power factor angle:
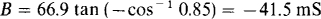
Because the added capacitor provides the change in susceptance, its capacitance is
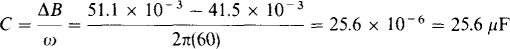
Naturally, less capacitance is required to improve the power factor to 0.85 lagging than to 1.
15.39 An induction motor draws 50 kW at a 0.6 lagging power factor from a 480-V, 60-Hz source. What parallel capacitor will increase the overall power factor to 0.9 lagging? What is the resulting decrease in input current?
The pertinent capacitance formula is
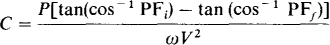
So, here,
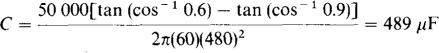
From P = VI × PF, the decrease in input current is
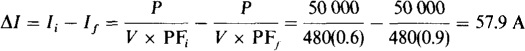
15.40 A factory draws 30 MVA at a 0.7 lagging power factor from a 12 470-V, 60-Hz line. Find the capacitance of the parallel capacitors required to improve the power factor to 0.85 lagging. Also, find the resulting decrease in line current.
The power absorbed by the factor is P = 30(0.7) = 21 MW. So, from the capacitance formula specified in Prob. 15.39, the capacitance required is
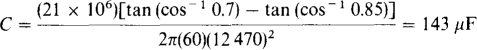
The decrease in line current is equal to the decrease in apparent power divided by the line voltage. The initial apparent power is the specified 30 MVA, and the final apparent power is P/PFf = 21 × 106/0.85 = 24.7 × 106 VA. So,
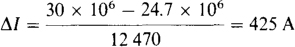
15.41 A 20-MW industrial load supplied from a 12 470-V, 60-Hz line has its power factor improved to 0.9 lagging by the addition of a 230-μF bank of capacitors. Find the power factor of the original load.
The initial reactive power is needed. It is equal to the final reactive power plus that added by the capacitors:
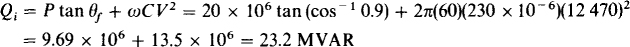
The real power and the initial reactive power can be used to find the initial power factor angle:
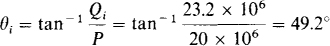
Finally, the initial power factor is PFi = cos θ = cos 49.2° = 0.653 lagging.
15.42 A 480-V, 60-Hz source energizes a load consisting of an induction motor and a synchronous motor. The induction motor draws 50 kW at a 0.65 lagging power factor, and the synchronous motor draws 10 kW at a 0.6 leading power factor. Find the capacitance of the parallel capacitor required to produce an overall power factor of 0.9 lagging.
The required change in reactive power is needed. The initial absorbed reactive power is the sum of that of the two motors, which from Q = P tan θ is
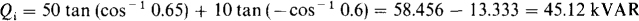
The final reactive power is, from Qf = PT tan (cos–1 PFf),
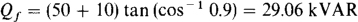
So the change ΔQ in reactive power is ΔQ = 45.12 – 29.06 = 16.1 kVAR and
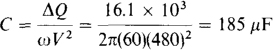
15.43 The instantaneous power absorbed by a circuit is p = 6 + 4 cos2 (2t + 30°) W. Find the maximum, minimum, and average powers absorbed.
Ans. pmax = 10W, Pmin = 6W, P = 8W
15.44 With 170sin(377i + 10°) V applied, a circuit draws 8 sin (377t + 35°) A. Find the power factor and the maximum, minimum, and average powers absorbed.
Ans. PF = 0.906 leading, pmax = 1.3kW, pmin = –63.7W, P = 616W
15.45 For each following load voltage and current pair, find the corresponding power factor and average power absorbed:
(a) v = 170 sin(50t – 40°)V, i = 4.3 sin (50t + 10°) A
(b) v = 340 cos (377t – 50°) V, i = 6.1 sin (377t + 30°) A
(c) v = 679 sin (377t + 40°) V, i = – 7.2 cos (377t + 50°) A
Ans. (a) 0.643 leading, 235 W; (b) 0.985 lagging, 1.02 kW; (c) 0.174 lagging, 424 W
15.46 Find the power factor of a fully loaded 5-hp induction motor that operates at 85 percent efficiency while drawing 15 A from a 480-V line.
Ans. 0.609 lagging
15.47 What is the power factor of a circuit that has an input impedance of 5∠ –25 Ω? Also, what is the power absorbed when 50 V is applied?
Ans. 0.906 leading, 453 W
15.48 If a circuit has an input admittance of 40 + j20 S and an applied voltage of 180 V, what is the power factor and the power absorbed?
Ans. 0.894 leading, 1.3 MW
15.49 A resistor in parallel with an inductor absorbs 25 W when the combination is connected to a 120-V, 60-Hz source. If the total current is 0.3 A, what are the resistance and inductance?
Ans. 576 Ω, 1.47 H
15.50 A coil absorbs 20 W when connected to a 240-V, 400-Hz source. If the current is 0.2 A, find the resistance and inductance of the coil.
Ans. 500 Ω, 0.434 H
15.51 A resistor and series capacitor draw 1 A from a 120-V, 60-Hz source at a 0.6 leading power factor. Find the resistance and capacitance.
Ans. 72 Ω, 27.6 μF
15.52 A resistor and parallel capacitor draw 0.6 A from a 120-V, 400-Hz source at a 0.7 leading power factor. Find the resistance and capacitance.
Ans. 286 Ω, 1.42 μF
15.53 A 100-kW load operates at a 0.6 lagging power factor from a 480-V, 60-Hz line. What current does the load draw? What current does the load draw if it operates at unity power factor instead?
Ans. 347 A, 208 A
15.54 A fully loaded 100-hp induction motor operates at 85 percent efficiency from a 480-V line. If the power factor is 0.65 lagging, what current does the motor draw? If the power factor is 0.9 lagging, instead, what current does this motor draw?
Ans. 281 A, 203 A
15.55 Find the wattmeter reading for the circuit shown in Fig. 15-8.
Fig. 15-8
Ans. 16 W
15.56 Find each wattmeter reading for the circuit shown in Fig. 15-9.
Fig. 15-9
Ans. WM1 = 1.54 kW, WM2 = 656 W
15.57 With 200 sin (754t + 35°) V applied, a circuit draws 456 sin (754f + 15°) mA. What is the reactive factor, and what is the reactive power absorbed?
Ans. 0.342, 15.6 VAR
15.58 With 300 cos (377t – 75°) V applied, a circuit draws 2.1 sin (377f + 70°) A. What is the reactive factor, and what is the reactive power absorbed?
Ans. –0.819, –258 VAR
15.59 What is the reactive factor of a circuit that has an input impedance of 50∠35° Ω? What reactive power does the circuit absorb when the input current is 4 A?
Ans. 0.574, 459 VAR
15.60 What is the reactive factor of a circuit that has an input impedance of 600∠ – 30° Ω? What is the reactive power absorbed when 480 V is applied?
Ans. –0.5, –192 VAR
15.61 When 120 V is applied across a circuit with an input admittance of 1.23∠40° S, what reactive power does the circuit absorb?
Ans. –11.4k VAR
15.62 When 4.1 A flows into a circuit with an input admittance of 0.7 – j1.1 S, what reactive power does the circuit absorb?
Ans. 10.9 VAR
15.63 A load consumes 500 VAR when energized from a 240-V source. If the reactive factor is 0.35, what current does the load draw and what is the load impedance?
Ans. 5.95 A, 40.3∠20.5° Ω
15.64 Two circuit elements in parallel consume 90 VAR when connected to a 120-V, 60-Hz source. If the reactive factor is 0.8, what are the two components and what are their values?
Ans. A 213-Ω resistor and a 0.424-H inductor
15.65 Two circuit elements in series consume –80 VAR when connected to a 240-V, 60-Hz source. If the reactive factor is –0.7, what are the two components and what are their values?
Ans. A 360-Ω resistor and a 7.52-μF capacitor
15.66 A 300-mA, 60-Hz current flows through a 10-μF capacitor. Find the average, peak, and reactive powers absorbed.
Ans. P = 0 W, pmax = 23.9 W, Q = –23.9 VAR
15.67 What are the power components resulting from a 3.6-A current flowing through a load of 50∠ –30° Ω?
Ans. S = 648∠–30° VA, S = 648 VA, P = 561 W, Q = –324 VAR
15.68 Find the power components of a fully loaded 10-hp synchronous motor operating at an 87 percent efficiency and a 0.7 leading power factor.
Ans. S= 12.2∠–45.6°kVA, S = 12.2kVA, P = 8.57 kW, Q = –8.74kVAR
15.69 A load draws 3 A with 75 V applied. If the load power factor is 0.6 lagging, find the power components of the load.
Ans. S = 225∠53.1° VA, S = 225 VA, P = 135 W. Q = 180 VAR
15.70 Find the power components of a load that draws 8.1∠36° A with 480∠10° V applied.
Ans. S = 3.89∠ –26° kVA, S = 3.89 kVA, P = 3.49 kW, Q = –1.7kVAR
15.71 A 120-mH inductor and a parallel 30-Ω resistor draw 6.1 A at 60-Hz. Find the power components.
Ans. S = 930/33.6° VA, S = 930 VA, P = 775 W, Q = 514 VAR
15.72 A fully loaded 15-hp induction motor operates from a 480-V, 60-Hz line at an efficiency of 83 percent and a 0.7 lagging power factor. Find the overall power factor when a 75-∠μF capacitor is placed in parallel with the motor.
Ans. 0.881 lagging
15.73 Two loads are connected in parallel across a 277-V line. One is a fully loaded 5-hp induction motor that operates at an 80 percent efficiency and a 0.7 lagging power factor. The other is a 5-kW resistive heater. Find the overall power factor and line current.
Ans. 0.897 lagging, 38.9 A
15.74 Two loads are connected in parallel across a 12 470-V line. One load takes 23 kVA at a 0.75 lagging power factor and the other load takes 10 kVA at a 0.6 leading power factor. Find the total line current and also the impedance of the combination.
Ans. 1.95 A, 6.39∠17.2°kQ
15.75 Three loads are connected across a 480-V line. One is a fully loaded 10-hp induction motor operating at an 80 percent efficiency and a 0.6 lagging power factor. Another is a fully loaded 5-hp synchronous motor operating at a 75 percent efficiency and a 0.6 leading power factor. The third is a 7-kW resistive heater. Find the total line current and the overall power factor.
Ans. 46 A, 0.965 lagging
15.76 In the circuit shown in Fig. 15-10, load 1 absorbs 6.3 kW and 9.27 kVAR, and load 2 absorbs 5.26 kW and generates 2.17 kVAR. Find the total power components, the source voltage V, and the impedance of each load.
Fig. 15-10
Ans.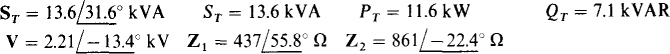
15.77 How much reactive power must be supplied by parallel capacitors to a 50-kVA load with a 0.65 lagging power factor to increase the overall power factor to 0.85 lagging?
Ans. 17.9 kVAR
15.78 An electric motor delivers 50 hp while operating from a 480-V line at an 83 percent efficiency and a 0.65 lagging power factor. If it is paralleled with a capacitor that increases the overall power factor to 0.9 lagging, what is the decrease in line current?
Ans. 40 A
15.79 A load energized from a 480-V, 60-Hz line has a power factor of 0.6 lagging. If placing a 100-μF capacitor across the line raises the overall power factor to 0.85 lagging, find the real power of the load and the decrease in line current.
Ans. 12.2 kW, 12.4 A
15.80 A factory draws 90 A at a 0.75 lagging power factor from a 25 000-V, 60-Hz line. Find the capacitance of a parallel capacitor that will increase the overall power factor to 0.9 lagging.
Ans. 2.85 μF
15.81 A fully loaded 75-hp induction motor operates from a 480-V, 60-Hz line at an 80 percent efficiency and a 0.65 lagging power factor. The power factor is to be raised to 0.9 lagging by placing a capacitor across the motor terminals. Find the capacitance required and the resulting decrease in line current.
Ans. 551μF, 62.2 A
15.82 A load of 50∠60° Ω is connected to a 480-V, 60-Hz source. What capacitor connected in parallel with the load will produce an overall power factor of 0.9 lagging?
Ans. 33.1 μF
15.83 At 400 Hz, what is the power factor of the circuit shown in Fig. 15-11 What capacitor connected across the input terminals causes the overall power factor to be 0.9 lagging?
Fig. 15-11
Ans. 0.77 lagging, 8.06 μF
15.84 For a load energized by a 277-V, 60-Hz source, an added parallel 5-μF capacitor improves the power factor from 0.65 lagging to 0.9 lagging. What is the source current both before and after the capacitor is added?
Ans. 1.17 A, 0.847 A
