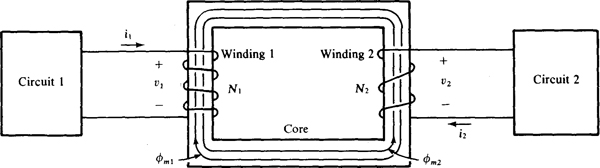
A transformer has two or more windings, also called coils, that are magnetically coupled. As shown in Fig. 16-1, a typical transformer has two windings wound on a core that may be made from iron. Each winding encirclement of the core is called a turn, and is designated by N. Here, winding 1 has N1 = 4 turns and winding 2 has N2 = 3 turns. (Windings of practical transformers have many more turns than these.) Circuit 1, connected to winding 1, is often a source, and circuit 2, connected to winding 2, is often a load. In this case, winding 1 is called the primary winding or just primary, and winding 2 is called the secondary winding or just secondary.

Fig. 16-1
In the operation, current i1 flowing in winding 1 produces a magnetic flux φm1 that, for power transformers, is ideally confined to the core and so passes through or couples winding 2. The m in the subscript means “mutual”—the flux is mutual to both windings. Similarly, current i2 flowing in winding 2 produces a flux φm2 that couples winding 1. When these currents change in magnitude or direction, they produce corresponding changes in the fluxes and these changing fluxes induce voltages in the windings. In this way, the transformer couples circuit 1 and circuit 2 so that electric energy can flow from one circuit to the other.
Although flux is a convenient aid for understanding transformer operation, it is not used in the analyses of transformer circuits. Instead, either transformer turns ratios or inductances are used, as will be explained.
Transformers are very important electrical components. At high efficiencies, they change voltage and current levels, which is essential for electric power distribution. In electronic applications they match load impedances to source impedances for maximum power transfer. And they couple amplifiers together without any direct metallic connections that would conduct dc currents. At the same time they may act with capacitors to filter signals.
In Fig. 16-1 the flux φm1 produced by i1, has a clockwise direction, but φm2 produced by i2 has a counterclockwise direction. The direction of the flux produced by current flowing in a winding can be determined from a version of the right-hand rule that is different from that presented in Chap. 9 for a single wire. As shown in Fig. 16-2, if the fingers of a right hand encircle a winding in the direction of the current, the thumb points in the direction of the flux produced in the winding by the current.
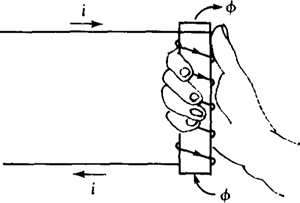
Fig. 16-2
Using dots at winding terminals in agreement with the dot convention is a convenient method for specifying winding direction relations. One terminal of each winding is dotted, with the dotted terminals selected such that currents flowing into the dotted terminals produce adding fluxes. Because these dots specify the transformer winding relations, they are used in circuit diagrams with inductor symbols in place of illustrated windings. A transformer circuit diagram symbol consists of two adjacent inductor symbols with dots. If the winding relations are not important, the dots may be omitted.
Figure 16-3 shows the use of dots. In a circuit diagram, the more convenient transformer representation with dots in Fig. 16-3b is used instead of the one with windings in Fig. 16-3a. But both are equivalent. An actual transformer may have some marking other than dots. In Fig. 16-3b, the two vertical lines between the inductor symbols designate the transformer as either an iron-core transformer or an ideal transformer, which is considered next.
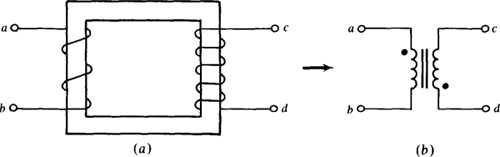
Fig. 16-3
In most respects, an ideal transformer is an excellent model for a transformer with an iron core—an iron-core transformer. Power transformers, the transformers used in electric power distribution systems, are iron-core transformers. Being a model, an ideal transformer is a convenient approximation of the real thing. The approximations are zero winding resistance, zero core loss, and infinite core permeability. Having windings of zero resistance, an ideal transformer has no winding ohmic power loss (I2R loss) and no resistive voltage drops. The second property, zero core loss, means that there is no power loss in the core—no hysteresis or eddy-current losses. And since there is no power loss in the windings either, there is no power loss in the entire ideal transformer—the power out equals the power in. The third and last feature, infinite core permeability, means that no current is required to establish the magnetic flux to produce the induced voltages. It also means that all the magnetic flux is confined to the core, coupling both windings. All flux is mutual, and there is no leakage flux, which is flux that couples only one winding.
In the analysis of a circuit containing an ideal transformer, the transformer turns ratio, also called transformation ratio, is used instead of flux. The turns ratio, with symbol a, is a = N1/N2. This is the ratio of the number of primary turns to secondary turns. In many electric circuits books, however, this ratio is defined as the number of secondary turns to primary turns, and sometimes the symbol n or N is used.
In a circuit diagram, the turns ratio of an iron-core or ideal transformer is specified over the transformer symbol by a designation such as 20:1, which means that the winding on the left of the vertical bars has 20 times as many turns as the winding on the right. If the designation were 1:25, instead, the winding on the right would have 25 times as many turns as the winding on the left.
The turns ratio is convenient because it relates the winding voltages. By Faraday’s law, v1 = ±N1d(φ)/dt and v2 = ±N2d(φ)/dt. (The same flux φ is in both equations because an ideal transformer has no leakage flux.) The ratio of these equations is
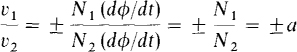
The positive sign must be selected when both dotted terminals have the same reference voltage polarity. Otherwise the negative sign must be selected. The justification for this selection is that, as can be shown by Lenz's law, at any one time the dotted terminals of an ideal transformer always have the same actual polarities—either both positive or both negative with respect to the other terminals. Incidentally, these actual polarities have nothing to do with the selection of voltage reference polarities, which is completely arbitrary.
It is obvious from v1/v2 = ±a that if a transformer has a turns ratio less than one (a < 1), the secondary rms voltage is greater than the primary rms voltage. Such a transformer is called a step-up transformer. But if the turns ratio is greater than one (a > 1), the secondary rms voltage is less than the primary rms voltage, and the transformer is called a step-down transformer.
As can be shown from the property of infinite permeability, or from zero power loss, the primary and secondary currents have a relation that is the inverse of that for the primary and secondary voltages. Specifically,
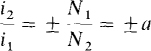
The positive sign must be selected if one current reference is into a dotted terminal and the other current reference is out of a dotted terminal. Otherwise the negative sign must be selected. The reason for this selection is that, at any one time, actual current flow is into the dotted terminal of one winding and out of the dotted terminal of the other. So, only the specified selection of signs will give the correct signs for the currents. But this selection of signs has nothing to do with the selection of current reference directions, which is completely arbitrary.
It is important to remember that the winding with the greater number of turns has more voltage but less current.
In the analysis of a circuit containing ideal transformers, a common approach is to eliminate the transformers by reflecting impedances and, if necessary, sources. This approach applies only if there are no current paths between the primary and secondary circuits, as is usually the case. For an understanding of this reflecting approach, consider the circuit shown in Fig. 16-4a. The impedance Zr “looking into” the primary winding, is called the reflected impedance, which is the turns ratio squared times the secondary circuit impedance Z2. If Zr replaces the primary winding, as shown in Fig. 16-4b, the primary current I1 is unchanged. As can be proven by trying all different dot arrangements, the dot locations have no effect on this reflected impedance.
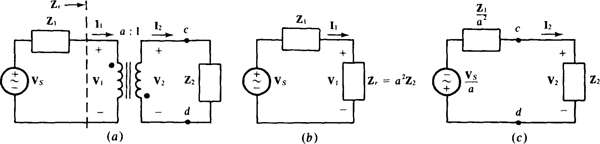
Fig. 16-4
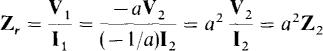
So if the primary circuit voltages and currents are of interest, the transformer can be eliminated by replacing the transformer primary winding with the reflected impedance of the secondary circuit, assuming this circuit contains no independent sources. The resulting primary circuit can be analyzed in the usual manner. Then if the secondary winding voltage and current are also of interest, they can be obtained from the primary winding voltage and current.
If the secondary circuit is not a lumped impedance, but a circuit with individual resistive and reactive components, the total impedance can be found and reflected. Alternatively, the whole secondary circuit can be reflected into the primary circuit. In this reflection, the circuit configuration is kept the same and each individual impedance is multiplied by the square of the turns ratio. Of course, the transformer is eliminated.
Reflection can also be from the primary to the secondary. To see this, consider making cuts at terminals c and d in the circuit shown in Fig. 16-4a and finding the Thévenin equivalent of the circuit to the left. Because of the open circuit created by the cuts, the secondary current is zero: I2 = 0 A, which in turn means that the primary current is zero: I1 = 0 A. Consequently, there is 0 V across Z1 and all the source voltage is across the primary winding. As a result, the Thévenin voltage referenced positive toward terminal c is VTh = V2 = –V1/a = – Vs/a. From impedance reflection the Thévenin impedance is ZTh = Z1/a2, with a2 being in the denominator instead of the numerator because the winding being “looked into” is the secondary winding. The result is shown in the circuit of Fig. 16-4c. Note that the source voltage polarity reverses because the dots are at opposite ends of the windings. By use of Norton's theorem in a similar way, it can be shown that a source of current Is would have reflected into the secondary as aIs and would have been reversed in direction because the dots are not at the same ends of the windings. Whole circuits can be reflected in this way.
An alternative to the reflection analysis approach is to write the circuit equations, which are usually mesh equations, with the transformer voltages and currents as variables. Since the number of unknowns will exceed the number of equations, these equations must be augmented with the transformer voltage and current turns-ratio equations. As an illustration, for the circuit of Fig. 16-4a, these equations are
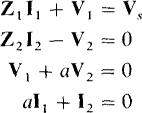
The fact that this approach requires more equations than does the reflection approach is not a significant disadvantage if an advanced scientific calculator is used in the calculations, and this approach may be easier overall.
For ac voltages and currents, an ideal transformer gives results that are within a few percent of those of the corresponding actual power transformer. But for dc voltages and currents, an ideal transformer gives incorrect results. The reason is that an ideal transformer will transform dc voltages and currents while an actual transformer will not.
The ideal transformer approximation is not valid for a transformer with a core constructed of nonmagnetic material, as may be required for operation at radio and higher frequencies. A transformer with such a core is often called an air-core transformer or a linear transformer.
Figure 16-5 shows two circuits coupled by an air-core transformer. Current i1 produces a mutual flux (φ)m1 and a leakage flux φi1, and current i2 produces a mutual flux φm2 and leakage flux φi2. As mentioned, a mutual flux couples both windings, but a leakage flux couples only one winding.
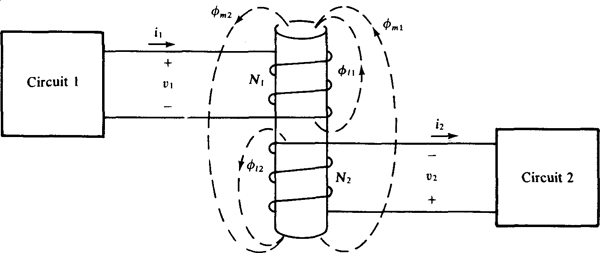
Fig. 16-5
The coefficient of coupling, with symbol k, indicates the closeness of coupling, which in turn means the fraction of total flux that is mutual. Specifically,
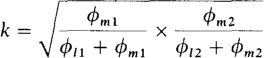
Clearly k cannot have a value greater than 1 or less than 0. And the greater each fraction of mutual flux, the greater the coefficient of coupling. The coefficient of coupling of a good power transformer is very close to 1, but an air-core transformer typically has a coefficient of coupling less than 0.5.
The voltages induced by changing fluxes are given by Faraday's law:

The positive signs in ±φm2 and. ±φm1 are selected if and only if both mutual fluxes have the same direction in each winding.
For circuit analysis, it is better to use inductances instead of fluxes. The self-inductances of the windings are

These are just the ordinary winding inductances as defined in Chap. 9. There is, however, another inductance called the mutual inductance with symbol M. It accounts for the flux linkages of one winding caused by current flow in the other winding. Specifically,
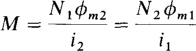
With these substitutions, the voltage equations become
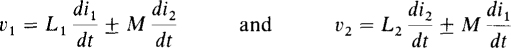
in which the ± signs for the L di/dt terms have been deleted because of the assumption of associated voltage and current references. For a sinusoidal analysis the corresponding equations are
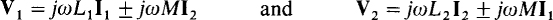
In these equations, the negative signs of ± are used if one current has a reference into a dotted terminal and the other has a reference out of a dotted terminal. Otherwise the positive signs are used. Put another way, if positive i1 and i2 or I1 and I2 produce adding mutual fluxes, then the L and M terms add. As mentioned, these equations are based on associated voltage and current references. If a pair of these references are not associated, the v or V of the corresponding equation should have a negative sign. Everything else, though, remains the same.
In a time-domain circuit diagram the self-inductances are specified adjacent to the corresponding windings in the usual manner. The mutual inductances are specified with arrows to designate which pair of windings each mutual inductance is for. In a phasor-domain circuit, of course, jωL1, jωL2, and jωM are used instead of L1 L2, and M.
If substitutions are made for the fluxes in the coefficient of coupling equation, the result is k = 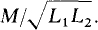
Mesh and loop analyses are best for analyzing circuits containing air-core transformers since nodal analysis is difficult to use. Writing the KVL equations is the same as for other circuits except for the necessity of including the jω MI terms resulting from the magnetic coupling. Also, voltage variables are not assigned to the windings.
If the secondary circuit contains no independent sources and no current paths to the primary circuit, it is possible to reflect impedances in a manner similar to that used for ideal transformers. For an understanding of this reflection, consider the circuit shown in Fig. 16-6. The mesh equations are
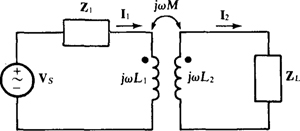
Fig. 16-6
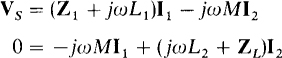
The mutual terms are negative in both equations because one winding current is referenced into a dotted terminal while the other is referenced out of a dotted terminal. If I2 is solved for in the second equation and a substitution made for I2 in the first equation, the result is
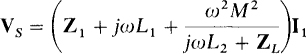
which indicates that the secondary circuit reflects into the primary circuit as an impedance ω2M2/(jωL2 + ZL) in series with the primary winding. As can be found by trying different dot locations, this impedance does not depend on those locations. Some authors of circuits books call this impedance a “reflected impedance.” Others, however, use the term “coupled impedance.”
An autotransformer is a transformer with a single winding that has an intermediate terminal that divides the winding into two sections. For an understanding of autotransformer operation, it helps to consider the two sections of the winding to be the two windings of a power transformer, as is done next.
Consider a 50-kVA power transformer that has a voltage rating of 10 000/200 V. From the kVA and voltage ratings, the full-load current of the high voltage winding is 50 000/10 000 = 5 A and that of the low voltage winding is 50 000/200 = 250 A. Figure 16-7a shows such a transformer, fully loaded, with its windings connected such that the dotted end of one winding is connected to the undotted end of the other. As shown, the 10 000-V secondary circuit can be loaded to a maximum of 250 + 5 = 255 A without either of the windings being current overloaded. Since the source current is 250 A, the transformer can deliver 10 200 × 250 = 2550 kVA. This can also be determined from the secondary circuit: 10 000 × 255 = 2550 kVA. In effect, the autotransformer connection has increased the transformer kVA rating from 50 to 2550 kVA.
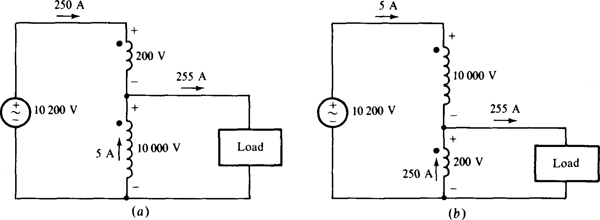
Fig. 16-7
The explanation for this increase is that the original 50-kVA transformer had no metallic connections between the two windings, and so the 50 kVA of a full load had to pass through the transformer by magnetic coupling. But with the windings connected to provide autotransformer operation, there is a metallic connection between the windings that passes 2550 — 50 = 2500 kVA without being magnetically transformed. So, it is the direct metallic connection that provides the kVA increase. Although advantageous in this respect, such a connection destroys the isolation property that conventional transformers have, which in turn means that autotransformers cannot be used in every transformer application.
If the windings are connected as in Fig. 16-7b, the kVA rating is just 10 200 × 5 = 200 × 255 = 51 kVA. This slight increase of 2 percent in kVA rating is the result of the greatly different voltage levels of the two circuits connected to the autotransformer. In general, the closer the voltage levels are to being the same, the greater the increase in kVA rating. This is why autotransformers are used as links between power systems usually only if the systems are operating at nearly the same voltage levels.
In Fig. 16-7a, the load and the voltage source can be interchanged. Then the load is connected across both windings and the voltage source across just one. This arrangement is used when the load voltage is greater than the source voltage. The increase in kVA rating is the same.
In the analysis of a circuit containing an autotransformer, an ideal transformer model can be assumed, and its turns ratio used in much the same way as for a conventional transformer connection. Along with this can be used the fact that the lines with the lower voltage carry the sum of the two winding currents. Also, part of the winding carries only the difference of the source and load currents. This is the part that is common to both the source and load circuits.
Contrary to what Fig. 16-7 suggests, autotransformers are preferably purchased as such and not constructed from conventional power transformers. An exception, however, is the “buck and boost” transformer. A typical one can be used to reduce 120 or 240 V to 12 or 24 V. The principal use, though, is as an autotransformer with the primary and secondary interconnected to give a slight adjustment in voltage, either greater or lesser.
PSpice does not have a built-in ideal transformer component, but a model for one can be constructed with dependent sources. To see how to do this, consider the ideal transformer of Fig. 16-8a. There are, of course, just two constraints on its operation: v1 = –av2 and i2 = yai1, as obtained from the turns ratio and also the dot locations. As shown in Fig. 16-8b, and also in Fig. 16-8c, these constraints can be satisfied with two dependent sources: a voltage-controlled voltage source to obtain the voltage constraint and a current-controlled current source to obtain the current constraint. Also needed is a dummy voltage source to sense the controlling current. Naturally, if the dot locations are at the same ends of the windings, instead of opposite ends as in Fig. 16-8a, the polarity of the dependent voltage source and the current direction of the dependent current source must be reversed.
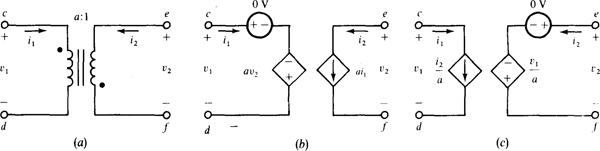
Fig. 16-8
PSpice does provide for an air-core transformer. Self-inductance statements are used for the two windings in the same manner as for ordinary inductors. The ordering of the node numbers informs PSpice of the dot locations, with the first node being at the dot location. The only other requirement is a coefficient of coupling statement that has a name beginning with the letter K. Following this name are the names of the two coupled inductors, in either order. Last is the coefficient of coupling. For example, the following statements could be used for the air-core transformer of Fig. 16-9.
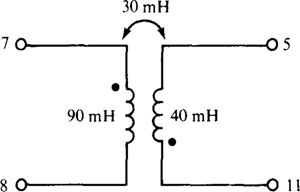
Fig. 16-9

The indicated coefficient of coupling of 0.5 is obtained from 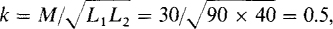 where the inductances are expressed in millihenries.
where the inductances are expressed in millihenries.
16.1 For the winding shown in Fig. 16-10a, what is the direction of flux produced in the core by current flowing into terminal a?
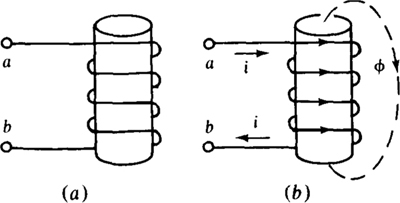
Fig. 16-10
Current that flows into terminal a flows over the core to the right, underneath to the left, then over the core to the right again, and so on, as is shown in Fig. 16-10b. For the application of the right-hand rule, fingers of a right hand should be imagined grasping the core with the fingers directed from left to right over the core. Then the thumb will point up, which means that the direction of the flux is up inside the core.
16.2 Supply the missing dots for the transformers shown in Fig. 16-11.
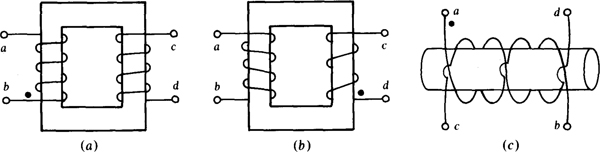
Fig. 16-11
(a) By the right-hand rule, current flowing into dotted terminal b produces clockwise flux. By trial and error it can be found that current flowing into terminal c also produces clockwise flux. So, terminal c should have a dot.
(b) Current flowing into dotted terminal d produces counterclockwise flux. Since current flowing into terminal b also produces counterclockwise flux, terminal b should have a dot.
(c) Current flowing into dotted terminal a produces flux to the right inside the core. Since current flowing into terminal d also produces flux to the right inside the core, terminal d should have a dot.
16.3 What is the turns ratio of a transformer that has a 684-turn primary winding and a 36-turn secondary winding?
The turns ratio a is the ratio of the number of primary turns to secondary turns: a = 684/36 = 19.
16.4 Find the turns ratio of a transformer that transforms the 12 470 V of a power line to the 240 V supplied to a house.
Since the high-voltage winding is connected to the power lines, it is the primary. The turns ratio is equal to the ratio of the primary to secondary voltages: a = 12 470/240 = 51.96.
16.5 What are the full-load primary and secondary currents of a 25 000/240-V, 50-kVA transformer? Assume, of course, that the 25 000-V winding is the primary.
The current rating of a winding is the transformer kVA rating divided by the winding voltage rating. So, the full-load primary current is 50 000/25 000 = 2 A, and the full-load secondary current is 50 000/240 = 208 A.
16.6 A power transformer with a voltage rating of 12 500/240 V has a primary current rating of 50 A. Find the transformer kVA rating and the secondary current rating if the 240 V is the secondary voltage rating.
The transformer has a kVA rating that is equal to the product of the primary voltage rating and the primary current rating: 12 500(50) = 625 000 VA = 625 kVA. Since this is also equal to the product of the secondary voltage and current ratings, the secondary current rating is 625 000/240 = 2.6 × 103 A = 2.6 kA. As a check, the secondary current rating is equal to the primary current rating times the turns ratio, which is a = 12 500/240 = 52.1. So the secondary current rating is 52.1(50) = 2.6 × 103A = 2.6kA, which checks.
16.7 A transformer has a 500-turn winding linked by flux changing at the rate of 0.4 Wb/s. Find the induced voltage.
If the polarity of the voltage is temporarily ignored, then by Faraday's law, v = N dφ/dt. The quantity dφ/dt is the time rate of change of flux, which is specified as 0.4 Wb/s. So, v = 500(0.4) = 200 V; the magnitude of the induced voltage is 200 V. The voltage polarity can be either positive or negative depending on the voltage reference polarity, the direction of the winding, and the direction in which the magnetic flux is either decreasing or increasing, none of which are specified. So the most that can be determined is that the magnitude of the induced voltage is 200 V at the time that the flux is changing at the rate of 0.4 Wb/s.
16.8 An iron-core transformer has 400 primary turns and 100 secondary turns. if the applied primary voltage is 240 V rms at 60 Hz, find the secondary rms voltage and the peak magnetic flux.
Since the transformer has an iron core, the turns ratio can be used to find the secondary rms voltage: V2 = (1/a)V1 = (100/400)(240) = 60 V rms. Because the voltages vary sinusoidally, they are induced by a sinusoidally varying flux that can be considered to be φ = φm sin ωt, where φm is the peak value of flux and ω is the radian frequency of ω = 2π(60) = 377 rad/s. The time rate of change of flux is dφ/dt = d(φm sin ωt)/dt = ωφm cos ωt, which has a peak value of wφm. Since the peak voltage is 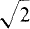 Vrms it follows from v = N dφ/dt that the peak voltage and flux values are related by
Vrms it follows from v = N dφ/dt that the peak voltage and flux values are related by 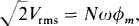 If φm is solved for and primary quantities used, the result is
If φm is solved for and primary quantities used, the result is
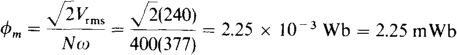
Alternatively, the secondary voltage and turns could have been used since the same flux is assumed to couple both windings.
Incidentally, from 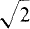 Vrms = N ωφm, the voltage Vrms can be expressed as
Vrms = N ωφm, the voltage Vrms can be expressed as
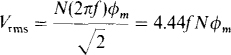
This is called the general transformer equation.
16.9 If a 50-turn transformer winding has a 120-V rms applied voltage, and if the peak coupling flux is 20 mWb, find the frequency of the applied voltage.
From rearranging the general transformer equation defined in Prob. 16.8,
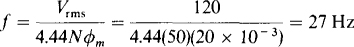
16.10 An iron-core transformer has 1500 primary turns and 500 secondary turns. A 12-Ω resistor is connected across the secondary winding. Find the resistor voltage when the primary current is 5 A.
Since no voltage or current references are specified, only rms values are of interest and are to be assumed without specific mention of them. The secondary current is equal to the turns ratio times the primary current: (1500/500)(5) = 15 A. When this current flows through the 12-ω resistor, it produces a voltage of 15(12)= 180 V.
16.11 The output stage of an audio system has an output resistance of 2 kΩ. An output transformer provides resistance matching with a 6-Q speaker. If this transformer has 400 primary turns, how many secondary turns does it have?
The term “resistance matching” means that the output transformer presents a reflected resistance of 2 kΩ to the output audio stage so that there is maximum power transfer to the 6-Ω speaker. Since, in general, the reflected resistance Rr is equal to the turns ratio squared times the resistance RL of the load connected to the secondary (Rr = a2RL), the turns ratio of the output transformer is
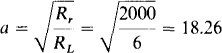
and the number of secondary turns is
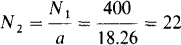
16.12 In the circuit shown in Fig. 16-12, find R for maximum power absorption. Also, find I for R = 3 Ω. Finally, determine if connecting a conductor between terminals d and f would change these results.
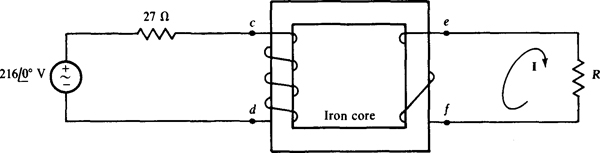
Fig. 16-12
The value of R for maximum power absorption is that value for which the reflected resistance a2R is equal to the source resistance of 27 Ω. Since the primary winding has 4 turns, and the secondary winding has 2 turns, the turns ratio is a = N1/N2 = 4/2 = 2. And, from 27 = 22R, the value of R for maximum power absorption is R = 27/4 = 6.75 Ω
For R = 3 Ω, the reflected resistance is 22(3) = 12 Ω. So the primary current directed into terminal c is 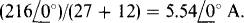 If terminal c is dotted, then terminal e should be dotted, as is evident from the right-hand rule. And, since I is directed out of terminal e while the calculated current is into terminal c, I is just the turns ratio times the current entering terminal c:
If terminal c is dotted, then terminal e should be dotted, as is evident from the right-hand rule. And, since I is directed out of terminal e while the calculated current is into terminal c, I is just the turns ratio times the current entering terminal c: 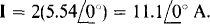
A conductor connected between terminals d and f does not affect these results since current cannot flow in a single conductor. For current to flow there would have to be another conductor to provide a return path.
16.13 Find i1, i2, and i3 for the circuit shown in Fig. 16-13. The transformers are ideal.
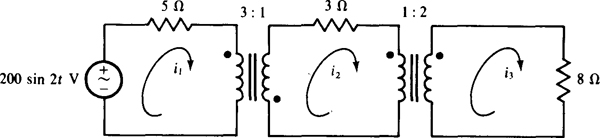
Fig. 16-13
A good procedure is to find i1 using reflected resistances, then find i2 from i1, and last find i3 from i2. The 8 Ωreflects into the middle circuit as 8/22 = 2 Ω, making a total resistance of 2 + 3 = 5 Ω in the middle circuit. This 5 Ω reflects into the source circuit as 32(5) = 45 Ω. Consequently,
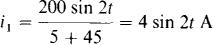
Because i 1 and i2 both have reference directions into dotted terminals of the first transformer, i2 is equal to the negative of the turns ratio times i1: i2 = – 3(4 sin 2t) = – 12 sin 2t A. Finally, since i2 has a reference direction into a dotted terminal of the second transformer, and i3 has a reference direction out of a dotted terminal of this transformer, i3 is equal to the turns ratio (1/2 = 0.5) times i2: i3 = 0.5(– 12 sin 2t) = 6 sin 2t A.
16.14 Find I1 and I2 for the circuit shown in Fig. 16-14.
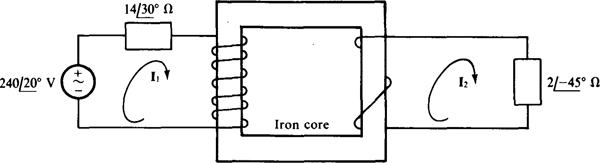
Fig. 16-14
Because the primary has 6 turns and the secondary has 2 turns, the turns ratio is a = 6/2 = 3 and so the impedance reflected into the primary circuit is 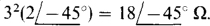 Thus,
Thus,
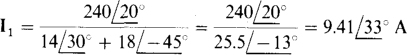
If the upper primary terminal is dotted, the bottom secondary terminal should be dotted. Then both I1 and I2 will be referenced into dots, and so I2 is equal to the negative of the turns ratio times I1:
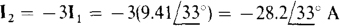
16.15 Find I1 and I2 for the circuit shown in Fig. 16-15a.
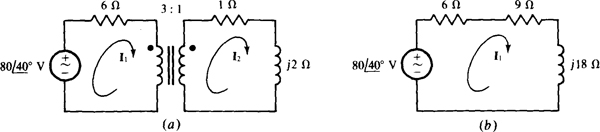
Fig. 16-15
The 1-Ω resistance and the j2-Ω inductive impedance in the secondary circuit reflect into the primary circuit as 32(1) = 9Ω and 32(j2)=j18Ω in series with the 6-Ω resistance, as shown in Fig. 16-15b. In
effect, these reflected elements replace the primary winding. From the simplified circuit, the primary current is
Because I1 is referenced into a dotted terminal and I2 is referenced out of a dotted terminal, I2 is equal to just the turns ratio times It (no negative sign):
16.16 Find Il5 I2, and I3 for the circuit shown in Fig. 16-16a.
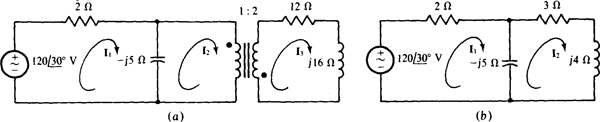
Fig. 16-16
The 12-Ω resistance and the j16-Ω inductive impedance reflect into the primary circuit as a (1/2)2(12) = 3-Ω resistance and a series (1/2)2(j16) = j4-Ω inductive impedance in parallel with the –j5-Ω capacitive impedance, as shown in Fig. 16-16b. The impedance of the parallel combination is
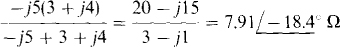
So,

By current division,
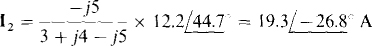
Finally, since I2 and I3 both have reference directions into dotted terminals, I3 is equal to the negative of the turns ratio times I2:
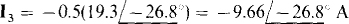
16.17 Find V for the circuit shown in Fig. 16-17a.
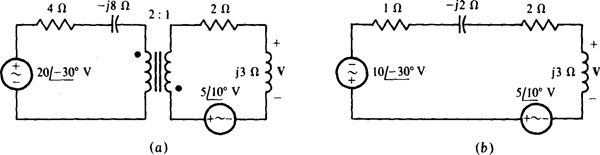
Fig. 16-17
Although reflection can be used, a circuit must be reflected instead of just an impedance because each circuit has a voltage source. And, because a voltage in the secondary circuit is desired, it is slightly preferable to reflect the primary circuit into the secondary. Of course, each reflected impedance is (1/a)2 times the original impedance, and the voltage of the reflected voltage source is 1/a times the original voltage. Also, the polarity of the reflected voltage source is reversed because the dots are located at opposite ends of the windings. The result is shown in Fig. 16-17b. By voltage division,
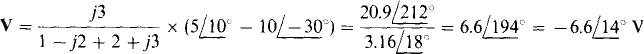
16.18 Use PSpice to determine V in the circuit of Fig. 16-17a of Prob. 16.17.
Figure 16-18 shows the corresponding PSpice circuit for a frequency of ω = 1 rad/s. Following is the circuit file and the answers obtained from the output file when this circuit file is run with PSpice. The answer of 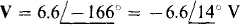 agrees with the answer obtained in the solution to Prob. 16.17.
agrees with the answer obtained in the solution to Prob. 16.17.
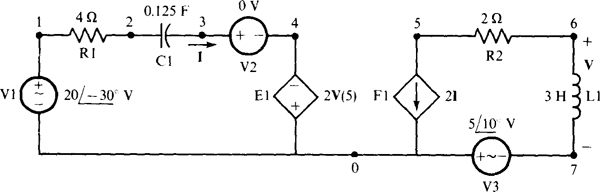
Fig. 16-18
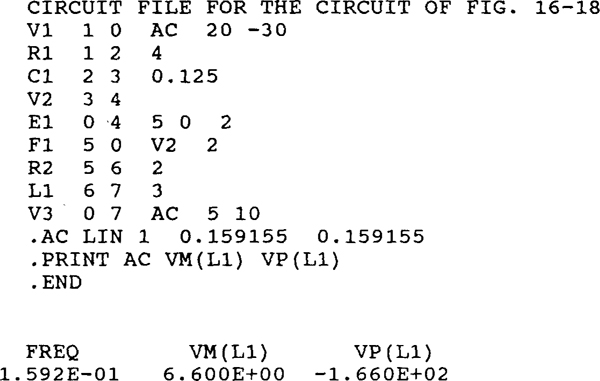
16.19 Find I1 and I2 in the circuit of Fig. 16-19.
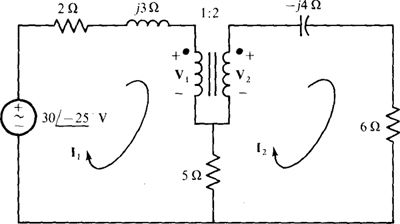
Fig. 16-19
Because the 5-Ω resistor directly couples both halves of the circuit, the reflection approach cannot be used. However, two mesh equations can be written, and then these equations augmented with the voltage and current transformer equations to obtain four equations in terms of four unknowns:
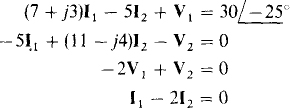
In matrix form, these equations are
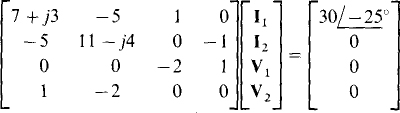
A scientific calculator can be used to solve for I1 and I2. The results are I1 = 5.821 ∞–47.83° A and I2 = 2.910∞–47.83° A.
16.20 Repeat Prob. 16.19 using PSpice.
Figure 16-20 is the PSpice circuit corresponding to the circuit of Fig. 16-19, with the inductor and capacitor values based on a frequency of w = 1 rad/s. Resistor R4 is inserted to prevent a capacitor (Cl) from being in series with a current source (Fl), since PSpice does not allow this. But the resistance of R4 is so large that the presence of this resistor will not significantly affect the answer. Dummy voltage source V2 is inserted, of course, to sense the controlling current for dependent current source Fl.
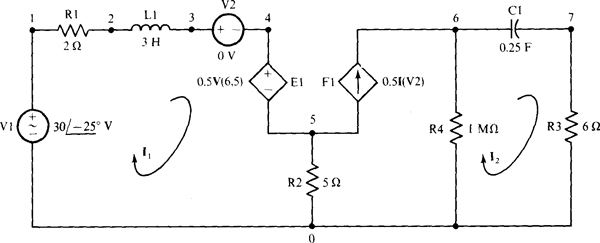
Fig. 16-20
Following is the corresponding circuit file along with the answers obtained from the output file when the circuit file is run with PSpice. The answers of 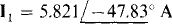 and
and 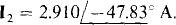 agree with the answers obtained in the solution to Prob. 16.19.
agree with the answers obtained in the solution to Prob. 16.19.

16.21 Determine the branch currents I1 I2, and I3 in the circuit of Fig. 16-21.
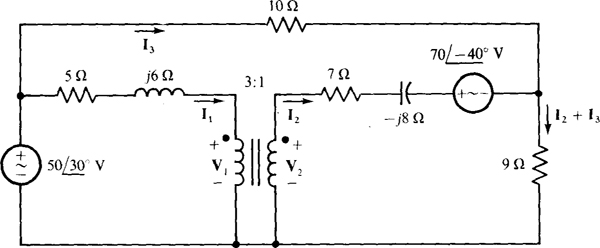
Fig. 16-21
Reflection cannot be used here because of the presence of the 10-Q resistor that along with the common ground provides a current path between the two winding circuits. For reflection to be applicable, the two windings must be only magnetically coupled. KVL can, however, be applied, and is best done around the two winding meshes and the outside loop. The resulting three equations will contain five variables, and must be augmented with the voltage and current transformer equations. These five equations are
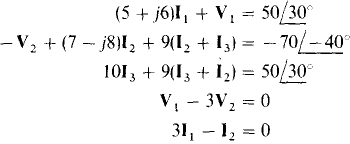
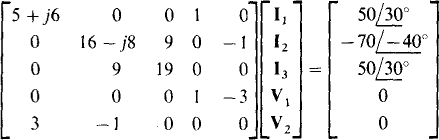
If a scientific calculator is used to obtain solutions, the results are 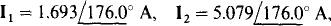 and
and 
16.22 Repeat Prob. 16.21 using PSpice.
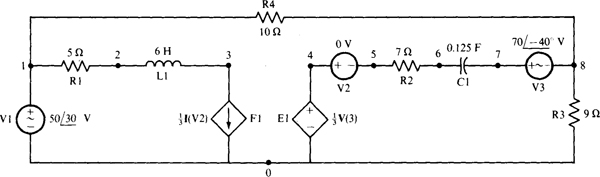
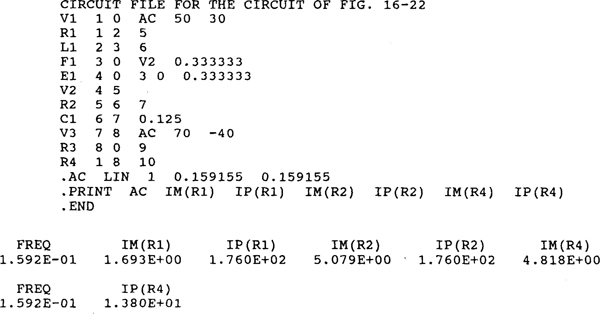
Fig. 16-22
Figure 16-22 shows the PSpice circuit corresponding to the circuit of Fig. 16-21. The inductor and capacitor values are based on a frequency of ω = 1 rad/s. A dummy voltage source V2 has been inserted to sense the controlling current for the dependent current source Fl. Following is the corresponding circuit file along with the answers obtained from the output file when this circuit file is run with PSpice. The answers agree with those obtained in the solution to Prob. 16.21.
16.23 An air-core transformer has primary and secondary currents of i1 = 0.2 A and i2 = 0.4 A that produce fluxes of φm1 = 100 μμb, φl 1 = 250 wWb, and φl2 = 300 μWb. Find φm2, M, L1, L2, and k if N1 = 25 turns and N2 = 40 turns.
By the mutual inductance formulas,
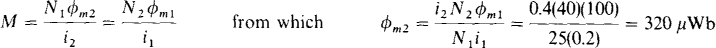
Also
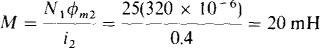
From the self-inductance formulas,
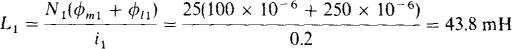
and
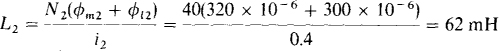
The coefficient of coupling is
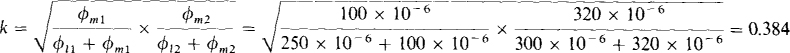
Alternatively,
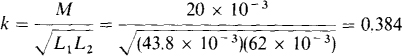
16.24 What is the greatest mutual inductance that an air-core transformer can have if its self-inductances are 0.3 and 0.7 H?
From 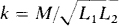 rearranged to
rearranged to 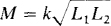 and the fact that k has a maximum value of 1,
and the fact that k has a maximum value of 1, 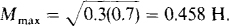
16.25 For each of the following, find the missing quantity—either self-inductance, mutual inductance, or coefficient of coupling:
(a) L1 = 0.3 H, L2 = 0.4 H, M = 0.2 H
(b) L1 = 4 mH, M = 5 mH, k = 0.4
(c) L1 = 30 μH, L2 = 40μH, K= 0.5
(d) L2 = 0.4 H, M = 0.2 H, K = 0.2
(a) 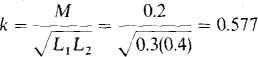
(b) 
(c) 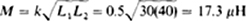
(d) 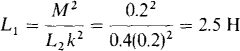
16.26 An air-core transformer has an open-circuited secondary winding with 50 V across it when the primary current is 30 mA at 3 kHz. If the primary self-inductance is 0.3 H, find the primary voltage and the mutual inductance.
Since phasors are not specified or mentioned, presumably the electric quantities specified and wanted are rms. Because the secondary is open-circuited, I2 = 0 A, which means that to ωMI2 = 0 and ωL2I2 = 0 in the voltage equations. So, the rms primary voltage is
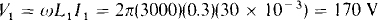
Also, the secondary voltage equation is V2 = ωMIi, from which
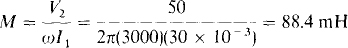
16.27 An air-core transformer has an open-circuited secondary with 80 V across it when the primary carries a current of 0.4 A and has a voltage of 120 V at 60 Hz. What are the primary self-inductance and also the mutual inductance?
Because the secondary is open-circuited, there is no current in this winding and so no mutually induced voltage in the primary winding. As a consequence, the rms voltage and current of the primary are related by the primary winding reactance: ωL1 = V1/I1 from which
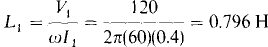
With the open-circuited secondary carrying zero current, the voltage of this winding is solely the mutually induced voltage: V2 = ωMI1, from which
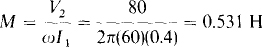
16.28 Find the voltage across the open-circuited secondary of an air-core transformer when 35 V at 400 Hz is applied to the primary. The transformer inductances are L1 = 0.75 H, L2 = 0.83 H, and M = 0.47 H.
Because the secondary is open-circuited, I2 = 0 A, which means that the rms primary voltage is V1 = ωL1Ii and the rms secondary voltage is V2 = ωMI1. The ratio of these equations is

16.29 An air-core transformer with an open-circuited secondary has inductances of L1 = 20mH, L2 = 32 mH, and M = 13 mH. Find the primary and secondary voltages when the primary current is increasing at the rate of 0.4 kA/s.
With the assumption of associated references,
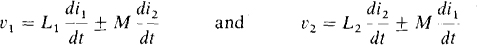
In the first equation, di2/dt is zero because of the open circuit, and di1/dt is the specified 0.4 kA/s. So, v1 =(20 × 103)(0.4 × 103) = 8 V. Similarly, the secondary voltage is v2=±Mdi,tdt = ±(13 × 10-3)(0.4 × 103) = ±5.2 V. Since the reference for v2 is not specified, the sign of v2 cannot be determined.
16.30 A transformer with a short-circuited secondary has inductances of Ll = 0.3 H, L2 = 0.4 H, and M = 0.2 H. Find the short-circuit secondary current I2 when the primary current is I1 = 0.5 A at 60 Hz.
V2 = j ω L2I2 ± j ω MI1 = 0 from which jωL2I2 = ±jωMIl and L2I2 = ±MI1
Since only rms quantities are of interest, as must be assumed from the problem specification, the angles of I1 and I2 can be neglected and the + sign of ± used, giving L2I2 = MI1. From this, the short-circuit secondary current I2 is
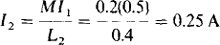
The same result would have been obtained by dividing ωMIt, the rms induced generator voltage, by ω)L2, the reactance that the short-circuit secondary current I2 flows through.
16.31 When connected in series, two windings of an air-core transformer have a total inductance of 0.4 H. With the reversal of the connections to one winding, though, the total inductance is 0.8 H. Find the mutual inductance of the transformer.
Because the windings are in series, the same current i’ flows through them during the inductance measurement, producing a voltage drop of L1 di/dt ± M di/dt = (L1 ± M) di/dt in one winding and a voltage drop of L2 di/dt ± M di/dt = (L2 + M) di/dt in the other. If the windings are arranged such that i flows into the dotted terminal of one winding but out of the dotted terminal of the other, both mutual terms are negative. But if i flows into both dotted terminals or out of them, both mutual terms are positive. Since the M di/dt terms have the same sign, either both positive or both negative, the total voltage drop is (L1 + L2 ± 2M) di/dt. The L1 + L2 ± 2M coefficient of di/dt is the total inductance. Obviously, the larger measured inductance must be for the positive sign, L1 + L2 + 2M = 0.8 H, and the smaller measured inductance must be for the negative sign, L1 + L 2 – 2M = 0.4 H. if the second equation is subtracted from the first, the result is

from which 4M = 0.4 and M = 0.1 H.
Consequently, a method for finding the mutual inductance of an air-core transformer is to connect the two windings in series and measure the total inductance, then reverse one winding connection and measure the total inductance. The mutual inductance is one-fourth of the difference of the larger measurement minus the smaller measurement. Obviously, the self-inductance of a winding can be measured directly if the other winding is open-circuited.
16.32 An air-core transformer has 3-mH mutual inductance and a 5-mH secondary self-inductance. A 5-Ω resistor and a 100-μF capacitor are in series with the secondary winding. Find the impedance coupled into the primary for ω = 1 krad/s.
The coupled impedance is (ωM)2/Z2, where Z2 is the total impedance of the secondary circuit. Here, ωM = 103(3 × 10–3) = 3 μ. and
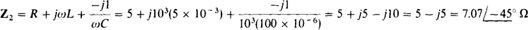
and so the coupled impedance is
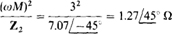
Notice that the capacitive secondary impedance couples into the primary circuit as an inductive impedance. This change in the nature of the impedance always occurs on coupling because the secondary circuit impedance is in the denominator of the coupling impedance formula. In contrast, there is no such change in reflected impedance with an ideal transformer.
16.33 A l-kΩ resistor is connected across the secondary of a transformer for which L1 = 0.1 H, L2 = 2 H, and k = 0.5. Find the resistor voltage when 250 V at 400 Hz is applied to the primary.
A good approach is to first find ωMI1, which is the induced mutual secondary voltage, and then use it to find the voltage across the 1-kΩ resistor. Since both M and I1, in (ωMI1 are unknown, they must be found. The mutual inductance M is
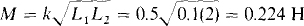
With M known, the coupled impedance can be used to obtain I1. This impedance is
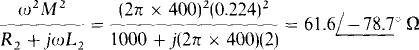
The current It is equal to the applied primary voltage divided by the magnitude of the sum of the coupled impedance and the primary winding impedance:
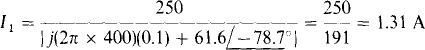
Now, with M and Ii known, the induced secondary voltage ωMl1 can be found:
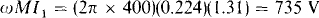
Voltage division can be used to find the desired voltage V2 from this induced voltage. The voltage V2 is equal to this induced voltage times the quotient of the load resistance and the magnitude of the total impedance of the secondary circuit:
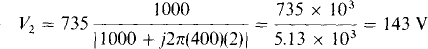
16.34 Find v for the circuit shown in Fig. 16-23a.
Fig. 16-23
The first step is the construction of the phasor-domain circuit shown in Fig. 16-23b. Next, the mesh equations are written:
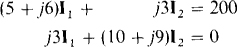
Notice that the mutual terms are positive because both I1 and I2 have reference directions into dotted terminals. By Cramer’s rule,
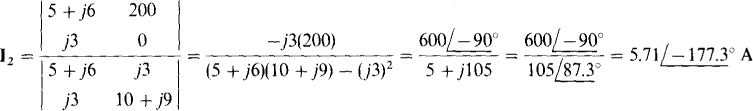
And 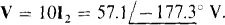 The corresponding voltage is
The corresponding voltage is
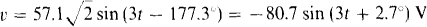
16.35 Find I2 for the circuit shown in Fig. 16-24.
Fig. 16-24
Before mesh equations can be written, the magnitude wM of jwM must be determined. From multiplying both sides of 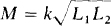 by ω,
by ω,
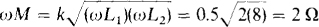
Now the mesh equations can be written:

Notice that the mutual voltage terms have an opposite sign (negative) from that (positive) of the self-induced voltage terms because one current reference direction is into a dotted terminal and the other one is not. In matrix form, these equations are
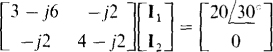
from which 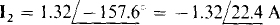 can be obtained by using a scientific calculator.
can be obtained by using a scientific calculator.
16.36 What is the total inductance of an air-core transformer with its windings connected in parallel if both dots are at the same end and if the mutual inductance is 0.1 H and the self-inductances are 0.2 and 0.4 H?
Because of the mutual-inductance effects, it is not possible to simply combine inductances. Instead, a source must be applied and the total inductance found from the ratio of the source voltage to source current, which ratio is the input impedance. Of course a phasor-domain circuit will have to be used. For this circuit the most convenient frequency is ω = 1 rad/s, and the most convenient source is 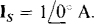 The circuit is shown in Fig. 16-25. The transformer impedances should be obvious from the specified inductances and the radian frequency of w = 1 rad/s. As shown, It of the
The circuit is shown in Fig. 16-25. The transformer impedances should be obvious from the specified inductances and the radian frequency of w = 1 rad/s. As shown, It of the 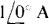 input current flows through the left-hand winding, leaving a current of
input current flows through the left-hand winding, leaving a current of 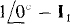 for the right-hand winding.
for the right-hand winding.
The voltage drops across the windings are
Fig. 16-25
The mutual voltage terms have the same signs as the self-induced voltage terms because both current reference directions are into dotted ends. Upon rearrangement and simplification, these equations become
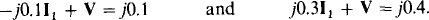
The unknown I1 can be eliminated by multiplying the first equation by 3 and adding corresponding sides of the equations. The result is
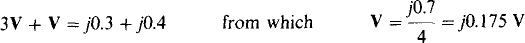
But
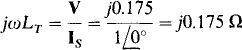
Finally, since ω = 1 rad/s, the total inductance is Lr =0.175 H.
16.37 Find i2 for the circuit shown in Fig. 6-2a.
Fig. 16-26
The first step is the construction of the phasor-domain circuit shown in Fig. 16-26b from which mesh equations can be written. These are
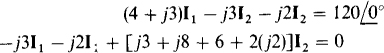
In the first equation, the 4 + j3 coefficient of I1 is, of course, the self-impedance of mesh 1, and the –j3 coefficient of I2 is the negative of the mutual impedance. The – j2I2 term is the voltage induced in the left-hand winding by I2 flowing in the right-hand winding. This term is negative because I1 enters a dotted terminal but I2 does not. In the second equation, the –j3I1, term is the mutual-impedance voltage, and –j2I1 is the voltage induced in the right-hand winding by I1 flowing in the left-hand winding. This term is negative for the same reason that –j2I2 is negative in the first equation, as has been explained. The j3 + j8 + 6 part of the coefficient of I2 is the self-impedance of mesh 2. The 2(j2) part of this coefficient is from a voltage j2I2 induced in each winding by I2 flowing in the other winding. It is positive because I2 enters undotted terminals of both windings.
These equations simplify to
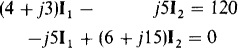
By Cramer’s rule,
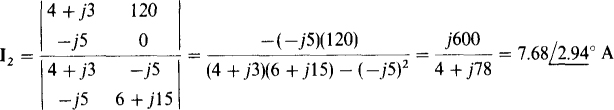
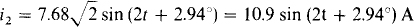
16.38 Find V for the circuit shown in Fig. 16-27. Then replace the 15-Ω resistor with an open circuit and find V again.
Fig. 16-27
The mesh equations are
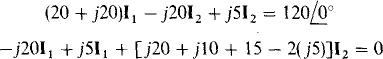
All the terms should be apparent except, perhaps, those for the mutually induced voltages. The j5I2 in the first equation is the voltage induced in the vertical winding by I2 flowing in the horizontal winding. It is positive because both I1 and I2 enter dotted terminals. The j5I1 term in the second equation is the voltage induced in the horizontal winding by I1 flowing in the vertical winding. It is positive for the same reason that j5I2 is positive in the first equation. The – 2(j5)I2 term is the result of a voltage of j’5I2, induced in each winding by I2 flowing in the other winding. It is negative because I2 enters a dotted terminal of one winding, but not of the other. These equations simplify to
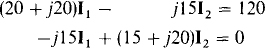
from which
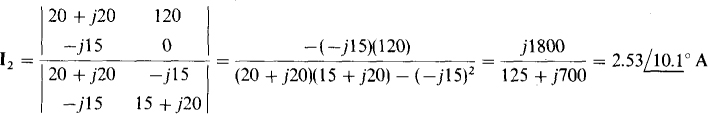
Finally,
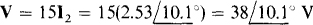
If the 15-Ω resistor is removed, then I2 = 0 A and V is equal to the sum of the voltage drops across the two windings. The only current that flows is I1; which is
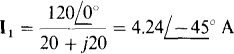
Across the vertical winding, ll produces a self-inductive voltage drop of
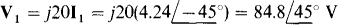
referenced positive on the dotted end. Across the horizontal winding, It produces a mutually induced voltage of
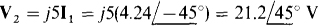
Like the other induced voltage, it also has a positive reference on a dotted end since part of the same flux produces it. (Actually, a changing flux produces the corresponding voltages v1 and v2) Finally, since the dotted ends of the two windings are adjacent, V is equal to the difference in the two winding voltages:
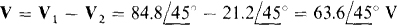
16.39 Repeat the first part of Prob. 16.38 using PSpice.
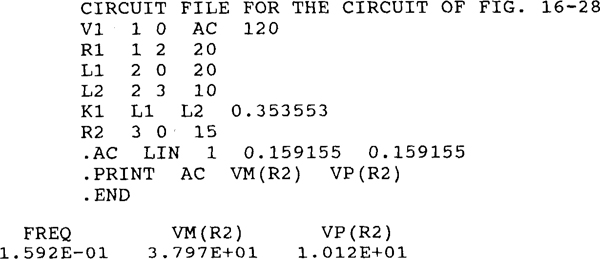
Fig. 16-28
Figure 16-28 shows the PSpice circuit corresponding to the phasor-domain circuit of Fig. 16-27. The inductance values are based on a frequency of ω = 1 rad/s, which is selected for convenience. The coefficient of coupling needed for the circuit file is 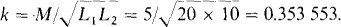
Following is the corresponding circuit file along with the answer from the output file obtained when PSpice is run with this circuit file. The answer of 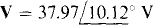 agrees to three significant digits with the first answer of Prob. 16.38.
agrees to three significant digits with the first answer of Prob. 16.38.
16.40 Determine the mesh currents in the circuit of Fig. 16-29.
Fig. 16-29
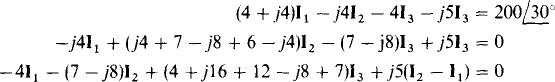
In the I1, mesh equation, the mutual term – j5I3 has a negative sign because I, is directed into a dotted end of a transformer winding but I3 is not. In the I2 mesh equation, the mutual term j5I3 does not have a negative sign because both I2 and I3 have directions into undotted ends of the transformer windings. And in the I3 mesh equation, the mutual term is j5(I2 – I2) because both I2 and I3 have directions into undotted ends of the transformer windings but I1 does not. When simplified and placed in matrix form, these equations are
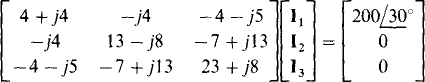
The solutions to these equations can be obtained by using a scientific calculator. They are I1 = 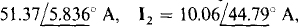 and
and 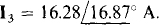
16.41 Repeat Prob. 16.40 using PSpice.
Fig. 16-30
Figure 16-30 shows the PSpice circuit corresponding to the phasor-domain circuit of Fig. 16-29 of Prob. 16.40. As usual, the inductances and capacitances are based on the frequency ω = 1 rad/s. The coefficient of coupling needed for the circuit file is 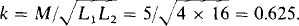
Following is the corresponding circuit file along with the answers from the output file obtained when PSpice is run with this circuit file. The answers agree with those obtained in the solution to Prob. 16.40.

16.42 What is the turns ratio of a two-winding transformer that can be connected as a autotransformer of 500/350 kV?
As can be seen from Fig. 16-7, the lower voltage is the voltage across one winding, and the higher voltage is the sum of the winding voltages. So, for this transformer, one winding voltage rating is 350 kV and the other is 500-350= 150 kV. The turns ratio is, of course, equal to the ratio of these ratings: a = 350/150 = 2.33 or a = 150/350 = 0.429, depending upon which winding is the primary and which is the secondary.
16.43 Compare the winding currents of a fully loaded 277/120-V, 50-kVA two-winding transformer and an autotransformer with the same rating.
The high-voltage winding of the conventional transformer must carry 50 000/277 = 181 A, and the low-voltage winding must carry 50 000/120 = 417 A. So, one winding carries the source current and the other winding carries the load current. In contrast, and as shown in the circuit of Fig. 16-31, part of the autotransformer winding must carry only the difference in the source and load currents, which is 417 — 181 = 236 A, as compared to the 417 A that the low-voltage winding of the conventional transformer must carry. Consequently, smaller wire can be used in the autotransformer, which results in a savings in the cost of copper. Also, the autotransformer can be smaller and lighter.
Fig. 16-31
16.44 A 12 470/277-V, 50-kVA transformer is connected as an autotransformer. What is the kVA rating if the windings are connected as shown in Fig. 16-7a? And what is this rating if the windings are connected as shown in Fig. 16-7b?
For either connection the maximum applied voltage is the sum of the voltage ratings of the windings: 12 470 + 277 = 12 747 V. Since, for the connection shown in Fig. 16-7b, the source current flows through the low-voltage winding, the maximum input current is the current rating of this winding, which is 50 000/277 = 181 A. So, the kVA rating for this connection is 12 747 × 181 VA = 2300 kVA. For the other connection, that illustrated in Fig. 16-7a, the source current flows through the high-voltage winding. Consequently, the maximum input current is the current rating of this winding, which is 50 000/12 470 = 4.01 A, and the kVA rating is only 12 747 × 4.01 VA = 51.1 kVA.
16.45 Find the three currents I1 I2, and I3 for the circuit shown in Fig. 16-32.
Fig. 16-32
The resistor current is obviously I3 = 120/100 = 1.2 A. And the resistor receives 120 × 1.2 = 144 VA. Since this is also the voltamperes supplied by the source, then 277I1 = 144 and I1 = 144/277 = 0.52 A. Last, from KCL applied at the transformer winding tap, I2 = I3 – I1 = 1.2 – 0.52 = 0.68 A. Scalar addition can be used here since all three currents are in phase.
16.46 In the transformer shown in Fig. 16-33, what is the direction of flux produced in the core by current flow into (a) terminal a, (b) terminal b, (c) terminal c, and (d) terminal d
Ans. (a) Clockwise, (b) counterclockwise, (c) counterclockwise, (d) clockwise
Fig. 16-33
16.47 Supply the missing dots for the transformers shown in Fig. 16-34.
Ans. (a) Dot on terminal d; (b) dot on terminal b; (c) dots on terminals b, c, and g.
Fig. 16-34
16.48 What is the turns ratio of a power transformer that has a 6.25-A primary current at the same time that it has a 50-A secondary current?
Ans. a = 8
16.49 Find the turns ratio of a power transformer that transforms the 12 470 V of a power line to the 480 V used in a factory.
Ans. a = 26.
16.50 What are the full-load primary and secondary currents of a 7200/120-V, 25-kVA power transformer? Assume that the 7200-V winding is the primary.
Ans. 3.47-A primary current and 208-A secondary current
16.51 A power transformer with a 13 200/480-V rating has a full-load primary current rating of 152 A. Find the transformer kVA rating and the full-load secondary current rating if the 480 V is the secondary voltage rating.
Ans. 2000 kVA, 4.18 kA
16.52 A 7200/120 V, 60-Hz transformer has 1620 turns on the primary. What is the peak rate of change of magnetic flux? (Hint: Remember that the voltage ratings are in rms.)
Ans. 6.29 Wb/s
16.53 An iron-core transformer has 3089 primary turns and 62 secondary turns. if the applied primary voltage is 13 800 V rms at 60 Hz, find the secondary rms voltage and the peak magnetic flux.
Ans. 277 V, 16.8 mWb
16.54 If a 27-turn transformer winding has 120 V rms applied, and if the peak coupling flux is 20 mWb, what is the frequency of the applied voltage?
Ans. 50 Hz
16.55 An iron-core transformer has 1620 primary turns and 54 secondary turns. A 10-Ω resistor is connected across the secondary winding. Find the resistor voltage when the primary current is 0.1 A.
Ans. 30 V
16.56 What should be the turns ratio of an output transformer that connects a 4-Ω speaker to an audio system that has an output resistance of 1600 Ω?
Ans. a = 20
16.57 In the circuit shown in Fig. 16-35, what should a and Xc be for maximum average power absorption by the load impedance, and what is this power?
Ans. 3.19, –4.52 Ω, 376 W
Fig. 16-35
16.58 Find i1, i2, and i3 in the circuit shown in Fig. 16-36.
Ans. i1 = 4 sin (3t – 36.9°) A
i2 = 8 sin (3t – 36.9°) A
i3 = –24 sin (3t – 36.9°) A
Fig. 16-36
16.59 Find V in the circuit shown in Fig. 16-37.
Ans. 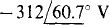
Fig. 16-37
16.60 Find I1, I2, and I3 in the circuit shown in Fig. 16-38.
Ans. 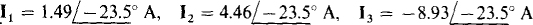
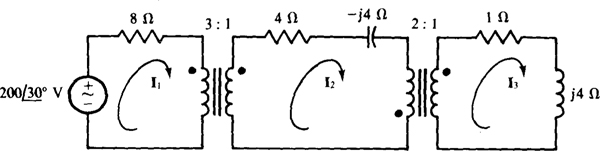
Fig. 16-38
16.61 What is υ in the circuit shown in Fig. 16-39?
Ans. –23.7 sin (2t – 6.09°) V
Fig. 16-39
16.62 Find I in the circuit shown in Fig. 16-40.
Ans. 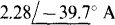
Fig. 16-40
16.63 For the following PSpice circuit file, construct a corresponding phasor-domain circuit diagram that contains an ideal transformer. Then use this diagram to calculate the answer that will appear in the output file when PSpice is run with this circuit file.
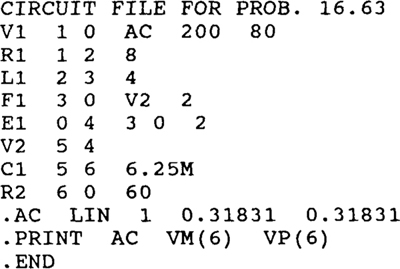
Ans. 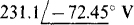
16.64 Repeat Prob. 16.63 for the following PSpice circuit file.
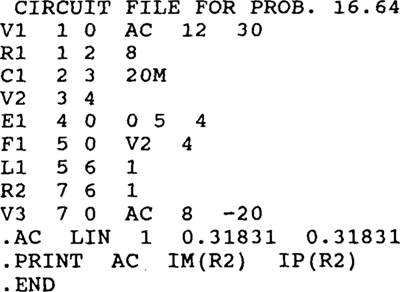
Ans. 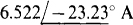
16.65 Repeat Prob. 16.63 for the following PSpice circuit file.
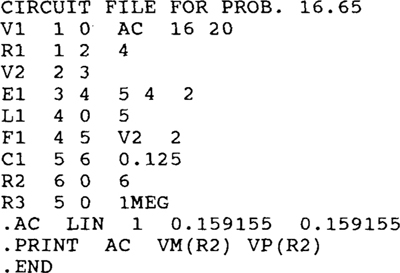
Ans. 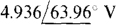
16.66 An air-core transformer has a primary current of 0.2 A and a secondary current of 0.1 A that produce fluxes of ϕn = 40ΩWb, ϕm2 = 10ΩWb, and ϕ12 = 30 Ω Wb. Find Ωm1 L1, L2, M, and k if N1, = 30 turns and N2 = 50 turns.
Ans. ϕm1 = 12 ΩWb, L1 = 7.8mH, L2 = 20 mH, M = 3mH, k = 0.24
16.67 What is the greatest possible mutual inductance of an air-core transformer that has self-inductances of 120 and 90 mH?
Ans. 104 mH
16.68 For each of the following, find the missing quantity—either self-inductance, mutual inductance, or coefficient of coupling.
(a) L1 = 130mH, L2 = 200mH, M = 64.5 mH
(b) L1 = 2.6ΩH, L2 = 3 ΩH, k = 0.4
(c) Ll = 350 mH, M = 100 mH, k = 0.3
Ans. (a) k = 0.4, (b) M = 1.12ΩH, (c) L2 = 317 mH
16.69 An air-core transformer has an open-circuited secondary winding with 70 V induced in it when the primary winding carries a 0.3-A current and has a 120-V, 600-Hz voltage across it. What is the mutual inductance and the primary self-inductance?
Ans. M = 61.9mH. L1 = 106 mH
16.70 An air-core transformer with an open-circuited secondary has inductances of L1 = 200 mH, L2 = 320 mH, and M = 130 mH. Find the primary and secondary voltages, referenced positive at the dotted terminals, when the primary current is increasing at the rate of 0.3 kA/s into the dotted terminal of the primary winding.
Ans. V1 = 60 V, v2 = 39 V
16.71 An air-core transformer has inductances of L1 = 0.3 H, L2 = 0.7 H, and M = 0.3 H. The primary current is increasing into the dotted primary terminal at the rate of 200 A/s, and the secondary current is increasing into the dotted secondary terminal at the rate of 300 A/s. What are the primary and secondary voltages referenced positive at the dotted terminals?
Ans. v1 = 150V, v2 = 270V
16.72 An air-core transformer with a shorted secondary has a 90-mA short-circuit secondary current and a 150-mA primary current when 50 V at 400 Hz is applied to the primary. If the mutual inductance is 110 mH, find the self-inductances.
Ans. L1 = 199 mH, L2 = 183 mH
16.73 An air-core transformer with a shorted secondary has inductances of L1 = 0.6 H, L2 = 0.4 H, and M = 0.2 H. Find the winding currents when a primary voltage of 50 V at 60 Hz is applied.
Ans. I1 = 265 mA, I2= 133 mA
16.74 A transformer has self-inductances of 1 and 0.6 H. One series connection of the windings results in a total inductance of 1 H. What is the coefficient of coupling?
Ans. k = 0.387
16.75 The transformer windings of a transformer are connected in series with dotted terminals adjacent. Find the total inductance of the series-connected windings if L1 = 0.6 H, L2 = 0.4 H, and k = 0.35.
Ans. 0.657 H
16.76 An air-core transformer has an 80-mH mutual inductance and a 200-mH secondary self-inductance. A 2-kΩ resistor and a 100-mH inductor are in series with the secondary winding. Find the impedance coupled into the primary for ω = 10 krad/s.
Ans. 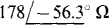
16.77 Find V in the circuit of Fig. 16-41.
Ans. 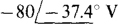
Fig. 16-41
16.78 A 6.8-kΩ resistor is connected across the secondary of a transformer having inductances of L1 = 150 mH, L2 = 300 mH, and M = 64 mH. What is the resistor current when 40 V at 10 krad/s is applied to the primary?
Ans. 2.33 mA
16.79 Find i in the circuit of Fig. 16-42.
Ans. 103 sin (l000t – 73.1°) mA
Fig. 16-42
16.80 What is the total inductance of the parallel-connected windings of an air-core transformer if the dots are at opposite ends and if the mutual inductance is 100 mH and the self-inductances are 200 and 400 mH?
Ans. 87.5 mH
16.81 Find i in the circuit of Fig. 16-43.
Ans. 24 sin (2t – 76.6°) A
Fig. 16-43
16.82 Find V in the circuit of Fig. 16-44. Then switch the dot on one winding and find V again.
Ans. 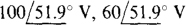
Fig. 16-44
16.83 In the circuit shown in Fig. 16-44, place a short circuit across terminals a and b and find the short-circuit current directed from terminal a to terminal b.
Ans. 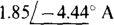
16.84 For the circuit shown in Fig. 16-44, what load connected to terminals a and b absorbs maximum power and what is this power?
Ans. 
16.85 Find I in the circuit of Fig. 16-45.
Ans. 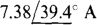
Fig. 16-45
16.86 Calculate the answer that will appear in the output file when PSpice is run with the following circuit file.
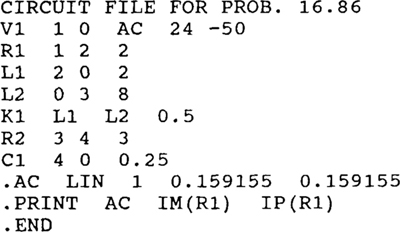
Ans. 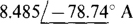
16.87 Calculate the answer that will appear in the output file when PSpice is run with the following circuit file.
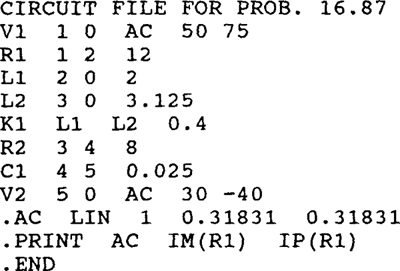
Ans. 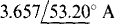
16.88 Calculate the answer that will appear in the output file when PSpice is run with the following circuit file.
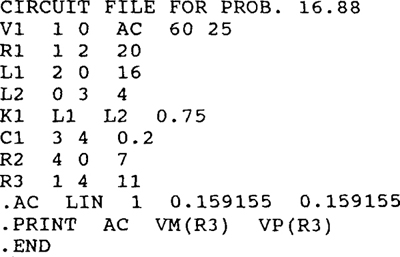
Ans. 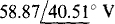
16.89 What is the turns ratio of a two-winding iron-core transformer that can be connected as a 277/120 V autotransformer?
Ans. a = 1.31 or a = 0.764
16.90 A 4800/240-V, 75-kVA power transformer is connected as an autotransformer. What is the kVA rating of the autotransformer for the connection shown in Fig. 16-7a? What is the kVA rating for the connection shown in Fig. 16–7b
Ans. 1575 kVA, 78.75 kVA
16.91 Find the currents I1 I2, and I3 in the circuit of Fig. 16-46.
Ans. I1 = 800 A, I2 = 343 A, I3 = 1.14 kA
Fig. 16-46