Chapter 2
Origins of a Habitable Universe
Humanity’s first communications satellite, named Echo 1, was little more than a passive mirror. Launched in 1960, the satellite consisted of a metalized balloon, about 70 m in diameter, placed to reflect radio waves from a transmitter on one side of the Atlantic to a receiver on the other side. After a few years, the Echo program was replaced by the first “active” communications satellites, which detect and electronically amplify signals before sending them on to the recipient, rendering the sensitive antennas and receivers built for the earlier system redundant.
In 1965, Arno Penzias and Robert Wilson, radio physicists working for AT&T’s Bell Labs in New Jersey, realized that a semiretired radio receiver built for the Echo program and located at nearby Crawford Hill might be of use for the astronomical detection of radio waves emanating from our galaxy. To use the receiver to measure these presumably very faint signals, however, they first had to characterize, and eliminate, the various sources of electronic noise that were sure to plague the instrument—which, after all, had not been designed to serve as a telescope. Not surprisingly, when they pointed the 6 m diameter, horn-shaped antenna at “empty” presumably radio-silent parts of the sky to calibrate it, they detected a faint radio frequency “hiss” that they assumed was due to instrument artifacts. However, when systematically trying to “fix” the antenna and its associated amplifiers, eliminating one by one any potential sources of electronic noise, the hiss persisted. Ultimately, the physicists began to suspect that pigeons that were roosted in the horn might be the source of the offending static. But even after chasing them away and cleaning up years’ worth of droppings (the life of a physicist is not as glamorous as it may appear), the hiss remained. They were flummoxed; for more than a year, the source of the problem eluded them. Finally, they started to consider the possibility that, although the hiss remained the same no matter where in the sky the antenna was pointed, the noise might not be instrument noise but might instead reflect some authentic astrophysical phenomenon. Upon hearing this, several colleagues suggested that they call Bob Dicke (1917–1997) at Princeton University, just an hour to the south. This, it turns out, was a fortuitous idea. With his colleagues Jim Peebles and David Wilkinson (1935–2002), Dicke had just written a paper outlining an important prediction of a theory regarding the origins of the Universe. This theory, they said, predicted that the entire Universe would be filled with microwave radiation at precisely the frequency and intensity observed in the horn antenna.
Unbeknownst to Dicke and his team, a similar theory had been described as far back as 1948 by the Hungarian-born American physicist George Gamow (1904–1968) and his student Ralph Alpher (1921–2007), who theorized that the Universe formed from an initially superdense, superhot state from which today, billions of years later, it continues to expand and cool. And although this key theoretical advance was ignored for many years after its publication, the paper describing it is now well known, both for its prescient scientific prediction and its being an example of Gamow’s famously puckish sense of humor. Specifically, Gamow added the name of his friend and Cornell colleague Hans Bethe (1906–2005) to the paper simply because it amused him that the authors’ names, Alpher, Bethe, and Gamow, would then parallel the first three letters of the Greek alphabet.
The theory that Gamow and company and Dicke and company had independently derived was based, in part, on observations made by astronomers in the first decades of the last century. By 1917, the American astronomer Vesto Slipher (1875–1969) had shown that nearly all the many spiral-shaped nebulae (from the Latin word for “cloud”) astronomers had spied in the heavens with their telescopes were “red shifted.” That is, their spectral lines—atom-specific wavelengths of emitted light—were shifted to longer wavelengths than those seen in laboratories on Earth. A possible reason for such a systematic red shift was that all the nebulae were moving away from us; the Austrian physicist Christian Doppler (1803–1853) had described a century before how frequency changes with the motion of the source, an effect now known as a Doppler shift. But at the time, it was not even clear what the nebulae were, much less why they would nearly all be receding. Even the very notion of that was an anathema; since Copernicus had shown that the Earth orbits around the Sun and not, as the Catholic church had taught, the other way around, a central precept of science had been that there is nothing particularly “special” about our place in the Universe (see sidebar 2.3). And yet, here it appeared that we were the center of some monstrous offense that the rest of the cosmos was fleeing from.
The question of what spiral nebulae are was put to rest by the British-American astronomer Edwin Hubble (1889–1953). In 1924, Hubble was in charge of the largest and best telescope in the world at the time, the “100 inch” (2.54 m) Mount Wilson telescope sitting in the mountains above the then small town of Los Angeles. From that perch, he turned the telescope’s unprecedented resolving power on Andromeda, the largest nebula by apparent size and thus likely one of the closest. Doing so, Hubble was able to resolve individual stars, confirming earlier speculation that Andromeda and its sister spiral “clouds” are galaxies like our own Milky Way. He was even able to identify a cepheid variable, a class of star whose variations in brightness correlate with its absolute brightness. A comparison of the cepheid’s apparent brightness with its absolute brightness indicated that Andromeda is nearly a million light-years away, a distance much greater than that to the farthest stars in the Milky Way, thus offering further confirmation that Andromeda is a galaxy in its own right.* By 1929, Hubble had estimated the distances to two dozen “galactic nebulae,” finding that they are galaxies in their own right. Moreover, upon comparing these distances to Slipher’s red shifts, Hubble discovered something startling: the rate with which other galaxies are receding from us is proportional to how far away from us they are. The mystery of why they are receding, however, remained unanswered in Hubble’s time.
Gamow and Alpher’s theory (and Dicke and company’s later, independent work) posited an answer to the riddle of the receding galaxies. Specifically, they proposed that the Universe is expanding uniformly from an initially ultradense state, nicely rationalizing both Slipher’s and Hubble’s observations: space, itself, was expanding, and thus from the perspective of every galaxy, it would appear that all other galaxies are receding (i.e., there is nothing special about our galaxy), and the more space there is between two galaxies (i.e., the farther apart they are), the more space there is expanding between them and thus the faster they recede from one another.
Thinking deeper, the theorists realized that if this “big bang” theory* were correct, the early Universe would not only have been unimaginably dense but also unimaginably hot and the heat of Universe’s fiery origins should still be observable today, albeit “cooled down” as relic radiation at microwave (centimeter) wavelengths. Consider this: as we look farther and farther away in distance, the finite speed of light ensures that we are looking at events that happened further and further back in time. And if you look far enough away (i.e., far enough back in time), you can see the big bang itself—photons from it are arriving on Earth from all directions, even today. But farther away also means greater red shift, and so, although the light of the big bang, which originally corresponded to a very hot object indeed, is all around us, it should be red-shifted so much as to appear cold. Based on then current estimates of the age of the Universe, Gamow predicted that this relic image of the big bang should glow like a blackbody at a temperature of approximately 4 K (4°C above absolute zero). And the radio hiss observed from New Jersey? Based on Peebles and Wilkinson’s observations, it corresponded to a blackbody with a temperature of about 5 K (both the theoretical prediction and the observed temperature have since been refined to 2.725 ± 0.002 K; fig. 2.1). Rather than the prosaic hiss of pigeon droppings, the physicists Penzias and Wilson were hearing the red-shifted hum of the big bang itself, now termed the “cosmic microwave background.”
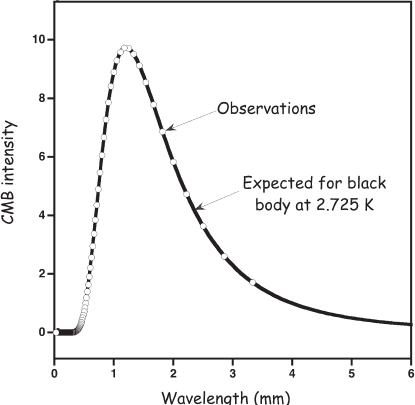
Figure 2.1 Echoes of the big bang are seen in the cosmic microwave background (CMB). The radio-wave photons that make up this spectrum are the red-shifted, cooled remnants of the hot sea of photons that filled the Universe at the time of recombination (discussed later in the chapter), some 370,000 years after its origins. As shown by the fitted line, the cosmic microwave background now exhibits the spectral characteristics of a blackbody (a perfect radiator) at a temperature of precisely 2.725 K. These data were obtained by NASA’s Cosmic Background Explorer (COBE) satellite.
The Big Bang
Our contemporary understanding of physics is sufficiently advanced such that cosmologists have been able to refine the big bang model into a detailed description of the origins of the Universe that, it is generally thought, is fairly accurate and detailed to as far back as within 10−34 seconds of the origins of time itself, and cosmologists are actively trying to push that back another billionfold, to as far back as 10−43 seconds (see sidebar 2.1). This is all the more impressive when one considers that, according to the current best estimates, these events happened 13.799 billion years ago (give or take 21 million years). Here we describe some of the many observations that compellingly support this hypothesis and explore the impact that the Universe’s big bang birth has had on the origins and evolution of life within it.
From our perspective as astrobiologists, the “interesting bits” started a million trillion trillion times later than the 10−34 seconds beyond which cosmologists are now trying to probe, when the Universe was, in relative terms, an ancient millionth of a second old. At this point, everything in our Universe, all the matter—and energy—now in you, in Pluto’s moon Charon, and in the most distant stars we see in the heavens, was compacted together in a dense, unimaginably hot plasma estimated to be at a temperature of 1013 K (at these sorts of temperatures, the Kelvin scale is equivalent to the Celsius scale). At this temperature, the mean energy per photon is higher than the energy bound up in the mass of a proton or neutron (which can be calculated from their mass by Einstein’s E = mc2), and, thus, when two such photons collide, they can spontaneously convert into a proton-antiproton or neutron-antineutron pair. Conversely, when proton-antiproton or neutron-antineutron pairs collide, they annihilate one another, producing—you guessed it—two high-energy photons. Before the first millionth of a second, the rate at which neutrons and protons were produced equaled the rate at which they were destroyed. After this point, however, further expansion of the Universe led to further cooling until, eventually, no new neutron-antineutron or proton-antiproton pairs were formed. (Protons and antiprotons are about 0.1% less massive than neutrons and antineutrons, which is enough to ensure that, when these pairs “froze out” of the mix of photons and nucleons, protons and antiprotons outnumbered neutrons and antineutrons by a factor of five.)
Although at this point the relic big bang photons lacked sufficient energy to create proton-antiproton and neutron-antineutron pairs, the opposite was not true. That is, existing nucleon-antinucleon pairs remained quite capable of annihilating one another to produce two γ-ray photons. But, for reasons that remain perhaps one of physics’ bigger unsolved mysteries, the “particles” outnumbered the “antiparticles” at this point by one part in a few billion. That is, for every annihilation, a pair of photons was added to what is now the cosmic microwave background (which is estimated to contain 90% of all the photons ever emitted over the history of our Universe), and for every few billion such photons, a single proton or neutron was left to create the atoms in our Universe. Without this tiny asymmetry between matter and antimatter, there would be no matter left in the Universe, so this cosmological mystery speaks to our very existence.
The electron and its antiparticle, the positron, are 1,836 times lighter than a proton. Thus, not until the Universe was 14 seconds old and the temperature had fallen to a much more “moderate” 3 billion kelvins, did electron-positron pair formation freeze and the total number of electrons (again, for some reason, electrons outnumbered positrons by one part in a few billion) settle down to its current value.
At this point, the Universe consisted of a hot, dense sea of electrons and nucleons. Nucleons, that is, neutrons and protons, not nuclei. The strong nuclear force, which holds together neutrons and protons to form atomic nuclei is weaker than the thermal energies seen above a billion kelvins, so any conglomeration of neutrons and protons that might have been transiently formed quickly dissociated under the onslaught of the highly energetic collisions taking place in this hot, unimaginably dense state.
It wasn’t until the Universe was about a minute and a half old that it cooled below a billion kelvins, the temperature at which the mean thermal energy of its matter (nucleons, electrons, and photons) was sufficiently low that neutrons and protons came together to form the first composite nucleus—deuterium, an isotope of hydrogen containing one neutron and one proton—faster than thermal collisions broke it apart. Deuterium, however, which is denoted 2H to reflect its atomic mass of two, is less stable than either tritium (3H, consisting of one proton and two neutrons) or helium-3 (3He, consisting of two protons and a neutron), and thus deuterium readily fuses to form these nuclei (fig. 2.2). Such fusion could be with a free neutron or a free proton, but the energy released would then have nowhere to go and would most likely tear the newly formed nucleus back apart. In contrast, when a deuterium fuses with another deuterium, the resulting composite nucleus can release a free proton or a free neutron that carries the energy away, producing either tritium or 3He. Tritium and 3He, in turn, are less stable than helium-4 (4He, two neutrons and two protons), and thus they rapidly undergo fusion with deuterium to create 4He, again with the release of either a free neutron or a free proton to carry away the excess energy.*
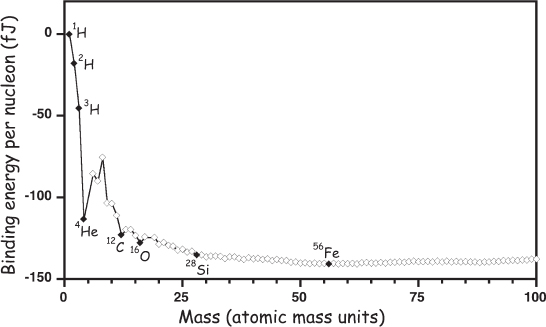
Figure 2.2 A plot of nuclear binding energies (a measure of the stability of a given nucleus) shows that helium-4 (4He) is significantly more stable (further “downhill”) than hydrogen (1H), deuterium (2H), and helium-3 (3He). Because of this, the fusion of these nuclei to form 4He dominated nucleosynthesis during the first few minutes of the big bang. It is also the primary energy source for stars. The dinuclear fusion of 4He with itself or with any of the lighter nuclei is prohibited by the instability (relative to 4He) of all the nuclei between the masses of four and 12. Fusion reactions to form heavier elements require instead the trinuclear fusion of three 4He to form carbon-12 (12C) in a single reaction. Once this barrier is surmounted, additional dinuclear reactions can continue until iron-56 (56Fe) is synthesized. Further fusion consumes rather than produces energy.
And then? And then nothing but more of the same. Between the ages of 1.5 and 3 minutes, the Universe converted 20% of its original (“primordial”) hydrogen into 4He, leaving behind tiny traces of deuterium, tritium, 3He, and lithium. And then, before it produced significant quantities of any heavier nuclei, the fusion stopped. A plot of nuclear stabilities (see fig. 2.2) reveals why: none of the nuclei consisting of five to 11 nucleons are as stable as 4He; it is not until carbon-12 (12C) that we find the first nucleon that is more stable. But the formation of this nucleus requires that three 4He simultaneously collide (or, more precisely, that a highly unstable beryllium-8 nucleus collide with a 4He nucleus during the incredibly brief 10−16 second lifetime of the former). Thus, the formation of 12C is a third-order reaction, a reaction whose rate scales with the concentration of reactants cubed. But, in addition to cooling, the Universe was also expanding. So much so that, by the time appreciable amounts of 4He had formed, the concentration of 4He was too low to support a third-order, trinuclear reaction at any appreciable rate. Thus, only 3 minutes after the start of the big bang and after a fifth of its initial complement of nucleons had been converted to 4He, primordial nucleosynthesis ground to a halt, leaving mainly protons, neutrons (which convert into protons with a half-life of about 14.5 minutes*), and 4He. Beyond this were only trace, one part in 20,000 amounts of deuterium, one part in 100,000 of 3He and tritium (which decays into 3He with a half-life of 12.35 years), and a few parts in 10 billion of the heavier nucleus lithium-7 (7Li).
The ratios of the primordial nuclei provide a stringent test of the big bang model. The ratios of 1H to 2H, 1H to 3He, and 1H to 7Li produced during big bang nucleosynthesis are exquisitely sensitive to the precise density of matter in the expanding early Universe, with greater density leading to the conversion of more hydrogen into the heavier nuclei (fig. 2.3). If the density of matter in the early Universe had varied even a little, these ratios would differ very significantly from their current values. (The 92:8 ratio of 1H to 4He, in contrast, is a result of the 6:1 ratio of protons to neutrons at the beginning of nucleosynthesis, up from the 5:1 ratio at the end of nucleon synthesis due to the decay of neutrons into protons in the intervening few minutes. Unlike the other ratios, this one is thus relatively independent of the density of the early Universe.) Since we do not know a priori what the density of the original Universe was, we cannot use big bang models to predict what the ratios of these nuclei were at the end of the nucleosynthesis era. But, if we measure these three ratios in the current Universe (and correct for the fact that stars have been converting some of the hydrogen to nonprimordial helium over the intervening 13.8 billion years) and find that all point to the same density, this provides powerful evidence in favor of the big bang hypothesis (see sidebar 2.2). The best current measurements of these ratios do, in fact, all point, more or less, to the same density (fig. 2.3), an observation that provides strong, quantitative support for the big bang model.

Figure 2.3 The production of deuterium (2H), 3He, and lithium-7 (7Li) during the first few minutes after the big bang depended sensitively on the density of the Universe. The curves in this figure indicate the relative abundance of the various nuclei expected as a function of nucleon density, with the latter being presented relative to Ω, the ratio of the actual density to the “critical density” that would produce a closed universe (see sidebar 2.2). Current best estimates for these abundances, which are indicated by the boxes, are internally consistent and point to a big bang nucleon density of about 4% to 5% of the critical density (vertical grey bar). Note that the production of 4He was tied to the 6:1 ratio of protons to neutrons at the beginning of nucleosynthesis and thus was only weakly dependent on density. For this reason, the 4He curve is presented on a narrower, non-logarithmic scale.
Nuclear binding energy, the energy that holds protons and neutrons together to form the nucleus, is about a million times stronger than the electromagnetic forces that bind electrons to nuclei to form atoms, which is why nuclear bombs are so much more powerful than traditional explosives. Thus, even though it took only 3 minutes for the Universe to cool sufficiently for nuclear reactions to freeze, it took much longer to cool to the point where electrons and nuclei could join together to form stable atoms. This “recombination event” (a misnomer, given that electrons had not previously been combined with nuclei) occurred when the temperature dropped below about 3,000 K, the temperature at which the energy of background photons was low enough that they would no longer rip electrons from nuclei. Current estimates are that the Universe cooled to this temperature some 370,000 years after the big bang.
The recombination event forever altered the relationship between photons and matter in the Universe. Before recombination, the Universe consisted of plasma, a cloud of naked nuclei and electrons. Photons are scattered by such charged particles and, in being scattered, exchange kinetic energy with them, ensuring that the photons and matter in the pre-recombination Universe reflected the same temperature. The scattering would also have made the pre-recombination Universe opaque, much the same way water droplets scatter light, rendering fog opaque. Neutral hydrogen and helium, in contrast, are transparent to the visible and infrared photons that filled the Universe at the time and thus, after recombination, the scattering stopped. This also put a stop to the thermal equilibration between matter and the primordial photons, and the two parted company. The matter evolved into galaxies, stars, and, eventually, us. The primordial photons, in contrast, sped off into space. Some of those, which were emitted from recombining gas that was 13.8 billion light-years away from our current location, are just arriving today, red-shifted a thousandfold by the expansion of the Universe, lengthening their wavelength by the same factor of 1,000, from wavelengths corresponding to a blackbody at the approximate 3000 K temperature of recombination to wavelengths corresponding to the 2.725 K of the cosmic microwave background.*
Fine details of the pervasive cosmic microwave background provide further, compelling evidence in favor of the accuracy of our understanding of the big bang. Before recombination, the photons, protons, and electrons in the Universe were in thermal equilibrium: because the photons were scattered by, and thus exchanged momentum with, the charged particles making up the plasma, anything that affected the temperature of matter affected the energy of the photons. And the early Universe was filled with something that affected the temperature of its matter: sound waves—not exactly music, but density fluctuations obeying similar physics. Under the influence of gravity, tiny fluctuations in the density of the matter tended to grow—the denser a region, the stronger its gravity and the better it pulled in matter from surrounding regions of space. And with this infalling matter came a small increase in temperature as gravitational potential energy was converted into kinetic energy. Before recombination, however, the scattering of primordial photons—which, as you’ll recall, outnumber protons and electrons by a billion to one—tended to tear apart any denser regions. Under such circumstances, random density fluctuations (and with these, temperature fluctuations) grew, dissipated, and grew again in a process that produced waves akin to a violin string responding to random strikes by emitting a note and its various harmonics. The wavelengths and amplitudes of waves are dependent on the density of the medium in which they occur, and, so, if we could measure the wavelength of these primordial waves, this would provide a second, independent measure of the density of the early Universe. As it turns out, we can.
The recombination event decoupled the big bang photons from the nuclei and electrons in the Universe, and thus a “fossil record” of the conditions in the Universe at the time of recombination is imprinted on the cosmic microwave background. If the Universe at recombination were perfectly homogeneous (if the plasma had the same density everywhere), the cosmic microwave background we see today would be isotropic, from the Greek ísos, meaning “equal,” and tropos, meaning “turning.” That is, the background would correspond to the same temperature in any direction we look. If, instead, the matter in the early Universe were filled with waves, the cosmic microwave background would also exhibit fluctuations corresponding to the density fluctuations (and their commensurate temperature fluctuations) that these waves set up, and the cosmic microwave background would be slightly anisotropic. In the early 1990s, the predicted small (10 parts in a million) anisotropies were finally detected by the Cosmic Background Explorer (COBE) satellite in a discovery that won the lead scientists on the project, George Smoot of the University of California, Berkeley, and John Mather of NASA’s Goddard Space Flight Center, the 2006 Nobel Prize in Physics.

Figure 2.4 A full-sky map of the cosmic microwave background shows miniscule, 10-parts-per-million variations in the 2.725 K mean temperature of the background. The angular scale of these fluctuations is a measure of the size—and thus the wavelength—of the acoustic perturbations that filled the Universe during recombination, some 370,000 years after the big bang. Recent high-precision measurement of the size of these oscillations by the Planck spacecraft are consistent with a nucleon density of 4.90 ± 0.02% of that necessary to produce a closed universe (see sidebar 2.2), which falls within the narrow range of densities consistent with the observed relative abundances of the light nuclei (see Figure 2.3). (Courtesy of NASA / WMAP Science Team)
High-resolution follow-on studies using the Wilkinson Microwave Anisotropy Probe (WMAP), named after David Wilkinson, mentioned in the introduction to this chapter, and launched in 2001, and the Planck mission, launched in 2009, provide a means of accurately measuring the wavelengths and amplitudes of the sound waves that created the cosmic microwave background anisotropies when the Universe was just a few hundred thousand years old (fig. 2.4). These measurements, in turn, produced an estimate of the density of nucleons in the early Universe that is within experimental error of the density derived—completely independently—from the known ratios of hydrogen to the heavier primordial nuclei (see fig. 2.3). That two completely independent estimates of the nucleon density of the Universe derived from the big bang model would converge on precisely the same value provides extremely strong support for the big bang theory, and the scientific community now considers this model rock solid, with only the details remaining to argue about.
Stars and Galaxies
By the time it was 370,000 years old, the Universe consisted of relic big bang photons zipping through transparent clouds of primordial, free hydrogen and helium atoms. Soon after, though, the first chemistry was born as atoms bound together to create the first molecules. As helium has a much stronger affinity for electrons than hydrogen does, it was the first to form neutral atoms. By combining with a still ionized hydrogen atom (i.e., a proton), these early helium atoms formed the first covalent bonds, resulting in the molecular ion helium hydride (HeH+), a molecular ion so unstable it would have destroyed itself by violently reacting with any other molecule had there been any other molecules for it to react with at the time. Eventually, though, things cooled down enough to allow molecular hydrogen (H2) to form, a far more stable molecule that then became the most common thing in the Universe.
The very limited chemistry available to hydrogen and helium is obviously not very promising fodder for life to arise; life requires both far more complex molecules than these two atoms can muster as well as seriously concentrated forms of disequilibrium (energy) to drive the replicative reactions of those more complex molecules. How did these come about? Initially they arose from the subtle, parts-per-million inhomogeneities produced by those early density waves and reflected today in anisotropies in the cosmic microwave background.
Despite their scant, 10-parts-per-million level, the inhomogeneities in the early Universe had a profound impact on its later evolution. The slightly denser regions exerted an equally slightly stronger gravitational pull than the less populated ones, and thus these regions began to accumulate even more matter. This new matter amplified the originally small density fluctuation, further accelerating the infall of matter. Within a few hundred million years after recombination, the once nearly homogeneous, post–big bang cloud of hydrogen and helium had been pulled into trillions of lumps, each a few billion times more massive than the Sun. These “protogalaxies” were the seeds of the galaxies we know today; over the next few billion years, merging protogalaxies would form the billions of galaxies that now make up the observable Universe, the sphere of space centered on the Earth that is close enough that light from objects within it has had time to reach us since the big bang (see fig. P.1 in the preface).
But we have gotten ahead of ourselves. When the Universe was young, it was filled with nothing but hydrogen and helium, contracting here and there to form the first protogalaxies. It wasn’t until the Universe was several hundred million years old that the next astonishing thing happened: the first stars were born, shedding fresh light on the Universe, which had descended into darkness as the primordial photons red-shifted toward infrared and then microwave wavelengths.
Stars are simply enormous piles of hydrogen and helium compressed under the weight of their own mass to such densities, pressures, and temperatures (the latter due initially to the kinetic energy associated with all that mass falling inward toward the center) that lighter atoms fuse to form heavier atoms through reactions like those last seen when the Universe was but 3 minutes old. Due to an interesting interplay between chemistry and physics, the first-generation stars are generally thought to have been quite massive. This was first realized by James Jeans (1877–1946), who, in 1940, turned his keen, physics-oriented mind toward the clouds of gas from which stars are born, which are called “proto-stellar” nebulae (again, nebula being the astronomer’s generic word for “thing that looks like a cloud”). Doing so, Jeans found that, in attempting to compress the gas, gravity is fighting against pressure. If the mass is too low, the gas’s pressure prevents collapse. Above a certain, minimum mass, however, gravity wins. The minimum mass, now known as the Jeans mass, is proportional to the square of the initial temperature of the gas (higher temperatures = higher pressures = greater mass required to ensure collapse). But because of this, it also depends on the chemistry of the cloud. Hydrogen and helium, the only significant components of the early Universe, are transparent to infrared and visible light, and transparent things are inefficient radiators (the ideal radiator, in fact, would be perfectly black). Because of this, the earliest proto-stellar clouds tended to heat up significantly as they collapsed, causing them to rebound and dissipate instead of collapsing to form stars. In the early, hydrogen-and-helium-only Universe, Jeans estimated, a proto-stellar cloud could not collapse to form a star unless it was hundreds of times the mass of the Sun. The first generation of stars born after the big bang were truly massive.
More massive stars require more vigorous fusion to overcome the inward pull of gravity (more on this below), leading to greater energy output and higher surface temperatures. In fact, the very first stars were so prodigiously hot that they put out copious amounts of UV radiation. This UV radiation allows us to date the time of their formation: the light put out by these stars was the first thing since the recombination event that was higher in energy than the energy of an electron bound to a proton to form hydrogen. Thus, as the first stars ignited, electrons once again found themselves ripped away from their atoms. Like sunlight burning off a morning fog, the light of these early stars “re-ionized” the clouds of neutral hydrogen and helium created by recombination and turned them once again into a plasma of free electrons and nuclei. Using the Hubble Space Telescope to peer at the most distant observable objects—which is the equivalent to looking back 13 billion years to what was happening just 800 million years after the big bang—astronomers have observed the spectral fingerprints of neutral hydrogen, suggesting that the re-ionization was not yet complete at that time.
The Heavy Elements
The first-generation stars, known for rather arbitrary, historical reasons as “population III stars,” were composed solely of the hydrogen and helium synthesized in the big bang. This is not the stuff of which life can be made; life requires chemistry, and, again, the only chemistry based on hydrogen and helium is the formation of molecular hydrogen (H2). Life is based on heavier atoms, which astronomers (erroneously, from a chemist’s perspective) refer to as “metals.” Where did these metals, so critical to the origins of life, come from? They are produced in the life and death of stars.
The center of the Sun, to pick our own star as an example, is a toasty 16 million kelvins, a temperature at which the kinetic energy of protons is sufficient to overcome the electrostatic repulsion between two like-charged protons and allow fusion to occur. As we discussed above, the nuclei intermediate in mass between 1H and 4He are unstable relative to 4He, and thus the deuterium, tritium, and 3He that are formed as intermediates are quickly consumed, with the net result being the production of 4He, two electrons (to balance the charge), and a great deal of energy.* This energy, of course, ultimately provides the disequilibrium on which most Terrestrial life is based. It also prevents the Sun from collapsing under the weight of its own massive bulk.
The outward pressure caused by fusion in the Sun’s core counteracts gravity’s incessant attempts to cause the star to collapse further, and a “truce” is set up in which they are perfectly balanced. And although this truce can last a long time, it is nevertheless still temporary; in another 6 billion years, for example, the Sun will consume all the hydrogen in its core (it’s currently down to just 33% hydrogen), fusion will stop, and gravity will begin to win. Since the gravitational pull of a larger star is, of course, larger, the counteracting pressure induced by fusion must also be higher. Thus, the equilibrium between the forces that want to tear the star apart and those that want to collapse it generally settles at higher values, meaning higher temperature, higher density, and higher rates of fusion. For this reason, and perhaps counterintuitively, larger stars burn faster and live shorter lives than smaller stars: if the mass of a star is doubled, the rate of fusion must increase tenfold to overcome the increased gravity, thus shortening the star’s life fivefold (twice the fuel burning at 10 times the rate). A tenfold increase in mass leads to a 3200-fold increase in the rate of fusion and a 320-fold decrease in lifetime, such that a star 10 times the mass of the Sun will barely live to see 30 million years.
And what happens when a star runs out of hydrogen fuel in its core? As fusion slows, the outward pressure it produces decreases, and gravity begins to win this stellar tug-of-war. Eventually, the temperature and pressure in the shell of unfused hydrogen immediately surrounding the star’s core rise sufficiently to cause fusion in a zone just outside the core. With the sudden production of energy so near its surface, the outer layers of the star expand dramatically; when this happens to the Sun, it will swell enough to engulf the terrestrial planets, and the Earth will have ended its 11-billion-year run. We suppose there is a philosophical point in that, as well, but what to make of it, we’ll leave to the reader.
This bloated phase of a star’s life history, called the red giant stage, lasts for only a few hundred million years. Meanwhile, the star’s helium-rich core continues to contract and, with that, heat up. When it gets hot enough, two new reactions kick in: the fusion of three 4He to produce 12C and the fusion of 4He with 12C to produce 16O. Because these larger nuclei are more highly charged than the hydrogen nucleus, they repel one another more strongly, and so their fusion requires core temperatures of at least 150 million kelvins. Such high temperatures are only reached in stars at least 80% as massive as the Sun; smaller stars never ignite helium fusion, so, after completing their red giant stage, they cool and contract into white dwarfs before eventually dying.
Helium fusion differs significantly from hydrogen fusion in that the former requires the simultaneous fusion of three nuclei rather than two. This occurs because, as we’ve noted, none of the nuclei intermediate in mass between 4He and 12C are stable relative to 4He (see fig. 2.2), and thus the formation of nuclei intermediate between them does not produce energy. Remember that 12C was not formed during the expanding big bang because trinuclear collisions were too rare at the low densities found by the time the fusion of hydrogen to helium had progressed significantly. In fact, even in the highly compressed core of the post–red giant Sun, the density should still be too low for the efficient formation of carbon.
The deeper problem with trinuclear reactions is that the vast majority of nuclear collisions are nonproductive. For example, the first fusion step in hydrogen burning—the fusion of two protons to form deuterium (and an electron)—takes place only a few times for every trillion collisions. This startlingly poor efficiency occurs because the fusion reaction liberates energy, and this excess energy tears the newly formed nucleus apart, reversing the reaction. The low efficiency isn’t much of a problem, though, for dinuclear reactions; dinuclear collisions occur frequently enough that, even if very few of them are productive, fusion hums along at a reasonable pace. This is not true for trinuclear reactions, for which low efficiency would be prohibitive. Considering this problem in 1939, Hans Bethe, whom, six years later, Gamow would humorously add to his big bang paper author list, concluded that “there is no way in which nuclei heavier than helium can be produced permanently in the interior of stars under present conditions. We can therefore drop the discussion of the building up of elements entirely and confine ourselves to the energy production, which is, in fact, the only observable process in stars.”* Bethe was probably right in focusing on energy production in stars as this is what won him the 1967 Nobel Prize. But he was wrong about their inability to create carbon.
Pondering the carbon issue, the astrophysicist Fred Hoyle (author of the “life in space” novel mentioned in the previous chapter) later realized that, in order for carbon to exist, the carbon nucleus must contain a resonance. That is, the carbon nucleus must be able to form an “excited state” exactly equal in energy to (i.e., is “resonant” with) the energy liberated by the fusion of three 4He nuclei. Nuclear excited states such as this are analogous to the electronic excited states of molecules; that is, states in which electrons have been “excited” into higher-energy, previously unoccupied atomic or molecular orbitals. The energy required for an electron to jump from its “normal,” low-energy orbital into one of these higher-energy, excited orbitals is the reason that many molecules absorb light and are thus colored. In the case of this particular nuclear excited state, the energy it absorbs prevents the energy liberated by fusion from rupturing the nascent nucleus, increasing the reaction’s efficiency to one in 104, a 10-millionfold improvement over the efficiency estimated for the reaction in the absence of such a resonance.
Hoyle predicted this resonance in 1953, and it was confirmed just a few months later by Ward Whaling (1923–2020) and Willie Fowler (1911–1995) at the California Institute of Technology (Caltech), the latter of whom received the 1983 Nobel Prize for his work on nucleosynthesis. To test Hoyle’s prediction, the Caltech researchers bombarded 14N with a deuteron (2H nucleus) to produce 12C and an α-particle (4He nucleus). Per Hoyle’s prediction, the resulting α-particles emerged with two energies: some had the energy expected for the reaction, but others had less energy, with the difference corresponding to the energy left behind to form the excited carbon nucleus at exactly the energy level predicted by Hoyle.
Although he did not pitch it in these terms at the time, Hoyle’s argument, it was later realized, was an early invocation of what is now known as the anthropic principle (fig. 2.5). That is, Hoyle did not necessarily know the precise details of the structure of the carbon nucleus, but because such a resonance had to occur in order for carbon to be formed, and because carbon had to be common for us to be here to ponder this issue, there must be such a resonance.
More broadly, the anthropic principle simply notes that living observers will always find themselves in universes capable of supporting life, an observation that profoundly influences what our existence tells us about the broader relationship between life and the Universe. Specifically, physicists should not be surprised to find the physical parameters of our Universe, including, for example, the parameters that go into defining the carbon nuclear resonance, seemingly perfectly “fine-tuned” to allow for living physicists to arise, no matter how “coincidental” such tuning may appear. More generally, if the Universe were not suitable to support life, living observers like us would not have arisen to study the Universe and raise the point in the first place. We touch on this issue (which we discuss in detail in sidebar 2.3) time and again throughout the rest of this book, so you may as well get comfortable with it.
Leaving aside, for the moment, the discovery of carbon’s nuclear resonance, let’s return to the story at hand. The helium in the Sun’s core will run out only a couple of billion years after helium fusion begins, rather significantly less than the 11-billion-year span of hydrogen fusion. The shorter duration of helium fusion occurs for two reasons. The first is that helium fusion produces less energy per nucleon than hydrogen fusion (see fig. 2.2), and thus, in order to balance the Sun’s gravitational contraction, the helium core must fuse more vigorously than the earlier hydrogen core. The second is that, because helium fusion requires higher temperatures than hydrogen fusion, it is limited to a smaller volume nearer the Sun’s center, so there is less helium that can fuse. Thus, after only 2 billion years, helium fusion will stop and the Sun will consist of a carbon-rich core surrounded by a helium-rich shell, surrounded in turn by a thick outer shell of primordial hydrogen and helium. When this happens, the Sun is doomed; bad news for any surviving Earthlings who may have escaped to Saturn’s moon Titan when the Earth was destroyed during the onset of the red giant stage a couple of billion years earlier. That is, although the Sun will begin to contract again after the helium burning stage, it doesn’t have enough mass to achieve the pressures and temperatures required to ignite the fusion of carbon and oxygen. The Sun will thus slowly collapse under its own weight, forming a white dwarf that cools over billions of years into a black, cold ember.
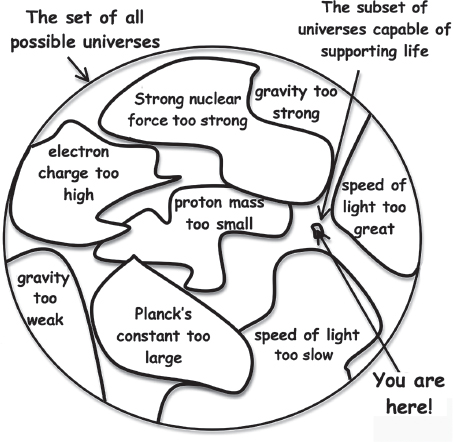
Figure 2.5 How many ways can a universe be constructed, each with different values of the many fundamental constants that describe it? And of the myriad possible universes, how many are capable of supporting life? The most likely answer to the latter question is “a vanishingly small fraction.” Nevertheless, it is not simply a lucky coincidence that our Universe just happens to be one of these rare, “special” universes that are habitable.
Of course, for the purpose discussed here—namely, how to enrich the Universe with heavier elements—metals locked in some cold, dark dwarf star are of little use. During the red giant phase, however, some of the heavier elements do leak out. The rate of helium fusion is extremely sensitive to temperature: it is proportional to temperature to the fortieth power, so even a 2% change in temperature will double the rate of fusion. As a result, any small increase in temperature accelerates helium burning, causing the temperature—and thus the fusion rate—to rise further. This increase in temperature, however, also causes the outer shell of the star to expand, which reduces the pressure in the core, ultimately slowing fusion. This oscillation drives the outer regions of the star to pulse in and out until, eventually, the motion becomes so vigorous that the star tosses its outermost atmosphere into space. The resulting explosion, which seeds the Universe with the heavier elements that the star has produced, is so bright that it often shows up in the sky as a new star, and thus its name: nova, from the Latin word for “new” (fig. 2.6, left).
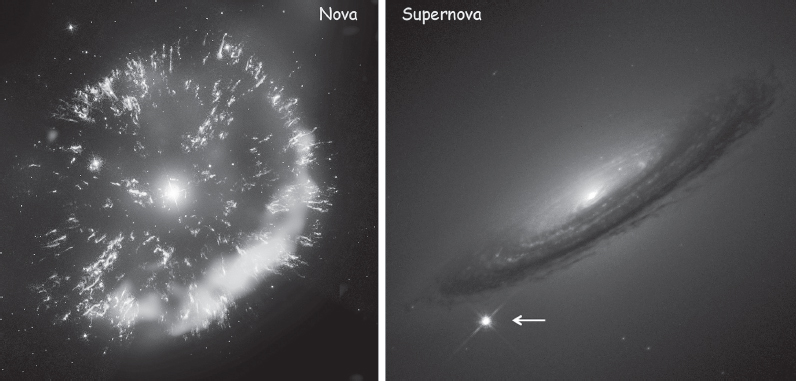
Figure 2.6 Stars seed the Universe with heavier elements, some as novae, others as supernovae. Novae occur when stars at least 80% the mass of our Sun evolve into red giants, which shed their outer atmospheres into space. Shown on the left is GK Persei, the remnants of a nova 1,500 light-years away that was, for a few weeks in 1901, the fourth brightest star in our sky. In contrast, a star of at least eight times the mass of the Sun ultimately collapses and rebounds in an enormously more powerful “supernova” explosion, which can shine as brightly as all the other stars in its host galaxy together. Shown by the arrow on the right is supernova 1994D, which took place in the galaxy NGC 4526, 55 million light-years from Earth. (Left image courtesy of NASA/CXC/RIKEND/STSci/NRAO/D, Takei et al.; right image courtesy of NASA/STScI)
We are all made of stardust. But stars such as the Sun stop their fusion reactions at helium burning and thus are not the source of many key biological elements. Stars much larger than the Sun, however, go on to create heavier atoms. In stars at least eight times heavier than the Sun, for example, the rise in pressure and temperature is sufficient to ignite the fusion of carbon with its own kind and with oxygen-16 (produced by the fusion of carbon and helium) to form magnesium-24, magnesium-23 (releasing a free neutron), sodium-23 (liberating a free proton), and silicon-28. Given that these reactions require still higher temperatures and pressures (the larger charges associated with carbon and oxygen nuclei require higher temperatures to overcome the associated larger electrostatic repulsions), they occur in a still smaller volume of the central core and continue for an even shorter time than the helium fusion era. In fact, the fusion phase of carbon and oxygen lasts only about a thousand years! And when the core becomes depleted of elements? You guessed it. More contraction, higher core temperatures, and fusion that forms heavier nuclei, with each fusion reaction phase lasting for shorter and shorter periods. This leaves behind concentric layers of hydrogen, helium, carbon, and so on, like a weird, spherical layer cake.
But this cycle does not continue ad infinitum. Eventually, silicon-28 fuses to form iron-56 (56Fe), but if you look at the chart of nuclear binding energies (see fig. 2.2), you’ll see that, at this isotope, we’ve hit rock bottom. Any further fusion consumes rather than liberates energy. In just hours, the silicon fusion reaction burns to completion, leaving behind a small, iron-rich core in which no further fusion is possible. Catastrophic collapse, postponed so long, can be averted no longer.
When energy production in the core stops, the core collapses under its own gravity, which is so strong that electrons are forced into protons to produce neutrons: what was once a billion-kelvin ball of plasma a few million kilometers across rapidly collapses to form a neutron star just 10 km in diameter. The outer layers of the star, no longer supported by the core, fall into this mass of neutrons within seconds. The resulting rebound causes a massive shockwave that ricochets through the outer, lighter, still fusible layers, heating and compressing them and producing a massive pulse of fusion. This, in turn, produces an extraordinary density of free neutrons, which, because they are neutral and need not overcome the electrostatic repulsion of the nucleus, avidly combine with any nuclei with which they collide to produce massive amounts of heavier, more neutron-rich nuclei. Many neutron-rich nuclei, however, are unstable and rapidly decay, typically by emitting electrons. This converts the excess neutrons into protons, raising the atomic number (while retaining the atomic mass) of nuclei and producing many of the stable nuclei heavier than iron. With the rebound of the infalling material off the core, and the intense burst of fusion as the lighter, outer layers collapse inward, this new material spews into space at speeds approaching a few percent of the speed of light. Within seconds, a star that was many times as massive as the Sun is torn asunder in a titanic “supernova” explosion that, for a short time, is comparable in brightness to all the rest of its galaxy (fig. 2.6, right). The core of the star, in contrast, remains behind as either a neutron star or a black hole. That is, if the mass of the remaining core is less than 2.4 times that of the Sun, the force of its gravity crushes its electrons into its protons, producing a solid mass of neutrons a few tens of kilometers across, but if its mass is more than 2.4 times that of the Sun, its gravity can overcome even neutron-neutron repulsion, and it collapses further to form a black hole.
While supernovae seed galaxies with elements up to and a bit beyond iron’s atomic mass (what with all those neutrons whizzing about, some additional, energetically “uphill” nuclei are formed during the final, cataclysmic explosion), it had long proven difficult to account for the abundances of the still heavier elements. Their source became clear, however, in August 2017 when the Laser Interferometer Gravitational-Wave Observatory (fig. 2.7, left) observed a gravitational wave signature indicative of the merger of two neutron stars that had hitherto been in close orbit around one another.* Subsequent telescopic studies at visible, x-ray, and γ-ray wavelengths identified the formation of 16,000 Earth-masses of neutron-rich, high-mass nuclei in the matter splashed out by this “kilonova” (so named because it is about 1,000 times brighter than the nova described above), which occurred in the elliptical galaxy NGC 4993, some 140 million light-years from Earth (fig. 2.7, right). We now believe that such mergers, which happen about once every 10,000 years in the Milky Way, are responsible for the creation of about half of all matter heavier than iron.
Some 100 million high-mass stars have died during the more than 12-billion-year lifetime of the Milky Way to date, going nova, supernova and, rarely, kilonova in the process. That is fewer than one-tenth of 1% of all the stars ever born in our galaxy, but it’s still been enough to convert about 2% of the original hydrogen and helium into heavier elements, leaving later-generation stars like ours relatively enriched in such atoms. Indeed, studies of the elemental and isotopic composition of the Sun indicate that it is a third-generation star (termed a “population I star”—again, for historical reasons). “Population II stars,” the second generation of stars formed after the big bang, are also extremely common. In fact, spectroscopic measurements, which allow us to assay the metal content of stars by the colors of the light they emit, indicate that the majority of stars in the outer half of our galaxy are from this second generation, with membership in this population indicated by the relative paucity of “metallic” atoms heavier than helium. Careful inspection of the spectra of these stars indicates, however, that they do contain some metal, so they are not the first generation of stars. But unlike our third-generation, relatively metal-rich Sun, these stars were born very shortly after formation of the galaxy. And what of the Sun’s grandparents, the population III stars formed from the primordial gas of the big bang? As noted above, the first stars to form were probably quite large because the paucity of metals in the early Universe prevented the cooling required for smaller gas clouds to collapse to form stars. Those massive, first-generation, population III stars would have gone supernova within a few million years, neatly accounting for the fact that, while we see many metal-poor, population II stars in the Milky Way, intensive searches have identified only two candidate stars that are very nearly metal free. The metal abundance in the two stars is less than 1/300,000 that of the Sun, and so these may be among the most ancient of stars. The metals so rapidly produced—and released in supernova explosions—by the population III stars would have contributed, in turn, to the metal composition of the second-generation, population II stars.

Figure 2.7 On August 17, 2017, the Laser Interferometer Gravitational-Wave Observatory (LIGO), shown on the left, detected the gravitational waves produced by two co-orbiting neutron stars, each of mass similar to that of our Sun, as they spiraled toward one another at near light speed before coalescing to form a black hole. LIGO achieved this by monitoring the distance between test masses at the ends of the observatory’s 4 km long arms (shown); as the gravitational wave rhythmically warped space itself, the distances between the masses changed by an amount equivalent to a thousandth of the diameter of a proton. Immediate follow-up studies with optical (shown on the right are visible light images), x-ray, and γ-ray telescopes captured the radioactive decay of the neutron-rich, high atomic weight nuclei produced as the merger sprayed neutron-rich material into space. (Left image courtesy of Caltech/MIT/LIGO Laboratory; right image courtesy of NASA and ESA)
Stellar Requirements for the Origins and Evolution of Life
So far it seems easy: make a universe, fill it with hydrogen and helium, let those elements contract and ignite, and let the resulting stars go nova, supernova, and, rarely, kilonova for a couple of generations to seed space with heavier elements, eventually producing metal-rich, third-generation stars and setting the stage for life, or at least potentially habitable solar systems, to arise. But it may not be so simple. Evidence collected over the past few decades suggests that stars capable of supporting inhabitable planets may be rather rare.
The Sun is not all that typical a star. For example, even a cursory survey of the map of nearby stars reveals that ours is different. For one, the Sun is solitary. Because they are born in densely packed stellar nurseries (more on this in chapter 3), about 85% of all stars occur in multiple-star systems in which two or more stars are in orbit around their common center of mass. Given the complex gravitational tugs associated with being in orbit around—or even near—two or more stars, stable planetary orbits are more difficult to achieve in such systems.
The Sun’s size also bodes well for its ability to support life while further rendering it somewhat special. The massiveness of the Sun is often underappreciated because it lies more or less in the middle of the size range between the most and least massive stars. But because they form more rarely and because they have much shorter life spans, larger stars are exponentially less common than smaller stars, and thus the Sun is in the top 10% of all stars in terms of its mass.* And the size of the Sun is a critical element in its ability to support the origins and evolution of life. Were the Sun smaller, like the red dwarf stars that outnumber it more than tenfold, it would be so cool and dim that the volume of its “habitable zone”—the region in which liquid water can form—would be positively puny.** For example, the habitable zone of Barnard’s star, a typical red dwarf, six light-years away and thus the second closest stellar system to our own, extends out to only one-twentieth the distance of Mercury’s orbit around the Sun. This is a problem. Specifically, the height of tides (like the nearly twice-daily rise and fall of the Earth’s oceans) drops off inversely with the cube of orbital radius, an effect that has important consequences here. The friction generated as this tidal “bulge” is dragged around a planet (or moon) has the net effect of bleeding rotational energy away as heat, thus slowing the rotation (the length of the day on Earth, for example, has increased by about two hours in the past 600 million years). Ultimately, the length of the “day” would increase so much that it would match the length of the “year,” causing the bulge to stop moving around the planet and the planet to spend the rest of eternity with one face locked forever toward its star and the other in perpetual cold and darkness. (By analogy, tides raised by the Earth in the Lunar crust long ago forced the Moon into such a resonance, which is why we only ever see one side of it.) For a planet in the habitable zone of a red dwarf, the tides would be so large that this “tidal locking” would occur within a few hundred million years. Not, perhaps, the most likely environment to support life, because—apart from any other reason—volatiles such as water would rapidly migrate from the warm, dayside of the planet to the bitterly cold nightside, where water would freeze and remain forever unavailable. Calculations suggest that the habitable zone does not move out beyond the zone of tidal locking until a star is at least 40% the mass of the Sun (fig. 2.8).
Conversely, it is also important that the Sun is not too large, lest it burn out before life had time to arise. As noted above, the Sun is small enough that it will remain in its hydrogen-burning phase for some 11 billion years, which is plenty of time for life to arise and evolve. A star twice the mass of the Sun, in contrast, would last for less than a billion years. All in all, only about 5% of all stars lie within the narrow range between being massive enough to push the habitable zone beyond the reach of rapid tidal locking, yet small enough to remain stable for hundreds of millions of years.
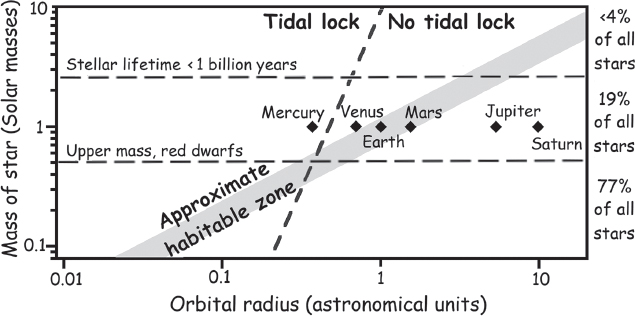
Figure 2.8 Both the habitable zone (gray band in the figure) and the tidal locking zone (in which one face of a planet is locked forever toward its star) shrink as stellar mass decreases. Because red dwarf stars are dim, their habitable zones lie within their tidal locking zones, rendering it far less likely that such stars—which are by far the most abundant stars in the Universe—can support life. For scale, our Solar System is shown. Mercury is just within the tidal locking region but, due to its highly eccentric (noncircular) orbit, is locked into a 2:3 resonance in which the planet revolves three times for each two orbits it makes around the Sun.
Galactic Requirements for the Origins and Evolution of Life
To make matters worse for potential extraterrestrials, the Sun’s special nature may not be limited to its size and lack of stellar companions. It may also extend to its placement in our galaxy. Research on the topic suggests that the origins of life are in line with so many other aspects of existence in which the three secrets to success are “location, location, location.”
The Sun orbits the center of the Milky Way at a distance of 26,700 light-years (plus or minus 1,300 light-years), taking 230 million years to complete each, nearly perfectly circular trip. This distance is near optimal in terms of the Sun’s ability to support a life-bearing planet. Nearer to the center of the Milky Way, the density of stars becomes greater, rapidly climbing to densities so high that supernova explosions are frequent enough and close enough to sterilize planets on a rapid timescale compared with life’s evolution. Nearer still to the center, the x-rays produced by the massive (four million Solar masses) black hole that resides there would destroy the complex molecules associated with life (fig. 2.9). Much farther out than the Sun’s orbit, all the stars are metal-poor, population II stars. Without the heavier elements, planet formation is likely inhibited, and what planets exist are probably poor substrates for life. In combination, these conditions produce what is known as the galactic habitable zone. And whereas the galactic habitable zone does make up a fair fraction of the volume of our galaxy, it is a sparsely populated fraction. Our best estimate is that, at any given time, only approximately 10% of the stars in the Milky Way reside within its habitable zone. The existence of life on our planet, from simple microorganisms to human beings, is a result of the unique conditions that exist in this zone.
Of course, merely being in the galactic habitable zone at a given time is only part of the equation. Just as critically, in order to bear life, a star must remain in the habitable zone for a sufficient length of time. And most stars do not. The eccentricity of the Sun’s orbit around the galactic center is extremely small; that is, the Sun’s orbit traces out an almost perfect circle. Because of this, the Sun—and with it the Earth—remains at a near constant distance from the galactic center, which provides a safe haven from the potentially disruptive effects we’ve just described. Such low-eccentricity orbits are relatively rare, however, and the large majority of the Sun-like stars currently in our neighborhood spend a significant fraction of each galactic orbit far too close to the galactic center for comfort. Taken together with the relatively small size of the galactic habitable zone, the eccentricity of the majority of Sun-type stars is sufficiently great that fewer than 5% of the stars in the Milky Way remain permanently in its life-supporting zone. Thus, when considered together with the stellar size limits and the frequency of multiple-star systems, only a tiny fraction of the stars in the Milky Way seem to be well placed to support life (see sidebar 2.4).

Figure 2.9 In 2019, astronomers of the Event Horizon Telescope project captured the first image of a black hole silhouetted against the glowing ring of plasma spiraling into it. The feat required connecting radio telescopes at eight sites around the globe (including the South Pole) to create a single virtual telescope with the resolving power of a single telescope nearly as large as the Earth itself. The black hole, which weighs in at 6.5 billion times the mass of the Sun, lies at the center of the galaxy M87, some 55 million light-years from Earth. In contrast, the black hole at the center of our own galaxy, called Sagittarius A*, weighs in at only 4 million solar masses. (Courtesy of ETH collaboration)
Conclusions
Our understanding of the origins of the Universe is reaching a fair degree of maturity. The big bang model is now a highly quantitative and compellingly confirmed model of how everything within and around us came into being. With this understanding of our origins, though, comes an appreciation of the vast number of things that had to be right for a universe to be habitable. If the Universe were too dense, it wouldn’t have survived long enough to make us. If it were too sparse, galaxies and their associated stars and heavy elements would not have formed. Were there no resonance in the 12C nucleus, there would be no heavy atoms, no chemistry, no life. And on, and on. Of course, these fundamental properties of the Universe are not the only things that had to be just right to create conditions for life. The size of the Sun, its location in our galaxy (and thus its metal content), and its low-eccentricity galactic orbit all seem to be critical aspects of the recipe that makes our planet habitable.
And what of Gamow, Alpher, Penzias, Wilson, Dicke, Peebles, and Wilkinson? Gamow died in 1968, just three years after Penzias and Wilson’s striking confirmation of his theory. A decade later, the latter two shared the 1978 Nobel Prize in Physics for their discovery—although, perhaps unfairly, they did not share it with either Alpher, Gamow’s then still-living student, or the Princeton group who were the first to explain the implications of that annoyingly persistent radiofrequency hiss.*
Further Reading
The Big Bang
Weinberg, Steven. The First Three Minutes: A Modern View of the Origin of the Universe. New York: Basic Books, 2020.
Stellar Nucleosynthesis
Bethe, Hans. “Energy Production in Stars.” Physical Review 55 (1939): 434–56.
The Anthropic Principle
Barrow, John D., and Frank J Tippler. The Anthropic Cosmological Principle. Oxford, UK: Oxford University Press, 1988.
The Galactic Habitable Zone
Lineweaver, Charles H., Yeshe Fenner, and Brad K. Gibson. “The Galactic Habitable Zone and the Age Distribution of Complex Life in the Milky Way.” Science 303, no. 5654 (2004): 59–62.
- * Hubble’s value for the absolute brightness of his cepheid was off; Andromeda is actually 2.54 million light-years from Earth.
- * The name was coined by the theorist Fred Hoyle, who, as mentioned in the prior chapter, was a proponent of the competing, but now disproven, “steady state” theory of the origins of the Universe, which postulated, despite the expansion first observed by Hubble, that the Universe remains statistically unchanged as new matter is constantly created from nothing, keeping the density of the Universe constant despite its propensity to expand. In coining the phrase “big bang,” a term Hoyle thought derisive, he was trying to belittle the hypothesis. He seems to have failed.
- * Hydrogen bombs are, in fact, tritium and deuterium bombs; because there are spare nucleons to carry off the energy liberated in fusion, these nuclei fuse much more efficiently than hydrogen, rendering it easier to detonate such a bomb.
- * Although the lifetime of the neutron has been studied for decades, and measurements from individual experiments now have precisions of better than a second, the two main experimental methods to this end (“bottle” and “beam”) produce values that differ by nine seconds. It’s a mystery.
- * In the olden days, when our television sets were hooked up to antennas rather than the internet, we had the pleasure of seeing these ourselves. About 1% of the “snow” seen when an antenna-linked, analog TV is tuned to a nontransmitting channel represents relic big bang photons red-shifted to television transmission frequencies.
- * That said, the 275 W/m3 produced in the Sun’s core (much less its outer layers) is far less than the 1,250 W/m3 produced by human flesh. The Sun, however, is rather larger than the human body.
- * Hans Bethe, “Energy Production in Stars,” Physical Review 55 (1939): 434–56.
- * Gravitational waves, which are sinusoidal oscillations of space itself, are detected by monitoring the distance between two test masses 4 km apart. As the gravitational wave passes, the space between the masses rhythmically expands and contracts by an amount equivalent to one-thousandth of the diameter of a proton.
- * That is, in galaxies like ours. In elliptical galaxies, which are quite common, dwarf stars outnumber Sun-like stars by an even larger margin.
- **Admittedly, this argument ignores potential habitats outside the traditional habitable zone, such as within the geothermally heated crust of a moon or planet. This is a topic we’ll explore in detail in chapter 9.
- * Jim Peebles, though, did win the 2019 Nobel Prize in Physics for his many contributions to theoretical cosmology.