Chapter 4

Stereochemistry and Conformation

The discussions in Chapters 1–3 focused on electron distribution in organic molecules. In this chapter, the focus will be on the 3D structure of organic compounds.¹ The structure may be such that stereoisomerism² is possible. Stereoisomers are compounds made up of the same atoms bonded by the same sequence of bonds, but having different 3D structures that are not interchangeable. These structures are called configurations.

4.A. Optical Activity and Chirality3

Any material that rotates the plane of polarized light is said to be optically active. If a pure compound is optically active, the molecule is nonsuperimposable on its mirror image. If a molecule is superimposable on its mirror image, the two structures constitute the same compound and the compound does not rotate the plane of polarized light; it is optically inactive. The property of nonsuperimposability of an object on its mirror image is called chirality. If a molecule is not superimposable on its mirror image, it is chiral. If it is superimposable on its mirror image, it is achiral. The relationship between optical activity and chirality is absolute. No exceptions are known, and many thousands of cases have been found in accord with it (however, see Sec. 4.C). The ultimate criterion, then, for optical activity is chirality (nonsuperimposability on the mirror image). This finding is both a necessary and a sufficient condition.⁴ This fact has been used as evidence for the structure determination of many compounds, and historically the tetrahedral nature of carbon was deduced from the hypothesis that the relationship might be true. Note that parity violation represents an essential property of particle and atomic handedness, and has been related to chirality.⁵

If a molecule is nonsuperimposable on its mirror image, the mirror image must be a different molecule, since superimposability is the same as identity. In each case of optical activity of a pure compound there are two and only two isomers, called enantiomers (sometimes enantiomorphs), which differ in structure only in the left- and right-handedness of their orientations (see the enantiomers for 2-butanol in Fig. 4.1). Enantiomers have identical⁶ physical and chemical properties except in two important respects:

1. They rotate the plane of polarized light in opposite directions, although in equal amounts. The isomer that rotates the plane to the left (counterclockwise) is called the levo isomer and is designated (−), while the one that rotates the plane to the right (clockwise) is called the dextro isomer and is designated (+). Because they differ in this property they are often called optical antipodes.

2. They may react at different rates with other chiral compounds. These rates may be so close together that the distinction is practically useless, or they may be so far apart that one enantiomer undergoes the reaction at a convenient rate while the other does not react at all. This finding is the reason that many compounds are biologically active while their enantiomers are not. Enantiomers react at the same rate with achiral compounds.⁷

Fig. 4.1 Enantiomers of 2-butanol.

In general, it may be said that enantiomers have identical properties in a symmetrical environment, but their properties may differ in an unsymmetrical environment.⁸ Besides the important differences previously noted, enantiomers may react at different rates with achiral molecules if an optically active catalyst is present; they may have different solubilities in an optically active solvent; they may have different indexes of refraction or absorption spectra when examined with circularly polarized light, and so on. In most cases, these differences are too small to be useful and are often too small to be measured.

Although pure compounds are always optically active if they are composed of chiral molecules, mixtures of equal amounts of enantiomers are optically inactive since the equal and opposite rotations cancel. Such mixtures are called racemic mixtures⁹ or racemates.¹⁰ Their properties are not always the same as those of the individual enantiomers. The properties in the gaseous or liquid state or in solution usually are the same, since such a mixture is nearly ideal, but properties involving the solid state¹¹ (e.g., melting points, solubilities, and heats of fusion), are often different. Thus racemic tartaric acid has a melting point of 204–206 °C and a solubility in water at 20 °C of 206 g L⁻¹ while for the (+) or the (−) enantiomer, the corresponding figures are 170 °C and 1390 g L⁻¹. The separation of a racemic mixture into its two optically active components is called resolution. The presence of optical activity always proves that a given compound is chiral, but its absence does not prove that the compound is achiral. A compound that is optically inactive may be achiral, or it may be a racemic mixture (see also, Sec. 4.C).

4.A.i. Dependence of Rotation on Conditions of Measurement

The amount of rotation α is not a constant for a given enantiomer; it depends on the length of the sample vessel, the temperature, the solvent¹² and concentration (for solutions), the pressure (for gases), and the wavelength of light.¹³ Of course, rotations determined for the same compound under the same conditions are identical. The length of the vessel and the concentration or pressure determine the number of molecules in the path of the beam, and α is linear with this. To make it possible for one value of α for a pure compound to be compared with another α for that compound taken under different circumstances, a physical property is defined, called the specific rotation [α], which is

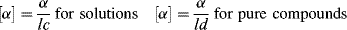
where α is the observed rotation, l is the cell length in decimeters, c is the concentration in grams per milliliter, and d is the density in the same units. The specific rotation is usually given along with the temperature and wavelength of light used for the measurement, in this manner: 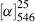. These conditions must be duplicated for comparison of rotations, since there is no way to put them into a simple formula. The expression [α]_D means that the rotation was measured with sodium D light; that is, λ = 589 nm. The molar rotation 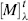is the specific rotation times the molecular weight divided by 100.

It must be emphasized that the value of α changes with conditions, but the molecular structure is unchanged. This finding is true even when the changes in conditions are sufficient to change not only the amount of rotation, but even the direction. Thus one of the enantiomers of aspartic acid, when dissolved in water, has [α]_D equal to +4.36° at 20°C and −1.86° at 90 °C, although the molecular structure is unchanged. A consequence of such cases is that there is a temperature at which there is no rotation (in this case 75°C). Of course, the other enantiomer exhibits opposite behavior.

Other cases are known in which the direction of rotation is reversed by changes in wavelength, solvent, and even concentration.¹⁴ In theory, there should be no change in [α] with concentration, since this is taken into account in the formula, but associations, dissociations, and solute–solvent interactions often cause nonlinear behavior. For example, 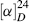for (−)-2-ethyl-2-methylsuccinic acid in CHCl₃ is −5.0° at c = 16.5 g 100 mL⁻¹ (0.165 g mL⁻¹), −0.7° at c = 10.6, +1.7° at c = 8.5, and +18.9° at c = 2.2.¹⁵ Note that the concentration is sometimes reported in g 100 mL⁻¹ (as shown) or as g dL⁻¹ (decaliters) rather than the standard g mL⁻¹. One should always check the concentration term to be certain. Note that calculation of the optical rotation of (R)-(−)-3-chloro-1-butene found a remarkably large dependence on the C=C–C–C torsional angle.¹⁶ However, the observed rotations are a factor of 2.6 smaller than the calculated values, independent of both conformation and wavelength from 589 to 365 nm.

4.B. What Kinds of Molecules Display Optical Activity?

Although the ultimate criterion is, of course, nonsuperimposability on the mirror image (chirality), other tests may be used that are simpler to apply, but not always accurate. One such test is the presence of a plane of symmetry.17 A plane of symmetry¹⁸ (also called a mirror plane) is a plane passing through an object such that the part on one side of the plane is the exact reflection of the part on the other side (the plane acting as a mirror). Compounds possessing such a plane are always optically inactive, but there are a few cases known in which compounds lack a plane of symmetry and are nevertheless inactive. Such compounds possess a center of symmetry (e.g., in α-truxillic acid), or an alternating axis of symmetry as in 1.¹⁹ A center of symmetry¹⁸ is a point within an object such that a straight line drawn from any part or element of the object to the center and extended an equal distance on the other side encounters an equal part or element. An alternating axis of symmetry¹⁸ of order n is an axis such that when an object containing such an axis is rotated by 360°/n about the axis and then reflection is effected across a plane at right angles to the axis, a new object is obtained that is indistinguishable from the original one. Compounds that lack an alternating axis of symmetry are always chiral.

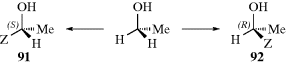
A molecule that contains just one stereogenic carbon atom (defined as a carbon atom connected to four different groups; also called a chiral atom or an asymmetric carbon atom) is always chiral, and hence optically active.²⁰ As seen in Fig. 4.1, such a molecule cannot have a plane of symmetry, whatever the identity of the four atoms or groups, as long as they are all different. However, optical activity may be present in molecules with no stereogenic atom.²¹ Some molecules with two or more steroegenic carbon atoms, however, are superimposable on their mirror images (called meso compounds), and hence inactive principally because there is symmetry. Examples of such compounds will be discussed subsequently.

Optically active compounds may be classified into several categories.

1. Compounds with a Stereogenic Carbon Atom. If there is only one such atom, the molecule must be optically active, no matter how slight the differences are among the four groups. An example is 1,12-dibromo-6-methyldodecane, which has one stereogenic carbon and will be optically active. Optical activity has been detected even in cases²² (e.g., 1-butanol-1-d), where one group is hydrogen and another deuterium:²³ The stereogenic carbon is connected to OH, H, D, and a propyl group.

Although enantiomers will exhibit specific rotation of equal magnitude but opposite sign, the difference may be too small to be measured accurately. In optically active compounds, the amount of rotation is greatly dependent on the nature of the four groups, in general increasing with increasing differences in polarizabilities among the groups. Alkyl groups have very similar polarizabilities²⁴ and the optical activity of 5-ethyl-5-propylundecane is too low to be measurable at any wavelength between 280 and 580 nm.²⁵

2. Compounds with Other Quadrivalent Stereogenic Atoms.²⁶ Any molecule with an atom that has four bonds pointing to the corners of a tetrahedron will be optically active if the four groups are different. Among atoms in this category are Si,²⁷ Ge, Sn,²⁸ and N (in quaternary salts or N-oxides).²⁹ In sulfones, the sulfur bonds have a tetrahedral array, but since two of the groups are always oxygen, no chirality results. However, the preparation³⁰ of an optically active sulfone (2) in which one oxygen is ¹⁶O and the other is ¹⁸O illustrates the point that slight differences in groups are all that is necessary. This point has been taken even further with the preparation of ester 3, both enantiomers of which have been prepared.³¹ Optically active chiral phosphates (4) have similarly been made.³²

3. Compounds with Tervalent Stereogenic Atoms. Atoms with pyramidal bonding³³ might be expected to give rise to optical activity if the atom is connected to three different groups, since the unshared pair of electrons is analogous to a fourth group, necessarily different from the others. For example, a secondary or tertiary amine

where X, Y, and Z are different and the fourth group is the electron pair would be expected to be chiral and thus resolvable. Many attempts have been made to resolve such compounds, but until 1968 all of them failed because of pyramidal inversion (also called fluxional inversion), which is a rapid oscillation of the unshared pair from one side of the XYZ plane to the other, thus converting the molecule into its enantiomer.³⁴ For ammonia, there are 2 × 10¹¹ inversions every second. The inversion is less rapid in substituted ammonia derivatives³⁵ (amines, amides, etc.). The interconversion barrier for endo versus exo methyl in N-methyl-2-azabicyclo[2.2.1]heptane, for example, is 0.3 kcal mol⁻¹ (1.26 kJ mol⁻¹).³⁶ In this case, torsional strain plays a significant role, along with angle strain, in determining inversion barriers. Two types of nitrogen atom invert particularly slowly, namely, a nitrogen atom in a three-membered ring and a nitrogen atom connected to another atom bearing an

unshared pair. Even in such compounds, however, pyramidal inversion proved too rapid to permit isolation of separate isomers for many years. This goal was accomplished²⁹ only when compounds were synthesized in which both features are combined: a nitrogen atom in a three-membered ring connected to an atom containing an unshared pair. For example, the two isomers of 1-chloro-2-methylaziridine (5 and 6) were separated and do not interconvert at room temperature.³⁷ In suitable cases, this barrier to inversion can result in compounds that are optically active solely because of a chiral tervalent nitrogen atom. For example, 7 has been resolved into its separate enantiomers.³⁸ Note that in this case too, the nitrogen is connected to an atom with an unshared pair. Conformational stability has also been demonstrated for oxaziridines,³⁹ diaziridines (e.g., 8),⁴⁰ triaziridines (e.g., 9),⁴¹ and 1,2-oxazolidines (e.g., 10),⁴² even though in this case the ring is five membered. However, note that the nitrogen atom in 10 is connected to two oxygen atoms.

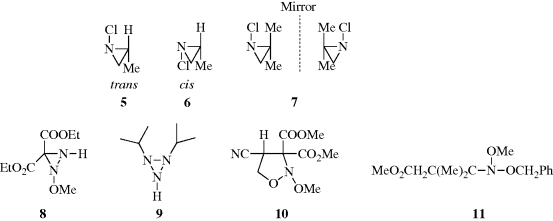
Compound 11 is another example in which nitrogen is connected to two oxygen atoms. In this case there is no ring at all, but it has been resolved into (+) and (−) enantiomers .⁴³ This compound and several similar ones reported in the same paper are the first examples of compounds whose optical activity is solely due to an acyclic tervalent chiral nitrogen atom. However, 11 is not optically stable and racemizes at 20°C with a half-life of 1.22 h. A similar compound (11, with OCH₂Ph replaced by OEt) has a longer half-life, 37.5 h at 20°C.

In molecules in which the nitrogen atom is at a bridgehead, pyramidal inversion is of course prevented. Such molecules, if chiral, can be resolved even without the presence of the two structural features noted above. For example, optically active 12 (Tröger's base) has been prepared.⁴⁴ Phosphorus inverts more slowly and arsenic still more slowly.⁴⁵ Nonbridgehead phosphorus,⁴⁶ arsenic, and antimony compounds have also been resolved (e.g., 13).⁴⁷ Sulfur exhibits pyramidal bonding in sulfoxides, sulfinic esters, sulfonium salts, and sulfites. Examples of each of these have been resolved.⁴⁸ An interesting example is (+)-Ph¹²CH₂SO¹³CH₂Ph, a sulfoxide in which the two alkyl groups differ only in ¹²C versus ¹³C, but which has [α]₂₈₀ = +0.71°.⁴⁹ A computational study indicates that base-catalyzed inversion at sulfur in sulfoxides is possible via a tetrahedral intermediate.⁵⁰

4. Suitably Substituted Adamantanes. Adamantanes bearing four different substituents at the bridgehead positions are chiral and optically active and 14, for example, has been resolved.⁵¹ This type of molecule is a kind of expanded tetrahedron and has the same symmetry properties as any other tetrahedron.

5. Restricted Rotation Giving Rise to Perpendicular Disymmetric Planes. Certain compounds that do not contain asymmetric atoms are nevertheless chiral, as illustrated in Fig. 4.2. For such compounds, there are two perpendicular planes (see I), neither of which can be bisected by a plane of symmetry (as illustrated by II). If either plane could be so bisected, the molecule would be superimposable on its mirror image, since such a plane would be a plane of symmetry. These points will be illustrated by examples.

Biphenyls that contain four large groups in the ortho positions cannot freely rotate about the central bond because of steric hindrance.⁵² For example, the activation energy (rotational barrier) for the enantiomerization process of the chiral 2-carboxy-2′-methoxy-6-nitrobiphenyl was determined, ΔG^‡ = 21.8 ± 0.1 kcal mol⁻¹(91.3 kJ mol⁻¹).⁵³ In such compounds, the two rings are in perpendicular planes. If either ring is symmetrically substituted, the molecule has a plane of symmetry. For example, consider the biaryls:

Ring B is symmetrically substituted. A plane drawn perpendicular to ring B contains all the atoms and groups in ring A; hence, it is a plane of symmetry and the compound is achiral. On the other hand, consider

In this molecule, there is no plane of symmetry and the molecule is chiral; many such compounds have been resolved. Note that groups in the para position cannot cause lack of symmetry. Isomers that can be separated only because rotation about single bonds is prevented or greatly slowed are called atropisomers.⁵⁴ 9,9′-Bianthryls also show hindered rotation and exhibit atropisomers.⁵⁵ Low-temperature NMR is sometimes used to detect atropisomers in certain systems [1,2,4,5-tetra(o-tolyl)benzene, e.g.].⁵⁶ Configurationally stable atropisomers are known.⁵⁷

It is not always necessary for four large ortho groups to be present in order for rotation to be prevented. Compounds with three and even two groups, if large enough, can have hindered rotation and, if suitably substituted, can be resolved. An example is biphenyl-2,2′-bis-sulfonic acid.⁵⁸ In some cases, the groups may be large enough to slow rotation greatly, but not to prevent it completely. In such cases, optically active compounds can be prepared that slowly racemize on standing. Thus, 15 loses its optical activity with a half-life of 9.4 min in ethanol at 25°C.⁵⁹ Compounds with greater rotational stability can often be racemized if higher temperatures are used to supply the energy necessary to force the groups past each other.⁶⁰

Atropisomerism occurs in other systems as well, including monopyrroles.⁶¹ Sulfoxide (16), for example, forms atropisomers with an interconversion barrier with its atropisomer of 18–19 kcal mol⁻¹ (75.4–79.5 kJ mol⁻¹).⁶² The atropisomers of hindered naphthyl alcohols (e.g., 17) exist as the sp-atropisomer (17a) and the ap-atropisomer (17b).⁶³ Atropisomers can also be formed in organometallic compounds, [e.g., the bis(phosphinoplatinum) complex (see 18)] generated by reaction with (R)-BINAP [(2R₁ 3S)-2,2′-bis(diphenylphosphino)-1,1′-binaphyl, see Reaction 19-36].⁶⁴

It is possible to isolate isomers in some cases, often due to restricted rotation. In 9,10-bis(trifluorovinyl)phenanthrene (19) torsional diastereomers (see Sec. 4.G) are formed. The value of K for interconversion of 19a and 19b is 0.48, with ΔG⁰ = 15.1 kcal mol⁻¹.⁶⁵ The ability to isolate atropisomers can depend on interactions with solvent, as in the isolation of atropisomeric colchicinoid alkaloids, which have been isolated, characterized, and their dichroic behavior described.⁶⁶

In allenes, the central carbon is sp hybridized. The remaining two p orbitals are perpendicular to each other and each overlaps with the p orbital of one adjacent carbon atom, forcing the two remaining bonds of each carbon into perpendicular planes. Thus allenes fall into the category represented by Fig. 4.2. Like biphenyls, allenes are chiral only if both sides are unsymmetrically substituted.⁶⁷ These cases are completely different from the cis–trans isomerism of compounds with one double bond (Sec. 4.K). In the latter cases, the four groups are all in one plane, the isomers are not enantiomers, and neither is chiral, while in allenes the groups are in two perpendicular planes and the isomers are a pair of optically active enantiomers.

When a molecule has three, five, or any odd number of cumulative double bonds, orbital overlap causes the four groups to occupy one plane and cis–trans isomerism is observed. When four, six, or any even number of cumulative double bonds exist, the situation is analogous to that in the allenes and optical activity is possible. Compound 20 has been resolved.⁶⁸

Other types of compounds that contain the system illustrated in Fig. 4.2 and that are similarly chiral if both sides are dissymmetric include spiranes (e.g., 21), and compounds with exocyclic double bonds (e.g., 22). Atropisomerism exists in (1,5)-bridgedcalix[8]arenes (see Sec. 3.C.ii).⁶⁹

6. Chirality due to a Helical Shape.⁷⁰ Several compounds have been prepared that are chiral because they have a shape that is actually helical and can therefore be left or right handed in orientation. The entire molecule is usually less than one full turn of the helix, but this does not alter the possibility of left- and right handedness. An example is hexahelicene,⁷¹ in which one side of the molecule must lie above the other because of crowding.⁷² The rotational barrier for helicene is ~22.9 kcal mol⁻¹(95.9 kJ mol⁻¹), and significantly higher when substituents are present.⁷³ It has been shown that the dianion of helicene retains its chirality.⁷⁴ Chiral discrimination of helicenes is possible.⁷⁵ 1,16-Diazo[6]helicene has also been prepared and, interestingly, does not act as a proton sponge (see Sec. 8.F) because the helical structure leaves the basic nitrogen atoms too far apart. Heptalene is another compound that is not planar (Sec. 2.I.iii). Its twisted structure makes it chiral, but the enantiomers rapidly interconvert.⁷⁶

trans-Cyclooctene (see also, Sec. 4.K.i) also exhibits helical chirality because the carbon chain must lie above the double bond on one side and below it on the other.⁷⁷ Similar helical chirality also appears in fulgide 23⁷⁸ and dispiro-1,3-dioxane (24), shows two enantiomers (24a and 24b).⁷⁹

7. Optical Activity Caused by Restricted Rotation of Other Types. Substituted paracyclophanes may be optically active⁸⁰ and 25, for example, has been resolved.⁸¹ In this case, chirality results because the benzene ring cannot rotate in such a way that the carboxyl group goes through the alicyclic ring. Many chiral layered cyclophanes (e.g., 26), have been prepared.⁸² Another cyclophane⁸³ with a different type of chirality is [12][12]paracyclophane (27), where the chirality arises from the relative orientation of the two rings attached to the central benzene ring.⁸⁴ An acetylenic cyclophane was shown to have helical chirality.⁸⁵ Metallocenes (Sec. 2.I.ii) substituted with at least two different groups on one ring are also chiral.⁸⁶ Several hundred such compounds have been resolved, one being 28. Chirality is also found in other metallic complexes of suitable geometry.⁸⁷ Fumaric acid–iron tetracarbonyl (29) has been resolved,⁸⁸ and 1,2,3,4-tetramethylcyclooctatetraene (30) is also chiral.⁸⁹ This molecule, which exists in the tub form (Sec. 2.K), has

neither a plane nor an alternating axis of symmetry. Another compound that is chiral solely because of hindered rotation is the propeller-shaped perchlorotriphenylamine, which has been resolved.⁹⁰ The 2,5-dideuterio derivative (31) of barrelene is chiral, though the parent hydrocarbon and the monodeuterio derivative are not. Compound 25 has been prepared in optically active form⁹¹ and is another case where chirality is due to isotopic substitution.

The main molecular chain in compound 32 has the form of a Möbius strip (see Fig. 15.7 and 3D model 33).⁹² This molecule has no stereogenic carbons, nor does it have a rigid shape, a plane, nor an alternating axis of symmetry. However, 32 has been synthesized and shown to be chiral.⁹³ Rings containing 50 or more members should be able to exist as knots (34, and see 39 on Sec. 3.D). Such a knot would be nonsuperimposable on its mirror image. Calixarenes,⁹⁴ crown ethers,⁹⁵ catenanes, and rotaxanes (see Sec. 3.D) can also be chiral if suitably substituted.⁹⁶ For example, 40 and 41 are nonsuperimposable mirror images.

A stereogenic center may be created from an achiral molecule via a chemical reaction. One example is the α-bromination of a carboxylic acid (Hell–Volhardt–Zelenskii reaction, 12-05) to form the α-bromo acid.

In this case, the α-carbon in the product is the stereogenic carbon. If there are no asymmetric components in the reaction, the product must be racemic. This means that no optically active material can be created if all starting materials and conditions are optically inactive.⁹⁷ This statement also holds when one begins with a racemic mixture, unless there is kinetic resolution (Sec. 4.I). Thus racemic 2-butanol, treated with HBr, must give racemic 2-bromobutane.

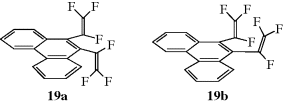
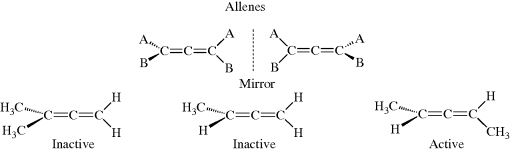
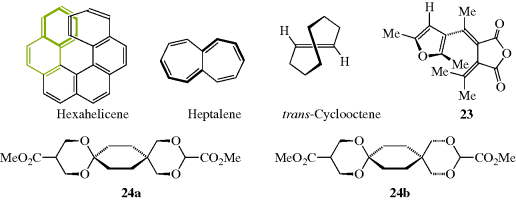
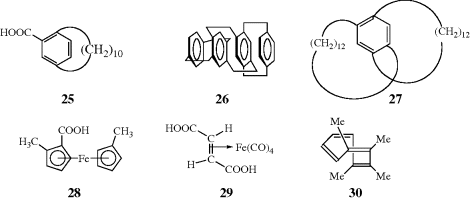
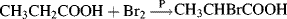
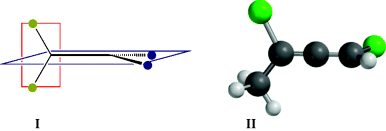
Fig. 4.2 Perpendicular dissymmetric planes and a chiral molecule with no stereogenic center.

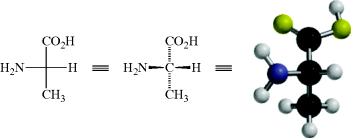
4.C. The Fischer Projection

For a thorough understanding of stereochemistry, it is useful to examine molecular models (like those depicted in Fig. 4.1). However, this is not feasible when writing on paper. In 1891, Emil Fischer displayed amino acids and some carbohydrates in a particular way known as a Fischer projection. This is simply a method of representing and “edge-viewed” tetrahedral on paper. By this convention, the model is held so that the two bonds in front of the paper are horizontal and those behind the paper are vertical, as shown for 2-aminopropanoic acid (alanine). With modern computers, molecular models are readily available, but the ability to write structures in two dimensions to represent a 3D form remains important.

In order to obtain proper results with these formulas, remember that they are projections and must be treated differently from the models in testing for superimposability. Every plane is superimposable on its mirror image; hence with these formulas there must be added the restriction that they may not be taken out of the plane of the blackboard or paper. Also, they may not be rotated 90°, although 180° rotation is permissible:

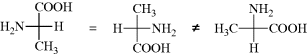
It is also permissible to keep any one group fixed and to rotate the other three clockwise or counterclockwise (because this can be done with models):

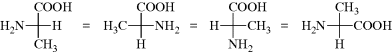
However, the interchange of any two groups results in the conversion of an enantiomer into its mirror image (this applies to models, as well as to the Fischer projections).

With these restrictions Fischer projections may be used instead of models to test whether a molecule containing a stereogenic carbon is superimposable on its mirror image. However, there are no such conventions for molecules whose chirality arises from anything other than chiral atoms (category 5 in Sec. 4.C).

4.D. Absolute Configuration

Suppose there are two test tubes, one containing (−)-lactic acid and the other the (+) enantiomer. One test tube contains 37 and the other 38. How can they be distinguished?

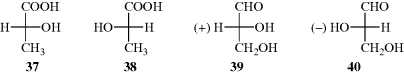
To generate a model to answer this question, Rosanoff proposed that one compound be chosen as a standard and a configuration arbitrarily assigned to it. The compound chosen was glyceraldehyde because of its relationship to the sugars. The (+) isomer was assigned the configuration shown in 39 and given the label D. The (−) isomer, designated to be 39, was given the label l. With a standard, other compounds could then be related to it. For example, (+)-glyceraldehyde, oxidized with mercuric oxide, gives (−)-glyceric acid:

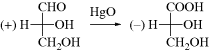
Since it is highly improbable that the configuration at the central carbon changed, it can be concluded that (−)-glyceric acid has the same configuration as (+)-glyceraldehyde and therefore (−)-glyceric acid is also called d. This example emphasizes that molecules with the same configuration need not rotate the plane of polarized light in the same direction. This fact should not surprise us when we remember that the same compound can rotate the plane in opposite directions under different conditions.

Once the configuration of the glyceric acids was known (in relation to the glyceraldehydes), it was then possible to relate other compounds to either of these, and each time a new compound was related, others could be related to it. In this way, many thousands of compounds were related, indirectly, to d- or l-glyceraldehyde. It was determined that 37, which has the d configuration, is the isomer that rotates the plane of polarized light to the left. Even compounds without asymmetric atoms (e.g., biphenyls and allenes), have been placed in the d or l series.98 When a compound has been placed in the d or l series, its absolute configuration is said to be known.⁹⁹

In 1951, it became possible to determine that Rosanoff's guess was right. Ordinary X-ray crystallography cannot distinguish between a d and a l isomer, but by use of a special technique, Bijvoet et al.¹⁰⁰ was able to examine sodium rubidium tartrate, compared it with glyceraldehyde, and found that Rosanoff had made the correct choice. It was perhaps historically fitting that the first true absolute configuration should have been determined on a salt of tartaric acid, since Pasteur made his great discoveries on another salt of this acid.

In spite of the former widespread use of d and l to denote absolute configuration, the method is not without faults. This method does not apply to all compounds that have a stereogenic center, but only those that can be structurally related to glyceraldehyde. The dl system is rarely used, therefore, except for certain groups of compounds (e.g., carbohydrates and amino acids). A more general model is required to distinguish the stereogenic centers of enantiomers.

4.D.i. The Cahn–Ingold–Prelog System

The system that is used universally is the Cahn–Ingold–Prelog system (or the CIP system), in which the four groups on a stereogenic carbon are ranked (prioritized) according to a set of sequence rules.¹⁰¹ For the most part, only a few of these rules are sufficient to deal with the vast majority of chiral compounds.

1. Prioritize substituents in order of decreasing atomic number of the atom directly joined to the carbon.

2. A tritium atom takes precedence over deuterium, which in turn takes precedence over ordinary hydrogen. Similarly, any higher isotope (e.g., ¹⁴C) takes precedence over any lower one.

3. Where two or more of the atoms connected to the stereogenic carbon are the same, the atomic number of the second atom determines the order. For example, in the molecule Me₂CH–CHBr–CH₂OH, the CH₂OH group takes precedence over the Me₂CH group because oxygen has a higher atomic number than carbon. Note that this is so even though there are two carbons in Me₂CH, and only one oxygen in CH₂OH. If two or more atoms connected to the second atom are the same, the third atom determines the precedence, and so on.

4. All atoms except hydrogen are formally given a valence of 4. Where the actual valence is less (as in nitrogen, oxygen, or a carbanion), phantom atoms (designated by a subscript 0) are used to bring the valence up to 4. These phantom atoms are assigned an atomic number of zero and necessarily rank lowest. Thus the ligand –⁺NHMe₂ ranks higher than –NMe₂.

5. Double and triple bonds are counted as if they were split into two or three single bonds, respectively, as in the examples in Table 4.1 (note the treatment of the phenyl group). Note that in a C=C double bond, the two carbon atoms are each regarded as being connected to two carbon atoms and that one of the latter is counted as having three phantom substituents.

Table 4.1 How Four Common Groups Are Treated in the Cahn–Ingold–Prelog System.

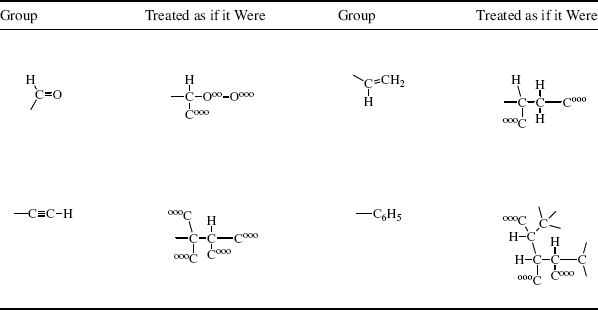
Using the four groups in Table 4.1 (aldehyde, vinyl, alkynyl, phenyl), the first atoms are connected, respectively, to (H, O, O), (H, C, C), (C, C, C), and (C, C, C). That is enough to establish that –CHO ranks first and –CH=CH₂ last, since even one oxygen outranks three carbons and three carbons outrank two carbons and a hydrogen. To classify the remaining two groups, proceed further along the chains. Note that –C₆H₅ has two of its (C, C, C) carbons connected to (C, C, H), while the third is (₀₀₀) and is thus preferred to –CCH, which has only one (C, C, H) and two (₀₀₀)s.

By application of the above rules, some groups in descending order of precedence are COOH, COPh, COMe, CHO, CH(OH)₂, o-tolyl, m-tolyl, p-tolyl, phenyl, CCH, tert-butyl, cyclohexyl, vinyl, isopropyl, benzyl, neopentyl, allyl, n-pentyl, ethyl, methyl, deuterium, and hydrogen. Using the CIP rules, the four groups of glyceraldehyde are arranged in the sequence: OH, CHO, CH₂OH, H.

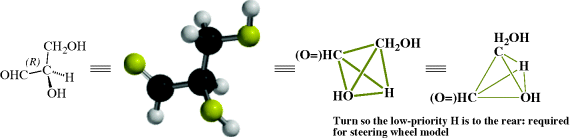
Once the order is determined, a model is required to determine the absolute configuration (i.e., which structure correlates to which enantiomer). The model used is known as the steering wheel model, where the molecule is held so that the lowest group in the sequence is pointed away from the viewer. Once the lowest priority group is held in that position, if the other groups, in the order listed, are oriented clockwise, the molecule is designated (R), and if counterclockwise (S). For glyceraldehyde, the (+) enantiomer is shown here and the CIP rules and the steering wheel model was used to assign an absolute configuration of (R).

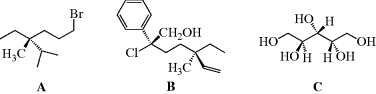
The CIP rules and steering wheel model are used to assign an absolute configuration to the following molecules. In A, the isopropyl carbon is higher in priority than the bromine-containing chain, and the methyl group is the lowest priority. Turning the molecule to place the methyl group to the rear makes this an (R) configuration. In B, there are two stereogenic centers, where the (S) center has the chain containing the (R) center as the lowest priority, and the (R) center has the methyl group as the low priority. In C, there are two (S) centers, but the hydroxyl-bearing carbon in the middle of the molecule is not a stereogenic carbon. Close inspection of C shows that this carbon has two identical groups [CH(OH)CH₂OH].

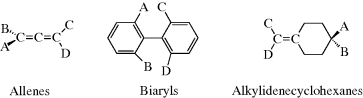
The CIP system is unambiguous and easily applicable in most cases. The CIP system also has been extended to chiral compounds that do not contain stereogenic centers, but rather have a chiral axis.¹⁰² Compounds having a chiral axis include unsymmetrical allenes, biaryls that exhibit atropisomerism (see Sec. 4.C, category 5), and alkylidene cyclohexane derivatives, molecular propellers and gears, helicenes, cyclophanes, annulenes, trans-cycloalkenes, and metallocenes. A series of rules have been proposed to address these cases based on what is called an “extended tetrahedron mode”, but the rules can be ambiguous in the case of cyclophanes and a few other systems.¹⁰³

4.D.ii. Methods of Determining Configuration¹⁰⁴

In all the methods,¹⁰⁵ it is necessary to relate the compound of unknown configuration to another whose configuration is known. The most important methods of doing this follow:

1. Conversion of the Unknown to, or Formation of the Unknown from, a Compound of Known Configuration Without Disturbing the Stereogenic Center. The glyceraldehyde–glyceric acid example above is

one example. The stereogenic center was not disturbed, and the configuration of the product (glyceric acid) is the same as the starting material (glyceraldehyde). Retention of the same absolute configuration such as with glyceraldehyde-to-glyceric acid is not always the case. If the reaction sequence does not disturb (change) the stereogenic center, the absolute configuration depends on the nature of the groups. For example, when (R)-1-bromo-2-butanol is reduced to 2-butanol without disturbing the stereogenic center, the product is the (S) enantiomer because CH₃CH₂ ranks lower than BrCH₂, but higher than CH₃.

2. Conversion at the Stereogenic Center if the Mechanism is Known. An S_N2 mechanism proceeds with inversion of configuration at a stereogenic carbon (Sec. 10.A.i). Indeed, a series of such transformations allowed the stereogenic center in lactic acid to be correlated to that in alanine.

3. Biochemical Methods. In a series of similar compounds (e.g., amino acids or certain types of steroids), a given enzyme will usually attack only molecules with one kind of configuration. If the enzyme attacks only the l form of eight amino acids, say, then attack on the unknown ninth amino acid will demonstrate that it is also the l form.

4. Optical Comparison. It is sometimes possible to use the sign and extent of rotation to determine which isomer has which configuration. In a homologous series, the rotation usually changes gradually and in one direction. If the configurations of enough members of the series are known, the configurations of the missing ones can be determined by extrapolation. Also, certain groups contribute more or less fixed amounts to the rotation of the parent molecule, especially when the parent is a rigid system (e.g., a steroid).

5. The Special X-Ray Method of Bijvoet. This method gives direct answers and has been used in a number of cases.⁸⁶

6. Derivatize the Alcohol with a Chiral Nonracemic Reagent and Examine the Ratio of Resulting Diastereomers by Gas Chromatography.¹⁰⁶ This methods is one of the most useful for determining enantiomeric composition. Many derivatizing agents are available, but one class widely used are derivatives of α-methoxy-α-trifluoromethylphenyl acetic acid (MTPA, Mosher's acid, 41).¹⁰⁷ Reaction with a chiral nonracemic alcohol (R^∗OH) generates a Mosher's ester (42) that can be analyzed for diastereomeric composition by ¹H or ¹⁹F NMR, as well as by chromatographic techniques.¹⁰⁸ Complexation with lanthanide shift reagents allow the signals of the MTPA ester to be resolved and used to determine enantiomeric composition.¹⁰⁹ This NMR method, as well as other related methods,¹¹⁰ are effective for determining the absolute configuration of an alcohol of interest (R^∗OH, where R^∗ is a group containing a stereogenic center).¹¹¹ Two, of many other reagents that have been developed to determine the enantiopurity of alcohols and amines, include 43 and 44. Chloromethyl lactam (43) reacts with R^∗OH or R^∗NHR (R^∗NH₂),¹¹² forming derivatives that allow analysis by ¹H NMR and 44 reacts with alkoxides (R^∗O⁻)¹¹³ to form a derivative that can be analyzed by ³¹P NMR. For a more detailed discussion of methods to determine optical purity, see Section 4.J.

7. Other Methods. Other method have also been used for determining absolute configuration in a variety of molecules, including optical rotatory dispersion,¹¹⁴ circular dichroism (CD),¹¹⁵ and asymmetric synthesis (Sec. 4.H). Optical rotatory dispersion (ORD) is a measurement of specific rotation [α] as a function of wavelength.¹¹⁶ The change of specific rotation [α] or molar rotation [Φ] with wavelength is measured, and a plot of either versus wavelength is often related to the sense of chirality or the substance under consideration. In general, the absolute value of the rotation increases as the wavelength decreases. The plot of CD is the differential absorption of left and right circularly polarized radiation by a nonracemic sample, taking place only in spectral regions in which absorption bands are found in the isotropic UV or visible (vis) electronic spectrum.¹¹⁷ The primary application of both ORD and CD is for the assignment of configuration or conformation.¹¹⁸ Configurational and conformational analyses have been carried out using IR and vibrational circular dichroism (VCD) spectroscopies.¹¹⁹

One example, and one of the more effective methods for derivatizing 1,2-diols, is the method employing dimolybdenum tetraacetate [Mo₂(AcO)₄] developed by Snatzke and Frelek.¹²⁰ Exposure of the resulting complex to air leads, in most cases, to a significant induced CD spectrum (known as ICD). The method can be used for a variety of 1,2-diols.¹²¹

8. NMR Dabtabases. Kishi and co-worker's¹²² developed an NMR database¹²³ of various molecules in chiral solvents, for the assignment of relative and absolute stereochemistry without derivatization or degradation. Kishi referred to this database as a “universal NMR database.”¹²⁴ The diagram provided for diols 45 illustrates the method (see Fig. 4.3). The graph presents the difference in carbon chemical shifts between the average and the values for 45 (100 MHz) in DMBA (N,α-dimethylbenzylamine). Spectra were recorded in both enantiomers of the solvent, where the solid bar was recorded in (R)-DMBA and the shaded bar in (S)-DMBA. The x- and y-axes represent the carbon number and Δδ (δ_45a–h - δ_ave in ppm), respectively. The graphs are taken from “the ¹³C NMR database in (R)- and (S)-DMBA as a deviation in chemical shift for each carbon of a given diastereomer from the average chemical shift of the carbon in question. Each diastereomer exhibits an almost identical NMR profile for (R)- and (S)-DMBA, but shows an NMR profile distinct and differing from the other diastereomers, demonstrating that the database in (R)- and/or (S)-DMBA can be used for prediction of the relative stereochemistry of structural motifs in an intact form.”¹²⁵

A ¹H NMR analysis method has been developed that leads to the assignment of the stereochemistry of β-hydroxy ketones, by visual inspection of the ABX patterns for the (R)-methylene unit of the β-hydroxyketones.¹²⁶ Since β-hydroxy ketones are derived from the aldol reaction (16-34), this method is particularly useful in organic synthesis. A method has also been developed that uses ¹³C NMR to determine the relative stereochemistry of 2,3-dialkylpentenoic acids.¹²⁷

Fig. 4.3 Proton NMR analysis for assignment of stereochemistry.

4.E. The Cause of Optical Activity

The question may be asked: Just why does a chiral molecule rotate the plane of polarized light? Theoretically, the answer to this question is known, and in a greatly simplified form may be explained as follows.128

Whenever any light hits any molecule in a transparent material, the light is slowed because of interactions with the molecule. This phenomenon on a gross scale is responsible for the refraction of light, and the decrease in velocity is proportional to the refractive index of the material. The extent of interaction depends on the polarizability of the molecule. Plane-polarized light may be regarded as being made up of two kinds of circularly polarized light. Circularly polarized light has the appearance (or would have, if one could see the wave) of a helix propagating around the axis of light motion, and one kind is a left and the other is a right-handed helix. As long as the plane-polarized light is passing through a symmetrical region, the two circularly polarized components travel at the same speed. However, a chiral molecule has a different polarizability depending on whether it is approached from the left or the right. One circularly polarized component approaches the molecule, so to speak, from the left and sees a different polarizability (hence on a gross scale, a different refractive index) than the other and is slowed to a different extent. This would seem to mean that the left- and right-handed circularly polarized components travel at different velocities, since each has been slowed to a different extent. However, it is not possible for two components of the same light to be traveling at different velocities. What actually takes place, therefore, is that the faster component “pulls” the other toward it, resulting in rotation of the plane. Empirical methods for the prediction of the sign and amount of rotation based on bond refractions and polarizabilities of groups in a molecule have been devised,¹²⁹ and have given fairly good results in many cases.

In liquids and gases, the molecules are randomly oriented. A molecule that is optically inactive because it has a plane of symmetry will very seldom be oriented so that the plane of the polarized light coincides with the plane of symmetry. When it is so oriented, that particular molecule does not rotate the plane, but all others not oriented in that manner do rotate the plane, even though the molecules are achiral. There is no net rotation because even though the molecules are present in large numbers and randomly oriented, there will always be another molecule later on in the path of the light that is oriented exactly opposite and will rotate the plane back again. Even if nearly all molecules rotate the plane individually, the total rotation is zero. For chiral molecules, however (if there is no racemic mixture), no opposite orientation is present and there is a net rotation.

An interesting phenomenon was observed when the CD of chiral molecules was measured in achiral solvents. The chiral solvent contributed as much as 10–20% to the CD intensity in some cases. Apparently, the chiral compound can induce a solvation structure that is chiral, even when the solvent molecules themselves are achiral.¹³⁰

4.F. Molecules with more than One Stereogenic Center

When a molecule has two stereogenic centers, each has its own configuration and can be classified (R) or (S) by the CIP method. There are a total of four isomers, since the first center may be (R) or (S) and so may the second. Each is drawn as both the Fischer projection and in the extended conformation. Since a molecule can have only one mirror image, only one of the other three can be the enantiomer of A. This enantiomer is B [the mirror image of an (R) center is always an (S) center]. Both C and D are a second pair of enantiomers and the relationship of C and D to A and B is designated by the term diastereomer. Diastereomers may be defined as stereoisomers that are not enantiomers (they are stereoisomers that are not mirror images, and not superimposable). Since C and D are enantiomers, they must have identical properties, except as noted in Section 4.A, and the same is true for A and B. However, the properties of A and B are not identical with those of C and D. They are different compounds, which means that they have different melting points, boiling points, solubilities, reactivity, and all other physical, chemical, and spectral properties. The properties are usually similar, but not identical. In particular, diastereomers have different specific rotations; indeed one diastereomer may be chiral and rotate the plane of polarized light while another may be achiral and not rotate at all (an example is presented below).

It is now possible to see why, as mentioned in Section 4.A, enantiomers react at different rates with other chiral molecules, but at the same rate with achiral molecules. In the latter case, the activated complex formed from the (R) enantiomer and the other molecule is the mirror image of the activated complex formed from the (S) enantiomer and the other molecule. Since the two activated complexes are enantiomeric, their energies are the same and the rates of the reactions in which they are formed must be the same (see Chapter 6). However, when an (R) enantiomer reacts with a chiral molecule that has, say, the (R) configuration, the activated complex has two chiral centers with configurations (R) and (R), while the activated complex formed from the (S) enantiomer has the configurations (S) and (R). The two activated complexes are diastereomeric, do not have the same energies, and consequently are formed at different rates.

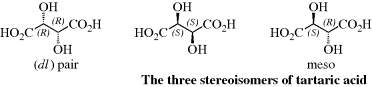
Although four is the maximum possible number of isomers when the compound has two stereogenic centers (chiral compounds without a stereogenic carbon, or with one stereogenic carbon and another type of stereogenic center, also follow the rules described here), some compounds have fewer. When the three groups on one stereogenic atom are the same as those on the other, one of the isomers (called a meso form) has a plane of symmetry, and hence is optically inactive, even though it has two stereogenic carbons. Tartaric acid is a typical case. As shown, there are only three isomers of tartaric acid: a pair of enantiomers and an inactive meso form. For compounds that have two stereogenic atoms, meso forms are found only where the four groups on one of the chiral atoms are the same as those on the other chiral atom.

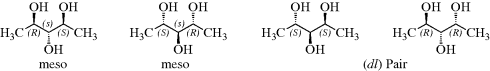
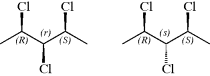
In compounds with two or more stereogenic centers, the maximum number of isomers can be calculated from the formula 2ⁿ, where n is the number of stereogenic centers. The actual number may be less than this, owing to meso forms,131 but never more. An interesting case is that of 2,3,4-pentanetriol (or any similar molecule). The middle carbon is not asymmetric when the 2- and 4-carbons are both (R) [or both (S)]; labeled the dl pair. The compound when one of them is (R) and the other (S) is asymmetric (labeled meso). The middle carbon in such compounds is called a pseudoasymmetric carbon. In such cases, there are four isomers: two meso forms and one dl pair. Remember that the meso forms are superimposable on their mirror images, and that there are no other stereoisomers. Two diastereomers that have a different configuration at only one chiral center are called epimers.

The small letters used for the psuedoasymmetric center are assigned using established rules. An atom that is tetrahedrally substituted and bonded to four different entities, two and only two of which have opposite configurations, is stereogenic. The descriptors “r” and “s” are used to denote such centers; they are assigned in accordance with Sequence Rule 5, taking into consideration that “(R)” has precedence over “(S)” in the order of priority.¹³² Step 1: configuration “(R)” or “(S)” is assigned to stereogenic centers C-2 and C-4; Using 1,2,3-trichloropentane as an example, Step 2: Configuration at C-3 is assigned by applying sequence rule, “(R)” precedes “(S)”, and if (R) precedes (S), then Cl is the highest priority, followed by (R) and then (S): C-3 is r. The exchange of the Cl and H atoms at C-3 of the compound on the left generates the compound on the right, and “3r” becomes “3s”

In compounds with two or more steroegenic centers, the absolute configuration must be separately determined for each center. The usual procedure is to determine the configuration at one center by the methods discussed in Section 4.E.ii, and then to relate the configuration at that center to the others in the molecule. One method is X-ray crystallography, which, as previously noted, cannot be used to determine the absolute configuration at any stereogenic center. This method does give relative configurations of all the stereogenic centers in a molecule, and if the absolute configuration of one stereogenic center is independently determined, the absolute configurations of all are then known. Other physical and chemical methods have also been used for this purpose.

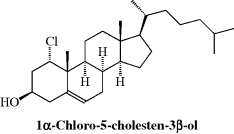
How to name the different stereoisomers of a compound when there are more than two is potentially a problem.² Enantiomers have the same IUPAC name, being distinguished by (R) and (S) or d and l or (+) or (−). In the early days of organic chemistry, it was customary to give each pair of enantiomers a different name or at least a different prefix (e.g., epi-, peri-, etc.). Thus the aldohexoses are called glucose, mannose, idose, and so on, although they are all 2,3,4,5,6-pentahydroxyhexanal (in their open-chain forms). This practice was partially due to lack of knowledge about which isomers had which configurations.¹³³ Today it is customary to describe each chiral position separately as either (R) or (S) or, in special fields, to use other symbols. Thus, in the case of steroids, groups above the “plane” of the ring system are designated β, and those below it α. Solid lines are typically used to depict β groups and dashed lines for α groups. An example is 1α-chloro-5-cholesten-3β-ol, showing the OH group on the top side of the molecule (up) and the chlorine atom on the bottom side (down).

For many open-chain compounds, prefixes are used that are derived from the names of the corresponding sugars and that describe the whole system rather than each chiral center separately. Two such common prefixes are erythro- and threo-, which are applied to systems containing two stereogenic carbons when two of the

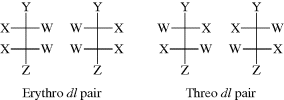
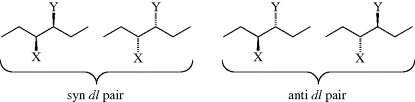
groups are the same and the third is different.¹³⁴ The erythro pair has the identical groups on the same side when drawn in the Fischer convention, and if Y were changed to Z, it would be meso. The threo pair has them on opposite sides, and if Y were changed to Z, it would still be a dl pair. Another system¹³⁵ for designating stereoisomers¹³⁶ uses the terms syn and anti. The “main chain” of the molecule is drawn in the common zigzag manner. Then if two non-hydrogen substituents are on the same side of the plane defined by the main chain, the designation is syn; otherwise it is anti.

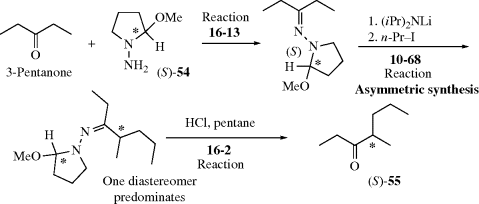
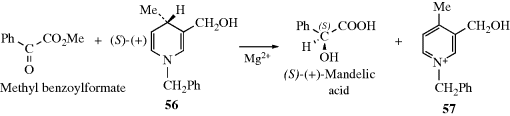
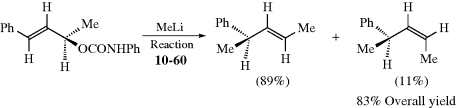
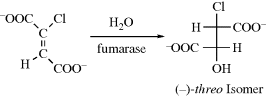
4.G. Asymmetric Synthesis

Organic chemists often wish to synthesize a chiral compound in the form of a single enantiomer or diastereomer, rather than as a mixture of stereoisomers. There are two basic ways in which this can be done.137 The first way, which is more common, is to begin with a single stereoisomer, and to use a synthesis that does not affect the stereogenic center (or centers). The optically active starting compound can be obtained by a previous synthesis, or by resolution of a racemic mixture (Sec. 4.I). If possible, the starting material is obtained from Nature, since many compounds (e.g., amino acids, sugars, and steroids), are present in Nature in the form of a single enantiomer or diastereomer. These compounds have been referred to as a chiral pool; that is, readily available compounds that can be used as starting materials.¹³⁸ This term is not used much now.

The other basic method is called asymmetric synthesis,¹³⁹ or stereoselective synthesis. As mentioned earlier, optically active materials cannot be created from inactive starting materials and conditions, except in the manner previously noted.⁹⁷ However, when a new stereogenic center is created, the two possible enantiomers need not be formed in equal amounts if anything is present that is not symmetric. Asymmetric synthesis may be categorized into four headings:

1. Active Substrate. If a new stereogenic center is created in a molecule that is already optically active, the product will generate diastereomers and the two diastereomers may not (except fortuitously) be formed in equal amounts. The reason is that the direction of attack by the reagent is determined by the groups already there. For certain additions to the carbon–oxygen double bond of ketones containing an asymmetric α carbon, Cram's rule predicts which of two diastereomers will predominate (diastereoselectivity).^140,141 The reaction of 46, which has a stereogenic center at the α-carbon, and HCN can generate two possible diastereomers (47 and 48).

If 46 is observed along its axis, it may be represented as in 49 (Sec. 4.O.i), where S, M, and L stand for small, medium, and large, respectively. The oxygen of the carbonyl orients itself between the small- and the medium-sized groups. The rule requires that the incoming group preferentially attacks on the side of the plane containing the small group. By this rule, it can be predicted that 48 will be formed in larger amounts than 47.

Another model uses transition state models 50 and 51 to predict diastereoselectivity in what is known as the Felkin–Anh model.¹⁴². This model assumes the favored transition state will be that with the greatest separation between the incoming group and any electronegative substituent at the α-carbon. The so-called Cornforth model has also been presented as a model for carbonyl addition to halogenated compounds,¹⁴³ and it assumes that the electron pairs on the carbonyl oxygen and on the halogen repel and assume an anti-conformation.

Many reactions of this type are known, and in some the extent of favoritism approaches 100% (e.g., see Reaction 12-12).¹⁴⁴ The farther away the reaction site is from the chiral center, the less influence the latter has and the more equal the amounts of diastereomers formed. There are many examples of asymmetric induction via nucleophilic acyl addition to carbonyl compounds (Reactions 16-24 and 16-25). Enolborane addition to α-heteroatom substituted aldehydes has been evaluated using the Cornforth and the Felkin–Anh models.¹⁴⁵

In a special case of this type of asymmetric synthesis, a compound (52) with achiral molecules, but whose crystals are chiral, was converted by UV light to a single enantiomer of a chiral product (53).¹⁴⁶

It is often possible to convert an achiral compound to a chiral compound by (1) addition of a chiral group; (2) running an asymmetric synthesis, and (3) cleavage of the original chiral group. The original chiral group is called a chiral auxiliary. An example is conversion of the achiral 2-pentanone to the chiral 4-methyl-3-heptanone, (55).¹⁴⁷ In this case, >99% of the product was the (S) enantiomer. As noted, compound 54 is called a chiral auxiliary because it is used to induce asymmetry and is then removed.

2. Active Reagent. A pair of enantiomers can be separated by an active reagent that reacts faster with one of them than it does with the other (this is also a method of resolution). If the absolute configuration of the reagent is known, the configuration of the enantiomers can often be determined by a knowledge of the mechanism and

by determining which diastereomer is preferentially formed.¹⁴⁸ Creation of a new stereogenic center in an inactive molecule can also be accomplished with an optically active reagent, although it is rare for 100% selectivity to be observed. An example^149,150 is the reduction of methyl benzoylformate with optically active N-benzyl-3-(hydroxymethyl)-4-methyl-1,4-dihydropyridine (56) to produce mandelic acid (after hydrolysis) that contained ~97.5% of the (S)-(+) isomer and 2.5% of the (R)-(−) isomer (for another example, see Reaction 15-16). Note that the other product, (57), is not chiral. Reactions like this, in which one reagent (in this case 56) gives up its chirality to another, are called self-immolative. In another example:

chirality is transferred from one atom to another in the same molecule.¹⁵¹

A reaction in which an inactive substrate is converted selectively to one of two enantiomers is called an enantioselective reaction, and the process is called asymmetric induction. These terms apply to reactions in this category and in categories 3 and 4.

When an optically active substrate reacts with an optically active reagent to form two new stereogenic centers, it is possible for both centers to be created in the desired sense. This type of process is called double asymmetric synthesis¹⁵² (for an example, see Reaction 16-34).

3. Optically Active Catalyst or Solvent.¹⁵³ Many such examples are found in the literature, among them reduction of ketones and substituted alkenes to optically active (though not optically pure) secondary alcohols and substituted alkanes by treatment with hydrogen and a chiral homogeneous hydrogenation catalyst (reactions 16-23 and 15-11),¹⁵⁴ the treatment of aldehydes or ketones with organometallic compounds in the presence of a chiral catalyst (see Reaction 16-24), and the conversion of alkenes to optically active epoxides by treatment with a hydroperoxide and a chiral catalyst (see Reaction 15-50). In some instances, the ratio of enantiomers prepared in this way is 99:1 or more.¹⁵⁵ Other examples of the use of a chiral catalyst or solvent are the conversion of chlorofumaric acid (in the form of its diion) to the (−)-threo isomer of the diion of chloromalic acid by treatment with H₂O and the enzyme fumarase,¹⁵⁶ as well as the preparation of optically active aldols (aldol condensation, see Reaction 16-35) by the condensation of enolate anions with optically active substrates.¹⁵⁷

4. Reactions in the Presence of Circularly Polarized Light.¹⁵⁸ If the light used to initiate a photochemical reaction (see Chap. 07) of achiral reagents is circularly polarized, then, in theory, a chiral product richer in one enantiomer might be obtained. However, such experiments have not proved fruitful. In certain instances, the use of left- and right-circularly polarized light has given products with opposite rotations¹⁵⁹ (showing that the principle is valid), but up to now the extent of favoritism has always been <1%.

4.H. Methods of Resolution160

A pair of enantiomers can be separated in several ways, but conversion to diastereomers and separation of these by fractional crystallization or chromatographic methods are used most often. In this method and in some of the others, both isomers can be recovered, but in some methods it is necessary to destroy one.

1. Conversion to Diastereomers. If the racemic mixture to be resolved contains a carboxyl group (and no strongly basic group), it is possible to form a salt with an optically active base. Since the base used is, say, the (S) form, there will be a mixture of two salts produced having the configurations (SS) and (RS). Although the acids are enantiomers, the salts are diastereomers and have different properties. The property most often used for separation is differential solubility. The mixture of diastereomeric salts is allowed to crystallize from a suitable solvent. Since the solubilities are different, the initial crystals formed will be richer in one diastereomer. Filtration at this point will already have achieved a partial resolution. Unfortunately, the difference in solubility is rarely if ever great enough to effect total separation with one crystallization. When fractional crystallizations must be used, the process is long and tedious. Fortunately, naturally occurring optically active bases (mostly alkaloids) are readily available. Among the most commonly used are brucine, ephedrine, strychnine, and morphine. Once the two diastereomers have been separated, it is easy to convert the salts back to the free acids and the recovered base can be used again.

Most resolution of this type is done on carboxylic acids and often, when a molecule does not contain a carboxyl group, it is converted to a carboxylic acid before resolution is attempted. Racemic compounds (e.g., 2-aminocylohexanol derivatives) react with carboxylic acids (e.g., optically active mandelic acid), to give diastereomers that are separated and then converted to enantiopure compounds.¹⁶¹ Racemic bases can be converted to diastereomeric salts with active acids. The principle of conversion to diastereomers is not confined to carboxylic acids, and other functional groups¹⁶² may be coupled to an optically active reagent.¹⁶³ Alcohols¹⁶⁴ can be converted to diastereomeric esters, aldehydes to diastereomeric hydrazones, and so on. Amino alcohols have been resolved using boric acid and chiral binaphthols.¹⁶⁵ Phosphine oxides¹⁶⁶ and chiral calix[4]arenes¹⁶⁷ have been resolved. Chiral crown ethers have been used to separate mixtures of enantiomeric alkylammonium and arylammonium ions, by the formation of diastereomeric complexes¹⁶⁸ (see also, category 3, below). Even hydrocarbons can be converted to diastereomeric inclusion compounds,¹⁶⁹ with urea. Urea is not chiral, but the cage structure is.¹⁷⁰ Racemic unsaturated hydrocarbons have been resolved as inclusion complex crystals with a chiral host compound derived from tartaric acid.¹⁷¹trans-Cyclooctene (Sec. 4.C, category 6) was resolved by conversion to a Pt complex containing an optically active amine.¹⁷²

Fractional crystallization has always been the most common method for the separation of diastereomers. When it can be used, binary phase diagrams for the diastereomeric salts have been used to calculate the efficiency of optical resolution.¹⁷³ However, it is tedious and the fact that it is limited to solids prompted a search for other methods. Fractional distillation has given only limited separation, but gas chromatography (GC)¹⁷⁴ and preparative liquid chromatography using chiral columns¹⁷⁵ have proved to be more useful. In many cases, they have supplanted fractional crystallization, especially where the quantities to be resolved are small.¹⁷⁶

2. Differential Absorption. When a racemic mixture is placed on a chromatographic column, if the column consists of chiral substances, then in principle the enantiomers should move along the column at different rates and should be separable without having to be converted to diastereomers.¹⁷⁶ This has been successfully accomplished with paper, column, thin-layer,¹⁷⁷ and gas and liquid chromatography.¹⁷⁸ For example, racemic mandelic acid has been almost completely resolved by column chromatography on starch.¹⁷⁹ Many workers have achieved separations with gas and liquid chromatography by the use of columns packed with chiral absorbents.¹⁸⁰ Columns packed with chiral materials are now commercially available and are capable of separating the enantiomers of certain types of compounds.¹⁸¹

3. Chiral Recognition. The use of chiral hosts to form diastereomeric inclusion compounds was mentioned above. But in some cases it is possible for a host to form an inclusion compound with one enantiomer of a racemic guest, but not the other. This is called chiral recognition. One enantiomer fits into the chiral host cavity, the other does not. More often, both diastereomers are formed, but one forms more rapidly than the other, so that if the guest is removed it is already partially resolved (this is a form of kinetic resolution, see category 6). An example is use of the chiral crown ether (58) partially to resolve the racemic amine salt (59).¹⁸² When an aqueous solution of 59 was mixed with a solution of optically active 58 in chloroform, and the layers separated, the chloroform layer contained about twice as much of the complex between 58 and (R)-59 as of the diastereomeric complex. Many other chiral crown ethers and cryptands have been used, as have been cyclodextrins,¹⁸³ cholic acid,¹⁸⁴ and other kinds of hosts.¹⁶⁹ Of course, enzymes are generally very good at chiral recognition, and much of the work in this area has been an attempt to mimic the action of enzymes.

4. Biochemical Processes.¹⁸⁵ Reactions catalyzed by enzymes can be utilized for this kind of resolution.¹⁸⁶ Biological molecules may react at different rates with the two enantiomers. For example, a certain bacterium may digest one enantiomer, but not the other. Pig liver esterase has been used for the selective cleavage of one enantiomeric ester.¹⁸⁷ This method is limited, since it is necessary to find the proper organism and since one of the enantiomers is destroyed in the process. However, when the proper organism is found, the method leads to a high extent of resolution since biological processes are usually very stereoselective. This process has been called chemoenzymatic dynamic kinetic resolution.¹⁸⁸

5. Mechanical Separation.¹⁸⁹ This is the method by which Pasteur proved that racemic tartaric acid was actually a mixture of (+)- and (−)-tartaric acids.¹⁹⁰ In the case of racemic sodium ammonium tartrate, the enantiomers crystallize separately: all the (+) molecules going into one crystal and all the (−) into another. Since the crystals too are nonsuperimposable, their appearance is not identical and a trained crystallographer can separate them with tweezers.¹⁹¹ However, this is seldom a practical method, since few compounds crystallize in this manner. Even sodium ammonium tartrate does so only when it is crystallized <27°C. A more useful variation of the method, although still not very common, is the seeding of a racemic solution with something that will cause only one enantiomer to crystallize.¹⁹² An interesting example of the mechanical separation technique was reported in the isolation of heptahelicene (Sec. 4.C. Category 7). One enantiomer of this

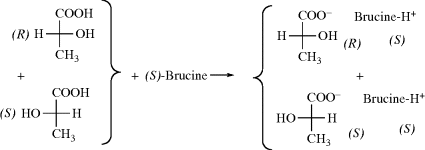
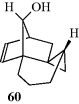
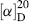compound, which incidentally has the extremely high rotation of = +6200° spontaneously crystallizes from benzene.¹⁹³ In the case of 1,1′-binaphthyl, optically active crystals can be formed simply by heating polycrystalline racemic samples of the compound at 76–150°C. A phase change from one crystal form to another takes place.¹⁹⁴ Note that 1,1′-binaphthyl is one of the few compounds that can be resolved by the Pasteur tweezer method. In some cases, resolution can be achieved by enantioselective crystallization in the presence of a chiral additive.¹⁹⁵ Spontaneous resolution has also been achieved by sublimation. In the case of the norborneol derivative 60, when the racemic solid is subjected to sublimation, the (+) molecules condense into one crystal and the (−) molecules into another.¹⁹⁶ In this case, the crystals are superimposable, unlike the situation with sodium ammonium tartrate, but the investigators were able to remove a single crystal, which proved optically active.

6. Kinetic Resolution.¹⁹⁷ Since enantiomers react with chiral compounds at different rates, it is sometimes possible to effect a partial separation by stopping the reaction before completion. This method is very similar to the asymmetric syntheses discussed in Section 4.C, category 5. A method has been developed to evaluate the enantiomeric ratio of kinetic resolution using only the extent of substrate conversion.¹⁹⁸ An important application of this method is the resolution of racemic alkenes by treatment with optically active diisopinocampheylborane,¹⁹⁹ since alkenes do not easily lend themselves to conversion to diastereomers if no

other functional groups are present. Another example is the resolution of allylic alcohols (e.g., 61) with one enantiomer of a chiral epoxidation agent (see Reaction 15-50).²⁰⁰ In the case of 61, the discrimination was extreme. One enantiomer was converted to the epoxide and the other was not, the rate ratio (hence the selectivity factor) being >100. Of course, in this method only one of the enantiomers of the original racemic mixture is obtained, but there are at least two possible ways of getting the other: (1) use of the other enantiomer of the chiral reagent and (2) conversion of the product to the starting compound by a reaction that preserves the stereochemistry.

Kinetic resolution of racemic allylic acetates²⁰¹ has been accomplished via asymmetric dihydroxylation (Reation 15-48), and 2-oxoimidazolidine-4-carboxylates have been developed as new chiral auxiliaries for the kinetic resolution of amines.²⁰² A planar chiral cyclic ether was found to be stable at ambient temperatures, but resolved by kinetic resolution.²⁰³

7. Deracemization. In this type of process, one enantiomer is converted to the other, so that a racemic mixture is converted to a pure enantiomer, or to a mixture enriched in one enantiomer (enantioenriched). This finding is not quite the same as the methods of resolution previously mentioned, although an outside optically active substance is required. To effect the deracemization, two conditions are necessary: (1) the enantiomers must complex differently with the optically active substance and (2) they must interconvert under the conditions of the experiment. When racemic thioesters were placed in solution with a specific optically active amide for 28 days, the solution contained 89% of one enantiomer and 11% of the other.²⁰⁴ In this case, the presence of a base (Et₃N) was necessary for the interconversion to take place. Biocatalytic deracemization processes induce deracemization of chiral secondary alcohols.²⁰⁵ In a specific example, Sphingomonas paucimobilis NCIMB 8195 catalyzes the efficient deracemization of many secondary alcohols in up to 90% yield of the (R)-alcohol.²⁰⁶

4.I. Optical Purity207

An attempt to resolve a racemic mixture by one of the methods described in Section 4.I has given either a pure compound or a new mixture. How can the purity of the two enantiomers obtained be determined? If the (+) isomer is contaminated by, say, 20% of the (−) isomer, how can this be determined? If the value of [α] for the pure material ([α]_max) is known, the purity of a sample is easily determined by measuring its rotation. For example, if [α]_max is +80° and the resolved (+) enantiomer contains 20% of the (−) isomer, [α] for the sample will be +48°.²⁰⁸ Optical purity is defined as

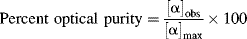
Assuming a linear relationship between [α] and concentration, which is true for most cases, the optical purity is equal to the percent excess of one enantiomer over the other:²⁰⁹

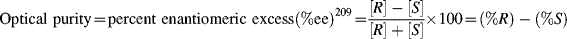
How is the value of [α]_max determined? It is plain that we have two related problems here; namely, what are the optical purities of our two samples and what is the value of [α]_max. Finding the properties of one also gives the other. Several methods for solving these problems are known.

One of these methods involves the use of NMR²¹⁰ (see Sec. 4.E.ii, category 7). If there is a nonracemic mixture of two enantiomers and the proportions constitute an unknown, convert the mixture into a mixture of diastereomers with an optically pure reagent and look at the NMR spectrum of the resulting mixture, for example,

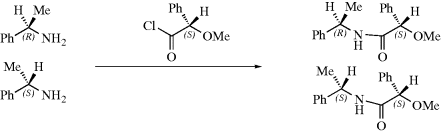
If the NMR spectrum of the starting mixture is examined, only one peak would be found (split into a doublet by the C–H) for the Me protons, since enantiomers give identical NMR spectra.²¹¹ But the two amides are not enantiomers and each Me gives its own doublet. From the intensity of the two peaks, the relative proportions of the two diastereomers (and hence of the original enantiomers) can be determined. Alternatively, the “unsplit” OMe peaks could have been used. This method was satisfactorily used to determine the optical purity of a sample of 1-phenylethylamine (the case shown above),²¹² as well as other cases, but it is obvious that sometimes corresponding groups in diastereomeric molecules will give NMR signals that are too close together for resolution. In such cases, one may resort to the use of a different optically pure reagent. The ¹³C NMR can be used in a similar manner.²¹³ It is also possible to use these spectra to determine the absolute configuration of the original enantiomers by comparing the spectra of the diastereomers with those of the original enantiomers.²¹⁴ From a series of experiments with related compounds of known configurations it can be determined in which direction one or more of the ¹H or ¹³C NMR peaks are shifted by formation of the diastereomer. It is then assumed that the peaks of the enantiomers of unknown configuration will be shifted the same way.

A closely related method does not require conversion of enantiomers to diastereomers, but relies on the fact that (in principle, at least) enantiomers have different NMR spectra in a chiral solvent, or when mixed with a chiral molecule (in which case transient diastereomeric species may form, see Sec. 4.E.ii). In such cases, the peaks may be separated enough to permit the proportions of enantiomers to be determined from their intensities.²¹⁵ Another variation, which gives better results in many cases, is to use an achiral solvent, but with the addition of a chiral lanthanide shift reagent [e.g., tris[3-trifluoroacetyl-d-camphorato]europium(III)].²¹⁶ Lanthanide shift reagents have the property of spreading NMR peaks of compounds with which they can form coordination compounds (e.g., alcohols, carbonyl compounds, and amines). Chiral lanthanide shift reagents shift the peaks of the two enantiomers of many such compounds to different extents.

Another method, involving GC,²¹⁷ is similar in principle to the NMR chiral complex method. A mixture of enantiomers whose purity is to be determined is converted by means of an optically pure reagent into a mixture of two diastereomers. These diastereomers are then separated by GC and the ratios are determined from the peak areas. Once again, the ratio of diastereomers is the same as that of the original enantiomers. High-pressure liquid chromatography has been used in a similar manner and has wider applicability.²¹⁸ The direct separation of enantiomers by gas or liquid chromatography on a chiral column has also been used to determine optical purity.²¹⁹

Other methods²²⁰ involve isotopic dilution,²²¹ kinetic resolution,^{222 13}C NMR relaxation rates of diastereomeric complexes,²²³ and circular polarization of luminescence.²²⁴

4.J. cis–trans Isomerism

Compounds in which rotation is restricted may exhibit cis–trans isomerism.225 These compounds do not rotate the plane of polarized light (unless they also happen to be chiral), and the properties of the isomers are not identical. The two most important types are isomerism resulting from double bonds and that resulting from rings.

4.J.i. cis-trans Isomerism Resulting from Double Bonds

It has been mentioned (Sec. 1.D) that the two carbon atoms of a C=C d=ble bond and the four atoms directly attached to them are all in the same plane and that the presence of the π-bond prevents rotation around the double bond. This means that in the case of a molecule WXC=CYZ, stereoisomerism exists when W ≠ X and Y ≠ Z. There are two and only two isomers (62 and 63), each superimposable on its mirror image unless one of the groups happens to carry a stereogenic center. Note that 62 and 63 are diastereomers, by the definition given in Section 4.E.i. There are two ways to name such isomers. In the older and less versatile method, one isomer is called cis and the other trans. When each carbon of the C=C unit has an identical group (W in 62 and 63), but fits the substitution pattern of 62 and 63, the cis-trans nomenclature system may be applied. When the two identical groups are on the same side (W and W in 62), it is labeled cis. cis-3-Hexene is shown as an example. When the two identical groups are on opposite side (W and W in 63) it is labeled trans. trans-3-Hexene is shown as an example. Unfortunately, there is no obvious way to apply this method when the four groups are different.

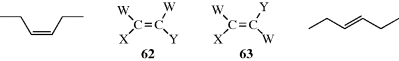
The newer and more widely applicable method can be applied to all cases, and is based on the CIP system (Sec. 4.E.i). The two groups at each carbon of the C=C unit are ranked by the sequence rules. The isomer with the two higher ranking groups on the same side of the double bond is called (Z) (for the German word zusammen meaning together). The isomer with the two higher ranking groups on opposite sides of the double bond is called (E) (for entgegen meaning opposite).²²⁶ A few examples are shown. Note that the (Z) isomer is not necessarily the one that would be called cis under the older system (e.g., 64 and 65). Like cis and trans, (E) and (Z) are used as prefixes; for example, 65 is called (E)-1-bromo-1,2-dichloroethene.

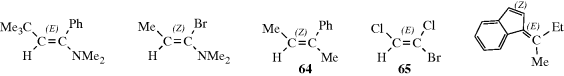
This type of isomerism is also possible with other double bonds (e.g., C=N,²²⁷ N=N,²²⁸ or even C=S),²²⁹ although in these cases only two or three groups are connected to the double-bond atoms. In the case of imines, oximes, and other C=N compounds, if W = Y, 66 may be called syn and 67 anti, but (E) and (Z) are used here too.²³⁰ In azo compounds there is no ambiguity. Compound 68 is always syn or (Z) regardless of the nature of W and Y.

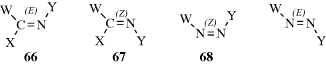
If there is more than one double bond²³¹ in a molecule and if W ≠ X and Y ≠ Z for each, the number of isomers in the most general case is 2ⁿ, although this number may be decreased if some of the substituents are the same, as in the three 2,5-heptadienes shown.

When a molecule contains a double bond and a stereogenic carbon, there are four isomers, a cis pair of enantiomers and a trans pair, shown for 4-methylhex-2-ene.

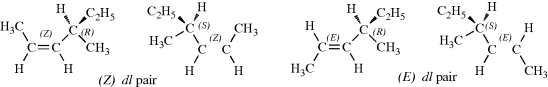
Double bonds in small rings are so constrained that they must be cis. From cyclopropene (a known system) to cycloheptene, double bonds in a stable ring cannot be trans. However, the cyclooctene ring is large enough to permit trans double bonds to exist (see Sec. 4.C, category 7), and for rings larger than 10- or 11-membered, trans isomers are more stable²³² (see also, Sec. 4.Q.ii).

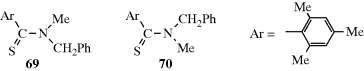
In a few cases, single-bond rotation is so slowed that cis and trans isomers can be isolated even where no double bond exists²³³ (see also, Sec. 4.Q.iv). One example is N-methyl-N-benzylthiomesitylide (69 and 70).²³⁴ The isomers are stable in the crystalline state, but interconvert with a half-life of ~25 h in CDCl₃ at 50°C.²³⁵ This type of isomerism is rare; it is found chiefly in certain amides and thioamides, because resonance gives the single-bond some double-bond character and slows rotation.⁵⁴ (For other examples of restricted rotation about single bonds, see Sec. 4.Q.iv.)

Conversely, there are compounds in which nearly free rotation is possible around what are formally C=C double bonds. These compounds, called push–pull or captodative ethylenes, have two electron-withdrawing groups on one carbon and two electron-donating groups on the other (71).²³⁶ The contribution of diionic

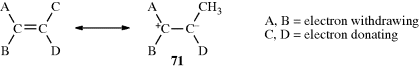
canonical forms, such as the one shown, decreases the double-bond character and allows easier rotation. For example, compound 72 has a barrier to rotation of 13 kcal mol⁻¹ (55 kJ mol⁻¹),²³⁷ compared to a typical value of ~62–65 kcal mol⁻¹(260–270 kJ mol⁻¹) for simple alkenes.

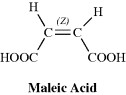
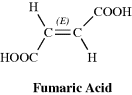
Since they are diastereomers, cis-trans isomers always differ in properties; the differences may range from very slight to considerable. The properties of maleic acid are so different from those of fumaric acid (Table 4.2) that it is not surprising that they have different names. Since they generally have more symmetry than cis isomers, trans isomers in most cases have higher melting points and lower solubilities in inert solvents. The cis isomer usually has a higher heat of combustion, which indicates a lower thermochemical stability. Other noticeably different properties are densities, acid strengths, boiling points, and various types of spectra, but the differences are too involved to be discussed here.

Table 4.2 Some Properties of Maleic and Fumaric Acids.

Property	Maleic Acid	Fumaric Acid
Melting point (°C)	130	286
Solubility in water at 25 °C (g L−1)	788	7
K1 (at 25°C)	1.5 × 10−2	1 × 10−3
K2 (at 25°C)	2.6 × 10−7	3 × 10−5

It is also important to note that trans-alkenes are often more stable than cis-alkenes due to diminished steric hindrance (Sec. 4.Q.iv), but this is not always the case. It is known, for example, that cis-1,2-difluoroethene is thermodynamically more stable than trans-1,2-difluoroethene. This appears to be due to delocalization of halogen lone-pair electrons and an antiperiplanar effect between vicinal antiperiplanar bonds.²³⁸

4.J.ii cis–trans Isomerism of Monocyclic Compounds

Although rings of four carbons and larger are not generally planar (see Sec. 4.O), they will be treated as such in this section, since the correct number of isomers can be determined when this is done²³⁹ and the principles are easier to visualize (see Sec. 4.O).

The presence of a ring, like that of a double bond, prevents rotation. cis and trans isomers are possible whenever there are two carbons on a ring, each of which is substituted by two different groups. The two carbons need not be adjacent. Examples follow:

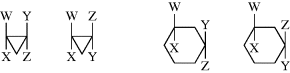
In some cases, the two stereoisomers can interconvert. In cis- and trans-disubstituted cyclopropanones, for example, there is reversible interconversion that favors the more stable trans isomer. This fluxional isomerization occurs via ring opening to an unseen oxyallyl valence bond isomer.²⁴⁰

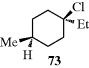
While cis and trans isomers are possible for rings, the restrictions are that W may equal Y and X may equal Z, but W may not equal X and Y may not equal Z. There is an important difference from the double-bond case: The substituted carbons may be stereogenic carbons. This means that there may be more than two isomers. In the most general case, where W, X, Y, and Z are all different, there are four isomers since neither the cis nor the trans isomer is superimposable on its mirror image. This is true regardless of ring size or which carbons are involved, except that in rings of even-numbered size when W, X, Y, and Z are at opposite corners. Cyclohexane derivative 73, for example, has no stereogenic carbons because there is a plane of symmetry. Imagine a focus on the chlorine-bearing carbon, and view each “arm” of the ring as a group. There are two identical groups so the carbon will not be stereogenic. When W = Y and X = Z, the cis isomer is always superimposable on its mirror image. Hence, this isomer is a meso compound, while the trans isomer consists of a dl pair, except in the case noted above. Again, the cis isomer has a plane of symmetry while the trans does not.

Rings with more than two differently substituted carbons can be dealt with using similar principles. In some cases, it is not easy to tell the number of isomers by inspection.¹⁰⁷ The best method may be to count the number n of differently substituted carbons (these will usually be asymmetric, but not always, e.g., in 73), and then to draw 2ⁿ structures, crossing out those that can be superimposed on others (usually the easiest method is to look for a plane of symmetry). By this means, it can be determined that for 1,2,3-cyclohexanetriol there are two meso compounds and a dl pair; and for 1,2,3,4,5,6-hexachlorocyclohexane there are seven meso compounds and a dl pair. Similar principles apply to heterocyclic rings as long as there are carbons (or other ring atoms) containing two different groups.

Cyclic stereoisomers containing only two differently substituted carbons are named either cis or trans, as previously indicated. The (Z, E) system is not used for cyclic compounds. However, cis-trans nomenclature will not suffice for compounds with more than two differently substituted atoms. For these compounds, a system is used in which the configuration of each group is given with respect to a reference group, which is chosen as the group attached to the lowest-numbered ring member bearing a substituent giving rise to cis-trans isomerism. The reference group is indicated by the symbol r. Three stereoisomers named according to this system are 3(S), 5(R)-dimethylcyclohexan-s-1-ol (74), 3(S), 5(R)-dimethylcyclohexan-r-1-ol (75), and 3(S), 5(S)-dimethylcyclohexan-s-1-ol (76). The last example demonstrates the rule that when there are two otherwise equivalent ways of going around the ring, one chooses the path that gives the cis designation to the first substituent after the reference. Another example is 2(S), 4(S)-dimethyl-6s-ethyl-1,3-dioxane (77).

4.J.iii. cis–trans Isomerism of Fused and Bridged Ring Systems

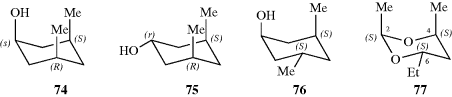
Fused bicyclic systems are those in which two rings share two and only two atoms. In such systems, there is no new principle. The fusion may be cis or trans, as illustrated by cis- and trans-decalin. However, when the rings are small enough, the trans configuration is impossible and the junction must be cis. The smallest trans junction that has been prepared when one ring is four membered is a four–five junction; trans-bicyclo[3.2.0]heptane (78) is known.²⁴¹ For the bicyclo[2.2.0] system (a four–four fusion), only cis compounds have been made. The smallest known trans junction when one ring is three membered is a six–three junction (a bicyclo[4.1.0] system). An example is 79.²⁴² When one ring is three-membered and the other eight-membered (an eight–three junction), the trans-fused isomer is more stable than the corresponding cis-fused isomer.²⁴³

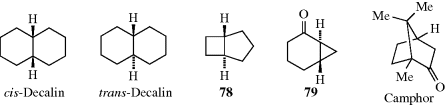
In bridged bicyclic ring systems, two rings share more than two atoms. In these cases, there may be fewer than 2ⁿ isomers, because of the structure of the system. For example, there are only two isomers of camphor (a pair of enantiomers), although it has two stereogenic carbons. In both isomers, the methyl and hydrogen are cis. The trans pair of enantiomers is impossible in this case, since the bridge must be cis. The smallest bridged system so far prepared in which the bridge is trans is the [4.3.1] system; the trans ketone (80) has been prepared.²⁴⁴ In this case, there are four isomers, since both the trans and the cis, which has also been prepared, are pairs of enantiomers.

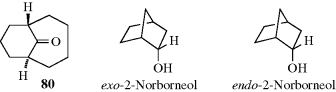
When one of the bridges contains a substituent, the question arises as to how to name the isomers involved. When the two bridges that do not contain the substituent are of unequal length, the rule generally followed is that the prefix endo- is used when the substituent is closer to the longer of the two unsubstituted bridges; the prefix exo- is used when the substituent is closer to the shorter bridge; for example, When the two bridges not containing the substituent are of equal length, this convention cannot be applied, but in some cases a decision can still be made. For example, if one of the two bridges contains a functional group, the endo isomer is the one in which the substituent is closer to the functional group:

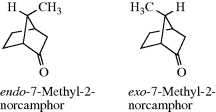
4.K. Out–In Isomerism

Another type of stereoisomerism, called out–in isomerism (or in–out),245 is found in salts of tricyclic diamines with nitrogen at the bridgeheads. In medium-sized bicyclic ring systems, in–out isomerism is possible,²⁴⁶ and the bridgehead nitrogen atoms adopt the arrangement that is more stable.²⁴⁷ A focus on the nitrogen lone pairs reveals that 1,4-diazabicyclo[2.2.2]octane (81) favors the out–out isomer, that 1,6-diazabicyclo[4.4.4]tetradecane (82) the in–in,²⁴⁸ that 1,5-diazabicyclo[3.3.3]undecane (83) has nearly planar nitrogen atoms,²⁴⁹ and that 1,9-diazabicyclo[7.3.1]tridecane (84) is in–out.²⁵⁰ One can also focus on the NH unit in the case of ammonium salts.

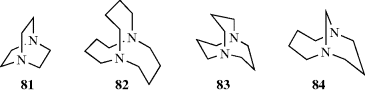
In the examples 85–87, when k, l, and m > 6, the N–H bonds can be inside the molecular cavity or outside, giving rise to three isomers, as shown. Simmons and Park²⁵¹ isolated several such isomers with k, l, and m varying from 6 to 10. In the 9,9,9 compound, the cavity of the in–in isomer is large enough to encapsulate a

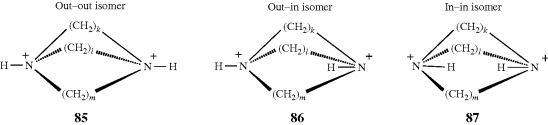
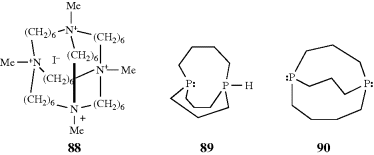
chloride ion that is hydrogen bonded to the two N–H groups. The species thus formed is a cryptate, but differs from the cryptates discussed at Section 3.C.ii in that there is a negative rather than a positive ion enclosed.²⁵² Even smaller ones (e.g., the 4,4,4 compound) have been shown to form mono-inside-protonated ions.²⁵³ In compound 88, which has four quaternary nitrogen atoms, a halide ion has been encapsulated without a hydrogen being present on a nitrogen.²⁵⁴ This ion does not display in–out isomerism. Out–in and in–in isomers have also been prepared in analogous all-carbon tricyclic systems.²⁵⁵

It is known that chiral phosphanes are more pyramidal and that inversion is more difficult, usually requiring temperatures well over 100°C for racemization.²⁵⁶ Alder and Read²⁵⁷ found that deprotonation of bis(phosphorane) 89, which is known to have an in–out structure with significant P–P bonding, leads to a rearrangement and the out–out diphosphane 90. Reprotonation gives 89,²⁵⁸ with inversion at the nonprotonated phosphorus atom occurring at room temperature.

4.L. Enantiotopic and Diastereotopic Atoms, Groups, and Faces259

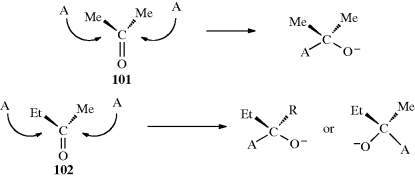
Many molecules contain atoms or groups that appear to be equivalent, but a close inspection will show them to be actually different. We can test whether two atoms are equivalent by replacing each of them in turn with some other atom or group. If the new molecules created by this process are identical, the original atoms are equivalent; otherwise they are not. There are three cases.

1. In the case of malonic acid [CH₂(COOH)₂], propane (CH₂Me₂), or any other molecule of the form CH₂Y₂,²⁶⁰ replacing either of the CH₂ hydrogens by a group Z will give the identical compound. The two hydrogens are thus equivalent. Equivalent atoms and groups need not, of course, be located on the same carbon atom. For example, all the chlorine atoms of hexachlorobenzene are equivalent as are the two bromine atoms of 1,3-dibromopropane.

2. In the case of ethanol, replacing one of the CH₂ hydrogens by a group Z will give one enantiomer of the compound ZCHMeOH (91), while replacement of the other hydrogen gives the other enantiomer (92). Since the two compounds that result upon replacement of H by Z (91 and 92) are not identical but enantiomeric, the hydrogens are not equivalent. Two atoms or groups that upon replacement with a third group give enantiomers are defined as enantiotopic. In any symmetrical environment, the two hydrogens behave as equivalent, but in a dissymmetrical environment they may behave differently. For example, in a reaction

with a chiral reagent they may be attacked at different rates. This has important consequences in enzymatic reactions,²⁶¹ since enzymes are capable of much greater discrimination than ordinary chiral reagents. An example is found in the Krebs cycle, in biological organisms, where oxaloacetic acid (93) is converted to α-oxoglutaric acid (95) by a sequence that includes citric acid (94) as an intermediate. When 93 is labeled with ¹⁴C at the 4 position, the label is found only at C-1 of 95, despite the fact that 94 is not chiral. The two

CH₂COOH groups of 94 are enantiotopic and the enzyme easily discriminates between them.²⁶² Note that the X atoms or groups of any molecule of the form CX₂WY are always enantiotopic if neither W nor Y is chiral. However, enantiotopic atoms and groups may also be found in other molecules (e.g., the hydrogen atoms in 3-fluoro-3-chlorocyclopropene, 96). In this case, substitution of an H by a group Z makes the C-3 atom asymmetric and substitution at C-1 gives the opposite enantiomer from substitution at C-2.

The term prochiral²⁶³ is used for a compound or group that has two enantiotopic atoms or groups (e.g., CX₂WY). That atom or group X that would lead to an R compound if preferred to the other is called pro-(R). The other is pro-(S); for example,

3. Where two atoms or groups in a molecule are in such positions that replacing each of them in turn by a group Z gives rise to diastereomers, the atoms or groups are called diastereotopic. Some examples are the CH₂ groups of 2-chlorobutane (97), vinyl chloride (98), and chlorocyclopropanone (99), as well as the two alkenyl hydrogens

of 100. Diastereotopic atoms and groups are different in any environment, chiral or achiral. These hydrogens react at different rates with achiral reagents, but an even more important consequence is that in NMR spectra, diastereotopic hydrogens theoretically give different peaks and split each other. This is in sharp contrast to equivalent or enantiotopic hydrogens, which are indistinguishable in the NMR, except when chiral solvents are used, in which case enantiotopic (but not equivalent) protons give different peaks.²⁶⁴ The term isochronous is used for hydrogens that are indistinguishable in the NMR.²⁶⁵ In practice, the NMR signals from diastereotopic protons are often found to be indistinguishable, but this is merely because they are very close together. Theoretically they are distinct, and they have been resolved in many cases. When they appear together, it is sometimes possible to resolve them by the use of lanthanide shift reagents (Sec. 4.J) or by changing the solvent or concentration. Note that X atoms or groups (CX₂WY) are diastereotopic if either W or Y is chiral.

Just as there are enantiotopic and diastereotopic atoms and groups, enantiotopic and diastereotopic faces in trigonal molecules may be distinguished. Again, there are three cases: (1) In formaldehyde or acetone (101), attack by an achiral reagent A from either face of the molecule gives rise to the same transition state and product; the two faces are thus equivalent and there is only one product. (2) In 2-butanone (102) or acetaldehyde, attack by an achiral A at one face gives a chiral transition state and the enantiomeric products arise from attack at one or the other face. Such faces are enantiotopic. Attack at an enantiotopic face by a chiral reagent will generate another stereogenic center, which gives diastereomers that may not be formed in equal amounts. (3) In a case like 103, the two faces are obviously not equivalent and are called diastereotopic. Enantiotopic and diastereotopic faces can be named by an extension of the CIP system (Sec. 4.E.i).²⁶³ If the three groups as arranged by the sequence rules have the order X > Y > Z, that face in which the groups in this sequence are clockwise (as in 104) is the Re face (from Latin rectus), whereas 105 shows the Si face (from Latin sinister).

Note that new terminology has been proposed.²⁶⁶ The concept of sphericity is used, and the terms homospheric, enantiospheric, and hemispheric have been coined to specify the nature of an orbit (an equivalent class) assigned to a coset representation.²⁶⁷ Using these terms, prochirality can be defined: If a molecule has at least one enantiospheric orbit, the molecule is defined as being prochiral.²⁵⁸

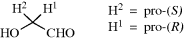
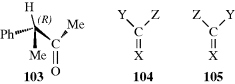
4.M. Stereospecific and Stereoselective Syntheses

Any reaction in which only one of a set of stereoisomers is formed predominantly is called a stereoselective synthesis.268 The same term is used when a mixture of two or more stereoisomers is exclusively or predominantly formed at the expense of other stereoisomers. In a stereospecific reaction, a given isomer leads to one product while another stereoisomer leads to the opposite product. All stereospecific reactions are necessarily stereoselective, but the converse is not true. These terms are best illustrated by examples. Thus, if maleic acid treated with bromine gives the dl pair of 2,3-dibromosuccinic acid while fumaric acid gives the meso isomer (this is the case), the reaction is stereospecific as well as stereoselective because two opposite isomers give two opposite isomers, However, if both maleic and fumaric acid gave the dl pair or a mixture in which the dl pair predominated, the reaction would be stereoselective, but not stereospecific. If more or less equal amounts of dl and meso forms were produced in each case, the reaction would be nonstereoselective. A consequence of these definitions is that if a reaction is carried out on a compound that has no stereoisomers, it cannot be stereospecific, but at most stereoselective. For example, addition of bromine to methylacetylene could (and does) result in preferential formation of trans-1,2-dibromopropene, but this can be only a stereoselective, not a stereospecific reaction.

4.N. Conformational Analysis

For acyclic molecules with single covalent bonds, there is rotation about those bonds. As a practical matter, such rotation leads to different arrangements of the atoms with respect to a given bond, but all arrangements constitute the same molecule. The different arrangements for a molecule due to such rotation are called rotamers. In principle, there is rotation about every single bond and a near infinite number of rotamers. If two different 3D spatial arrangements of the atoms in an acyclic molecule are interconvertible merely by free rotation about bonds, they are called conformations.269 If they are not interconvertible, they are called configurations.²⁷⁰ Configurations represent isomers that can be separated, as previously discussed in this chapter. Conformations represent conformers, which are rapidly interconvertible and thus nonseparable. The terms “conformational isomer” or more commonly “rotamer”²⁷¹ are used to identify one of many structures that result from rotation about single covalent bonds. Typically, the conformation is the average of the collection of lower energy rotatmers for an acyclic compound. A number of methods have been used to determine conformations.²⁷² These include X-ray and electron diffraction, IR, Raman, UV, NMR,²⁷³ and microwave spectra,²⁷⁴ PES,²⁷⁵ supersonic molecular jet spectroscopy,²⁷⁶ and ORD and CD measurements.²⁷⁷ Ring current NMR anisotropy has been applied to conformational analysis,²⁷⁸ as has chemical shift simulation.²⁷⁹ Some of these methods are useful only for solids. It must be kept in mind that the conformation of a molecule in the solid state is not necessarily the same as in solution.²⁸⁰ Conformations can be calculated by a method called molecular mechanics (Sec. 4.P). A method was reported that characterized six-membered ring conformations as a linear combination of ideal basic conformations.²⁸¹ The term absolute conformation has been introduced for molecules where one conformation is optically inactive but, by internal rotation about a C(sp³)–C(sp³) bond, optically active conformers are produced.²⁸²

Note that “free” rotation about single bonds is not possible in cyclic molecules, but rather pseudorotation that leads to different conformations. This discussion will therefore separate rotation in acyclic molecules from pseudorotation in cyclic molecules.

4.N.i. Conformation in Open-Chain Systems²⁸³

For any open-chain molecule with a single bond that connects two sp³ carbon atoms, an infinite number of rotatmers are possible, each of which has a certain energy associated with it, which leads to an infinite number of conformations. As a practical matter, the number of conformations is much less. If one ignores duplications due to symmetry, the number of conformations can be estimated as being > 3ⁿ, where n = the number of internal C–C bonds. For example, n-pentane, has 11, n-hexane 35, n-heptane 109, n-octane 347, n-nonane 1101, and n-decane 3263.²⁸⁴ For ethane, there are two important rotamers that are taken as the extremes, a conformation of highest (marked eclipsed) and one of lowest (marked staggered) potential energy, depicted in two ways as sawhorse diagrams or Newman projections. In Newman projection formulas, the observer looks at the C–C bond head on. The three lines emanating from the center of the circle represent the bonds coming from the front carbon, with respect to the observer.

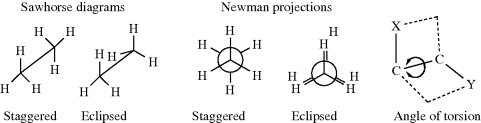
The staggered conformation is the conformation of lowest potential energy for ethane. As rotation about the bond occurs, the energy gradually increases until the eclipsed conformation is reached, when the energy is at a maximum. Further rotation decreases the energy again. Figure 4.4 illustrates this finding. The angle of torsion, which is a dihedral angle, is the angle between the X–C–C and the C–C–Y planes, as shown in the diagram. For ethane, the difference in energy is ~2.9 kcal mol⁻¹ (12 kJ mol⁻¹).²⁸⁵ This difference is called the energy barrier or rotational barrier,²⁸⁶ since in free rotation about a single bond there must be enough rotational energy present to cross the barrier every time two hydrogen atoms are opposite each other. There was much speculation about the cause of the barriers and many explanations have been suggested.²⁸⁷ It has been concluded from MO calculations (see Sec. 4.P) that the barrier is caused by repulsion between overlapping filled molecular orbitals.²⁸⁸ The staggered conformation of ethane is lowest in energy because the orbitals of the C–H bonds in this conformation have the least amount of overlap with the C–H orbitals of the adjacent carbon.

Fig. 4.4 Conformational energy diagram for ethane.

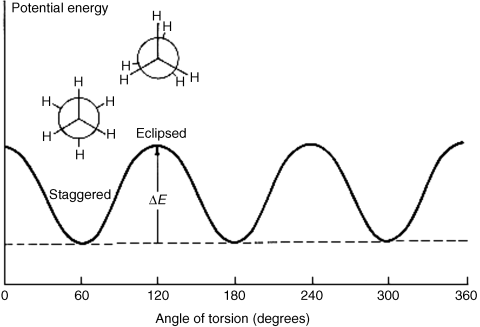
At ordinary temperatures, enough rotational energy is present for the ethane molecule to rotate rapidly, but it spends most of its time at or near the energy minimum. Groups larger than hydrogen cause larger barriers, presumably due to steric interactions between the larger units.²⁸⁹ When the barriers are large enough, as in the case of suitably substituted biphenyls (Sec. 4.C, category 5) or the diadamantyl compound mentioned (see 107 and 108) rotation at room temperature is completely prevented, which is described as a q configuration not a conformations. Even for compounds with small barriers, cooling to low temperatures may remove enough rotational energy for what would otherwise be conformational isomers to become configurational isomers.

A 1,2-disubstituted ethane (YCH₂–CH₂Y or YCH₂–CH₂X,²⁹⁰ e.g., n-butane),²⁹¹ is somewhat more complicated. There are four extremes: a fully staggered conformation, called anti, trans, or antiperiplanar; another staggered conformation, called gauche or synclinal; and two types of eclipsed conformations, called synperiplanar and anticlinal.

An energy diagram for this system is given in Fig. 4.5. Although there is constant rotation about the central bond, it is possible to estimate what percentage of the molecules are in each conformation at a given time. For example, a consideration of dipole moment and polarizability measurements led to the conclusion that for 1,2-dichloroethane in CCl₄ solution at 25°C ~ 70% of the molecules are in the anti and ~ 30% in the gauche conformation.²⁹² The corresponding figures for 1,2-dibromoethane are 89% anti and 11% gauche.²⁹³ The eclipsed conformations are unpopulated and serve only as pathways from one staggered conformation to another. Solids normally consist of a single conformer.

Fig. 4.5 Conformational energy for YCH₂–CH₂Y or YCH₂–CH₂X. For n-butane, ΔE₁ = 4–6, ΔE₂ = 0.9, and ΔE₃ = 3.4 kcal mol⁻¹ (17–25, 3.8, 14 kJ mol⁻¹, respectively).

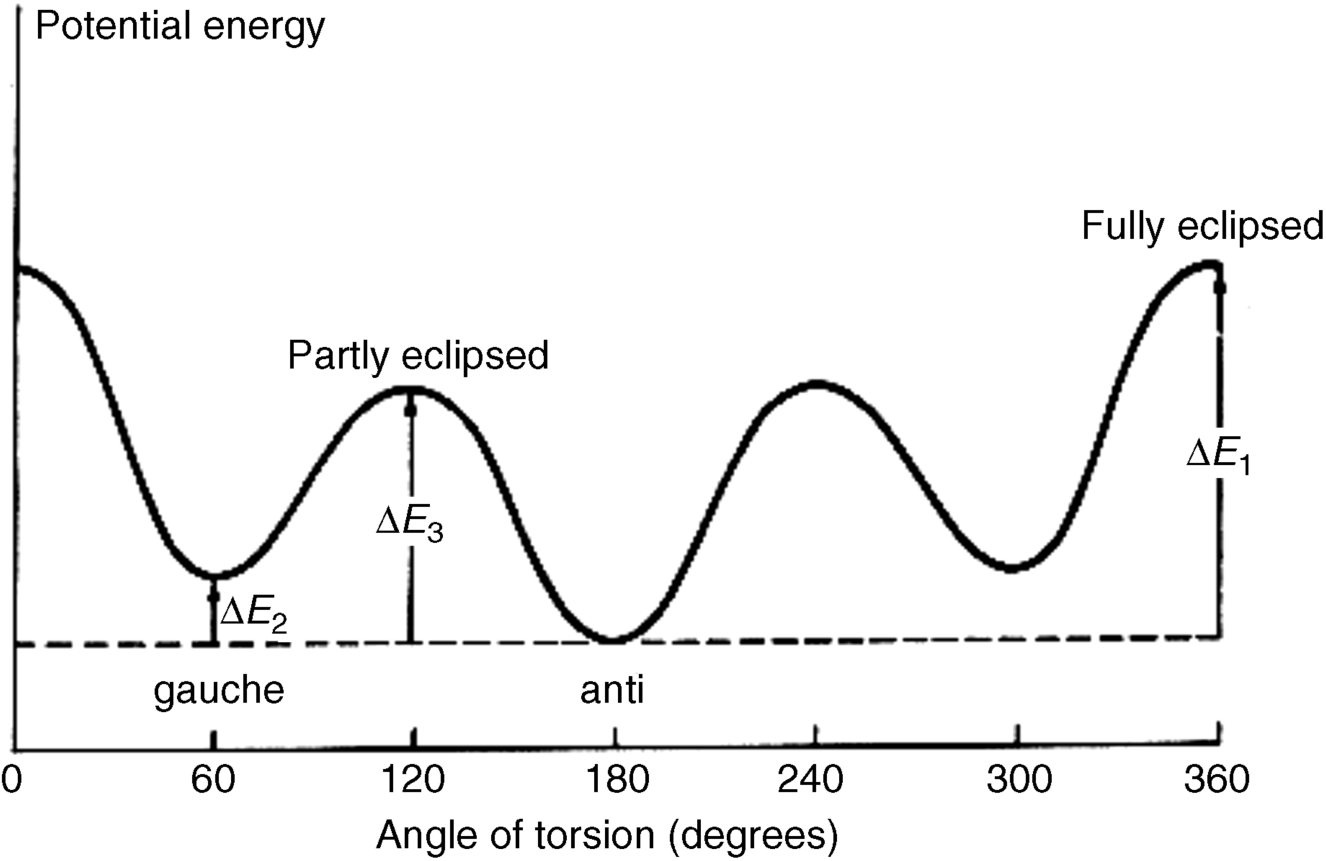
It may be observed that the gauche conformation of butane (see 106), or any other similar molecule, appears to be chiral. It is not. The lack of optical activity in such compounds arises from the fact that 106 is not a static molecule, but is in dynamic equilibrium with many other conformations, including its mirror image. In effect, they interconvert too rapidly for separation.

For butane and for most other molecules of the forms YCH₂–CH₂Y and YCH₂– CH₂X, the anti conformer is the most stable, but exceptions are known. One group of exceptions consists of molecules containing small electronegative atoms, especially fluorine and oxygen. Thus 2-fluoroethanol,²⁹⁴ 1,2-difluoroethane,²⁹⁵ and 2-fluoroethyl trichloroacetate (FCH₂CH₂OCOCCl₃)²⁹⁶ exist predominantly in the gauche form and compounds, such as, 2-chloroethanol and 2-bromoethanol,²⁹⁴ also prefer the gauche form. It has been proposed that the preference for the gauche conformation in these molecules is an example of a more general phenomenon, known as the gauche effect; that is, a tendency to adopt that structure that has the maximum number of gauche interactions between adjacent electron pairs or polar bonds.²⁹⁷ It was believed that the favorable gauche conformation of 2-fluoroethanol was the result of intramolecular hydrogen bonding, but this explanation does not do for molecules like 2-fluoroethyl trichloroacetate. It has in fact been ruled out for 2-fluoroethanol as well.²⁹⁸ The effect of β-substituents in Y–C–C–OX systems where Y = F or SiR₃ has been examined and there is a small bond shortening effect on C–OX that is greatest when OX is a good leaving group. Bond lengthening was also observed with the β-silyl substituent.²⁹⁹ Other exceptions are known, where small electronegative atoms are absent. For example 1,1,2,2-tetrachloroethane and 1,1,2,2-tetrabromoethane both prefer the gauche conformation,³⁰⁰ even though 1,1,2,2-tetrafluoroethane prefers the anti.³⁰¹ Also, both 2,3-dimethylpentane and 3,4-dimethylhexane prefer the gauche conformation,³⁰² and 2,3-dimethylbutane shows no preference for either.³⁰³ Furthermore, the solvent can exert a powerful effect. For example, the compound 2,3-dinitro-2,3-dimethylbutane exists entirely in the gauche conformation in the solid state, but in benzene, the gauche/anti ratio is 79:21; while in CCl₄ the anti form is actually favored (gauche/anti ratio 42:58).³⁰⁴ In many cases, there are differences in the conformation of these molecules between the gas and the liquid phase (as when X = Y = OMe) because of polar interactions with the solvent.³⁰⁵

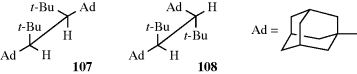
In one case, two conformational isomers of a single aliphatic hydrocarbon, 3,4-di(1-adamantyl)-2,2,5,5-tetramethylhexane, have proven stable enough for isolation at room temperature.³⁰⁶ The two isomers 107 and 108 were separately crystallized, and the structures were proven by X-ray crystallography. The actual dihedral angles are distorted from the 60° angles shown in the drawings, due to steric hindrance between the large adamantyl and tert-butyl groups.

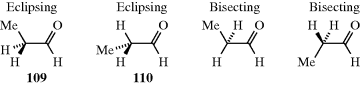
All the conformations so far discussed have involved rotation about sp³–sp³ bonds. Many studies have also been made of compounds with sp³–sp² bonds.³⁰⁷ For example, propanal (or any similar molecule) has four extreme conformations, two of which are called eclipsing and the other two bisecting. For propanal, the eclipsing conformations have lower energy than the other two, with 109 favored over 110 by ~1 kcal mol⁻¹ (4 kJ mol⁻¹).³⁰⁸ As already pointed out (Sec. 4.K.i), for a few of these compounds, rotation is slow enough to permit cis-trans isomerism, although for simple compounds rotation is rapid. The cis conformer of acetic acid was produced in solid Ar,³⁰⁹ and it was reported that acetaldehyde has a lower rotational barrier (~1 kcal mol⁻¹ or 4 kJ mol⁻¹) than ethane.³¹⁰ Calculations have examined the rotational barriers around the CO and CC bonds in formic acid, ethanedial, and glycolaldehyde molecules.³¹¹

Other carbonyl compounds exhibit rotation about sp³–sp³ bonds, including amides.³¹² In N-acetyl-N-methylaniline, the cis- conformation (111) is more stable than the trans- (112) by 3.5 kcal mol⁻¹ (14.6 kJ mol⁻¹).³¹³ This is due to destabilization of (S) due to steric hindrance between two methyl groups, and to electronic repulsion between the carbonyl lone-pair electrons and the phenyl π-electrons in the twisted phenyl orientation.³¹³

A similar conformational analysis has been done with formamide derivatives,³¹⁴ with secondary amides,³¹⁵ and for hydroxamide acids.³¹⁶ It is known that thioformamide has a larger rotational barrier than formamide, which can be explained by a traditional picture of amide “resonance” that is more appropriate for the thioformamide than formamide itself.³¹⁷ Torsional barriers in α-keto amides have been reported,³¹⁸ and the C–N bond of acetamides,³¹⁹ thioamides,³²⁰ enamides³²¹ carbamates (R₂N–CO₂R′),³²² and enolate anions derived from amides³²³ have been examined. It is known that substituents influence rotational barriers.³²⁴

In Section 4.C, category 5, atropisomerism was possible when ortho substituents on biphenyl derivatives and certain other aromatic compounds prevented rotation about the bond. The presence of ortho-substituents can also influence the conformation of certain groups.³²⁵ In 113, R = alkyl and the carbonyl unit is planar, with the trans C=OF conformer is more stable when X = F. When X = CF₃, the cis and trans are planar and the trans predominates.³²⁶ When R = alkyl, there is one orthogonal conformation, but there are two interconverting nonplanar conformations when R = O-alkyl.³²⁶ In 1,2-diacylbenzenes, the carbonyl units tend to adopt a twisted conformation to minimize steric interactions.³²⁷

4.N.ii. Conformation in Six-Membered Rings³²⁸

For cyclic compounds, complete rotation (360°) about a single bond is impossible. However, repulsion between atoms and groups leads to motion about each bond called pseudorotation. Pseudorotation leads to a variety of different conformations, depending on the size of the ring. In many such conformations, the ring is said to be puckered. For cyclohexane, there are two extreme conformations in which all the angles are tetrahedral (the C–C–C angles in cyclohexane are actually 111.5°).³²⁹ These are called the boat and the chair conformations. The chair conformation is the low-energy structure that participates in a dynamic equilibrium (there are two chair conformations that are equivalent in energy for cyclohexane), and the boat form is a higher energy form³³⁰ in equilibrium with a somewhat more stable form

known as the twist conformation. The twist form is ~1.5 kcal mol⁻¹ (6.3 kJ mol⁻¹) more stable than the boat because it has less eclipsing interaction (see below).³³¹ The chair form is more stable than the twist form by ~5 kcal mol⁻¹ (21 kJ mol⁻¹).³³² In the vast majority of compounds containing a cyclohexane ring, the molecules exist almost entirely as equilibrating chair forms.³³³ It is known that the boat or twist form exists transiently. In some cases, chair and twist–boat conformations have actually been observed (cis-1,4-di-tert-butylcyclohexane, e.g.).³³⁴

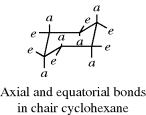
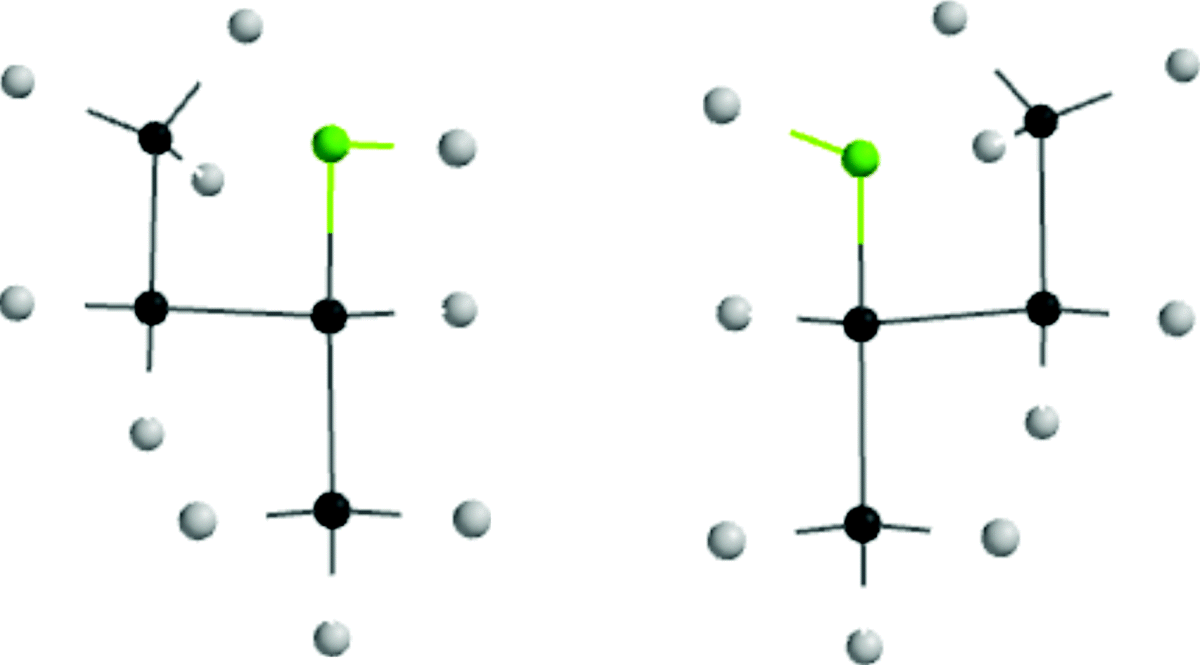
An inspection of the chair form shows that six of its bonds are directed differently from the other six. On each carbon, one bond is directed up or down and the other more or less in the “plane” of the ring. The up or down bonds are called axial and the others are equatorial. The axial bonds point alternately up and down. If a molecule were frozen into a chair form, there would be isomerism in monosubstituted cyclohexanes. For example, there would be an equatorial methylcyclohexane and an axial isomer. This result is incorrect, however, as it has never been possible to isolate isomers of this type at room temperature.³³⁵ In order for the two types of methylcyclohexane to be nonseparable, there must be rapid interconversion of one chair form to another (in which all axial bonds become equatorial and vice versa) and this is possible only if the boat or twist conformations are transient species. Conversion of one chair form to another requires an activation energy of ~10 kcal mol⁻¹ (42 kJ mol⁻¹)³³⁶ and is very rapid at room temperature.³³⁷ However, by working at low temperatures, Jensen and Bushweller³³⁸ were able to obtain the pure equatorial conformers of chlorocyclohexane and trideuteriomethoxycyclohexane as solids and in solution. Equatorial chlorocyclohexane has a half-life of 22 years in solution at −160°C.

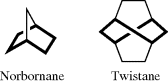
In some molecules, the twist conformation is actually preferred.³³⁹ Of course, in certain bicyclic compounds, the six-membered ring is forced to maintain a boat or twist conformation, as in norbornane or twistane.

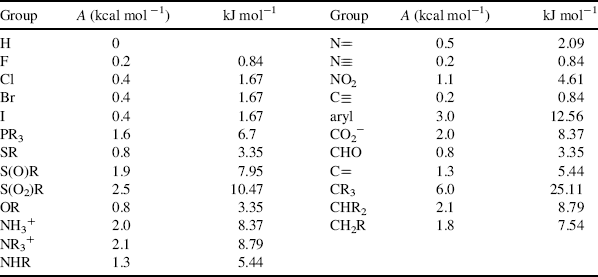
In monosubstituted cyclohexanes, the substituent normally prefers the equatorial position because there is an interaction between the substituent and the axial hydrogens in the axial 3 and 5 positions, but the extent of this preference depends greatly on the nature of the group.³⁴⁰ Alkyl groups have a greater preference for the equatorial position than polar groups. For alkyl groups, the preference increases with size, although size seems to be unimportant for polar groups. Both the large HgBr³⁴¹ and HgCl³⁴² groups and the small F group have been reported to have little or no conformational preference (the HgCl group actually shows a slight preference for the axial position). Table 4.3 gives approximate values of the free energy required for various groups to go from the equatorial position to the axial (these are called A values),³⁴³ although it must be kept in mind that they vary somewhat with physical state, temperature, and solvent.³⁴⁴ Values for other groups in kcal mol⁻¹ include D³⁴⁵ (0.008), NH₂³⁴⁶ (1.4), CH=CH₂³⁴⁷ (1.7), CH₃³⁴⁸ (1.74), C₆H₁₁³⁴⁹ (2.15), Si(CH₃),³⁵⁰ (2.4–2.6), OCH₃³⁵¹ (0.75), C₆H₅³⁵² (2.7), and t-(CH₃)₃C³⁵³ (4.9).

Table 4.3 Free-Energy Differences between Equatorial and Axial Substituents on a Cyclohexane Ring^a,b

[Reprinted with permission from Corey, E.J.; Feiner, N.F. J. Org. Chem. 1980, 45, 765. Copyright © 1980 American Chemical Society.]

a. See Ref. 343.

b. The A values or A^1,3-strain.

For alkyl groups in disubstituted compounds, the conformation is such that as many groups as possible adopt the equatorial position. This conformation will minimize the axial interactions (known as A^1,3-strain), and will be the lower energy conformation. The preference for one chair conformation over the other depends on the groups attached to the cyclohexane ring, and their relative positions on that ring. In a cis-1,2-disubstituted cyclohexane, one substituent must be axial and the other equatorial. In a trans-1,2, compound both may be equatorial or both axial. This finding is also true for 1,4-disubstituted cyclohexanes, but the reverse holds for 1,3-compounds: the trans isomer must have the age conformation and the cis isomer may be a or ee. For alkyl groups, the ee conformation predominates over the a, but for other groups this is not necessarily so. For example, both trans-1,4-dibromocyclohexane and the corresponding dichloro compound have the ee and a conformations about equally populated³⁵⁴ and most trans-1,2-dihalocyclohexanes exist predominantly in the a conformation.³⁵⁵ Note that in the latter case the two halogen atoms are anti in the a conformation, but gauche in the ee conformation.³⁵⁶

Since compounds with alkyl equatorial substituents are generally more stable, trans-1,2 compounds, which can adopt the ee conformation, are thermodynamically more stable than their cis-1,2 isomers, which must exist in the age conformation. For the 1,2-dimethylcyclohexanes, the difference in stability is ~2 kcal mol⁻¹ (8 kJ mol⁻¹). Similarly, trans-1,4 and cis-1,3 compounds are more stable than their stereoisomers.

An interesting anomaly is all-trans-1,2,3,4,5,6-hexaisopropylcyclohexane, in which the six isopropyl groups prefer the axial position, although the six ethyl groups of the corresponding hexaethyl compound prefer the equatorial position.³⁵⁷ The alkyl groups of these compounds can of course only be all axial or all equatorial, and it is likely that the molecule prefers the all-axial conformation because of unavoidable strain in the other conformation.

Incidentally, it is now apparent, at least in one case, why the correct number of stereoisomers could be predicted by assuming planar rings, even though they are not planar (Sec. 4.K.ii). In the case of both a cis-1,2-X,X-disubstituted and a cis-1,2-X,Y-disubstituted cyclohexane, the molecule is nonsuperimposable on its mirror image; neither has a plane of symmetry. However, in the former case (114) conversion of one chair form to the other which of course happens rapidly, turns the molecule into its mirror image, while in the latter case (115) rapid interconversion does not give the mirror image, but merely the conformer in which the original axial and equatorial substituents exchange places. Thus the optical inactivity of 114 is not due to a plane of symmetry, but to a rapid interconversion of the molecule and its mirror image. A similar situation holds for cis-1,3 compounds. However, for cis-1,4 isomers (both X,X and X,Y) optical inactivity arises from a plane of symmetry in both conformations. All trans-1,2- and trans-1,3-disubstituted cyclohexanes are chiral (whether X,X or X,Y), while trans-1,4 compounds (both X,X and X,Y) are achiral, since all conformations have a plane of symmetry. It has been shown that the equilibrium is very dependent on both the solvent and the concentration of the disubstituted cyclohexane.³⁵⁸ A theoretical study of the 1,2-dihalides showed a preference for the diaxial form with X = Cl, but predicted that the energy difference between diaxial and diequatorial was small when X = F.³⁵⁹

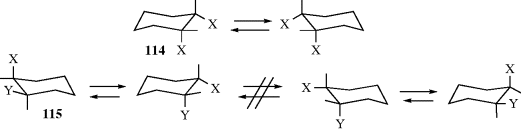
The conformation of a group can be frozen into a desired position by putting a large alkyl group into the ring (most often tert-butyl), which introduces significant A^1,3-strain and leads to a preference for the chair with the groups in the equatorial position.³⁶⁰ It is known that silylated derivatives of trans-1,4- and trans-1,2-dihydroxycyclohexane, some monosilyloxycyclohexanes and some silylated sugars have unusually large populations of chair conformations with axial substituents.³⁶¹ Adjacent silyl groups in the 1,2-disubstituted series show a stabilizing interaction in all conformations, generally leading to unusually large axial populations.

The principles involved in the conformational analysis of six-membered rings containing one or two trigonal atoms. For example, cyclohexanone and cyclohexene, are similar.^362–364 The barrier to interconversion in cyclohexane has been calculated to be 8.4–12.1 kcal mol⁻¹(35.2–50.7 kJ mol⁻¹).³⁶⁵ Cyclohexanone derivatives also assume a chair–conformation. Substituents at C-2 can assume an axial or equatorial position depending on steric and electronic influences. The proportion of the conformation with an axial X group is shown in Table 4.4 for a variety of substituents (X) in 2-substituted cyclohexanones.³⁶⁶

Table 4.4 Proportion of Axial Conformation in 2-Substituted Cyclohexanones, in CDCl₃^a

Reprinted with permission from Basso, E.A.; Kaiser, C.; Rittner, R.; Lambert, J.B. J. Org. Chem. 1993, 58, 7865. Copyright © 1993 American Chemical Society.

X	% Axial Conformation
F	17 ± 3
Cl	45 ± 4
Br	71 ± 4
I	88 ± 5
MeO	28 ± 4
MeS	85 ± 7
MeSe	(92)
Me2N	44 ± 3
Me	(26)
a. See Ref. 366.

4.N.iii. Conformation in Six-Membered Rings Containing Heteroatoms

In six-membered rings containing heteroatoms,³⁶⁷ the basic principles are the same; that is, there are chair, twist, and boat forms, axial, and equatorial groups. The conformational equilibrium for tetrahydropyridines, for example, has been studied.³⁶⁸ In certain compounds, a number of new factors enter the picture. Only two of these will be examined.³⁶⁹

1. In 5-alkyl-substituted 1,3-dioxanes, the 5-substituent has a much smaller preference for the equatorial position than in cyclohexane derivatives;³⁷⁰ the A^1,3-strain is much lower. This fact indicates that the lone pairs on the oxygens have a smaller steric requirement than the C–H bonds in the corresponding cyclohexane derivatives. There is some evidence of a homoanomeric interaction in these systems.³⁷¹ Similar behavior is found in the 1,3-dithianes,³⁷² and 2,3-disubstituted-1,4-dithianes have also been examined.³⁷³ With certain non-alkyl substituents (e.g., F, NO₂, SOMe,³⁷⁴ NMe₃⁺) the axial position is actually preferred.³⁷⁵

2. An alkyl group located on a carbon α to a heteroatom prefers the equatorial position, which is of course the normally expected behavior, but a polar group in such a location prefers the axial position. An example of this phenomenon, known as the anomeric effect,³⁷⁶ is the greater stability of α-glucosides over β-glucosides. A number of explanations have been offered for the anomeric

effect.³⁷⁷ The one³⁷⁸ that has received the most acceptance³⁷⁹ is that one of the lone pairs of the polar atom connected to the carbon (an oxygen atom in the case of 117) can be stabilized by overlapping with an antibonding orbital of the bond between the carbon and the other polar atom:

This can happen only if the two orbitals are in the positions shown. The situation can also be represented by this type of hyperconjugation (called “negative hyperconjugation,” see Sec. 2.M):

It is possible that simple repulsion between parallel dipoles in 116 also plays a part in the greater stability of 117. It has been shown that aqueous solvation effects reduce anomeric stabilization in many systems, particularly for tetrahydropyranosyls.³⁸⁰ In contrast to cyclic acetals, simple acyclic acetals rarely adopt the anomeric conformation, apparently because the eclipsed conformation better accommodates steric interactions of groups linked by relatively short carbon–oxygen bonds.³⁸¹ In all cis-2,5-di-tert-butyl-1,4-cyclohexanediol, hydrogen bonding stabilizes the otherwise high-energy form³⁸² and 1,3-dioxane (118) exists largely as the twist conformation shown.³⁸³ The conformational preference of 1-methyl-1-silacyclohexane (121) has been studied.³⁸⁴ A strongly decreased activation barrier in silacyclohexane was observed, as compared to that in the parent ring, and is explained by the longer endocyclic Si–C bonds.

Second-row heteroatoms are known to show a substantial anomeric effect.³⁸⁵ There appears to be evidence for a reverse anomeric effect in 2-aminotetrahydropyrans,³⁸⁶ but it has been called into question whether a reverse anomeric effect exists at all.³⁸⁷ In 119, the lone-pair electrons assume an axial conformation and there is an anomeric effect.³⁸⁸ In 120, however, the lone-pair electron orbitals are oriented gauche to both the axial and equatorial α-CH bond and there is no anomeric effect.³⁸⁸

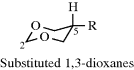
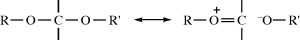
4.N.iv. Conformation in Other Rings³⁸⁹

Three-membered saturated rings are usually planar, but other small rings can have some flexibility. Cyclobutane³⁹⁰ is not planar, but exists as in 122, with an angle between the planes of ~35°.³⁹¹ The deviation from planarity is presumably caused by eclipsing in the planar form (see Sec. 4.Q.i). Oxetane is closer to

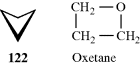
planarity because there is less eclipsing, with an angle between the planes of ~10°.³⁹² Cyclopentane might be expected to be planar, since the angles of a regular pentagon are 108°, but it is not so, also because of eclipsing effects.³⁹³ There are two puckered conformations for cyclopentane, the envelope and the half-chair. There is little energy difference between these two forms and many five-membered ring systems have conformations somewhere in between them.³⁹⁴ Although in the envelope conformation one carbon is shown above the others,

ring motions cause each of the carbons in rapid succession to assume this position. The puckering rotates around the ring in what is called a pseudorotation³⁹⁵ (see Sec. 4.O.ii). In substituted cyclopentanes and five-membered rings in which at least one atom does not contain two substituents [e.g., tetrahydrofuran (THF), cyclopentanone, C₃- and C₇-monosubstituted and disubstituted hexahydroazepin-2-ones (caprolactams),³⁹⁶ tetrahydrothiophene S-oxide³⁹⁷], one conformer may be more stable than the others. The barrier to planarity in cyclopentane has been reported to be 5.2 kcal mol⁻¹ (22 kJ mol⁻¹).³⁹⁸ Contrary to previous reports, there is only weak stabilization (<2 kcal mol⁻¹; <8 kJ mol⁻¹) of three-, four-, and five-membered rings by gem-dialkoxycarbonyl substituents (e.g., COOR).³⁹⁹

Rings larger than six-membered are always puckered⁴⁰⁰ unless they contain a large number of sp² atoms (see the section on strain in medium rings, Sec. 4.Q.ii). The energy and conformations of the alkane series cycloheptane to cyclodecane has been reported.⁴⁰¹ The conformation shown for oxacyclooctane (123), for example, appears to be the most abundant one.⁴⁰² The conformations of other large-ring compounds have been studied, including cycloundecane,⁴⁰³ 11-membered ring lactones,⁴⁰⁴ 10- and 11-membered ring ketones,⁴⁰⁵ and 11- and 14-membered ring lactams.⁴⁰⁶ Dynamic NMR was used to determine the conformation large-ring cycloalkenes and lactones,⁴⁰⁷ and C–H coupling constants have been used for conformational analysis.⁴⁰⁸ Strain estimates have been made for small-ring cyclic allenes and butatrienes.⁴⁰⁹ Note that axial and equatorial hydrogens are found only in the chair conformations of six-membered rings. In rings of other sizes, the hydrogens protrude at angles that generally do not lend themselves to classification in this way,⁴¹⁰ although in some cases the terms “pseudo-axial” and “pseudo-equatorial” have been used to classify hydrogens in rings of other sizes.⁴¹¹

4.O. Molecular Mechanics412

Molecular Mechanics⁴¹³ describes a molecule in terms of a collection of bonded atoms that have been distorted from some idealized geometry due to nonbonded van der Waals (steric) and Coulombic (charge–charge) interactions. This approach is fundamentally different from MO theory that is based on quantum mechanics and that make no reference whatsoever to chemical bonding. The success of molecular mechanics depends on the ability to represent molecules in terms of unique valence structures, on the notion that bond lengths and angles may be transferred from one molecule to another and on a predictable dependence of geometrical parameters on the local atomic environment.

The molecular mechanics energy of a molecule is given as a sum of contributions arising from distortions from ideal bond distances (stretch contributions), bond angles (bend contributions) and torsion angles (torsion contributions), together with contributions from non-bonded interactions. This energy is commonly referred to as a strain energy, meaning that it reflects the inherent strain in a real molecule relative to a hypothetical idealized (strain-free) form.

(4.1)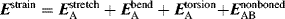

Stretch and bend terms are most simply given in terms of quadratic (Hooke's law) forms:

(4.2)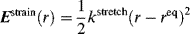

(4.3)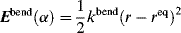

r and α are the bond distance and angle, respectively, and r^eq and α^eq are the ideal bond length and angle, respectively.

Torsion terms need to properly reflect the inherent periodicity of the particular bond involved in a rotation. For example, the threefold periodicity of the carbon–carbon bond in ethane may be represented by a simple cosine form.

(4.4)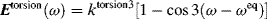

Ω is the torsion angle, ω^eq is the ideal torsion angle and k^torsion is a parameter. Torsion contributions to the strain energy usually will also need to include contributions that are onefold and twofold periodic. These can be represented in the same manner as the threefold term.

(4.5)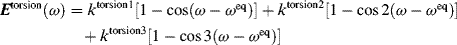

Nonbonded interactions involve a sum of van der Waals (VDW) interactions and Coulombic interactions. The Coulombic term accounts for charge–charge interactions.

(4.6)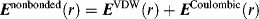

The VDW is made up of two parts, the first to account for strong repulsion on nonbonded atoms as they closely approach, and the second to account for weak long-range attraction, r is the nonbonded distance.

Molecular mechanics methods differ both in the form of the terms that make up the strain energy and in their detailed parameterization. Older methods (e.g., SYBYL⁴¹⁴) use very simple forms and relatively few parameters, while newer methods (e.g., MM3,⁴¹⁵ MM4,⁴¹⁶ and MMFF⁴¹⁷) use more complex forms and many more parameters. In general, the more complex the form of the strain energy terms and the more extensive the parameterization, the better the results. Of course, more parameters mean that more (experimental) data will be needed in their construction. Because molecular mechanics is not based on “physical fundamentals,” but rather is essentially an interpolation scheme, its success depends on the availability of either experimental or high-quality theoretical data for parameterization. A corollary is that molecular mechanics would not be expected to lead to good results for “new” molecules, that is, molecules outside the range of their parameterization.

The two most important applications of molecular mechanics are geometry calculations on very large molecules (e.g., on proteins) and conformational analysis on molecules for which there may be hundreds, thousands, or even tens of thousands of distinct structures. It is here that methods based on quantum mechanics are simply not (yet) practical. It should be no surprise that equilibrium geometries obtained from molecular mechanics are generally in good accord with experimental values. There are ample data with which to parameterize and evaluate the methods. However, because there are very few experimental data relating to the equilibrium conformations of molecules and energy differences among different conformations, molecular mechanics calculations for these quantities need to be viewed with a very critical eye. In time, high-quality data from quantum mechanics will provide the needed data and allow more careful parameterization (and assessment) than now possible.

The most important limitation of molecular mechanics is its inability to provide thermochemical data. The reason for this is that the mechanics strain energy is specific to a given molecule (it provides a measure of how much this molecule deviates from an ideal arrangement), and different molecules have different ideal arrangements. For example, acetone and methyl vinyl ether have different bonds and would be referenced to different standards. The only exception occurs for conformational energy differences or, more generally, for energy comparisons among molecules with exactly the same bonding (e.g., cis- and trans-2-butene).

Because a molecular mechanics calculation reveals nothing about the distribution of electrons or distribution of charge in molecules, and because mechanics methods have not (yet) been parameterized to reproduce transition state geometries, they are of limited value in describing either chemical reactivity or product selectivity. There are, however, situations where steric considerations associated with either the product or reactants are responsible for trends in reactivity and selectivity, and here molecular mechanics would be expected to be of some value.

Because of the different strengths and limitations of molecular mechanics and quantum chemical calculations, it is now common practice to combine the two, for example, to use molecular mechanics to establish conformation (or at least a set of reasonable conformations) and then to quantum calculations to evaluate energy differences.

In practical terms, molecular mechanics calculations may easily be performed on molecules comprising several thousand atoms. Additionally, molecular mechanics calculations are sufficiently rapid to permit extensive conformational searching on molecules containing upward of a hundred atoms. Modern graphical based programs for desktop computers make the methods available to all chemists.

4.P. Strain

Steric strain418 exists in a molecule when bonds are forced to make abnormal angles, usually due to repulsion of large atoms or groups attached to those bonds, but not always. This repulsion results in a higher energy than would be the case in the absence of the angle distortions. It has been shown that there is a good correlation between the ¹³C–H coupling constants in NMR and the bond angles and bond force angles in strained organic molecules.⁴¹⁹ There are, in general, two kinds of structural features that result in sterically caused abnormal bond angles. One of these is found in small-ring compounds, where the angles must be less than those resulting from normal orbital overlap.⁴²⁰ Such strain is called small-angle strain or Baeyer strain. The other arises when nonbonded atoms are forced into close proximity by the geometry of the molecule. These are called nonbonded interactions. This latter type of strain is most often associated with the term steric strain.

Strained molecules possess strain energy. That is, their potential energies are higher than they would be if strain were absent.⁴²¹ The strain energy for a particular molecule can be estimated from heat of atomization or heat of combustion data. A strained molecule has a lower heat of atomization than it would have if it were strain-free (Fig. 4.6). As in the similar case of resonance energies (Sec. 2.B), strain energies cannot be known exactly, because the energy of a real molecule can be measured, but not the energy of a hypothetical unstrained model. It is also possible to calculate strain energies by molecular mechanics, not only for real molecules, but also for those that cannot be made.⁴²²

Fig. 4.6 Strain energy calculation.

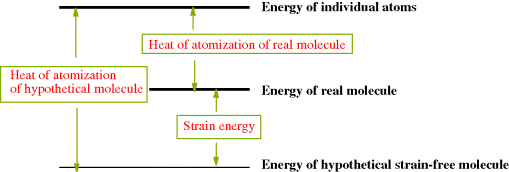
4.P.i Strain in Small Rings

Three-membered rings have a great deal of angle strain (also called Baeyer strain), since 60° angles represent a large departure from the “normal” tetrahedral angles. Calculations have been interpreted to say that Baeyer strain in small ring systems originates from a decrease in nucleus–electron attraction compared to acyclic compounds,⁴²³ but this has been challenged in later work.⁴²⁴ However, in sharp contrast to other ethers, ethylene oxide is quite reactive, the ring being opened by many reagents (see Sec. 10.G.iii). Ring opening, of course, relieves the strain.⁴²⁵ Cyclopropane,⁴²⁶ which is even more strained⁴²⁷ than ethylene oxide, is also cleaved more easily than would be expected for an alkane.⁴²⁸ Thus, pyrolysis at 450–500°C converts it to propene, bromination gives 1,3-dibromopropane,⁴²⁹ and it can be hydrogenated to propane (though at high pressure).⁴³⁰ Other three-membered rings are similarly reactive.⁴³¹ Alkyl substituents influence the strain energy of small ring compounds,⁴³² and carbonyl substitution also influences the strain energy.⁴³³ gem-Dimethyl substitution, for example, “lowers the strain energy of cyclopropanes, cyclobutanes, epoxides, and dimethyldioxirane by 6–10 kcal mol⁻¹ (25–42 kJ mol⁻¹) relative to an unbranched acyclic reference molecule.”⁴³² The CH bond dissociation energy also tends to increase ring strain in small-ring alkenes.⁴³⁴ Computation of the ring strain energy of 1,1-dimethylcyclobutane, however, shows “no significant enthalpic component of the gem-dimethyl effect as measured by the ring strain energy.”⁴³⁵

There is much evidence, chiefly derived from NMR coupling constants, that the bonding in cyclopropanes is not the same as in compounds that lack small-angle strain.⁴³⁶ For a normal carbon atom, one s and three p orbitals are hybridized to give four approximately equivalent sp³ orbitals, each containing ~25% s character. But for a cyclopropane carbon atom, the four hybrid orbitals are far from equivalent. The two orbitals directed to the outside bonds have more s character than a normal sp³ orbital, while the two orbitals involved in ring bonding have less, because the more p-like they are the more they resemble ordinary p orbitals, whose preferred bond angle is 90° rather than 109.5°. Since the small-angle strain in cyclopropanes is the difference between the preferred angle and the real angle of 60°, this additional p character relieves some of the strain. The external orbitals have ~33% s character, so that they are ~sp² orbitals, while the internal orbitals have ~17% s character, so that they may be called ~sp⁵ orbitals.⁴³⁷ Each of the three carbon–carbon bonds of cyclopropane is therefore formed by overlap of two sp⁵ orbitals. Molecular-orbital calculations show that such bonds are not completely s in character. In normal C–C bonds, sp³ orbitals overlap in such a way that the straight line connecting the nuclei becomes an axis about which the electron density is symmetrical. But in cyclopropane, the electron density is directed away from the ring.⁴³⁸ Figure 4.7 shows the direction of orbital overlap.⁴³⁹ For cyclopropane, the angle (marked θ) is 21°. Cyclobutane exhibits the same phenomenon but to a lesser extent, θ being 7°.⁴³⁹ Molecular orbital calculations also show that the maximum electron densities of the C–C σ orbitals are bent away from the ring, with θ = 9.4° for cyclopropane and 3.4° for cyclobutane.⁴⁴⁰ The bonds in cyclopropane are called bent bonds (sometimes, banana bonds), and are intermediate in character between σ and π, so that cyclopropanes behave in some respects like double-bond compounds.⁴⁴¹ For one thing, there is much evidence, chiefly from UV spectra,⁴⁴² that a cyclopropane ring is conjugated with an adjacent double bond. The conjugation is greatest for the conformation shown in Fig. 4.8a and is least or absent for the conformation shown in 4.8b, since overlap of the double-bond π orbital with two of the p-like orbitals of the cyclopropane ring is greatest in conformation a. However, the conjugation between a cyclopropane ring and a double bond is less than that between two double bonds.⁴⁴³ For other examples of the similarities in behavior of a cyclopropane ring and a double bond (see Sec. 4.O.iv).

Fig. 4.7 Orbital overlap in cyclopropane. The arrows point toward the center of electron density.

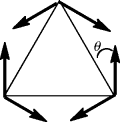
Fig. 4.8 Conformations of α-cyclopropylalkenes. Conformation (a) leads to maximum conjugation and conformation (b) to minimum conjugation

Four-membered rings also exhibit angle strain, but much less than three-membered rings, and for that reason are less easily opened. Cyclobutane is more resistant than cyclopropane to bromination, and although it can be hydrogenated to butane, more strenuous conditions are required. Nevertheless, pyrolysis at 420°C gives two molecules of ethylene. As mentioned earlier (Sec. 4.O.iv), cyclobutane is not planar.

Many highly strained compounds containing small rings in fused systems have been prepared,⁴⁴⁴ showing that organic molecules can exhibit much more strain than simple cyclopropanes or cyclobutanes.⁴⁴⁵ Table 4.5 shows a few of these compounds.⁴⁴⁶ Perhaps the most interesting are cubane, prismane,⁴⁶⁰ and the substituted tetrahedrane, since preparation of these ring systems had been the object of much endeavor. Prismane is tetracyclo[2.2.0.0^2,6.0^3,5]hexane and many derivatives are known,⁴⁶¹ including bis(homohexaprismane) derivatives.⁴⁶² The bicyclobutane molecule is bent, with the angle θ between the planes equal to 126 ± 3°.⁴⁶³ The rehybridization effect, described above for cyclopropane, is even more extreme in this molecule. Calculations have shown that the central bond is essentially formed by overlap of two p orbitals with little or no

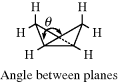
s character.⁴⁶⁴ Propellanes are compounds in which two carbons, directly connected, are also connected by three other bridges. [1.1.1]Propellane is in the table and it is the smallest possible propellane.⁴⁶⁵ It is in fact more stable than the larger [2.1.1]propellane and [2.2.1]propellane, which have been isolated only in solid matrixes at low temperature.⁴⁶⁶ The bicyclo[1.1.1]pentanes are related to the propellanes except that the central connecting bond is missing, and several derivatives are known.⁴⁶⁷ Even more complex systems are known.⁴⁶⁸

Table 4.5 Some Strained Small-Ring Compounds.

In certain small-ring systems, including small propellanes, the geometry of one or more carbon atoms is so constrained that all four of their valences are directed to the same side of a plane (inverted tetrahedron), as in 124.⁴⁶⁹ An example is 1,3-dehydroadamantane, 125, which is also a propellane.⁴⁷⁰ X-ray crystallography of the 5-cyano derivative of 125 shows that the four carbon valences at C-1 and C-3 are all directed “into” the molecule and none point outside.⁴⁷¹ Compound 125 is quite reactive; it is unstable in air, readily adds hydrogen, water, bromine, or acetic acid to the C-1–C-3 bond, and is easily polymerized. When two such atoms are connected by a bond (as in 125), the bond is very long (the C-1–C-3 bond length in the 5-cyano derivative of 125 is 1.64 Å), as the atoms try to compensate in this way for their enforced angles. The high reactivity of the C-1–C-3 bond of 125 is not only caused by strain, but also by the fact that reagents find it easy to approach these atoms since there are no bonds (e.g., C–H bonds on C-1 or C-3) to get in the way.

4.P.ii. Strain in Other Rings⁴⁷²

In rings larger than four-membered, there is no strain due to small bond angles, but there are three other kinds of strain. In the chair form of cyclohexane, which does not exhibit any of the three kinds of strain, all six carbon–carbon bonds have the two attached carbons in the gauche conformation. However, in five-membered rings and in rings containing from 7 to 13 carbons, any conformation in which all the ring bonds are gauche contains transannular interactions, that is, interactions between the substituents on C-1 and C-3 or C-1 and C-4, and so on. These interactions occur because the internal space is not large enough for all the quasi-axial hydrogen atoms to fit without coming into conflict. The molecule can adopt other conformations in which this transannular strain is reduced, but then some of the carbon–carbon bonds must adopt eclipsed or partially eclipsed conformations. The strain resulting from eclipsed conformations is called Pitzer strain. For saturated rings from 3- to 13-membered (except for the chair form of cyclohexane) there is no escape from at least one of these two types of strain. In practice, each ring adopts conformations that minimize both sorts of strain as much as possible. For cyclopentane, as seen in Section 4.O.iv, this means that the molecule is not planar. In rings larger than nine-membered, Pitzer strain seems to disappear, but transannular strain is still present.⁴⁷³ For 9- and 10-membered rings, some of the transannular and Pitzer strain may be relieved by the adoption of a third type of strain, large-angle strain. Thus, C–C–C angles of 115–120° have been found in X-ray diffraction of cyclononylamine hydrobromide and 1,6-diaminocyclodecane dihydrochloride.⁴⁷⁴

Strain can exert other influences on molecules. 1-Aza-2-adamantanone (126) is an extreme case of a twisted amide.⁴⁷⁵ The overlap of the lone-pair electrons on nitrogen with the π-system of the carbonyl is prevented.⁴⁷⁵ In chemical reactions, 126 reacts more or less like a ketone, giving a Wittig reaction (16-44) and it can form a ketal (16-7). A twisted biadamantylidene compound has been reported.⁴⁷⁶

The amount of strain in cycloalkanes is shown in Table 4.6,⁴⁷⁷ which lists heats of combustion per CH₂ group. As can be seen, cycloalkanes > 13-membered are as strain-free as cyclohexane.

Table 4.6 Heats of Combustion in the Gas Phase for Cycloalkanes, per CH₂ Group^a

[Reprinted with permission. Gol'dfarb, Ya.L.; Belen'kii, L.I. Russ. Chem. Rev. 1960, 29, 214, p. 218].

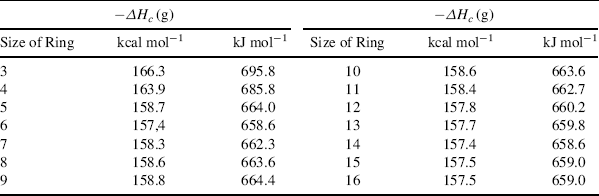
a. See Ref. 472.

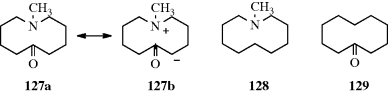
Transannular interactions can exist across rings from 8- to 11-membered and even larger.⁴⁷⁸ Such interactions can be detected by dipole and spectral measurements. For example, that the carbonyl group in 127a is affected by the nitrogen (127b is probably another canonical form) has been demonstrated by photoelectron spectroscopy, which shows that the ionization potentials of the nitrogen n and C=O π orbitals in 127 differ from those of the two comparison molecules 128 and 129.⁴⁷⁹ It is significant that when 127 donates electrons to a proton, it goes to the oxygen rather than to the nitrogen. Many examples of transannular reactions are known, including the following:

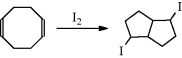	Ref. 480
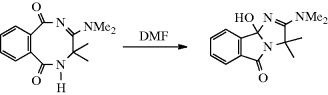	Ref. 481

where DMF = N, N-dimethylformamide (Solvent)

In summary, saturated rings may be divided into four groups, of which the first and third are more strained than the other two.⁴⁸²

1. Small rings (three- and four-membered). Small-angle strain predominates.

2. Common rings (five-, six-, and seven-membered). Largely unstrained. The strain that is present is mostly Pitzer strain.

3. Medium rings (8- to 11-membered). Considerable strain; Pitzer, transannular, and large-angle strain.

4. Large rings (12-membered and larger). Little or no strain.⁴⁸³

4.P.iii. Unsaturated Rings⁴⁸⁴

Double bonds can exist in rings of any size. As expected, the most highly strained are the three-membered rings (e.g., cyclopropene). Small-angle strain, which is so important in cyclopropane, is even greater in cyclopropene⁴⁸⁵ because the ideal angle is more distorted. In cyclopropane, the bond angle is forced to be 60°, ~50° smaller than the tetrahedral angle; but in cyclopropene, the angle, also ~60°, is now ~60° smaller than the ideal angle of 120° for an alkene Thus, the angle of cyclopropene is ~10° more strained than in cyclopropane. However, this additional strain is offset by a decrease in strain arising from another factor. Cyclopropene, lacking two hydrogens, has none of the eclipsing strain present in cyclopropane. Cyclopropene has been prepared⁴⁸⁶ and is stable at liquid-nitrogen temperatures, although on warming even to −80°C it rapidly polymerizes. Many other cyclopropenes are stable at room temperature and above.⁴⁶⁴ The highly strained benzocyclopropene,⁴⁸⁷ in which the cyclopropene ring is fused to a benzene ring, has been prepared⁴⁸⁸ and is stable for weeks at room temperature, although it decomposes on distillation at atmospheric pressure.

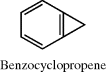
As previously mentioned, double bonds in relatively small rings must be cis. A stable trans double bond⁴⁸⁹ first appears in an eight-membered ring (trans-cyclooctene, Sec. 4.C, category 6), although the transient existence of trans-cyclohexene and cycloheptene has been demonstrated.⁴⁹⁰ Above ~11 members, the trans isomer is more stable than the cis.²³² It has proved possible to prepare compounds in which a trans double bond is shared by two cycloalkene rings (e.g., 130). Such compounds have been called [m.n]betweenanenes, and several have been prepared with m and n values from 8 to 26.⁴⁹¹ The double bonds of the smaller betweenanenes, as might be expected from the fact that they are deeply buried within the bridges, are much less reactive than those of the corresponding cis–cis isomers.

The smallest unstrained cyclic triple bond is found in cyclononyne.⁴⁹² Cyclooctyne has been isolated,⁴⁹³ but its heat of hydrogenation shows that it is considerably strained. There have been a few compounds isolated with triple bonds in seven-membered rings. 3,3,7,7-Tetramethylcycloheptyne (131) is known and dimerizes within 1 h at room temperature,⁴⁹⁴ but the thia derivative (132), in which the C–S bonds are longer than the corresponding C–C bonds in 131, is indefinitely stable even at 140°C.⁴⁹⁵ Cycloheptyne itself has not been isolated, although its transient existence has been shown.⁴⁹⁶ Cyclohexyne⁴⁹⁷ and its 3,3,6,6-tetramethyl derivative⁴⁹⁸ have been trapped at 77 K, and in an Ar π matrix at 12 K, respectively. Its IR spectra have also been

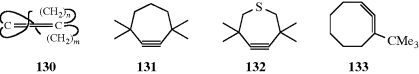
obtained. Transient six- and even five-membered rings containing triple bonds have also been demonstrated.⁴⁹⁹ A derivative of cyclopentyne has been trapped in a matrix.⁵⁰⁰ Although cycloheptyne and cyclohexyne have not been isolated at room temperatures, Pt(0) complexes of these compounds have been prepared and are stable.⁵⁰¹ The smallest cyclic allene⁵⁰² so far isolated is 1-tert-butyl-1,2-cyclooctadiene (133).⁵⁰³ The parent 1,2-cyclooctadiene has not been isolated. It has been shown to exist as a transient species, but rapidly dimerizes.⁵⁰⁴ Incorporation of the tert-butyl group apparently prevents this. The transient existence of 1,2-cycloheptadiene has also been shown,⁵⁰⁵ and both 1,2-cyclooctadiene and 1,2-cycloheptadiene have been isolated in Pt complexes.⁵⁰⁶ 1,2-Cyclohexadiene has been trapped at low temperatures, and its structure has been proved by spectral studies.⁵⁰⁷ Cyclic allenes in general are less strained than their acetylenic isomers.⁵⁰⁸ The cyclic cumulene 1,2,3-cyclononatriene also has been synthesized and is reasonably stable in solution at room temperature in the absence of air.⁵⁰⁹

There are many examples of polycyclic molecules and bridged molecules that have one or more double bonds. There is flattening of the ring containing the C=C unit, and this can have a significant effect on the molecule. Norbornene (bicyclo[2.2.1]hept-2-ene, 134) is a simple example and it has been calculated that it contains a distorted π-face.⁵¹⁰ The double bond can appear away from the bridgehead carbon atoms, as in bicyclo[4.2.2]dec-3-ene (135), which flattens that part of the molecule. The C=C units in pentacyclo[8.2.1.1^2,5.1^4,7.1^8,11]hexadeca-1,7-diene (136) are held in a position where there is significant π–π interactions across the molecule.⁵¹¹

Double bonds at the bridgehead of bridged bicyclic compounds are impossible in small systems. This result is the basis of Bredt's rule,⁵¹² which states that elimination to give a double bond in a bridged bicyclic system (e.g., 137) always leads away from the bridgehead. This rule no longer applies when the rings are large enough. In

determining whether a bicyclic system is large enough to accommodate a bridgehead double bond, the most reliable criterion is the size of the ring in which the double bond is located.⁵¹³ Bicyclo[3.3.1]non-1-ene⁵¹⁴ (138) and bicyclo[4.2.1]non-1(8)ene⁵¹⁵ (139) are stable compounds. Both can be looked upon as derivatives of trans-cyclooctene, which is of course a known compound. Compound 138 has been shown to have a strain

energy of the same order of magnitude as that of trans-cyclooctene.⁵¹⁶ On the other hand, in bicyclo[3.2.2]non-1-ene (140), the largest ring that contains the double bond is a trans-cycloheptene, which is as yet unknown. Compound 140 has been prepared, but dimerized before it could be isolated.⁵¹⁷ Even smaller systems ([3.2.1] and [2.2.2]), but with imine double bonds (141–143), have been obtained in matrixes at low temperatures.⁵¹⁸ These compounds are destroyed on warming. Compounds 141 and 142 are the first reported example of (E–Z) isomerism at a strained bridgehead double bond.⁵¹⁹

4.P.iv. Strain Due to Unavoidable Crowding⁵²⁰

In some molecules, large groups are so close to each other that they cannot fit into the available space in such a way that normal bond angles are maintained. It has proved possible to prepare compounds with a high degree of this type of strain. For example, success has been achieved in synthesizing benzene rings containing ortho tert-butyl groups. Two examples that have been prepared, of several, are 1,2,3-tri-tert-butyl compound 144⁵²¹ and the 1,2,3,4-tetra-tert-butyl compound 145.⁵²² That these molecules are strained is demonstrated by UV and IR spectra, which show that the ring is not planar in 1,2,4-tri-tert-butylbenzene, and by a comparison of the heats of reaction of this compound and its 1,3,5 isomer, which show that the 1,2,4 compound possesses ~22 kcal mol⁻¹ (92 kJ mol⁻¹) more strain energy than its isomer⁵²³ (see also Reaction 18-27). Although SiMe₃ groups are larger

than CMe₃ groups, it has proven possible to prepare C₆(SiMe₃)₆. This compound has a chair-shaped ring in the solid state, and a mixture of chair and boat forms in solution.⁵²⁴ Even smaller groups can sterically interfere in ortho positions. In hexaisopropylbenzene, the six isopropyl groups are so crowded that they cannot rotate, but are lined up around the benzene ring, all pointed in the same direction.⁵²⁵ This compound is an example of a geared molecule.⁵²⁶ The isopropyl groups fit into each other in the same manner as interlocked

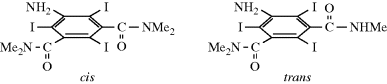
gears. Another example is 146, which is a stable enol.⁵²⁷ In this case, each ring can rotate about its C–aryl bond only by forcing the other to rotate as well. In the case of triptycene derivatives (e.g., 147), a complete 360° rotation of the aryl group around the O–aryl bond requires the aryl group to pass over three rotational barriers; one of which is the C–X bond and the other two the “top” C–H bonds of the other two rings. As expected, the C–X barrier is the highest, ranging from 10.3 kcal mol⁻¹ (43.1 kJ mol⁻¹) for X = F to 17.6 kcal mol⁻¹ (73.6 kJ mol⁻¹) for X = tert-butyl.⁵²⁸ In another instance, it has proved possible to prepare cis and trans isomers of 5-amino-2,4,6-triiodo-N,N,N′,N′-tetramethylisophthalamide because there is no room for the CONMe₂ groups to rotate, caught as they are between two bulky iodine atoms.⁵²⁹ The trans isomer is chiral and has been resolved, while the cis isomer is a meso form. Another example of cis-trans isomerism resulting from restricted rotation about single bonds⁵³⁰ is found in 1,8-di-o-tolylnapthalene⁵³¹ (see also, Sec. 4.K.i).

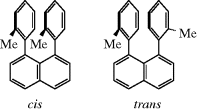
There are many other cases of intramolecular crowding that result in the distortion of bond angles. Hexahelicene (Sec. 4.C, category 6) and bent benzene rings (Sec. 2.G) have been mentioned previously. The compounds tri-tert-butylamine, and tetra-tert-butylmethane are as yet unknown. In the latter, there is no way for the strain to be relieved and it is questionable whether this compound can ever be made. In tri-tert-butylamine, the crowding can be eased somewhat if the three bulky groups assume a planar instead of the normal pyramidal configuration. In tri-tert-butylcarbinol, coplanarity of the three tert-butyl groups is prevented by the presence of the OH group, and yet this compound has been prepared.⁵³² Tri-tert-butylamine should have less steric strain than tri-tert-butylcarbinol and it should be possible to prepare it.⁵³³ The tetra-tert-butylphosphonium cation (t-Bu)₄P⁺ has been prepared.⁵³⁴ Although steric effects are nonadditive in crowded molecules, a quantitative measure has been proposed by DeTar, based on molecular mechanics calculations. This is called formal steric enthalpy (FSE), and values have been calculated for alkanes, alkenes, alcohols, ethers, and methyl esters⁵³⁵ For example, some FSE values for alkanes are butane 0.00; 2,2,3,3-tetramethylbutane 7.27; 2,2,4,4,5-pentamethylhexane 11.30; and tri-tert-butylmethane 38.53.

The two carbon atoms of a C=C double bond and the four groups attached to them are normally in a plane, but if the groups are large enough, significant deviation from planarity can result.⁵³⁶ The compound tetra-tert-butylethene (148) has not been prepared,⁵³⁷ but the tetraaldehyde (149), which should have about the same amount of strain, has been made. X-ray crystallography shows that 149 is twisted out of a planar shape by an angle of 28.6°.⁵³⁸ Also, the C=C double bond distance is 1.357 Å, significantly longer than normal C=C bond of 1.32 Å (Table 1.5). (Z)-1,2-Bis(tert-butyldimethylsilyl)-1,2-bis(trimethylsilyl)ethene (150) has an even greater twist, but could not be made to undergo conversion to the (E) isomer, probably because the groups are too large to slide past each other.⁵³⁹ A different kind of double-bond strain is found in tricyclo[4.2.2.2²,⁵]dodeca-1,5-diene (151),⁵⁴⁰ cubene (152),⁵⁴¹ and homocub-4(5)-ene (153).⁵⁴² In these molecules, the four groups on the

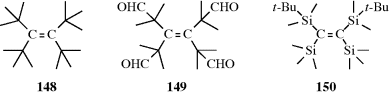
double bond are all forced to be on one side of the double-bond plane.⁵⁴³ In 151, the angle between the line C1–C2 (extended) and the plane defined by C2, C3, and C11 is 27°. An additional source of strain in this molecule is the fact that the two double bonds are pushed into close proximity by the four bridges. In an effort to alleviate this sort of strain, the bridge bond distances (C-3–C-4) are 1.595 Å, which is considerably longer than the 1.53 Å expected for a normal sp³–sp³ C–C bond (Table 1.5). Compounds 152 and 153 have not been isolated, but have been generated as intermediates that were trapped by reaction with other compounds.^541,542

Notes

1. See Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds, Wiley-Interscience, NY, 1994; Sokolov, V.I. Introduction to Theoretical Stereochemistry, Gordon and Breach, NY, 1991; Nógrádi, M. Sterochemistry, Pergamon, Elmsford, NY, 1981; Kagan, H. Organic Sterochemistry, Wiley, NY, 1979; Testa, B. Principles of Organic Stereochemistry, Marcel Dekker, NY, 1979; Izumi, Y.; Tai, A. Stereo-Differentiating Reactions, Academic Press, NY, Kodansha Ltd., Tokyo, 1977; Natta, G.; Farina, M. Stereochemistry, Harper and Row, NY, 1972; Eliel, E.L. Elements of Stereochemistry, Wiley, NY, 1969; Mislow, K. Introduction to Stereochemistry, W.A. Benjamin, NY, 1965. For a historical treatment, see Ramsay, O.B. Stereochemistry, Heyden & Son, Ltd., London, 1981.

2. See Pure Appl. Chem. 1976, 45, 13 and in Nomenclature of Organic Chemistry, Pergamon, Elmsford, NY, 1979 (the Blue Book).

3. See Cintas, P. Angew. Chem. Int. Ed. 2007, 46, 4016.

4. For a discussion of the conditions for optical activity in liquids and crystals, see O'Loane, J.K. Chem. Rev. 1980, 80, 41. For a discussion of chirality as applied to molecules, see Quack, M. Angew. Chem. Int. Ed. 1989, 28, 571.

5. Avalos, M.; Babiano, R.; Cintas, P.; Jiménez, J.L.; Palacios, J.C. Tetrahedron Asymm. 2000, 11, 2845.

6. Interactions among electrons, nucleons, and certain components of nucleons (e.g., bosons), called weak interactions, violate parity; that is, mirror image interactions do not have the same energy. It has been contended that interactions of this sort cause one of a pair of enantiomers to be (slightly) more stable than the other. See Tranter, G.E. J. Chem. Soc. Chem. Commun. 1986, 60, and references cited therein. See also, Barron, L.D. Chem. Soc. Rev. 1986, 15, 189.

7. For a reported exception, see Hata, N. Chem. Lett. 1991, 155.

8. See Craig, D.P.; Mellor, D.P. Top. Curr. Chem. 1976, 63, 1.

9. Strictly speaking, the term racemic mixture applies only when the mixture of molecules is present as separate solid phases, but in this book this expression refers to any equimolar mixture of enantiomeric molecules, liquid, solid, gaseous, or in solution.

10. See Jacques, J.; Collet, A.; Wilen, S.H. Enantiomers, Racemates, and Resolutions, Wiley, NY, 1981.

11. See Wynberg, H.; Lorand, J.P. J. Org. Chem. 1981, 46, 2538 and references cited therein.

12. A good example is found in Kumata, Y.; Furukawa, J.; Fueno, T. Bull. Chem. Soc. Jpn. 1970, 43, 3920.

13. For a review of polarimetry see Lyle, G.G.; Lyle, R.E. in Morrison, J.D. Asymmetric Synthesis, Vol. 1, Academic Press, NY, 1983, pp. 13–27.

14. For examples, see Shriner, R.L.; Adams, R.; Marvel, C.S. in Gilman, H. Advanced Organic Chemistry, Vol. 1, 2nd ed. Wiley, NY, 1943, pp. 291–301.

15. Krow, G.; Hill, R.K. Chem. Commun. 1968, 430.

16. Wiberg, K. B.; Vaccaro, P. H.; Cheeseman, J.R. J. Am. Chem. Soc. 2003, 125, 1888.

17. See Barron L.D. Chem. Soc. Rev. 1986, 15, 189.

18. The definitions of plane, center, and alternating axis of symmetry are taken from Eliel, E.L. Elements of Stereochemistry, Wiley, NY, 1969, pp. 6,7. See also, Lemière, G.L.; Alderweireldt, F.C. J. Org. Chem. 1980, 45, 4175.

19. McCasland, G.E.; Proskow, S. J. Am. Chem. Soc. 1955, 77, 4688.

20. For discussions of the relationship between a chiral carbon and chirality, see Mislow, K.; Siegel, J. J. Am. Chem. Soc. 1984, 106, 3319; Brand, D.J.; Fisher, J. J. Chem. Educ. 1987, 64, 1035.

21. For a review of such molecules, see Nakazaki, M. Top. Stereochem. 1984, 15, 199.

22. See Barth, G.; Djerassi, C. Tetrahedron 1981, 24, 4123; Verbit, L. Prog. Phys. Org. Chem. 1970, 7, 51; Floss, H.G.; Tsai, M.; Woodard, R.W. Top. Stereochem. 1984, 15, 253.

23. Streitwieser, Jr., A.; Schaeffer, W.D. J. Am. Chem. Soc. 1956, 78, 5597.

24. For a discussion of optical activity in paraffins, see Brewster, J.H. Tetrahedron 1974, 30, 1807.

25. Ten Hoeve, W.; Wynberg, H. J. Org. Chem. 1980, 45, 2754.

26. For compounds with asymmetric atoms other than carbon, see Aylett, B.J. Prog. Stereochem. 1969, 4, 213; Belloli, R. J. Chem. Educ. 1969, 46, 640; Sokolov, V.I.; Reutov, O.A. Russ. Chem. Rev. 1965, 34, 1.

27. See Corriu, R.J.P.; Guérin, C.; Moreau, J.J.E. in Patai, S.; Rappoport, Z. The Chemistry of Organic Silicon Compounds, pt. 1, Wiley, NY, 1989, pp. 305–370; Top. Stereochem. 1984, 15, 43; Maryanoff, C.A.; Maryanoff, B.E. in Morrison, J.D. Asymmetric Synthesis, Vol. 4, Academic Press, NY, 1984, pp. 355–374.

28. See Gielen, M. Top. Curr. Chem. 1982, 104, 57; Top. Stereochem. 1981, 12, 217.

29. See Davis, F.A.; Jenkins Jr., R.H. in Morrison, J.D. Asymmetric Synthesis, Vol. 4, Academic Press, NY, 1984, pp. 313–353; Pope, W, J.; Peachey, S.J. J. Chem. Soc. 1899, 75, 1127.

30. Stirling, C.J.M. J. Chem. Soc. 1963, 5741; Sabol, M.A.; Andersen, K.K. J. Am. Chem. Soc. 1969, 91, 3603; Annunziata, R.; Cinquini, M.; Colonna, S. J. Chem. Soc. Perkin Trans. 1 1972, 2057.

31. Lowe, G.; Parratt, M.J. J. Chem. Soc. Chem. Commun. 1985, 1075.

32. Abbott, S.J.; Jones, S.R.; Weinman, S.A.; Knowles, J.R. J. Am. Chem. Soc. 1978, 100, 2558; Cullis, P.M.; Lowe, G. J. Chem. Soc. Chem. Commun. 1978, 512. See Lowe, G. Acc. Chem. Res. 1983, 16, 244.

33. For a review of the stereochemistry at trivalent nitrogen, see Raban, M.; Greenblatt, J. in Patai, S. The Chemistry of Functional Groups, Supplement F, pt. 1, Wiley, NY, 1982, pp. 53–83.

34. See Lambert, J.B. Top. Stereochem. 1971, 6, 19; Rauk, A.; Allen, L.C.; Mislow, K. Angew. Chem. Int. Ed. 1970, 9, 400; Lehn, J.M. Fortschr. Chem. Forsch. 1970, 15, 311.

35. For example, see Stackhouse, J.; Baechler, R.D.; Mislow, K. Tetrahedron Lett. 1971, 3437, 3441.

36. Forsyth, D.A.; Zhang, W.; Hanley, J.A. J. Org. Chem. 1996, 61, 1284. Also see, Adams, D.B. J. Chem. Soc. Perkin Trans. 2 1993, 567.

37. Brois, S.J. J. Am. Chem. Soc. 1968, 90, 506, 508. See also, Shustov, G.V.; Kadorkina, G.K.; Kostyanovsky, R.G.; Rauk, A. J. Am. Chem. Soc. 1988, 110, 1719; Lehn, J.M.; Wagner, J. Chem. Commun. 1968, 148; Felix, D.; Eschenmoser, A. Angew. Chem. Int. Ed. 1968, 7, 224. For a review, see Brois, S.J. Trans. N.Y. Acad. Sci. 1969, 31, 931.

38. Schurig, V.; Leyrer, U. Tetrahedron Asymm. 1990, 1, 865.

39. Bucciarelli, M.; Forni, A.; Moretti, I.; Torre, G.; Brückner, S.; Malpezzi, L. J. Chem. Soc. Perkin Trans. 2 1988, 1595. See also, Forni, A.; Moretti, I.; Torre, G.; Brückner, S.; Malpezzi, L.; Di Silvestro, G.D. J. Chem. Soc. Perkin Trans. 2 1984, 791. See Schmitz, E. Adv. Heterocycl. Chem. 1979, 24, 63.

40. Shustov, G.V.; Denisenko, S.N.; Chervin, I.I.; Asfandiarov, N.L.; Kostyanovsky, R.G. Tetrahedron 1985, 41, 5719 and cited references. See also, Mannschreck, A.; Radeglia, R.; Gründemann, E.; Ohme, R. Chem. Ber. 1967, 100, 1778.

41. Hilpert, H.; Hoesch, L.; Dreiding, A.S. Helv. Chim. Acta 1985, 68, 1691; 1987, 70, 381.

42. See Wu, G.; Huang, M. Chem. Rev. 2006, 106 , 2596.

43. Kostyanovsky, R.G.; Rudchenko, V.F.; Shtamburg, V.G.; Chervin, I.I.; Nasibov, S.S. Tetrahedron 1981, 37, 4245; Kostyanovsky, R.G.; Rudchenko, V.F. Doklad. Chem. 1982, 263, 121. See also, Rudchenko, V.F.; Ignatov, S.M.; Chervin, I.I.; Kostyanovsky, R.G. Tetrahedron 1988, 44, 2233.

44. Prelog, V.; Wieland, P. Helv. Chim. Acta 1944, 27, 1127.

45. For reviews, see Yambushev, F.D.; Savin, V.I. Russ. Chem. Rev. 1979, 48, 582; Gallagher, M.J.; Jenkins, I.D. Top. Stereochem. 1968, 3, 1; Kamai, G.; Usacheva, G.M. Russ. Chem. Rev. 1966, 35, 601.

46. See Valentine, Jr., D.J. in Morrison, J.D. Asymmetric Synthesis, Vol. 4, Academic Press, NY, 1984, pp. 263–312.

47. Horner, L.; Fuchs, H. Tetrahedron Lett. 1962, 203.

48. See Andersen, K.K. in Patai, S.; Rappoport, Z.; Stirling, C. The Chemistry of Sulphones and Sulphoxides, Wiley, NY, 1988, pp. 55–94; and in Stirling, C.J.M. The Chemistry of the Sulphonium Group, pt. 1, Wiley, NY, 1981, pp. 229–312; Barbachyn, M.R.; Johnson, C.R. in Morrison, J.D. Asymmetric Synthesis, Vol. 4, Academic Press, NY, 1984, pp. 227–261; Cinquini, M.; Cozzi, F.; Montanari, F. in Bernardi, F.; Csizmadia, I.G.; Mangini, A. Organic Sulfur Chemistry, Elsevier, NY, 1985, pp. 355–407; Miko /ajczyk, M.; Drabowicz, J. Top. Stereochem. 1982, 13, 333.

49. Andersen, K.K.; Colonna, S.; Stirling, C.J.M. J. Chem. Soc. Chem. Commun. 1973, 645.

50. Balcells, D.; Maseras, F.; Khiar, N. Org. Lett. 2004, 6, 2197.

51. Hamill, H.; McKervey, M.A. Chem. Commun. 1969, 864; Applequist, J.; Rivers, P.; Applequist, D.E. J. Am. Chem. Soc. 1969, 91, 5705.

52. When the two rings of a biphenyl are connected by a bridge, rotation is of course impossible. For a review of such compounds, see Hall, D.M. Prog. Stereochem. 1969, 4, 1.

53. Ceccacci, F.; Mancini, G.; Mencarelli, P.; Villani, C. Tetrahedron Asymm. 2003, 14, 3117.

54. For a review, see Öki, M. Top. Stereochem. 1983, 14, 1. Also see Miljani, O.S.; Han, S.; Holmes, D.; Schaller, G.R.; Vollhardt, K.P.C. Chem. Commun. 2005, 2606.

55. Becker, H.-D.; Langer, V.; Sieler, J.; Becker, H.-C. J. Org. Chem. 1992, 57, 1883.

56. Lunazzi, L.; Mazzanti, A.; Minzoni, M. J. Org. Chem. 2005, 70, 10062.

57. Casarini, D.; Coluccini, C.; Lunazzi, L.; Mazzanti, A. J. Org. Chem. 2005, 70, 5098.

58. Patterson, W.I.; Adams, R. J. Am. Chem. Soc. 1935, 57, 762.

59. Stoughton, R.W.; Adams, R. J. Am. Chem. Soc. 1932, 54, 4426.

60. See Öki, M. Applications of Dynamic NMR Spectroscopy to Organic Chemistry, VCH, NY, 1985.

61. Boiadjiev, S.E.; Lightner, S.A. Tetrahedron Asymm. 2002, 13, 1721.

62. Casarini, D.; Foresti, E.; Gasparrini, F.; Lunazzi, L.; Macciantelli, D.; Misiti, D.; Villani, C. J. Org. Chem. 1993, 58, 5674.

63. See Berthod, M.; Mignani, G.; Woodward, G.; Lemaire, M. Chem. Rev. 2005, 105, 1801. For a review of BINOL, see Brunel, J.M. Chem. Rev. 2005, 105, 857.

64. Alcock, N.W.; Brown, J.M.; Pérez-Torrente, J.J. Tetrahedron Lett. 1992, 33, 389. See also, Mikami, K.; Aikawa, K.; Yusa, Y.; Jodry, J.J.; Yamanaka, M. Synlett 2002, 1561.

65. Dolbier Jr., W.R.; Palmer, K.W. Tetrahedron Lett. 1992, 33, 1547.

66. Cavazza, M.; Zandomeneghi, M.; Pietra, F. Tetrahedron Lett. 2000, 41, 9129.

67. For reviews of allene chirality, see Runge, W. in Landor, S.R. The Chemistry of the Allenes, Vol. 3, Academic Press, NY, 1982, pp. 579–678, and in Patai, S. The Chemistry of Ketenes, Allenes, and Related Compounds, pt. 1, Wiley, NY, 1980, pp. 99–154; Rossi, R.; Diversi, P. Synthesis 1973, 25.

68. Nakagawa, M.; Shing, K.; Naemura, K. Tetrahedron Lett. 1961, 802.

69. Consoli, G.M.L.; Cunsolo, F.; Geraci, C.; Gavuzzo, E.; Neri, P. Org. Lett. 2002, 4, 2649.

70. For a review, see Meurer, K.P.; Vögtle, F. Top. Curr. Chem. 1985, 127, 1. See also, Laarhoven, W.H.; Prinsen, W.J.C. Top. Curr. Chem. 1984, 125, 63; Martin, R.H. Angew. Chem. Int. Ed. 1974, 13, 649.

71. Martin, R.H.; Baes, M. Tetrahedron 1975, 31, 2135; Bernstein, W.J.; Calvin, M.; Buchardt, O. J. Am. Chem. Soc. 1973, 95, 527; Defay, N.; Martin, R.H. Bull. Soc. Chim. Belg. 1984, 93, 313; Bestmann, H.J.; Roth, W. Chem. Ber. 1974, 107, 2923.

72. For reviews of the helicenes, see Laarhoven, W.H.; Prinsen, W.J.C. Top. Curr. Chem. 1984, 125, 63; Martin, R.H. Angew. Chem. Int. Ed. 1974, 13, 649.

73. Janke, R.H.; Haufe, G.; Würthwein, E.-U.; Borkent, J.H. J. Am. Chem. Soc. 1996, 118, 6031.

74. Frim, R.; Goldblum, A.; Rabinovitz, M. J. Chem. Soc. Perkin Trans. 2 1992, 267.

75. Murguly, E.; McDonald, R.; Branda, N.R. Org. Lett. 2000, 2, 3169.

76. Staab, H.A.; Diehm, M.; Krieger, C. Tetrahedron Lett. 1994, 35, 8357.

77. Cope, A.C.; Ganellin, C.R.; Johnson, Jr., H.W.; Van Auken, T.V.; Winkler, H.J.S. J. Am. Chem. Soc. 1963, 85, 3276. Also see, Levin, C.C.; Hoffmann, R. J. Am. Chem. Soc. 1972, 94, 3446.

78. Yokoyama, Y.; Iwai, T.; Yokoyama, Y.; Kurita, Y. Chem. Lett. 1994, 225.

79. Grosu, I.; Mager, S.; Plé, G.; Mesaros, E. Tetrahedron 1996, 52, 12783.

80. For an example, see Rajakumar, P.; Srisailas, M. Tetrahedron 2001, 57, 9749.

81. Blomquist, A.T.; Stahl, R.E.; Meinwald, Y.C.; Smith, B.H. J. Org. Chem. 1961, 26, 1687. For a review of chiral cyclophanes and related molecules, see Schlögl, K. Top. Curr. Chem. 1984, 125, 27.

82. Nakazaki, M.; Yamamoto, K.; Tanaka, S.; Kametani, H. J. Org. Chem. 1977, 42, 287. Also see, Pelter, A.; Crump, R.A.N.C.; Kidwell, H. Tetrahedron Lett. 1996, 37, 1273. For an example of a chiral [2.2]-paracyclophane.

83. For a treatise on the quantitative chirality of helicenes, see Katzenelson, O.; Edelstein, J.; Avnir, D. Tetrahedron Asymm. 2000, 11, 2695.

84. Chan, T.-L.; Hung, C.-W.; Man, T.-O.; Leung, M.-k. J. Chem. Soc. Chem. Commun. 1994, 1971.

85. Collins, S.K.; Yap, G.P.A.; Fallis, A.G. Org. Lett. 2000, 2, 3189.

86. For reviews on the stereochemistry of metallocenes, see Schlögl, K. J. Organomet. Chem. 1986, 300, 219; Top. Stereochem. 1967, 1, 39; Pure Appl. Chem. 1970, 23, 413.

87. For reviews of such complexes, see Paiaro, G. Organomet. Chem. Rev. Sect. A 1970, 6, 319.

88. Paiaro, G.; Palumbo, R.; Musco, A.; Panunzi, A. Tetrahedron Lett. 1965, 1067. Also see, Paiaro, G.; Panunzi, A. J. Am. Chem. Soc. 1964, 86, 5148.

89. Paquette, L.A.; Gardlik, J.M.; Johnson, L.K.; McCullough, K.J. J. Am. Chem. Soc. 1980, 102, 5026.

90. Okamoto, Y.; Yashima, E.; Hatada, K.; Mislow, K. J. Org. Chem. 1984, 49, 557. See Grilli, S.; Lunazzi, L.; Mazzanti, A.; Casarini, D.; Femoni, C. J. Org. Chem. 2001, 66, 488.

91. Lightner, D.A.; Paquette, L.A.; Chayangkoon, P.; Lin, H.; Peterson, J.R.J. Org. Chem. 1988, 53, 1969.

92. See Walba, D.M. Tetrahedron 1985, 41, 3161.

93. Walba, D.M.; Richards, R.M.; Haltiwanger, R.C. J. Am. Chem. Soc. 1982, 104, 3219.

94. Iwanek, W.; Wolff, C.; Mattay, J. Tetrahedron Lett. 1995, 36, 8969.

95. de Vries, E.F.J.; Steenwinkel, P.; Brussee, J.; Kruse, C.G.; van der Gen, A. J. Org. Chem. 1993, 58, 4315; Pappalardo, S.; Palrisi, M.F. Tetrahedron Lett. 1996, 37, 1493; Geraci, C.; Piattelli, M.; Neri, P. Tetrahedron Lett. 1996, 37, 7627.

96. See Schill, G. Catenanes, Rotaxanes, and Knots, Academic Press, NY, 1971, pp. 11–18.

97. There is one exception to this statement. In a very few cases, racemic mixtures may crystalize from solution in such a way that all the (+) molecules go into one crystal and the (−) molecules into another. If one of the crystals crystallizes before the other, a rapid filtration results in optically active material. For a discussion, see Pincock, R.E.; Wilson, K.R. J. Chem. Educ. 1973, 50, 455.

98. The use of small d and l is now discouraged, since some authors used it for rotation, and some for configuration. However, a racemic mixture is still a dl mixture, since there is no ambiguity here.

99. For lists of absolute configurations of thousands of compounds, with references, mostly expressed as (R) or (S) rather than d or l, see Klyne, W.; Buckingham, J. Atlas of Stereochemistry, 2nd ed., 2 Vols., Oxford University Press, Oxford, 1978; Jacques, J.; Gros, C.; Bourcier, S.; Brienne, M.J.; Toullec, J. Absolute Configurations (Vol. 4 of Kagan, H. Stereochemistry), Georg Thieme Publishers, Stuttgart, 1977.

100. Bijvoet, J.M.; Peerdeman, A.F.; van Bommel, A.J. Nature (London) 1951, 168, 271. For a list of organic structures whose absolute configurations have been determined by this method, see Neidle, S.; Rogers, D.; Allen, F.H. J. Chem. Soc. C 1970, 2340.

101. For descriptions of the system and sets of sequence rules, see Pure Appl. Chem. 19767, 45, 13; Nomenclature of Organic Chemistry, Pergamon, Elmsford, NY, 1979 (the Blue Book); Cahn, R.S.; Ingold, C.K.; Prelog, V. Angew. Chem. Int. Ed. 1966, 5, 385; Cahn, R.S. J. Chem. Educ. 1964, 41, 116; Fernelius, W.C.; Loening, K.; Adams, R.M. J. Chem. Educ. 1974, 51, 735. See also, Prelog, V.; Helmchen, G. Angew. Chem. Int. Ed. 1982, 21, 567. Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds, Wiley-Interscience, NY, 1994, pp. 101–147. Also see, Smith, M.B. Organic Synthesis, 3rd ed., Wavefunction Inc./Elsevier, Irvine, CA/London, England, 2010, pp. 15–23.

102. Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds, Wiley, NY, 1994, pp. 1119–1190. See Krow, G. Top. Stereochem. 1970, 5, 31.

103. Mata, P.; Lobo, A.M.; Marshall, C.; Johnson, A.P. Tetrahedron Asymm. 1993, 4, 657; Perdih, M.; Razinger, M. Tetrahedron Asymm. 1994, 5, 835.

104. See Kagan, H.B. Determination of Configuration by Chemical Methods (Vol. 3 of Kagan, H.B. Stereochemistry), Georg Thieme Publishers, Stuttgart, 1977; Brewster, J.H. in Bentley, K.W.; Kirby, G.W. Elucidation of Organic Structures by Physical and Chemical Methods, 2nd ed. (Vol. 4 of Weissberger, A. Techniques of Chemistry), pt. 3, Wiley, NY, 1972, pp. 1–249; Klyne, W.; Scopes, P.M. Prog. Stereochem.1969, 4, 97; Schlenk, Jr., W. Angew. Chem. Int. Ed. 1965, 4, 139. Also see Addadi, L.; Berkovitch-Yellin, Z.; Weissbuch, I.; Lahav, M.; Leiserowitz, L. Top. Stereochem. 1986, 16, 1.

105. Except the X-ray method of Bijvoet.

106. Parker, D. Chem. Rev. 1991, 91, 1441.

107. Dale, J. A.; Dull, D.L.; Mosher, H. S. J. Org. Chem. 1969, 34, 2543; Dale, J.A.; Mosher, H.S. J. Am. Chem. Soc. 1973, 95, 512.

108. See Mori, K.; Akao, H. Tetrahedron Lett. 1978, 4127; Plummer, E.L.; Stewart, T.E.; Byrne, K.; Pearce, G.T.; Silverstein, R.M. J. Chem. Ecol. 1976, 2, 307. See also, Seco, J.M.; Quiñoá, E.; Riguera, R. Tetrahedron Asymm. 2000, 11, 2695.

109. Yamaguchi, S.; Yasuhara, F.; Kabuto, K. Tetrahedron 1976, 32, 1363; Yasuhara, F.; Yamaguchi, S. Tetrahedron Lett. 1980, 21, 2827; Yamaguchi, S.; Yasuhara, F. Tetrahedron Lett. 1977, 89.

110. Latypov, S.K.; Ferreiro, M.J.; Quiñoá, E.; Riguera, R. J. Am. Chem. Soc. 1998, 120, 4741; Latypov, S.K.; Seco, J.M.; Quiñoá, E.; Riguera, R. J. Org. Chem. 1995, 60, 1538.

111. Seco, J.M.; Quiñoá, E.; Riguera, R. Chem. Rev. 2004, 104, 17.

112. Smith, M.B.; Dembofsky, B.T.; Son, Y.C. J. Org. Chem. 1994, 59, 1719; Latypov, S.K.; Riguera, R.; Smith, M.B.; Polivkova, J. J. Org. Chem. 1998, 63, 8682. For a chiral compound used to determine the enantiomeric purity of primary amines, see Pérez-Fuertes, Y.; Kelly, A.M.; Johnson, A.L.; Arimori, S.; Bull, S.D.; James, T.D. Org. Lett. 2006, 8, 609.

113. Alexakis, A.; Mutti, S.; Mangeney, P. J. Org. Chem. 1992, 57, 1224.

114. See Ref. 277 for books and reviews on optical rotatory dispersion and CD. For predictions about anomalous ORD, see Polavarapu, P.L.; Zhao, C. J. Am. Chem. Soc. 1999, 121, 246.

115. Gawronski, J.; Grajewski, J. Org. Lett. 2003, 5, 3301. See Ref. 277; Stephens, P.J.; Aamouche, A.; Devlin, F.J.; Superchi, S.; Donnoli, M.I.; Rosini, C. J. Org. Chem. 2001, 66, 3671; McCann, D.M.; Stephens, P.J. J. Org. Chem. 2006, 71, 6074.

116. Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds, Wiley, NY, 1994, pp. 1203, 999–1003.

117. Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds, Wiley, NY, 1994, pp. 1195, 1003–1007.

118. Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds, Wiley, NY, 1994, pp. 1007–1071; Nakanishi, K.; Berova, N.; Woody, R.W. Circular Dichroism: Principles and Applications, VCH, NY, 1994; Purdie, N.; Brittain, H.G. Analytical Applications of Circular Dichroism, Elsevier, Amsterdam, The Netherlands, 1994.

119. Devlin, F.J.; Stephens, P.J.; Osterle, C.; Wiberg, K.B.; Cheeseman, J.R.; Frisch, M.J. J. Org. Chem. 2002, 67, 8090.

120. Frelek, J.; Geiger, M.; Voelter, W. Curr. Org. Chem. 1999, 3, 117–146 and references cited therein; Snatzke, G.; Wagner, U.; Wolff, H. P. Tetrahedron 1981, 37, 349; Pakulski, Z.; Zamojski, A. Tetrahedron Asymm. 1996, 7, 1363; Frelek, J.; Ikekawa, N.; Takatsuto, S.; Snatzke, G. Chirality 1997, 9, 578.

121. Di Bari, L.; Pescitelli, G.; Pratelli, C.; Pini, D.; Salvadori, P. J. Org. Chem. 2001, 66, 4819.

122. Kobayashi, Y.; Hayashi, N.; Tan, C.-H.; Kishi, Y. Org. Lett. 2001, 3, 2245; Hayashi, N.; Kobayashi, Y.; Kishi, Y. Org. Lett. 2001, 3, 2249; Kobayashi, Y.; Hayashi, N.; Kishi, Y. Org. Lett. 2001, 3, 2253.

123. For another protocol, see Dambruoso, P.; Bassarello, C.; Bifulco, G.; Appendino, G.; Battaglia, A.; Fontana, G.; Gomez-Paloma, L. Org. Lett. 2005, 7, 983.

124. Kobayashi, Y.; Tan, C.-H.; Kishi, Y. J. Am. Chem. Soc. 2001, 123, 2076.

125. Kobayashi, Y.; Hayashi, N.; Tan, C.-H.; Kishi, Y. Org. Lett. 2001, 3, 2245.

126. Roush, W.R.; Bannister, T.D.; Wendt, M.D.; VanNieuwenhze, M.S.; Gustin, D.J.; Dilley, G.J.; Lane, G.C.; Scheidt, K.A.; Smith, III, W.J. J. Org. Chem. 2002, 67, 4284.

127. Hong, S.-p.; McIntosh, M.C. Tetrahedron 2002, 57, 5055.

128. See Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds, Wiley–Interscience, NY, 1994, pp. 93–94, 992–999; Wheland, G.W. Advanced Organic Chemistry, 3rd ed., Wiley, NY, 1960, pp. 204–211; Caldwell, D.J.; Eyring, H. The Theory of Optical Activity Wiley, NY, 1971; Buckingham, A.D.; Stiles, P.J. Acc. Chem. Res. 1974, 7, 258; Mason, S.F. Q. Rev. Chem. Soc. 1963, 17, 20.

129. Brewster, J.H. Top. Stereochem. 1967, 2, 1, J. Am. Chem. Soc. 1959, 81, 5475, 5483, 5493; Sathyanarayana, B.K.; Stevens, E.S. J. Org. Chem. 1987, 52, 3170; Wroblewski, A.E.; Applequist, J.; Takaya, A.; Honzatko, R.; Kim, S.; Jacobson, R.A.; Reitsma, B.H.; Yeung, E.S.; Verkade, J.G. J. Am. Chem. Soc. 1988, 110, 4144.

130. Fidler, J.; Rodger, P.M.; Rodger, A. J. Chem. Soc. Perkin Trans. 2 1993, 235.

131. For a method of generating all stereoisomers consistent with a given empirical formula, suitable for computer use, see Nourse, J.G.; Carhart, R.E.; Smith, D.H.; Djerassi, C. J. Am. Chem. Soc. 1979, 101, 1216; 1980, 102, 6289.

132. Available at http://old.iupac.org/reports/provisional/abstract04/favre_310305.html, Preferred IUPAC Names, Chapter 9, September, 2004, p. 6.

133. A method has been developed for the determination of stereochemistry in six-membered chair-like rings using residual dipolar couplings. See Yan, J.; Kline, A. D.; Mo, H.; Shapiro, M. J.; Zartler, E. R. J. Org. Chem. 2003, 68, 1786.

134. See Carey, F.A.; Kuehne, M.E. J. Org. Chem. 1982, 47, 3811; Boguslavskaya, L.S. J. Org. Chem. USSR 1986, 22, 1412; Seebach, D.; Prelog, V. Angew. Chem. Int. Ed. 1982, 21, 654; Brewster, J.H. J. Org. Chem. 1986, 51, 4751. See also, Tavernier, D. J. Chem. Educ. 1986, 63, 511; Brook, M.A. J. Chem. Educ. 1987, 64, 218.

135. For still another system, see Seebach, D.; Prelog, V. Angew. Chem. Int. Ed. 1982, 21, 654.

136. Masamune, S.; Kaiho, T.; Garvey, D.S. J. Am. Chem. Soc. 1982, 104, 5521.

137. See Morrison, J.D.; Scott, J.W. Asymmetric Synthesis, Vol. 4; Academic Press, NY, 1984; Williams, R.M. Synthesis of Optically Active α-Amino Acids, Pergamon, Elmsford, NY, 1989; Crosby, J. Tetrahedron 1991, 47, 4789; Mori, K. Tetrahedron 1989, 45, 3233.

138. See Coppola, G.M.; Schuster, H.F. Asymmetric Synthesis, Wiley, NY, 1987; Hanessian, S. Total Synthesis of Natural Products: The Chiron Approach, Pergamon, Elmsford, NY, 1983; Hanessian, S. Aldrichim. Acta 1989, 22, 3; Jurczak, J.; Gotebiowski, A. Chem. Rev. 1989, 89, 149.

139. See Morrison, J.D. Asymmetric Synthesis 5 Vols. [Vol. 4 coedited by Scott, J.W.], Academic Press, NY, 1983–1985; Nógrádi, M. Stereoselective Synthesis, VCH, NY, 1986; Eliel, E.L.; Otsuka, S. Asymmetric Reactions and Processes in Chemistry, American Chemical Society, Washington, 1982; Morrison, J.D.; Mosher, H.S. Asymmetric Organic Reactions, Prentice-Hall, Englewood Cliffs, NJ, 1971, paperback reprint, American Chemical Society, Washington, 1976. For reviews, see Ward, R.S. Chem. Soc. Rev. 1990, 19, 1; Whitesell, J.K. Chem. Rev. 1989, 89, 1581; Fujita, E.; Nagao, Y. Adv. Heterocycl. Chem. 1989, 45, 1; Kochetkov, K.A.; Belikov, V.M. Russ. Chem. Rev. 1987, 56, 1045; Oppolzer, W. Tetrahedron 1987, 43, 1969; Seebach, D.; Imwinkelried, R.; Weber, T. Mod. Synth. Methods, 1986, 4, 125; ApSimon, J.W.; Collier, T.L. Tetrahedron 1986, 42, 5157.

140. Leitereg, T.J.; Cram, D.J. J. Am. Chem. Soc. 1968, 90, 4019. For discussions, see Anh, N.T. Top. Curr. Chem, 1980, 88, 145, pp. 151–161; Eliel, E.L. in Morrison, J.D. Asymmetric Synthesis, Vol. 2, Academic Press, NY, 1983, pp. 125–155. See Smith, R.J.; Trzoss, M; Bühl, M.; Bienz, S. Eur. J. Org. Chem. 2002, 2770.

141. See Eliel, E.L. The Stereochemistry of Carbon Compounds, McGraw-Hill, NY, 1962, pp. 68–74; Bartlett, P.A. Tetrahedron 1980, 36, 2, pp. 22–28; Ashby, E.C.; Laemmle, J.T. Chem. Rev. 1975, 75, 521; Goller, E.J. J. Chem. Educ. 1974, 51, 182; Toromanoff, E. Top. Stereochem. 1967, 2, 157.

142. Chérest, M.; Felkin, H.; Prudent, N. Tetrahedron Lett. 1968, 2199; Chérest, M.; Felkin, H. Tetrahedron Lett. 1968, 2205; Anh, N.T.; Eisenstein, O. Nov. J. Chem. 1977, 1, 61. For experiments that show explanations for certain systems based on the Felkin–Anh model to be weak, see Yadav, V.K.; Gupta, A.; Balamurugan, R.; Sriramurthy, V.; Kumar, N.V. J. Org. Chem. 2006, 71, 4178.

143. Cornforth, J.W.; Cornforth, R.H.; Mathew, K.K. J. Chem. Soc. 1959, 112; Evans, D.A.; Siska, S.J.; Cee, V.J. Angew. Chem. Int. Ed. 2003, 42, 1761.

144. See Eliel, E.L. in Morrison, J.D. Asymmetric Synthesis, Vol. 2, Academic Press, NY, 1983, pp. 125–155; Eliel, E.L.; Koskimies, J.K.; Lohri, B. J. Am. Chem. Soc. 1978, 100, 1614; Still, W.C.; McDonald, J.H. Tetrahedron Lett. 1980, 21, 1031; Still, W.C.; Schneider, J.A. Tetrahedron Lett. 1980, 21, 1035.

145. Cee, V.J.; Cramer, C.J.; Evans, D.A. J. Am. Chem. Soc. 2006, 128, 2920.

146. Evans, S.V.; Garcia-Garibay, M.; Omkaram, N.; Scheffer, J.R.; Trotter, J.; Wireko, F. J. Am. Chem. Soc. 1986, 108, 5648; Garcia-Garibay, M.; Scheffer, J.R.; Trotter, J.; Wireko, F. Tetrahedron Lett. 1987, 28, 4789. For an earlier example, see Penzien, K.; Schmidt, G.M.J. Angew. Chem. Int. Ed. 1969, 8, 608.

147. Enders, D.; Eichenauer, H.; Baus, U.; Schubert, H.; Kremer, K.A.M. Tetrahedron 1984, 40, 1345.

148. See Brockmann, Jr., H.; Risch, N. Angew. Chem. Int. Ed. 1974, 13, 664; Potapov, V.M.; Gracheva, R.A.; Okulova, V.F. J. Org. Chem. USSR 1989, 25, 311.

149. Meyers, A.I.; Oppenlaender, T. J. Am. Chem. Soc. 1986, 108, 1989. For reviews of asymmetric reduction, see Morrison, J.D. Surv. Prog. Chem. 1966, 3, 147; Yamada, S.; Koga, K. Sel. Org. Transform., 1970, 1, 1. See also, Morrison, J.D. Asymmetric Synthesis, Vol. 2, Academic Press, NY, 1983.

150. See, in Morrison, J.D. Asymmetric Synthesis, Vol. 5, Academic Press, NY, 1985, the reviews by Halpern, J. pp. 41–69, Koenig, K.E. pp. 71–101, Harada, K. pp. 345–383; Ojima, I.; Clos, N.; Bastos, C. Tetrahedron 1989, 45, 6901, pp. 6902–6916; Jardine, F.H. in Hartley, F.R. The Chemistry of the Metal–Carbon Bond, Vol. 4, Wiley, NY, 1987, pp. 751–775; Nógrádi, M. Stereoselective Synthesis, VCH, NY, 1986, pp. 53–87; Knowles, W.S. Acc. Chem. Res. 1983, 16, 106; Brunner, H. Angew. Chem. Int. Ed. 1983, 22, 897; Sathyanarayana, B.K.; Stevens, E.S. J. Org. Chem. 1987, 52, 3170; Wroblewski, A.E.; Applequist, J.; Takaya, A.; Honzatko, R.; Kim, S.; Jacobson, R.A.; Reitsma, B.H.; Yeung, E.S.; Verkade, J.G. J. Am. Chem. Soc. 1988, 110, 4144.

151. Goering, H.L.; Kantner, S.S.; Tseng, C.C. J. Org. Chem. 1983, 48, 715.

152. For a review, see Masamune, S.; Choy, W.; Petersen, J.S.; Sita, L.R. Angew. Chem. Int. Ed. 1985, 24, 1.

153. For a monograph, see Morrison, J.D. Asymmetric Synthesis, Vol. 5, Academic Press, NY, 1985. For reviews, see Tomioka, K. Synthesis 1990, 541; Consiglio, G.; Waymouth, R.M. Chem. Rev. 1989, 89, 257; Brunner, H. in Hartley, F.R. The Chemistry of the Metal–Carbon Bond, Vol. 5, Wiley, NY, 1989, pp. 109–146; Noyori, R.; Kitamura, M. Mod. Synth. Methods 1989, 5, 115; Pfaltz, A. Mod. Synth. Methods 1989, 5, 199; Kagan, H.B. Bull. Soc. Chim. Fr. 1988, 846; Brunner, H. Synthesis 1988, 645; Wynberg, H. Top. Stereochem. 1986, 16, 87.

154. For reviews of these and related topics, see Zief, M.; Crane, L.J. Chromatographic Separations, Marcel Dekker, NY, 1988; Brunner, H. J. Organomet. Chem. 1986, 300, 39; Bosnich, B.; Fryzuk, M.D. Top. Stereochem. 1981, 12, 119.

155. See Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds, Wiley–Interscience, NY, 1994. Also see, Smith, M.B. Organic Synthesis, 3rd ed., Wavefunction Inc./Elsevier, Irvine, CA/London, England, 2010. For random examples, see Wu, Q.-F.; He, H.; Liu, W.-B.; You, S.-L. J. Am. Chem. Soc. 2010, 132, 11418; Berhal, F.; Wu, Z.; Genet, J.-P.; Ayad, T.; Ratovelomanana-Vidal, V. J. Org. Chem. 2011, 76, 6320; He, P.; Liu, X.; Shi, J.; Lin, L.; Feng, X. Org. Lett. 2011, 13, 936; Yang, H.-M.; Li, L.; Li, F.; Jiang, K.-Z.; Shang, J.-Y.; Lai, G.-Q.; Xu, L.-W. Org. Lett. 2011, 13, 6508.

156. Findeis, M.A.; Whitesides, G.M. J. Org. Chem. 1987, 52, 2838; Réty, J.; Robinson, J.A. Stereospecificity in Organic Chemistry and Enzymology, Verlag Chemie, Deerfield Beach, FL, 1982. For reviews, see Klibanov, A.M. Acc. Chem. Res. 1990, 23, 114; Jones, J.B. Tetrahedron 1986, 42, 3351; Jones, J.B. in Morrison, J.D. Asymmetric Synthesis, Vol. 5, Academic Press, NY, 1985, pp. 309–344.

157. Heathcock, C.H.; White, C.T. J. Am. Chem. Soc. 1979, 101, 7076.

158. For a review, See Buchardt, O. Angew. Chem. Int. Ed. 1974, 13, 179. For a discussion, see Barron L.D. J. Am. Chem. Soc. 1986, 108, 5539.

159. See Bernstein, W.J.; Calvin, M.; Buchardt, O. J. Am. Chem. Soc. 1973, 95, 527; Nicoud, J.F.; Kagan, J.F. Isr. J. Chem. 1977, 15, 78. See also, Zandomeneghi, M.; Cavazza, M.; Pietra, F. J. Am. Chem. Soc. 1984, 106, 7261.

160. Faigl, F.; Fogassy, E.; Nógrádi, M.; Pálovics, E.; Schindler, J. Tetrahedron Asymm. 2008, 19, 519. See Wilen, S.H.; Collet, A.; Jacques, J. Tetrahedron 1977, 33, 2725; Boyle, P.H. Q. Rev. Chem. Soc. 1971, 25, 323; Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds, Wiley–Interscience, NY, 1994, pp. 297–424; Jacques, J.; Collet, A.; Wilen, S.H. Enantiomers, Racemates, aand Resolutions, Wiley, NY, 1981.

161. Schiffers, I.; Rantanen, T.; Schmidt, F.; Bergmans, W.; Zani, L.; Bolm, C. J. Org. Chem. 2006, 71, 2320.

162. See Boyle, P.H. Q. Rev. Chem. Soc. 1971, 25, 323; Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds, Wiley–Interscience, NY, 1994, pp. 322–424.

163. For an extensive list of reagents that have been used for this purpose and of compounds resolved, see Wilen, S.H. Tables of Resolving Agents and Optical Resolutions, University of Notre Dame Press, Notre Dame, IN, 1972.

164. See Klyashchitskii, B.A.; Shvets, V.I. Russ. Chem. Rev. 1972, 41, 592.

165. Periasamy, M.; Kumar, N.S.; Sivakumar, S.; Rao, V.D.; Ramanathan, C.R.; Venkatraman, L. J. Org. Chem. 2001, 66, 3828.

166. Andersen, N.G.; Ramsden, P.D.; Che, D.; Parvez, M.; Keay, B.A. J. Org. Chem. 2001, 66, 7478.

167. Caccamese, S.; Bottino, A.; Cunsolo, F.; Parlato, S.; Neri, P. Tetrahedron Asymm. 2000, 11, 3103.

168. See Slingenfelter, D.S.; Helgeson, R.C.; Cram, D.J. J. Org. Chem. 1981, 46, 393; Davidson, R.B.; Bradshaw, J.S.; Jones, B.A.; Dalley, N.K.; Christensen, J.J.; Izatt, R.M.; Morin, F.G.; Grant, D.M. J. Org. Chem. 1984, 49, 353.

169. See Prelog, V.; Kovaevi, M.; Egli, M. Angew. Chem. Int. Ed. 1989, 28, 1147; Worsch, D.; Vögtle, F. Top. Curr. Chem. 1987, 140, 21; Toda, F. Top. Curr. Chem. 1987, 140, 43; Stoddart, J.F. Top. Stereochem. 1987, 17, 207; Arad-Yellin, R.; Green, B.S.; Knossow, M.; Tsoucaris, G. in Atwood, J.L.; Davies, J.E.D.; MacNicol, D.D. Inclusion Compounds, Vol. 3, Academic Press, NY, 1984, pp. 263–295.

170. See Schlenk, Jr., W. Liebigs Ann. Chem. 1973, 1145, 1156, 1179, 1195. See Arad-Yellin, R.; Green, B.S.; Knossow, M.; Tsoucaris, G. J. Am. Chem. Soc. 1983, 105, 4561.

171. Miyamoto, H.; Sakamoto, M.; Yoskioka, K.; Takaoka, R.; Toda, F. Tetrahedron Asymm. 2000, 11, 3045.

172. For a review, see Tsuji, J. Adv. Org. Chem. 1969, 6, 109, see p. 220.

173. Amos, R.D.; Handy, N.C.; Jones, P.G.; Kirby, A.J.; Parker, J.K.; Percy, J.M.; Su, M.D. J. Chem. Soc. Perkin Trans. 2 1992, 549.

174. See Westley, J.W.; Halpern, B.; Karger, B.L. Anal. Chem. 1968, 40, 2046; Kawa, H.; Yamaguchi, F.; Ishikawa, N. Chem. Lett. 1982, 745.

175. See Meyers, A.I.; Slade, J.; Smith, R.K.; Mihelich, E.D.; Hershenson, F.M.; Liang, C.D. J. Org. Chem. 1979, 44, 2247; Goldman, M.; Kustanovich, Z.; Weinstein, S.; Tishbee, A.; Gil-Av, E. J. Am. Chem. Soc. 1982, 104, 1093.

176. See Lough, W.J. Chiral Liquid Chromatography; Blackie and Sons: London, 1989; Krstulovi, A.M. Chiral Separations by HPLC, Ellis Horwood, Chichester, 1989; Zief, M.; Crane, L.J. Chromatographic Separations, Marcel Dekker, NY, 1988. For a review, see Karger, B.L. Anal. Chem. 1967, 39(8), 24A.

177. Weinstein, S. Tetrahedron Lett. 1984, 25, 985.

178. See Allenmark, S.G. Chromatographic Enantioseparation, Ellis Horwood, Chichester, 1988; König, W.A. The Practice of Enantiomer Separation by Capillary Gas Chromatography, Hüthig, Heidelberg, 1987. For reviews, see Schurig, V.; Nowotny, H. Angew. Chem. Int. Ed. 1990, 29, 939; Pirkle, W.H.; Pochapsky, T.C. Chem. Rev. 1989, 89, 347; Blaschke, G. Angew. Chem. Int. Ed. 1980, 19, 13; Rogozhin, S.V.; Davankov, V.A. Russ. Chem. Rev. 1968, 37, 565. See also, many articles in the journal Chirality.

179. Ohara, M.; Ohta, K.; Kwan, T. Bull. Chem. Soc. Jpn. 1964, 37, 76. See also, Blaschke, G.; Donow, F. Chem. Ber. 1975, 108, 2792; Hess, H.; Burger, G.; Musso, H. Angew. Chem. Int. Ed. 1978, 17, 612.

180. See Schurig, V.; Nowotny, H.; Schmalzing, D. Angew. Chem. Int. Ed. 1989, 28, 736; Ôi, S.; Shijo, M.; Miyano, S. Chem. Lett. 1990, 59; Erlandsson, P.; Marle, I.; Hansson, L.; Isaksson, R.; Pettersson, C.; Pettersson, G. J. Am. Chem. Soc. 1990, 112, 4573.

181. See, for example, Pirkle, W.H.; Welch, C.J. J. Org. Chem. 1984, 49, 138.

182. Kanoh, S.; Hongoh, Y.; Katoh, S.; Motoi, M.; Suda, H. J. Chem. Soc. Chem. Commun. 1988, 405; Bradshaw, J.S.; Huszthy, P.; McDaniel, C.W.; Zhu, C.Y.; Dalley, N.K.; Izatt, R.M.; Lifson, S. J. Org. Chem. 1990, 55, 3129.

183. See, for example, Hamilton, J.A.; Chen, L. J. Am. Chem. Soc. 1988, 110, 5833.

184. See Miyata, M.; Shibakana, M.; Takemoto, K. J. Chem. Soc. Chem. Commun. 1988, 655.

185. For a review, see Sih, C.J.; Wu, S. Top. Stereochem. 1989, 19, 63.

186. See Nakamura, K.; Inoue, Y.; Ohno, A. Tetrahedron Lett. 1994, 35, 4375; Kazlauskas, R.J. J. Am. Chem. Soc. 1989, 111, 4953; Schwartz, A.; Madan, P.; Whitesell, J.K.; Lawrence, R.M. Org. Synth. 69, 1. For resolution with Subtilisin, see Savile, C.K.; Magloire, V.P.; Kazlauskas, R.J. J. Am. Chem. Soc. 2005, 127, 2104. For the chemoenzymatic kinetic resolution of primary amines, see Paetzold, J.; Bäckvall, J.E. J. Am. Chem. Soc. 2005, 127, 17620.

187. For an example, see Gais, H.-J.; Jungen, M.; Jadhav, V. J. Org. Chem. 2001, 66, 3384.

188. For an example of the resolution of acyloins, see Ödman, P.; Wessjohann, L.A.; Bornscheuer, U.T. J. Org. Chem. 2005, 70, 9551.

189. For reviews, see Collet, A.; Brienne, M.; Jacques, J. Chem. Rev. 1980, 80, 215; Bull. Soc. Chim. Fr. 1972, 127; 1977, 494. For a discussion, see Curtin, D.Y.; Paul, I.C. Chem. Rev. 1981, 81, 525 pp. 535–536.

190. Besides discovering this method of resolution, Pasteur also discovered the method of conversion to diastereomers and separation by fractional crystallization and the method of biochemical separation (and, by extension, kinetic resolution).

191. This is a case of optically active materials arising from inactive materials. However, it may be argued that an optically active investigator is required to use the tweezers. Perhaps a hypothetical human being constructed entirely of inactive molecules would be unable to tell the difference between left- and right-handed crystals.

192. For a review of the seeding method, see Secor, R.M. Chem. Rev. 1963, 63, 297.

193. Martin, R.H; Baes, M. Tetrahedron 1975, 31, 2135. See also, Wynberg, H.; Groen, M.B. J. Am. Chem. Soc. 1968, 90, 5339; McBride, J.M.; Carter, R.L. Angew. Chem. Int. Ed. 1991, 30, 293.

194. Kress, R.B.; Duesler, E.N.; Etter, M.C.; Paul, I.C.; Curtin, D.Y. J. Am. Chem. Soc. 1980, 102, 7709. See also, Gottarelli, G.; Spada, G.P. J. Org. Chem. 1991, 56, 2096. For a discussion and other examples, see Agranat, I.; Perlmutter-Hayman, B.; Tapuhi, Y. Nouv. J. Chem. 1978, 2, 183.

195. Addadi, L.; Weinstein, S.; Gati, E.; Weissbuch, I.; Lahav, M. J. Am. Chem. Soc. 1982, 104, 4610. See also, Weissbuch, I.; Addadi, L.; Berkovitch-Yellin, Z.; Gati, E.; Weinstein, S.; Lahav, M.; Leiserowitz, L. J. Am. Chem. Soc. 1983, 105, 6615.

196. Paquette, L.A.; Lau, C.J. J. Org. Chem. 1987, 52, 1634.

197. For reviews, see Pellissier, H. Tetrahedron 2008, 64, 1563; Ward, R.S. Tetrahedron Asymm. 1995, 6, 1475; Pellissier, H. Tetrahedron 2003, 59, 8291.

198. Lu, Y.; Zhao, X.; Chen, Z.-N. Tetrahedron Asymm. 1995, 6, 1093.

199. Brown, H.C.; Ayyangar, N.R.; Zweifel, G. J. Am. Chem. Soc. 1964, 86, 397.

200. Carlier, P.R.; Mungall, W.S.; Schröder, G.; Sharpless, K.B. J. Am. Chem. Soc. 1988, 110, 2978; Discordia, R.P.; Dittmer, D.C. J. Org. Chem. 1990, 55, 1414. For other examples, see Katamura, M.; Ohkuma, T.; Tokunaga, M.; Noyori, R. Tetrahedron Asymm. 1990, 1, 1; Hayashi, M.; Miwata, H.; Oguni, N. J. Chem. Soc. Perkin Trans. 2 1991, 1167.

201. Lohray, B.B.; Bhushan, V. Tetrahedron Lett. 1993, 34, 3911.

202. Kubota, H.; Kubo, A.; Nunami, K. Tetrahedron Lett. 1994, 35, 3107.

203. Tomooka, K.; Komine, N.; Fujiki, D.; Nakai, T.; Yanagitsuru, S. J. Am. Chem. Soc. 2005, 127, 12182.

204. Pirkle, W.H.; Reno, D.S. J. Am. Chem. Soc. 1987, 109, 7189. For another example, see Reider, P.J.; Davis, P.; Hughes, D.L.; Grabowski, E.J.J. J. Org. Chem. 1987, 52, 955.

205. Stecher, H.; Faber, K. Synthesis 1997, 1.

206. Allan, G. R.; Carnell, A. J. J. Org. Chem. 2001, 66, 6495.

207. For a review, see Raban, M.; Mislow, K. Top. Stereochem. 1967, 2, 199.

208. If a sample contains 80% (+) and 20% (−) isomer, the (−) isomer cancels an equal amount of (+) isomer and the mixture behaves as if 60% of it were (+) and the other 40% inactive. Therefore the rotation is 60% of 80° or 48°. This type of calculation, however, is not valid for cases in which [α] is dependent on concentration (Sec. 4.B); see Horeau, A. Tetrahedron Lett. 1969, 3121.

209. For a method to measure %ee using electrooptics, see Walba, D.M.; Eshdat, L.; Korblova, E.; Shao, R.; Clark, N.A. Angew. Chem. Int. Ed. 2007, 46, 1473.

210. Raban, M.; Mislow, K. Tetrahedron Lett. 1965, 4249, 1966, 3961; Jacobus, J.; Raban, M. J. Chem. Educ. 1969, 46, 351; Tokles, M.; Snyder, J.K. Tetrahedron Lett. 1988, 29, 6063. For a review, see Yamaguchi, S. in Morrison, J.D. Asymmetric Synthesis, Vol. 1, Academic Press, NY, 1983, pp. 125–152. See also, Raban, M.; Mislow, K. Top. Stereochem. 1967, 2, 199.

211. Though enantiomers give identical NMR spectra, the spectrum of a single enantiomer may be different from that of the racemic mixture, even in solution. See Williams, T.; Pitcher, R.G.; Bommer, P.; Gutzwiller, J.; Uskokovi, M. J. Am. Chem. Soc. 1969, 91, 1871.

212. Raban, M.; Mislow, K. Top. Stereochem. 1967, 2, 199, see pp. 216–218.

213. For a method that relies on diastereomer formation without a chiral reagent, see Feringa, B.L.; Strijtveen, B.; Kellogg, R.M. J. Org. Chem. 1986, 51, 5484. See also, Pasquier, M.L.; Marty, W. Angew. Chem. Int. Ed. 1985, 24, 315; Luchinat, C.; Roelens, S. J. Am. Chem. Soc. 1986, 108, 4873.

214. See Trost, B.M.; Belletire, J.L.; Godleski, S.; McDougal, P.G.; Balkovec, J.M.; Baldwin, J.J.; Christy, M.E.; Ponticello, G.S.; Varga, S.L.; Springer, J.P. J. Org. Chem. 1986, 51, 2370.

215. For reviews of NMR chiral solvating agents, see Weisman, G.R. in Morrison, J.D. Asymmetric Synthesis, Vol. 1, Academic Press, NY, 1983, pp. 153–171; Pirkle, W.H.; Hoover, D.J. Top. Stereochem. 1982, 13, 263. Sweeting, L.M.; Anet, F.A.L. Org. Magn. Reson. 1984, 22, 539. See also, Pirkle, W.H.; Tsipouras, A. Tetrahedron Lett. 1985, 26, 2989; Parker, D.; Taylor, R.J. Tetrahedron 1987, 43, 5451.

216. Sweeting, L.M.; Crans, D.C.; Whitesides, G.M. J. Org. Chem. 1987, 52, 2273; Morrill, T.C. Lanthanide Shift Reagents in Stereochemical Analysis, VCH, NY, 1986; Fraser, R.R. in Morrison, J.D. Asymmetric Synthesis, Vol. 1, Academic Press, NY, 1983, pp. 173–196; Sullivan, G.R. Top. Stereochem. 1978, 10, 287.

217. See Westley, J.W.; Halpern, B. J. Org. Chem. 1968, 33, 3978.

218. For a review, see Pirkle, W.H.; Finn, J. in Morrison, J.D. Asymmetric Synthesis, Vol. 1, Academic Press, NY, 1983, pp. 87–124.

219. For reviews, see in Morrison, J.D. Asymmetric Synthesis, Vol. 1, Academic Press, NY, 1983, the articles by Schurig, V. pp. 59–86 and Pirkle, W.H.; Finn, J. pp. 87–124.

220. See Hill, H.W.; Zens, A.P.; Jacobus, J. J. Am. Chem. Soc. 1979, 101, 7090; Matsumoto, M.; Yajima, H.; Endo, R. Bull. Chem. Soc. Jpn. 1987, 60, 4139.

221. Berson, J.A.; Ben-Efraim, D.A. J. Am. Chem. Soc. 1959, 81, 4083; Andersen, K.K.; Gash, D.M.; Robertson, J.D. in Morrison, J.D. Asymmetric Synthesis, Vol. 1, Academic Press, NY, 1983, pp. 45–57.

222. Horeau, A.; Guetté, J.; Weidmann, R. Bull. Soc. Chim. Fr. 1966, 3513. For a review, see Schoofs, A.R.; Guetté, J. in Morrison, J.D. Asymmetric Synthesis, Vol. 1, Academic Press, NY, 1983, pp. 29–44.

223. Hofer, E.; Keuper, R. Tetrahedron Lett. 1984, 25, 5631.

224. Schippers, P.H.; Dekkers, H.P.J.M. Tetrahedron 1982, 38, 2089.

225. cis-trans isomerism was formerly called geometrical isomerism.

226. For a complete description of the system, see Pure Appl. Chem. 1976, 45, 13; Nomenclature of Organic Chemistry, Pergamon, Elmsford, NY, 1979 (the Blue Book).

227. See in Patai, S. The Chemistry of the Carbon–Nitrogen Double Bond, Wiley, NY, 1970, the articles by McCarty, C.G. pp. 363–464 (pp. 364–408), and Wettermark, G. pp. 565–596 (pp. 574–582).

228. Wang, Y.-N.; Bohle, D.S.; Bonifant, C.L.; Chmurny, G.N.; Collins, J.R.; Davies, K.M.; Deschamps, J.; Flippen-Anderson, J.L.; Keefer, L.K.; Klose, J.R.; Saavedra, J.E.; Waterhouse, D.J.; Ivanic, J. J. Am. Chem. Soc. 2005, 127, 5388.

229. King, J.F.; Durst, T. Can. J. Chem. 1966, 44, 819.

230. A mechanism has been reported for the acid-catalyzed Z/E isomerization of imines. See Johnson, J.E.; Morales, N.M.; Gorczyca, A.M.; Dolliver, D.D.; McAllister, M.A. J. Org. Chem. 2001, 66, 7979.

231. This rule does not apply to allenes, which do not show cis--trans isomerism (see Sec. 4.C, category 5).

232. Cope, A.C.; Moore, P.T.; Moore, W.R. J. Am. Chem. Soc. 1959, 81, 3153.

233. Öki, M. Applications of Dynamic NMR Spectroscopy to Organic Chemistry, VCH, NY, 1985, pp. 41–71.

234. Mannschreck, A. Angew. Chem. Int. Ed. 1965, 4, 985. See also, Völter, H.; Helmchen, G. Tetrahedron Lett. 1978, 1251; Walter, W.; Hühnerfuss, H. Tetrahedron Lett. 1981, 22, 2147.

235. This is another example of atropisomerism (Sec. 4.C, category 5).

236. For reviews, see Sandström, J. Top. Stereochem. 1983, 14, 83; Öki, M. Applications of Dynamic NMR Spectroscopy to Organic Chemistry, VCH, NY, 1985, pp. 111–125.

237. Sandström, J.; Wennerbeck, I. Acta Chem. Scand. Ser. B, 1978, 32, 421.

238. Yamamoto, T.; Tomoda, S. Chem. Lett. 1997, 1069.

239. See Leonard, J.E.; Hammond, G.S.; Simmons, H.E. J. Am. Chem. Soc. 1975, 97, 5052.

240. Sorensen, T.S.; Sun, F. J. Chem. Soc. Perkin Trans. 2 1998, 1053.

241. Meinwald, J.; Tufariello, J.J.; Hurst, J.J. J. Org. Chem. 1964, 29, 2914.

242. Paukstelis, J.V.; Kao, J. J. Am. Chem. Soc. 1972, 94, 4783. For references to other examples, see Dixon, D.A.; Gassman, P.G. J. Am. Chem. Soc. 1988, 110, 2309.

243. Corbally, R.P.; Perkins, M.J.; Carson, A.S.; Laye, P.G.; Steele, W.V. J. Chem. Soc. Chem. Commun. 1978, 778.

244. Winkler, J.D.; Hey, J.P.; Williard, P.G. Tetrahedron Lett. 1988, 29, 4691.

245. See Alder, R.W. Acc. Chem. Res. 1983, 16, 321.

246. Alder, R.W.; East, S.P. Chem. Rev. 1996, 96, 2097.

247. Alder, R.W. Tetrahedron 1990, 46, 683.

248. Alder, R.W.; Orpen, A.G.; Sessions, R.B. J. Chem. Soc., Chem. Commun. 1983, 999.

249. Alder, R.W.; Goode, N.C.; King, T.J.; Mellor, J.M.; Miller, B.W. J. Chem. Soc., Chem. Commun. 1976, 173; Alder, R.W.; Arrowsmith, R.J.; Casson, A.; Sessions, R.B.; Heilbronner, E.; Kovac, B.; Huber, H.; Taagepera, M. J. Am. Chem. Soc. 1981, 103, 6137.

250. Alder, R.W.; Heilbronner, E.; Honegger, E.; McEwen, A.B.; Moss, R.E.; Olefirowicz, E.; Petillo, P.A.; Sessions, R.B.; Weisman, G.R.; White, J.M.; Yang, Z.-Z. J. Am. Chem. Soc. 1993, 115, 6580.

251. Simmons, H.E.; Park, C.H. J. Am. Chem. Soc. 1968, 90, 2428; Park, C.H.; Simmons, H.E. J. Am. Chem. Soc. 1968, 90, 2429, 2431; Simmons, H.E.; Park, C.H.; Uyeda, R.T.; Habibi, M.F. Trans. N.Y. Acad. Sci. 1970, 32, 521. See also, Dietrich, B.; Lehn, J.M.; Sauvage, J.P. Tetrahedron 1973, 29, 1647; Dietrich, B.; Lehn, J.M.; Sauvage, J.P.; Blanzat, J. Tetrahedron 1973, 29, 1629.

252. See Schmidtchen, F.P.; Gleich, A.; Schummer, A. Pure. Appl. Chem. 1989, 61, 1535; Pierre, J.; Baret, P. Bull. Soc. Chim. Fr. 1983, II-367. See also, Hosseini, M.W.; Lehn, J. Helv. Chim. Acta 1988, 71, 749.

253. Dietrich, B.; Lehn, J.M.; Guilhem, J.; Pascard, C. Tetrahedron Lett. 1989, 30, 4125; Wallon, A.; Peter-Katalini, J.; Werner, U.; Müller, W.M.; Vögtle, F. Chem. Ber. 1990, 123, 375.

254. Schmidtchen, F.P.; Müller, G. J. Chem. Soc. Chem. Commun. 1984, 1115. See also, Schmidtchen, F.P. J. Am. Chem. Soc. 1986, 108, 8249, Top. Curr. Chem. 1986, 132, 101.

255. McMurry, J.E.; Hodge, C.N. J. Am. Chem. Soc. 1984, 106, 6450; Winkler, J.D.; Hey, J.P.; Williard, P.G. J. Am. Chem. Soc. 1986, 108, 6425.

256. See Baechler, R.D.; Mislow, K. J. Am. Chem. Soc. 1970, 92, 3090; Rauk, A.; Allen, L.C.; Mislow, K. Angew. Chem. Int. Ed. 1970, 9, 400.

257. Alder, R.W.; Read, D. Angew. Chem. Int. Ed. 2000, 39, 2879.

258. Alder, R.W.; Ellis, D.D.; Gleiter, R.; Harris, C.J.; Lange, H.; Orpen, A.G.; Read, D.; Taylor, P.N. J. Chem. Soc., Perkin Trans. I 1998, 1657.

259. These terms were coined by Mislow. See Eliel, E.L. Top. Curr. Chem. 1982, 105, 1; Mislow, K.; Raban, M. Top. Stereochem. 1967, 1, 1. See also, Jennings, W.B. Chem. Rev. 1975, 75, 307.

260. In the case where Y is itself a chiral group, this statement is only true when the two Y groups have the same configuration.

261. For a review, see Benner, S.A.; Glasfeld, A.; Piccirilli, J.A. Top. Stereochem. 1989, 19, 127. For a nonenzymatic example, see Job, R.C.; Bruice, T.C. J. Am. Chem. Soc. 1974, 96, 809.

262. The experiments were carried out by Evans Jr., E.A.; Slotin, L. J. Biol. Chem. 1941, 141, 439; Wood, H.G.; Werkman, C.H.; Hemingway, A.; Nier, A.O. J. Biol. Chem. 1942, 142, 31. The correct interpretation was given by Ogston, A.G. Nature (London) 1948, 162, 963. For discussion, see Eliel, E.L. Top. Curr. Chem. 1982, 105, 1, pp. 5–7, 45–70.

263. Hirschmann, H.; Hanson, K.R. Tetrahedron 1974, 30, 3649.

264. Pirkle, W.H. J. Am. Chem. Soc. 1966, 88, 1837; Burlingame, T.G.; Pirkle, W.H. J. Am. Chem. Soc. 1966, 88, 4294; Pirkle, W.H.; Burlingame, T.G. Tetrahedron Lett. 1967, 4039.

265. For a review of isochronous and nonisochronous nuclei in NMR, see van Gorkom, M.; Hall, G.E. Q. Rev. Chem. Soc. 1968, 22, 14. For a discussion, see Silverstein, R.M.; LaLonde, R.T. J. Chem. Educ. 1980, 57, 343.

266. Fujita, S. J. Org. Chem. 2002, 67, 6055.

267. Fujita, S. J. Am. Chem. Soc. 1990, 112, 3390.

268. For a further discussion of these terms and of stereoselective reactions in general, see Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds, Wiley–Interscience, NY, 1994, pp. 835–990.

269. See Bonchev, D.; Rouvray, D.H. Chemical Topology, Gordon and Breach, Australia, 1999.

270. See Dale, J. Stereochemistry and Conformational Analysis, Verlag Chemie, Deerfield Beach, FL, 1978; Chiurdoglu, G. Conformational Analysis, Academic Press, NY, 1971; Eliel, E.L.; Allinger, N.L.; Angyal, S.J.; Morrison, G.A. Conformational Analysis, Wiley, NY, 1965; Hanack, M. Conformation Theory, Academic Press, NY, 1965. For reviews, see Dale, J. Top. Stereochem. 1976, 9, 199; Truax, D.R.; Wieser, H. Chem. Soc. Rev. 1976, 5, 411; Eliel, E.L. J. Chem. Educ. 1975, 52, 762; Bastiansen, O.; Bushweller, C.H.; Gianni, M.H. in Patai, S. The Chemistry of Functional Groups, Supplement E, Wiley, NY, 1980, pp. 215–278.

271. Öki, M. The Chemistry of Rotational Isomers, Springer–Verlag, Berlin, 1993.

272. For a review, see Eliel, E.L.; Allinger, N.L.; Angyal, S.J.; Morrison, G.A. Conformational Analysis, Wiley, NY, 1965, pp. 129–188.

273. See Öki, M. Applications of Dynamic NMR Spectroscopy to Organic Chemistry, VCH, NY, 1985; Marshall, J.L. Carbon–Carbon and Carbon–Proton NMR Couplings, VCH, NY, 1983. For reviews, see Anet, F.A.L.; Anet, R. in Nachod, F.C.; Zuckerman, J.J. Determination of Organic Structures by Physical Methods, Vol. 3, Academic Press, NY, 1971, pp. 343–420; Kessler, H. Angew. Chem. Int. Ed. 1970, 9, 219; Ivanova, T.M.; Kugatova-Shemyakina, G.P. Russ. Chem. Rev. 1970, 39, 510; See also, Whitesell, J.K.; Minton, M. Stereochemical Analysis of Alicyclic Compounds by C-13 NMR Spectroscopy, Chapman and Hall, NY, 1987.

274. For a review see Wilson, E.B. Chem. Soc. Rev. 1972, 1, 293.

275. For a review, see Klessinger, M.; Rademacher, P. Angew. Chem. Int. Ed. 1979, 18, 826.

276. Breen, P.J.; Warren, J.A.; Bernstein, E.R.; Seeman, J.I. J. Am. Chem. Soc. 1987, 109, 3453.

277. See Kagan, H.B. Determination of Configurations by Dipole Moments, CD, or ORD (Vol. 2 of Kagan, H.B. Stereochemistry), Georg Thieme Publishers, Stuttgart, 1977; Crabbé, P. ORD and CD in Chemistry and Biochemistry, Academic Press, NY, 1972; Snatzke, G. Optical Rotatory Dispersion and Circular Dichroism in Organic Chemistry, Sadtler Research Laboratories, Philadelphia, 1967; Velluz, L.; Legrand, M.; Grosjean, M. Optical Circular Dichroism, Academic Press, NY, 1965. For reviews, see Smith, H.E. Chem. Rev. 1983, 83, 359; Håkansson, R. in Patai, S. The Chemistry of Acid Derivatives, pt. 1, Wiley, NY, 1979, pp. 67–120; Hudec, J.; Kirk, D.N. Tetrahedron 1976, 32, 2475; Schellman, J.A. Chem. Rev. 1975, 75, 323.

278. Chen, J.; Cammers-Goodwin, A. Eur. J. Org. Chem. 2003, 3861.

279. Iwamoto, H.; Yang, Y.; Usui, S.; Fukazawa, Y. Tetrahedron Lett. 2001, 42, 49.

280. See Kessler, H.; Zimmermann, G.; Förster, H.; Engel, J.; Oepen, G.; Sheldrick, W.S. Angew. Chem. Int. Ed. 1981, 20, 1053.

281. Bérces, A.; Whitfield, D.M.; Nukada, T. Tetrahedron 2001, 57, 477.

282. Öki, M.; Toyota, S. Eur. J. Org. Chem. 2004, 255.

283. See Berg, U.; Sandström, J. Adv. Phys. Org. Chem. 1989, 25, 1. Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds, Wiley–Interscience, NY, 1994, pp. 597–664. Also see, Smith, M.B. Organic Synthesis, 3rd ed., Wavefunction Inc./Elsevier, Irvine, CA/London, England, 2010, pp. 35–47.

284. Goto, H.; Osawa, E.; Yamato, M. Tetrahedron 1993, 49, 387.

285. Lide Jr., D.R. J. Chem. Phys. 1958, 29, 1426; Weiss, S.; Leroi, G.E. J. Chem. Phys. 1968, 48, 962; Hirota, E.; Saito, S.; Endo, Y. J. Chem. Phys. 1979, 71, 1183.

286. Mo, Y.; Gao, J. Acc. Chem. Res. 2007, 40, 113.

287. See Lowe, J.P. Prog. Phys. Org. Chem. 1968, 6, 1; Oosterhoff, L.J. Pure Appl. Chem. 1971, 25, 563; Wyn-Jones, E.; Pethrick, R.A. Top. Stereochem. 1970, 5, 205; Pethrick, R.A.; Wyn-Jones, E. Q. Rev. Chem. Soc. 1969, 23, 301; Brier, P.N. J. Mol. Struct. 1970, 6, 23; Lowe, J.P. Science, 1973, 179, 527.

288. See Pitzer, R.M. Acc. Chem. Res. 1983, 16, 207. See, however, Bader, R.F.W.; Cheeseman, J.R.; Laidig, K.E.; Wiberg, K.B.; Breneman, C. J. Am. Chem. Soc. 1990, 112, 6530.

289. See Bader, W.; Cortés-Guzmán, F. Can. J. Chem. 2009, 87, 1583.

290. See Wiberg, K.B.; Murcko, M.A. J. Am. Chem. Soc. 1988, 110, 8029; Allinger, N.L.; Grev, R.S.; Yates, B.F.; Schaefer, III, H.F. J. Am. Chem. Soc. 1990, 112, 114.

291. Cormanich, R.A.; Freitas, M.P. J. Org. Chem. 2009, 74, 8384; Mo, Y. J. Org. Chem. 2010, 75, 2733.

292. Le Fèvre, R.J.W.; Orr, B.J. Aust. J. Chem. 1964, 17, 1098.

293. See Schrumpf, G. Angew. Chem. Int. Ed. 1982, 21, 146.

294. See Davenport, D.; Schwartz, M. J. Mol. Struct. 1978, 50, 259; Huang, J.; Hedberg, K. J. Am. Chem. Soc. 1989, 111, 6909.

295. See Friesen, D.; Hedberg, K. J. Am. Chem. Soc. 1980, 102, 3987; Fernholt, L.; Kveseth, K. Acta Chem. Scand. Ser. A 1980, 34, 163.

296. Abraham, R.J.; Monasterios, J.R. Org. Magn. Reson. 1973, 5, 305.

297. See Wolfe, S. Acc. Chem. Res. 1972, 5, 102. See also, Phillips, L.; Wray, V. J. Chem. Soc. Chem. Commun. 1973, 90; Radom, L.; Hehre, W.J.; Pople, J.A. J. Am. Chem. Soc. 1972, 94, 2371; Zefirov, N.S. J. Org. Chem. USSR 1974, 10, 1147; Juaristi, E. J. Chem. Educ. 1979, 56, 438.

298. Griffith, R.C.; Roberts, J.D. Tetrahedron Lett. 1974, 3499.

299. Amos, R.D.; Handy, N.C.; Jones, P.G.; Kirby, A.J.; Parker, J.K.; Percy, J.M.; Su, M.D. J. Chem. Soc. Perkin Trans. 2 1992, 549.

300. Kagarise, R.E. J. Chem. Phys. 1956, 24, 300.

301. Brown, D.E.; Beagley, B. J. Mol. Struct. 1977, 38, 167.

302. Ritter, W.; Hull, W.; Cantow, H. Tetrahedron Lett. 1978, 3093.

303. Lunazzi, L.; Macciantelli, D.; Bernardi, F.; Ingold, K.U. J. Am. Chem. Soc. 1977, 99, 4573.

304. Tan, B.; Chia, L.H.L.; Huang, H.; Kuok, M.; Tang, S. J. Chem. Soc. Perkin Trans. 2 1984, 1407.

305. Smith, G.D.; Jaffe, R.L.; Yoon, D.Y. J. Am. Chem. Soc. 1995, 117, 530. For an analysis of N,N-dimethylacetamide, see Mack, H.-G.; Oberhammer, H. J. Am. Chem. Soc. 1997, 119, 3567.

306. Flamm-ter Meer; Beckhaus, H.; Peters, K.; von Schnering, H.; Fritz, H.; Rüchardt, C. Chem. Ber. 1986, 119, 1492; Rüchardt, C.; Beckhaus, H. Angew. Chem. Int. Ed. 1985, 24, 529.

307. See Sinegovskaya, L.M.; Keiko, V.V.; Trofimov, B.A. Sulfur Rep. 1987, 7, 337 (for enol ethers and thioethers); Karabatsos, G.J.; Fenoglio, D.J. Top. Stereochem. 1970, 5, 167; Jones, G.I.L.; Owen, N.L. J. Mol. Struct. 1973, 18, 1 (for carboxylic esters). See also, Cossé-Barbi, A.; Massat, A.; Dubois, J.E. Bull. Soc. Chim. Belg. 1985, 94, 919; Dorigo, A.E.; Pratt, D.W.; Houk, K.N. J. Am. Chem. Soc. 1987, 109, 6591.

308. Allinger, N.L.; Hickey, M.J. J. Mol. Struct. 1973, 17, 233; Gupta, V.P. Can. J. Chem. 1985, 63, 984.

309. Macoas, E.M.S.; Khriachtchev, L.; Pettersson, M.; Fausto, R.; Rasanen, M. J. Am. Chem. Soc. 2003, 125, 16188.

310. Davidson, R.B.; Allen, L.C. J. Chem. Phys. 1971, 54, 2828.

311. Ratajczyk, T.; Pecul, M.; Sadlej, J. Tetrahedron 2004, 60, 179.

312. Avalos, M.; Babiano, R.; Barneto, J.L.; Bravo, J.L.; Cintas, P.; Jiménez, J.L.; Palcios, J.C. J. Org. Chem. 2001, 66, 7275. Also see Modarresi-Alam, A.R.; Najafi, P.; Rostamizadeh, M.; Keykha, H.; Bijanzadeh, H.-R.; Kleinpeter, E. J. Org. Chem. 2007, 72, 2208.

313. Saito, S.; Toriumi, Y.; Tomioka, A.; Itai, A. J. Org. Chem. 1995, 60, 4715.

314. Axe, F.U.; Renugopalakrishnan, V.; Hagler, A.T. J. Chem. Res. 1998, 1. For an analysis of DMF see Wiberg, K.B.; Rablen, P.R.; Rush, D.J.; Keith, T.A. J. Am. Chem. Soc. 1995, 117, 4261.

315. Avalos, M.; Babiano, R.; Barneto, J.L.; Cintas, P.; Clemente, F.R.; Jiménez, J.L.; Palcios, J.C. J. Org. Chem. 2003, 68, 1834.

316. Kakkar, R.; Grover, R.; Chadha, P. Org. Biomol. Chem. 2003, 1, 2200.

317. Wiberg, K.B.; Rablen, P.R. J. Am. Chem. Soc. 1995, 117, 2201.

318. Bach, R.D.; Mintcheva, I.; Kronenberg, W.J.; Schlegel, H.B. J. Org. Chem. 1993, 58, 6135.

319. Ilieva, S.; Hadjieva, B.; Galabov, B. J. Org. Chem. 2002, 67, 6210.

320. Wiberg, K. B.; Rush, D. J. J. Am. Chem. Soc. 2001, 123, 2038; J. Org. Chem. 2002, 67, 826.

321. Rablen, P.R.; Miller, D.A.; Bullock, V.R.; Hutchinson, P.H.; Gorman, J.A. J. Am. Chem. Soc. 1999, 121, 218.

322. Deetz, M.J.; Forbes, C.C.; Jonas, M.; Malerich, J.P.; Smith, B.D.; Wiest, O. J. Org. Chem. 2002, 67, 3949.

323. Kim, Y.-J.; Streitwieser, A.; Chow, A.; Fraenkel, G. Org. Lett. 1999, 1, 2069.

324. Smith, B.D.; Goodenough-Lashua, D.M.; D'Souza, C.J.E.; Norton, K.J.; Schmidt, L.M.; Tung, J.C. Tetrahedron Lett. 2004, 45, 2747.

325. For an analysis of barriers to rotation in such compounds, see Mazzanti, A.; Lunazzi, L.; Minzoni, M.; Anderson, J.E. J. Org. Chem. 2006, 71, 5474.

326. Abraham, R.J.; Angioloni, S.; Edgar, M.; Sancassan, F. J. Chem. Soc. Perkin Trans. 2 1997, 41.

327. Casarini, D.; Lunazzi, L.; Mazzanti, A. J. Org. Chem. 1997, 62, 7592.

328. See Jensen, F.R.; Bushweller, C.H. Adv. Alicyclic Chem. 1971, 3, 139; Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds, Wiley–Interscience, NY, 1994, pp. 686–753. Also see, Smith, M.B. Organic Synthesis, 3rd ed., Wavefunction Inc./Elsevier, Irvine, CA/London, England, 2010, pp. 54–67.

329. See Geise, H.J.; Buys, H.R.; Mijlhoff, F.C. J. Mol. Struct. 1971, 9, 447; Bastiansen, O.; Fernholt, L.; Seip, H.M.; Kambara, H.; Kuchitsu, K. J. Mol. Struct. 1973, 18, 163.

330. See Dunitz, J.D. J. Chem. Educ. 1970, 47, 488.

331. For a review of nonchair forms, see Kellie, G.M.; Riddell, F.G. Top. Stereochem. 1974, 8, 225.

332. Squillacote, M.; Sheridan, R.S.; Chapman, O.L.; Anet, F.A.L. J. Am. Chem. Soc. 1975, 97, 3244.

333. See Wiberg, K.B.; Castejon, H.; Bailey, W.F.; Ochterski, J. J. Org. Chem. 2000, 65, 1181.

334. Gill, G.; Pawar, D.M.; Noe, E.A. J. Org. Chem. 2005, 70, 10726.

335. See Wehle, D.; Fitjer, L. Tetrahedron Lett. 1986, 27, 5843.

336. See Anet, F.A.L.; Bourn, A.J.R. J. Am. Chem. Soc. 1967, 89, 760. See also, Strauss, H.L. J. Chem. Educ. 1971, 48, 221.

337. See Oki, M. Applications of Dynamic NMR Spectroscopy to Organic Chemistry, VCH, NY, 1985, pp. 287–307; Anderson, J.E. Top. Curr. Chem. 1974, 45, 139.

338. See Jensen, F.R.; Bushweller, C.H.; J. Chem. Soc. 1969, 91, 3223.

339. Weiser, J.; Golan, O.; Fitjer, L.; Biali, S.E. J. Org. Chem. 1996, 61, 8277.

340. For a study of thioether, sulfoxide and sulfone substituents, see Juaristi, E.; Labastida, V.; Antúnez, S. J. Org. Chem., 2000, 65, 969.

341. Jensen, F.R.; Gale, L.H. J. Am. Chem. Soc. 1959, 81, 6337.

342. Anet, F.A.L.; Krane, J.; Kitching, W.; Dodderel, D.; Praeger, D. Tetrahedron Lett. 1974, 3255.

343. These values are from Corey, E.J.; Feiner, N.F. J. Org. Chem. 1980, 45, 765. Also see Jensen, F.R.; Bushweller, C.H. Adv. Alicyclic Chem. 1971, 3, 139. See also, Schneider, H.; Hoppen, V. Tetrahedron Lett. 1974, 579 and see Smith, M.B. Organic Synthesis, 3rd ed., Wavefunction Inc./Elsevier, Irvine, CA/London, England, 2010, pp. 54–67.

344. See Ford, R.A.; Allinger, N.L. J. Org. Chem. 1970, 35, 3178. For a critical review of the methods used to obtain these values, see Jensen, F.R.; Bushweller, C.H. Adv. Alicyclic Chem. 1971, 3, 139.

345. Anet, F.A.L.; O'Leary, D.J. Tetrahedron Lett. 1989, 30, 1059.

346. Buchanan, G.W.; Webb, V.L. Tetrahedron Lett. 1983, 24, 4519.

347. Eliel, E.L.; Manoharan, M. J. Org. Chem. 1981, 46, 1959.

348. Booth, H.; Everett, J.R. J. Chem. Soc. Chem. Commun. 1976, 278.

349. Hirsch, J.A. Top. Stereochem. 1967, 1, 199.

350. Kitching, W.; Olszowy, H.A.; Drew, G.M.; Adcock, W. J. Org. Chem. 1982, 47, 5153.

351. Schneider, H.; Hoppen, V. Tetrahedron Lett. 1974, 579.

352. Squillacote, M.E.; Neth, J.M. J. Am. Chem. Soc. 1987, 109, 198. Values of 2.59–2.92 kcal mol⁻¹(10.84–12.23 kJ mol⁻¹) were determined for 4-X-C₆H₄– substituents (X = NO₂, Cl, MeO): see Kirby, A.J.; Williams, N.H. J. Chem. Soc. Chem. Commun. 1992, 1285, 1286.

353. Manoharan, M.; Eliel, E.L. Tetrahedron Lett. 1984, 25, 3267.

354. Abraham, R.J.; Rossetti, Z.L. J. Chem. Soc. Perkin Trans. 2 1973, 582. See also, Hammarström, L.; Berg, U.; Liljefors, T. Tetrahedron Lett. 1987, 28, 4883.

355. Abraham, M.H.; Xodo, L.E.; Cook, M.J.; Cruz, R. J. Chem. Soc. Perkin Trans. 2 1982, 1503; Samoshin, V.V.; Svyatkin, V.A.; Zefirov, N.S. J. Org. Chem. USSR 1988, 24, 1080, and references cited therein. See Zefirov, N.S.; Samoshin, V.V.; Subbotin, O.A.; Sergeev, N.M. J. Org. Chem. USSR 1981, 17, 1301.

356. For a case of a preferential diaxial conformation in 1,3 isomers, see Ochiai, M.; Iwaki, S.; Ukita, T.; Matsuura, Y.; Shiro, M.; Nagao, Y. J. Am. Chem. Soc. 1988, 110, 4606.

357. Golan, O.; Goren, Z.; Biali, S.E. J. Am. Chem. Soc. 1990, 112, 9300.

358. Abraham, R.J.; Chambers, E.J.; Thomas, W.A. J. Chem. Soc. Perkin Trans. 2 1993, 1061.

359. Wiberg, K.B. J. Org. Chem. 1999, 64, 6387.

360. This idea was suggested by Winstein, S.; Holness, N.J. J. Am. Chem. Soc. 1955, 77, 5561. See Saunders, M.; Wolfsberg, M.; Anet, F.A.L.; Kronja, O. J. Am. Chem. Soc. 2007, 129, 10276.

361. Marzabadi, C. H.; Anderson, J. E.; Gonzalez-Outeirino, J.; Gaffney, P. R. J.; White, C. G. H.; Tocher, D. A.; Todaro, L. J. J. Am. Chem. Soc. 2003, 125, 15163.

362. See Rabideau, P.W. The Conformational Analysis of Cyclohexenes, Cyclohexadienes, and Related Hydroaromatic Compounds, VCH, NY, 1989; Vereshchagin, A.N. Russ. Chem. Rev. 1983, 52, 1081; Johnson, F. Chem. Rev. 1968, 68, 375. See also, Lambert, J.B.; Clikeman, R.R.; Taba, K.M.; Marko, D.E.; Bosch, R.J.; Xue, L. Acc. Chem. Res. 1987, 20, 454.

363. See Dale, J. Stereochemistry and Conformational Analysis, Verlag Chemie, Deerfield Beach, FL, 1978; Chiurdoglu, G. Conformational Analysis, Academic Press, NY, 1971; Eliel, E.L.; Allinger, N.L.; Angyal, S.J.; Morrison, G.A. Conformational Analysis, Wiley, NY, 1965; Dale, J. Top. Stereochem. 1976, 9, 199; Truax, D.R.; Wieser, H. Chem. Soc. Rev. 1976, 5, 411; Eliel, E.L. J. Chem. Educ. 1975, 52, 762; Bushweller, C.H.; Gianni, M.H. in Patai, S. The Chemistry of Functional Groups, Supplement E, Wiley, NY, 1980, pp. 215–278.

364. See Jensen, F.R.; Bushweller, C.H. Adv. Alicyclic Chem. 1971, 3, 139; Robinson, D.L.; Theobald, D.W. Q. Rev. Chem. Soc. 1967, 21, 314; Eliel, E.L. Angew. Chem. Int. Ed. 1965, 4, 761; Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds, Wiley-Interscience, NY, 1994, pp. 686–753. Also see, Smith, M.B. Organic Synthesis, 3rd ed., Wavefunction Inc./Elsevier, Irvine, CA/London, England, 2010, pp. 61–65.

365. Laane, J.; Choo, J. J. Am. Chem. Soc. 1994, 116, 3889.

366. Basso, E.A.; Kaiser, C.; Rittner, R.; Lambert, J.B. J. Org. Chem. 1993, 58, 7865.

367. See Glass, R.S. Conformational Analysis of Medium-Sized Heterocycle, VCH, NY, 1988; Riddell, F.G. The Conformational Analysis of Heterocyclic Compounds, Academic Press, NY, 1980; Juaristi, E. Acc. Chem. Res. 1989, 22, 357; Crabb, T.A.; Katritzky, A.R. Adv. Heterocycl. Chem. 1984, 36, 1; Eliel, E.L. Angew. Chem. Int. Ed. 1972, 11, 739; Pure Appl. Chem. 1971, 25, 509; Acc. Chem. Res. 1970, 3, 1; Lambert, J.B. Acc. Chem. Res. 1971, 4, 87.

368. Bachrach, S.M.; Liu, M. Tetrahedron Lett. 1992, 33, 6771.

369. These factors are discussed by Eliel, E.L. Angew. Chem. Int. Ed. 1972, 11, 739.

370. Riddell, F.G.; Robinson, M.J.T. Tetrahedron 1967, 23, 3417; Eliel, E.L.; Knoeber, M.C. J. Am. Chem. Soc. 1968, 90, 3444. See also, Eliel, E.L.; Alcudia, F. J. Am. Chem. Soc. 1974, 96, 1939. See Cieplak, P.; Howard, A.E.; Powers, J.P.; Rychnovsky, S.D.; Kollman, P.A. J. Org. Chem. 1996, 61, 3662 for conformational energy differences in 2,2,6-trimethyl-4-alkyl-1,3-dioxane.

371. Cai, J.; Davies, A.G.; Schiesser, C.H. J. Chem. Soc. Perkin Trans. 2 1994, 1151.

372. Hutchins, R.O.; Eliel, E.L. J. Am. Chem. Soc. 1969, 91, 2703. See also, Juaristi, E.; Cuevas, G. Tetrahedron 1999, 55, 359.

373. Strelenko, Y.A.; Samoshin, V.V.; Troyansky, E.I.; Demchuk, D.V.; Dmitriev, D.E.; Nikishin, G.I.; Zefirov, N.S. Tetrahedron 1994, 50, 10107.

374. Gordillo, B.; Juaristi, E.; Matínez, R.; Toscano, R.A.; White, P.S.; Eliel, E.L. J. Am. Chem. Soc. 1992, 114, 2157.

375. Kaloustian, M.K.; Dennis, N.; Mager, S.; Evans, S.A.; Alcudia, F.; Eliel, E.L. J. Am. Chem. Soc. 1976, 98, 956. See also, Eliel, E.L.; Kandasamy, D.; Sechrest, R.C. J. Org. Chem. 1977, 42, 1533.

376. See Kirby, A.J. The Anomeric Effect and Related Stereoelectronic Effects at Oxygen, Springer, NY, 1983; Szarek, W.A.; Horton, D. Anomeric Effect, American Chemical Society, Washington, 1979; Deslongchamps, P. Stereoelectronic Effects in Organic Chemistry, Pergamon, Elmsford, NY, 1983, pp. 4–26; Zefirov, N.S. Tetrahedron 1977, 33, 3193; Lemieux, R.U. Pure Appl. Chem. 1971, 27, 527.

377. Juaristi, E.; Cuevas, G. Tetrahedron 1992, 48, 5019.

378. See Romers, C.; Altona, C.; Buys, H.R.; Havinga, E. Top. Stereochem. 1969, 4, 39, pp. 73–77; Wolfe, S.; Whangbo, M.; Mitchell, D.J. Carbohydr. Res. 1979, 69, 1.

379. See Praly, J.; Lemieux, R.U. Can. J. Chem. 1987, 65, 213; Booth, H.; Khedhair, K.A.; Readshaw, S.A. Tetrahedron 1987, 43, 4699. For evidence against it, see Box, V.G.S. Heterocycles 1990, 31, 1157.

380. Cramer, C.J. J. Org. Chem. 1992, 57, 7034; Booth, H.; Dixon, J.M.; Readshaw, S.A. Tetrahedron 1992, 48, 6151.

381. Anderson, J.E. J. Org. Chem. 2000, 65, 748.

382. Stolow, R.D. J. Am. Chem. Soc. 1964, 86, 2170; Stolow, R.D.; McDonagh, P.M.; Bonaventura, M.M. J. Am. Chem. Soc. 1964, 86, 2165. Also see Fitjer, L.; Scheuermann, H.; Klages, U.; Wehle, D.; Stephenson, D.S.; Binsch, G. Chem. Ber. 1986, 119, 1144.

383. Rychnovsky, S.D.; Yang, G.; Powers, J.P. J. Org. Chem. 1993, 58, 5251.

384. Arnason, I.; Kvaran, A.; Jonsdottir, S.; Gudnason, P. I.; Oberhammer, H. J. Org. Chem. 2002, 67, 3827.

385. Salzner, U.; Schleyer, P.v.R. J. Am. Chem. Soc. 1993, 115, 10231; Aggarwal, V.K.; Worrall, J.M.; Adams, H.; Alexander, R.; Taylor, B.F. J. Chem. Soc. Perkin Trans. 1 1997, 21.

386. Salzner, U.; Schleyer, P.v.R. J. Org. Chem. 1994, 59, 2138.

387. Perrin, C.L. Tetrahedron 1995, 51, 11901.

388. Anderson, J.E.; Cai, J.; Davies, A.G. J. Chem. Soc. Perkin Trans. 2 1997, 2633. For some controversy concerning the anomeric effect a related system, see Perrin, C.L.; Armstrong, K.B.; Fabian, M.A. J. Am. Chem.Soc. 1994, 116, 715; Salzner, U. J. Org. Chem. 1995, 60, 986.

389. Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds, Wiley–Interscience, NY, 1994, pp. 675–685 and 754–770.

390. For reviews of the stereochemistry of four-membered rings, see Legon, A.C. Chem. Rev. 1980, 80, 231; Moriarty, R.M. Top. Stereochem. 1974, 8, 271; Cotton, F.A.; Frenz, B.A. Tetrahedron 1974, 30, 1587.

391. Miller, F.A.; Capwell, R.J.; Lord, R.C.; Rea, D.G. Spectrochim. Acta Part A, 1972, 28, 603. However, see Margulis, T.N. J. Am. Chem. Soc. 1971, 93, 2193.

392. Luger, P.; Buschmann, J. J. Am. Chem. Soc. 1984, 106, 7118.

393. See Fuchs, B. Top. Stereochem. 1978, 10, 1; Legon, A.C. Chem. Rev. 1980, 80, 231.

394. Willy, W.E.; Binsch, G.; Eliel, E.L. J. Am. Chem. Soc. 1970, 92, 5394; Lipnick, R.L. J. Mol. Struct. 1974, 21, 423.

395. Lipnick, R.L. J. Mol. Struct. 1974, 21, 411; Poupko, R.; Luz, Z.; Zimmermann, H. J. Am. Chem. Soc. 1982, 104, 5307; Riddell, F.G.; Cameron K.S.; Holmes, S.A.; Strange, J.H. J. Am. Chem. Soc. 1997, 119, 7555.

396. Matallana, A.; Kruger, A.W.; Kingsbury, C.A. J. Org. Chem. 1994, 59, 3020.

397. Abraham, R.J.; Pollock, L.; Sancassan, F. J. Chem. Soc. Perkin Trans. 2 1994, 2329.

398. Carreira, L.A.; Jiang, G.J.; Person, W.B.; Willis, Jr., J.N. J. Chem. Phys. 1972, 56, 1440.

399. Verevkin, S.P.; Kümmerlin, M.; Beckhaus, H.-D.; Galli, C.; Rüchardt, C. Eur. J. Org. Chem. 1998, 579.

400. See Arshinova, R.P. Russ. Chem. Rev. 1988, 57, 1142; Ounsworth, J.P.; Weiler, L. J. Chem. Educ. 1987, 64, 568; Öki, M. Applications of Dynamic NMR Spectroscopy to Organic Chemistry, VCH, NY, 1985, pp. 307–321; Casanova, J.; Waegell, B. Bull. Soc. Chim. Fr. 1975, 911; Anet, F.A.L. Top. Curr. Chem. 1974, 45, 169; Dunitz, J.D. Pure Appl. Chem. 1971, 25, 495. See Glass, R.S. Conformational Analysis of Medium-Sized Heterocycles VCH, NY, 1988.

401. Wiberg, K.B. J. Org. Chem. 2003, 68, 9322.

402. Meyer, W.L.; Taylor, P.W.; Reed, S.A.; Leister, M.C.; Schneider, H.-J.; Schmidt, G.; Evans, F.E.; Levine, R.A. J. Org. Chem. 1992, 57, 291.

403. Pawar, D.M.; Brown II, J.; Chen, K.-H.; Allinger, N.L.; Noe, E.A. J. Org. Chem. 2006, 71, 6512.

404. Spracklin, D.K.; Weiler, L. J. Chem. Soc. Chem. Commun. 1992, 1347; Keller, T.H.; Neeland, E.G.; Rettig, S.; Trotter, J.; Weiler, L. J. Am. Chem. Soc. 1988, 110, 7858.

405. Pawar, D.M.; Smith, S.V.; Moody, E.M.; Noe, E.A. J. Am. Chem. Soc. 1998, 120, 8241.

406. Borgen, G.; Dale, J.; Gundersen, L.-L.; Krivokapic, A.; Rise, F.; Øverås, A.T. Acta Chem. Scand. B, 1998, 52, 1110.

407. Pawar, D.M.; Davids, K.L.; Brown, B.L.; Smith, S.V.; Noe, E.A. J. Org. Chem. 1999, 64, 4580; Pawar, D.M.; Moody, E.M.; Noe, E.A. J. Org. Chem. 1999, 64, 4586.

408. Kleinpeter, E.; Koch, A.; Pihlaja, K. Tetrahedron 2005, 61, 7349.

409. Daoust, K.J.; Hernandez, S.M.; Konrad, K.M.; Mackie, I.D.; Winstanley, Jr., J.; Johnson, R.P. J. Org. Chem. 2006, 71, 5708.

410. For definitions of axial, equatorial, and related terms for rings of any size, see Anet, F.A.L. Tetrahedron Lett. 1990, 31, 2125.

411. For a discussion of the angles of the ring positions, see Cremer, D. Isr. J. Chem. 1980, 20, 12.

412. Thanks to Dr. Warren Hehre, Wavefunction, Inc., Irvine, CA. Personal communication. See Hehre, W.J. A Guide to Molecular Mechanics and Quantum Chemical Calculations, Wavefunction, Inc., Irvine, CA, 2003, pp. 56–57.

413. For a review, see Rappe, A.K.; Casewit, C.J. Molecular Mechanics Across Chemistry, University Science Books, Sausalito, CA, 1997.

414. Clark, M.; Cramer, III, R.D.; van Opdenbosch, N. J. Computational Chem. 1989, 10, 982.

415. Allinger, N.L.; Li, F.; Yun, Y.H. J. Computational Chem. 1990, 11, 855, and later papers in this series.

416. Allinger, N.L.; Chen, K.; Lii, J.-H. J. Computational Chem. 1996, 17, 642, and later papers in this series.

417. Halgren, T.A. J. Computational Chem 1996, 17, 490, and later papers in this series.

418. See Greenberg, A.; Liebman, J.F. Strained Organic Molecules, Academic Press, NY, 1978; Wiberg, K.B. Angew. Chem. Int. Ed. 1986, 25, 312; Greenberg, A.; Stevenson, T.A. Mol. Struct. Energ. 1986, 3, 193; Liebman, J.F.; Greenberg, A. Chem. Rev. 1976, 76, 311; Cremer, D.; Kraka, E. Mol. Struct. Energ. 1988, 7, 65.

419. Zhao, C.-Y.; Duan, W.-S.; Zhang, Y.; You, X.-Z. J. Chem. Res. (S) 1998, 156.

420. Wiberg, K.B. Accts. Chem. Res. 1996, 29, 229.

421. For discussions, see Wiberg, K.B.; Bader, R.F.W.; Lau, C.D.H. J. Am. Chem. Soc. 1987, 109, 985, 1001.

422. For a review, see Rüchardt, C.; Beckhaus, K. Angew. Chem. Int. Ed. 1985, 24, 529. See also, Burkert, U.; Allinger, N.L. Molecular Mechanisms, American Chemical Society, Washington, 1982, pp. 169–194; Allinger, N.L. Adv. Phys. Org. Chem. 1976, 13, 1, 45–47.

423. Bari, D.; Maksi, Z.B. Theor. Chem. Acc.2005, 114, 222.

424. Hohlneicher, G.; Packschies, L. Tetrahedron Lett. 2007, 48, 6429. However, see Bari, D.; Maksi, Z.B. Tetrahedron Lett. 2008, 49, 1428.

425. For reviews of reactions of cyclopropanes and cyclobutanes, see Trost, B.M. Top. Curr. Chem. 1986, 133, 3; Wong, H.N.C.; Lau, C.D.H.; Tam, K. Top. Curr. Chem. 1986, 133, 83.

426. For a treatise, see Rappoport, Z. The Chemistry of the Cyclopropyl Group, 2 pts.; Wiley, NY, 1987.

427. See in Rappoport, Z. The Chemistry of the Cyclopropyl Group, 2 pts, Wiley, NY, 1987, the papers by Wiberg, K.B. pt. 1., pp. 1–26; Liebman, J.F.; Greenberg, A. pt. 2, pp. 1083–1119; Liebman, J.F.; Greenberg, A. Chem. Rev. 1989, 89, 1225.

428. See Wong, H.N.C.; Hon, M.; Ts, C.e; Yip, Y.; Tanko, J.; Hudlicky, T. Chem. Rev. 1989, 89, 165; Reissig, H. in Rappoport, Z. The Chemistry of the Cyclopropyl Group, pt. 1, Wiley, NY, 1987, pp. 375–443.

429. Ogg, Jr., R.A.; Priest, W.J. J. Am. Chem. Soc. 1938, 60, 217.

430. Shortridge, R.W.; Craig, R.A.; Greenlee, K.W.; Derfer, J.M.; Boord, C.E. J. Am. Chem. Soc. 1948, 70, 946.

431. See Frey, H.M. Adv. Phys. Org. Chem. 1966, 4, 147.

432. Bach, R. D.; Dmitrenko, O. J. Org. Chem. 2002, 67, 2588.

433. Bach, R.D.; Dmitrenko, O. J. Am. Chem. Soc. 2006, 128, 4598.

434. Bach, R. D.; Dmitrenko, O. J. Am. Chem. Soc. 2004, 126, 4444; Tian, Z.; Fattahi, A.; Lis, L.; Kass, S.R. J. Am. Chem. Soc. 2006, 128, 17087.

435. Bachrach, S.M. J. Org. Chem. 2008, 73, 2466. Also see Ringer, A.L.; Magers, D.H. J. Org. Chem. 2007, 72, 2533.

436. See Cremer, D.; Kraka, E. J. Am. Chem. Soc. 1985, 107, 3800, 3811; Slee, T.S. Mol. Struct. Energ. 1988, 5, 63; Casaarini, D.; Lunazzi, L.; Mazzanti, A. J. Org. Chem. 1997, 62, 7592.

437. Randi, M.; Maksi, Z. Theor. Chim. Acta 1965, 3, 59; Weigert, F.J.; Roberts, J.D. J. Am. Chem. Soc. 1967, 89, 5962.

438. Wiberg, K.B. Accts. Chem. Res. 1996, 29, 229.

439. See Hoffmann, R.; Davidson, R.B. J. Am. Chem. Soc. 1971, 93, 5699. See also Ref. 438

440. Wiberg, K.B.; Bader, R.F.W.; Lau, C.D.H. J. Am. Chem. Soc. 1987, 109, 985, 1001.

441. See Tidwell, T.T. in Rappoport, Z. The Chemistry of the Cyclopropyl Groups, pt. 1, Wiley, NY, 1987, pp. 565–632; Charton, M. in Zabicky, J. The Chemistry of Alkenes, Vol. 2, pp. 511–610, Wiley, NY, 1970.

442. See Tsuji, T.; Shibata, T.; Hienuki, Y.; Nishida, S. J. Am. Chem. Soc. 1978, 100, 1806; Drumright, R.E.; Mas, R.H.; Merola, J.S.; Tanko, J.M. J. Org. Chem. 1990, 55, 4098.

443. Staley, S.W. J. Am. Chem. Soc. 1967, 89, 1532; Pews, R.G.; Ojha, N.D. J. Am. Chem. Soc. 1969, 91, 5769. See, however, Noe, E.A.; Young, R.M. J. Am. Chem. Soc. 1982, 104, 6218.

444. See the reviews in Chem. Rev. 1989, 89, 975, and the following: Jefford, C.W. J. Chem. Educ. 1976, 53, 477; Seebach, D. Angew. Chem. Int. Ed. 1965, 4, 121; Greenberg, A.; Liebman, J.F. Strained Organic Molecules, Academic Press, NY, 1978, pp. 210–220; Eliel, E.L.; Wilen, S.H.; Mander, L.N. Stereochemistry of Organic Compounds, Wiley–Interscience, NY, 1994, pp. 771–811.

445. For a useful classification of strained polycyclic systems, see Gund, P.; Gund, T.M. J. Am. Chem. Soc. 1981, 103, 4458.

446. For a computer program that generates IUPAC names for complex bridged systems, see Rücker, G.; Rücker, C. Chimia 1990, 44, 116.

460. Gribanova, T.N.; Minyaev, R.M.; Minkin, V.I. Russ. J. Org. Chem. 2007, 43, 1144.

461. Gleiter, R.; Treptow, B.; Irngartinger, H.; Oeser, T. J. Org. Chem. 1994, 59, 2787.

462. Golobish, T.D.; Dailey, W.P. Tetrahedron Lett. 1996, 37, 3239.

463. Haller, I.; Srinivasan, R. J. Chem. Phys. 1964, 41, 2745.

464. Newton, M.D.; Schulman, J.M. J. Am. Chem. Soc. 1972, 94, 767.

465. Wiberg, K.B.; Waddell, S.T. J. Am. Chem. Soc. 1990, 112, 2194; Seiler, S.T. Helv. Chim. Acta 1990, 73, 1574; Bothe, H.; Schlüter, A. Chem. Ber. 1991, 124, 587; Lynch, K.M.; Dailey, W.P. J. Org. Chem. 1995, 60, 4666. See Wiberg, K.B. Chem. Rev. 1989, 89, 975; Ginsburg, D. in Rappoport, Z The Chemistry of the Cyclopropyl Group, pt. 2, Wiley, NY, 1987, pp. 1193–1221; Ginsburg, D. Top. Curr. Chem. 1987, 137, 1. For a discussion of charge density and bonding, see Coppens, P. Angew. Chem. Int. Ed. 2005, 44, 6810.

466. Wiberg, K.B.; Walker, F.H.; Pratt, W.E.; Michl, J. J. Am. Chem. Soc. 1983, 105, 3638.

467. Della, E.W.; Taylor, D.K. J. Org. Chem. 1994, 59, 2986.

468. See Kuck, D.; Krause, R.A.; Gestmann, D.; Posteher, F.; Schuster, A. Tetrahedron 1998, 54, 5247.

447. Lemal, D.M.; Menger, F.M.; Clark, G.W. J. Am. Chem. Soc. 1963, 85, 2529; Wiberg, K.B.; Lampman, G.M. Tetrahedron Lett. 1963, 2173; Hoz, S. in Rappoport, Z The Chemistry of the Cyclopropyl Group, pt. 2, Wiley, NY, 1987, pp. 1121–1192; Wiberg, K.B. Adv. Alicyclic Chem. 1968, 2, 185. For a review of [n.1.1] systems, see Meinwald, J.; Meinwald, Y.C. Adv. Alicyclic Chem. 1966, 1, 1.

448. Casanova, J.; Bragin, J.; Cottrell, F.D. J. Am. Chem. Soc. 1978, 100, 2264.

449. Irngartinger, H.; Goldmann, A.; Jahn, R.; Nixdorf, M.; Rodewald, H.; Maier, G.; Malsch, K.; Emrich, R. Angew. Chem. Int. Ed. 1984, 23, 993; Maier, G.; Fleischer, F. Tetrahedron Lett. 1991, 32, 57. Also see Maier, G. Angew. Chem. Int. Ed. 1988, 27, 309; Maier, G.; Rang, H.; Born, D. in Olah, G.A. Cage Hydrocarbons, Wiley, NY, 1990, pp. 219–259; Maier, G.; Born, D. Angew. Chem. Int. Ed. 1989, 28, 1050.

450. Rücker, C.; Trupp, B. J. Am. Chem. Soc. 1988, 110, 4828.

451. Von Seebach, M.; Kozhushkov, S.I.; Boese, R.; Benet-Buchholz, J.; Yufit, D.S.; Howard, J.A.K.; de Meijere, A. Angew. Chem. Int. Ed. 2000, 39, 2495.

452. Katz, T.J.; Acton, N. J. Am. Chem. Soc. 1973, 95, 2738. See also, Wilzbach, K.E.; Kaplan, L. J. Am. Chem. Soc. 1965, 87, 4004.

453. Hedberg, L.; Hedberg, K.; Eaton, P.E.; Nodari, N.; Robiette, A.G. J. Am. Chem. Soc. 1991, 113, 1514. For a review of cubanes, see Griffin, G.W.; Marchand, A.P. Chem. Rev. 1989, 89, 997.

454. Paquette, L.A.; Fischer, J.W.; Browne, A.R.; Doecke, C.W. J. Am. Chem. Soc. 1985, 105, 686.

455. Eaton, P.E.; Or, Y.S.; Branca, S.J.; Shankar, B.K.R. Tetrahedron 1986, 42, 1621. See also, Dauben, W.G.; Cunningham Jr., A.F. J. Org. Chem. 1983, 48, 2842.

456. Otterbach, A.; Musso, H. Angew. Chem. Int. Ed. 1987, 26, 554.

457. Allred, E.L.; Beck, B.R. J. Am. Chem. Soc. 1973, 95, 2393.

458. Hoffmann, V.T.; Musso, H. Angew. Chem. Int. Ed. 1987, 26, 1006.

459. Rihs, G. Tetrahedron Lett. 1983, 24, 5857. See Mathew, T.; Keller, M.; Hunkler, D.; Prinzbach, H. Tetrahedron Lett. 1996, 37, 4491 for the synthesis of azapagodanes (also called azadodecahedranes).

469. For a review, see Wiberg, K.B. Acc. Chem. Res. 1984, 17, 379.

470. Scott, W.B.; Pincock, R.E. J. Am. Chem. Soc. 1973, 95, 2040.

471. Gibbons, C.S.; Trotter, J. Can. J. Chem. 1973, 51, 87.

472. See Raphael, R.A. Proc. Chem. Soc. 1962, 97; Sicher, J. Prog. Stereochem. 1962, 3, 202.

473. Huber-Buser, E.; Dunitz, J.D. Helv. Chim. Acta 1960, 43, 760.

474. Dunitz, J.D.; Venkatesan, K. Helv. Chim. Acta 1961, 44, 2033.

475. Kirby, A.J.; Komarov, I.V.; Wothers, P.D.; Feeder, N. Angew. Chem. Int. Ed., 1998, 37, 785. Also see Madder, R.D.; Kim, C.-Y.; Chandra, P.P.; Doyon, J.B.; Barid, Jr., T.A.; Fierke, C.A.; Christianson, D.W.; Voet, J.G.; Jain, A. J. Org. Chem. 2002, 67, 582.

476. Okazaki, T.; Ogawa, K.; Kitagawa, T.; Takeuchi, K. J. Org. Chem. 2002, 67, 5981.

477. Gol'dfarb, Ya.L.; Belen'kii, L.I. Russ. Chem. Rev. 1960, 29, 214, p. 218.

478. For a review, see Cope, A.C.; Martin, M.M.; McKervey, M.A. Q. Rev. Chem. Soc. 1966, 20, 119.

479. Spanka, G.; Rademacher, P. J. Org. Chem. 1986, 51, 592. See also, Spanka, G.; Rademacher, P.; Duddeck, H. J. Chem. Soc. Perkin Trans. 2 1988, 2119.

480. Uemura, S.; Fukuzawa, S.; Toshimitsu, A.; Okano, M.; Tezuka, H.; Sawada, S. J. Org. Chem. 1983, 48, 270.

481. Schläpfer-Dähler, M.; Prewo, R.; Bieri, J.H.; Germain, G.; Heimgartner, H. Chimia 1988, 42, 25.

482. See Granik, V.G. Russ. Chem. Rev. 1982, 51, 119.

483. An example is the calculated strain of 1.4–3.2 kcal mol⁻¹(5.9–13.4 kJ mol⁻¹) in cyclotetradecane. See Chickos, J.S.; Hesse, D.G.; Panshin, S.Y.; Rogers, D.W.; Saunders, M.; Uffer, P.M.; Liebman, J.F. J. Org. Chem. 1992, 57, 1897.

484. For a review of strained double bonds, see Zefirov, N.S.; Sokolov, V.I. Russ. Chem. Rev. 1967, 36, 87. For a review of double and triple bonds in rings, see Johnson, R.P. Mol. Struct. Energ. 1986, 3, 85.

485. See Baird, M.S. Top. Curr. Chem. 1988, 144, 137; Halton, B.; Banwell, M.G. in Rappoport, Z. The Chemistry of the Cyclopropyl Group, pt. 2, Wiley, NY, 1987, pp. 1223–1339; Closs, G.L. Adv. Alicyclic Chem. 1966, 1, 53; For a discussion of the bonding and hybridization, see Allen, F.H. Tetrahedron 1982, 38, 645.

486. Dem'yanov, N.Ya.; Doyarenko, M.N. Ber. 1923, 56, 2200; Schlatter, M.J. J. Am. Chem. Soc. 1941, 63, 1733; Stigliani, W.M.; Laurie, V.W.; Li, J.C. J. Chem. Phys. 1975, 62, 1890.

487. See Halton, B. Chem. Rev. 1989, 89, 1161; 1973, 73, 113; Billups, W.E.; Rodin, W.A.; Haley, M.M. Tetrahedron 1988, 44, 1305; Billups, W.E. Acc. Chem. Res. 1978, 11, 245.

488. Vogel, E.; Grimme, W.; Korte, S. Tetrahedron Lett. 1965, 3625. Also see Müller, P.; Bernardinelli, G.; Thi, H.C.G. Chimia 1988, 42, 261; Neidlein, R.; Christen, D.; Poignée, V.; Boese, R.; Bläser, D.; Gieren, A.; Ruiz-Pérez, C.; Hübner, T. Angew. Chem. Int. Ed. 1988, 27, 294.

489. For reviews of trans cycloalkenes, see Nakazaki, M.; Yamamoto, K.; Naemura, K. Top. Curr. Chem. 1984, 125, 1; Marshall, J.A. Acc. Chem. Res. 1980, 13, 213.

490. Wallraff, G.M.; Michl, J. J. Org. Chem. 1986, 51, 1794; Squillacote, M.; Bergman, A.; De Felippis, J. Tetrahedron Lett. 1989, 30, 6805.

491. Marshall, J.A.; Flynn, K.E. J. Am. Chem. Soc. 1983, 105, 3360. For reviews, see Nakazaki, M.; Yamamoto, K.; Naemura, K. Top. Curr. Chem. 1984, 125, 1; Marshall, J.A. Acc. Chem. Res. 1980, 13, 213. For a review of these and similar compounds, see Borden, W.T. Chem. Rev. 1989, 89, 1095.

492. See Meier, H. Adv. Strain Org. Chem. 1991, 1, 215; Krebs, A.; Wilke, J. Top. Curr. Chem. 1983, 109, 189; Nakagawa, M. in Patai, S. The Chemistry of the CC Triple Bond, pt. 2, Wiley, NY, 1978, pp. 635–712; Krebs, A. in Viehe, H.G. Acetylenes, Marcel Dekker, NY, 1969, pp. 987–1062. See Meier, H.; Hanold, N.; Molz, T.; Bissinger, H.J.; Kolshorn, H.; Zountsas, J. Tetrahedron 1986, 42, 1711.

493. Blomquist, A.T.; Liu, L.H. J. Am. Chem. Soc. 1953, 75, 2153. See also, Bühl, H.; Gugel, H.; Kolshorn, H.; Meier, H. Synthesis 1978, 536.

494. Schmidt, H.; Schweig, A.; Krebs, A. Tetrahedron Lett. 1974, 1471.

495. Krebs, A.; Kimling, H. Tetrahedron Lett. 1970, 761.

496. Bottini, A.T.; Frost II, K.A.; Anderson, B.R.; Dev, V. Tetrahedron 1973, 29, 1975.

497. Wentrup, C.; Blanch, R.; Briehl, H.; Gross, G. J. Am. Chem. Soc. 1988, 110, 1874.

498. See Sander, W.; Chapman, O.L. Angew. Chem. Int. Ed. 1988, 27, 398.

499. See Bolster, J.M.; Kellogg, R.M. J. Am. Chem. Soc. 1981, 103, 2868; Gilbert, J.C.; Baze, M.E. J. Am. Chem. Soc. 1983, 105, 664.

500. Chapman, O.L.; Gano, J.; West, P.R.; Regitz, M.; Maas, G. J. Am. Chem. Soc. 1981, 103, 7033.

501. Bennett, M.A.; Robertson, G.B.; Whimp, P.O.; Yoshida, T. J. Am. Chem. Soc. 1971, 93, 3797.

502. See Johnson, R.P. Chem. Rev. 1989, 89, 1111; Thies, R.W. Isr. J. Chem. 1985, 26, 191; Schuster, H.F.; Coppola, G.M. Allenes in Organic Synthesis; Wiley, NY, 1984, pp. 38–56.

503. Price, J.D.; Johnson, R.P. Tetrahedron Lett. 1986, 27, 4679.

504. See Marquis, E.T.; Gardner, P.D. Tetrahedron Lett. 1966, 2793.

505. Wittig, G.; Dorsch, H.; Meske-Schüller, J. Liebigs Ann. Chem. 1968, 711, 55.

506. Visser, J.P.; Ramakers, J.E. J. Chem. Soc. Chem. Commun. 1972, 178.

507. Wentrup, C.; Gross, G.; Maquestiau, A.; Flammang, R. Angew. Chem. Int. Ed. 1983, 22, 542. 1,2,3-Cyclohexatriene has also been trapped: Shakespeare, W.C.; Johnson, R.P. J. Am. Chem. Soc. 1990, 112, 8578.

508. Moore, W.R.; Ward, H.R. J. Am. Chem. Soc. 1963, 85, 86.

509. Angus Jr., R.O.; Johnson, R.P. J. Org. Chem. 1984, 49, 2880.

510. Ohwada, T. Tetrahedron 1993, 49, 7649.

511. Lange, H.; Schäfer, W.; Gleiter, R.; Camps, P.; Vázquez, S. J. Org. Chem. 1998, 63, 3478.

512. See Shea, K.J. Tetrahedron 1980, 36, 1683; Buchanan, G.L. Chem. Soc. Rev. 1974, 3, 41; Köbrich, G. Angew. Chem. Int. Ed. 1973, 12, 464. See Billups, W.E.; Haley, M.M.; Lee, G. Chem. Rev. 1989, 89, 1147; Warner, P.M. Chem. Rev. 1989, 89, 1067; Keese, R. Angew. Chem. Int. Ed. 1975, 14, 528. Also see, Smith, M.B. Organic Synthesis, 3rd ed., Wavefunction Inc./Elsevier, Irvine, CA/London, England, 2010, pp. 553–555.

513. See Maier, W.F.; Schleyer, P.v.R. J. Am. Chem. Soc. 1981, 103, 1891.

514. Kim, M.; White, J.D. J. Am. Chem. Soc. 1975, 97, 451; Becker, K.B. Helv. Chim. Acta 1977, 60, 81. See Nakazaki, M.; Naemura, K.; Nakahara, S. J. Org. Chem. 1979, 44, 2438.

515. Wiseman, J.R.; Chan, H.; Ahola, C.J. J. Am. Chem. Soc. 1969, 91, 2812; Carruthers, W.; Qureshi, M.I. Chem. Commun. 1969, 832; Becker, K.B. Tetrahedron Lett. 1975, 2207.

516. Lesko, P.M.; Turner, R.B. J. Am. Chem. Soc. 1968, 90, 6888; Burkert, U. Chem. Ber. 1977, 110, 773.

517. Wiseman, J.R.; Chong, J.A. J. Am. Chem. Soc. 1969, 91, 7775.

518. Sheridan, R.S.; Ganzer, G.A. J. Am. Chem. Soc. 1983, 105, 6158; Radziszewski, J.G.; Downing, J.W.; Wentrup, C.; Kaszynski, P.; Jawdosiuk, M.; Kovacic, P.; Michl, J. J. Am. Chem. Soc. 1985, 107, 2799.

519. Radziszewski, J.G.; Downing, J.W.; Wentrup, C.; Kaszynski, P.; Jawdosiuk, M.; Kovacic, P.; Michl, J. J. Am. Chem. Soc. 1985, 107, 2799.

520. See Tidwell, T.T. Tetrahedron 1978, 34, 1855; Mosher, H.S.; Tidwell, T.T. J. Chem. Educ. 1990, 67, 9. For a review of van der Waals radii, see Zefirov, Yu.V.; Zorkii, P.M. Russ. Chem. Rev. 1989, 58, 421.

521. Arnett, E.M.; Bollinger, J.M. Tetrahedron Lett. 1964, 3803.

522. Maier, G.; Schneider, K. Angew. Chem. Int. Ed. 1980, 19, 1022. For another example, see Krebs, A.; Franken, E.; Müller, S. Tetrahedron Lett. 1981, 22, 1675.

523. Arnett, E.M.; Sanda, J.C.; Bollinger, J.M.; Barber, M. J. Am. Chem. Soc. 1967, 89, 5389;. See also, Barclay, L.R.C.; Brownstein, S.; Gabe, E.J.; Lee, F.L. Can. J. Chem. 1984, 62, 1358.

524. Sakurai, H.; Ebata, K.; Kabuto, C.; Sekiguchi, A. J. Am. Chem. Soc. 1990, 112, 1799.

525. Siegel, J.; Gutiérrez, A.; Schweizer, W.B.; Ermer, O.; Mislow, K. J. Am. Chem. Soc. 1986, 108, 1569. Also see Kahr, B.; Biali, S.E.; Schaefer, W.; Buda, A.B.; Mislow, K. J. Org. Chem. 1987, 52, 3713.

526. See Iwamura, H.; Mislow, K. Acc. Chem. Res. 1988, 21, 175; Mislow, K. Chemtracts: Org. Chem. 1989, 2, 151; Berg, U.; Liljefors, T.; Roussel, C.; Sandström, J. Acc. Chem. Res. 1985, 18, 80.

527. Nugiel, D.A.; Biali, S.E.; Rappoport, Z. J. Am. Chem. Soc. 1984, 106, 3357.

528. Yamamoto, G.; Öki, M. Bull. Chem. Soc. Jpn. 1986, 59, 3597. See Yamamoto, G. Pure Appl. Chem. 1990, 62, 569; Öki, M. Applications of Dynamic NMR Spectroscopy to Organic Chemistry, VCH, NY, 1985, pp. 269–284.

529. Ackerman, J.H.; Laidlaw, G.M.; Snyder, G.A. Tetrahedron Lett. 1969, 3879; Ackerman, J.H.; Laidlaw, G.M. Tetrahedron Lett. 1969, 4487. See also, Cuyegkeng, M.A.; Mannschreck, A. Chem. Ber. 1987, 120, 803.

530. See Öki, M. Applications of Dynamic NMR Spectroscopy to Organic Chemistry, VCH, NY, 1985; Förster, H.; Vögtle, F. Angew. Chem. Int. Ed. 1977, 16, 429; Öki, M. Angew. Chem. Int. Ed. 1976, 15, 87.

531. Clough, R.L.; Roberts, J.D. J. Am. Chem. Soc. 1976, 98, 1018. For a study of rotational barriers in this system, see Cosmo, R.; Sternhell, S. Aust. J. Chem. 1987, 40, 1107.

532. Bartlett, P.D.; Tidwell, T.T. J. Am. Chem. Soc. 1968, 90, 4421.

533. See Back, T.G.; Barton, D.H.R. J. Chem. Soc. Perkin Trans 1, 1977, 924; Kopka, I.E.; Fataftah, Z.A.; Rathke, M.W. J. Org. Chem. 1980, 45, 4616.

534. Schmidbaur, H.; Blaschke, G.; Zimmer-Gasser, B.; Schubert, U. Chem. Ber. 1980, 113, 1612.

535. DeTar, D.F.; Binzet, S.; Darba, P. J. Org. Chem. 1985, 50, 2826, 5298, 5304.

536. For reviews, see Luef, W.; Keese, R. Top. Stereochem. 1991, 20, 231; Sandström, J. Top. Stereochem. 1983, 14, 83, pp. 160–169.

537. For a list of crowded alkenes that have been made, see Drake, C.A.; Rabjohn, N.; Tempesta, M.S.; Taylor, R.B. J. Org. Chem. 1988, 53, 4555. See also, Garratt, P.J.; Payne, D.; Tocher, D.A. J. Org. Chem. 1990, 55, 1909.

538. Krebs, A.; Nickel, W.; Tikwe, L.; Kopf, J. Tetrahedron Lett. 1985, 26, 1639.

539. Sakurai, H.; Ebata, K.; Kabuto, C.; Nakadaira, Y. Chem. Lett. 1987, 301.

540. Wiberg, K.B.; Matturo, M.G.; Okarma, P.J.; Jason, M.E. J. Am. Chem. Soc. 1984, 106, 2194; Wiberg, K.B.; Adams, R.D.; Okarma, P.J.; Matturo, M.G.; Segmuller, B. J. Am. Chem. Soc. 1984, 106, 2200.

541. Eaton, P.E.; Maggini, M. J. Am. Chem. Soc. 1988, 110, 7230.

542. Hrovat, D.A.; Borden, W.T. J. Am. Chem. Soc. 1988, 110, 7229.

543. For a review of such molecules, see Borden, W.T. Chem. Rev. 1989, 89, 1095. See also, Hrovat, D.A.; Borden, W.T. J. Am. Chem. Soc. 1988, 110, 4710.