Chapter 9
Effects of Structure and Medium on Reactivity
When the equation for a reaction of, say, carboxylic acids, is written, it is customary to use the formula RCOOH, where R is a generic alkyl group, which implies that all carboxylic acids undergo the reaction. Since most compounds with a given functional group usually give more or less the same reactions, the custom is useful, and the practice is used in this text. It allows a large number of individual reactions to be classified together and serves as an aid both for memory and understanding. Nevertheless, it must be borne in mind that a given functional group does not always react the same way, regardless of what molecule it is a part of. In other words, a reaction at the functional group is influenced by the rest of the molecule. This influence may be great enough to stop the reaction completely or to make it take an entirely different course. Even when two compounds with the same functional group undergo the same reaction, the rates and/or the positions of equilibrium are usually different, sometimes slightly, sometimes greatly, depending on the structures of the compounds. The greatest variations may be expected when additional functional groups are present.
The effects of structure on reactivity can be divided into three major types: field, resonance (or mesomeric), and steric.1 In most cases, two or all three of these are operating, and it is usually not easy to tell how much of the rate enhancement (or decrease) is caused by each of the three effects.
9.A. Resonance and Field Effects
It is often particularly difficult to separate resonance and field effects; they are frequently grouped together under the heading of electrical effects.2 Field effects were discussed in Section 1.I. Table 1.3 contains a list of some +I and −I groups. As for resonance effects, in Section 2.F it was shown how the electron density distribution in aniline is not the same as it would be if there were no resonance interaction between the ring and the NH2 group. Most groups that contain an unshared pair on an atom connected to an unsaturated system display a similar effect; that is, the electron density on the group is less than expected, and the density on the unsaturated system is greater. Such groups are said to be electron donating by the resonance effect (+M groups). Alkyl groups, which do not have an unshared pair, are also +M groups, presumably because of hyperconjugation (see Sec. 2.M).
On the other hand, groups that have a multiple-bonded electronegative atom directly connected to an unsaturated system are −M groups. In such cases, canonical forms can be drawn in which electrons are delocalized from the unsaturated system into the group, as in nitrobenzene (1). Table 9.1 contains a list of some +M and −M groups.
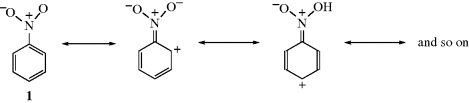
Table 9.1 Some Groups with +M and −M Effects, Not Listed in Order of Strength of Effecta
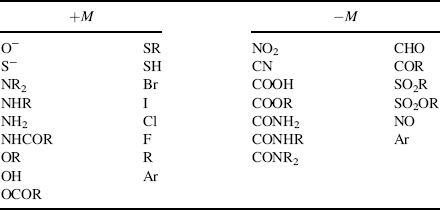
a. Argon (Ar) appears in both lists because it is capable of both kinds of effect.
The resonance effect of a group, whether +M or −M, operates only when the group is directly connected to an unsaturated system, so that, for example, in explaining the effect of the CH3O group on the reactivity of the COOH in CH3OCH2CH2COOH, only the field effect of the CH3O need be considered. This is one way of separating the two effects. In p-methoxybenzoic acid both effects must be considered. The field effect operates through space, solvent molecules, or the σ bonds of a system, while the resonance effect operates through π electrons.
It must be emphasized once again that neither by the resonance nor by the field effect are any electrons actually being donated or withdrawn, though these terms are convenient (and we will use them). As a result of both effects, the electron-density distribution is not the same as it would be without the effect (see Sec. 1.I, 2.F). Complicating the study of these effects on the reactivity of compounds is the fact that a given group may have an effect in the transition state that is considerably more or less than it has in the molecule that does not react.
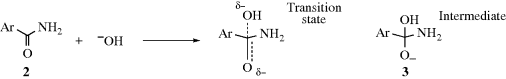
In the alkaline hydrolysis of aromatic amides (Reaction 16-60), the rate-determining step is the attack of hydroxide ion at the carbonyl carbon. The conversion of 2 to 3 illustrates the nature of electrical effects (resonance and field) on reactivity. In the transition state, which has a structure somewhere between that of the starting amide (2) and the intermediate (3), the electron density on the carbonyl carbon is increased. Therefore, electron-withdrawing groups (−I or −M) on the aromatic ring will lower the free energy of the transition state (by spreading the negative charge). These groups have much less effect on the free energy of 2. Since G is lowered for the transition state, but not substantially for 2, ΔG‡ is lowered and the reaction rate is increased (Chapter 6). Conversely, electron-donating groups (+I or +M) should decrease the rate of this reaction. Of course, many groups are −I and +M, and for these it is not always possible to predict which effect will predominate.
9.B. Steric Effects
It occasionally happens that a reaction proceeds much faster or much slower than expected on the basis of electrical effects alone. In these cases, it can often be shown that steric effects have a significant influence on the rate. For example, Table 9.2 lists relative rates for the SN2 ethanolysis of certain alkyl halides (see Sec. 10.A.i).3 All these compounds are primary bromides; the branching is on the second carbon, so that field-effect differences should be small. As Table 9.2 shows, the rate decreases with increasing b branching and reaches a very low value for neopentyl bromide. This reaction is known to involve an attack by the nucleophile from a position opposite to that of the bromine (see Sec. 10.A.i). The great decrease in rate can be attributed to steric hindrance in the transition state of the reaction, which makes attack of the nucleophile more difficult. Another example of steric hindrance is found in 2,6-disubstituted benzoic acids, which are difficult to esterify no matter what the resonance or field effects of the groups in the 2 or the 6 positions. Similarly, once 2,6-disubstituted benzoic acids are esterified, the esters are difficult to hydrolyze.
Table 9.2 Relative Rates of Reaction of RBr with Ethanola
| R | Relative Rate |
| CH3 | 17.6 |
| CH3CH2 | 1 |
| CH3CH2CH2 | 0.28 |
| (CH3)2CHCH2 | 0.030 |
| (CH3)3CCH2 | 4.2 × 10−6 |
| Reproduced from Hughes, E.D. Q. Rev. Chem. Soc. 1948, 2, 107 with permission from the Royal Society of Chemistry. | |
| a. See Ref. 3. | |
Not all steric effects decrease reaction rates. In the hydrolysis of RCl by an SN1 mechanism (see Sec. 10.A.ii), the first step, which is rate determining, involves ionization of the alkyl chloride to a carbocation:
The central carbon in the alkyl chloride is sp3 hybridized, with angles of ~109.5°, but when it is converted to the carbocation, the hybridization becomes sp2 and the preferred angle is 120°. If the halide is tertiary and the three alkyl groups are large enough, they will be pushed together by the enforced tetrahedral angle, resulting in strain (see Sec. 4.Q.iv). This type of strain is called B strain4 (for back strain), and can be relieved by ionization to the carbocation.5
The rate of ionization (and hence the solvolysis rate) of a molecule in which there is B strain is expected to be larger than in cases where B strain is not present. Table 9.3 shows that this is so.6 Substitution of ethyl groups for the methyl groups of tert-butyl chloride does not cause B strain; the increase in rate is relatively small, and the rate smoothly rises with the increasing number of ethyl groups. The increase is caused by normal field and resonance (hyperconjugation) effects. Substitution by one isopropyl group is not greatly different. But with the second isopropyl group the crowding is now great enough to cause B strain, and the rate is increased 10-fold. Substitution of a third isopropyl group increases the rate still more. Another example where B strain increases the rate of solvolysis is found with the highly crowded molecules tri-tert-butylcarbinol, di-tert-butylneopentylcarbinol, tert-butyldineopentylcarbinol, and trineopentylcarbinol, where rates of solvolysis of the p-nitrobenzoate esters are faster than that of tert-butyl nitrobenzoate by factors of 13,000, 19,000, 68,000, and 560, respectively.7
Table 9.3 Rates of Hydrolysis of Tertiary Alkyl Chlorides at 25 °C in 80% Aqueous Ethanola
Reproduced with permission Brown, H.C.; Fletcher, R.S. J. Am. Chem. Soc. 1949, 71, 1845. Copyright © 1949 American Chemical Society.
a. See Ref. 6.
Another type of strain, which can affect rates of cyclic compounds, is called I strain (internal strain).8 This type of strain results from changes in ring strain in going from a tetrahedral to a trigonal carbon or vice versa. For example, as mentioned above, SN1 solvolysis of an alkyl halide involves a change in the bond angle of the central carbon from ~109.5° to ~120°. This change is highly favored in 1-chloro-1-methylcyclopentane because it relieves eclipsing strain (Sec. 4.Q.iv); thus this compound undergoes solvolysis in 80% ethanol at 25 °C, 43.7 times faster than the reference compound tert-butyl chloride.9 In the corresponding cyclohexyl compound, this factor is absent because the substrate does not have eclipsing strain (Sec. 4.Q.iv), and this compound undergoes the reaction at about one-third the rate of tert-butyl chloride. The reasons for this small decrease in rate are not clear. Corresponding behavior is found in the other direction, in changes from a trigonal to a tetrahedral carbon. Thus cyclohexanone undergoes addition reactions faster than cyclopentanone. Similar considerations apply to larger rings. Rings of 7–11 members exhibit eclipsing and transannular strain; and in these systems reactions in which a tetrahedral carbon becomes trigonal generally proceed faster than in open-chain systems.10 I-Strain has been shown to be a factor in other reactions as well.11
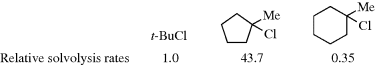
Conformational effects on reactivity can be considered under the heading of steric effects,12 but in these cases the effect of a group X and that of another group X′ upon reactivity at a site Y are not considered. But the effect of the conformation of the molecule must be considered. Many reactions fail entirely unless the molecules are able to assume the proper conformation. An example is the rearrangement of N-benzoylnorephedrine. The two diastereomers of this compound (4 and 5) behave very differently when treated with alcoholic HCl. In one of the isomers, nitrogen-to-oxygen migration takes place, while the other does not react at all.13 In order for the migration to take place, the nitrogen must be near the oxygen (gauche to it). When 4 assumes this conformation, the methyl and phenyl groups are anti to each other, which is a favorable position, but when 5 has the nitrogen gauche to the oxygen, the methyl must be gauche to the phenyl, which is so unfavorable that the reaction does not occur. Other examples are electrophilic additions to C=C double bonds (see Sec. 15.A.i) and E2 elimination reactions (see Sec. 17.A.i.). Also, many examples are known where axial and equatorial groups behave differently.14
In steroids and other rigid systems, a functional group in one part of the molecule can strongly affect the rate of a reaction taking place at a remote part of the same molecule by altering the conformation of the whole skeleton. An example of this effect, called conformational transmission, is found in ergost-7-en-3-one (6) and cholest-6-en-3-one (7), where 7 condenses with benzaldehyde 15 times faster than 6.15 The reaction site in both cases is the carbonyl group, and the rate increases because moving the double bond from the 7 to the 6 position causes a change in conformation at the carbonyl group (the difference in the side chain at C-17 does not affect the rate). Molecular models of 6 and 7 are provided for illustration.
9.C. Quantitative Treatments of the Effect of Structure on Reactivity16
Suppose a reaction is performed on a substrate molecule that can be represented as XGY, where Y is the site of the reaction, X a variable substituent, and G is a skeleton group to which X and Y are attached. In such a molecule, changing X from H to CH3 results in a rate increase by a factor, of say, 10. What part of the increase is due to each of the effects previously mentioned? The obvious way to approach such a problem is to try to find compounds in which one or two of the factors are absent or at least negligible. This is difficult because factors that seem negligible to one investigator do not always appear so to another. The first attempt to give numerical values was that of Hammett.17 For the cases of m- and p-XC6H4Y, Hammett set up the equation
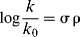
where k0 is the rate constant or equilibrium constant for X = H, k is the constant for the group X, ρ is a constant for a given reaction under a given set of conditions, and σ is a constant characteristic of the group X. The equation is called the Hammett equation.
The value of ρ was set at 1.00 for ionization of XC6H4COOH in water at 25°C. The values of σm and σp were then calculated for each group (for a group X, σ is different for the meta and para positions). Once a set of σ values was obtained, ρ values could be obtained for other reactions from the rates of just two X-substituted compounds, if the s values of the X groups were known (in practice, at least four well-spaced values are used to calculate ρ because of experimental error and because the treatment is not exact). With the ρ value calculated and the known s values for other groups, rates can be predicted for reactions that have not yet been run.
The σ values are numbers that sum up the total electrical effects (resonance plus field) of a group X when attached to a benzene ring. The treatment usually fails for the ortho position. The Hammett treatment has been applied to many reactions and to many functional groups. It correlates an enormous amount of data quite well. Jaffé's review article17 listed ρ values for 204 reactions,18 many of which have different ρ values for different conditions. Among them are reactions as disparate as the following reactions.
Rate constants for the following:
Equilibrium constants for
The Hammett equation also has been shown to apply to many physical measurements, including IR frequencies and NMR chemical shifts.19 The treatment is reasonably successful whether the substrates are attacked by electrophilic, nucleophilic, or free radical reagents, the important thing being that the mechanism be the same within a given reaction series.
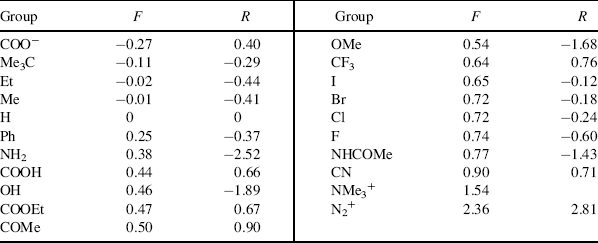
However, there are many reactions that do not fit the treatment. These are mostly reactions where the attack is directly on the ring and where the X group can enter into direct resonance interaction with the reaction site in the transition state (i.e., the substrate is XY rather than XGY). For these cases, two new sets of σ values have been devised: σ+ values (proposed by H.C. Brown) for cases in which an electron-donating group interacts with a developing positive charge in the transition state (this includes the important case of electrophilic aromatic substitutions; see Chapter 11), and σ values, where electron-withdrawing groups interact with a developing negative charge. Table 9.4 gives σ, σ+, and σ− values for some common X groups.20 As shown in the table, σ is not very different from σ+ for most electron-withdrawing groups. The values of 
are not shown in the table, since they are essentially the same as the σm values.
Table 9.4 The σ, σ+, and σ− Values for Some Common Groupsa
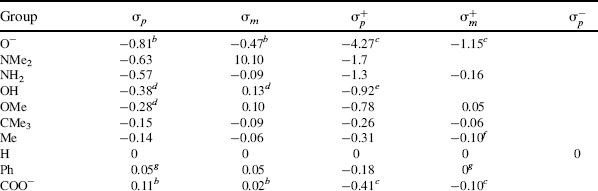
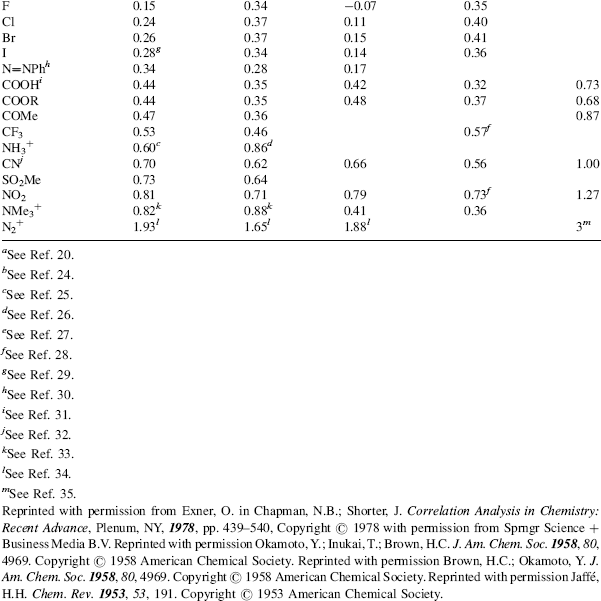
A positive value of σ indicates an electron-withdrawing group and a negative value an electron-donating group.21 The constant ρ measures the susceptibility of the reaction to electrical effects.22 Reactions with a positive ρ are helped by electron-withdrawing groups and vice versa. The following ρ values for the ionization of some carboxylic acids illustrate this:23
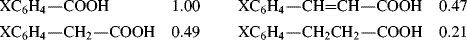
This example shows that the insertion of a CH2 or a CH=CH group diminishes electrical effects to about the same extent, while a CH2CH2 group diminishes them much more. A ρ > 1 would mean that the reaction is more sensitive to electrical effects than is the ionization of XC6H4COOH (ρ = 1.00).
Similar calculations have been made for compounds with two groups X and X′ on one ring, where the σ values are sometimes additive and sometimes not,36 for other ring systems, (e.g., naphthalene)37 and heterocyclic rings,38 and for ethylenic and acetylenic systems.39
The Hammett equation is a linear free energy relationship (LFER). This relationship can be demonstrated as follows for the case of equilibrium constants (for rate constants a similar demonstration can be made with ΔG‡ instead of ΔG). For each reaction, where X is any group,
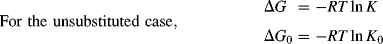
The Hammett equation can be rewritten
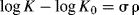
so that
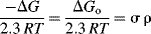
and
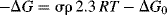
For a given reaction under a given set of conditions, σ, R, T, and ΔG0 are all constant, so that σ is linear with ΔG.
The Hammett equation is not the only LFER.40 Some, like the Hammett equation, correlate structural changes in reactants, but the Grunwald–Winstein relationship (see Sec. 10.G.iv) correlates changes in solvent and the Br
nsted relation (see Sec. 8.D) relates acidity to catalysis. The Taft equation is a structure–reactivity equation that correlates only field effects.41
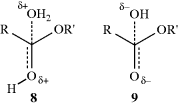
Taft, following Ingold,42 assumed that for the hydrolysis of carboxylic esters, steric and resonance effects will be the same whether the hydrolysis is catalyzed by acid or base (see the discussion of ester-hydrolysis mechanisms, Reaction 16-59). Rate differences would therefore be caused only by the field effects of R and R′ in RCOOR′. This system is presumably good to use for this purpose because the transition state for acid-catalyzed hydrolysis (8) has a greater positive charge (and is hence destabilized by −I and stabilized by +I substituents) than the starting ester, while the transition state for base-catalyzed hydrolysis (9) has a greater negative charge than the starting ester. Field effects of substituents X could therefore be determined by measuring the rates of acid- and base-catalyzed hydrolysis of a series XCH2COOR′,43 where R′ is held constant.38 From these rate constants, a value σI could be determined by the equation44
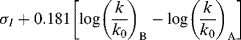
In this equation, (k/k0)B is the rate constant for basic hydrolysis of XCH2COOR′ divided by the rate constant for basic hydrolysis of CH3COOR′, (k/k0)A is the similar rate-constant ratio for acid catalysis, and 0.181 is an arbitrary constant. The substituent constant σI is for a group X, substituted at a saturated carbon, which reflects only field effects.45 Once a set of σI values was obtained, it was found that the equation holds for a number of reactions, among them:46
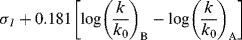
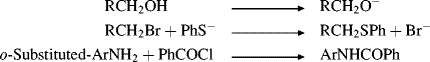
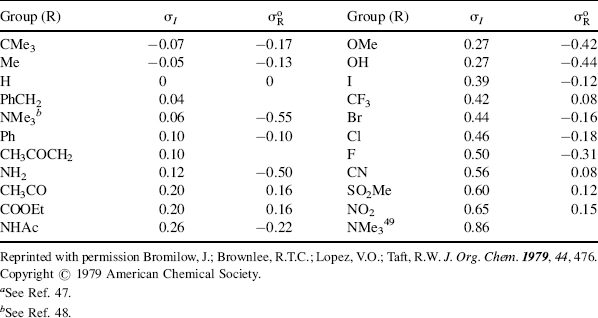
As with the Hammett equation, σI is constant for a given reaction under a given set of conditions. For very large groups, the relationship may fail because of the presence of steric effects, which are not constant. The equation also fails when X enters into resonance with the reaction center to different extents in the initial and transition states. A list of some σI values is given in Table 9.5.47 The σI values are4849 about what is expected for pure field-effect values (see Sec. 1.I) and are additive, as field effects (but not resonance or steric effects) would be expected to be. Thus, in moving a group one carbon down the chain, there is a decrease by a factor of 2.8 ± 0.5 (cf. the values of R in Table 9.5 for R = Ph and CH3CO). An inspection of Table 9.5 shows that σI values for most groups are fairly close to the σm values (Table 9.4) for the same groups. This result is not surprising, since σm values would be expected to arise almost entirely from field effects, with little contribution from resonance.
Table 9.5 The σI and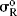 
Values for Some Groupsa
Since σp values represent the sum of resonance and field effects, these values can be divided into resonance and field contributions if σI is taken to represent the field-effect portion.50 The resonance contribution σR51 is defined as:
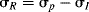
As it stands, however, this equation is not very useful because the σR value for a given group, which should be constant if the equation is to have any meaning, is actually not constant, but depends on the nature of the reaction.52 In this respect, the σI values are much better. Although they vary with solvent in some cases, σI values are essentially invariant throughout a wide variety of reaction series. However, it is possible to overcome53 the problem of varying σR values by using a special set of σR values, called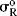 
,54 that measure the ability to delocalize π electrons into or out of an unperturbed or “neutral” benzene ring. Several 
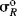scales have been reported; the most satisfactory values are obtained from 
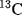chemical shifts of substituted benzenes.55 Table 9.5 lists some values of 
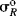, most of which were obtained in this way.56
An equation, for example,
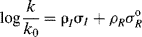
which treats resonance and field effects separately, is known as a dual substituent parameter equation.57
The only groups in Table 9.5 with negative values of σI are the alkyl groups methyl and tert-butyl. There has been some controversy on this point.58 One opinion is that σI values decrease in the series methyl, ethyl, isopropyl, tert-butyl (respectively, −0.046, −0.057, −0.065, −0.074).59 Other evidence, however, has led to the belief that all alkyl groups have approximately the same field effect and that the σI values are invalid as a measure of the intrinsic field effects of alkyl groups.60
Another attempt to divide σ values into resonance and field contributions61 is that of Swain and Lupton, who show that the large number of sets of σ values (σm, σp, σp−, σp+, σI,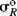 
, etc., as well as others we have not mentioned) are not entirely independent and that linear combinations of two sets of new values F (which expresses the field-effect contribution) and R (the resonance contribution) satisfactorily express 43 sets of values.62 Each set is expressed as:
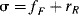
where f and r are weighting factors. Some F and R values for common groups are given in Table 9.6.63 From the calculated values of f and r, Swain and Lupton63 calculated that the importance of resonance, %R, is 20% for σm, 38% for σp, and 62% for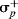 
.64 This is another dual substituent parameter approach.
Table 9.6 The F and R Values for Some Groupsa
Reprinted with permission Swain, C.G.; Unger, S.H.; Rosenquist, N.R.; Swain, M.S. J. Am. Chem. Soc. 1983, 105, 492. Copyright © 1983 American Chemical Society.
a. See Ref. 63.
Taft and co-workers63 were also able to isolate steric effects.65 For the acid-catalyzed hydrolysis of esters in aqueous acetone, long (k/k0) was shown to be insensitive to polar effects.66 In cases where resonance interaction was absent, this value was proportional only to steric effects (and any others67 that are not field or resonance). The equation is
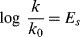
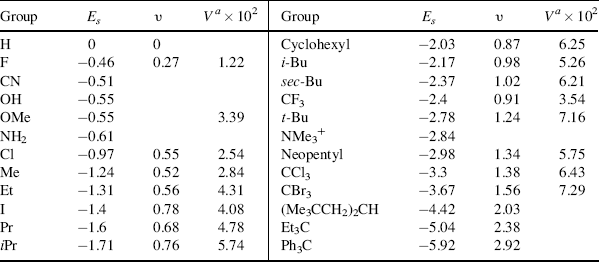
Some Es values are given in Table 9.7,68 where hydrogen is taken as standard, with a value of 0.69 This treatment is more restricted than those previously discussed, since it requires more assumptions, but the Es values are approximately in order of the size of the groups. Charton70 show that Es values for substituents of types CH2X, CHX2, and CX3 are linear functions of the van der Waals radii for these groups.
Table 9.7 The Es, υ, and Va Values for Some Groupsa
Reprinted with permission from Gallo, R.; Roussel, C.; Berg, U. Adv. Heterocycl. Chem. 1988, 43, 173, Copyright © 1988, with permission from Elsevier Science.
a. See Ref. 68.
Two other steric parameters are independent of any kinetic data. Charton's υ values are derived from van der Waals radii,71 and Meyer's Va values from the volume of the portion of the substituent that is within 0.3 nm of the reaction center.72 The Va values are obtained by molecular mechanics calculations based on the structure of the molecule. Table 9.7 gives υ and Va values for some groups.73 As can be seen in the table, there is a fair, but not perfect, correlation among the Es, υ, and Va values. Other sets of steric values (e.g., 
,74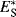 
,75 Ωs76 and δf,77 have also been proposed.73
Since the Hammett equation has been so successful in the treatment of the effects of groups in the meta and para positions, it is not surprising that attempts have been made to apply it to ortho positions also.78 The effect on a reaction rate or equilibrium constant of a group in the ortho position is called the ortho effect.79 Despite the many attempts made to quantify ortho effects, no set of values has so far commanded general agreement. However, the Hammett treatment is successful for ortho compounds when the group Y in o-XC6H4Y is separated from the ring; for example, ionization constants of o-XC6H4OCH2CO2H can be successfully correlated.80
Linear free energy relationships can have mechanistic implications. If log k/k0 is linear with the appropriate σ, it is likely that the same mechanism operates throughout the series. If not, a smooth curve usually indicates a gradual change in mechanism, while a pair of intersecting straight lines indicates an abrupt change,81 although nonlinear plots can also be due to other causes (e.g., complications arising from side reactions). If a reaction series follows σ+ or σ− better than σ it generally means that there is extensive resonance interaction in the transition state.82
Information can also be obtained from the magnitude and sign of ρ. For example, a strongly negative ρ value indicates a large electron demand at the reaction center, from which it may be concluded that a highly electron-deficient center, perhaps an incipient carbocation, is involved. Conversely, a positive ρ value is associated with a developing negative charge in the transition state.83 The σρ relationship even applies to free radical reactions, because free radicals can have some polar character (Sec. 14.A.ii), though ρ values here are usually small (less than ~1.5) whether positive or negative. Reactions involving cyclic transition states (Sec. 6.B) also exhibit very small ρ values.
9.D. Effect of Medium on Reactivity and Rate
There is no question that the solvent chosen for a given reaction has a profound influence on the course of that reaction. Protic versus aprotic solvents, as well as polar versus nonpolar solvents, can have effects ranging from solubility to solvent assisted ionization or stabilization of transition states. Reactions can also be done neat in one of the reactants, in the gas phase, on solid support, or in the solid phase. Environmental friendly chemistry (green chemistry) is becoming increasingly important, and chemical reactions in nonpolluting (often non-organic) solvents are of particular interest.84 This section will describe alternative reaction media as well as other medium-related things that influence chemical reactions.
9.D.i High Pressure
Acceleration of some chemical reactions is possible when high-pressure techniques are employed.85,86 The effects on a given reaction can be predicted to a certain extent because the thermodynamic properties of solutions are well known. The rate of a reaction can be expressed in terms of the activation volume, (ΔV‡)
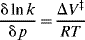
so rate constants vary with pressure.86 “The activation volume87 is the difference in partial molal volume between the transition state and the initial state. From a synthetic point of view, this could be approximated by the molar volume.”86 If the volume of activation is negative, the rate of the reaction will be accelerated by increasing pressure. As the pressure increases, the value of ΔV‡ decreases and the system does not strictly obey the equation shown above at pressures > 10 kbar (1 bar = 0.986924 atm = 1.1019716 kg cm−2). If the transition state of a reaction involves bond formation, concentration of charge, or ionization, a negative volume of activation often results. There is a correlation between pressure and steric interactions in organic reactions.88 Cleavage of a bond, dispersal of charge, or neutralization of the transition state and diffusion control lead to a positive volume of activation. Matsumoto et al. summarized the reactions for which rate enhancement is expected at high pressure.86
Many high-pressure reactions are done neat, but if a solvent is used, the influence of pressure on that solvent is important. The melting point generally increases at elevated pressures, and this influences the viscosity of the medium (the viscosity of liquids increases approximately two times per kilobar increase in pressure). Controlling the rate of diffusion of reactants in the medium is also important, leading to another influence of high pressure on reactivity.86,89 In most reactions, pressure is applied (5–20 kbar) at room temperature and then the temperature is increased until reaction takes place. The temperature is lowered and the pressure is reduced to isolate the products.
9.D.ii Water and Other Non-Organic Solvents
Although some reactions may be done in water,90 chemical reactions of organic substrates usually employ an organic solvent (e.g., a hydrocarbon, ether, dichloromethane, small molecular weight alcohols, and so on), but other more exotic solvents are available. For example, poly(ethylene glycol), or PEG, has been used as a solvent medium for catalytic hydrogenation (Reaction 15-11).91 For some reactions in organic solvents, the presence of water may cause unwanted side reactions, and methods have been developed to detect the presence of water in those solvents.92
With the exception of small molecular weight molecules with polar functional groups and polyfunctional molecules or salts, organic chemicals have poor solubility in water. Nonetheless, some reactions show a faster rate of reaction in water or in aqueous media.93 The first indication that water accelerated a reaction was in a patent by Hopff and Rautenstrauch in 1939,94 who reported that yields in the Diels–Alder Reaction (15-60) were enhanced in aqueous detergent solutions. In an early study, Berson et al.95 showed a clear relationship between the endo/exo product ratio and solvent polarity, in the Diels–Alder reaction of cyclopentadiene and acrylates. Breslow and Rideout.96 showed there was a hydrophobic acceleration for an intermolecular Diels–Alder reaction in which cyclopentadiene reacted with methyl vinyl ketone. Clearly, there is an accelerating effect on some chemical reactions when done in water that is useful in organic chemistry.97
When nonpolar compounds are suspended in water, their relative insolubility causes them to associate, diminishing the water–hydrocarbon interfacial area (a hydrophobic effect).98 This association is greater in water than in methanol and brings the reactive partners into close proximity, increasing the rate of reaction. Any additive that increases the hydrophobic effect will increase the rate.96
Organic chemical reactions have been done is supercritical fluids, including supercritical water.99 A supercritical fluid can be either liquid or gas, but it is used in a state above the temperature and pressure where gases and liquids can coexist. The properties of a supercritical fluid are different from those of either gases or liquids under standard conditions, with no distinct liquid and gas phases at temperatures and pressures above its critical point. The critical point is the temperature, pressure, and so on, at which there are no phase boundaries. Carbon dioxide can be used as a reaction solvent when pressurized (supercritical carbon dioxide, scCO2). Carbon dioxide is nontoxic, inexpensive, abundant, and easily recycled. These properties have made it attractive as an extraction solvent.100 The low critical temperature of CO2 (Tc) 31.1 °C ensures that scCO2 is a safe solvent for many applications.101 There are solubility issues that suggest scCO2 is a rather polar solvent.102 For example, many systems with hydrocarbon chains are not very soluble in CO2.103 Water/carbon dioxide emulsions have also been employed.104 The use of (scCO2) has been explored in many reactions,105 including catalysis.106 Some applications of this technique include the electrochemical synthesis of conducting polymers107 and highly cross-linked polymers108 in scCO2, the synthesis of octyl palmitate,109 of carbonated fatty methyl esters,110 and of methyl carbamates.111 A carbonylation reaction was done is scCO2 in the course of a synthesis of trisubstituted cyclopentanes and cyclohexanes as key components of substance P antagonists.112 A continuous flow acid-catalyzed dehydration of alcohols was accomplished in scCO2.113 Supercritical fluids are playing an increasingly important role in synthetic organic chemistry.114
Other supercritical fluids can be used for chemical reactions, such as supercritical ammonia in the synthesis of labeled guanidines.115
9.D.iii Ionic Solvents
Environmentally friendly solvents,116 which include ionic liquids, are of great interest.117 An ionic liquid is a salt in which the ions are poorly coordinated, usually leading to their being liquid at <100 °C and sometimes at room temperature.118 In such ionic species, there is usually at least one ion with a delocalized charge, whereas the other component is usually organic. This combination inhibits the formation of a stable crystal lattice. The structure and solvation properties of solutes in ionic liquids have been studied.119 It was discovered that some ionic liquids are suitable as a medium for chemical reactions.120 Both methylimidazolium and pyridinium ions form the basis of common ionic liquids that have been used in organic chemistry.121 One of the most common ionic liquids used as a solvent is 1-butyl-3-methylimidazolium as the hexafluorophosopahte, (10, Bmim PF6).122 Hydrogenbutylimidazolium tetrafluoroborate (HBuIm, 11) and 1,3-dibutylimidazolium, tetrafluoroborate (DiBuIm, 12), for example,123 have been reported to facilitate Diels–Alder Reactions (15-60).124 It is known that a proton on C-2 of imidazolium cations (e.g., 10-12) is relatively acidic.125 Carbene formation is common and the anion generated by treatment with base can undergo substitution reactions.125 These facts lead to a caution that undesired side reactions are possible when these ionic liquids are employed as solvents.125,126 Pyridinium-based ionic liquids [e.g., ethylpyridinium tetrafluoroborate (13)] have also been used.127 Several room temperature ionic liquids have been synthesized from amino acids.128
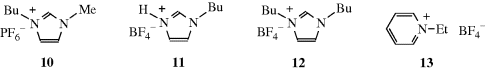
Ionic solvents have been used to facilitate heterocyclic reactions,129 several catalytic reactions,130 the Heck Reaction (13-9)131 and other Pd catalyzed C–C bond-forming reactions,132 the oxidation of alcohols with hypervalent iodine reagents (19-3),133 and the catalytic asymmetric dihydroxylation of alkenes (15-48) using a recoverable and reusable Os/ligand complex.134 The camphorsulfonate anion has been used as a counterion for imidazolium salts, and shown to increase the number of unsolvated imidazolium cations.135 This ionic liquid was then shown to influence the endo/exo ratio in a stereoselective Diels–Alder Reaction (15-60).135 Other catalytic reactions in ionic liquids are known.136 Other chiral ionic liquids are known.137 Reactions performed in an ionic liquid are a rapidly growing area of organic chemistry, and has been expanded to include microwave reactions (see Sec. 7.C) in ionic solvents.138 The development and use of ionic solvents is a growth area of organic chemistry.139 Also note that some ionic liquids are categorized as Lewis base (Sec. 8.E), which will influence the acidity of dissolved compounds.140 There are also acidic Brnsted ionic liquids.141
9.D.iv. Solventless Reactions
In some cases, it should be possible to accomplish a chemical transformation without the use of a solvent. Dry media reaction under microwave irradiation is an important area of study (see Sec. 7.C).142 There are several advantages of solventless reactions: (1) the possibility of direct formation of high-purity compounds, (2) the possibility of sequential reactions, (3) fast kinetics, (4) lower energy usage, (5) minimal need for preformed salts and metal–metalloid complexes, (6) simplicity and low equipment cost, and (7) the possibility of avoiding functional group protection–deprotection.143 Potential difficulties include the possibility of hot spots and runaway reactions, and difficulties in handling solid or highly viscous materials.144 An example of this approach is the aldol condensation, where a single aldol product was obtained in high yield.145 3-Carboxylcoumarins have been produced via a solventless aldol.143
Notes
1. See Klumpp, G.W. Reactivity in Organic Chemistry, Wiley, NY, 1982. For a general theoretical approach to organic reactivity, see Pross, A. Adv. Phys. Org. Chem. 1985, 21, 99.
2. See Topsom, R.D. Prog. Phys. Org. Chem. 1987, 16, 125, Mol. Struct. Energ. 1987, 4, 235.
3. Hughes, E.D. Q. Rev. Chem. Soc. 1948, 2, 107.
4. Brown, H.C. Boranes in Organic Chemistry, Cornell University Press, Ithaca, NY, 1972, pp. 114–121.
5. See Stirling, C.J.M. Tetrahedron 1985, 41, 1613; Pure Appl. Chem. 1984, 56, 1781.
6. Brown, H.C.; Fletcher, R.S. J. Am. Chem. Soc. 1949, 71, 1845.
7. Bartlett, P.D.; Tidwell, T.T. J. Am. Chem. Soc. 1968, 90, 4421.
8. See Brown, H.C. Boranes in Organic Chemistry, Cornell University Press, Ithaca, NY, 1972, pp. 105–107, 126–128.
9. Brown, H.C.; Borkowski, M. J. Am. Chem. Soc. 1952, 74, 1894. See also, Brown, H.C.; Ravindranathan, M.; Peters, E.N.; Rao, C.G.; Rho, M.M. J. Am. Chem. Soc. 1977, 99, 5373.
10. See Schneider, H.; Thomas, F. J. Am. Chem. Soc. 1980, 102, 1424.
11. Sands, R.D. J. Org. Chem. 1994, 59, 468.
12. See Green, B.S.; Arad-Yellin, R.; Cohen, M.D. Top. Stereochem. 1986, 16, 131; Öki, M. Acc. Chem. Res. 1984, 17, 154; Seeman, J.I. Chem. Rev. 1983, 83, 83. See also, Öki, M.; Tsukahara, J.; Moriyama, K.; Nakamura, N. Bull. Chem. Soc. Jpn. 1987, 60, 223, and other papers in this series.
13. Fodor, G.; Bruckner, V.; Kiss, J.; Óhegyi, G. J. Org. Chem. 1949, 14, 337.
14. See Eliel, E.L. Stereochemistry of Carbon Compounds, McGraw-Hill, NY, 1962, pp. 219–234.
15. Barton, D.H.R.; McCapra, F.; May, P.J.; Thudium, F. J. Chem. Soc. 1960, 1297.
16. See Exner, O. Correlation Analysis of Chemical Data, Plenum, NY, 1988; Johnson, C.D. The Hammett Equation, Cambridge University Press, Cambridge, 1973; Shorter, J. Correlation Analysis of Organic Reactivity, Wiley, NY, 1982; Chapman, N.B.; Shorter, J. Correlation Analysis in Chemistry: Recent Advances, Plenum, NY, 1978. Also see Connors, K.A. Chemical Kinetics, VCH, NY, 1990, pp. 311–383; Lewis, E.S. in Bernasconi, C.F. Investigation of Rates and Mechanisms of Reactions (Vol. 6 of Weissberger, A. Techniques of Chemistry), 4th ed., Wiley, NY, 1986, pp. 871–901; Jones, R.A.Y. Physical and Mechanistic Organic Chemistry, 2nd ed., Cambridge University Press, Cambridge, 1984, pp. 38–68; Hine, J. Structural Effects in Organic Chemistry, Wiley, NY, 1975, pp. 55–102. For a historical perspective, see Grunwald, E. CHEMTECH 1984, 698.
17. For a review, see Jaffé, H.H. Chem. Rev. 1953, 53, 191.
18. Additional ρ values are given in Wells, P.R. Chem. Rev. 1963, 63, 171 and van Bekkum, H.; Verkade, P.E.; Wepster, B.M. Recl. Trav. Chim. Pays-Bas 1959, 78, 821.
19. For a review of Hammett treatment of NMR chemical shifts, see Ewing, D.F. in Chapman, N.B.; Shorter, J. Correlation Analysis in Chemistry: Recent Advances, Plenum, NY, 1978, pp. 357–396.
20. Unless otherwise noted, σ values are from Exner, O. in Chapman, N.B.; Shorter, J. Correlation Analysis in Chemistry: Recent Advances, Plenum, NY, 1978, pp. 439–540, and σ+ values from Okamoto, Y.; Inukai, T.; Brown, H.C. J. Am. Chem. Soc. 1958, 80, 4969; Brown, H.C.; Okamoto, Y. J. Am. Chem. Soc. 1958, 80, 4979. σ− values, except as noted, are from Jaffé, H.H. Chem. Rev. 1953, 53, 191. Also see Hansch, C.; Leo, A.; Taft, R.W. Chem. Rev. 1991, 91, 165; Egorochkin, A.N.; Razuvaev, G.A. Russ. Chem. Rev. 1987, 56, 846. For values for heteroaromatic groups, see Mamaev, V.P.; Shkurko, O.P.; Baram, S.G. Adv. Heterocycl. Chem. 1987, 42, 1.
24. Hine, J. J. Am. Chem. Soc. 1960, 82, 4877; Jones, R.A.Y. Physical and Mechanistic Organic Chemistry, 2nd ed., Cambridge Univ. Press, Cambridge, 1984, p. 42.
25. See Hine, J. J. Am. Chem. Soc. 1960, 82, 4877.
26. Matsui, T.; Ko, H.C.; Hepler, L.G. Can. J. Chem. 1974, 52, 2906.
27. de la Mare, P.B.D.; Newman, P.A. Tetrahedron Lett. 1982, 23, 1305 give this value as –1.6.
28. Amin, H.B.; Taylor, R. Tetrahedron Lett. 1978, 267.
29. Sjöström, M.; Wold, S. Chem. Scr. 1976, 9, 200.
30. Byrne, C.J.; Happer, D.A.R.; Hartshorn, M.P.; Powell, H.K.J. J. Chem. Soc. Perkin Trans. 2 1987, 1649.
31. For a review of directing and activating effects of C=O, C=C, C=N, and C=S groups, see Charton, M. in Patai, S. The Chemistry of Double-Bonded Functional Groups, Vol. 2, pt. 1, Wiley, NY, 1989, pp. 239–298.
32. For a review of directing and activating effects of C
N and CC groups, see Charton, M. in Patai, S.; Rappoport, Z. The Chemistry of Functional Groups, Supplement C, pt. 1, Wiley, NY, 1983, pp. 269–323.
33. McDaniel, D.H.; Brown, H.C. J. Org. Chem. 1958, 23, 420.
34. Ustynyuk, Yu.A.; Subbotin, O.A.; Buchneva, L.M.; Gruzdneva, V.N.; Kazitsyna, L.A. Doklad. Chem. 1976, 227, 175.
35. Lewis, E.S.; Johnson, M.D. J. Am. Chem. Soc. 1959, 81, 2070.
21. See Dubois, J.E.; Ruasse, M.; Argile, A. J. Am. Chem. Soc. 1984, 106, 4840; Ruasse, M.; Argile, A.; Dubois, J.E. J. Am. Chem. Soc. 1984, 106, 4846; Lee, I.; Shim, C.S.; Chung, S.Y.; Kim, H.Y.; Lee, H.W. J. Chem. Soc. Perkin Trans. 2 1988, 1919.
22. Hine, J. J. Am. Chem. Soc. 1960, 82, 4877.
23. Binev, I.G.; Kuzmanova, R.B.; Kaneti, J.; Juchnovski, I.N. J. Chem. Soc. Perkin Trans. 2 1982, 1533.
36. Stone, R.M.; Pearson, D.E. J. Org. Chem. 1961, 26, 257.
37. Berliner, E.; Winikov, E.H. J. Am. Chem. Soc. 1959, 81, 1630; See also, Well, P.R.; Ehrenson, S.; Taft, R.W. Prog. Phys.Org. Chem. 1968, 6, 147.
38. See Charton, M. in Chapman, N.B.; Shorter, J. Correlation Analysis in Chemistry: Recent Advances, Plenum, NY, 1978, pp. 175–268; Tomasik, P.; Johnson, C.D. Adv. Heterocycl. Chem. 1976, 20, 1.
39. See Ford, G.P.; Katritzky, A.R.; Topsom, R.D. in Correlation Analysis in Chemistry: Recent Advances, Plenum, NY, ,1978, pp. 269–311; Charton, M. Prog. Phys. Org. Chem. 1973, 10, 81.
40. See Exner, O. Prog. Phys. Org. Chem. 1990, 18, 129.
41. For reviews of the separation of resonance and field effects, see Charton, M. Prog. Phys. Org. Chem. 1981, 13, 119; Shorter, J. Q. Rev. Chem. Soc. 1970, 24, 433; Chem. Ber. 1969, 5, 269. For a review of field and inductive effects, see Reynolds, W.F. Prog. Phys. Org. Chem. 1983, 14, 165. For a review of field effects on reactivity, see Grob, C.A. Angew. Chem. Int. Ed. 1976, 15, 569.
42. Ingold, C.K. J. Chem. Soc. 1930, 1032.
43. Also see Draffehn, J.; Ponsold, K. J. Prakt. Chem. 1978, 320, 249.
44. The symbol σF is also used in the literature; sometimes in place of σI, and sometimes to indicate only the field (not the inductive) portion of the total effect (Sec. 1.G).
45. There is another set of values (called σ∗ values) that are also used to correlate field effects. These are related to σI values by σI(X) = 0.45σ. Only σI, and not σ∗ values are discussed.
46. Wells, P.R. Chem. Rev. 1963, 63, 171, p. 196.
47. These values are from Bromilow, J.; Brownlee, R.T.C.; Lopez, V.O.; Taft, R.W. J. Org. Chem. 1979, 44, 4766, but the values for NHAc, OH, and I are from Wells, P.R.; Ehrenson, S.; Taft, R.W. Prog. Phys. Org. Chem. 1968, 6, 147, the values for Ph and NMe3+ are from Taft, R.W.; Ehrenson, S.; Lewis, I.C.; Glick, R. J. Am.Chem. Soc. 1959, 81, 5352; Taft, R.W.; Deno, N.C.; Skell, P.S. Annu. Rev. Phys. Chem. 1958, 8, 287, and the value for CMe3 is from Seth-Paul, W.A.; de Meyer-van Duyse, A.; Tollenaere, J.P. J. Mol. Struct. 1973, 19, 811. The values for the CH2Ph and CH2COCH3 groups were calculated from σ∗ values by the formula given in ref. 45. Also see Charton, M. Prog. Phys. Org. Chem. 1981, 13, 119; Taylor, P.J.; Wait, A.R. J. Chem. Soc. Perkin Trans. 2 1986, 1765.
48. For values for some other NR2 groups, see Korzhenevskaya, N.G.; Titov, E.V.; Chotii, K.Yu.; Chekhuta, V.G. J. Org. Chem. USSR 1987, 28, 1109.
49. It has been shown that charged groups (called polar substituents) cannot be included with uncharged groups (dipolar substituents) in one general scale of electrical substituent effects: Marriott, S.; Reynolds, J.D.; Topsom, R.D. J. Org. Chem. 1985, 50, 741.
50. Taft, R.W. J. Phys. Chem. 1960, 64, 1805; Taft, R.W.; Lewis, I.C. J. Am. Chem. Soc. 1958, 80, 2436; Taft, R.W.; Deno, N.C.; Skell, P.S. Annu. Rev. Phys. Chem. 1958, 9, 287, see pp. 290–293.
51. Ehrenson, S.; Brownlee, R.T.C.; Taft, R.W. Prog. Phys. Org. Chem. 1973, 10, 1. See also, Taft, R.W.; Topsom, R.D. Prog. Phys. Org. Chem. 1987, 16, 1; Charton, M. Prog. Phys. Org. Chem. 1987, 16, 287.
52. Taft, R.W.; Lewis, I.C. J. Am. Chem. Soc. 1959, 81, 5343; Reynolds, W.F.; Dais, P.; MacIntyre, D.W.; Topsom, R.D.; Marriott, S.; von Nagy-Felsobuki, E.; Taft, R.W. J. Am. Chem. Soc. 1983, 105, 378.
53. Also see Happer, D.A.R.; Wright, G.J. J. Chem. Soc. Perkin Trans. 2 1979, 694.
54. Taft, R.W.; Ehrenson, S.; Lewis, I.C.; Glick, R.E. J. Am. Chem. Soc. 1959, 81, 5352.
55. Bromilow, J.; Brownlee, R.T.C.; Lopez, V.O.; Taft, R.W. J. Org. Chem. 1979, 44, 4766. See also, Marriott, S.; Topsom, R.D. J. Chem. Soc. Perkin Trans. 2 1985, 1045.
56. For a set of σR values for use in XY+ systems, see Charton, M. Mol. Struct. Energ. 1987, 4, 271.
57. See de Ligny, C.L.; van Houwelingen, H.C. J. Chem. Soc. Perkin Trans. 2 1987, 559.
58. See Shorter, J. in Chapman, N.B.; Shorter, J. Advances in Linear Free Energy Relationships, Plenum, NY, 1972, pp. 98–103.
59. See Screttas, C.G. J. Org. Chem. 1979, 44, 3332; Hanson, P. J. Chem. Soc. Perkin Trans. 2 1984, 101.
60. See DeTar, D.F. J. Org. Chem. 1980, 45, 5166; J. Am. Chem. Soc. 1980, 102, 7988.
61. See Shorter, J. in Chapman, N.B.; Shorter, J. Correlation Analysis in Chemistry: Recent Advances, Plenum, NY, 1978, pp. 119–173, pp. 126–144; Afanas'ev, I.B. J. Chem. Soc. Perkin Trans. 2 1984, 1589; Ponec, R. Coll. Czech. Chem. Commun. 1983, 48, 1564.
62. Swain, C.G.; Unger, S.H.; Rosenquist, N.R.; Swain, M.S. J. Am. Chem. Soc. 1983, 105, 492 and references cited therin.
63. From Swain, C.G.; Unger, S.H.; Rosenquist, N.R.; Swain, M.S. J. Am. Chem. Soc. 1983, 105, 492. Also see Hansch, C.; Leo, A.; Taft, R.W. Chem. Rev. 1991, 91, 165.
64. The Swain-Lupton treatment has been criticized by Reynolds, W.F.; Topsom, R.D. J. Org. Chem. 1984, 49, 1989; Hoefnagel, A.J.; Oosterbeek, W.; Wepster, B.M. J. Org. Chem. 1984, 49, 1993; Charton, M. J. Org. Chem. 1984, 49, 1997. For a reply, see Swain, C.G. J. Org. Chem. 1984, 49, 2005. See Charton, M. Prog. Phys. Org. Chem. 1981, 13, 119; Nakazumi, H.; Kitao, T.; Zollinger, H. J. Org. Chem. 1987, 52, 2825.
65. See Gallo, R.; Roussel, C.; Berg, U. Adv. Heterocycl. Chem. 1988, 43, 173; Gallo, R. Prog. Phys. Org. Chem. 1983, 14, 115; Unger, S.H.; Hansch, C. Prog. Phys. Org. Chem. 1976, 12, 91.
66. Also see De Tar, D.F.; Delahunty, C. J. Am. Chem. Soc. 1983, 105, 2734.
67. See McClelland, R.A.; Steenken, S. J. Am. Chem. Soc. 1988, 110, 5860.
68. Taken from Gallo, R.; Roussel, C.; Berg, U. Adv. Heterocycl. Chem. 1988, 43, 173; Gallo, R. Prog. Phys. Org. Chem. 1983, 14, 115; Unger, S.H.; Hansch, C. Prog. Phys. Org. Chem. 1976, 12, 91. Charton, M. J. Org. Chem. 1976, 41, 2217; and Meyer, A.Y. J. Chem. Soc. Perkin Trans. 2 1986, 1567.
69. In Taft's original work, Me was given the value 0. The Es values in Table 9.7 can be converted to the orginal values by adding 1.24.
70. Charton, M. J. Am. Chem. Soc. 1969, 91, 615.
71. Charton, M. J. Am. Chem. Soc. 1975, 97, 1552; J. Org. Chem. 1976, 41, 2217. See also, Charton, M. J. Org. Chem. 1978, 43, 3995; Idoux, J.P.; Schreck, J.O. J. Org. Chem. 1978, 43, 4002.
72. Meyer, A.Y. J. Chem. Soc. Perkin Trans. 2 1986, 1567.
73. See DeTar, D.F. J. Org. Chem. 1980, 45, 5166; J. Am. Chem. Soc. 1980, 102, 7988.
74. MacPhee, J.A.; Panaye, A.; Dubois, J.E. J. Org. Chem. 1980, 45, 1164; Dubois, J.E.; MacPhee, J.A.; Panaye, A. Tetrahedron 1980, 36, 919. See also, Datta, D.; Sharma, G.T. J. Chem. Res. (S) 1987, 422.
75. Fellous, R.; Luft, R. J. Am. Chem. Soc. 1973, 95, 5593.
76. Komatsuzaki, T.; Sakakibara, K.; Hirota, M. Tetrahedron Lett. 1989, 30, 3309; Chem. Lett. 1990, 1913.
77. Beckhaus, H. Angew. Chem. Int. Ed. 1978, 17, 593.
78. See Fujita, T.; Nishioka, T. Prog. Phys. Org. Chem. 1976, 12, 49; Charton, M. Prog. Phys. Org. Chem. 1971, 8, 235. See also, Robinson, C.N.; Horton, J.L.; Fosheé, D.O.; Jones, J.W.; Hanissian, S.H.; Slater, C.D. J. Org. Chem. 1986, 51, 3535.
79. This is not the same as the ortho effect discussed in Section 11.B.iv.
80. Charton, M. Can. J. Chem. 1960, 38, 2493.
81. See Schreck, J.O. J. Chem. Educ. 1971, 48, 103.
82. See, however, Gawley, R.E. J. Org. Chem. 1981, 46, 4595.
83. Also see Williams, A. Acc. Chem. Res. 1984, 17, 425.
84. Clark, J.H. Green Chem. 1999, 1, 1; Cave, G.W.V.; Raston, C.L.; Scott, J.L. Chem. Commun. 2001, 2159.
85. Jenner, G. Tetrahedron 2002, 58, 5185; Matsumoto, K.; Morris, A.R. Organic Synthesis at High Pressure, Wiley, New York, 1991.
86. Matsumoto, K.; Sera, A.; Uchida, T. Synthesis 1985, 1; Matsumoto, K.; Sera, A. Synthesis. 1985, 999. Also see Benito-López, F.; Egberink, R.J.M.; Reinhoudt, D.N.; Verboom, W. Tetrahedron 2008, 64, 10023.
87. See le Noble, W.J. Progr. Phys. Org. Chem. 1967, 5, 207; Isaacs, N.S. Liquid Phase High Pressure Chemistry, Wiley, Chichester, 1981; Asano, T.; le Noble, W.J. Chem. Rev. 1978,78, 407.
88. Jenner, G. Tetrahedron 2005, 61, 3621.
89. Firestone, R.A.; Vitale, M.A. J. Org. Chem. 1981, 46, 2160.
90. Organic Reactions in Water: Principles, Strategies and Applications, Lindström, U.M. (Ed.), Blackwell, Oxford, 2007; Chanda, A.; Fokin, V.V. Chem. Rev. 2009, 109, 725.
91. Chandrasekhar, S.; Prakash, S.J.; Rao, C.L. J. Org. Chem. 2006, 71, 2196. PEG has also been used for the synthesis of β-amino sulfides. See Kamal, A.; Reddy, D.R.; Rajendar Tetrahedron Lett. 2006, 47, 2261.
92. Sun, H.; Wang, B.; DiMagno, S.G. Org. Lett. 2008, 10, 4413.
93. See Pirrung, M.C. Chemistry: European J. 2006, 12, 1312.
94. Hopff, H.; Rautenstrauch, C.W. U.S. Patent 2,262,002, 1939 [Chem. Abstr. 36: 10469, 1942].
95. Berson, J.A.; Hamlet, Z.; Mueller, W.A. J. Am. Chem. Soc. 1962, 84, 297.
96. Rideout, D.; Breslow, R. J. Am. Chem. Soc. 1980, 102, 7816.
97. Engberts, J.B.F.N.; Blandamer, M.J. Chem. Commun. 2001, 1701; Lindström, U.M. Chem. Rev. 2002, 102, 2751; Ribe, S.; Wipf, P. Chem. Commun. 2001, 299.
98. For a review of chemical reactions in aqueous media with a focus on C–C bond formation, see Li, C.-J. Chem. Rev. 2005, 105, 3095. For microwave assisted synthesis in water, see Dallinger, D.; Kappe, C.O. Chem. Rev. 2007, 107, 2563.
99. Weingärtner, H.; Franck, E.U. Angew. Chem. Int. Ed.2005, 44, 2672; Fraga-Dubreuil, J.; Poliakoff, M. Pure Appl. Chem. 2006, 78,1971.
100. See Raynie, D.E. Anal. Chem. 2004, 76, 4659.
101. Subramaniam, B.; Rajewski, R. A.; Snavely, K. J. Pharm. Sci. 1997, 86, 885.
102. Raveendran, P.; Ikushima, Y.; Wallen, S.L. Acc. Chem. Res. 2005, 38, 478.
103. Consani, K.A.; Smith, R.D.J. Supercrit. Fluids 1990, 3, 51.
104. Jacobson, G.B.; Lee, Jr., C.T.; da Rocha, S.R.P.; Johnston, K.P. J. Org. Chem. 1999, 64, 1207; Jacobson, G.B.; Lee, Jr., C.T.; Johnston, K.P. J. Org. Chem. 1999, 64, 1201.
105. Gopalan, A.D.; Wai, C.M.; Jacobs, H.K. Supercritical Carbon Dioxide: Separations and Processes, American Chemical Society (distributed by Oxford University Press), Washington, DC. 2003; Beckman, E.J. Ind. Eng. Chem. Res. 2003, 42, 1598; Wang, S.; Kienzle, F. Ind. Eng. Chem. Res. 2000, 39, 4487.
106. Leitner, W. Acc. Chem. Res. 2002, 35, 746.
107. Anderson, P.E.; Badlani, R.N.; Mayer, J.; Mabrouk, P.A. J. Am. Chem. Soc. 2002, 124, 10284.
108. Cooper, A.I.; Hems, W.P.; Holmes, A.B. Macromolecules 1999, 32, 2156.
109. Madras, G.; Kumar, R.; Modak, J. Ind. Eng. Chem. Res. 2004, 43, 7697,1568.
110. Doll, K.M.; Erhan, S.Z. J. Agric. Food Chem. 2005, 53, 9608.
111. Selva, M.; Tundo, P.; Perosa, A.; Dall'Acqua, F. J. Org. Chem. 2005, 70, 2771.
112. Kuethe, J.T.; Wong, A.; Wu, J.; Davies, I.W.; Dormer, P.G.; Welch, C.J.; Hillier, M.C.; Hughes, D.L.; Reider, P.J. J. Org. Chem. 2002, 67, 5993.
113. Gray, W.K.; Smail, F.R.; Hitzler, M.G.; Ross, S.K.; Poliakoff, M. J. Am. Chem. Soc. 1999, 121, 10711.
114. See Prajapati, D.; Gohain, M. Tetrahedron 2004, 60, 815.
115. Jacobson, G.B.; Westerberg, G.; Markides, K.E.; Langstrom, B. J. Am. Chem. Soc. 1996, 118, 6868.
116. Alternative Solvents for Green Chemistry, Kerton, F.M.; Clark J.M.; Kraus, G.A. Royal Society of Chemistry, Cambridge, 2009.
117. But also see Scammells, P.J.; Scott, J.L.; Singer, R.D. Austr. J. Chem. 2005, 58, 155.
118. For a discussion of physical properties, see Ludwig, R.; Kragl, U. Angew. Chem. Int. Ed. 2007, 46, 6582.
119. Hardacre, C.; Holbrey, J.D.; Nieuwenhuyzen, M.; Youngs, T.G.A. Acc. Chem. Res. 2007, 40, 1146; Greaves, T.L.; Drummond, C.J. Chem. Rev. 2008, 108, 206. See also Lungwitz, R.; Strehmel, V.; Spange, S. New J. Chem. 2010, 34, 1135.
120. Wasserscheid, P.; Keim, W. Angew. Chem. Int. Ed. 2000, 39, 3772; Earle, M.J.; Seddon, K.R. Pure. Appl. Chem. 2000, 72, 1391; Ionic Liquids in Synthesis, Wasserscheid, P.; Welton, T.; Wiley–VCH, NY, 2002; Chemistry in Alternative Reaction Media, Adams, D.J.; Dyson, P.J.; Taverner, S.J.; Wiley, 2003. For a discussion of the solvating ability, see Chiappe, C.; Malvaldi, M.; Pomelli, C.S. Pure Appl. Chem. 2009, 81, 767.
121. Rogers, R.D.; Voth, G.A. Acc. Chem. Res. 2007, 40,1077;
122. Dupont, J.; Consorti, C.S.; Suarez, P.A.Z.; de Souza, R.F. Org. Synth. Coll. Vol. X, 184.
123. For discussion of HBuIM and DiBuIm, see Harlow, K.J.; Hill, A.F.; Welton, T. Synthesis 1996, 697; Holbrey, J.D.; Seddon, K.R. J. Chem. Soc., Dalton Trans. 1999, 2133; Larsen, A.S.; Holbrey, J.D.; Tham, F.S.; Reed, C.A. J. Am. Chem. Soc. 2000, 122, 7264.
124. Jaegar, D.A.; Tucker, C.E. Tetrahedron Lett. 1989, 30, 1785.
125. Handy, S.T.; Okello, M. J. Org. Chem. 2005, 70, 1915.
126. For a discussion of the reactivity of ionic liquids, see Chowdhury, S.; Mohan, R.S.; Scott, J.L. Tetrahedron 2007, 63, 2363.
127. See Xiao, Y.; Malhotra, S.V. Tetrahedron Lett. 2004, 45, 8339.
128. Fukumoto, K.; Yoshizawa, M.; Ohno, H. J. Am. Chem. Soc. 2005, 127, 2398. Also see Chen, X.; Li, X.; Hu, A.; Wang, F. Tetrahedron Asymmetry 2008, 19, 1.
129. Martins, M.A.P.; Frizzo, C.P.; Moreira, D.N.; Zanatta, N.; Bonacorso, H.G. Chem. Rev. 2008, 108, 2015.
130. See Toma, Š.; Me
iarová. M.; Šebesta, R. Eur. J. Org. Chem. 2009, 321.
131. Handy, S.T.; Okello, M.; Dickenson, G. Org. Lett. 2003, 5, 2513.
132. Calò, V.; Nacci, A.; Monopoli, A. Eur. J. Org. Chem. 2006, 3791.
133. Yadav, J.S.; Reddy, B.V.S.; Basak, A.K.; Narsaiah, A.V. Tetrahedron 2004, 60, 2131.
134. Branco, L.C.; Afonso, C.A.M. J. Org. Chem. 2004, 69, 4381.
135. Nobuoka, K.; Kitaoka, S.; Kunimitsu, K.; Iio, M.; Harran, T.; Wakisaka, A.; Ishikawa, Y. J. Org. Chem. 2005, 70, 10106.
136. Pârvulescu, V.I.; Hardacre, C. Chem. Rev. 2007, 107, 2615.
137. Baudequin, C.; Brégeon, D.; Levillain, J.; Guillen, F.; Plaquevent, J.-C.; Gaumont, A.C. Tetrahedron Asymmetry 2005, 16, 3921; Pernak, J.; Feder-Kubis, J. Tetrahedron Asymmetry 2006, 17, 1728; Luo, S.-P.; Xu, D.-Q.; Yue, H.-D.; Wang, L.-P.; Yang, W.-L.; Xu, Z.-Y. Tetrahedron Asymmetry 2006, 17, 2028.
138. See Leadbeater, N.E.; Torenius, H.M. J. Org. Chem. 2002, 67, 3145.
139. For studies to expand the polarity range of ionic solvents see Dzyuba, S.V.; Bartsch, R.A. Tetrahedron Lett. 2002, 43, 4657. See Ionic Liquids: From Knowledge to Application, Plechkova, N.V.; Rogers, R.D.; Seddon, K.R. (Eds.), American Chemical Society, Washington, DC (distributed by Oxford University Press), 2010.
140. MacFarlane, D.R.; Pringle, J.M.; Johansson, K.M.; Forsyth, S.A.; Forsyth, M. Chem. Commun. 2006, 1905.
141. Hajipour, A.R.; Rafiee, F. Org. Prep. Proceed. Int. 2010, 42, 285.
142. Kidwai, M. Pure Appl. Chem. 2001, 73, 147.
143. Cave, G.W.V.; Raston, C.L.; Scott, J.L. Chem. Commun. 2001, 2159; Toda, F.; Tanaka, K. Chem. Rev. 2000, 100, 1025.
144. Raston, C.L. Chemistry in Australia 2004, 10.
145. Toda, F.; Tanaka, K.; Hamai, K. J. Chem. Soc., Perkin Trans. 1 1990, 3207.