Chapter 11. Word Embeddings

Word embeddings are part of distributional semantics, similar to the topic models we discussed in the previous chapter. Unlike topic models, word embeddings do not work on term-document relationships. Instead, word embeddings work with smaller contexts like sentences or subsequences of tokens in a sentence.

The field of word embeddings is a rapidly evolving set of techniques. The most popular technique, Word2vec, was developed in 2013 by Tomas Mikolov et al. at Google. Since then, there has been much research (and hype). The idea is that you use a neural network to build a language model. Once this model is learned, you can take some of the intermediate values in the network as representations of the input term.

In this chapter, we will look at the implementation of Word2vec in code. This will help give us a clear understanding of the fundamentals of this family of techniques. We will discuss the more recent approaches at a higher level because they can be quite resource intensive.

Word2vec

One of the ideas behind deep learning is that the hidden layers are “higher level” representations of the data. This comes from analysis of the visual cortex. As the information travels from the eye through the brain, neurons appear to be associated with more complex shapes. The early layers of neurons recognize only points of light and dark, later neurons recognize lines and curves, and so on. Using this assumption, if we train a language model using a neural network, the hidden layers will be a “higher level” representation of the words.

There are two ways that Word2vec is commonly implemented: continuous bag-of-words (CBOW) and continuous skip grams (often just skip grams). In CBOW, we build a model that tries to predict a word based on the nearby words. In the skip-gram approach, a word is used to predict the context.

In either approach, the model is trained using a neural network with one hidden layer. Let’s say we want to represent words as K dimensional vectors, and let’s say we have N words in our vocabulary. The weights we learn will become the vectors. The intuition behind this is based on how neural networks function. A neural network learns higher-level representations of input features. These higher-level representations are the intermediate values produced in evaluating a neural-network model. In classic CBOW, the vectors that are fed into the hidden layer are these higher-level features. This means that we can simply take the rows of the first weight matrix as our word vectors. Let’s implement CBOW, so we can get a clearer understanding.

First, let’s define our imports and load our data.

import sparknlp
from nltk.corpus import brown

spark = sparknlp.start()

def detokenize(sentence):
    text = ''
    for token in sentence:
        if text and any(c.isalnum() for c in token):
            text += ' '
        text += token
    return text
texts = []

for fid in brown.fileids():
    text = [detokenize(s) for s in brown.sents(fid)]
    text = ' '.join(text)
    texts.append((text,))
    
texts = spark.createDataFrame(texts, ['text'])

Now that we have our data, let’s process and prepare it for building our model.

from pyspark.ml import Pipeline

from sparknlp import DocumentAssembler, Finisher
from sparknlp.annotator import *

assembler = DocumentAssembler()\
    .setInputCol('text')\
    .setOutputCol('document')
sentence = SentenceDetector() \
    .setInputCols(["document"]) \
    .setOutputCol("sentences") \
    .setExplodeSentences(True)
tokenizer = Tokenizer()\
    .setInputCols(['sentences'])\
    .setOutputCol('token')
normalizer = Normalizer()\
    .setCleanupPatterns([
        '[^a-zA-Z.-]+', 
        '^[^a-zA-Z]+', 
        '[^a-zA-Z]+$',
    ])\
    .setInputCols(['token'])\
    .setOutputCol('normalized')\
    .setLowercase(True)
finisher = Finisher()\
    .setInputCols(['normalized'])\
    .setOutputCols(['normalized'])\
    .setOutputAsArray(True)

pipeline = Pipeline().setStages([
    assembler, sentence, tokenizer, 
    normalizer, finisher
]).fit(texts)

sentences = pipeline.transform(texts)
sentences = sentences.select('normalized').collect()
sentences = [r['normalized'] for r in sentences]

print(len(sentences)) # number of sentences

59091

Now we have performed the text processing, so let’s build our encoding. There are tools to do this in most deep learning libraries, but let’s do it ourselves.

from collections import Counter
import numpy as np
import pandas as pd
UNK = '???'
PAD = '###'
w2i = {PAD: 0, UNK: 1}
df = Counter()

for s in sentences:
    df.update(s)

df = pd.Series(df)
df = df[df > 10].sort_values(ascending=False)

for word in df.index:
    w2i[word] = len(w2i)
    

i2w = {ix: w for w, ix in w2i.items()}
vocab_size = len(i2w)

print(vocab_size)
7814

We include a marker for padding and a marker for unknown words. We will be tiling over our sentences, creating windows of tokens. The middle token is what we are trying to predict, and the surrounding tokens are our context. We need to pad our sentences, otherwise we will lose words at the beginning and ending of the sentences.

Let’s also make some utility functions that will convert a sequence of tokens to a sequence of indices, and one that does the inverse.

def texts_to_sequences(texts):
    return [[w2i.get(w, w2i[UNK]) for w in s] for s in texts]

def sequences_to_texts(seqs):
    return [' '.join([i2w.get(ix, UNK) for ix in s]) for s in seqs]

seqs = texts_to_sequences(sentences)

Now let’s build our context windows. We will go over each sentence and create a window for each token in the sentence.

w = 4
windows = []
Y = []

for k, seq in enumerate(seqs):
    for i in range(len(seq)):
        if seq[i] == w2i[UNK] or len(seq) < 2*w:
            continue
        window = []
        for j in range(-w, w+1):
            if i+j < 0:
                window.append(w2i[PAD])
            elif i+j >= len(seq):
                window.append(w2i[PAD])
            else:
                window.append(seq[i+j])
        windows.append(window)
        
windows = np.array(windows)

We can’t just turn all of our data into vectors because that would take up too much memory. So we will need to implement a generator. First, let’s write the function that will turn a collection of windows into numpy arrays. This will take the windows and produce a matrix containing the one-hot–encoded words and a matrix containing the one-hot–encoded target words.

def windows_to_batch(batch_windows):
    w = batch_windows.shape[1] // 2
    X = []
    Y = []
    for window in batch_windows:
        X.append(np.concatenate((window[:w], window[w+1:])))
        Y.append(window[w])
        
    X = np.array(X)
    Y = ku.to_categorical(Y, vocab_size)
    return X, Y

Now we write the function that actually produces the generator. The training method takes a Python generator, so we need a utility function that creates a generator of batches.

def generate_batch(windows, batch_size=100):
    while True:
        indices = np.arange(windows.shape[0])
        indices = np.random.choice(indices, batch_size)
        batch_windows = windows[indices, :]
        yield windows_to_batch(batch_windows)

Now we can implement our model. Let’s define our model. We will be creating 50-dimension word vectors. The number of dimensions should be based on the size of your corpus. However, there is no hard-and-fast rule.

from keras.models import Sequential
from keras.layers import *
import keras.backend as K
import keras.utils as ku
dim = 50

model = Sequential()
model.add(Embedding(vocab_size, dim, input_length=w*2))
model.add(Lambda(lambda x: K.mean(x, axis=1), (dim,)))
model.add(Dense(vocab_size, activation='softmax'))

The first layer is the actual embeddings we will be learning. The second layer collapses the context into a single vector. The last layer makes the prediction of what the word in the middle of the window should be.

print(model.summary())
Model: "sequential_2"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
embedding_2 (Embedding)      (None, 8, 50)             390700    
_________________________________________________________________
lambda_2 (Lambda)            (None, 50)                0         
_________________________________________________________________
dense_2 (Dense)              (None, 7814)              398514    
=================================================================
Total params: 789,214
Trainable params: 789,214
Non-trainable params: 0
_________________________________________________________________
None
model.compile(loss='categorical_crossentropy', optimizer='adam')

This is a relatively simple Word2vec model, yet we still need to learn more than 700,000 parameters. Word embeddings models get complicated quickly.

Let’s store the weights for every 50 epochs. We make 50 calls to the generator for each epoch.

batch_size = 1000
steps = 100
generator = generate_batch(windows, batch_size)

mc = ModelCheckpoint('weights{epoch:05d}.h5', 
                     save_weights_only=True, 
                     period=50)

model.fit_generator(generator, steps_per_epoch=steps, 
                    epochs=500, callbacks=[mc])

Now let’s look at the data. First, let’s implement a class to represent the embeddings data. We will be using cosine similarity to compare vectors.

class Word2VecData(object):
    def __init__(self, word_vectors, w2i, i2w):
        self.word_vectors = word_vectors
        self.w2i = w2i
        self.i2w = i2w
        ## the implementation of cosine similarity uses the 
        ## normalized vectors. This means that we can precalculate
        ## the vectors of our vocabulary
        self.normed_wv = np.divide(
            word_vectors.T, 
            np.linalg.norm(word_vectors, axis=1)
        ).T
        self.all_sims = np.dot(self.normed_wv, self.normed_wv.T)
        self.all_sims = np.triu(self.all_sims)
        self.all_sims = self.all_sims[self.all_sims > 0]
        
    ## this transforms a word into a vector
    def w2v(self, word):
        return self.word_vectors[self.w2i[word],:]

    ## this calculates cosine similarity of the input word to all words
    def _get_sims(self, word):
        if isinstance(word, str):
            v = self.w2v(word)
        else:
            v = word
        v = np.divide(v, np.linalg.norm(v))
        return np.dot(self.normed_wv, v)

    def nearest_words(self, word, k=10):
        sims = self._get_sims(word)
        nearest = sims.argsort()[-k:][::-1]
        ret = []
        for ix in nearest:
            ret.append((self.i2w[ix], sims[ix]))
        return ret

    def compare_words(self, u, v):
        if isinstance(u, str):
            u = self.w2v(u)
        if isinstance(v, str):
            v = self.w2v(v)
        u = np.divide(u, np.linalg.norm(u))
        v = np.divide(v, np.linalg.norm(v))
        return np.dot(u, v)

Let’s also implement something to output the results. We want to look at a couple things when looking at Word2vec. We want to find what words are similar to other words. If the model has learned information about the words, you should see related words.

There are also word analogies. One of the interesting uses of Word2vec was a word “algebra.” The common example is king – man + woman ~ queen. This means that you subtract the man vector from the king vector, then add the woman vector. The result is approximately the queen vector. This generally works well only with a large diverse vocabulary. Our vocabulary is more limited because our data set is small.

Let’s plot the histogram of all word-to-word similarities.

import matplotlib.pyplot as plt
%matplotlib inline
def display_Word2vec(model, weight_path, words, analogies):
    model.load_weights(weight_path)
    word_vectors = model.layers[0].get_weights()[0]
    W2V = Word2VecData(word_vectors, w2i, i2w)

    for word in words:
        for w, sim in W2V.nearest_words(word):
            print(w, sim)
        print()
        
    for w1, w2, w3, w4 in analogies:
        v1 = W2V.w2v(w1)
        v2 = W2V.w2v(w2)
        v3 = W2V.w2v(w3)
        v4 = W2V.w2v(w4)
        x = v1 - v2 + v3
        for w, sim in W2V.nearest_words(x):
            print(w, sim)
        print()
        print(w4, W2V.compare_words(x, v4))
        print()
        print('{}-{}+{}~{} quantile'.format(w1, w2, w3, w4), 
              (W2V.all_sims < W2V.compare_words(x, v4)).mean())
        print()

    plt.hist(W2V.all_sims)
    plt.title('Word-to-Word similarity histogram')
    
    plt.show()

Let’s look at the results from the 50th epoch. First, let’s look at the words similar to “space.” This is a list of the nearest 10 words to “space” by cosine similarity.

space 0.9999999
shear 0.96719706
section 0.9615698
chapter 0.9592927
output 0.958699
phase 0.9580841
corporate 0.95798546
points 0.9575049
density 0.9573466
institute 0.9545017

Now let’s look at the words similar to “polynomial.”

polynomial 1.0000001
formula 0.9805055
factor 0.9684353
positive 0.96643007
produces 0.9631797
remarkably 0.96068406
equation 0.9601216
assumption 0.95971704
moral 0.9586859
unique 0.95754766

Now let’s look at the king – man + woman ~ queen analogy. We will print out the words closest to the result vector, king – man + woman. Then we can look at the similarity of the result to the queen vector. Finally, let’s look at what the quantile is for queen. The higher it is, the better the analogy works.

mountains 0.96987706
emperor 0.96913254
crowds 0.9688335
generals 0.9669207
masters 0.9664976
kings 0.9663711
roof 0.9653381
ceiling 0.96467453
ridge 0.96467185
woods 0.96466273

queen 0.9404894

king-man+woman~queen quantile 0.942

That the queen vector is closer than 94% of other words is a good sign, but that some of the other top results, like “ceiling,” are so close is a sign that our data set may be too small and perhaps too specialized to learn such general relationships.

Finally, let’s look at the histogram, as shown in Figure 11-1.

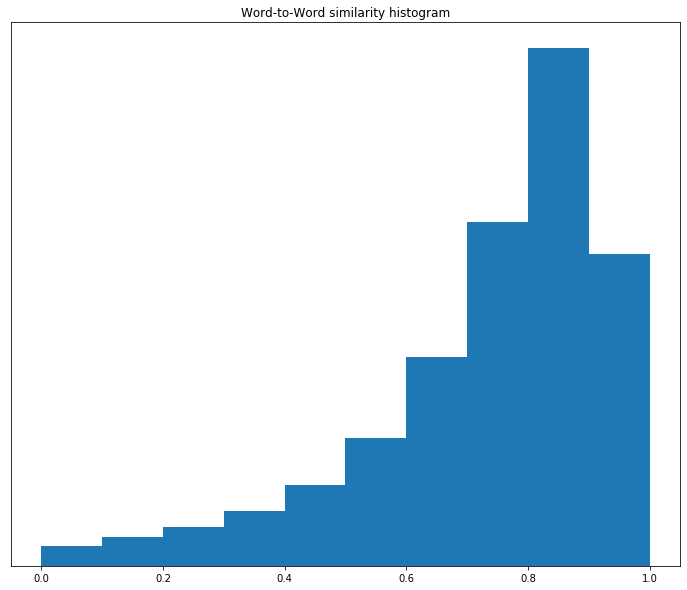
Figure 11-1. Histogram of word-to-word similarities at epoch 50

Most of the similarities are on the high side. This means that at epoch 50 the words are quite similar. Let’s look at the histogram at epoch 100, as shown in Figure 11-2.

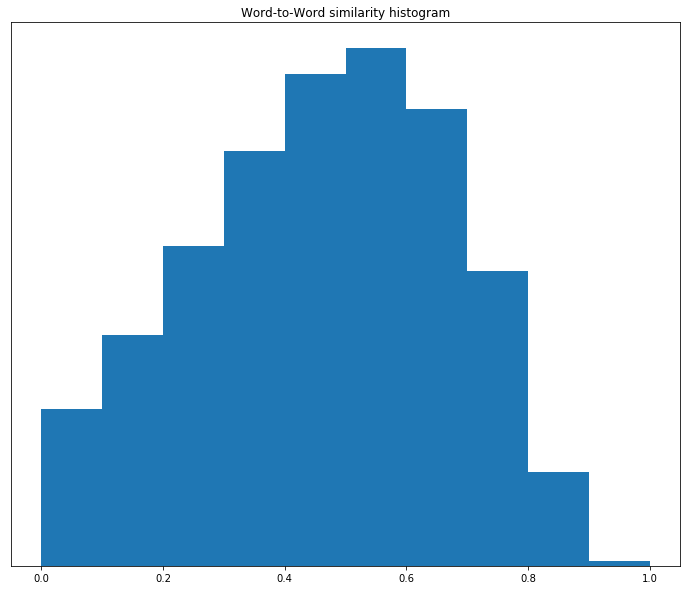
Figure 11-2. Histogram of word-to-word similarities at epoch 100

The weight of the histogram has moved toward the middle. This means that we are seeing more differentiation between our words. Now let’s look at 500 epochs, as shown in Figure 11-3.

Note how the mass of the histogram has moved to the left, so most words are dissimilar to each other. This means that the words are more separated in the word-vector space. But remember that this may mean that we are overfitting to this data set.

Spark NLP lets us incorporate externally trained Word2vec models. Let’s see how we can use these word embeddings in Spark NLP. First, let’s write the embeddings to a file in a format that Spark NLP is familiar with.

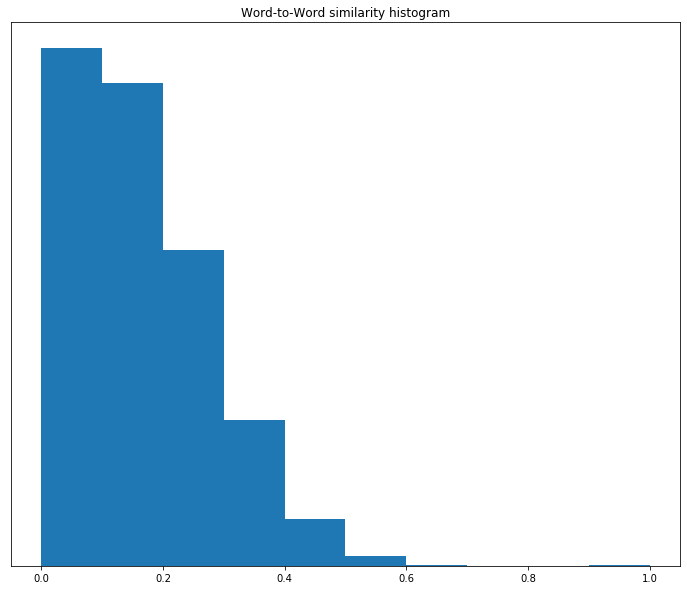
Figure 11-3. Histogram of word-to-word similarities at epoch 500
model.load_weights('weights00500.h5')
word_vectors = model.layers[0].get_weights()[0]

with open('cbow.csv', 'w') as out:
    for ix in range(vocab_size):
        word = i2w[ix]
        vec = list(word_vectors[ix, :])
        line = ['{}'] + ['{:.18e}'] * dim
        line = ' '.join(line) + '\n'
        line = line.format(word, *vec)
        out.write(line)

Now we can create an embeddings annotator.

Word2vec = WordEmbeddings() \
    .setInputCols(['document', 'normalized']) \
    .setOutputCol('embeddings') \
    .setDimension(dim) \
    .setStoragePath('cbow.csv', 'TEXT')

pipeline = Pipeline().setStages([
    assembler, sentence, tokenizer, 
    normalizer, Word2vec
]).fit(texts)

Let’s get out the embeddings generated by our model.

pipeline.transform(texts).select('embeddings.embeddings') \
    .first()['embeddings']

[[0.6336007118225098,
  0.7607026696205139,
  1.1777857542037964,
  ...]]

Spark has an implementation of the skip-gram approach. Let’s look at how to use that.

from pyspark.ml.feature import Word2Vec
Word2vec = Word2Vec() \
    .setInputCol('normalized') \
    .setOutputCol('word_vectors') \
    .setVectorSize(dim) \
    .setMinCount(5)
finisher = Finisher()\
    .setInputCols(['normalized'])\
    .setOutputCols(['normalized'])\
    .setOutputAsArray(True)

pipeline = Pipeline().setStages([
    assembler, sentence, tokenizer, 
    normalizer, finisher, Word2vec
]).fit(texts)

pipeline.transform(texts).select('word_vectors') \
    .first()['word_vectors']
DenseVector([0.0433, -0.0003, 0.0281, 0.0791, ...])

Transformers

In 2017, researchers at Google created a new approach for modeling attention. Attention is a concept from sequence modeling. A sequence model that does not have a fixed context must learn how long to retain information from earlier in the sequence. Being able to better capture long-distance relationships is very important to automatic machine translation. Most words have multiple senses or meanings, and clarifying requires broader context. In linguistics, the property of having multiple senses is known as polysemy or homonymy.

Polysemy is when the senses are different but related, and homonymy is when the senses are not related in meaning. For example, let’s look at the word “rock.” When used as a noun, “rock” means a piece of stone. This is completely unrelated to the other meaning, the verb “to rock.” The verb “to rock” refers to a back-and-forth motion, and it can also mean to perform or enjoy rock-and-roll music. So “rock” (a stone) is a homonym of “rock” (to move back and forth), which is polyseme that also has the meaning to perform or enjoy rock-and-roll music.

Cues to disambiguate homonyms and polysemes generally come from other words in the context. The example given in the paper defines the Transformer (Vaswani et al.) as a “bank,” which has two meanings. The first is a financial institution, and the second is the edge of a river. This homonymous relationship does not translate. For example, in Spanish, the institution is “banco,” and the edge of a river is “orilla.” So if you are translating, using a neural network, it would be advantageous to represent the two words differently. To do this, you must encode your words with their context.

The word vectors of previous methods represent aggregations of these different senses. This allows a much richer representation of the text. However, it comes at a severe cost. These models are computationally much more intense to train and use. In fact, most of the current methods, at the time of writing in 2019, are not feasible without using GPUs or even more specialized hardware.

ELMo, BERT, and XLNet

Newer embedding techniques are based on the idea of representing words in a context-dependent way. This means that a full neural-network model is needed to use the embeddings, unlike in static embeddings where there is simply a lookup.

Embeddings from language models (ELMo) is a model that was developed at the Allen Institute in 2018. The language model that is being learned is bidirectional. This means that the model is learning to predict a word based on the words that come both before it and after it. The model learns at the character level, but the embeddings themselves are actually word based.

Bidirectional Encoder Representations from Transformers (BERT), published in 2018, is doing something very similar to ELMo, but it is using Google’s Transformers—hence the name. The intent is that this model can be fine-tuned. This is done by building a generic pretrained model on a data set. There are other approaches that allow fine-tuning, but the authors of the BERT paper note that those are either unidirectional approaches, or more specialized bidirectional approaches. BERT is intended to solve the problem of needing to choose by building a model that tries to identify randomly masked words.

BERT became very popular by achieving high scores on a number of benchmarks. Roughly a year later, XLNet was published. XLNet was built to learn a model without the masking needed by BERT. The idea is that the masking is creating discrepancies between what the BERT model sees at training time and what it sees at time of use. XLNet then went on to achieve yet higher benchmarks.

Let’s look at how to use BERT embeddings in Spark NLP.

bert = BertEmbeddings.pretrained() \
      .setInputCols(["sentences", "normalized"]) \
      .setOutputCol("bert")

pipeline = Pipeline().setStages([
    assembler, sentence, tokenizer, 
    normalizer, bert
]).fit(texts)

pipeline.transform(texts).select('bert.embeddings') \
    .first()['embeddings']
[[-0.43669646978378296,
  0.5360171794891357,
  -0.051413312554359436,
  ...]]

A caveat to those interested in these techniques: one must always return to first principles when evaluating such new and complicated approaches. First, always consider what your product actually needs. Is your product similar to one of the tasks for which the BERT and XLNet achieved high scores? What is the level of accuracy you need versus the amount you are willing to spend on developer time, training time, and hardware? Just because these techniques are very popular with people in the field of NLP does not mean they are the best for every application.

In fact, there is the possibility that these techniques can overfit in difficult-to-detect ways. Researchers at the National Cheng Kung University in Taiwan created an adversarial data set for a question-and-answer task called Argument Reasoning Comprehension Task. Here, a model must take in a piece of text that makes some arguments and draw a conclusion. BERT was able to achieve scores higher than human scores on this task. The researchers modified the data set with examples that were contradictory. The BERT model was evaluated on this new adversarial data set, and it performed worse than humans and little better than models built with older, simpler techniques. A model should be able to make a conclusion based solely on the input text; that is, it should not be using statements in other examples.

doc2vec

Doc2vec is the set of techniques that lets us turn a document into a vector. Often, we want to use embeddings as sparser features for other tasks, like classification. How can we combine these word-level features into document-level features? One common way is to simply average the word-level vectors. This makes intuitive sense because we are hoping that the vector space represents a vague idea of meaning. So if we average all the vectors in a document, we should get the “average” meaning of the document.

The problem with this approach comes in when we consider rarity of words. Recalling our conversation on TF.IDF, it is often the case that unimportant words have a high frequency. For example, consider a clinical note. We may find a large number of generic words that are common to all notes. This can present a problem because these words will pull all of our documents toward a small number of places in our vector space. A model could still separate them, but it will converge more slowly. Worse yet, if there are natural clusters within the corpus, in other words, clinical notes from different departments, we may have a number of tightly packed clusters of documents. What we want is to be able to characterize a document by the words that are most important to that unique document. There are a few approaches for doing this.

You can perform weighted averaging on the word vectors by using IDF values as weights. This will help reduce the effect that more common words have on the document vector. This approach has the benefit of being simple to implement. Indeed, if you are using a static embedding technique, you can simply scale the vectors by the IDF values. There will be no need to compute this at evaluation time. The downside is that this is a bag-of-words approach and does not take into account the relationships between words.

Another approach is called distributed memory paragraph vectors. This is essentially CBOW, but with an additional set of weights that needs to be learned. In CBOW, we are predicting a word from its context, so we have vectors representing the context as input. For distributed memory paragraph vectors, we concatenate a one-hot encoding of our document IDs to input. This allows us to represent the document with the same dimension as the words.

A third approach to doc2vec parallels the skip-gram approach, distributed bag-of-words paragraph vectors. Recall that skip grams predict the context from a word. In distributed bag-of-words paragraph vectors, you learn to predict a context of the document from its document ID.

These last two approaches have the benefit of learning the relationships between co-occurring words. They are also relatively straightforward to implement if you can implement Word2vec. Their downside is that they learn only documents you have on hand. If you get a new document, you will not be able to produce a vector for it. So these approaches can be used only on offline processes.

When talking about doc2vec, also sometimes known as paragraph2vec, it’s important to keep in mind that it can be applied to different sizes of text, from phrases to whole documents. However, if you are interested in converting phrases to vectors, you may also want to consider incorporating this into your tokenization. You can produce phrases as tokens and then learn one of the word-level embeddings discussed previously.

Exercises

Let’s see how these techniques work on our classification problem from Chapter 9.

This time, writing code is up to you. Try Spark’s skip-gram implementation, Spark NLP’s pretrained GloVe model, and Spark NLP’s BERT model.