“George, I really like doing things backward. Can we do differentiation backward?”
“Sure we can, Lenny. It’s called integration.”
Differential calculus has to do with rates of change. Integral calculus has to do with sums of many tiny incremental quantities. It’s not immediately obvious that these have anything to do with each other, but they do.
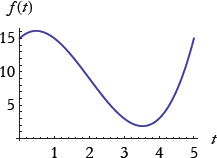
We begin with the graph of a function f(t), as in Figure 1.

Figure 1: The behavior of f(t).
The central problem of integral calculus is to calculate the area under the curve defined by f(t). To make the problem well defined, we consider the function between two values that we call limits of integration, t = a and t = b. The area we want to calculate is the area of the shaded region in Figure 2.
Figure 2: The limits of integration.
In order to do this, we break the region into very thin rectangles and add their areas (see Figure 3).
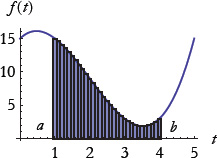
Figure 3: An illustration of integration.
Of course this involves an approximation, but it becomes accurate if we let the width of the rectangles tend to zero. In order to carry out this procedure, we first divide the interval between t = a and t = b into a number, N, of subintervals—each of width Δ t. Consider the rectangle located at a specific value of t. The width is Δ t and the height is the local value of f(t). It follows that the area of a single rectangle, δ A, is

Now we add up all the areas of the individual rectangles to get an approximation to the area that we are seeking. The approximate answer is
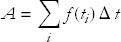
where the uppercase greek letter sigma, Σ, indicates a sum of successive values defined by i. So, if N = 3, then
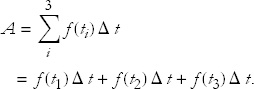
Here ti is the position of the ith rectangle along the t axis.
To get the exact answer, we take the limit in which Δ t shrinks to zero and the number of rectangles increases to infinity. That defines the definite integral of f(t) between the limits t = a and t = b. We write this as
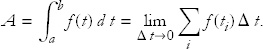
The integral sign, called summa, ∫, replaces the summation sign, and—as in differential calculus—Δ t is replaced by d t. The function f(t) is called the integrand.
Let’s make a notational change and call one of the limits of integration T. In particular, replace b by T and consider the integral
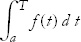
where we are going to think of T as a variable instead of as a definite value of t. In this case, this integral defines a function of T, which can take on any value of t. The integral is a function of T because it has a definite value for each value of T.

Thus a given function f(t) defines a second function F(T). We could also let a vary, but we won’t. The function F(T) is called the indefinite integral of f(t). It is indefinite because instead of integrating from a fixed value to a fixed value, we integrate to a variable. We usually write such an integral without limits of integration,
|
(1) |
The fundamental theorem of calculus is one of the simplest and most beautiful results in mathematics. It asserts a deep connection between integrals and derivatives. What it says is that if F(T) = ∫ f(t) d t, then
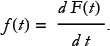
To see this, consider a small incremental change in T from T to T + Δ t. Then we have a new integral,
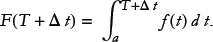
In other words, we have added one more rectangle of width Δ t at t = T to the area shaded in Figure 3. In fact, the difference F(T + Δ t) − F(T) is just the area of that extra rectangle, which happens to be f(T) Δ t, so
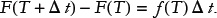

we obtain the fundamental theorem connecting F and f, when we take the limit where Δ t → 0:

We can simplify the notation by ignoring the difference between t and T,
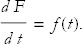
In other words, the processes of integration and differentiation are reciprocal: The derivative of the integral is the original integrand.
Can we completely determine F(t) knowing that its derivative is f(t)? Almost, but not quite. The problem is that adding a constant to F(t) does not change its derivative. Given f(t), its indefinite integral is ambiguous, but only up to adding a constant.
To see how the fundamental theorem is used, let’s work out some indefinite integrals. Let’s find the integral of a power f(t) = tn. Consider,
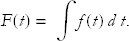
It follows that
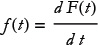
or
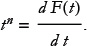
All we need to do is find a function F whose derivative is tn, and that is easy.
In the last chapter we found that for any m,
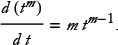
If we substitute m = n + 1, this becomes
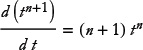
or, dividing by n + 1,
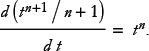
Thus we find that tn is the derivative of 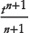 . Substituting the relevant values, we get
. Substituting the relevant values, we get

The only thing missing is the ambiguous constant that we can add to F. We should write

where c is a constant that has to be determined by other means.
The ambiguous constant is closely related to the ambiguity in choosing the other endpoint of integration that we earlier called a. To see how a determines the ambiguous constant c, let’s consider the integral
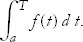
in the limit where the two limits of integration come together—that is, T = a. In this case, the integral has to be zero. You can use that fact to determine c.
In general, the fundamental theorem of calculus is written
|
|
(2) |
Another way to express the fundamental theorem is by a single equation:
|
(3) |
In other words, integrating a derivative gives back the original function (up to the usual ambiguous constant). Integration and differentiation undo each other.
Here are some integration formulas:
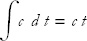
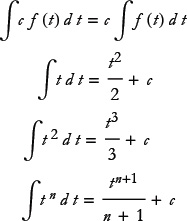
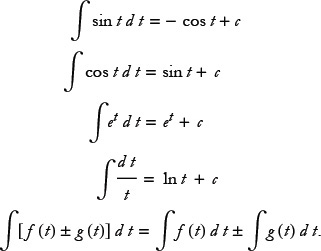
Exercise 1: Determine the indefinite integral of each of the following expressions by reversing the process of differentiation and adding a constant.
Exercise 2: Use the fundamental theorem of calculus to evaluate each integral from Exercise 1 with limits of integration being t = 0 to t = T.
Exercise 3: Treat the expressions from Exercise 1 as expressions for the acceleration of a particle. Integrate them once, with respect to time, and determine the velocities, and a second time to determine the trajectories. Because we will use t as one of the limits of integration we will adopt the dummy integration variable t'. Integrate them from t' = 0 to t' = t.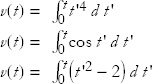
There are some tricks to doing integrals. One trick is to look them up in a table of integrals. Another is to learn to use Mathematica. But if you’re on your own and you don’t recognize the integral, the oldest trick in the book is integration by parts. It’s just the reverse of using the product rule for differentiation. Recall from Lecture 2 that to differentiate a function, which itself is a product of two functions, you use the following rule:
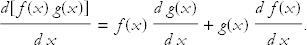
Now let’s integrate both sides of this equation between limits a and b.
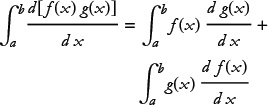
The left side of the equation is easy. The integral of a derivative (the derivative of f g) is just the function itself. The left side is
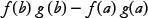
which we often write in the form
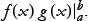
Now let’s subtract one of the two integrals on the right side and shift it to the left side.
|
(4) |
Suppose we have some integral that we don’t recognize, but we notice that the integrand happens to be a product of a function f(x) and the derivative of another function g(x). In other words, after some inspection, we see that the integral has the form of the right side of Eq. (4), but we don’t know how to do it. Sometimes we are lucky and recognize the integral on the left side of the equation.
Let’s do an example. Suppose the integral that we want to do is
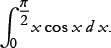
That’s not in our list of integrals. But notice that
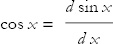
so the integral is
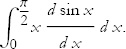
Equation (4) tells us that this integral is equal to
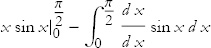
or just
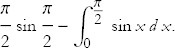
Now it’s easy. The integral ∫ sin x d x is on our list: it’s just –cos x. I’ll leave the rest to you.
Exercise 4: Finish evaluating 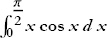 .
.
You might wonder how often this trick works. The answer is quite often, but certainly not always. Good luck.