10
First Draft of a Report on the EDVAC (1945)
John von Neumann
The so-called “von Neumann architecture” described but not named in this report has the logical structure of the “universal computing machine” described by Turing (1936, here chapter 6), though the similarity seems to be something of a coincidence (see page xviii). The same memory that holds the data on which a program operates holds the program itself (pages 94, 104). Alan Turing cites this report but not his own theoretical work in his plan for an Automatic Calculating Engine (Turing, 1945).
In 1944 Arthur Burks (1915–2008) and Herman Goldstine (1913–2004) were two members of the team led by Presper Eckert and John Mauchly designing an electronic computer known as the EDVAC at the Moore School of the University of Pennsylvania—the successor to the Eckert–Mauchly ENIAC that was already grinding out ballistics calculations for the U.S. Army. After Goldstine happened to meet the eminent mathematician John von Neumann (1903–1957) and told him about the EDVAC project, von Neumann joined the group. John von Neumann wrote up the design in this memo, which Goldstine typed and released in 1945, listing only von Neumann as author. That was regrettable: the document was von Neumann’s, but the design was the group’s, and the stored program was already part of the ENIAC (though in that machine, the program resided in read-only memory).
Figure 10.1 shows the cover page of the typescript, which is very rough. Where possible, we have supplied section cross-references that in the original were left to be filled in later. A revised report (Burks et al., 1947) was issued in 1946 under the name “Preliminary discussion of the logical design of an electronic computing instrument,” adding Goldstine and Burks as co-authors.
Figure 10.1: Title page of “First draft” typescript
These reports set the direction for computer design that would eventually make the software industry possible, since programs could be processed and loaded into memory like any other kind of data. The reports analyze the device into memory and control units (“organs”) using binary notation, and the later “Preliminary discussion” adds explanations of memory addresses (“location-numbers”), registers of various kinds, floating-point representation, and use of the first six letters of the Roman alphabet as hexadecimal digits. But in the short run, the reports’ failure to acknowledge the contributions of others caused resentment among the founding members of the design team—in particular Mauchly, who had authored the proposal under which the EDVAC and its predecessor machine the ENIAC had been funded and designed. After the war, Mauchly and Eckert broke off to start a computer business, in 1947 filing patents that were ultimately invalidated because of the prior release of this report. (The subsequent history of the Eckert–Mauchly Computer Corporation is sketched on page 169.) Burks and Goldstine pursued academic careers, joining von Neumann at Princeton.
By the time von Neumann joined the EDVAC team, he was already one of the most accomplished mathematicians in the world, having made contributions to a great variety of mathematical fields, to mathematical economics, and to quantum mechanics. Born and educated in Hungary, he moved to Berlin in 1930 to be part of the circle surrounding David Hilbert (see chapter 5). He emigrated to the US before the outbreak of the Second World War and was an important contributor to the Manhattan Project, which designed the atomic bomb. He witnessed the work of hundreds of human “computers” using individual mechanical calculators to solve the equations he had worked out in the design of a fission bomb, and though he could not discuss that classified work with the groups he worked with at the Moore School or at Princeton, it provided motivation for his work developing high-speed automatic computers.
Some of the terminology of the “First draft” is confusingly implementation-specific. The memory was in the form of a delay line, organized in what we would today call 32-bit words—von Neumann called them “minor cycles.” One of the 32 bits was a flag to indicate whether the word represented a number or an instruction (“order”). Numbers used another bit for the sign, with the remaining bits representing a binary fraction between − 1 and 1. 32 minor cycles constituted a “major cycle” or delay line organ (DLA). The full memory comprised 256 DLAs, so to specify, for example, the address of a number in memory required 8 bits to identify the DLA and 5 more bits to single out the minor cycle.
To achieve a level of design abstraction, the “First draft” posits a bistable “element” that might have a variety of physical realizations. In §10.4.2, von Neumann cites McCulloch and Pitts at some length, but he does not mention Turing. In an omitted section, the report goes on to note that “an element which stimulates itself will hold a stimulus indefinitely,” exactly as “A Logical Calculus” had said of neurons (page 87). And von Neumann’s use of circuitry synchronized by a clock is reminiscent of the discrete time variable McCulloch and Pitts imposed on neuronal circuits to subject their behavior to logical analysis. In fact the analogy between a vacuum tube and a neuron is not heavily used in the design, though it was of interest to von Neumann in his speculations about the computational power of the brain, and the EDVAC’s program was stored in fast memory, rather than on cards or tape as in Aiken’s Mark I, simply so that successive instructions could be accessed at electronic speeds.
The discussion of neuronal computing in this “First draft” disappeared in the “Preliminary discussion,” but von Neumann never lost interest in the idea of the brain as a computer and was still working on it at the time of his death from cancer at age 53. The Computer and the Brain (von Neumann, 2000) was published posthumously.
10.1 Definitions
10.1.1 The considerations which follow deal with the structure of a very high speed automatic digital computing system, and in particular with its logical control. Before going into specific details, some general explanatory remarks regarding these concepts may be appropriate.
10.1.2 An automatic computing system is a (usually highly composite) device, which can carry out instructions to perform calculations of a considerable order of complexity—e.g. to solve a non-linear partial differential equation in 2 or 3 independent variables numerically.
The instructions which govern this operation must be given to the device in absolutely exhaustive detail. They include all numerical information which is required to solve the problem under consideration: Initial and boundary values of the dependent variables, values of fixed parameters (constants), tables of fixed functions which occur in the statement of the problem. These instructions must be given in some form which the device can sense: Punched into a system of punchcards or on teletype tape, magnetically impressed on steel tape or wire, photographically impressed on motion picture film, wired into one or more fixed or exchangeable plugboards—this list being by no means necessarily complete. All these procedures require the use of some code to express the logical and the algebraical definition of the problem under consideration, as well as the necessary numerical material (cf. above).
Once these instructions are given to the device, it must be able to carry them out completely and without any need for further intelligent human intervention. At the end of the required operations the device must record the results again in one of the forms referred to above. The results are numerical data; they are a specified part of the numerical material produced by the device in the process of carrying out the instructions referred to above.
10.1.3 It is worth noting, however, that the device will in general produce essentially more numerical material (in order to reach the results) than the (final) results mentioned. Thus only a fraction of its numerical output will have to be recorded as indicated in §10.1.2, the remainder will only circulate in the interior of the device, and never be recorded for human sensing. This point will receive closer consideration subsequently ….
10.1.4 The remarks of §10.1.2 on the desired automatic functioning of the device must, of course, assume that it functions faultlessly. Malfunctioning of any device has, however, always a finite probability—and for a complicated device and a long sequence of operations it may not be possible to keep this probability negligible. Any error may vitiate the entire output of the device. For the recognition and correction of such malfunctions intelligent human intervention will in general be necessary.
However, it may be possible to avoid even these phenomena to some extent. The device may recognize the most frequent malfunctions automatically, indicate their presence and location by externally visible signs, and then stop. Under certain conditions it might even carry out the necessary correction automatically and continue (cf. §10.3.3).
10.2 Main Subdivision of the System
10.2.1 In analyzing the functioning of the contemplated device, certain classificatory distinctions suggest themselves immediately.
10.2.2 First: Since the device is primarily a computer, it will have to perform the elementary operations of arithmetics most frequently. These are addition, subtraction, multiplication and division: +, −, ×, ÷. It is therefore reasonable that it should contain specialized organs for just these operations.
It must be observed, however, that while this principle as such is probably sound, the specific way in which it is realized requires close scrutiny. Even the above list of operations: +, −, ×, ÷, is not beyond doubt. It may be extended to include such operation as 
sgn, | |, also log10, log2, ln, sin and their inverses, etc. One might also consider restricting it, e.g. omitting ÷ and even ×. One might also consider more elastic arrangements. For some operations radically different procedures are conceivable, e.g. using successive approximation methods or function tables. … At any rate a central arithmetical part of the device will probably have to exist, and this constitutes the first specific part: CA.
10.2.3 Second: The logical control of the device, that is the proper sequencing of its operations, can be most efficiently carried out by a central control organ. If the device is to be elastic, that is as nearly as possible all purpose, then a distinction must be made between the specific instructions given for and defining a particular problem, and the general control organs which see to it that these instructions—no matter what they are—are carried out. The former must be stored in some way—in existing devices this is done as indicated in §10.1.2—the latter are represented by definite operating parts of the device. By the central control we mean this latter function only, and the organs which perform it form the second specific part: CC.
10.2.4 Third: Any device which is to carry out long and complicated sequences of operations (specifically of calculations) must have a considerable memory. At least the four following phases of its operation require a memory:
(a) Even in the process of carrying out a multiplication or a division, a series of intermediate (partial) results must be remembered. This applies to a lesser extent even to additions and subtractions (when a carry digit may have to be carried over several positions), and to a greater extent to 
, if these operations are wanted. …
(b) The instructions which govern a complicated problem may constitute a considerable material, particularly so, if the code is circumstantial (which it is in most arrangements). This material must be remembered.
(c) In many problems specific functions play an essential role. They are usually given in form of a table. Indeed in some cases this is the way in which they are given by experience (e.g. the equation of state of a substance in many hydrodynamical problems), in other cases they may be given by analytical expressions, but it may nevertheless be simpler and quicker to obtain their values from a fixed tabulation, than to compute them anew (on the basis of the analytical definition) whenever a value is required. It is usually convenient to have tables of a moderate number of entries only (100–200) and to use interpolation. Linear and even quadratic interpolation will not be sufficient in most cases, so it is best to count on a standard of cubic or biquadratic (or even higher order) interpolation ….
Some of the functions mentioned in the course of §10.2.2 may be handled in this way: log10, log2, ln, sin and their inverses, possibly also 
. Even the reciprocal might be treated in this manner, thereby reducing ÷ to ×.
(d) For partial differential equations the initial conditions and the boundary conditions may constitute an extensive numerical material, which must be remembered throughout a given problem.
(e) For partial differential equations of the hyperbolic or parabolic type, integrated along a variable t, the (intermediate) results belonging to the cycle t must be remembered for the calculation of the cycle t + dt. This material is much of the type (d), except that it is not put into the device by human operators, but produced (and probably subsequently again removed and replaced by the corresponding data for t + dt) by the device itself, in the course of its automatic operation.
(f) For total differential equations (d), (e) apply too, but they require smaller memory capacities. Further memory requirements of the type (d) are required in problems which depend on given constants, fixed parameters, etc.
(g) Problems which are solved by successive approximations (e.g. partial differential equations of the elliptic type, treated by relaxation methods) require a memory of the type (e): The (intermediate) results of each approximation must be remembered, while those of the next one are being computed.
(h) Sorting problems and certain statistical experiments (for which a very high speed device offers an interesting opportunity) require a memory for the material which is being treated.
10.2.5 To sum up the third remark: The device requires a considerable memory. While it appeared that various parts of this memory have to perform functions which differ somewhat in their nature and considerably in their purpose, it is nevertheless tempting to treat the entire memory as one organ, and to have its parts even as interchangeable as possible for the various functions enumerated above. This point will be considered in detail ….
At any rate the total memory constitutes the third specific part of the device: M.
10.2.6 The three specific parts CA, CC (together C) and M correspond to the associative neurons in the human nervous system. It remains to discuss the equivalents of the sensory or afferent and the motor or efferent neurons. These are the input and the output organs of the device, and we shall now consider them briefly.
In other words: All transfers of numerical (or other) information between the parts C and M of the device must be effected by the mechanisms contained in these parts. There remains, however, the necessity of getting the original definitory information from outside into the device, and also of getting the final information, the results, from the device into the outside.
By the outside we mean media of the type described in §10.1.2: Here information can be produced more or less directly by human action (typing, punching, photographing light impulses produced by keys of the same type, magnetizing metal tape or wire in some analogous manner, etc.), it can be statically stored, and finally sensed more or less directly by human organs.
The device must be endowed with the ability to maintain the input and output (sensory and motor) contact with some specific medium of this type (cf. §10.1.2): That medium will be called the outside recording medium of the device: R. Now we have:
10.2.7 Fourth: The device must have organs to transfer (numerical or other) information from R into its specific parts, C and M. These organs form its input, the fourth specific part: I. It will be seen that it is best to make all transfers from R (by I) into M, and never directly into C (cf. §10.14.1).
10.2.8 Fifth: The device must have organs to transfer (presumably only numerical information) from its specific parts C and M into R. These organs form its output, the fifth specific part: O. It will be seen that it is again best to make all transfers from M (by O) into R, and never directly from C, (cf. §10.14.1).
10.2.9 The output information, which goes into R, represents, of course, the final results of the operation of the device on the problem under consideration. These must be distinguished from the intermediate results, discussed e.g. in §10.2.4, (e)–(g), which remain inside M. At this point an important question arises: Quite apart from its attribute of more or less direct accessibility to human action and perception R has also the properties of a memory. Indeed, it is the natural medium for long time storage of all the information obtained by the automatic device on various problems. Why is it then necessary to provide for another type of memory within the device M? Could not all, or at least some functions of M—preferably those which involve great bulks of information—be taken over by R?
Inspection of the typical functions of M, as enumerated in §10.2.4, (a)–(h), shows this: It would be convenient to shift (a) (the short-duration memory required while an arithmetical operation is being carried out) outside the device, i.e. from M into R. (Actually (a) will be inside the device, but in CA rather than in M. …) All existing devices, even the existing desk computing machines, use the equivalent of M at this point. However (b) (logical instructions) might be sensed from outside, i.e. by I from R, and the same goes for (c) (function tables) and (e), (g) (intermediate results). The latter may be conveyed by O to R when the device produces them, and sensed by I from R when it needs them. The same is true to some extent of (d) (initial conditions and parameters) and possibly even of (f) (intermediate results from a total differential equation). As to (h) (sorting and statistics), the situation is somewhat ambiguous: In many cases the possibility of using M accelerates matters decisively, but suitable blending of the use of M with a longer range use of R may be feasible without serious loss of speed and increase the amount of material that can be handled considerably.
Indeed, all existing (fully or partially automatic) computing devices use R—as a stack of punchcards or a length of teletype tape—for all these purposes (excepting (a), as pointed out above). Nevertheless it will appear that a really high speed device would be very limited in its usefulness unless it can rely on M, rather than on R, for all the purposes enumerated in §10.2.4, (a)–(h), with certain limitations in the case of (e), (g), (h) ….
10.3 Procedure of Discussion
10.3.1 The classification of §10.2 being completed, it is now possible to take up the five specific parts into which the device was seen to be subdivided, and to discuss them one by one. Such a discussion must bring out the features required for each one of these parts in itself, as well as in their relations to each other. It must also determine the specific procedures to be used in dealing with numbers from the point of view of the device, in carrying out arithmetical operations, and providing for the general logical control. All questions of timing and of speed, and of the relative importance of various factors, must be settled within the framework of these considerations.
10.3.2 The ideal procedure would be, to take up the five specific parts in some definite order, to treat each one of them exhaustively, and go on to the next one only after the predecessor is completely disposed of. However, this seems hardly feasible. The desirable features of the various parts, and the decisions based on them, emerge only after a somewhat zigzagging discussion. It is therefore necessary to take up one part first, pass after an incomplete discussion to a second part, return after an equally incomplete discussion of the latter with the combined results to the first part, extend the discussion of the first part without yet concluding it, then possibly go on to a third part, etc. Furthermore, these discussions of specific parts will be mixed with discussions of general principles, of arithmetical procedures, of the elements to be used, etc.
In the course of such a discussion the desired features and the arrangements which seem best suited to secure them will crystallize gradually until the device and its control assume a fairly definite shape. As emphasized before, this applies to the physical device as well as to the arithmetical and logical arrangements which govern its functioning.
10.3.3 In the course of this discussion the viewpoints of §10.1.4, concerned with the detection, location, and under certain conditions even correction, of malfunctions must also receive some consideration. That is, attention must be given to facilities for checking errors. We will not be able to do anything like full justice to this important subject, but we will try to consider it at least cursorily whenever this seems essential ….
10.4 Elements, Synchronism, Neuron Analogy
10.4.1 We begin the discussion with some general remarks:
Every digital computing device contains certain relay like elements, with discrete equilibria. Such an element has two or more distinct states in which it can exist indefinitely. These may be perfect equilibria, in each of which the element will remain without any outside support, while appropriate outside stimuli will transfer it from one equilibrium into another. Or, alternatively, there may be two states, one of which is an equilibrium which exists when there is no outside support, while the other depends for its existence upon the presence of an outside stimulus. The relay action manifests itself in the omission of stimuli by the element whenever it has itself received a stimulus of the type indicated above. The emitted stimuli must be of the same kind as the received one, that is, they must be able to stimulate other elements. There must, however, be no energy relation between the received and the emitted stimuli, that is, an element which has received one stimulus, must be able to emit several of the same intensity. In other words: Being a relay, the element must receive its energy supply from another source than the incoming stimulus.
In existing digital computing devices various mechanical or electrical devices have been used as elements: Wheels, which can be locked into any one of ten (or more) significant positions, and which on moving from one position to another transmit electric pulses that may cause other similar wheels to move; single or combined telegraph relays, actuated by an electromagnet and opening or closing electric circuits; combinations of these two elements;—and finally there exists the plausible and tempting possibility of using vacuum tubes, the grid acting as a valve for the cathode-plate circuit. In the last mentioned case the grid may also be replaced by deflecting organs, i.e. the vacuum tube by a cathode ray tube—but it is likely that for some time to come the greater availability and various electrical advantages of the vacuum tubes proper will keep the first procedure in the foreground.
Any such device may time itself autonomously, by the successive reaction times of its elements. In this case all stimuli must ultimately originate in the input. Alternatively, they may have their timing impressed by a fixed clock, which provides certain stimuli that are necessary for its functioning at definite periodically recurrent moments. This clock may be a rotating axis in a mechanical or a mixed, mechanico-electrical device; and it may be an electrical oscillator (possibly crystal controlled) in a purely electrical device. If reliance is to be placed on synchronisms of several distinct sequences of operations performed simultaneously by the device, the clock impressed timing is obviously preferable. We will use the term element in the above defined technical sense, and call the device synchronous or asynchronous, according to whether its timing is impressed by a clock or autonomous, as described above.
10.4.2 It is worth mentioning, that the neurons of the higher animals are definitely elements in the above sense. They have all-or-none character, that is two states: Quiescent and excited. They fulfill the requirements of §10.4.1 with an interesting variant: An excited neuron emits the standard stimulus along many lines (axons). Such a line can, however, be connected in two different ways to the next neuron: First: In an excitatory synapse, so that the stimulus causes the excitation of the neuron. Second: In an inhibitory synapse, so that the stimulus absolutely prevents the excitation of the neuron by any stimulus on any other (excitatory) synapse. The neuron also has a definite reaction time, between the reception of a stimulus and the emission of the stimuli caused by it, the synaptic delay.
Following McCulloch and Pitts (1943, here chapter 9) we ignore the more complicated aspects of neuron functioning: Thresholds, temporal summation, relative inhibition, changes of the threshold by after-effects of stimulation beyond the synaptic delay, etc. It is, however, convenient to consider occasionally neurons with fixed thresholds 2 and 3, that is, neurons which can be excited only by (simultaneous) stimuli on 2 or 3 excitatory synapses (and none on an inhibitory synapse). …
It is easily seen that these simplified neuron functions can be imitated by telegraph relays or by vacuum tubes. Although the nervous system is presumably asynchronous (for the synaptic delays), precise synaptic delays can be obtained by using synchronous setups. …
10.4.3 It is clear that a very high speed computing device should ideally have vacuum tube elements. Vacuum tube aggregates like counters and scalers have been used and found reliable at reaction times (synaptic delays) as short as a microsecond ( = 10−6 seconds), this is a performance which no other device can approximate. Indeed: Purely mechanical devices may be entirely disregarded and practical telegraph relay reaction times are of the order of 10 milliseconds ( = 10−2 seconds) or more. It is interesting to note that the synaptic time of a human neuron is of the order of a millisecond ( = 10−3 seconds).
In the considerations which follow we will assume accordingly, that the device has vacuum tubes as elements. We will also try to make all estimates of numbers of tubes involved, timing, etc., on the basis that the types of tubes used are the conventional and commercially available ones. That is, that no tubes of unusual complexity or with fundamentally new functions are to be used. The possibilities for the use of new types of tubes will actually become clearer and more definite after a thorough analysis with the conventional types (or some equivalent elements …) has been carried out.
Finally, it will appear that a synchronous device has considerable advantages ….
10.5 Principles Governing the Arithmetical Operations
10.5.1 Let us now consider certain functions of the first specific part: The central arithmetical part CA.
The element in the sense of §10.4.3, the vacuum tube used as a current valve or gate, is an all-or-none device, or at least it approximates one: According to whether the grid bias is above or below cut-off, it will pass current or not. It is true that it needs definite potentials on all its electrodes in order to maintain either state, but there are combinations of vacuum tubes which have perfect equilibria: Several states in each of which the combination can exist indefinitely, without any outside support, while appropriate outside stimuli (electric pulses) will transfer it from one equilibrium into another. These are the so called trigger circuits, the basic one having two equilibria and containing two triodes or one pentode. The trigger circuits with more than two equilibria are disproportionately more involved.
Thus, whether the tubes are used as gates or as triggers, the all-or-none, two equilibrium, arrangements are the simplest ones. Since these tube arrangements are to handle numbers by means of their digits, it is natural to use a system of arithmetic in which the digits are also two valued. This suggests the use of the binary system.
The analogs of human neurons, discussed in §§10.4.2–10.4.3, are equally all-or-none elements. It will appear that they are quite useful for all preliminary, orienting, considerations of vacuum tube systems (cf. §§10.6.1–10.6.2). It is therefore satisfactory that here too the natural arithmetical system to handle is the binary one.
10.5.2 A consistent use of the binary system is also likely to simplify the operations of multiplication and division considerably. Specifically it does away with the decimal multiplication table, or with the alternative double procedure of building up the multiples of each multiplier or quotient digit by additions first, and then combining these (according to positional value) by a second sequence of additions or subtractions. In other words: Binary arithmetics has a simpler and more one-piece logical structure than any other, particularly than the decimal one.
It must be remembered, of course, that the numerical material which is directly in human use, is likely to have to be expressed in the decimal system. Hence, the notations used in R should be decimal. But it is nevertheless preferable to use strictly binary procedures in CA, and also in whatever numerical material may enter into the central control CC. Hence M should store binary material only.
This necessitates incorporating decimal-binary and binary-decimal conversion facilities into I and O. Since these conversions require a good deal of arithmetical manipulating, it is most economical to use CA, and hence for coordinating purposes also CC, in connection with I and O. The use of CA implies, however, that all arithmetics used in both conversions must be strictly binary. …
10.5.3 At this point there arises another question of principle. In all existing devices where the element is not a vacuum tube the reaction time of the element is sufficiently long to make a certain telescoping of the steps involved in addition, subtraction, and still more in multiplication and division, desirable. To take a specific case consider binary multiplication. A reasonable precision for many differential equation problems is given by carrying 8 significant decimal digits, that is by keeping the relative rounding-off errors below 10−8. This corresponds to 2−27 in the binary system, that is to carrying 27 significant binary digits. Hence a multiplication consists of pairing each one of 27 multiplicand digits with each one of 27 multiplier digits, and forming product digits 0 and 1 accordingly, and then positioning and combining them. These are essentially 272 = 729 steps, and the operations of collecting and combining may about double their number. So 1000–1500 steps are essentially right.
It is natural to observe that in the decimal system a considerably smaller number of steps obtains 82 = 64 steps, possibly doubled, that is about 100 steps. However, this low number is purchased at the price of using a multiplication table or otherwise increasing or complicating the equipment. At this price the procedure can be shortened by more direct binary artifices, too, which will be considered presently. For this reason it seems not necessary to discuss the decimal procedure separately.
10.5.4 As pointed out before, 1000–1500 successive steps per multiplication would make any non vacuum tube device unacceptably slow. All such devices, excepting some of the latest special relays, have reaction times of more than 10 milliseconds, and these newest relays (which may have reaction times down to 5 milliseconds) have not been in use very long. This would give an extreme minimum of 10–15 seconds per (8 decimal digit) multiplication, whereas this time is 10 seconds for fast modern desk computing machines, and 6 seconds for the standard IBM multipliers. (For the significance of these durations, as well as of those of possible vacuum tube devices, when applied to typical problems, cf. ….)
The logical procedure to avoid these long durations, consists of telescoping operations, that is of carrying out simultaneously as many as possible. The complexities of carrying prevent even such simple operations as addition or subtraction to be carried out at once. In division the calculation of a digit cannot even begin unless all digits to its left are already known. Nevertheless considerable simultaneisations are possible: In addition or subtraction all pairs of corresponding digits can be combined at once, all first carry digits can be applied together in the next step, etc. In multiplication all the partial products of the form (multiplicand) × (multiplier digit) can be formed and positioned simultaneously—in the binary system such a partial product is zero or the multiplicand, hence this is only a matter of positioning. In both addition and multiplication the above mentioned accelerated forms of addition and subtraction can be used. Also, in multiplication the partial products can be summed up quickly by adding the first pair together simultaneously with the second pair, the third pair, etc.; then adding the first pair of pair sums together simultaneously with the second one, the third one, etc.; and so on until all terms are collected. (Since 27 ≤ 25, this allows to collect 27 partial sums—assuming a 27 binary digit multiplier—in 5 addition times. This scheme is due to H. Aiken.)
Such accelerating, telescoping procedures are being used in all existing devices. (The use of the decimal system, with or without further telescoping artifices is also of this type, as pointed out at the end of §10.5.3. It is actually somewhat less efficient than purely dyadic procedures. The arguments of §§10.5.1–10.5.2 speak against considering it here.) However, they save time only at exactly the rate at which they multiply the necessary equipment, that is the number of elements in the device: Clearly if a duration is halved by systematically carrying out two additions at once, double adding equipment will be required (even assuming that it can be used without disproportionate control facilities and fully efficiently), etc.
This way of gaining time by increasing equipment is fully justified in non vacuum tube element devices, where gaining time is of the essence, and extensive engineering experience is available regarding the handling of involved devices containing many elements. A really all-purpose automatic digital computing system constructed along these lines must, according to all available experience, contain over 10,000 elements.
10.5.5 For a vacuum tube element device on the other hand, it would seem that the opposite procedure holds more promise.
As pointed out in §10.4.3, the reaction time of a not too complicated vacuum tube device can be made as short as one microsecond. Now at this rate even the unmanipulated duration of the multiplication, obtained in §10.5.3 is acceptable: 1000–1500 reaction times amount to 1–1.5 milliseconds, and this is so much faster than any conceivable non vacuum tube device, that it actually produces a serious problem of keeping the device balanced, that is to keep the necessarily human supervision beyond its input and output ends in step with its operations. …
Regarding other arithmetical operations this can be said: Addition and subtraction are clearly much faster than multiplication. On a basis of 27 binary digits (cf. §10.5.3) and taking carrying into consideration, each should take at most twice 27 steps, that is about 30–50 steps or reaction times. This amounts to.03–.05 milliseconds. Division takes, in this scheme where shortcuts and telescoping have not been attempted in multiplying and the binary system is being used, about the same number of steps as multiplication. … Square rooting is usually, and in this scheme too, not essentially longer than dividing.
10.5.6 Accelerating these arithmetical operations does therefore not seem necessary—at least not until we have become thoroughly and practically familiar with the use of very high speed devices of this kind, and also properly understood and started to exploit the entirely new possibilities for numerical treatment of complicated problems which they open up. Furthermore it seems questionable whether the method of acceleration by telescoping processes at the price of multiplying the number of elements required would in this situation achieve its purpose at all: The more complicated the vacuum tube equipment—that is, the greater the number of elements required—the wider the tolerances must be. Consequently any increase in this direction will also necessitate working with longer reaction times than the above mentioned one of one microsecond. The precise quantitative effects of this factor are hard to estimate in a general way—but they are certainly much more important for vacuum tube elements than for telegraph relay ones.
Thus it seems worthwhile to consider the following viewpoint: The device should be as simple as possible, that is, contain as few elements as possible. This can be achieved by never performing two operations simultaneously, if this would cause a significant increase in the number of elements required. The result will be that the device will work more reliably and the vacuum tubes can be driven to shorter reaction times than otherwise.
10.5.7 The point to which the application of this principle can be profitably pushed will, of course, depend on the actual physical characteristics of the available vacuum tube elements. It may be, that the optimum is not at a 100% application of this principle and that some compromise will be found to be optimal. However, this will always depend on the momentary state of the vacuum tube technique, clearly the faster the tubes are which will function reliably in this situation, the stronger the case is for uncompromising application of this principle. It would seem that already with the present technical possibilities the optimum is rather nearly at this uncompromising solution.
It is also worth emphasizing that up to now all thinking about high speed digital computing devices has tended in the opposite direction: Towards acceleration by telescoping processes at the price of multiplying the number of elements required. It would therefore seem to be more instructive to try to think out as completely as possible the opposite viewpoint: That of absolutely refraining from the procedure mentioned above, that is of carrying out consistently the principle formulated in §10.5.6.
We will therefore proceed in this direction. …
10.6 E-Elements
10.6.1 The considerations of §10.5 have defined the main principles for the treatment of CA. We continue now on this basis, with somewhat more specific and technical detail.
In order to do this it is necessary to use some schematic picture for the functioning of the standard element of the device: Indeed, the decisions regarding the arithmetical and the logical control procedures of the device, as well as its other functions, can only be made on the basis of some assumptions about the functioning of the elements.
The ideal procedure would be to treat the elements as what they are intended to be: as vacuum tubes. However, this would necessitate a detailed analysis of specific radio engineering questions at this early stage of the discussion, when too many alternatives are still open to be treated all exhaustively and in detail. Also, the numerous alternative possibilities for arranging arithmetical procedures, logical control, etc., would superpose on the equally numerous possibilities for the choice of types and sizes of vacuum tubes and other circuit elements from the point of view of practical performance, etc. All this would produce an involved and opaque situation in which the preliminary orientation which we are now attempting would be hardly possible.
In order to avoid this we will base our considerations on a hypothetical element, which functions essentially like a vacuum tube—e.g. like a triode with an appropriate associated RLC-circuit—but which can be discussed as an isolated entity, without going into detailed radio frequency electromagnetic considerations. We re-emphasize: This simplification is only temporary, only a transient standpoint, to make the present preliminary discussion possible. After the conclusions of the preliminary discussion the elements will have to be reconsidered in their true electromagnetic nature. But at that time the decisions of the preliminary discussion will be available, and the corresponding alternatives accordingly eliminated.
10.6.2 The analogs of human neurons, discussed in §§10.4.2–10.4.3 and again referred to at the end of §10.5.1, seem to provide elements of just the kind postulated at the end of §10.6.1. We propose to use them accordingly for the purpose described there: as the constituent elements of the device, for the duration of the preliminary discussion. We must therefore give a precise account of the properties which we postulate for these elements.
The element which we will discuss, to be called an E-element, will be represented to be a circle O, which receives the excitatory and inhibitory stimuli, and emits its own stimuli along a line attached to it: 
This axis may branch: 
. The emission along it follows the original stimulation by a synaptic delay, which we can assume to be a fixed time, the same for all E-elements, to be denoted by t. We propose to neglect the other delays (due to conduction of the stimuli along the lines) aside of t. We will mark the presence of the delay t by an arrow on the line: 
. This will also serve to identify the origin and the direction of the line.
10.6.3 At this point the following observation is necessary. In the human nervous system the conduction times along the lines (axons) can be longer than the synaptic delays, hence our above procedure of neglecting them aside of t would be unsound. In the actually intended vacuum tube interpretation, however, this procedure is justified: t is to be about a microsecond, an electromagnetic impulse travels in this time 300 meters, and as the lines are likely to be short compared to this, the conduction times may indeed be neglected. (It would take an ultra high frequency device—t = 10−8 seconds or less—to vitiate this argument.)
Another point of essential divergence between the human nervous system and our intended application consists in our use of a well-defined dispersionless synaptic delay t, common to all E-elements. (The emphasis is on the exclusion of a dispersion. We will actually use E-elements with a synaptic delay 2t, …) We propose to use the delays t as absolute units of time which can be relied upon to synchronize the functions of various parts of the device. The advantages of such an arrangement are immediately plausible, specific technical reasons will appear in [EDITOR: sentence ends here].
In order to achieve this, it is necessary to conceive the device as synchronous in the sense of §10.4.1. The central clock is best thought of as an electrical oscillator, which emits in every period t a short, standard pulse of a length t′ of about 
. The stimuli emitted nominally by an E-element are actually pulses of the clock, for which the pulse acts as a gate. There is clearly a wide tolerance for the period during which the gate must be kept open, to pass the clock-pulse without distortion. Cf. Figure 10.2. Thus the opening of the gate can be controlled by any electric delay device with a mean delay time t, but considerable permissible dispersion. Nevertheless, the effective synaptic delay will be t with the full precision of the clock, and the stimulus is completely renewed and synchronized after each step. …
Figure 10.2: Clock pulses
10.12 Capacity of the Memory M, General Principles
10.12.1 We consider next the third specific part: the memory M. …
10.12.2 Preceding this discussion, however, we must consider the capacity which we desire in M. It is the number of stimuli which this organ can remember, or more precisely, the number of occasions for which it can remember whether or not a stimulus was present. The presence or absence of a stimulus (at a given occasion, i.e. on a given line in a given moment) can be used to express the value 1 or 0 for a binary digit (in a given position). Hence the capacity of a memory is the number of binary digits (the values of) which it can retain. In other words:
The (capacity) unit of memory is the ability to retain the value of one binary digit.
We can now express the “cost” of various types of information in these memory units.
Let us consider first the memory capacity required to store a standard (real) number. As indicated …, we shall fix the size of such a number at 30 binary digits (at least for most uses …). This keeps the relative rounding-off errors below 2−30, which corresponds to 10−9, i.e. to carrying 9 significant decimal digits. Thus a standard number corresponds to 30 memory units. To this must be added one unit for its sign … and it is advisable to add a further unit in lieu of a symbol which characterizes it as a number (to distinguish it from an order, cf. §10.14). In this way we arrive at 32 = 26 units per number.
The fact that a number requires 32 memory units, makes it advisable to subdivide the entire memory in this way: First, obviously, into units, second into groups of 32 units, to be called minor cycles. … Each standard (real) number accordingly occupies precisely one minor cycle. It simplifies the organization of the entire memory, and various synchronization problems of the device along with it, if all other constants of the memory are also made to fit into this subdivision into minor cycles. …
10.14 CC and M
10.14.1 Our next aim is to go deeper into the analysis of CC. Such an analysis, however, is dependent upon a precise knowledge of the system of orders used in controlling the device, since the function of CC is to receive these orders, to interpret them, and then either to carry them out, or to stimulate properly those organs which will carry them out. It is therefore our immediate task to provide a list of the orders which control the device, i.e. to describe the code to be used in the device, and to define the mathematical and logical meaning and the operational significance of its code words.
Before we can formulate this code, we must go through some general considerations concerning the functions of CC and its relation to M.
The orders which are received by CC come from M, i.e. from the same place where the numerical material is stored. (Cf. §10.2.4 ….) The content of M consists of minor cycles …, hence by the above each minor cycle must contain a distinguishing mark which indicates whether it is a standard number or an order.
The orders which CC receives fall naturally into these four classes: (a) orders for CC to instruct CA to carry out one of its ten specific operations …; (b) orders for CC to cause the transfer of a standard number from one place to another; (c) orders for CC to transfer its own connection with M to a different point in M, with the purpose of getting its next order from there; (d) orders controlling the operation of the input and the output of the device (i.e. I of §10.2.7 and O of §10.2.8).
Let us now consider these classes (a)–(d) separately. We cannot at this time add anything to the statements … concerning (a) …. The discussion of (d) is also better delayed …. We propose, however, to discuss (b) and (c) now.
10.14.2 Ad (b): These transfers can occur within M, or within CA, or between M and CA. The first kind can always be replaced by two operations of the last kind, i.e. all transfers within M can be routed through CA. We propose to do this, since this is in accord with the general principle of §10.5.6 …, and in this way we eliminate all transfers of the first kind. Transfers of the second kind are obviously handled by the operating controls of CA. Hence those of the last kind alone remain. They fall obviously into two classes: Transfers from M to CA and transfers from CA to M. We may break up accordingly (b) into (b′) and (b′′), corresponding to these two operations.
10.14.3 Ad (c): In principle CC should be instructed, after each order, where to find the next order that it is to carry out. We saw, however, that this is undesirable per se, and that it should be reserved for exceptional occasions, while as a normal routine CC should obey the orders in the temporal sequence, in which they naturally appear at the output of the DLA organ to which CC is connected (cf. the corresponding discussion for the iconoscope memory …). There must, however, be orders available, which may be used at the exceptional occasions referred to, to instruct CC to transfer its connection to any other desired point in M. This is primarily a transfer of this connection to a different DLA organ (i.e. a delay line organ …). Since, however, the connection actually wanted must be with a definite minor cycle, the order in question must consist of two instructions: First, the connection of CC is to be transferred to a definite DLA organ. Second, CC is to wait there until a definite r-period, the one in which the desired minor cycle appears at the output of this DLA, and CC is to accept an order at this time only.
Apart from this, such a transfer order might provide that, after receiving and carrying out the order in the desired minor cycle, CC should return its connection to the DLA organ which contains the minor cycle that follows upon the one containing the transfer order, wait until this minor cycle appears at the output, and then continue to accept orders from there on in the natural temporal sequence. Alternatively, after receiving and carrying out the order in the desired minor cycle, CC should continue with that connection, and accept orders from there on in the natural temporal sequence. It is convenient to call a transfer of the first type a transient one, and one of the second type a permanent one.
It is clear that permanent transfers are frequently needed, hence the second type is certainly necessary. Transient transfers are undoubtedly required in connection with transferring standard numbers (orders (c′) and (c′′), cf. the end of §10.14.2 …). It seems very doubtful whether they are ever needed in true orders, particularly since such orders constitute only a small part of the contents of M …, and a transient transfer order can always be expressed by two permanent transfer orders. We will therefore make all transfers permanent, except those connected with transferring standard numbers, as indicated above. …
10.15 The Code
10.15.1 The considerations of §10.14 provide the basis for a complete classification of the contents of M, i.e. they enumerate a system of successive disjunctions which give together this classification. This classification will put us into the position to formulate the code which effects the logical control of CC, and hence of the entire device.
Let us therefore restate the pertinent definitions and disjunctions.
The contents of M are the memory units, each one being characterized by the presence or absence of a stimulus. It can be used to represent accordingly the binary digit 1 or 0, and we will at any rate designate its content by the binary digit i = 1 or 0 to which it corresponds in this manner. …These units are grouped together to form 32-unit minor cycles, and these minor cycles are the entities which will acquire direct significance in the code which we will introduce. … We denote the binary digits which make up the 32 units of a minor cycle, in their natural temporal sequence, by i0, i1, i2, …, i31. The minor cycles with these units may be written I = (i0, i1, i2, …, i31) = (iv).
Minor cycles fall into two classes: Standard numbers and orders. (Cf. …§10.14.1.) These two categories should be distinguished from each other by their respective first units … i.e. by the value of i0. We agree accordingly that i0 = 0 is to designate a standard number, and i0 = 1 an order.
10.15.2 The remaining 31 units of a standard number express its binary digits and its sign. It is in the nature of all arithmetical operations, specifically because of the role of carry digits, that the binary digits of the numbers which enter into them must be fed in from right to left, i.e. those with the lowest positional values first. (This is so because the digits appear in a temporal succession and not simultaneously…. The details are most simply evident in the discussion of the adder ….) The sign plays the role of the digit farthest left, i.e. of the highest positional value …. Hence it comes last, i.e. i31 = 0 designates the + sign and i31 = 1 the − sign. Finally … the binary point follows immediately after the sign digit, and the number ξ thus represented must be moved mod 2 into the interval − 1, 1. That is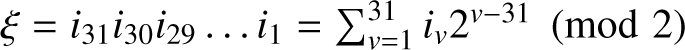 
, − 1 ≤ ξ < 1.
10.15.3 The remaining 31 units of an order, on the other hand, must express the nature of this order. The orders were classified in §10.14.1 into four classes (a)–(d), and these were subdivided further …. [EDITOR: Figure 10.3 shows the orders in tabular form.]
Figure 10.3: First draft EDVAC “orders” (instructions)
Reprinted from von Neumann (1993), with permission from the Institute for Electrical and Electronics Engineers.