15 The Best Way to Design an Automatic Calculating Machine (1951)

Maurice Wilkes

In 1946, Maurice Wilkes (1913–2010), then head of the Mathematics Laboratory at the University of Cambridge in England, attended a summer school taught at the Moore School of the University of Pennsylvania and learned about the EDVAC of Burks, Goldstine, von Neumann, et al. On the return voyage, he began the design of a machine he dubbed the Electronic Delay Storage Automatic Calculator, or EDSAC. By 1949, when the EDSAC was up and running, a stored-program computer called the Mark 1 was already operational in England at the University of Manchester—a project mentioned both by Wilkes in this piece and by Turing in chapter 14 (pages 150 and 159). The Manchester Mark 1 served more as an experimental prototype than as a computational workhorse (a follow-on machine was put into commercial production in 1951 as the Ferranti Mark 1).

The EDSAC, by contrast, was soon being used to capacity as a resource to the Cambridge scientific community, and Wilkes began work on a successor machine. As he designed the data formats and instruction set, he came to the crucial realization that it would be far easier to design a more primitive micro-instruction set for such micro-operations as shifting bits within a register or moving bits between registers, and then to implement the actual machine instructions as micro-programs of those micro-instructions—“giving the control unit the full flexibility of a programmed computer in miniature,” as he later put it (Wilkes, 1986). At the end of this article he even imagines that programmers might some day be able to choose their own instruction sets.

Microcode was indeed quickly recognized as the “best way” to design a computer. Later in the 1950s, IBM adopted microcode for the design of its System/360 line of computers, greatly easing the task of debugging and even field modifying the design of complex operations such as multiplication. The idea of flexible, hierarchical, updatable design is behind the ubiquitous use of firmware in modern systems.

Wilkes went on to a distinguished career as a professor at Cambridge and authored one of the earliest textbooks on computer programming. He received the Turing Award in 1967 for his many contributions to the field.

…I think that most people will agree that the first consideration for a designer at the present time is how he is to achieve the maximum degree of reliability in his machine. Amongst other things the reliability of the machine will depend on the following:

(a) The amount of equipment it contains.

(b) Its complexity.

By the complexity of a machine I mean the extent to which cross-connections between the various units obscure their logical interrelation. A machine is easier to repair if it consists of a number of units connected together in a simple way without cross-connections between them; it is also easier to construct since different people can work on the different units without getting in each other’s way.

As regards repetition I think everyone would prefer to have in a particular part of the machine a group of five identical units rather than a group of five different units. Most people would prefer to have six identical units rather than five different units. How far one ought to be prepared to go in the direction of accepting a greater quantity of equipment in order to achieve repetition is a matter of opinion. The matter may be put as follows. Suppose that it is regarded as being equally desirable to have a particular part of the machine composed of a group of n different units, or composed of a group of kn identical units, all the units being of similar size. What is the value of k? My conjecture is that k > 2. I should say that I am thinking of a machine which has about 10 groups of units and that n is approximately equal to 10.

The remarks I have just made are of general application. I will now try to be more specific. If one builds a parallel machine one has a good example, in the arithmetical unit, of a piece of equipment consisting of identical units repeated many times. Such an arithmetical unit is, however, much larger than that in a serial machine. On the other hand I think it is true to say that the control in a parallel machine is simpler than in a serial machine. I am using the word control here in a very general sense to include everything that does not appertain to the store proper (i.e., it includes the access circuits) or to the registers and adders in the arithmetical unit.…

We are thus led to think of an arithmetical unit composed of a number of standard units each containing four flip-flops (one belonging to each of four registers) together with an adder. Gates would be provided to make possible the transfer of numbers from one register to another, through the adder when necessary. These transfers would be effected by pulsing one or more of a set of wires emerging from the arithmetical unit.

It is also necessary to have registers in the control of a machine. These, with the names given to them respectively in the Manchester machine and in the EDSAC, are as follows:

Register for counting the number of steps in a multiplication or shifting operation (not needed with the fast multiplier on the Manchester machine, timing control tank in the EDSAC).

In addition the Manchester machine has a number of B registers.

If one B register is considered to be sufficient the parallel machine we are considering can use the same unit (containing 4 flip-flops and 1 adder) for the control registers as for arithmetical registers. In this way an extreme degree of repetition can be achieved.

It remains to consider the control proper, that is, the part of the machine which supplies the pulses for operating the gates associated with the arithmetical and control registers. The designer of this part of a machine usually proceeds in an ad hoc manner, drawing block diagrams until he sees an arrangement which satisfies his requirements and appears to be reasonably economical. I would like to suggest a way in which the control can be made systematic, and therefore less complex.

Each operation called for by an order in the order code of the machine involves a sequence of steps which may include transfers from the store to control or arithmetical registers, or vice versa, and transfers from one register to another. Each of these steps is achieved by pulsing certain of the wires associated with the control and arithmetical registers, and I will refer to it as a “micro-operation.” Each true machine operation is thus made up of a sequence of “micro-programme” of micro-operations.

Figure 15.1 shows the way in which pulses for performing the micro-operations may be generated. The timing pulse which initiates a micro-operation enters the decoding tree and is routed to one of the outputs according to the number set on the register R. It passes into the rectifier matrix A and gives rise to pulses on certain of the output wires of this matrix according to the arrangement of the rectifiers. These pulses operate the gates associated with the control and arithmetical registers, and cause the correct micro-operation to be performed. The pulse from the decoding tree also passes into matrix B and gives rise to pulses on certain of the output wires of this matrix. These pulses are conducted, via a short delay line, to the register R and cause the number set up on it to be changed. The result is that the next initiating pulse to enter the decoding tree will emerge from a different outlet and will consequently cause a different micro-operation to be performed. It will thus be seen that each row of rectifiers in matrix A corresponds to one of the micro-orders in the sequence required to perform a machine operation.

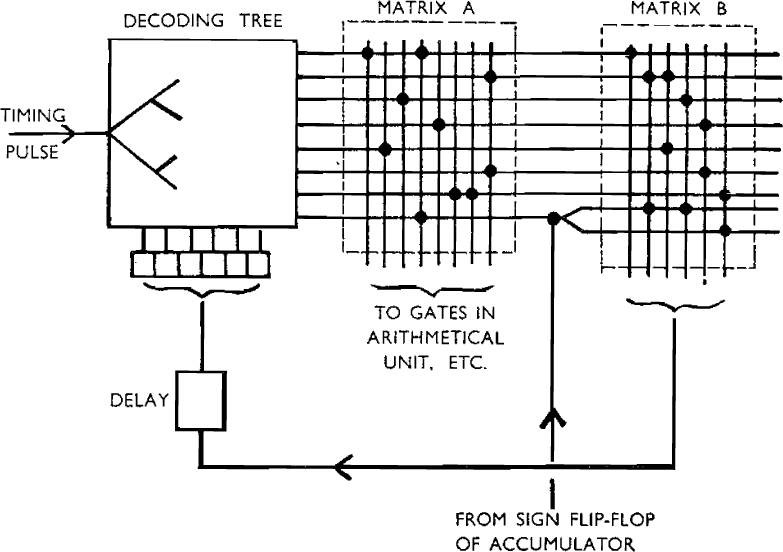
The system as described would enable a fixed cycle of operations only to be performed. Its utility can be greatly extended by making some of the micro-orders conditional in the sense that they are followed by one of two alternative micro-orders according to the state of the machine. This can be done by making the output of the decoding tree branch before it enters matrix B. The direction the pulse takes at the branch is controlled by the potential on a wire coming from another part of the machine; for example, it might come from the sign flip-flop of the accumulator. The bottom row of matrix A in Figure 15.1 corresponds to a conditional micro-order. The matrix A contains sequences of micro-orders for performing all the basic operations in the order code of the machine. All that is necessary to perform a particular operation is that “micro-control” shall be switched to the first micro-order in the appropriate sequence. This is done by causing the function digits of the order to be set up on the first four or five flip-flops of the register R, zero being set on the others.

A control system designed in this way is certainly very logical in structure but two comments, slightly contradictory in their implications, might be made. In the first place it might be said that there is nothing very new about the arrangement since it makes use of flip-flops, gates, and mixing diodes which are the elements out of which any control is built. With this criticism I would agree. In fact, the controls of various machines now in existence or being constructed could no doubt be drawn in some way closely resembling Figure 15.1. The other objection is that the scheme appears to be rather extravagant in equipment. This I think is not true, particularly if some departures from the precise form of Figure 15.1 are allowed. I think that by starting with a logical layout one is likely to arrive at a final arrangement which is both logical and economical. Moreover, one is able to see at each stage what one is sacrificing in the way of logical layout in order to achieve economy and vice versa. In order to get some idea of the number of micro-orders required I have constructed a micro-programme for a simple machine with the following orders: add, subtract, multiply (two orders, one for the multiplier, one for the multiplicand), right and left shift (any number of places), transfer from the accumulator to the store, conditional operation depending on the sign of the number in the accumulator, conditional operation depending on the sign of the number in the B register (one B register is assumed), transfer from the store to the B register, input, and output. The micro-programme also provides for the preliminary extraction of the order from the store (Stage 1 in EDSAC terminology). Only 40 micro-orders are required to perform all these operations.

The considerations involved in drawing-up a micro-programme resemble those involved in drawing-up an ordinary programme. The final details of the control are thus settled by a systematic process instead of by the usual ad hoc procedures based on the use of block diagrams. Of course, sound engineering would be necessary to produce designs for the decoding tree and the matrices which could be used for any desired micro-programme by arranging the rectifiers suitably in the matrices. One important advantage of this method of designing the control is that the order code need not be decided on finally until a late stage in the construction of the machine; it would even be possible to change it after the machine had been put into operation simply by rewiring the matrices.

Reprinted from Wilkes (1981), with permission from Elsevier.