18
The Perceptron: A Probabilistic Model for Information Storage and Organization (1958)
Frank Rosenblatt
The “perceptron” of Frank Rosenblatt (1928–1971) is at once a dramatic early step toward artificial intelligence, a temporary casualty of intellectual rivalry, and a case study in the faddishness of scientific research trends. Educated at Cornell as a psychologist, Rosenblatt began developing an artificial perceptual mechanism when he joined Cornell’s Aeronautical Laboratory after receiving his PhD in 1956. There he had access to what then counted as a large computer, the IBM 704. His first cut at a perceptron, in 1957, was an early experiment in training an artificial pattern-recognition system to improve its performance through reinforcement learning. This 1958 paper describes his refined model, complete with various tunable parameters and mathematics commonly used to describe physical systems. Rosenblatt pursued this line of research and other dramatically different experiments in neuroscience as a psychology professor until his death in a boating accident on his forty-third birthday.
Rosenblatt was ahead of his time, and the line of descent from his invention to today’s trained neural nets is anything but direct. In 1969 Marvin Minsky, a founding father of artificial intelligence at MIT, and Seymour Papert, his psychologist colleague there, published Perceptrons (Minsky and Papert, 1969), which studied the power of a restricted “one-layer” version of Rosenblatt’s model. Perceptrons correctly showed the limitations of one-layer nets. As a scientific matter, that should not have been enough to sidetrack research on the full perceptron model, but it seems to have had that effect, perhaps because it was published at a moment of frustratingly slow progress in producing nontrivial experimental results in artificial intelligence. Minsky (who had been one grade behind Rosenblatt at Bronx High School of Science) and his MIT colleagues (some soon to depart for Stanford) were championing a different approach to AI, through logic and other symbolic systems rather than through mimicking the architecture of the human brain.
Rosenblatt’s early research came out of mothballs in the 1980s, when computers began to be powerful enough to simulate multi-layer nets and to train them on sizable data sets. As a result neural computing models are now of great interest to researchers in artificial intelligence.
IF we are eventually to understand the capability of higher organisms for perceptual recognition, generalization, recall, and thinking, we must first have answers to three fundamental questions:
1. How is information about the physical world sensed, or detected, by the biological system?
2. In what form is information stored, or remembered?
3. How does information contained in storage, or in memory, influence recognition and behavior?
The first of these questions is in the province of sensory physiology, and is the only one for which appreciable understanding has been achieved. This article will be concerned primarily with the second and third questions, which are still subject to a vast amount of speculation, and where the few relevant facts currently supplied by neurophysiology have not yet been integrated into an acceptable theory.
With regard to the second question, two alternative positions have been maintained. The first suggests that storage of sensory information is in the form of coded representations or images, with some sort of one-to-one mapping between the sensory stimulus and the stored pattern. According to this hypothesis, if one understood the code or “wiring diagram” of the nervous system, one should, in principle, be able to discover exactly what an organism remembers by reconstructing the original sensory patterns from the “memory traces” which they have left, much as we might develop a photographic negative, or translate the pattern of electrical charges in the “memory” of a digital computer. This hypothesis is appealing in its simplicity and ready intelligibility, and a large family of theoretical brain models has been developed around the idea of a coded, representational memory (Culbertson, 1950, 1956; Köhler, 1951; Rashevsky, 1938). The alternative approach, which stems from the tradition of British empiricism, hazards the guess that the images of stimuli may never really be recorded at all, and that the central nervous system simply acts as an intricate switching network, where retention takes the form of new connections, or pathways, between centers of activity. In many of the more recent developments of this position (Hebb’s “cell assembly,” and Hull’s “cortical anticipatory goal response,” for example) the “responses” which are associated to stimuli may be entirely contained within the CNS itself. In this case the response represents an “idea” rather than an action. The important feature of this approach is that there is never any simple mapping of the stimulus into memory, according to some code which would permit its later reconstruction. Whatever information is retained must somehow be stored as a preference for a particular response; i.e., the information is contained in connections or associations rather than topographic representations. (The term response, for the remainder of this presentation, should be understood to mean any distinguishable state of the organism, which may or may not involve externally detectable muscular activity. The activation of some nucleus of cells in the central nervous system, for example, can constitute a response, according to this definition.)
Corresponding to these two positions on the method of information retention, there exist two hypotheses with regard to the third question, the manner in which stored information exerts its influence on current activity. The “coded memory theorists” are forced to conclude that recognition of any stimulus involves the matching or systematic comparison of the contents of storage with incoming sensory patterns, in order to determine whether the current stimulus has been seen before, and to determine the appropriate response from the organism. The theorists in the empiricist tradition, on the other hand, have essentially combined the answer to the third question with their answer to the second: since the stored information takes the form of new connections, or transmission channels in the nervous system (or the creation of conditions which are functionally equivalent to new connections), it follows that the new stimuli will make use of these new pathways which have been created, automatically activating the appropriate response without requiring any separate process for their recognition or identification.
The theory to be presented here takes the empiricist, or “connectionist” position with regard to these questions. The theory has been developed for a hypothetical nervous system, or machine, called a perceptron. The perceptron is designed to illustrate some of the fundamental properties of intelligent systems in general, without becoming too deeply enmeshed in the special, and frequently unknown, conditions which hold for particular biological organisms. The analogy between the perceptron and biological systems should be readily apparent to the reader.
During the last few decades, the development of symbolic logic, digital computers, and switching theory has impressed many theorists with the functional similarity between a neuron and the simple on-off units of which computers are constructed, and has provided the analytical methods necessary for representing highly complex logical functions in terms of such elements. The result has been a profusion of brain models which amount simply to logical contrivances for performing particular algorithms (representing “recall,” stimulus comparison, transformation, and various kinds of analysis) in response to sequences of stimuli—e.g., Rashevsky (1938); McCulloch (1951); McCulloch and Pitts (1943); Culbertson (1950); Kleene (1951); Minsky (1956). A relatively small number of theorists, like Ashby (1952), von Neumann (1951), and von Neumann (1956), have been concerned with the problems of how an imperfect neural network, containing many random connections, can be made to perform reliably those functions which might be represented by idealized wiring diagrams. Unfortunately, the language of symbolic logic and boolean algebra is less well suited for such investigations. The need for a suitable language for the mathematical analysis of events in systems where only the gross organization can be characterized, and the precise structure is unknown, has led the author to formulate the current model in terms of probability theory rather than symbolic logic.
The theorists referred to above were chiefly concerned with the question of how such functions as perception and recall might be achieved by a deterministic physical system of any sort, rather than how this is actually done by the brain. The models which have been produced all fail in some important respects (absence of equipotentiality, lack of neuroeconomy, excessive specificity of connections and synchronization requirements, unrealistic specificity of stimuli sufficient for cell firing, postulation of variables or functional features with no known neurological correlates, etc.) to correspond to a biological system. The proponents of this line of approach have maintained that, once it has been shown how a physical system of any variety might be made to perceive and recognize stimuli, or perform other brainlike functions, it would require only a refinement or modification of existing principles to understand the working of a more realistic nervous system, and to eliminate the shortcomings mentioned above. The writer takes the position, on the other hand, that these shortcomings are such that a mere refinement or improvement of the principles already suggested can never account for biological intelligence; a difference in principle is clearly indicated. The theory of statistical separability (Rosenblatt, 1958b), which is to be summarized here, appears to offer a solution in principle to all of these difficulties.
Those theorists—Hebb (1949); Milner (1957); Eccles (1953); Hayek (1952)—who have been more directly concerned with the biological nervous system and its activity in a natural environment, rather than with formally analogous machines, have generally been less exact in their formulations and far from rigorous in their analysis, so that it is frequently hard to assess whether or not the systems that they describe could actually work in a realistic nervous system, and what the necessary and sufficient conditions might be. Here again, the lack of an analytic language comparable in proficiency to the boolean algebra of the network analysts has been one of the main obstacles. The contributions of this group should perhaps be considered as suggestions of what to look for and investigate, rather than as finished theoretical systems in their own right. Seen from this viewpoint, the most suggestive work, from the standpoint of the following theory, is that of Hebb and Hayek.
The position, elaborated by Hebb (1949); Hayek (1952); Uttley (1956); Ashby (1952), in particular, upon which the theory of the perceptron is based, can be summarized by the following assumptions:
1. The physical connections of the nervous system which are involved in learning and recognition are not identical from one organism to another. At birth, the construction of the most important networks is largely random, subject to a minimum number of genetic constraints.
2. The original system of connected cells is capable of a certain amount of plasticity; after a period of neural activity, the probability that a stimulus applied to one set of cells will cause a response in some other set is likely to change, due to some relatively long-lasting changes in the neurons themselves.
3. Through exposure to a large sample of stimuli, those which are most “similar” (in some sense which must be defined in terms of the particular physical system) will tend to form pathways to the same sets of responding cells. Those which are markedly “dissimilar” will tend to develop connections to different sets of responding cells.
4. The application of positive and/or negative reinforcement (or stimuli which serve this function) may facilitate or hinder whatever formation of connections is currently in progress.
5. Similarity, in such a system, is represented at some level of the nervous system by a tendency of similar stimuli to activate the same sets of cells. Similarity is not a necessary attribute of particular formal or geometrical classes of stimuli, but depends on the physical organization of the perceiving system, an organization which evolves through interaction with a given environment. The structure of the system, as well as the ecology of the stimulus-environment, will affect, and will largely determine, the classes of “things” into which the perceptual world is divided.
18.1 The Organization of a Perceptron
The organization of a typical photo-perceptron (a perceptron responding to optical patterns as stimuli) is shown in Figure 18.1. The rules of its organization are as follows:
1. Stimuli impinge on a retina of sensory units (S-points), which are assumed to respond on an all-or-nothing basis, in some models, or with a pulse amplitude or frequency proportional to the stimulus intensity, in other models. In the models considered here, an all-or-nothing response will be assumed.
2. Impulses are transmitted to a set of association cells (A-units) in a “projection area” (AI). This projection area may be omitted in some models, where the retina is connected directly to the association area (AII). The cells in the projection area each receive a number of connections from the sensory points. The set of S-points transmitting impulses to a particular A-unit will be called the origin points of that A-unit. These origin points may be either excitatory or inhibitory in their effect on the A-unit. If the algebraic sum of excitatory and inhibitory impulse intensities is equal to or greater than the threshold (θ) of the A-unit, then the A-unit fires, again on an all-or-nothing basis (or, in some models, which will not be considered here, with a frequency which depends on the net value of the impulses received). The origin points of the A-units in the projection area tend to be clustered or focalized, about some central point, corresponding to each A-unit. The number of origin points falls off exponentially as the retinal distance from the central point for the A-unit in question increases. (Such a distribution seems to be supported by physiological evidence, and serves an important functional purpose in contour detection.)
3. Between the projection area and the association area (AII), connections are assumed to be random. That is, each A-unit in the AII set receives some number of fibers from origin points in the AI set, but these origin points are scattered at random throughout the projection area. Apart from their connection distribution, the AII units are identical with the AI units, and respond under similar conditions.
4. The “responses,” R1, R2, …, Rn are cells (or sets of cells) which respond in much the same fashion as the A-units. Each response has a typically large number of origin points located at random in the AII set. The set of A-units transmitting impulses to a particular response will be called the source-set for that response. (The source-set of a response is identical to its set of origin points in the A-system.) The arrows in Figure 18.1 indicate the direction of transmission through the network. Note that up to AII all connections are forward, and there is no feedback. When we come to the last set of connections, between AII and the R-units, connections are established in both directions. The rule governing feedback connections, in most models of the perceptron, can be either of the following alternatives:
(a) Each response has excitatory feedback connections to the cells in its own source-set, or
(b) Each response has inhibitory feedback connections to the complement of its own source-set (i.e., it tends to prohibit activity in any association cells which do not transmit to it).
The first of these rules seems more plausible anatomically, since the R-units might be located in the same cortical area as their respective source-sets, making mutual excitation between the R-units and the A-units of the appropriate source-set highly probable. The alternative rule (b) leads to a more readily analyzed system, however, and will therefore be assumed for most of the systems to be evaluated here. …
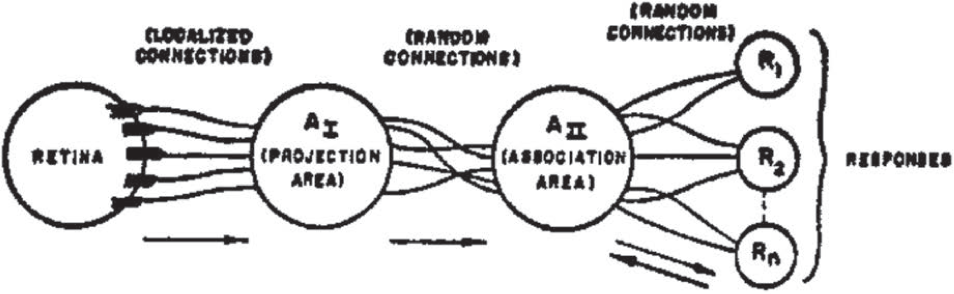
Figure 18.1: Organization of a perceptron.
18.2 Conclusions and Evaluation
The main conclusions of the theoretical study of the perceptron can be summarized as follows:
1. In an environment of random stimuli, a system consisting of randomly connected units, subject to the parametric constraints discussed above, can learn to associate specific responses to specific stimuli. Even if many stimuli are associated to each response, they can still be recognized with a better-than-chance probability, although they may resemble one another closely and may activate many of the same sensory inputs to the system.
2. In such an “ideal environment,” the probability of a correct response diminishes towards its original random level as the number of stimuli learned increases.
3. In such an environment, no basis for generalization exists.
4. In a “differentiated environment,” where each response is associated to a distinct class of mutually correlated, or “similar” stimuli, the probability that a learned association of some specific stimulus will be correctly retained typically approaches a better-than-chance asymptote as the number of stimuli learned by the system increases. This asymptote can be made arbitrarily close to unity by increasing the number of association cells in the system.
5. In the differentiated environment, the probability that a stimulus which has not been seen before will be correctly recognized and associated to its appropriate class (the probability of correct generalization) approaches the same asymptote as the probability of a correct response to a previously reinforced stimulus. This asymptote will be better than chance if the inequality Pc12 < Pa < Pc11 is met, for the stimulus classes in question.
6. The performance of the system can be improved by the use of a contour-sensitive projection area, and by the use of a binary response system, in which each response, or “bit,” corresponds to some independent feature or attribute of the stimulus.
7. Trial-and-error learning is possible in bivalent reinforcement systems.
8. Temporal organizations of both stimulus patterns and responses can be learned by a system which uses only an extension of the original principles of statistical separability, without introducing any major complications in the organization of the system.
9. The memory of the perceptron is distributed, in the sense that any association may make use of a large proportion of the cells in the system, and the removal of a portion of the association system would not have an appreciable effect on the performance of any one discrimination or association, but would begin to show up as a general deficit in all learned associations
10. Simple cognitive sets, selective recall, and spontaneous recognition of the classes present in a given environment are possible. The recognition of relationships in space and time, however, seems to represent a limit to the perceptron’s ability to form cognitive abstractions.
Psychologists, and learning theorists in particular, may now ask: “What has the present theory accomplished, beyond what has already been done in the quantitative theories of Hull, Bush and Mosteller, etc., or physiological theories such as Hebb’s?” The present theory is still too primitive, of course, to be considered as a full-fledged rival of existing theories of human learning. Nonetheless, as a first approximation, its chief accomplishment might be stated as follows:
For a given mode of organization (α, β, or γ; Σ or μ; monovalent or bivalent) the fundamental phenomena of learning, perceptual discrimination, and generalization can be predicted entirely from six basic physical parameters, namely:
x: the number of excitatory connections per A-unit,
y: the number of inhibitory connections per A-unit,
θ: the expected threshold of an A-unit,
ω: the proportion of R-units to which an A-unit is connected,
NA: the number of A-units in the system, and
NR: the number of R-units in the system.
NA (the number of sensory units) becomes important if it is very small. It is assumed that the system begins with all units in a uniform state of value; otherwise the initial value distribution would also be required. Each of the above parameters is a clearly defined physical variable, which is measurable in is own right, independently of the behavioral and perceptual phenomena which we are trying to predict.
As a direct consequence of its foundation on physical variables the present system goes far beyond existing learning and behavior theories in three main points: parsimony, verifiability, and explanatory power and generality. Let us consider each of these points in turn.
18.2.1 Parsimony Essentially all of the basic variables and laws used in this system are already present in the structure of physical and biological science, so that we have found it necessary to postulate only one hypothetical variable (or construct) which we have called V, the “value” of an association cell; this is a variable which must conform to certain functional characteristics which can clearly be stated, and which is assumed to have a potentially measurable physical correlate.
18.2.2 Verifiability Previous quantitative learning theories, apparently without exception, have had one important characteristic in common: they have all been based on measurements of behavior, in specified situations, using these measurements (after theoretical manipulation) to predict behavior in other situations. Such a procedure, in the last analysis, amounts to a process of curve fitting and extrapolation, in the hope that the constants which describe one set of curves will hold good for other curves in other situations. While such extrapolation is not necessarily circular, in the strict sense, it shares many of the logical difficulties of circularity, particularly when used as an “explanation” of behavior. Such extrapolation is difficult to justify in a new situation, and it has been shown that if the basic constants and parameters are to be derived anew for any situation in which they break down empirically (such as change from white rats to humans), then the basic “theory” is essentially irrefutable, just as any successful curve-fitting equation is irrefutable. It has, in fact, been widely conceded by psychologists that there is little point in trying to “disprove” any of the major learning theories in use today, since by extension, or a change in parameters, they have all proved capable of adapting to any specific empirical data. This is epitomized in the increasingly common attitude that a choice of theoretical model is mostly a matter of personal aesthetic preference or prejudice, each scientist being entitled to a favorite model of his own. In considering this approach, one is reminded of a remark attributed to Kistiakowsky, that “given seven parameters, I could fit an elephant.” This is clearly not the case with a system in which the independent variables, or parameters, can be measured independently of the predicted behavior. In such a system, it is not possible to “force” a fit to empirical data, if the parameters in current use should lead to improper results. In the current theory a failure to fit a curve in a new situation would be a clear indication that either the theory or the empirical measurements are wrong. Consequently, if such a theory does hold for repeated tests, we can be considerably more confident of its validity and of its generality than in the case of a theory which must be hand-tailored to meet each situation.
18.2.3 Explanatory power and generality The present theory, being derived from basic physical variables, is not specific to any one organism or learning situation. It can be generalized in principle to cover any form of behavior in any system for which the physical parameters are known. A theory of learning, constructed on these foundations, should be considerably more powerful than any which has previously been proposed. It would not only tell us what behavior might occur in any known organism, but would permit the synthesis of behaving systems, to meet special requirements. Other learning theories tend to become increasingly qualitative as they are generalized. Thus a set of equations describing the effects of reward on T-maze learning in a white rat reduces simply to a statement that rewarded behavior tends to occur with increasing probability when we attempt to generalize it from any species and any situation. The theory which has been presented here loses none of its precision through generality. …
Reprinted from Rosenblatt (1958a).