2
The True Method (1677)
Gottfried Wilhelm Leibniz
Gottfried Wilhelm Leibniz (1646–1716) was a polymath—a philosopher of great breadth and a legal and political thinker, as well as a profound and prolific mathematician. He would be in the running for the title of first computer scientist. Pascal might be considered for his adding machine, and others before and after, but Leibniz built a nested-loop calculator that could both multiply and divide (see page 62). More remarkably, he invented binary arithmetic (Figure 2.1) and designed a binary calculator (which was never built).
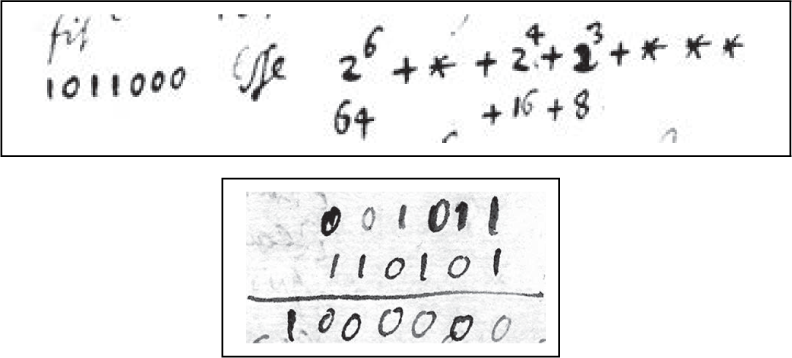
Figure 2.1: Binary to decimal conversion and a binary sum, from Leibniz’s De progressione dyadica (1679).
Leibniz shares credit with Isaac Newton for discovering what was then called the calculus of infinitesimals. Today the calculus is so identified with mathematics that we no longer hear the reference to the calculations that were its original motivations—for example, how to find the area of a figure by adding up the areas of thin slices. Leibniz’s notation dx for an infinitesimal change in x survives to this day, because the notation makes it easy to state plug-and-chug rules that are almost inexpressible in Newton’s dot notation. For example, the identity ![]() is very awkward to state using Newton’s notation
is very awkward to state using Newton’s notation ![]() for the derivative of y.
for the derivative of y.
Leibniz recognized how good notation can contribute to clear thought. He had been introduced to Aristotle at age 14, and as part of his education wrote a thesis on the use of a systematized logic in legal reasoning (Leibniz, 1666). He developed formal notations for logical reasoning, an early form of mathematical logic (Struik, 1969, page 123). His effort to capture reasoning in a logical system with formal rules evolved into a grand plan to unify all of human knowledge in a system that would settle all disputes; the facts, once established, would then yield incontestable answers. All of human reasoning would be reduced to plugging and chugging, and the result would be an unequivocally better world. Leibniz’s famous optimism—his confidence that the world we live in was the best of all possible worlds—thus melded with an early techno-utopianism.
Even as he was recognized for his mathematical contributions, he was ridiculed for his optimism. In 1759 Voltaire caricatured him as Dr. Pangloss in Candide. Today his dream of a perfect world through logic and mechanized reasoning seems naïve and a poor fit for the theological framework on which he stretched it. And yet his imagined logical reductionism reappears regularly—recognizably in McCulloch and Pitts (1943, here page 83) and Bush (1945a, here page 114), and generally in every automated decision support system.
SINCE happiness consists in contentment, and since enduring contentment depends on the assurance we have of the future—assurance based on the knowledge we should have of the nature of God and the soul—it follows that knowledge is necessary for true happiness.
But knowledge depends upon demonstration, and the invention of demonstrations by a certain method, which is not known to everyone. For although every man is capable of judging a demonstration (since it would not deserve this name if all those who consider it attentively were not convinced and persuaded by it), nevertheless not every man is capable of devising demonstrations on his own initiative, nor to propose them clearly once they are found, for want of leisure or method.
The true method taken in all of its extent is to my mind a thing hitherto quite unknown, and has not been practised except in mathematics. It is still very imperfect with regard to mathematics itself, as I had the good fortune to show to some (who are considered today to be among the foremost mathematicians of the century) by means of surprising proofs. And I expect to offer some examples of it, which will be perhaps not unworthy of posterity.
Yet if the method of mathematicians has not been sufficient to discover all that could be wished from them, it has at least been able to save them from mistakes, and if they have not said everything they ought to say, they have also said nothing they ought not to say.
If those who have cultivated the other sciences had imitated the mathematicians at least on this point, we would be very happy, and we would have long since had a secure metaphysics, as well as the morals which depend upon it, since metaphysics contains knowledge of God and the soul, knowledge which should govern our life.
Moreover, we would have the science of motion, which is the key to physics and, consequently, to medicine. It is true I believe we are now in a state to aspire to it, and some of my first thoughts, because of their wonderful simplicity, have been received with such applause by the most learned of our time that I believe we now have only to perform certain experiments properly designed and considered (rather than by chance and by trial and error, as commonly happens) in order to erect thereupon the bastion of a certain and demonstrative physics.
Now, the reason the art of demonstration has been until now found only in mathematics has not been properly fathomed by anyone, for if the cause of the difficulty had been known, the remedy would have long since been discovered. The reason is that mathematics carries its own test with it. For when I am presented with a false theorem, I do not need to examine it or even to know the demonstration, since I shall discover its falsity a posteriori by an easy experiment, which costs nothing but ink and paper, that is, by calculation, which will reveal the error, no matter how small it is. If it were as easy in other matters to verify reasoning by experiments then there would not be such differing opinions. But the trouble is that experiments in physics are difficult and have a high cost, and in metaphysics they are impossible unless God, for our sake, performs a miracle to make remote immaterial things known to us.
This difficulty is not insurmountable, although at first it seems to us that it is. But those who will want to consider what I am going to say about it will soon change their mind. It must be noted, then, that the tests or experiments performed in mathematics to guard against false reasoning (as are, for example, the test of casting out nines, the calculation of Ludolph of Cologne concerning the size of the circle, tables of sines or others) are not made on the thing itself, but on the characters we have substituted in place of the thing. [EDITOR: “Casting out nines” is to test whether a number is divisible by 9 by repeatedly adding up its digits. Aristotle had approximated the value of π by calculating the area of a regular 96-sided polygon; Ludolph (1540–1610) used a 262-sided polygon instead, thus calculating π to 35 decimal places, an effort that took years (Ludolph van Ceulen, 1596).] For to take a calculation of numbers, for example if 1677 times 365 makes 612,105, it would never have been done if one had to make 365 heaps and put 1677 small stones in each one and then at length count them all in order to know if the aforementioned number is found. That is why we are content to do it with characters on paper, by means of the test of nines or some other. Likewise, when someone proposes a supposedly exact quadrature of the circle, we do not need to make a material circle and tie a thread around it in order to see whether the length of this thread or the circumference to the diameter has the proportion proposed; that would be difficult, for even if the error is a thousandth (or less) part of the diameter, a large circle constructed with a great deal of accuracy would be required. Yet we nonetheless refute this false quadrature by experiment and by the calculation or test in numbers. But this test is performed only on paper, and consequently on the characters which represent the thing, and not on the thing itself.
This consideration is fundamental in this matter, and although many very able people, especially in our century, have claimed to give us demonstrations regarding physics, metaphysics, morals, and even in politics, jurisprudence, and medicine, nevertheless either they have been mistaken (because all the steps are slippery and it is difficult not to fall unless guided by some directions), or even if they did hit upon them, they have been unable to make their arguments accepted universally (because there has not yet been a way to examine arguments by some easy tests of which everyone is capable).
From this it is clear that, if we could find characters or signs appropriate for expressing all our thoughts as clearly and exactly as arithmetic expresses numbers or geometric analysis expresses lines, we could accomplish in all matters, insofar as they are amenable to reasoning, everything that can be done in arithmetic and geometry.
For all inquiries that depend upon reasoning would be performed by the transposition of these characters and by a kind of calculation, which would make the invention of beautiful things quite easy. For we would not have to rack our brains as much as we are forced to do today, and nevertheless we would be sure of being able to accomplish everything feasible, in accordance with the given facts.
Moreover, everyone would be made to agree on what had been found or concluded, since it would be easy to verify the calculation either by repeating it or by trying some tests similar to that of casting out nines in arithmetic. And if someone were to doubt what I had done, I would say to him, “Let us calculate, Sir,” and thus taking up pen and ink we should soon settle the matter.
I always add: insofar as can be done by reasoning, in accordance with the given facts. For although certain experiments are always needed to serve as a basis for reasoning, nevertheless, once these experiments are given, we would draw from them everything that anyone else could possibly draw from them, and would even discover the experiments which remain to be performed for the clarification of all remaining doubts. That would be an admirable help, even in politics and medicine, for reasoning about the given symptoms and circumstances in a steady and perfect way. For even though there will not be enough given circumstances to form an infallible judgement, we shall always be able to determine what is most probable from the given facts. And that is all reason can do.
Now the characters that will express all our thoughts will form a new language which can be written and spoken; this language will be very difficult to construct but very easy to learn. It will be quickly accepted by everyone on account of its great use and its surprising facility, and it will serve wonderfully for communication among many peoples, which will help make it accepted. Those who will write in this language will not make mistakes, provided they avoid the errors of calculation, barbarisms, solecisms, and other mistakes of grammar and construction. Moreover, this language will possess a wonderful property, namely that of silencing the ignorant. For one will be unable to speak or write in this language except about what he understands, or if one tries to do so, one of two things will happen: either the vanity of what is advanced will be obvious to everyone, or it will be learned by writing or speaking. Just as indeed those who calculate learn by writing and those who speak sometimes encounter success they did not imagine, with the tongue running ahead of the mind. This will happen especially in our language because of its exactness. So much so that there will be no equivocations or amphibolies, and everything that will be said intelligibly in it will be said with propriety.
I dare say that this is the highest effort of the human mind, and when the project is accomplished it will merely be up to men to be happy since they will have an instrument which will serve to exalt reason no less than the telescope serves to perfect vision.
It is one of my ambitions to finish this project if God grants me the time. I owe it only to myself, and I had the first thought about it at the age of eighteen, as I evidenced a little later in a printed discourse (Leibniz, 1666). And as I am certain there is no invention which comes close to this one, I believe there is nothing so capable of immortalizing the name of the inventor. But I have much stronger reasons for thinking about it, for the religion I follow closely assures me that the love of God consists in an ardent desire to procure the general good, and reason teaches me that there is nothing which contributes more to the general good of all men than what perfects reason.
Reprinted from Leibniz (2020), with permission from Lloyd Strickland. Images reproduced with permission from Gottfried Wilhelm Leibniz Bibliothek.