21
Recursive Functions of Symbolic Expressions and Their Computation by Machine (1960)
John McCarthy
John McCarthy (1927–2011) studied mathematics at Cal Tech as an undergraduate and at Princeton as a PhD student. While teaching at Dartmouth College in 1956, McCarthy hosted a summer school there on what he dubbed “Artificial Intelligence.” According to the proposal for the conference (McCarthy, 1960), co-authored by McCarthy, Shannon, Marvin Minsky (then a Junior Fellow at Harvard), and the IBM researcher Nathaniel Rochester, the subjects for the conference would include (1) “Automatic computers” (how to write programs to simulate “the higher functions of the human brain”); (2) “How can a computer be programmed to use a language”; (3) “Neuron nets” (citing McCulloch and Pitts); (4) “Theory of the size of a calculation” (“a theory of the complexity of functions”); (5) “Self-improvement”; (6) “Abstractions”; and (7) “Randomness and creativity.” All are still active research problems today!
McCarthy moved to MIT, where he was instrumental in the birth of time-sharing (chapter 23). There he invented the LISP programming language as a tool for the sort of symbolic reasoning he anticipated would be key to progress in AI. It was an audacious move, to borrow so directly from the lambda-calculus that Alonzo Church had developed as a mathematical language for resolving Hilbert’s Entscheidungsproblem. In this initial description of LISP, the language was purely interpretive; it would take years before compilers were developed. McCarthy had to develop the garbage collection technique of memory management in order to make even small programs executable on the memory-limited machines of the day. LISP has remained not only usable but influential; McCarthy was involved in the design of ALGOL 60, the first widely-used general purpose language featuring recursion, and LISP has influenced the design of every subsequent functional programming language.
In 1962 McCarthy moved to Stanford, where he started the Artificial Intelligence Laboratory (SAIL), the foundry of vast amounts of influential AI research. Not only McCarthy but fifteen other affiliates of the SAIL have been recognized with the Turing Award. Throughout his career, he almost uniquely combined a deeply rooted respect for formal, mathematical, logical foundations with the ambition to produce working code that emulated aspects of human thought.
21.1 Introduction
A programming system called LISP (for LISt Processor) has been developed for the IBM 704 computer by the Artificial Intelligence group at M.I.T. The system was designed to facilitate experiments with a proposed system called the Advice Taker, whereby a machine could be instructed to handle declarative as well as imperative sentences and could exhibit “common sense” in carrying out its instructions. The original proposal (McCarthy, 1961) for the Advice Taker was made in November 1958. The main requirement was a programming system for manipulating expressions representing formalized declarative and imperative sentences so that the Advice Taker system could make deductions.
In the course of its development the LISP system went through several stages of simplification and eventually came to be based on a scheme for representing the partial recursive functions of a certain class of symbolic expressions. This representation is independent of the IBM 704 computer, or of any other electronic computer, and it now seems expedient to expound the system by starting with the class of expressions called S-expressions and the functions called S-functions.
In this article, we first describe a formalism for defining functions recursively. We believe this formalism has advantages both as a programming language and as vehicle for developing a theory of computation. Next, we describe S-expressions and S-functions, give some examples, and then describe the universal S-function apply which plays the theoretical role of a universal Turing machine and the practical role of an interpreter. Then we describe the representation of S-expressions in the memory of the IBM 704 by list structures similar to those used by Newell and Shaw (1957), and the representation of S-functions by program. Then we mention the main features of the LISP programming system for the IBM 704. Next comes another way of describing computations with symbolic expressions, and finally we give a recursive function interpretation of flow charts.
We hope to describe some of the symbolic computations for which LISP has been used in another paper, and also to give elsewhere some applications of our recursive function formalism to mathematical logic and to the problem of mechanical theorem proving.
21.2 Functions and Function Definitions
We shall need a number of mathematical ideas and notations concerning functions in general. Most of the ideas are well known, but the notion of conditional expression is believed to be new, and the use of conditional expressions permits functions to be defined recursively in a new and convenient way.
a. Partial Functions. A partial function is a function that is defined only on part of its domain. Partial functions necessarily arise when functions are defined by computations because for some values of the arguments the computation defining the value of the function may not terminate. However, some of our elementary functions will be defined as partial functions.
b. Propositional Expressions and Predicates. A propositional expression is an expression whose possible values are T (for truth) and F (for falsity). We shall assume that the reader is familiar with the propositional connectives ∧ (“and”), ∨ (“or”), and ∼ (“not”), Typical propositional expressions are:
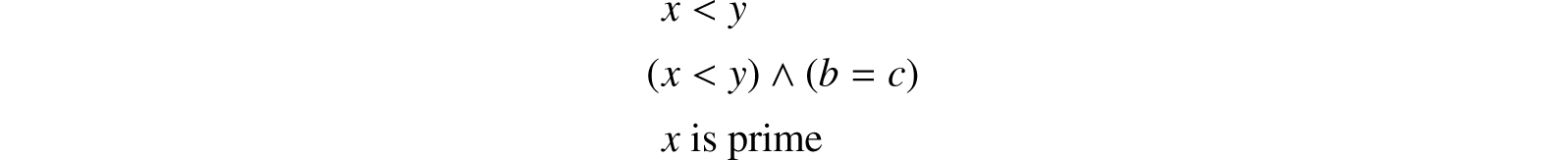
A predicate is a function whose range consists of the truth values T and F.
c. Conditional Expressions. The dependence of truth values on the values of quantities of other kinds is expressed in mathematics by predicates, and the dependence of truth values on other truth values by logical connectives. However, the notations for expressing symbolically the dependence of quantities of other kinds on truth-values is inadequate, so that English words and phrases are generally used for expressing these dependences in texts that describe other dependences symbolically. For example, the function |x| is usually defined in words.
Conditional expressions are a device for expressing the dependence of quantities on propositional quantities. A conditional expression has the form (p1 → e1, ⋯ , pn → en), where the p’s are propositional expressions and the e’s are expressions of any kind. It may be read, “If p1 then e1, otherwise if p2 then e2, ⋯, otherwise if pn then en,” or “p1 yields e1, ⋯, pn yields en.”
We now give the rules for determining whether the value (p1 → e1, ⋯ , pn → en) is defined, and if so what its value is. Examine the p’s from left to right. If a p whose value is T is encountered before any p whose value is undefined is encountered, then the value of the conditional expression is the value of the corresponding e (if this is defined). If any undefined p is encountered before a true p, or if all p’s are false, or if the e corresponding to the first true p is undefined, then the value of the conditional expression is undefined. We now give examples.
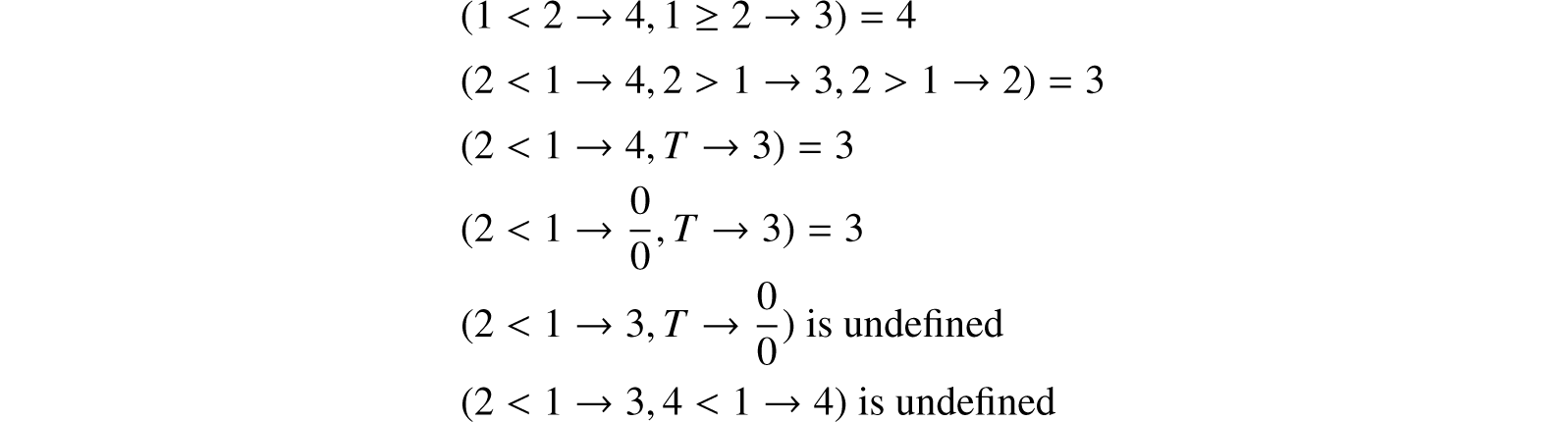
Some of the simplest applications of conditional expressions are in giving such definitions as

d. Recursive Function Definitions. By using conditional expressions we can, without circularity, define functions by formulas in which the defined function occurs. For example, we write

When we use this formula to evaluate 0! we get the answer 1; because of the way in which the value of a conditional expression was defined, the meaningless expression 0 · (0 − 1)! does not arise. The evaluation of 2! according to this definition proceeds as follows:
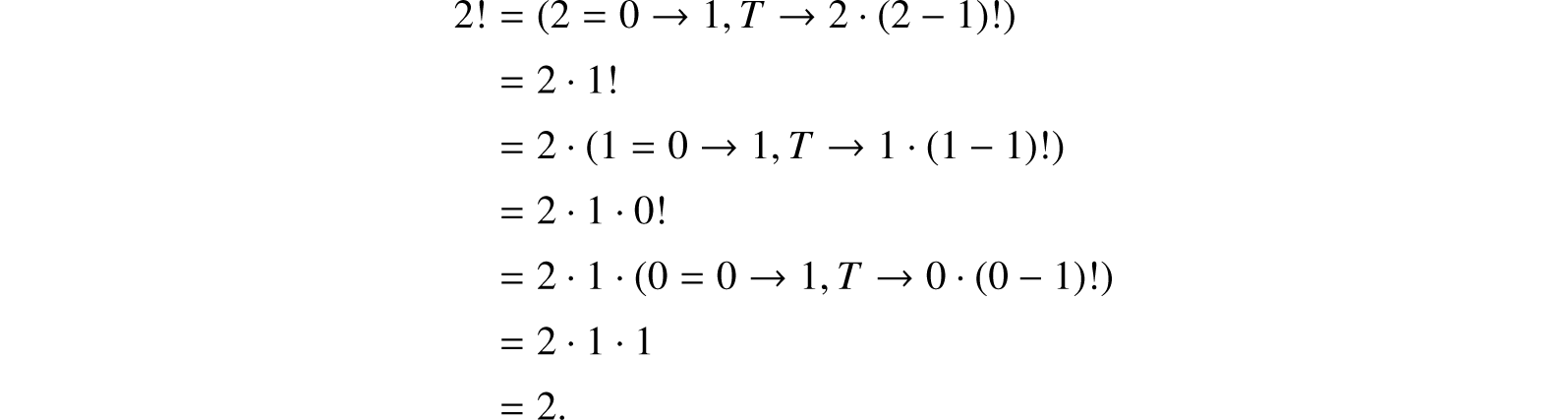
We now give two other applications of recursive function definitions. The greatest common divisor, gcd(m, n), of two positive integers m and n is computed by means of the Euclidean algorithm. This algorithm is expressed by the recursive function definition:
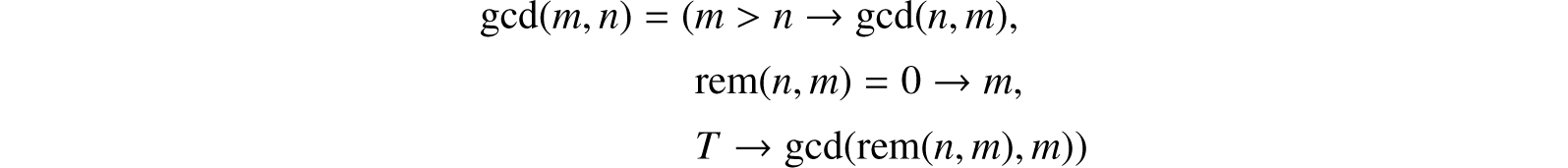
where rem(n, m) denotes the remainder left when n is divided by m.
The Newtonian algorithm for obtaining an approximate square root of a number a, starting with an initial approximation x and requiring that an acceptable approximation y satisfy |y2 − a| < ε, may be written
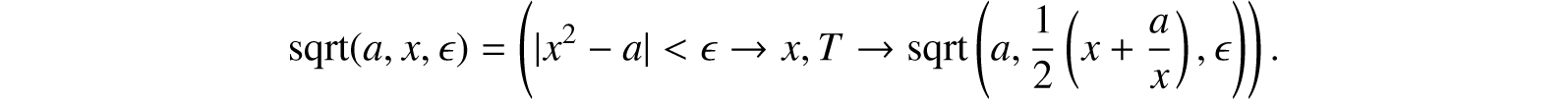
The simultaneous recursive definition of several functions is also possible, and we shall use such definitions if they are required. There is no guarantee that the computation determined by a recursive definition will ever terminate and, for example, an attempt to compute n! from our definition will only succeed if n is a non-negative integer. If the computation does not terminate, the function must be regarded as undefined for the given arguments.
The propositional connectives themselves can be defined by conditional expressions. We write

It is readily seen that the right-hand sides of the equations have the correct truth tables. If we consider situations in which p or q may be undefined, the connectives ∧ and ∨ are seen to be noncommutative. For example if p is false and q is undefined, we see that according to the definitions given above p ∧ q is false, but q ∧ p is undefined. For our applications this noncommutativity is desirable, since p ∧ q is computed by first computing p, and if p is false q is not computed. If the computation for p does not terminate, we never get around to computing q. We shall use propositional connectives in this sense hereafter.
e. Functions and Forms. It is usual in mathematics—outside of mathematical logic—to use the word “function” imprecisely and to apply it to forms such as y2 + x. Because we shall later compute with expressions for functions, we need a distinction between functions and forms and a notation for expressing this distinction. This distinction and a notation for describing it, from which we deviate trivially, is given by Church (1941).
Let f be an expression that stands for a function of two integer variables. It should make sense to write f(3, 4) and the value of this expression should be determined. The expression y2 + x does not meet this requirement; y2 + x(3, 4) is not a conventional notation, and if we attempted to define it we would be uncertain whether its value would turn out to be 13 or 19. Church calls an expression like y2 + x a form. A form can be converted into a function if we can determine the correspondence between the variables occurring in the form and the ordered list of arguments of the desired function. This is accomplished by Church’s λ-notation.
If ℰ is a form in variables x1, ⋯ , xn, then λ((x1, ⋯ , xn), ℰ) will be taken to be the function of n variables whose value is determined by substituting the arguments for the variables x1, ⋯, xn in that order in ℰ and evaluating the resulting expression. For example, λ((x, y), y2 + x) is a function of two variables, and λ((x, y), y2 + x)(3, 4) = 19.
The variables occurring in the list of variables of a λ-expression are dummy or bound, like variables of integration in a definite integral. That is, we may change the names of the bound variables in a function expression without changing the value of the expression, provided that we make the same change for each occurrence of the variable and do not make two variables the same that previously were different. Thus λ((x, y), y2 + x), λ((u, v), v2 + u) and λ((y, x), x2 + y) denote the same function.
We shall frequently use expressions in which some of the variables are bound by λ’s and others are not. Such an expression may be regarded as defining a function with parameters. The unbound variables are called free variables.
An adequate notation that distinguishes functions from forms allows an unambiguous treatment of functions of functions. It would involve too much of a digression to give examples here, but we shall use functions with functions as arguments later in this report. …
21.3 Recursive Functions of Symbolic Expressions
We shall first define a class of symbolic expressions in terms of ordered pairs and lists. Then we shall define five elementary functions and predicates, and build from them by composition, conditional expressions, and recursive definitions an extensive class of functions of which we shall give a number of examples. We shall then show how these functions themselves can be expressed as symbolic expressions, and we shall define a universal function apply that allows us to compute from the expression for a given function its value for given arguments. Finally, we shall define some functions with functions as arguments and give some useful examples.
a. A Class of Symbolic Expressions. We shall now define the S-expressions (S stands for symbolic). They are formed by using the special characters
.
(
)
and an infinite set of distinguishable atomic symbols. For atomic symbols, we shall use strings of capital Latin letters and digits with single imbedded blanks. Examples of atomic symbols are
A
ABA
APPLE PIE NUMBER 3
There is a twofold reason for departing from the usual mathematical practice of using single letters for atomic symbols. First, computer programs frequently require hundreds of distinguishable symbols that must be formed from the 47 characters that are printable by the IBM 704 computer. Second, it is convenient to allow English words and phrases to stand for atomic entities for mnemonic reasons. The symbols are atomic in the sense that any substructure they may have as sequences of characters is ignored. We assume only that different symbols can be distinguished.
S-expressions are then defined as follows:
1. Atomic symbols are S-expressions.
2. If e1 and e2 are S-expressions, so is (e1 · e2).
Examples of S-expressions are
AB
(A · B)
((AB · C) · D)
An S-expression is then simply an ordered pair, the terms of which may be atomic symbols or simpler S-expressions. We can represent a list of arbitrary length in terms of S-expressions as follows. The list (m1, m2, ⋯ , mn) is represented by the S-expression
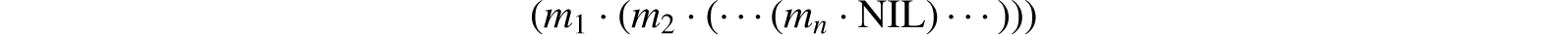
where NIL is an atomic symbol used to terminate lists.
Since many of the symbolic expressions with which we deal are conveniently expressed as lists, we shall introduce a list notation to abbreviate certain S-expressions. We have
1. (m) stands for (m · NIL).
2. (m1, ⋯ , mn) stands for (m1 · (⋯(mn · NIL)⋯ )).
3. (m1, ⋯ , mn · x) stands for (m1 · (⋯(mn · x)⋯ )).
Subexpressions can be similarly abbreviated. Some examples of these abbreviations are
((AB, C), D) for ((AB · (C · NIL)) · (D · NIL))
((A, B), C, D · E) for ((A · (B · NIL)) · (C · (D · E)))
Since we regard the expressions with commas as abbreviations for those not involving commas, we shall refer to them all as S-expressions.
b. Functions of S-expressions and the Expressions That Represent Them. We now define a class of functions of S-expressions. The expressions representing these functions are written in a conventional functional notation. However, in order to clearly distinguish the expressions representing functions from S-expressions, we shall use sequences of lower-case letters for function names and variables ranging over the set of S-expressions. We also use brackets and semicolons, instead of parentheses and commas, for denoting the application of functions to their arguments. Thus we write
car [x]
car [cons [(A · B); x]]
In these M-expressions (meta-expressions) any S-expressions that occur stand for themselves.
c. The Elementary S-functions and Predicates. We introduce the following functions and predicates:
1. atom. atom [x] has the value of T or F, accordingly as x is an atomic symbol or not. Thus
atom [X] = T
atom [(X · A)] = F
2. eq. eq[x; y] is defined if and only if both x and y are atomic. eq[x; y] = T if x and y are the same symbol, and eq[x; y] = F otherwise. Thus
eq[X; X] = T
eq[X; A] = F
eq[X; (X · A)] is undefined.
3. car. car[x] is defined if and only if x is not atomic. car[(e1 · e2)] = e1. Thus car[X] is undefined.
car[(X · A)] = X
car[((X · A) · Y)] = (X · A)
4. cdr. cdr[x] is also defined when x is not atomic. We have cdr[(e1 · e2)] = e2. Thus cdr[X] is undefined.
cdr[(X · A)] = A
cdr[((X · A) · Y)] = Y
5. cons. cons[x; y] is defined for any x and y. We have cons[e1; e2] = (e1 ·e2). Thus
cons[X; A] = (X · A)
cons[(X · A); Y] = ((X · A) · Y)
car, cdr, and cons are easily seen to satisfy the relations
car[cons[x; y]] = x
cdr[cons[x; y]] = y
cons[car[x]; cdr[x]] = x, provide that x is not atomic.
The names “car” and “cons” will come to have mnemonic significance only when we discuss the representation of the system in the computer. Compositions of car and cdr give the subexpressions of a given expression in a given position. Compositions of cons form expressions of a given structure out of pairs. The class of functions which can be formed in this way is quite limited and not very interesting.
d. Recursive S-functions. We get a much larger class of functions (in fact, all computable functions) when we allow ourselves to form new functions of S-expressions by conditional expressions and recursive definition.
We now give some examples of functions that are definable in this way.
ff[x]. The value of ff[x] is the first atomic symbol of the S-expression x with the parentheses ignored. Thus
ff[((A · B) · C)] = A
We have
ff[x] = [atom[x] → x; t → ff[car[x]]]
[EDITOR: Other function and predicate definitions and examples omitted.]
…
f. The Universal S-Function apply. There is an S-function apply with the property that if f is an S-expression for an S-function f′ and args is a list of arguments of the form (argl, ⋯, argn), where arg1, ⋯, argn are arbitrary S-expressions, then apply[f; args] and f′[arg1; ⋯; argn] are defined for the same values of arg1, ⋯, argn, and are equal when defined. For example,
λ[[x; y]; cons[car[x]; y]][(A, B); (C, D)]
= apply[(LAMBDA, (X, Y), (CONS, (CAR X), Y)) ((A, B), (C, D))]
= (A, C, D)
…
g. Functions with Functions as Arguments. There are a number of useful functions some of whose arguments are functions. They are especially useful in defining other functions. One such function is maplist [x; f] with an S-expression argument x and an argument f that is a function from S-expressions to S-expressions. We define
maplist [x; f] = [null [x] → NIL; T → cons [f[x]; maplist [cdr [x]; f]]]
The usefulness of maplist is illustrated by formulas for the partial derivative with respect to x of expressions involving sums and products of x and other variables. The S-expressions that we shall differentiate are formed as follows.
1. An atomic symbol is an allowed expression.
2. If e1, ⋯ , en are allowed expressions, (PLUS, e1, ⋯ , en) and (TIMES, e1, ⋯ , en) are also, and represent the sum and product, respectively, of e1, ⋯ , en.
This is, essentially, the Polish notation for functions except that the inclusion of parentheses and commas allows functions of variable numbers of arguments. An example of an allowed expression is (TIMES, X, (PLUS, X, A), Y), the conventional algebraic notation for which is X(X+A)Y.
Our differentiation formula, which gives the derivative of y with respect to x, is
diff[y; x] = [atom[y] → [eq[y; x] → ONE; T → ZERO];
eq[car[y]; PLUS] → cons[PLUS; maplist[cdr[y]; λ[[z]; diff[car[z]; x]]]];
eq[car[y]; TIMES] → cons[PLUS; maplist[cdr[y]; λ[[z]; cons[TIMES;
maplist[cdr[y]; λ[[w]; ∼ eq[z; w] → car[w]; T → diff[car[[w]; x]]]]]]]]]
The derivative of the allowed expression, as computed by this formula, is
(PLUS, (TIMES, ONE, (PLUS, X, A), Y), (TIMES, X, (PLUS, ONE, ZERO), Y),
(TIMES, X, (PLUS, X, A), ZERO))
…
21.4 The LISP Programming System
The LISP programming system is a system for using the IBM 704 computer to compute with symbolic information in the form of S-expressions. It has been or will be used for the following purposes:
1. Writing a compiler to compile LISP programs into machine language.
2. Writing a program to check proofs in a class of formal logical systems.
3. Writing programs for formal differentiation and integration.
4. Writing programs to realize various algorithms for generating proofs in predicate calculus.
5. Making certain engineering calculations whose results are formulas rather than numbers.
6. Programming the Advice Taker system.
The basis of the system is a way of writing computer programs to evaluate S-functions. This will be described in the following sections.
In addition to the facilities for describing S-functions, there are facilities for using S-functions in programs written as sequences of statements along the lines of FORTRAN (IBM, 1956) or ALGOL (Perlis and Samelson, 1958). These features will not be described in this article.
a. Representation of S-Expressions by List Structure. List structure is a collection of computer words arranged as in Figure 21.1a or 21.1b. Each word of the list structure is represented by one of the subdivided rectangles in the figure. The left box of a rectangle represents the address field of the word and the right box represents the decrement field. An arrow from a box to another rectangle means that the field corresponding to the box contains the location of the word corresponding to the other rectangle. [EDITOR: The IBM 704 provided convenient facilities for manipulating the “Contents of the Address field of the Register” (car) and the “Contents of the Decrement field of the Register” (cdr). Within each word of a list structure, early LISP implementations placed that word’s two pointers (to other words of the list structure) in the right bit positions to take advantage of those facilities.]
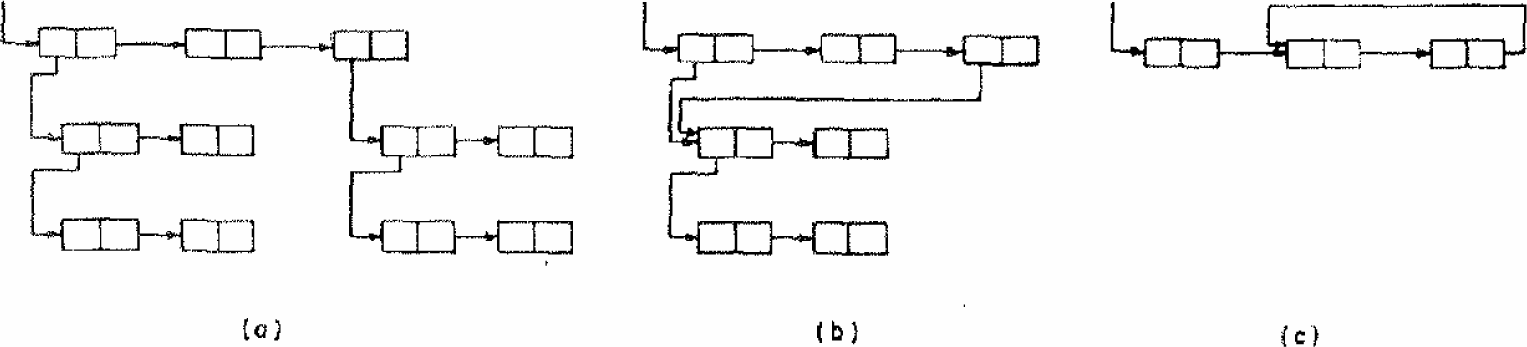
It is permitted for a substructure to occur in more than one place in a list structure, as in Figure 21.1b, but it is not permitted for a structure to have cycles, as in Figure 21.1c.
An atomic symbol is represented in the computer by a list structure of special form called the association list of the symbol. The address field of the first word contains a special constant which enables the program to tell that this word represents an atomic symbol. …
An S-expression x that is not atomic is represented by a word, the address and decrement parts of which contain the locations of the subexpressions car[x] and cdr[x], respectively. …
The advantages of list structures for the storage of symbolic expressions are:
1. The size and even the number of expressions with which the program will have to deal cannot be predicted in advance. Therefore, it is difficult to arrange blocks of storage of fixed length to contain them.
2. Registers can be put back on the free-storage list when they are no longer needed. Even one register returned to the list is of value, but if expressions are stored linearly, it is difficult to make use of blocks of registers of odd sizes that may become available.
3. An expression that occurs as a subexpression of several expressions need be represented in storage only once.
…
e. Free-Storage List. At any given time only a part of the memory reserved for list structures will actually be in use for storing S-expressions. The remaining registers (in our system the number, initially, is approximately 15,000) are arranged in a single list called the free-storage list. A certain register, FREE, in the program contains the location of the first register in this list. When a word is required to form some additional list structure, the first word on the free-storage list is taken and the number in register FREE is changed to become the location of the second word on the free-storage list. No provision need be made for the user to program the return of registers to the free-storage list.
This return takes place automatically, approximately as follows (it is necessary to give a simplified description of this process in this report): There is a fixed set of base registers in the program which contains the locations of list structures that are accessible to the program. Of course, because list structures branch, an arbitrary number of registers may be involved. Each register that is accessible to the program is accessible because it can be reached from one or more of the base registers by a chain of car and cdr operations. When the contents of a base register are changed, it may happen that the register to which the base register formerly pointed cannot be reached by a car–cdr chain from any base register. Such a register may be considered abandoned by the program because its contents can no longer be found by any possible program; hence its contents are no longer of interest, and so we would like to have it back on the free-storage list. This comes about in the following way.
Nothing happens until the program runs out of free storage. When a free register is wanted, and there is none left on the free-storage list, a reclamation cycle starts. First, the program finds all registers accessible from the base registers and makes their signs negative. This is accomplished by starting from each of the base registers and changing the sign of every register that can be reached from it by a car-cdr chain. If the program encounters a register in this process which already has a negative sign, it assumes that this register has already been reached.
After all of the accessible registers have had their signs changed, the program goes through the area of memory reserved for the storage of list structures and puts all the registers whose signs were not changed in the previous step back on the free-storage list, and makes the signs of the accessible registers positive again.
This process, because it is entirely automatic, is more convenient for the programmer than a system in which he has to keep track of and erase unwanted lists. Its efficiency depends upon not coming close to exhausting the available memory with accessible lists. This is because the reclamation process requires several seconds to execute, and therefore must result in the addition of at least several thousand registers to the free-storage list if the program is not to spend most of its time in reclamation. …
Reprinted from McCarthy (1960), with permission from the Association for Computing Machinery.