24
Sketchpad (1963)
Ivan E. Sutherland
While he was growing up, Ivan Sutherland (b. 1938) covered his school books with blueprints that his father, a civil engineer, had discarded. (His mother said that the family could not afford the college-themed book covers his schoolmates were using.) He learned the concise, elegant language of blueprints by staring at his book covers during moments of classroom boredom. When he studied engineering as an undergraduate, he had to create blueprints as well as to interpret them, and he lacked the dexterity and patience to draw them well. So when he entered MIT as a graduate student and found himself with time on the TX-2 computer and in need of a PhD thesis topic, it occurred to him to program the computer to help out with the drawing task. Sutherland was aware of the vision of both Bush (chapter 11) and Licklider (chapter 20), but nothing much like what they imagined had actually been built. This dissertation was written under the direction of Claude Shannon, and thus was born the entire field of computer graphics and interactive computing.
The TX-2 was transistorized, and at the time was the most powerful computer in the world. It had 64K of 36-bit words—twice as much memory as any other machine. It also had a primitive display—just a circular cathode ray tube, and a machine instruction that would flash a point at coordinates specified in the instruction. (Such displays were not new—they had been part of the EDVAC design. See page 210 for Licklider’s analysis of the limitations of display technology in 1960.) There were no raster, line-drawing, or character displays at the time; to draw a line, the software had to stipulate the coordinates of the successive points to be displayed, and then flash each point in rapid succession, repeating the process to give the illusion that the whole line was being displayed at once. More complicated images could be painted on the screen in the same way, as long as the whole process took less than a thirtieth of a second or so, in order to avoid annoying flicker.
To create a drawing program, Sutherland also needed a graphic input device. The TX-2 had a light pen—a photocell connected to the computer by an electric wire. If the photocell was held over part of the displayed image, the program could determine where it was by correlating the time the photocell was activated to the position of the point being displayed at that moment. By displaying a small cross at that position and checking which parts of the cross were visible to the photocell from one instant to the next, the program could determine the direction in which the user was moving the light pen.
All these instrumentalities were replaced by better ones in the following decade—fiber optic cables, tablets, touchscreens, raster displays, color displays, and so on. Sutherland’s durable intellectual contribution was a form of human–computer symbiosis, exactly what Licklider had predicted. Sketchpad allowed the user to stipulate constraints, for example about which lines should be parallel or should meet at their endpoints. The program did its best to keep all constraints satisfied as objects were dragged and distorted. Thus it understood the topology as well as the geometry of the drawing. Sketchpad had facilities for grouping, reduplicating, rotating, and moving objects around. It was the first computer-aided design program. Even more remarkably, its use of novel programming techniques such as constraint satisfaction and object hierarchies sowed the seeds of both non-procedural programming and of object-oriented system design.
When Sutherland visited Bell Helicopter Company in Texas around 1963, he was shown a clever contraption designed to aid pilots landing at night. An infrared camera mounted on the bottom of the helicopter was automatically oriented in coordination with the pilot’s head movements, and the camera image was projected through prisms into the pilot’s field of view. Sutherland had the idea of substituting a computer-generated image for the infrared camera image, and thus was born the first virtual reality system, built at Harvard in 1968. A head-mounted display was tethered to the ceiling by telescoping tubes, enabling the wearer to view a wire-frame cube floating in space and to walk through and around it. Sutherland went on to build the graphic system for the first practical flight simulator at the Evans and Sutherland Computer Company in Utah. As computer graphics developed toward extraordinary verisimilitude in the next decade, Sutherland shifted his efforts to the design of very fast electronic circuits, a field in which he remains active.
One other biographical detail has proved important to the development of computer science. When J. C. R. Licklider left ARPA in 1964 to go to private industry, he was replaced by Sutherland, then fresh out of graduate school and fulfilling the military obligation he had incurred as a ROTC cadet. During the tenure of Licklider and Sutherland at ARPA, visionary funding initiatives stimulated computer science research all across the U.S. That too was part of the creation of the future.
24.1 Abstract
THE Sketchpad system uses drawing as a novel communication medium for a computer. The system contains input, output, and computation programs which enable it to interpret information drawn directly on a computer display. It has been used to draw electrical, mechanical, scientific, mathematical, and animated drawings; it is a general purpose system. Sketchpad has shown the most usefulness as an aid to the understanding of processes, such as the notion of linkages, which can be described with pictures. Sketchpad also makes it easy to draw highly repetitive or highly accurate drawings and to change drawings previously drawn with it. The many drawings in this thesis were all made with Sketchpad.
A Sketchpad user sketches directly on a computer display with a “light pen.” The light pen is used both to position parts of the drawing on the display and to point to them to change them. A set of push buttons controls the changes to be made such as “erase,” or “move.” Except for legends, no written language is used. Information sketched can include straight line segments and circle arcs. Arbitrary symbols may be defined from any collection of line segments, circle arcs, and previously defined symbols. A user may define and use as many symbols as he wishes. Any change in the definition of a symbol is at once seen wherever that symbol appears.
Sketchpad stores explicit information about the topology of a drawing. If the user moves one vertex of a polygon, both adjacent sides will be moved. If the user moves a symbol, all lines attached to that symbol will automatically move to stay attached to it. The topological connections of the drawing are automatically indicated by the user as he sketches. Since Sketchpad is able to accept topological information from a human being in a picture language perfectly natural to the human, it can be used as an input program for computation programs which require topological data, e.g., circuit simulators.
Sketchpad itself is able to move parts of the drawing around to meet new conditions which the user may apply to them. The user indicates conditions with the light pen and push buttons. For example, to make two lines parallel, he successively points to the lines with the light pen and presses a button. The conditions themselves are displayed on the drawing so that they may be erased or changed with the light pen language. Any combination of conditions can be defined as a composite condition and applied in one step.
It is easy to add entirely new types of conditions to Sketchpad’s vocabulary. Since the conditions can involve anything computable, Sketchpad can be used for a very wide range of problems. For example, Sketchpad has been used to find the distribution of forces in the members of truss bridges drawn with it.
Sketchpad drawings are stored in the computer in a specially designed “ring” structure. The ring structure features rapid processing of topological information with no searching at all. The basic operations used in Sketchpad for manipulating the ring structure are described.
24.2 Introduction
The Sketchpad system makes it possible for a man and a computer to converse rapidly through the medium of line drawings. Heretofore, most interaction between men and computers has been slowed down by the need to reduce all communication to written statements that can be typed; in the past, we have been writing letters to rather than conferring with our computers. For many types of communication, such as describing the shape of a mechanical part or the connections of an electrical circuit, typed statements can prove cumbersome. The Sketchpad system, by eliminating typed statements (except for legends) in favor of line drawings, opens up a new area of man–machine communication.
The decision actually to implement a drawing system reflected our feeling that knowledge of the facilities which would prove useful could only be obtained by actually trying them. The decision actually to implement a drawing system did not mean, however, that brute force techniques were to be used to computerize ordinary drafting tools; it was implicit in the research nature of the work that simple new facilities should be discovered which, when implemented, should be useful in a wide range of applications, preferably including some unforeseen ones. It has turned out that the properties of a computer drawing are entirely different from a paper drawing not only because of the accuracy, ease of drawing, and speed of erasing provided by the computer, but also primarily because of the ability to move drawing parts around on a computer drawing without the need to erase them. Had a working system not been developed, our thinking would have been too strongly influenced by a lifetime of drawing on paper to discover many of the useful services that the computer can provide.
As the work has progressed, several simple and very widely applicable facilities have been discovered and implemented. They provide a subpicture capability for including arbitrary symbols on a drawing, a constraint capability for relating the parts of a drawing in any computable way, and a definition copying capability for building complex relationships from combinations of simple atomic constraints. When combined with the ability to point at picture parts given by the demonstrative light pen language, the subpicture, constraint, and definition copying capabilities produce a system of extraordinary power. As was hoped at the outset, the system is useful in a wide range of applications, and unforeseen uses are turning up.
To understand what is possible with the system at present let us consider using it to draw the hexagonal pattern of Figure 24.1. We will issue specific commands with a set of push buttons, turn functions on and off with switches, indicate position information and point to existing drawing parts with the light pen, rotate and magnify picture parts by turning knobs, and observe the drawing on the display system. This equipment as provided at Lincoln Laboratory’s TX-2 computer (Clark et al., 1957) is shown in Figure 24.2. When our drawing is complete it may be inked on paper, as were all the drawings in the thesis, by the plotter (EAI, 1959) shown in Figure 24.3. It is our intent with this example to show what the computer can do to help us draw while leaving the details of how it performs its functions for the chapters which follow.
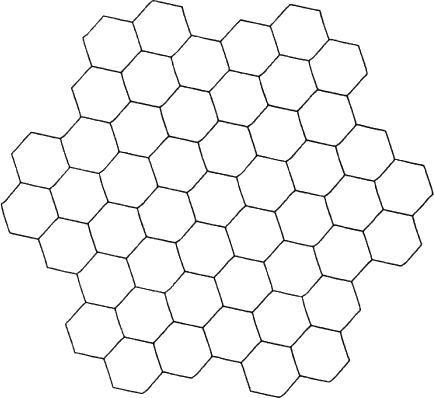
Figure 24.1: Hexagonal pattern.

Figure 24.2: TX-2 operating area—Sketchpad in use. On the display can be seen part of a bridge …. The Author is holding the Light pen. The push buttons used to control specific drawing functions are on the box in front of the Author. Part of the bank of toggle switches can be seen behind the Author. The size and position of the part of the total picture seen on the display is obtained through the four black knobs just above the table.

Figure 24.3: Plotter used with Sketchpad. A digital and analog control system makes the plotter draw straight lines and circles either under direct control of the TX-2 or off-line from punched paper tape.
24.2.1 An introductory example If we point the light pen at the display system and press a button called “draw,” the computer will construct a straight line segment which stretches like a rubber band from the initial to the present location of the pen as shown in Figure 24.4. Additional presses of the button will produce additional lines until we have made six, enough for a single hexagon. To close the figure we return the light pen to near the end of the first line drawn where it will “lock on” to the end exactly. A sudden flick of the pen terminates drawing, leaving the closed irregular hexagon shown in Figure 24.5A.
Figure 24.4: Line and circle drawing.

Figure 24.5: Illustrative example.
To make the hexagon regular, we can inscribe it in a circle. To draw the circle we place the light pen where the center is to be and press the button “circle center,” leaving behind a center point. Now, choosing a point on the circle (which fixes the radius), we press the button “draw” again, this time getting a circle arc whose length only is controlled by light pen position as shown in Figure 24.4.
Next we move the hexagon into the circle by pointing to a corner of the hexagon and pressing the button “move” so that the corner follows the light pen, stretching two rubber band line segments behind it. By pointing to the circle and giving the termination flick we indicate that the corner is to lie on the circle. Each corner is in this way moved onto the circle at roughly equal spacing around it as shown in Figure 24.5D.
We have indicated that the vertices of the hexagon are to lie on the circle, and they will remain on the circle throughout our further manipulations. If we also insist that the sides of the hexagon be of equal length, a regular hexagon will be constructed. This we can do by pointing to one side and pressing the “copy” button, and then to another side and giving the termination flick. The button in this case copies a definition of equal length lines and applies it to the lines indicated. We have said, in effect, make this line equal in length to that line. We indicate that all six lines are equal in length by five such statements. The computer satisfies all existing conditions (if it is possible) whenever we turn on a toggle switch. This done, we have a complete regular hexagon inscribed in a circle. We can erase the entire circle by pointing to any part of it and pressing the “delete” button. The completed hexagon is shown in Figure 24.5F.
To make the hexagonal pattern of Figure 24.1 we wish to attach a large number of hexagons together by their corners, and so we designate the six corners of our hexagon as attachment points by pointing to each and pressing a button. We now file away the basic hexagon and begin work on a fresh “sheet of paper” by changing a switch setting. On the new sheet we assemble, by pressing a button to create each hexagon as a subpicture, six hexagons around a central seventh in approximate position as shown in Figure 24.5G. Subpictures may be positioned, each in its entirety, with the light pen, rotated or scaled with the knobs and fixed in position by the pen flick termination signal; but their internal shape is fixed. By pointing to the corner of one hexagon, pressing a button, and then pointing to the corner of another hexagon we can fasten those corners together, because these corners have been designated as attachment points. If we attach two corners of each outer hexagon to the appropriate corners of the inner hexagon, the seven are uniquely related, and the computer will reposition them as shown in Figure 24.5H. An entire group of hexagons, once assembled, can be treated as a symbol. The entire group can be called up on another “sheet of paper” as a subpicture and assembled with other groups or with single hexagons to make a very large pattern. Using Figure 24.5H seven times we get the pattern of Figure 24.1. Constructing the pattern of Figure 24.1 takes less than five minutes with the Sketchpad system.
24.2.2 Interpretation of introductory example In the introductory example above we have seen how to draw lines and circles and how to move existing parts of the drawing around. We used the light pen both to position parts of the drawing and to point to existing parts. For example, we pointed to the circle to erase it, and while drawing the sixth line, we pointed to the end of the first line drawn to close the hexagon. We also saw in action the very general subpicture, constraint, and definition copying capabilities of the system.
24.2.2.1 Subpicture The original hexagon might just as well have been anything else: a picture of a transistor, a roller bearing, an airplane wing, a letter, or an entire figure for this report. Any number of different symbols may be drawn, in terms of other simpler symbols if desired, and any symbol may be used as often as desired.
24.2.2.2 Constraint When we asked that the vertices of the hexagon lie on the circle we were making use of a basic relationship between picture parts that is built into the system. Basic relationships (atomic constraints) to make lines vertical, horizontal, parallel, or perpendicular; to make points lie on lines or circles; to make symbols appear upright, vertically above one another or be of equal size; and to relate symbols to other drawing parts such as points and lines have been included in the system. It is so easy to program new constraint types that the set of atomic constraints was expanded from five to the seventeen listed in Appendix A in a period of about two days; specialized constraint types may be added as needed. [EDITOR: Appendix omitted.]
24.2.2.3 Definition copying In the introductory example above we asked that the sides of the hexagon be equal in length by pressing a button while pointing to the side in question. Here we were using the definition copying capability of the system. Had we defined a composite operation such as to make two lines both parallel and equal in length, we could have applied it just as easily. The number of operations which can be defined from the basic constraints applied to various picture parts is almost unlimited. Useful new definitions are drawn regularly; they are as simple as horizontal lines and as complicated as dimension lines complete with arrowheads and a number which indicates the length of the line correctly. The definition copying capability makes using the constraint capability easy.
24.2.3 Implications of the introductory example As we have seen in the introductory example, drawing with the Sketchpad system is different from drawing with an ordinary pencil and paper. Most important of all, the Sketchpad drawing itself is entirely different from the trail of carbon left on a piece of paper. Information about how the drawing is tied together is stored in the computer as well as the information which gives the drawing its particular appearance. Since the drawing is tied together, it will keep a useful appearance even when parts of it are moved. For example, when we moved the corners of the hexagon onto the circle, the lines next to each corner were automatically moved so that the closed topology of the hexagon was preserved. Again, since we indicated that the corners of the hexagon were to lie on the circle they remained on the circle throughout our further manipulations.
It is this ability to store information relating the parts of a drawing to each other that makes Sketchpad most useful. For example, the linkage shown in Figure 24.6 was drawn with Sketchpad in just a few minutes. Constraints were applied to the linkage to keep the length of its various members constant. Rotation of the short central link is supposed to move the left end of the dotted line vertically. Since exact information about the properties of the linkage has been stored in Sketchpad, it is possible to observe the motion of the entire linkage when the short central link is rotated. The value of the number in Figure 24.6 was constrained to indicate the length of the dotted line, comparing the actual motion with the vertical line at the right of the linkage. One can observe that for all positions of the linkage the length of the dotted line is constant, demonstrating that this is indeed a straight line linkage. Other examples of moving drawings made with Sketchpad may be found in the final chapter.
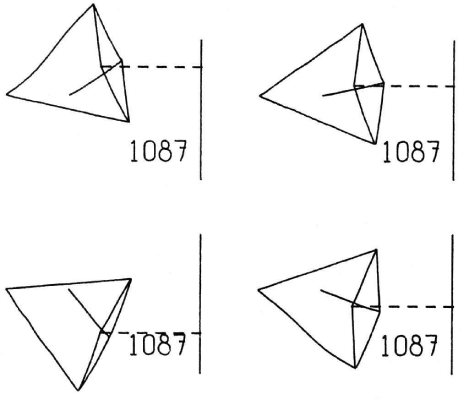
Figure 24.6: Four positions of linkage. Number shows length of dotted line.
As well as storing how the various parts of the drawing are related, Sketchpad stores the structure of the subpicture used. For example, the storage for the hexagonal pattern of Figure 24.1 indicates that this pattern is made of smaller patterns which are in turn made of smaller patterns which are composed of single hexagons. If the master hexagon is changed, the entire appearance of the hexagonal pattern will be changed. The structure of the pattern will, of course, be the same. For example, if we change the basic hexagon into a semicircle, the fish scale pattern shown in Figure 24.7 instantly results.
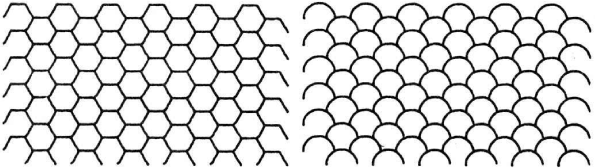
Figure 24.7: Half hexagons and semicircles on same lattice.
Since Sketchpad stores the structure of a drawing, a Sketchpad drawing explicitly indicates similarity of symbols. In an electrical drawing, for example, all transistor symbols are created from a single master transistor drawing. If some change to the basic transistor symbol is made, this change appears at once in all transistor symbols without further effort. Most important of all, the computer “knows” that a “transistor” is intended at that place in the circuit. It has no need to interpret the collection of lines which we would easily recognize as a transistor symbol. Since Sketchpad stores the topology of the drawing as we saw in closing the hexagon, one indicates both what a circuit looks like and its electrical connections when one draws it with Sketchpad. One can see that the circuit connections are stored because moving a component automatically moves any wiring on that component to maintain the correct connections. Sketchpad circuit drawings will soon be used as inputs for a circuit simulator. Having drawn a circuit one will find out its electrical properties.
24.2.4 Sketchpad and the design process Construction of a drawing with Sketchpad is itself a model of the design process. The locations of the points and lines of the drawing model the variables of a design, and the geometric constraints applied to the points and lines of the drawing model the design constraints which limit the values of design variables. The ability of Sketchpad to satisfy the geometric constraints applied to the parts of a drawing models the ability of a good designer to satisfy all the design conditions imposed by the limitations of his materials, cost, etc. In fact, since designers in many fields produce nothing themselves but a drawing of a part, design conditions may well be thought of as applying to the drawing of a part rather than to the part itself. If such design conditions were added to Sketchpad’s vocabulary of constraints the computer could assist a user not only in arriving at a nice looking drawing, but also in arriving at a sound design.
24.2.5 Present usefulness At the outset of the research no one had ever drawn engineering drawings directly on a computer display with nearly the facility now possible, and consequently no one knew what it would be like. We have now accumulated about a hundred hours of experience actually making drawings with a working system. As is shown in the final chapter, application of computer drawing techniques to a variety of problems has been made. As more and more applications have been made it has become clear that the properties of Sketchpad drawings make them most useful in four broad areas:
24.2.5.1 For making small changes to existing drawings Each time a drawing is made, a description of that drawing is stored in the computer in a form that is readily transferred to magnetic tape. Thus, as time passes, a library of drawings will develop, parts of which may be used in other drawings at only a fraction of the investment of time that was put into the original drawing. Since a drawing stored in the computer may contain explicit representation of design conditions in its constraints, manual change of a critical part will automatically result in appropriate changes to related parts.
24.2.5.2 For gaining scientific or engineering understanding of operations that can be described graphically The description of a drawing stored in the Sketchpad system is more than a collection of static drawing parts, lines and curves, etc. A drawing in the Sketchpad system may contain explicit statements about the relations between its parts so that as one part is changed the implications of this change become evident throughout the drawing. It is possible, as we saw in Figure 24.6, to give the property of fixed length to lines so as to study mechanical linkages, observing the path of some parts when others are moved. As we saw in Figure 24.7 any change made in the definition of a subpicture is at once reflected in the appearance of that subpicture wherever it may occur. By making such changes, understanding of the relationships of complex sets of subpictures can be gained. For example, one can study how a change in the basic element of a crystal structure is reflected throughout the crystal.
24.2.5.3 As a topological input device for circuit simulators, etc. Since the ring structure storage of Sketchpad reflects the topology of any circuit or diagram, it can serve as an input for many network or circuit simulating programs. The additional effort required to draw a circuit completely from scratch with the Sketchpad system may well be recompensed if the properties of the circuit are obtainable through simulation of the circuit drawn.
24.2.5.4 For highly repetitive drawings The ability of the computer to reproduce any drawn symbol anywhere at the press of a button, and to recursively include subpictures within subpictures makes it easy to produce drawings which are composed of huge numbers of parts all similar in shape. Great interest in doing this comes from people in such fields as memory development and micro logic where vast numbers of elements are to be generated at once through photographic processes. Master drawings of the repetitive patterns necessary can be easily drawn. Here again, the ability to change the individual element of the repetitive structure and have the change at once brought into all subelements makes it possible to change the elements of an array without redrawing the entire array. …
24.3 History of Sketchpad
… Had I the work to do again, I could start afresh with the sure knowledge that generic structure, separation of subroutines into general purpose ones applying to all types of picture parts and ones specific to particular types of picture parts, and unlimited applicability of functions (e.g. anything should be moveable) would more than recompense the effort involved in achieving them. I have great admiration for those people who were able to tell me these things all along, but I, personally, had to follow the stumbling trail described in this chapter to become convinced myself. It is to be hoped that future workers can either grasp the power of generality at once and strive for it or have the courage to stumble along a trail like mine until they achieve it. …
[T]here are possibilities for application of the system not yet even dreamed of. The richness of the possibilities of the definition copying function, and the new types of constraints which might easily be added to the system for special purposes suggest that further application will bring about a new body of knowledge of system application. For example, the bridge design examples shown at the end of this paper were not anticipated. There are, of course, limitations to the system. In the last chapter are suggested the improvements, some just minor changes, but some major additions which would change the entire character of the system. It is to be hoped that future work will far surpass my effort.
Reprinted from Sutherland (1963), with permission from the Massachusetts Institute of Technology.