32

A Relational Model of Large Shared Data Banks (1970)

Edgar F. Codd

It is common in academic circles to think that the science of computing is about algorithms. But in business, computing has always been about data. Of course the two perspectives are not opposed, but the world looks very different from a data-oriented view than from an algorithm-oriented view. A database scientist told me that data was the ocean, deep, eternal, and mysterious, and algorithms were just boats skimming its surface.

Until the 1960s, most practical applications of computers were for computing numbers—either values of mathematical functions (such as the tables generated by Aiken’s Mark I) or parameters of physical phenomena (astronomical calculations, for example, or the predicted behavior of an atom bomb). Of course any calculation involving physical phenomena requires numerical data, but early computers did not have enough storage to process large amounts of it. The scientific interest in computing was driven by the need to perform numerical calculations, plus the extraordinary discovery by Church and Turing of the ontology of algorithms. Turing’s remarkable codebreaking work at Bletchley Park was an exercise of logic and carefully controlled combinatorial search driven by very small amounts of data (intercepted encrypted messages).

Certainly Vannevar Bush had foreseen the importance of large-scale data manipulation (“Selection devices … will soon be speeded up from their present rate of reviewing data at a few hundred a minute,” page 115). Howard Aiken and Grace Hopper anticipated the importance of business applications, and the International Business Machines Corporation, which had grown out of companies supplying tabulating machines for the U.S. Census, came to dominate the business market for computers. Starting in the mid-1960s, IBM developed a database product to manage inventory for the Apollo space program. The data model of this system, known originally as IMS, drew ultimately on graph theory: mechanical parts had sub-parts, and the same sub-parts might be used in several different larger assemblies, so the connection between data entities resembled the links connecting nodes of a directed graph.

The quantity of data managed by such systems steadily grew, and it became clear that the way data were described and queried need not correspond to the memory structures used to store it. In much the same way as compilers had made it possible to abstract the statement of algorithms from the particulars of the machine code that executed them, there was a need to talk about data with some formal clarity, leaving to computer systems themselves the problem of optimally organizing the data in physical devices for most effective storage and retrieval.

For Edgar Frank Codd (1923–2003), the way to talk about data was to use a language derived from the predicate calculus. Data was to be organized as relations. A relation is a set of n-tuples, for example a set of ordered triples or ordered quadruples, where each position or “column” contains data of a particular type. The relation can be depicted as a table, with one n-tuple per row, but the order of the rows in the table is semantically irrelevant because the n-tuples are logically a set.

In this seminal paper Codd worked out the basics of the relational view of data, and most importantly, developed a relational algebra for combining relations. Codd spent much of his career with IBM, and this work emerged from his frustration that existing database systems entangled the database’s logical structure (and thus the logic of programs accessing the database) with its internal “physical” representation. IBM welcomed Codd’s innovations only tepidly, perhaps because a successful relational database system would compete with existing IBM products, so Codd left to start his own firm. Research implementations of the relational database model began to appear later in the 1970s, with IBM’s System R and the Ingres system of Michael Stonebraker at Berkeley. Oracle Corporation, Tandem Computers, Stonebraker’s Relational Technology Inc., and IBM all released commercial implementations between 1979 and 1981, establishing the model as a de facto standard. The model and the associated data management language SQL are now ubiquitous, and Codd was recognized with the Turing award for his contribution.

---

32.1    Relational Model and Normal Form

THIS paper is concerned with the application of elementary relation theory to systems which provide shared access to large banks of formatted data. Except for a paper by Childs (1968), the principal application of relations to data systems has been to deductive question-answering systems. Levien and Maron (1967) provide numerous references to work in this area.

In contrast, the problems treated here are those of data independence—the independence of application programs and terminal activities from growth in data types and changes in data representation—and certain kinds of data inconsistency which are expected to become troublesome even in nondeductive systems.

The relational view (or model) of data described in §32.1 appears to be superior in several respects to the graph or network model (Bachman, 1965; McGee, 1969) presently in vogue for noninferential systems. It provides a means of describing data with its natural structure only—that is, without superimposing any additional structure for machine representation purposes. Accordingly, it provides a basis for a high level data language which will yield maximal independence between programs on the one hand and machine representation and organization of data on the other.

A further advantage of the relational view is that it forms a sound basis for treating derivability, redundancy, and consistency of relations—these are discussed in §32.2. The network model, on the other hand, has spawned a number of confusions, not the least of which is mistaking the derivation of connections for the derivation of relations ….

Finally, the relational view permits a clearer evaluation of the scope and logical limitations of present formatted data systems, and also the relative merits (from a logical standpoint) of competing representations of data within a single system. Examples of this clearer perspective are cited in various parts of this paper. Implementations of systems to support the relational model are not discussed.

32.1.2    Data dependencies in present systems    The provision of data description tables in recently developed information systems represents a major advance toward the goal of data independence (IBM, 1965b,a; Bleier, 1967; IDS, 1968). Such tables facilitate changing certain characteristics of the data representation stored in a data bank. However, the variety of data representation characteristics which can be changed without logically impairing some application programs is still quite limited. Further, the model of data with which users interact is still cluttered with representational properties, particularly in regard to the representation of collections of data (as opposed to individual items). Three of the principal kinds of data dependencies which still need to be removed are: ordering dependence, indexing dependence, and access path dependence. In some systems these dependencies are not clearly separable from one another.

32.1.2.1    Ordering dependence    Elements of data in a data bank may be stored in a variety of ways, some involving no concern for ordering, some permitting each element to participate in one ordering only, others permitting each element to participate in several orderings. Let us consider those existing systems which either require or permit data elements to be stored in at least one total ordering which is closely associated with the hardware-determined ordering of addresses. For example, the records of a file concerning parts might be stored in ascending order by part serial number. Such systems normally permit application programs to assume that the order of presentation of records from such a file is identical to (or is a subordering of) the stored ordering. Those application programs which take advantage of the stored ordering of a file are likely to fail to operate correctly if for some reason it becomes necessary to replace that ordering by a different one. Similar remarks hold for a stored ordering implemented by means of pointers.

It is unnecessary to single out any system as an example, because all the well-known information systems that are marketed today fail to make a clear distinction between order of presentation on the one hand and stored ordering on the other. Significant implementation problems must be solved to provide this kind of independence.

32.1.2.2    Indexing dependence    In the context of formatted data, an index is usually thought of as a purely performance-oriented component of the data representation. It tends to improve response to queries and updates and, at the same time, slow down response to insertions and deletions. From an informational standpoint, an index is a redundant component of the data representation. If a system uses indices at all and if it is to perform well in an environment with changing patterns of activity on the data bank, an ability to create and destroy indices from time to time will probably be necessary. The question then arises: Can application programs and terminal activities remain invariant as indices come and go?

Present formatted data systems take widely different approaches to indexing. TDMS (Bleier, 1967) unconditionally provides indexing on all attributes. The presently released version of IMS (IBM, 1965b) provides the user with a choice for each file: a choice between no indexing at all (the hierarchic sequential organization) or indexing on the primary key only (the hierarchic indexed sequential organization). In neither case is the user’s application logic dependent on the existence of the unconditionally provided indices. IDS, however, permits the file designers to select attributes to be indexed and to incorporate indices into the file structure by means of additional chains. Application programs taking advantage of the performance benefit of these indexing chains must refer to those chains by name. Such programs do not operate correctly if these chains are later removed.

32.1.2.3    Access path dependence    Many of the existing formatted data systems provide users with tree-structured files or slightly more general network models of the data. Application programs developed to work with these systems tend to be logically impaired if the trees or networks are changed in structure. A simple example follows.

Suppose the data bank contains information about parts and projects. For each part, the part number, part name, part description, quantity-on-hand, and quantity-on-order are recorded. For each project, the project number, project name, project description are recorded. Whenever a project makes use of a certain part, the quantity of that part committed to the given project is also recorded. Suppose that the system requires the user or file designer to declare or define the data in terms of tree structures. Then, any one of the hierarchical structures may be adopted for the information mentioned above (see Structures 1–5, Figures 32.1–32.5).

Figure 32.1: Structure 1. Projects subordinate to parts

Figure 32.2: Structure 2. Parts subordinate to projects

Figure 32.3: Structure 3. Parts and projects as peers, commitment relationship subordinate to projects

Figure 32.4: Structure 4. Parts and projects as peers, commitment relationship subordinate to parts

Figure 32.5: Structure 5. Parts, projects, and commitment relationship as peers

Now, consider the problem of printing out the part number, part name, and quantity committed for every part used in the project whose project name is “alpha.” The following observations may be made regardless of which available tree-oriented information system is selected to tackle this problem. If a program P is developed for this problem assuming one of the five structures above—that is, P makes no test to determine which structure is in effect—then P will fail on at least three of the remaining structures. More specifically, if P succeeds with structure 5, it will fail with all the others; if P succeeds with structure 3 or 4, it will fail with at least 1, 2, and 5; if P succeeds with 1 or 2, it will fail with at least 3, 4, and 5. The reason is simple in each case. In the absence of a test to determine which structure is in effect, P fails because an attempt is made to execute a reference to a nonexistent file (available systems treat this as an error) or no attempt is made to execute a reference to a file containing needed information. The reader who is not convinced should develop sample programs for this simple problem.

Since, in general, it is not practical to develop application programs which test for all tree structurings permitted by the system, these programs fail when a change in structure becomes necessary.

Systems which provide users with a network model of the data run into similar difficulties. In both the tree and network cases, the user (or his program) is required to exploit a collection of user access paths to the data. It does not matter whether these paths are in close correspondence with pointer-defined paths in the stored representation—in IDS the correspondence is extremely simple, in TDMS it is just the opposite. The consequence, regardless of the stored representation, is that terminal activities and programs become dependent on the continued existence of the user access paths. One solution to this is to adopt the policy that once a user access path is defined it will not be made obsolete until all application programs using that path have become obsolete. Such a policy is not practical, because the number of access paths in the total model for the community of users of a data bank would eventually become excessively large.

32.1.3    A relational view of data    The term relation is used here in its accepted mathematical sense. Given sets S₁, S₂, …, S_n (not necessarily distinct), R is a relation on these n sets if it is a set of n-tuples each of which has its first element from S₁, its second element from S₂, and so on. We shall refer to S_j as the j^th domain of R. As defined above, R is said to have degree n. Relations of degree 1 are often called unary, degree 2 binary, degree 3 ternary, and degree n n-ary.

For expository reasons, we shall frequently make use of an array representation of relations, but it must be remembered that this particular representation is not an essential part of the relational view being expounded. An array which represents an n-ary relation R has the following properties:

1. Each row represents an n-tuple of R.

2. The ordering of rows is immaterial.

3. All rows are distinct.

4. The ordering of columns is significant—it corresponds to the ordering S₁, S₂, …, S_n of the domains on which R is defined (see, however, remarks below on domain-ordered and domain-unordered relations).

5. The significance of each column is partially conveyed by labeling it with the name of the corresponding domain.

The example in Figure 32.6 illustrates a relation of degree 4, called supply, which reflects the shipments-in-progress of parts from specified suppliers to specified projects in specified quantities.

Figure 32.6: A relation of degree 4

One might ask: If the columns are labeled by the name of corresponding domains, why should the ordering of columns matter? As the example in Figure 32.7 shows, two columns may have identical headings (indicating identical domains) but possess distinct meanings with respect to the relation. The relation depicted is called component. It is a ternary relation, whose first two domains are called part and third domain is called quantity. The meaning of component (x, y, z) is that part x is an immediate component (or subassembly) of part y, and z units of part x are needed to assemble one unit of part y. It is a relation which plays a critical role in the parts explosion problem.

Figure 32.7: A relation with two identical domains

It is a remarkable fact that several existing information systems (chiefly those based on tree-structured files) fail to provide data representations for relations which have two or more identical domains. The present version of IMS/360 (IBM, 1965b) is an example of such a system.

The totality of data in a data bank may be viewed as a collection of time-varying relations. These relations are of assorted degrees. As time progresses, each n-ary relation may be subject to insertion of additional n-tuples, deletion of existing ones, and alteration of components of any of its existing n-tuples.

In many commercial, governmental, and scientific data banks, however, some of the relations are of quite high degree (a degree of 30 is not at all uncommon). Users should not normally be burdened with remembering the domain ordering of any relation (for example, the ordering supplier, then part, then project, then quantity in the relation supply). Accordingly, we propose that users deal, not with relations which are domain-ordered, but with relationships which are their domain-unordered counterparts. (In mathematical terms, a relationship is an equivalence class of those relations that are equivalent under permutation of domains (see §32.2.1).) To accomplish this, domains must be uniquely identifiable at least within any given relation, without using position. Thus, where there are two or more identical domains, we require in each case that the domain name be qualified by a distinctive role name, which serves to identify the role played by that domain in the given relation. For example, in the relation component of Figure 32.7, the first domain part might be qualified by the role name sub, and the second by super, so that users could deal with the relationship component and its domains—sub.part, super.part, quantity—without regard to any ordering between these domains.

To sum up, it is proposed that most users should interact with a relational model of the data consisting of a collection of time-varying relationships (rather than relations). Each user need not know more about any relationship than its name together with the names of its domains (role qualified whenever necessary). (Naturally, as with any data put into and retrieved from a computer system, the user will normally make far more effective use of the data if he is aware of its meaning.) Even this information might be offered in menu style by the system (subject to security and privacy constraints) upon request by the user.

There are usually many alternative ways in which a relational model may be established for a data bank. In order to discuss a preferred way (or normal form), we must first introduce a few additional concepts (active domain, primary key, foreign key, nonsimple domain) and establish some links with terminology currently in use in information systems programming. In the remainder of this paper, we shall not bother to distinguish between relations and relationships except where it appears advantageous to be explicit.

Consider an example of a data bank which includes relations concerning parts, projects, and suppliers. One relation called part is defined on the following domains:

1. part number

2. part name

3. part color

4. part weight

5. quantity on hand

6. quantity on order

and possibly other domains as well. Each of these domains is, in effect, a pool of values, some or all of which may be represented in the data bank at any instant. While it is conceivable that, at some instant, all part colors are present, it is unlikely that all possible part weights, part names, and part numbers are. We shall call the set of values represented at some instant the active domain at that instant.

Normally, one domain (or combination of domains) of a given relation has values which uniquely identify each element (n-tuple) of that relation. Such a domain (or combination) is called a primary key. In the example above, part number would be a primary key, while part color would not be. A primary key is nonredundant if it is either a simple domain (not a combination) or a combination such that none of the participating simple domains is superfluous in uniquely identifying each element. A relation may possess more than one nonredundant primary key. This would be the case in the example if different parts were always given distinct names. Whenever a relation has two or more nonredundant primary keys, one of them is arbitrarily selected and called the primary key of that relation.

A common requirement is for elements of a relation to cross-reference other elements of the same relation or elements of a different relation. Keys provide a user-oriented means (but not the only means) of expressing such cross-references. We shall call a domain (or domain combination) of relation R a foreign key if it is not the primary key of R but its elements are values of the primary key of some relation S (the possibility that S and R are identical is not excluded). In the relation supply of Figure 32.6, the combination of supplier, part, project is the primary key, while each of these three domains taken separately is a foreign key.

In previous work there has been a strong tendency to treat the data in a data bank as consisting of two parts, one part consisting of entity descriptions (for example, descriptions of suppliers) and the other part consisting of relations between the various entities or types of entities (for example, the supply relation). This distinction is difficult to maintain when one may have foreign keys in any relation whatsoever. In the user’s relational model there appears to be no advantage to making such a distinction (there may be some advantage, however, when one applies relational concepts to machine representations of the user’s set of relationships).

So far, we have discussed examples of relations which are defined on simple domains—domains whose elements are atomic (nondecomposable) values. Nonatomic values can be discussed within the relational framework. Thus, some domains may have relations as elements. These relations may, in turn, be defined on nonsimple domains, and so on. For example, one of the domains on which the relation employee is defined might be salary history. An element of the salary history domain is a binary relation defined on the domain date and the domain salary. The salary history domain is the set of all such binary relations. At any instant of time there are as many instances of the salary history relation in the data bank as there are employees. In contrast, there is only one instance of the employee relation.

The terms attribute and repeating group in present data base terminology are roughly analogous to simple domain and nonsimple domain, respectively. Much of the confusion in present terminology is due to failure to distinguish between type and instance (as in “record”) and between components of a user model of the data on the one hand and their machine representation counterparts on the other hand (again, we cite “record” as an example).

32.1.4    Normal form    A relation whose domains are all simple can be represented in storage by a two-dimensional column-homogeneous array of the kind discussed above. Some more complicated data structure is necessary for a relation with one or more nonsimple domains. For this reason (and others to be cited below) the possibility of eliminating nonsimple domains appears worth investigating. There is, in fact, a very simple elimination procedure, which we shall call normalization.

Consider, for example, the collection of relations exhibited in Figure 32.8. Job history and children are nonsimple domains of the relation employee. Salary history is a nonsimple domain of the relation job history. The tree in Figure 32.8 shows just these interrelationships of the nonsimple domains.

Figure 32.8: Unnormalized set

Normalization proceeds as follows. Starting with the relation at the top of the tree, take its primary key and expand each of the immediately subordinate relations by inserting this primary key domain or domain combination. The primary key of each expanded relation consists of the primary key before expansion augmented by the primary key copied down from the parent relation. Now, strike out from the parent relation all nonsimple domains, remove the top node of the tree, and repeat the same sequence of operations on each remaining subtree.

The result of normalizing the collection of relations in Figure 32.8 is the collection in Figure 32.9. The primary key of each relation is italicized to show how such keys are expanded by the normalization.

Figure 32.9: Normalized set

If normalization as described above is to be applicable, the unnormalized collection of relations must satisfy the following conditions:

1. The graph of interrelationships of the nonsimple domains is a collection of trees.

2. No primary key has a component domain which is nonsimple.

The writer knows of no application which would require any relaxation of these conditions. Further operations of a normalizing kind are possible. These are not discussed in this paper.

The simplicity of the array representation which becomes feasible when all relations are cast in normal form is not only an advantage for storage purposes but also for communication of bulk data between systems which use widely different representations of the data. The communication form would be a suitably compressed version of the array representation and would have the following advantages:

1. It would be devoid of pointers (address-valued or displacement-valued).

2. It would avoid all dependence on hash addressing schemes.

3. It would contain no indices or ordering lists.

If the user’s relational model is set up in normal form, names of items of data in the data bank can take a simpler form than would otherwise be the case. A general name would take a form such as

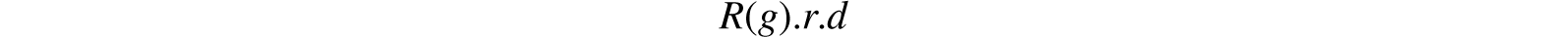
where R is a relational name; g is a generation identifier (optional); r is a role name (optional); d is a domain name. Since g is needed only when several generations of a given relation exist, or are anticipated to exist, and r is needed only when the relation R has two or more domains named d, the simple form R.d will often be adequate.

32.1.5    Some linguistic aspects    The adoption of a relational model of data, as described above, permits the development of a universal data sublanguage based on an applied predicate calculus. A first-order predicate calculus suffices if the collection of relations is in normal form. Such a language would provide a yardstick of linguistic power for all other proposed data languages, and would itself be a strong candidate for embedding (with appropriate syntactic modification) in a variety of host languages (programming, command- or problem-oriented). While it is not the purpose of this paper to describe such a language in detail, its salient features would be as follows.

Let us denote the data sublanguage by R and the host language by H. R permits the declaration of relations and their domains. Each declaration of a relation identifies the primary key for that relation. Declared relations are added to the system catalog for use by any members of the user community who have appropriate authorization. H permits supporting declarations which indicate, perhaps less permanently, how these relations are represented in storage. R permits the specification for retrieval of any subset of data from the data bank. Action on such a retrieval request is subject to security constraints.

The universality of the data sublanguage lies in its descriptive ability (not its computing ability). In a large data bank each subset of the data has a very large number of possible (and sensible) descriptions, even when we assume (as we do) that there is only a finite set of function subroutines to which the system has access for use in qualifying data for retrieval. Thus, the class of qualification expressions which can be used in a set specification must have the descriptive power of the class of well-formed formulas of an applied predicate calculus. It is well known that to preserve this descriptive power it is unnecessary to express (in whatever syntax is chosen) every formula of the selected predicate calculus. For example, just those in prenex normal form are adequate (Church, 1956).

Arithmetic functions may be needed in the qualification or other parts of retrieval statements. Such functions can be defined in H and invoked in R.

A set so specified may be fetched for query purposes only, or it may be held for possible changes. Insertions take the form of adding new elements to declared relations without regard to any ordering that may be present in their machine representation. Deletions which are effective for the community (as opposed to the individual user or sub-communities) take the form of removing elements from declared relations. Some deletions and updates may be triggered by others, if deletion and update dependencies between specified relations are declared in R.

One important effect that the view adopted toward data has on the language used to retrieve it is in the naming of data elements and sets. Some aspects of this have been discussed in the previous section. With the usual network view, users will often be burdened with coining and using more relation names than are absolutely necessary, since names are associated with paths (or path types) rather than with relations.

Once a user is aware that a certain relation is stored, he will expect to be able to exploit it using any combination of its arguments as “knowns” and the remaining arguments as “unknowns,” because the information (like Everest) is there. This is a system feature (missing from many current information systems) which we shall call (logically) symmetric exploitation of relations. Naturally, symmetry in performance is not to be expected.

To support symmetric exploitation of a single binary relation, two directed paths are needed. For a relation of degree n, the number of paths to be named and controlled is n factorial.

Again, if a relational view is adopted in which every n-ary relation (n > 2) has to be expressed by the user as a nested expression involving only binary relations (see Feldman’s LEAP System [Feldman and Rovner, 1968], for example) then 2n − 1 names have to be coined instead of only n + 1 with direct n-ary notation as described in §32.1.2. For example, the 4-ary relation supply of Figure 32.6, which entails 5 names in n-ary notation, would be represented in the form

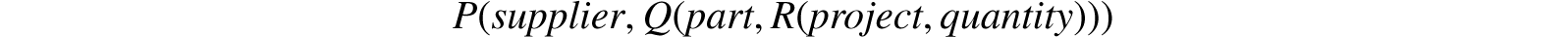
in nested binary notation and, thus, employ 7 names.

A further disadvantage of this kind of expression is its asymmetry. Although this asymmetry does not prohibit symmetric exploitation, it certainly makes some bases of interrogation very awkward for the user to express (consider, for example, a query for those parts and quantities related to certain given projects via Q and R).

32.1.6    Expressible, named, and stored relations    Associated with a data bank are two collections of relations: the named set and the expressible set. The named set is the collection of all those relations that the community of users can identify by means of a simple name (or identifier). A relation R acquires membership in the named set when a suitably authorized user declares R; it loses membership when a suitably authorized user cancels the declaration of R.

The expressible set is the total collection of relations that can be designated by expressions in the data language. Such expressions are constructed from simple names of relations in the named set; names of generations, roles and domains; logical connectives; the quantifiers of the predicate calculus; and certain constant relation symbols such as =, >. The named set is a subset of the expressible set—usually a very small subset.

Since some relations in the named set may be time-independent combinations of others in that set, it is useful to consider associating with the named set a collection of statements that define these time-independent constraints. We shall postpone further discussion of this until we have introduced several operations on relations (see §32.2).

One of the major problems confronting the designer of a data system which is to support a relational model for its users is that of determining the class of stored representations to be supported. Ideally, the variety of permitted data representations should be just adequate to cover the spectrum of performance requirements of the total collection of installations. Too great a variety leads to unnecessary overhead in storage and continual reinterpretation of descriptions for the structures currently in effect.

For any selected class of stored representations the data system must provide a means of translating user requests expressed in the data language of the relational model into corresponding—and efficient—actions on the current stored representation. For a high level data language this presents a challenging design problem. Nevertheless, it is a problem which must be solved—as more users obtain concurrent access to a large data bank, responsibility for providing efficient response and throughput shifts from the individual user to the data system.

32.2    Redundancy and Consistency

32.2.1    Operations on relations    Since relations are sets, all of the usual set operations are applicable to them. Nevertheless, the result may not be a relation; for example, the union of a binary relation and a ternary relation is not a relation.

The operations discussed below are specifically for relations. These operations are introduced because of their key role in deriving relations from other relations. Their principal application is in noninferential information systems—systems which do not provide logical inference services—although their applicability is not necessarily destroyed when such services are added.

Most users would not be directly concerned with these operations. Information systems designers and people concerned with data bank control should, however, be thoroughly familiar with them.

32.2.1.1    Permutation    A binary relation has an array representation with two columns. Interchanging these columns yields the converse relation. More generally, if a permutation is applied to the columns of an n-ary relation, the resulting relation is said to be a permutation of the given relation. There are, for example, 4! = 24 permutations of the relation supply in Figure 32.6, if we include the identity permutation which leaves the ordering of columns unchanged.

Since the user’s relational model consists of a collection of relationships (domain-unordered relations), permutation is not relevant to such a model considered in isolation. It is, however, relevant to the consideration of stored representations of the model. In a system which provides symmetric exploitation of relations, the set of queries answerable by a stored relation is identical to the set answerable by any permutation of that relation. Although it is logically unnecessary to store both a relation and some permutation of it, performance considerations could make it advisable.

32.2.1.2    Projection    Suppose now we select certain columns of a relation (striking out the others) and then remove from the resulting array any duplication in the rows. The final array represents a relation which is said to be a projection of the given relation.

A selection operator π is used to obtain any desired permutation, projection, or combination of the two operations. Thus, if L is a list of indices L = i₁, i₂, …, i_k and R is an n-ary relation (n ≥ k), then π_L(R) is the k-ary relation whose j^th column is column i_j of R (j = 1, 2, …, k) except that duplication in resulting rows is removed. Consider the relation supply of Figure 32.6. A permuted projection of this relation is exhibited in Figure 32.10. Note that, in this particular case, the projection has fewer n-tuples than the relation from which it is derived.

Figure 32.10: A permuted projection of the relation in Figure 32.6

32.2.1.3    Join    Suppose we are given two binary relations, which have some domain in common. Under what circumstances can we combine these relations to form a ternary relation which preserves all of the information in the given relations?

The example in Figure 32.11 shows two relations R, S, which are joinable without loss of information, while Figure 32.12 shows a join of R with S. A binary relation R is joinable with a binary relation S if there exists a ternary relation U such that π₁₂(U) = R and π₂₃(U) = S. Any such ternary relation is called a join of R with S. If R, S are binary relations such that π₂(R) = π₁(S), then R is joinable with S. One join that always exists in such a case is the natural join of R with S defined by

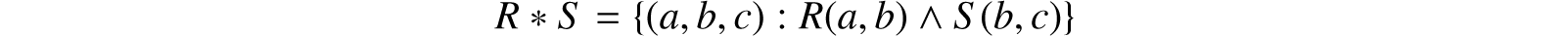
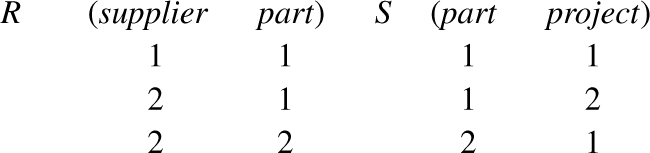
Figure 32.11: Two joinable relations

Figure 32.12: The natural join of R with S (from Figure 32.11)

where R(a, b) has the value true if (a, b) is a member of R and similarly for S(b, c). It is immediate that

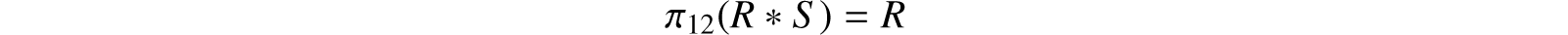
and

Note that the join shown in Figure 32.12 is the natural join of R with S from Figure 32.11. Another join is shown in Figure 32.13.

Figure 32.13: Another join of R with S (from Figure 32.11)

Inspection of these relations reveals an element (element 1) of the domain part (the domain on which the join is to be made) with the property that it possesses more than one relative under R and also under S. It is this element which gives rise to the plurality of joins. Such an element in the joining domain is called a point of ambiguity with respect to the joining of R with S.

If either π₂₁(R) or S is a function, no point of ambiguity can occur in joining R with S. In such a case, the natural join of R with S is the only join of R with S. Note that the reiterated qualification “of R with S” is necessary, because S might be joinable with R (as well as R with S), and this join would be an entirely separate consideration. In Figure 32.11, none of the relations R, π₂₁(R), S, π₂₁(S) is a function. …

32.2.2    Redundancy    …

32.2.3    Consistency    …

32.2.4    Summary    In §32.1 a relational model of data is proposed as a basis for protecting users of formatted data systems from the potentially disruptive changes in data representation caused by growth in the data bank and changes in traffic. A normal form for the time-varying collection of relationships is introduced.

In §32.2 operations on relations and two types of redundancy are defined and applied to the problem of maintaining the data in a consistent state. This is bound to become a serious practical problem as more and more different types of data are integrated together into common data banks. …

1. Reprinted from Codd (1970), with permission from the Association for Computing Machinery.