34 The Complexity of Theorem-Proving Procedures (1971)

Stephen A. Cook

While discussing maximal matchings in graphs a decade after Kruskal’s unelaborated claim that his spanning tree algorithm was “practical” (chapter 17), the computer scientist Jack Edmonds paused to draw the distinction between polynomial- and exponential-time algorithms (as we now call them). A “digression” near the beginning of Edmonds (1965) states, “An explanation is due on the use of the words ‘efficient algorithm.’… For practical purposes the difference between algebraic and exponential order is often more crucial than the difference between finite and non-finite.” At about the same time, the mathematician Alan Cobham (1965) formulated a machine-model-independent class he called ℒ, the functions computable in time “bounded by polynomials in the lengths of the numbers involved” represented in digital form.

In this seminal paper, Stephen Cook (b. 1939) defines as ℒ_* the class that Edmonds refers to as problems with “algebraic order” solutions and which are today known as 𝒫 or PTIME. That is, ℒ_* or 𝒫 is the set analog of Cobham’s class ℒ of functions. Cook then provides the crucial definition of polynomial-time reducibility between problems, and proves that all problems accepted in polynomial time by a nondeterministic Turing machine are polynomial-time reducible to the set of satisfiable formulas of the propositional calculus in conjunctive normal form. (The 𝒩𝒫 notation for this class was adopted soon after publication of this paper—see chapter 36 and Knuth (1974b). Also, the theorem is stated in terms of tautologyhood, which is in co-𝒩𝒫, rather than—as would be customary today—satisfiability, which is in 𝒩𝒫.)

Cook received his PhD in mathematics at Harvard in 1966, working under the direction of the logician Hao Wang on the complexity of multiplication and other mathematical functions. He joined the mathematics department at Berkeley as assistant professor. In what can only be considered a blunder, Cook was denied tenure at Berkeley in 1970 and moved to the University of Toronto. He presented this short paper at a major computer science theory conference, demonstrating that time-bounded nondeterministic computations could be described succinctly by boolean formulas, and therefore that a polynomial-time algorithm for boolean satisfiability would immediately result in polynomial-time algorithms for every 𝒩𝒫 problem. The proof is easy—the brilliant insight was to describe computations by formulas in a distant echo of Turing (1936, here page 60). Cook’s result set off the still unfinished search for an answer to the question of whether or not 𝒫 = 𝒩𝒫 and hundreds of other research threads in complexity theory.

There is one more important historical aspect of the 𝒫 = 𝒩𝒫 question. Working independently and in relative isolation in the Soviet Union, Leonid Levin (b. 1948) had identified the same class of “Universal Search Problems” (Levin, 1973) that came to be known as the 𝒩𝒫-complete problems. The discoveries by Cook and Levin were nearly simultaneous, though Levin’s publication was delayed. The existence of 𝒩𝒫-complete problems is now known as the Cook–Levin Theorem. Levin emigrated to the US in 1978 and is now a professor at Boston University.

34.0 Summary

IT is shown that any recognition problem solved by a polynomial time-bounded nondeterministic Turing machine can be “reduced” to the problem of determining whether a given propositional formula is a tautology. Here “reduced” means, roughly speaking, that the first problem can be solved deterministically in polynomial time provided an oracle is available for solving the second. From this notion of reducible, polynomial degrees of difficulty are defined, and it is shown that the problem of determining tautologyhood has the same polynomial degree as the problem of determining whether the first of two given graphs is isomorphic to a subgraph of the second. Other examples are discussed. A method of measuring the complexity of proof procedures for the predicate calculus is introduced and discussed.

Throughout this paper, a set of strings means a set of strings on some fixed, large, finite alphabet Σ. This alphabet is large enough to include symbols for all sets described here. All Turing machines are deterministic recognition devices, unless the contrary is explicitly stated.

34.1 Tautologies and Polynomial Reducibility

Let us fix a formalism for the propositional calculus in which formulas are written as strings on Σ. Since we will require infinitely many proposition symbols (atoms), each such symbol will consist of a member of Σ followed by a number in binary notation to distinguish that symbol. Thus a formula of length n can only have about n/log n distinct function and predicate symbols. The logical connectives are ∧ (and), ∨ (or), and ¬ (not).

The set of tautologies (denoted by {tautologies}) is a certain recursive set of strings on this alphabet, and we are interested in the problem of finding a good lower bound on its possible recognition times. We provide no such lower bound here, but Theorem 1 will give evidence that {tautologies} is a difficult set to recognize, since many apparently difficult problems can be reduced to determining tautologyhood. By reduced we mean, roughly speaking, that if tautologyhood could be decided instantly (by an “oracle”) then these problems could be decided in polynomial time. In order to make this notion precise, we introduce query machines, which are like Turing machines with oracles in Kreider and Ritchie (1964).

A query machine is a multitape Turing machine with a distinguished tape called the query tape, and three distinguished states called the query state, yes state, and no state, respectively. If M is a query machine and T is a set of strings, then a T-computation of M is a computation of M in which initially M is in the initial state and has an input string w on its input tape, and each time M assumes the query state there is a string u on the query tape, and the next state M assumes is the yes state if u ∈ T and the no state if u T. We think of an “oracle,” which knows T, placing M in the yes state or no state.

Definition. A set S of strings is P-reducible (P for polynomial) to a set T of strings iff there is some query machine M and a polynomial Q(n) such that for each input string w, the T-computation of M with input w halts within Q(|w|) steps (|w| is the length of w) and ends in an accepting state iff w ∈ S.

It is not hard to see that P-reducibility is a transitive relation. Thus the relation E on sets of strings, given by (S, T) ∈ E iff each of S and T is P-reducible to the other, is an equivalence relation. The equivalence class containing a set S will be denoted by deg(S) (the polynomial degree of difficulty of S).

Definition. We will denote deg({0}) by ℒ_*, where 0 denotes the zero function.

Thus ℒ_* is the class of sets recognizable in polynomial time. ℒ_* was discussed in Cook (1971a, p. 5), and is the string analog of Cobham’s class ℒ of functions (Cobham, 1965).

We now define the following special sets of strings.

1. The subgraph problem is the problem given two finite undirected graphs, determine whether the first is isomorphic to a subgraph of the second. A graph G can be represented by a string on the alphabet {0, 1, *} by listing the successive rows of its adjacency matrix, separated by *s. We let {subgraph pairs} denote the set of strings such that G₁ is isomorphic to a subgraph of G₂.

2. The graph isomorphism problem will be represented by the set, denoted by {isomorphic graph pairs}, of all strings such that G₁ is isomorphic to G₂.

3. The set {primes} is the set of all binary notations for prime numbers.

4. The set {DNF tautologies} is the set of strings representing tautologies in disjunctive normal form.

5. The set D₃ consists of those tautologies in disjunctive normal form in which each disjunct has at most three conjuncts (each of which is an atom or negation of an atom).

Theorem 1. If a set S of strings is accepted by some nondeterministic Turing machine within polynomial time, then S is P-reducible to {DNF tautologies}.

Corollary. Each of the sets in definitions 1–5 is P-reducible to {DNF tautologies}.

This is because each set, or its complement, is accepted in polynomial time by some nondeterministic Turing machine.

Proof of Theorem 1. Suppose a nondeterministic Turing machine M accepts a set S of strings within time Q(n), where Q(n) is a polynomial. Given an input w for M, we will construct a proposition formula A(w) in conjunctive normal form such that A(w) is satisfiable iff M accepts w. Thus ¬A(w) is easily put in disjunctive normal form (using De Morgan’s laws), and ¬A(w) is a tautology if and only if w S. Since the whole construction can be carried out in time bounded by a polynomial in |w| (the length of w), the theorem will be proved.

We may as well assume the Turing machine M has only one tape, which is infinite to the right but has a left-most square. Let us number the squares from left to right 1, 2, …. Let us fix an input w to M of length n, and suppose w ∈ S. Then there is a computation of M with input w that ends in an accepting state within T = Q(n) steps. The formula A(w) will be built from many different proposition symbols, whose intended meanings, listed below, refer to such a computation.

Suppose the tape alphabet for M is {σ₁, …, σ_ℓ}, and the set of states is {q₁, …, q_r}. Notice that since the computation has at most T = Q(n) steps, no tape square beyond T is scanned.

Proposition symbols:

for 1 ≤ i ≤ ℓ, 1 ≤ s, t ≤ T. is true iff tape square number s at step t contains the symbol σ_i.

for 1 ≤ i ≤ r, 1 ≤ t ≤ T. is true iff at step t the machine is in state q_i.

S _{s, t} for 1 ≤ s, t ≤ T is true iff at time t square number s is scanned by the tape head.

The formula A(w) is a conjunction B ∧ C ∧ D ∧ E ∧ F ∧ G ∧ H ∧ I formed as follows. Notice A(w) is in conjunctive normal form.

B will assert that at each step t, one and only one square is scanned. B is a conjunction B₁ ∧ B₂ ∧⋯∧ B_T, where B_t asserts that at time t one and only one square is scanned:

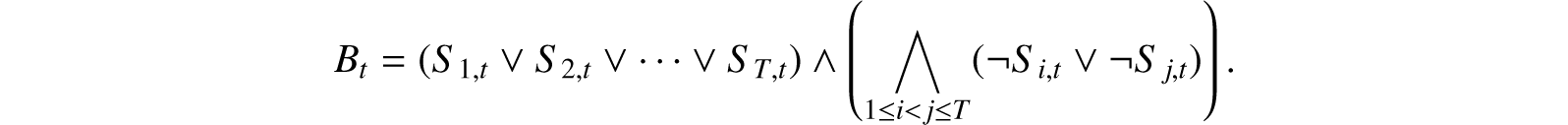
For 1 ≤ s ≤ Tand 1 ≤ t ≤ T, C_{s, t} asserts that at square s and time t there is one and only one symbol. C is the conjunction of all the C_{s, t}.

D asserts that for each t there is one and only one state.

E asserts the initial conditions are satisfied:

where w = σ_i₁…σ_{i_n}, q₀ is the initial state and σ₁ is the blank symbol.

F, G, and H assert that for each time t the values of the P’s, Q’s and S’s are updated properly. For example, G is the conjunction over all t, i, j of , where asserts that if at time t the machine is in state q_i scanning symbol σ_j, then at time t + 1 the machine is in state q_k, where q_k is the state given by the transition function for M. [EDITOR: The version of the original paper posted on Cook’s website includes a handwritten note here: “(or states: nondeterminism).” Indeed, the construction as presented is correct only if the machine is deterministic; it needs to be done somewhat differently for nondeterministic machines.]

Finally, the formula I asserts that the machine reaches an accepting state at some time. The machine M should be modified so that it continues to compute in some trivial fashion after reaching an accepting state, so that A(w) will be satisfied.

It is now straightforward to verify that A(w) has all the properties asserted in the first paragraph of the proof.

Theorem 2. The following sets are P-reducible to each other in pairs (and hence each has the same polynomial degree of difficulty): {tautologies}, {DNF tautologies}, D₃, {subgraph pairs}.

Remark. We have not been able to add either {primes} or {isomorphic graph pairs} to the above list. To show {tautologies} is P-reducible to {primes} would seem to require some deep results in number theory, while showing {tautologies} is P-reducible to {isomorphic graph pairs} would probably upset a conjecture of Corneil’s (Corneil and Gotlieb, 1970) from which he deduces that the graph isomorphism problem can be solved in polynomial time.

Incidentally, it is not hard to see from the Davis–Putnam procedure (Davis and Putnam, 1960) that the set D₂ consisting of all DNF tautologies with at most two conjuncts per disjunct, is in ℒ_*. Hence D₂ cannot be added to the list in Theorem 2 (unless all sets in the list are in ℒ_*).

Proof of Theorem 2. By the corollary to Theorem 1, each of the sets is P-reducible to {DNF tautologies}. Since obviously {DNF tautologies} is P-reducible to {tautologies}, it remains to show {DNF tautologies} is P-reducible to D₃ and D₃ is P-reducible to {subgraph pairs}.

To show {DNF tautologies} is P-reducible to D₃, let A be a proposition formula in disjunctive normal form. Say A = B₁ ∨B₂ ∨⋯∨B_k, where B₁ = R₁ ∧⋯∧R_s, and each R_i is an atom or negation of an atom, and s > 3. Then A is a tautology if and only if A′ is a tautology where

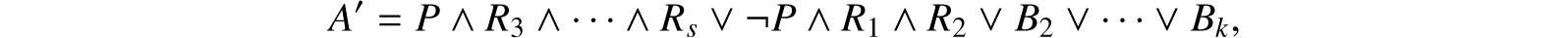
where P is a new atom. Since we have reduced the number of conjuncts in B₁, this process may be repeated until eventually a formula is found with at most three conjuncts per disjunct. Clearly the entire process is bounded in time by a polynomial in the length of A.

It remains to show that D₃ is P-reducible to {subgraph pairs}. Suppose A is a formula in disjunctive normal form with three conjuncts per disjunct. Thus A = C₁ ∨⋯∨ C_k,where C_i = R_i1 ∧ R_i2 ∧ R_i3, and each R_ij is an atom or a negation of an atom. Now let G₁ be the complete graph with vertices {v₁, v₂, …, v_k}, and let G₂ be the graph with vertices {u_ij}, 1 ≤ i ≤ k, 1 ≤ j ≤ 3, such that u_ij is connected by an edge to u_rs if and only if i ≠ r and the two literals (R_ij, R_rs) do not form an opposite pair (that is they are neither of the form (P, ¬P) nor of the form (¬P, P)). Thus there is a falsifying truth assignment to the formula A iff there is a graph homomorphism ϕ: G₁ → G₂ such that for each i, ϕ(v_i) = u_ij for some j. (The homomorphism tells for each i which of R_i1, R_i2, R_i3 should be falsified, and the selective lack of edges in G₂ guarantees that the resulting truth assignment is consistently specified.)

In order to guarantee that a one-one homomorphism ϕ: G₁ → G₂ has the property that for each i, ϕ(v_i) = u_ij for some j, we modify G₁ and G₂ as follows. We select graphs H₁, H₂, …, H_k which are sufficiently distinct from each other that if is formed from G₁ by attaching H_i to v_i, 1 ≤ i ≤ k, and is formed from G₂ by attaching H_i to each of u_i1 and u_i2 and u_i3, 1 ≤ i ≤ k, then every one-one homomorphism has the property just stated. It is not hard to see such a construction can be carried out in polynomial time. Then can be embedded in if and only if . This completes the proof of Theorem 2.

34.2 Discussion

Theorem 1 and its corollary give strong evidence that it is not easy to determine whether a given proposition formula is a tautology, even if the formula is in normal disjunctive form. Theorems 1 and 2 together suggest that it is fruitless to search for a polynomial decision procedure for the subgraph problem, since success would bring polynomial decision procedures to many other apparently intractable problems. Of course the same remark applies to any combinatorial problem to which tautologies is P-reducible.

Furthermore, the theorems suggest that {tautologies} is a good candidate for an interesting set not in ℒ_*, and I feel it is worth spending considerable effort trying to prove this conjecture. Such a proof would be a major breakthrough in complexity theory.

In view of the apparent complexity of {DNF tautologies}, it is interesting to examine the Davis–Putnam procedure (Davis and Putnam, 1960). This procedure was designed to determine whether a given formula in conjunctive normal form is satisfiable, but of course the “dual” procedure determines whether a given formula in disjunctive normal form is a tautology. I have not yet been able to find a series of examples showing the procedure (treated sympathetically to avoid certain pitfalls) must require more than polynomial time. Nor have I found an interesting upper bound for the time required.

If we let strings represent natural numbers (or k-tuples of natural numbers) using m-adic or other suitable notation, then the notions in the preceding sections can be made to apply to sets of numbers (or k-place relations on numbers). It is not hard to see that the set of relations accepted in polynomial time by some nondeterministic Turing machine is precisely the set ℒ⁺ of relations of the form

where , ℓ(z) is the dyadic length of z, and is an ℒ_* relation. (ℒ⁺ is the class of extended positive rudimentary relations of Bennett (1962).) If we remove the bound on the quantifier in formula (34.1), the class ℒ⁺ would become the class of recursively enumerable sets. Thus if ℒ⁺ is the analog of the class of r.e. sets, then determining tautologyhood is the analog of the halting problem; since, according to Theorem 1, {tautologies} has the complete ℒ⁺ degree just as the halting problem has the complete r.e. degree. Unfortunately, the diagonal argument which shows the halting problem is not recursive apparently cannot be adapted to show {tautologies} is not in ℒ_*. …

Reprinted from Cook (1971b), with permission from the Association for Computing Machinery.