45

A Method for Obtaining Digital Signatures and Public-Key Cryptosystems (1978)

Ronald Rivest, Adi Shamir, and Len Adleman

A copy of Diffie and Hellman (1976a, here chapter 42) quickly reached MIT, where Ronald Rivest (b. 1947), Leonard Adleman (b. 1945), and Adi Shamir (b. 1952) set to work on the problem of finding a public-key cryptosystem suitable for both the key distribution and digital signature problems. Eventually the three figured out how to use the factoring problem as the basis for such a system. The RSA algorithm became widely deployed in internet security software in the late 1990s when the World Wide Web began to be used commercially. Today, every banking transaction, e-commerce purchase, and rideshare summons involves an unspoken key exchange worked out between the user’s browser or app and the computers offering the service.

The paper is a remarkable testament to the beauty of algorithms and to the utility of even the purest mathematics. No one preparing to be a computer scientist when the authors were young could have decided to study number theory in the expectation that it would be important in building computer systems, but these three knew the subject well enough to brainstorm, challenge, and correct each other’s ideas of how to use it. The algorithm is elegant and easy to describe—if you know a bit of eighteenth-century mathematics about the properties of integers. Yet it depends on an unproven premise: that there is no fast algorithm for finding factors of large numbers.

The apparent difficulty of factoring was already well known. In 1801 Carl Friedrich Gauss observed that the best methods devised by both “ancient and modern” mathematicians “try the patience of even the practiced calculator,” and urged that “every possible means be explored for the solution of a problem so elegant and so celebrated” (Gauss, 1986, pages 396f.)—thus foreshadowing the agenda urged in the penultimate paragraph of this paper. William Jevons, inventor of the logic piano (page 27 of this volume), noted that factorization seemed to be only one of what we would now call one-way functions. “There are many cases in which we can easily and infallibly do a certain thing but may have much trouble in undoing it. … Given any two numbers, we may by a simple and infallible process obtain their product; but when a large number is given it is quite another matter to determine its factors” (Jevons, 1874, page 122). That factoring is exponentially costly has often been asserted (including by Jevons) but never proved, in spite of strenuous efforts since the widespread adoption of the RSA algorithm.

Fast factoring would break the RSA cryptosystem, and the system remains unbroken—as far as we know; there is always the possibility that some government agency or criminal has developed a secret technique for factoring large numbers. But as technology advanced, the key lengths suggested in this paper have been increased in actual practice. And while public-key systems based on other mathematical objects (for example, elliptic curves) have been developed, they too suffer from not, as yet, having been proved secure.

Though the authors suggest that readers familiar with Diffie and Hellman (1976a) can skip the first few sections of this paper, we include them because they straightforwardly lay out the context—and, notably, introduce “Alice” and “Bob,” who in much of the subsequent literature play the roles of the communicating parties.

Rivest remains on the faculty at MIT, while Adleman is at the University of Southern California and Shamir is at the Weizmann Institute in Israel. All three have contributed significantly to other areas of computer science (see chapter 46 in particular). In 1983 they founded a company to commercialize the discovery presented in this paper (RSA Security, which was acquired by Security Dynamics, which in turn was acquired by EMC, which was then acquired by Dell). In 2002 they were jointly recognized with the Turing Award.

---

45.0    Abstract

AN encryption method is presented with the novel property that publicly revealing an encryption key does not thereby reveal the corresponding decryption key. This has two important consequences.

1. Couriers or other secure means are not needed to transmit keys, since a message can be enciphered using an encryption key publicly revealed by the intended recipient. Only he can decipher the message, since only he knows the corresponding decryption key.

2. A message can be “signed” using a privately held decryption key. Anyone can verify this signature using the corresponding publicly revealed encryption key. Signatures cannot be forged, and a signer cannot later deny the validity of his signature. This has obvious applications in “electronic mail” and “electronic funds transfer” systems. A message is encrypted by representing it as a number M, raising M to a publicly specified power e and then taking the remainder when the result is divided by the publicly specified product n of two large secret prime numbers p and q. Decryption is similar, only a different, secret, power d is used, where e · d ≡ 1 (mod (p − 1) · (q − 1)). The security of the system rests in part on the difficulty of factoring the published divisor, n.

45.1    Introduction

The era of “electronic mail” (Potter, 1977) may soon be upon us; we must ensure that two important properties of the current “paper mail” system are preserved: (a) messages are private, and (b) messages can be signed. We demonstrate in this paper how to build these capabilities into an electronic mail system.

At the heart of our proposal is a new encryption method. This method provides an implementation of a “public-key cryptosystem,” an elegant concept invented by Diffie and Hellman (1976a, here chapter 42). Their article motivated our research, since they presented the concept but not any practical implementation of such a system. Readers familiar with Diffie and Hellman (1976a) may wish to skip directly to §45.5 for a description of our method.

45.2    Public-Key Cryptosystems

In a “public-key cryptosystem” each user places in a public file an encryption procedure E. That is, the public file is a directory giving the encryption procedure of each user. The user keeps secret the details of his corresponding decryption procedure D. These procedures have the following four properties:

(a) Deciphering the enciphered form of a message M yields M. Formally,

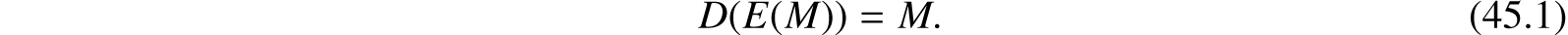
(b) Both E and D are easy to compute.

(c) By publicly revealing E the user does not reveal an easy way to compute D. This means that in practice only he can decrypt messages encrypted with E, or compute D efficiently.

(d) If a message M is first deciphered and then enciphered, M is the result. Formally,

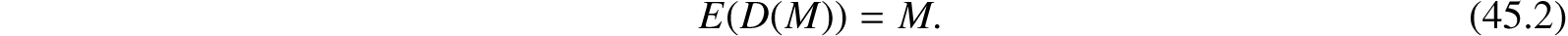
An encryption (or decryption) procedure typically consists of a general method and an encryption key. The general method, under control of the key, enciphers a message M to obtain the enciphered form of the message, called the ciphertext C. Everyone can use the same general method; the security of a given procedure will rest on the security of the key. Revealing an encryption algorithm then means revealing the key.

When the user reveals E he reveals a very inefficient method of computing D(C): testing all possible messages M until one such that E(M) = C is found. If property (c) is satisfied the number of such messages to test will be so large that this approach is impractical.

A function E satisfying (a)–(c) is a “trap-door one-way function”; if it also satisfies (d) it is a “trap-door one-way permutation.” Diffie and Hellman (1976a, here chapter 42) introduced the concept of trap-door one-way functions but did not present any examples. These functions are called “one-way” because they are easy to compute in one direction but (apparently) very difficult to compute in the other direction. They are called “trap-door” functions since the inverse functions are in fact easy to compute once certain private “trap-door” information is known. A trap-door one-way function which also satisfies (d) must be a permutation: every message is the ciphertext for some other message and every ciphertext is itself a permissible message. (The mapping is “one-to-one” and “onto.”) Property (d) is needed only to implement “signatures.”

The reader is encouraged to read Diffie and Hellman’s excellent article for further background, for elaboration of the concept of a public-key cryptosystem, and for a discussion of other problems in the area of cryptography. The ways in which a public-key cryptosystem can ensure privacy and enable “signatures” (described in §§45.3 and 45.4 below) are also due to Diffie and Hellman.

For our scenarios we suppose that A and B (also known as Alice and Bob) are two users of a public-key cryptosystem. We will distinguish their encryption and decryption procedures with subscripts: E_A, D_A, E_B, D_B.

45.3    Privacy

Encryption is the standard means of rendering a communication private. The sender enciphers each message before transmitting it to the receiver. The receiver (but no unauthorized person) knows the appropriate deciphering function to apply to the received message to obtain the original message. An eavesdropper who hears the transmitted message hears only “garbage” (the ciphertext) which makes no sense to him since he does not know how to decrypt it.

The large volume of personal and sensitive information currently held in computerized data banks and transmitted over telephone lines makes encryption increasingly important. In recognition of the fact that efficient, high-quality encryption techniques are very much needed but are in short supply, the National Bureau of Standards has recently adopted a “Data Encryption Standard,” developed at IBM (Federal Register: Vol. 40, No. 42, March 17, 1975; Vol. 40, No. 149, August 1, 1975). The new standard does not have property (c), needed to implement a public-key cryptosystem.

All classical encryption methods (including the NBS standard) suffer from the “key distribution problem.” The problem is that before a private communication can begin, another private transaction is necessary to distribute corresponding encryption and decryption keys to the sender and receiver, respectively. Typically a private courier is used to carry a key from the sender to the receiver. Such a practice is not feasible if an electronic mail system is to be rapid and inexpensive. A public-key cryptosystem needs no private couriers; the keys can be distributed over the insecure communications channel.

How can Bob send a private message M to Alice in a public-key cryptosystem? First, he retrieves E_A from the public file. Then he sends her the enciphered message E_A(M). Alice deciphers the message by computing D_A(E_A(M)) = M. By property (c) of the public-key cryptosystem only she can decipher E_A(M). She can encipher a private response with E_B, also available in the public file.

Observe that no private transactions between Alice and Bob are needed to establish private communication. The only “setup” required is that each user who wishes to receive private communications must place his enciphering algorithm in the public file.

Two users can also establish private communication over an insecure communications channel without consulting a public file. Each user sends his encryption key to the other. Afterwards all messages are enciphered with the encryption key of the recipient, as in the public-key system. An intruder listening in on the channel cannot decipher any messages, since it is not possible to derive the decryption keys from the encryption keys. (We assume that the intruder cannot modify or insert messages into the channel.) Ralph Merkle (1978) has developed another solution to this problem.

A public-key cryptosystem can be used to “bootstrap” into a standard encryption scheme such as the NBS method. Once secure communications have been established, the first message transmitted can be a key to use in the NBS scheme to encode all following messages. This may be desirable if encryption with our method is slower than with the standard scheme. (The NBS scheme is probably somewhat faster if special-purpose hardware encryption devices are used; our scheme may be faster on a general-purpose computer since multiprecision arithmetic operations are simpler to implement than complicated bit manipulations.)

45.4    Signatures

If electronic mail systems are to replace the existing paper mail system for business transactions, “signing” an electronic message must be possible. The recipient of a signed message has proof that the message originated from the sender. This quality is stronger than mere authentication (where the recipient can verify that the message came from the sender); the recipient can convince a “judge” that the signer sent the message. To do so, he must convince the judge that he did not forge the signed message himself! In an authentication problem the recipient does not worry about this possibility, since he only wants to satisfy himself that the message came from the sender.

An electronic signature must be message-dependent, as well as signer-dependent. Otherwise the recipient could modify the message before showing the message-signature pair to a judge. Or he could attach the signature to any message whatsoever, since it is impossible to detect electronic “cutting and pasting.”

To implement signatures the public-key cryptosystem must be implemented with trap-door one-way permutations (i.e. have property (d)), since the decryption algorithm will be applied to unenciphered messages.

How can user Bob send Alice a “signed” message M in a public-key cryptosystem? He first computes his “signature” S for the message M using D_B: S = D_B(M). (Deciphering an unenciphered message “makes sense” by property (d) of a public-key cryptosystem: each message is the ciphertext for some other message.) He then encrypts S using E_A (for privacy), and sends the result E_A(S) to Alice. He need not send M as well; it can be computed from S.

Alice first decrypts the ciphertext with D_A to obtain S. She knows who is the presumed sender of the signature (in this case, Bob); this can be given if necessary in plain text attached to S. She then extracts the message with the encryption procedure of the sender, in this case E_B (available on the public file): M = E_B(S). She now possesses a message-signature pair (M, S) with properties similar to those of a signed paper document.

Bob cannot later deny having sent Alice this message, since no one else could have created S = D_B(M). Alice can convince a “judge” that E_B(S) = M, so she has proof that Bob signed the document.

Clearly Alice cannot modify M to a different version M′, since then she would have to create the corresponding signature S′ = D_B(M′) as well.

Therefore Alice has received a message “signed” by Bob, which she can “prove” that he sent, but which she cannot modify. (Nor can she forge his signature for any other message.)

An electronic checking system could be based on a signature system such as the above. It is easy to imagine an encryption device in your home terminal allowing you to sign checks that get sent by electronic mail to the payee. It would only be necessary to include a unique check number in each check so that even if the payee copies the check the bank will only honor the first version it sees.

Another possibility arises if encryption devices can be made fast enough: it will be possible to have a telephone conversation in which every word spoken is signed by the encryption device before transmission.

When encryption is used for signatures as above, it is important that the encryption device not be “wired in” between the terminal (or computer) and the communications channel, since a message may have to be successively enciphered with several keys. It is perhaps more natural to view the encryption device as a “hardware subroutine” that can be executed as needed.

We have assumed above that each user can always access the public file reliably. In a “computer network” this might be difficult; an “intruder” might forge messages purporting to be from the public file. The user would like to be sure that he actually obtains the encryption procedure of his desired correspondent and not, say, the encryption procedure of the intruder. This danger disappears if the public file “signs” each message it sends to a user. The user can check the signature with the public file’s encryption algorithm E_PF. The problem of “looking up” E_PF itself in the public file is avoided by giving each user a description of E_PF when he first shows up (in person) to join the public-key cryptosystem and to deposit his public encryption procedure. He then stores this description rather than ever looking it up again. The need for a courier between every pair of users has thus been replaced by the requirement for a single secure meeting between each user and the public-file manager when the user joins the system. Another solution is to give each user, when he signs up, a book (like a telephone directory) containing all the encryption keys of users in the system.

45.5    Our Encryption and Decryption Methods

To encrypt a message M with our method, using a public encryption key (e, n), proceed as follows. (Here e and n are a pair of positive integers.)

First, represent the message as an integer between 0 and n − 1. (Break a long message into a series of blocks, and represent each block as such an integer.) Use any standard representation. The purpose here is not to encrypt the message but only to get it into the numeric form necessary for encryption.

Then, encrypt the message by raising it to the e^th power modulo n. That is, the result (the ciphertext C) is the remainder when M^e is divided by n.

To decrypt the ciphertext, raise it to another power d, again modulo n. The encryption and decryption algorithms E and D are thus:

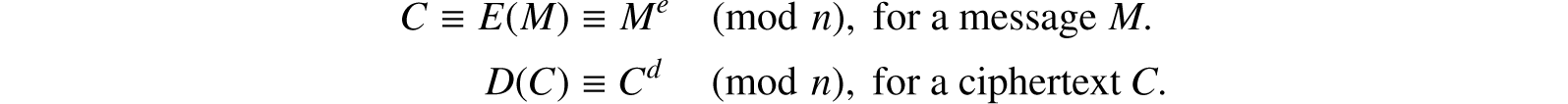
Note that encryption does not increase the size of a message; both the message and the ciphertext are integers in the range 0 to n − 1.

The encryption key is thus the pair of positive integers (e, n). Similarly, the decryption key is the pair of positive integers (d, n). Each user makes his encryption key public, and keeps the corresponding decryption key private. (These integers should properly be subscripted as in n_A, e_A, and d_A, since each user has his own set. However, we will only consider a typical set, and will omit the subscripts.)

How should you choose your encryption and decryption keys, if you want to use our method?

You first compute n as the product of two primes p and q: n = p · q. These primes are very large, “random” primes. Although you will make n public, the factors p and q will be effectively hidden from everyone else due to the enormous difficulty of factoring n. This also hides the way d can be derived from e.

You then pick the integer d to be a large, random integer which is relatively prime to (p− 1) · (q − 1). That is, check that d satisfies gcd(d, (p− 1) · (q − 1)) = 1 (“gcd” means “greatest common divisor”).

The integer e is finally computed from p, q, and d to be the “multiplicative inverse” of d, modulo (p− 1) · (q − 1). Thus we have e·d ≡ 1 (mod (p− 1) · (q − 1)).

We prove in the next section that this guarantees that (45.1) and (45.2) hold, i.e. that E and D are inverse permutations. §45.7 shows how each of the above operations can be done efficiently.

The aforementioned method should not be confused with the “exponentiation” technique presented by Diffie and Hellman (1976a, here chapter 42) to solve the key distribution problem. Their technique permits two users to determine a key in common to be used in a normal cryptographic system. It is not based on a trap-door one-way permutation. Pohlig and Hellman (1978) study a scheme related to ours, where exponentiation is done modulo a prime number.

45.6    The Underlying Mathematics

We demonstrate the correctness of the deciphering algorithm using an identity due to Euler and Fermat (Niven, 1972): for any integer (message) M which is relatively prime to n,

Here ϕ(n) is the Euler totient function giving the number of positive integers less than n which are relatively prime to n. For prime numbers p, ϕ(p) = p − 1. In our case, we have by elementary properties of the totient function:

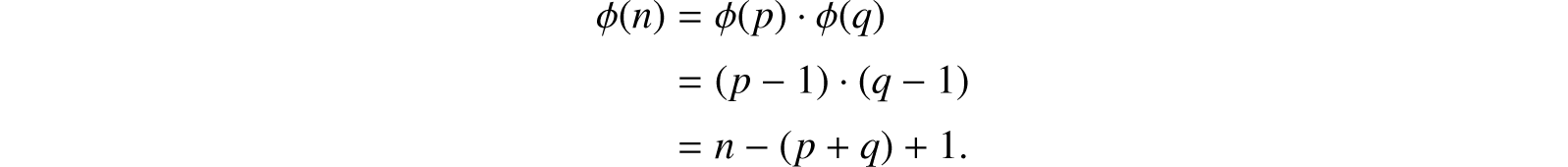
Since d is relatively prime to ϕ(n), it has a multiplicative inverse e in the ring of integers modulo ϕ(n):

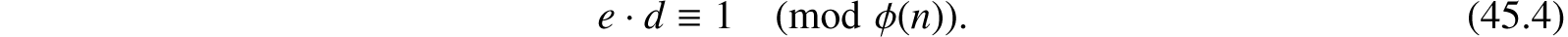
We now prove that equations (45.1) and (45.2) hold (that is, that deciphering works correctly if e and d are chosen as above). Now

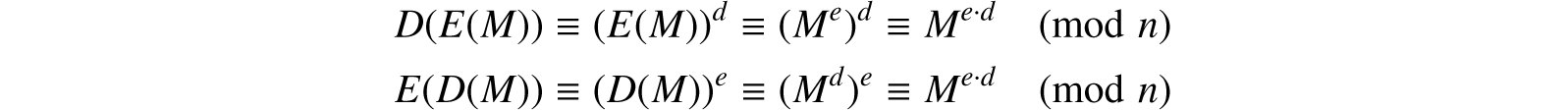
and

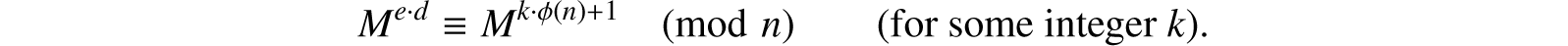
From (45.3) we see that for all M such that p does not divide M, M^p−1 ≡ 1 (mod p), and since (p − 1) divides ϕ(n),

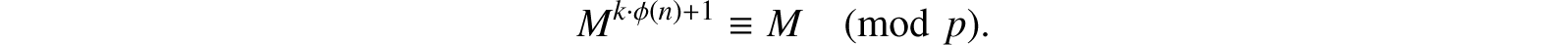
This is trivially true when M ≡ 0 (mod p), so that this equality actually holds for all M. Arguing similarly for q yields

Together these last two equations imply that for all M,

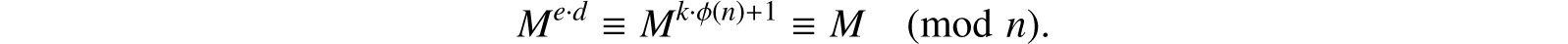
This implies (45.1) and (45.2) for all M, 0 ≤ M < n. Therefore E and D are inverse permutations. (We thank Rich Schroeppel for suggesting the above improved version of the authors’ previous proof.)

45.7    Algorithms

To show that our method is practical, we describe an efficient algorithm for each required operation.

45.7.1    How to encrypt and decrypt efficiently    Computing M^e (mod n) requires at most 2 log₂(e) multiplications and 2 log₂(e) divisions using the following procedure (decryption can be performed similarly using d instead of e):

1. Let e_ke_k−1…e₁e₀ be the binary representation of e.

2. Set the variable C to 1.

3. Repeat steps 3a and 3b for i = k, k − 1, …, 0:

3a. Set C to the remainder of C² when divided by n.

3b. If e_i = 1, then set C to the remainder of C · M when divided by n.

4. Halt. Now C is the encrypted form of M.

This procedure is called “exponentiation by repeated squaring and multiplication.” This procedure is half as good as the best; more efficient procedures are known. Knuth (1969) studies this problem in detail.

The fact that the enciphering and deciphering are identical leads to a simple implementation. (The whole operation can be implemented on a few special-purpose integrated circuit chips.)

A high-speed computer can encrypt a 200-digit message M in a few seconds; special-purpose hardware would be much faster. The encryption time per block increases no faster than the cube of the number of digits in n.

45.7.2    How to find large prime numbers    Each user must (privately) choose two large random prime numbers p and q to create his own encryption and decryption keys. These numbers must be large so that it is not computationally feasible for anyone to factor n = p · q. (Remember that n, but not p or q, will be in the public file.) We recommend using 100-digit (decimal) prime numbers p and q, so that n has 200 digits.

To find a 100-digit “random” prime number, generate (odd) 100-digit random numbers until a prime number is found. By the prime number theorem (Niven, 1972), about (ln10¹⁰⁰)/2 = 115 numbers will be tested before a prime is found.

To test a large number b for primality we recommend the elegant “probabilistic” algorithm due to Solovay and Strassen (1977). It picks a random number a from a uniform distribution on {1, …, b − 1}, and tests whether

where J(a, b) is the Jacobi symbol (Niven, 1972). If b is prime (45.5) is always true. If b is composite (45.5) will be false with probability at least . If (45.5) holds for 100 randomly chosen values of a then b is almost certainly prime; there is a (negligible) chance of one in 2¹⁰⁰ that b is composite. Even if a composite were accidentally used in our system, the receiver would probably detect this by noticing that decryption didn’t work correctly. When b is odd, a ≤ b, and gcd(a, b) = 1, the Jacobi symbol J(a, b) has a value in {−1, 1} and can be efficiently computed by the program:

(The computations of J(a, b) and gcd(a, b) can be nicely combined, too.) Note that this algorithm does not test a number for primality by trying to factor it. Other efficient procedures for testing a large number for primality are given in Miller (1976); Pollard (1974); Rabin (1976).

To gain additional protection against sophisticated factoring algorithms, p and q should differ in length by a few digits, both (p− 1) and (q − 1) should contain large prime factors, and gcd(p − 1, q − 1) should be small. The latter condition is easily checked.

To find a prime number p such that (p − 1) has a large prime factor, generate a large random prime number u, then let p be the first prime in the sequence i·u + 1, for i = 2, 4, 6, …. (This shouldn’t take too long.) Additional security is provided by ensuring that (u − 1) also has a large prime factor.

A high-speed computer can determine in several seconds whether a 100-digit number is prime, and can find the first prime after a given point in a minute or two.

Another approach to finding large prime numbers is to take a number of known factorization, add one to it, and test the result for primality. If a prime p is found it is possible to prove that it really is prime by using the factorization of p − 1. We omit a discussion of this since the probabilistic method is adequate.

45.7.3    How to choose d    It is very easy to choose a number d which is relatively prime to ϕ(n). For example, any prime number greater than max(p, q) will do. It is important that d should be chosen from a large enough set so that a cryptanalyst cannot find it by direct search.

45.7.4    How to compute e from d and ϕ(n)    To compute e, use the following variation of Euclid’s algorithm for computing the greatest common divisor of ϕ(n) and d. (See exercise 4.5.2.15 in Knuth (1969).) Calculate gcd(ϕ(n), d) by computing a series x₀, x₁, x₂, …, where x₀ = ϕ(n), x₁ = d, and x_i+1 = x_i−1 (mod x_i), until an x_k equal to 0 is found. Then gcd(x₀, x₁) = x_k−1. Compute for each x_i numbers a_i and b_i such that x_i = a_i · x₀ + b_i · x₁. If x_k−1 = 1 then b_k−1 is the multiplicative inverse of x₁ (mod x₀). Since k will be less than 2 · log₂(n), this computation is very rapid.

If e turns out to be less than log₂(n), start over by choosing another value of d. This guarantees that every encrypted message (except M = 0 or M = 1) undergoes some “wrap-around” (reduction modulo n). …

45.8    A Small Example …

45.9    Security of the Method: Cryptanalytic approaches

Since no techniques exist to prove that an encryption scheme is secure, the only test available is to see whether anyone can think of a way to break it. The NBS standard was “certified” this way; seventeen man-years at IBM were spent fruitlessly trying to break that scheme. Once a method has successfully resisted such a concerted attack it may for practical purposes be considered secure. (Actually there is some controversy concerning the security of the NBS method [Diffie and Hellman, 1977].)

We show in the next sections that all the obvious approaches for breaking our system are at least as difficult as factoring n. While factoring large numbers is not provably difficult, it is a well-known problem that has been worked on for the last three hundred years by many famous mathematicians. Fermat (1601?–1665) and Legendre (1752–1833) developed factoring algorithms; some of today’s more efficient algorithms are based on the work of Legendre. As we shall see in the next section, however, no one has yet found an algorithm which can factor a 200-digit number in a reasonable amount of time. We conclude that our system has already been partially “certified” by these previous efforts to find efficient factoring algorithms.

In the following sections we consider ways a cryptanalyst might try to determine the secret decryption key from the publicly revealed encryption key. We do not consider ways of protecting the decryption key from theft; the usual physical security methods should suffice. (For example, the encryption device could be a separate device which could also be used to generate the encryption and decryption keys, such that the decryption key is never printed out (even for its owner) but only used to decrypt messages. The device could erase the decryption key if it was tampered with.)

45.9.1    Factoring n    Factoring n would enable an enemy cryptanalyst to “break” our method. The factors of n enable him to compute ϕ(n) and thus d. Fortunately, factoring a number seems to be much more difficult than determining whether it is prime or composite. … [EDITOR: Discussion of factoring algorithms omitted]

45.9.2    Computing ϕ(n) without factoring n    If a cryptanalyst could compute ϕ(n) then he could break the system by computing d as the multiplicative inverse of e modulo ϕ(n) (using the procedure of §45.7.4).

We argue that this approach is no easier than factoring n since it enables the cryptanalyst to easily factor n using ϕ(n). This approach to factoring n has not turned out to be practical.

How can n be factored using ϕ(n)? First, (p + q) is obtained from n and ϕ(n) = n− (p + q) + 1. Then (p−q) is the square root of (p + q)² − 4n. Finally, q is half the difference of (p + q) and (p − q).

Therefore breaking our system by computing ϕ(n) is no easier than breaking our system by factoring n. (This is why n must be composite; ϕ(n) is trivial to compute if n is prime.)

45.9.3    Determining d without factoring n or computing ϕ(n)    Of course, d should be chosen from a large enough set so that a direct search for it is unfeasible.

We argue that computing d is no easier for a cryptanalyst than factoring n, since once d is known n could be factored easily. This approach to factoring has also not turned out to be fruitful.

A knowledge of d enables n to be factored as follows. Once a cryptanalyst knows d he can calculate e · d − 1, which is a multiple of ϕ(n). Miller has shown that n can be factored using any multiple of ϕ(n). Therefore if n is large a cryptanalyst should not be able to determine d any easier than he can factor n.

A cryptanalyst may hope to find a d′ which is equivalent to the d secretly held by a user of the public-key cryptosystem. If such values d′ were common then a brute-force search could break the system. However, all such d′ differ by the least common multiple of (p− 1) and (q − 1), and finding one enables n to be factored. (In (45.3) and (45.4), ϕ(n) can be replaced by lcm(p− 1, q − 1).) Finding any such d′ is therefore as difficult as factoring n.

45.9.4    Computing d in some other way    Although this problem of “computing e^th roots modulo n without factoring n” is not a well-known difficult problem like factoring, we feel reasonably confident that it is computationally intractable. It may be possible to prove that any general method of breaking our scheme yields an efficient factoring algorithm. This would establish that any way of breaking our scheme must be as difficult as factoring. We have not been able to prove this conjecture, however.

Our method should be certified by having the above conjecture of intractability withstand a concerted attempt to disprove it. The reader is challenged to find a way to “break” our method.

45.10    Avoiding “Reblocking” When Encrypting a Signed Message

A signed message may have to be “reblocked” for encryption since the signature n may be larger than the encryption n (every user has his own n). This can be avoided as follows. A threshold value h is chosen (say h = 10¹⁹⁹) for the public-key cryptosystem. Every user maintains two public (e, n) pairs, one for enciphering and one for signature-verification, where every signature n is less than h, and every enciphering n is greater than h. Reblocking to encipher a signed message is then unnecessary; the message is blocked according to the transmitter’s signature n.

Another solution uses a technique given in Levine and Brawley (1977). Each user has a single (e, n) pair where n is between h and 2h, where h is a threshold as above. A message is encoded as a number less than h and enciphered as before, except that if the ciphertext is greater than h, it is repeatedly re-enciphered until it is less than h. Similarly for decryption the ciphertext is repeatedly deciphered to obtain a value less than h. If n is near h re-enciphering will be infrequent. (Infinite looping is not possible, since at worst a message is enciphered as itself.)

45.11    Conclusions

We have proposed a method for implementing a public-key cryptosystem whose security rests in part on the difficulty of factoring large numbers. If the security of our method proves to be adequate, it permits secure communications to be established without the use of couriers to carry keys, and it also permits one to “sign” digitized documents.

The security of this system needs to be examined in more detail. In particular, the difficulty of factoring large numbers should be examined very closely. The reader is urged to find a way to “break” the system. Once the method has withstood all attacks for a sufficient length of time it may be used with a reasonable amount of confidence.

Our encryption function is the only candidate for a “trap-door one-way permutation” known to the authors. It might be desirable to find other examples, to provide alternative implementations should the security of our system turn out someday to be inadequate. There are surely also many new applications to be discovered for these functions.

1. Reprinted from Rivest et al. (1978), with permission from the Association for Computing Machinery.