8

A Symbolic Analysis of Relay and Switching Circuits (1938)

Claude Shannon

Electric wires connected by switches either conduct electricity or don’t, depending on the interconnection pattern and the settings of the switches. As early as 1886, the philosopher Charles Sanders Peirce had recognized the relation of logical connectives to series and parallel electric circuits. But it was Claude Shannon (1916–2001) who exploited the electric interpretation of Boole’s laws of thought. Shannon had tinkered with electric circuits while growing up in rural northern Michigan and had built a barbed wire telegraph to a friend’s house. By the 1930s the radio and telephone industries were flourishing, and Shannon studied electrical engineering at the University of Michigan. He encountered Boole’s writings in a philosophy class, and as an MIT graduate student he made the connection between the two binary-valued systems—thus giving birth to a profoundly elegant methodology for managing complex circuit design problems.

Today we take it for granted that the intended behavior of a circuit can be described mathematically, and that the resulting formulas can be manipulated using mathematical rules and then “compiled” into hardware. Shannon, in his Master’s thesis, was the first to do it. This selection is an excerpt from a paper that became part of that thesis; it has had immense impact on circuit design ever since. It deals with the analysis and synthesis of electrical circuits, some far more complicated than the simple ones in our brief selection. In a passage we do not include, Shannon’s paper goes on to prove upper and lower bounds on the size of circuits for certain boolean functions under particular restrictions about the form of those circuits, thus foreshadowing the rich and important field of circuit complexity.

---

8.1    Introduction

IN the control and protective circuits of complex electrical systems it is frequently necessary to make intricate interconnections of relay contacts and switches. Examples of these circuits occur in automatic telephone exchanges, industrial motor-control equipment, and in almost any circuits designed to perform complex operations automatically. In this paper a mathematical analysis of certain of the properties of such networks will be made. Particular attention will be given to the problem of network synthesis. Given certain characteristics, it is required to find a circuit incorporating these characteristics. The solution of this type of problem is not unique and methods of finding those particular circuits requiring the least number of relay contacts and switch blades will be studied. Methods will also be described for finding any number of circuits equivalent to a given circuit in all operating characteristics. It will be shown that several of the well-known theorems on impedance networks have roughly analogous theorems in relay circuits. Notable among these are the delta-wye and star-mesh transformations, and the duality theorem.

The method of attack on these problems may be described briefly as follows: any circuit is represented by a set of equations, the terms of the equations corresponding to the various relays and switches in the circuit. A calculus is developed for manipulating these equations by simple mathematical processes, most of which are similar to ordinary algebraic algorithms. This calculus is shown to be exactly analogous to the calculus of propositions used in the symbolic study of logic. For the synthesis problem the desired characteristics are first written as a system of equations, and the equations are then manipulated into the form representing the simplest circuit. The circuit may then be immediately drawn from the equations. By this method it is always possible to find the simplest circuit containing only series and parallel connections, and in some cases the simplest circuit containing any type of connection.

Our notation is taken chiefly from symbolic logic. Of the many systems in common use we have chosen the one which seems simplest and most suggestive for our interpretation. Some or our phraseology, such as node, mesh, delta, wye, etc., is borrowed from ordinary network theory for simple concepts in switching circuits.

8.2    Series-Parallel Two-Terminal Circuits: Definitions and Postulates

We shall limit our treatment of circuits containing only relay contacts and switches, and therefore at any given time the circuit between any two terminals must be either open (infinite impedance) or closed (zero impedance). Let us associate a symbol X_ab or more simply X, with the terminals a and b. This variable, a function of time, will be called the hindrance of the two-terminal circuit a − b. The symbol 0 (zero) will be used to represent the hindrance of a closed circuit, and the symbol 1 (unity) to represent the hindrance of an open circuit. Thus when the circuit a − b is open X_ab = 1 and when closed X_ab = 0. Two hindrances X_ab and X_cd will be said to be equal if whenever the circuit a − b is open, the circuit c − d is open, and whenever a − b is closed, c − d is closed. Now let the symbol + (plus) be defined to mean the series connection of the two-terminal circuits whose hindrances are added together. Thus X_ab + X_cd is the hindrance of the circuit a − d when b and c are connected together. Similarly the product of two hindrances X_ab · X_cd, or more briefly X_abX_cd will be defined to mean the hindrance of the circuit formed by connecting the circuits a − b and c − d in parallel. A relay contact or switch will be represented in a circuit by the symbol in Figure 8.1, the letter being the corresponding hindrance function. Figure 8.2 shows the interpretation of the plus sign and Figure 8.3 the multiplication sign. This choice of symbols makes the manipulation of hindrances very similar to ordinary numerical algebra.

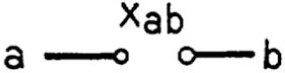
Figure 8.1: Symbol for hindrance function

Figure 8.2: Interpretation of addition

Figure 8.3: Interpretation of multiplication

It is evident that with the above definitions, the following postulates will hold:

			Postulates
1.	a.	0 · 0 = 0	A closed circuit in parallel with a closed circuit is a closed circuit.
	b.	1 + 1 = 1	An open circuit in series with an open circuit is an open circuit.
2.	a.	1 + 0 = 0 + 1 = 1	An open circuit in series with a closed circuit in either order (i.e., whether the open circuit is to the right or left of the closed circuit) is an open circuit.
	b.	0·1 = 1·0 = 0	A closed circuit in parallel with an open circuit in either order is a closed circuit.
3.	a.	0 + 0 = 0	A closed circuit in series with a closed circuit is a closed circuit.
	b.	1 · 1 = 1	An open circuit in parallel with an open circuit is an open circuit.
4.			At any given time either X = 0 or X = 1.

These are sufficient to develop all the theorems which will be used in connection with circuits containing only series and parallel connections. The postulates are arranged in pairs to emphasize a duality relationship between the operations of addition and multiplication and the quantities zero and one. Thus if in any of the a postulates the zero’s are replaced by one’s and the multiplications by additions and vice versa, the corresponding b postulate will result. This fact is of great importance. It gives each theorem a dual theorem, it being necessary to prove only one to establish both. The only one of these postulates which differs from ordinary algebra is 1b. However, this enables great simplifications in the manipulation of these symbols.

8.2.1    Theorems    In this section a number of theorems governing the combination of hindrances will be given. Inasmuch as any of the theorems may be proved by a very simple process, the proofs will not be given except for an illustrative example. The method of proof is that of “perfect induction,” i.e., the verification of the theorem for all possible cases. Since by Postulate 4 each variable is limited to the values 0 and 1, this is a simple matter. Some of the theorems may be proved more elegantly by recourse to previous theorems, but the method of perfect induction is so universal that it is probably to be preferred.

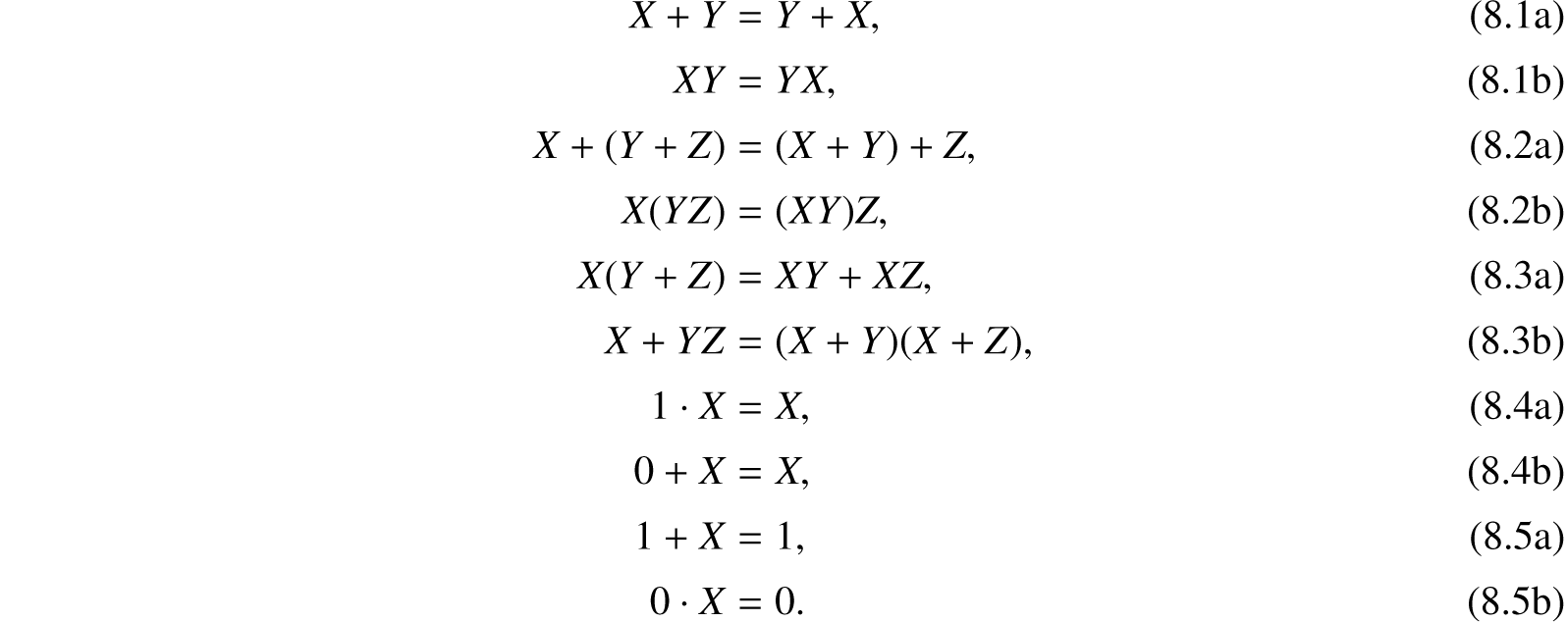
For example, to prove Theorem 8.4a, note that X is either 0 or 1. If it is 0, the theorem follows from Postulate 2b: if 1, it follows from Postulate 3b. Theorem 8.4b now follows by the duality principle, replacing the 1 by 0 and the · by +.

Due to the associative laws (8.2a and 8.2b) parentheses may be omitted in a sum or product of several terms without ambiguity. The Σ and Π symbols will be used as in ordinary algebra.

The distributive law (8.3a) makes it possible to “multiply out” products and to factor sums. The dual of this theorem, (8.3b), however, is not true in numerical algebra.

We shall now define a new operation to be called negation. The negative of a hindrance X will be written X′ and is defined to be a variable which is equal to 1 when X equals 0 and equal to 0 when X equals 1. If X is the hindrance of the make contacts of a relay, then X′ is the hindrance of the break contacts of the same relay. The definition of the negative of a hindrance gives the following theorems:

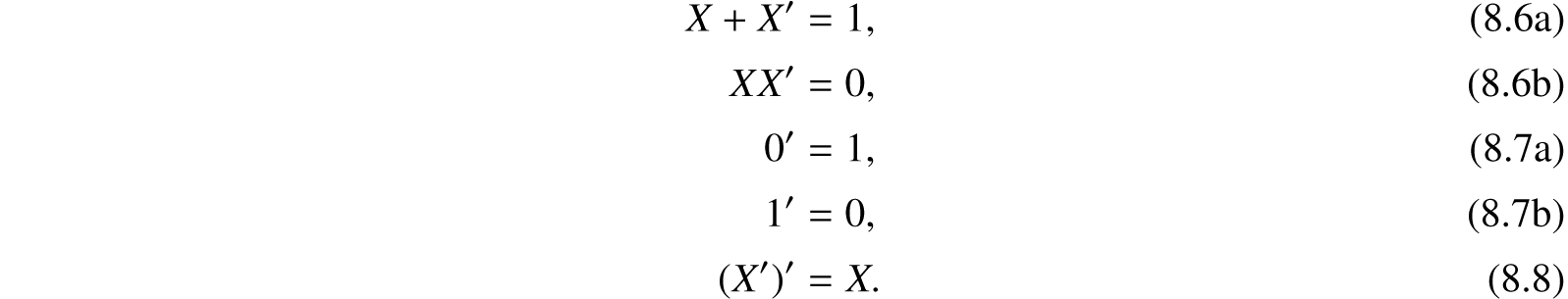
8.2.2    Analogue with the calculus of propositions    We are now in a position to demonstrate the equivalence of this calculus with certain elementary parts of the calculus of propositions. The algebra of logic, originated by George Boole, is a symbolic method of investigating logical relationships. The symbols of boolean algebra admit of two logical interpretations. If interpreted in terms of classes, the variables are not limited to the two possible values 0 and 1. This interpretation is known as the algebra of classes. If, however, the terms are taken to represent propositions, we have the calculus of propositions in which variables are limited to the values 0 and 1, as are the hindrance functions above. Usually the two subjects are developed simultaneously from the same set of postulates, except for the addition in the case of the calculus of propositions of a postulate equivalent to Postulate 4 above. E. V. Huntington gives the following set of postulates for symbolic logic:

1. The class K contains at least two distinct elements.

2. If a and b are in the class K then a + b is in the class K.

3. a + b = b + a.

4. (a + b) + c = a + (b + c).

5. a + a = a.

6. ab + ab′ = a where ab is defined as (a′ + b′)′.

If we let the class K be the class consisting of the two elements 0 and 1, then these postulates follow from those given in the first section. Also Postulates 1, 2, and 3 given there can be deduced from Huntington’s postulates. Adding 4 and restricting our discussion to the calculus of propositions, it is evident that a perfect analogy exists between the calculus for switching circuits and this branch of symbolic logic. The two interpretations of the symbols are shown in Figure 8.4.

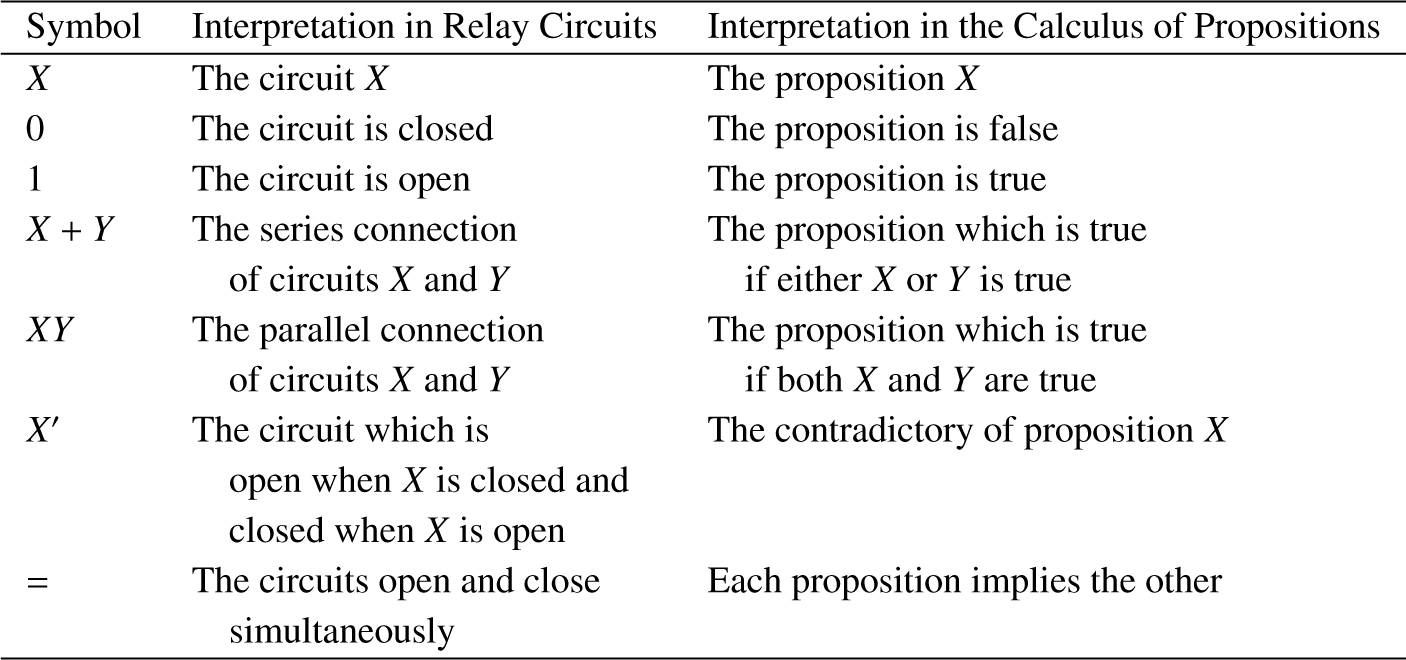
Figure 8.4: Analogue between the calculus of propositions and the symbolic relay analysis

Due to this analogy any theorem of the calculus of propositions is also a true theorem if interpreted in terms of relay circuits. The remaining theorems in this section are taken directly from this field.

De Morgan’s theorem:

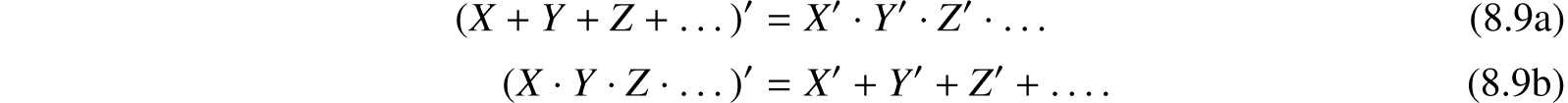
This theorem gives the negative of a sum or product in terms of the negatives of the summands or factors. It may be easily verified for two terms by substituting all possible values and then extended to any number n of variables by mathematical induction.

A function of certain variables X₁, X₂, …, X_n is any expression formed from the variables with the operations of addition, multiplication, and negation. The notation f(X₁, X₂, …, X_n) will be used to represent a function. Thus we might have f(X, Y, Z) = XY + X′(Y ′ + Z′). In infinitesimal calculus it is shown that any function (providing it is continuous and all derivatives are continuous) may be expanded in a Taylor series. A somewhat similar expansion is possible in the calculus of propositions. To develop the series expansion of functions first note the following equations: [EDITOR: Cf. Boole, page 44]

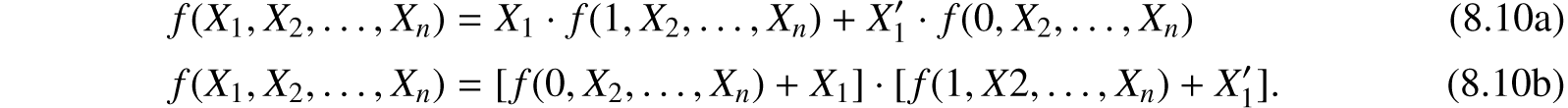
These reduce to identities if we let X₁ equal either 0 or 1. In these equations the function f is said to be expanded about X₁. The coefficients of X₁ and in (8.10a) are functions of the (n − 1) variables X₂, …, X_n and may thus be expanded about any of these variables in the same manner. The additive terms in (8.10b) also may be expanded in this manner. Expanding about X₂ we have:

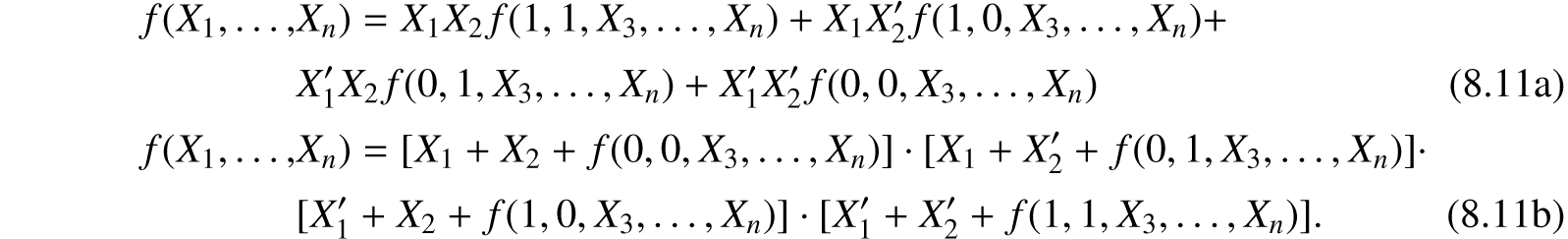
Continuing this process n times we will arrive at the complete series expansion having the form:

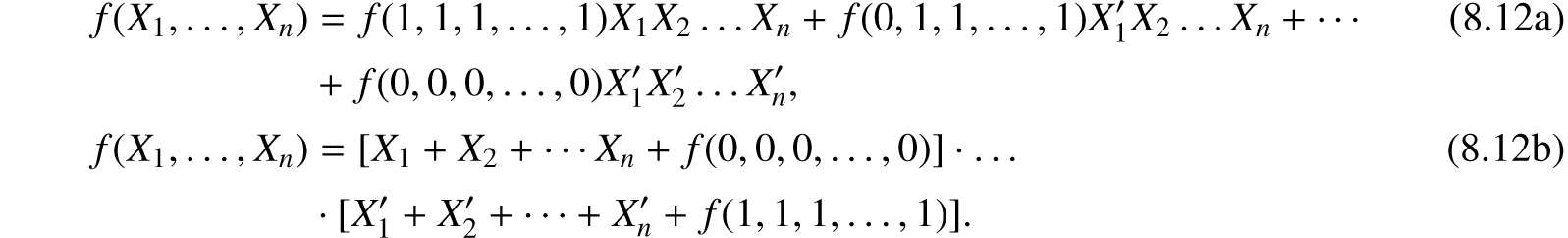
By (8.12a), f is equal to the sum of the products formed by permuting primes on the terms of X₁, X₂, …, X_n in all possible ways and giving each product a coefficient equal to the value of the function when that product is 1. Similarly for (8.12b).

As an application of the series expansion it should be noted that if we wish to find a circuit representing any given function we can always expand the function by either (8.10a) or (8.10b) in such a way that any given variable appears at most twice, once as a make contact and once as a break contact. This is shown in Figure 8.5. Similarly by (8.11a) and (8.11b) any other variable need appear no more than four times (two make and two break contacts), etc.

Figure 8.5: Expansion about one variable

A generalization of De Morgan’s theorem is represented symbolically in the following equation:

By this we mean that the negative of any function may be obtained by replacing each variable by its negative and interchanging the + and · symbols. Explicit and implicit parentheses will, of course, remain in the same places. For example, the negative of X + Y(Z + WX′) will be X′[Y′ + Z′(W′ + X)].

Some other theorems useful in simplifying expressions are given below:

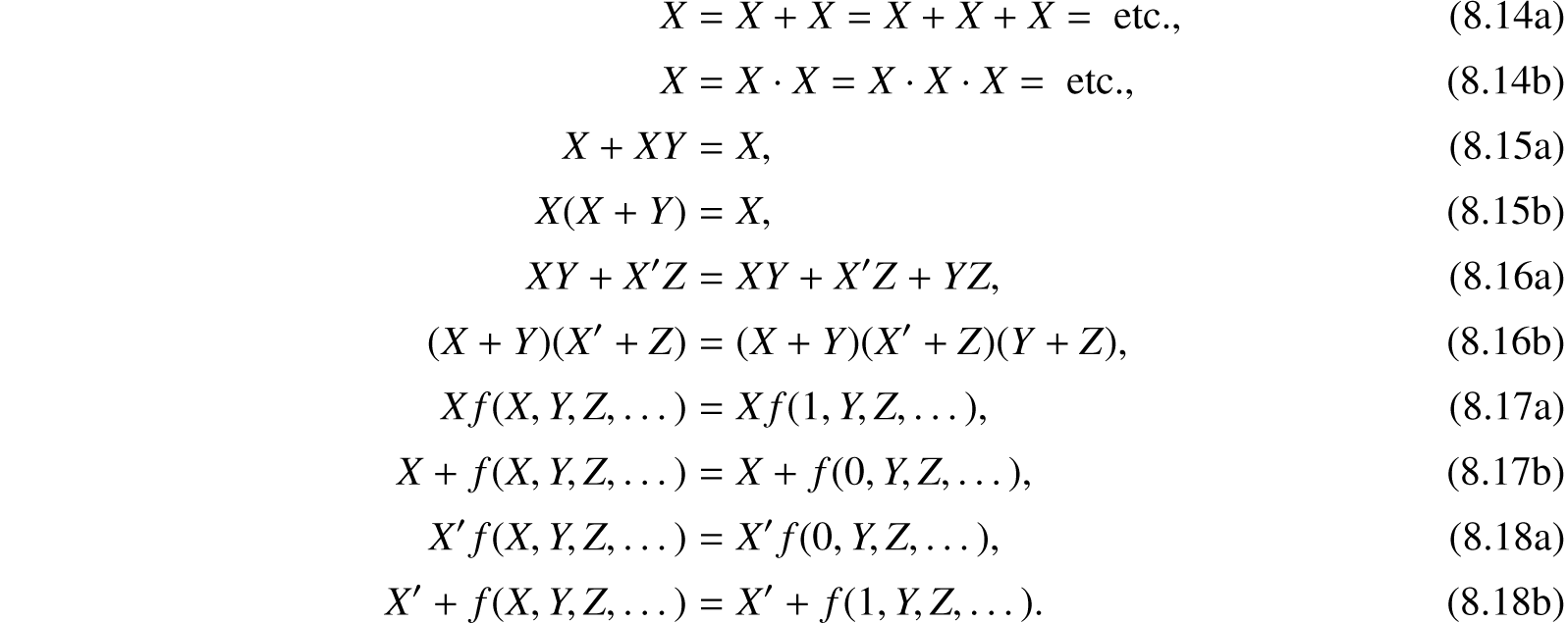
All of these theorems may be proved by the method of perfect induction.

Any expression formed with the operations of addition, multiplication, and negation represents explicitly a circuit containing only series and parallel connections. Such a circuit will be called a series-parallel circuit. Each letter in an expression of this sort represents a make or break relay contact, or a switch blade and contact. To find the circuit requiring the least number of contacts, it is therefore necessary to manipulate the expression into the form in which the least number of letters appear. The theorems given above are always sufficient to do this. A little practice in the manipulation of these symbols is all that is required. Fortunately most of the theorems are exactly the same as those of numerical algebra—the associative, commutative, and distributive laws of algebra hold here. The writer has found (8.3), (8.6), (8.9), (8.14), (8.15), (8.16a), (8.17), and (8.18) to be especially useful in the simplification of complex expressions. Frequently a function may be written in several ways, each requiring the same minimum number of elements. In such a case the choice of circuit may be made arbitrarily from among these, or from other considerations.

As an example of the simplification of expressions consider the circuit shown in Figure 8.6. The hindrance function X_ab for this circuit will be:

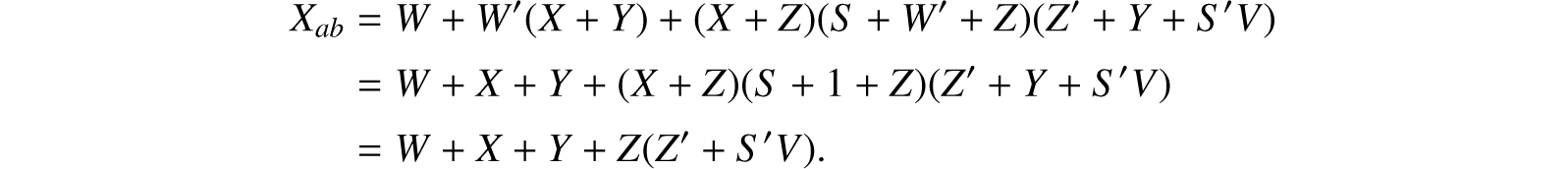
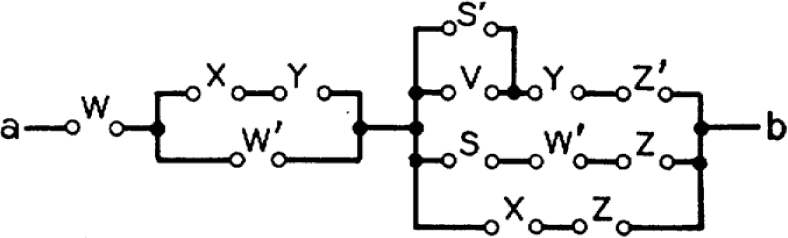
Figure 8.6: Circuit to be simplified

These reductions were made with (8.17b) using first W, then X and Y as the “X” of (8.17b). Now multiplying out:

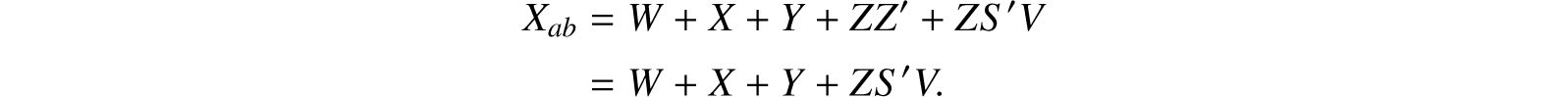
The circuit corresponding to this expression is shown in Figure 8.7. Note the large reduction in the number of elements. …

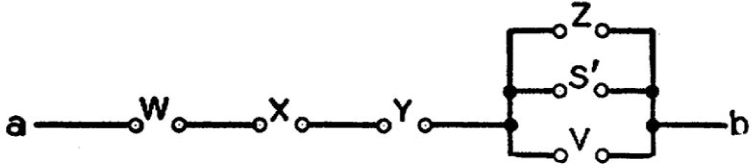
Figure 8.7: Simplification of Figure 8.6

1. Reprinted from Shannon (1938), with permission from the Massachusetts Institute of Technology.