9
A Logical Calculus of the Ideas Immanent in Nervous Activity (1943)
Warren McCulloch and Walter Pitts
This is a strange and wonderful paper, technically convoluted and hubristically prophetic, an admixture of wet neuroscience and austere mathematical abstraction unlike anything written before. It is complex in its notation and extravagant in its pretensions. Its goal is nothing less than to reduce the functioning of the human brain to mathematical logic, and thereby to explain thought, memory, and mind. In all its immodesty and naïveté, it is the bubbling source of ideas that have nourished computer science for decades.
The authors picture a neural network consisting of two kinds of neurons. Some receive inputs from no other neurons; they are the bearers of sensory data and are referred to as “peripheral afferents.” The others are switches, and can be in one of two states, either firing or not. A global clock synchronizes the system, and the state of each neuron at time t + 1 depends on the states of its inputs at time t. The inputs to a neuron are from peripheral afferents or from the outputs (“efferents”) of other neurons; the junction points, where the inputs arrive at a neuron, are synapses. A McCulloch–Pitts neuron i has a threshold θi; neuron i fires if more than θi of its inputs fire—except that the neuron also has an inhibitory input, and will not fire if the inhibitory input is activated. In their drawings of neurons (Figure 9.1 on page 86), the excitatory inputs are on the slanted sides of the triangular diagram, the inhibitory input is at the point on the left, and the output or efferent comes from the vertical side on the right.
Figure 9.1: The neuron ci is always marked with the numeral i upon the body of the cell, and the corresponding action is denoted by “N” with i as subscript, as in the text.
In short, this paper models the brain and all its functions as a digital system. The neurons of Figure 9.1 are gates in what would today be called a threshold logic. The authors’ goal is to determine what kinds of computations such a network can carry out. They do this by associating with each neuron i a predicate Ni(t) that is true if neuron i is firing at time t. With this background, it is worth working through some of the diagrams and formulas of Figure 9.1 before beginning to read the paper. (The single dots and vertical double dots are an alternative to parentheses; they tend to push formulas apart, two dots more strongly than one. A single dot can also denote conjunction. So the first line of part (e) corresponds to N3(t) ≡ [N1(t − 1) ∨ (N2(t − 3) ∧ ∼ N2(t − 2))], where ∼ stands for “not,” ∨ for “or,” and ∧ for “and.”)
The specific technical accomplishment of the paper is to prove that the set of predicates computable by neural nets is exactly the same as the set of predicates expressible in a certain very expressive logic. Particular attention is given to networks with feedback, in which the output of one neuron, after affecting a series of other neurons, loops back as an input to the original neuron. Such cycles of activity, the authors suggest, explain memory. So given a complete account of the network, they reasoned, “for prognosis, history is never necessary” (page 88). The brain is what we would now call a deterministic finite-state machine: its future is completely determined by its present state and its inputs going forward.
The paper’s formulas are ridden with errors and infelicities—“S” names the successor function, but boldface “S” is an unrelated variable standing for “sentence.” Stephen Cole Kleene simplified the model and used it in 1951 as the basis for his formalization of finite automata and regular expressions. Readers who find “A Logical Calculus” tough going should be reassured by Kleene’s take on it: “The present article is partly an exposition of the McCulloch–Pitts results; but we found the part of their paper which treats of arbitrary nerve nets obscure ….” (Kleene, 1951).
It soon became evident that the digital contraption McCulloch and Pitts described was a poor model for the brain. The discovery that “what the frog’s eye tells the frog’s brain” (Lettvin et al., 1959) was not a bitmap seemed to shatter Pitts’s hope of making logical sense of the world. And yet McCulloch and Pitts had given birth not just to finite automata theory but to the sprawling field of neural computing. Their audacity paid off—just not in the way they had hoped.
“A Logical Calculus” is the product of an extraordinary and tragic partnership. Warren McCulloch (1898–1969) was a neuroscientist who longed to understand the mind scientifically. A member of a successful family of lawyers and engineers, McCulloch was skeptical of the Freudian theories that dominated mid-twentieth century psychology. He had encountered the logic of Whitehead and Russell’s Principia Mathematica but could not marry it to his understanding of neural anatomy and function. Walter Pitts (1923–1969), the son of an abusive working-class father in Detroit, found shelter as a boy in a public library. He became remarkably learned through solitary study, and in particular read the Principia at the age of 12 and entered into a correspondence about it with Bertrand Russell. A few years later, hearing that Russell was lecturing at the University of Chicago, he ran away from home, never to return. He hung around the University, where he met McCulloch. (You would not be wrong to think of Good Will Hunting.) McCulloch, 42 at the time and a professor, and Pitts, a homeless 18-year-old runaway, had both read Leibniz and were determined to develop a Leibnizian calculus of thought with a sound mathematical and neuroanatomical basis. This paper is the upshot. For the first time, McCulloch later declared, “we know how we know.” In the last section, it proposes that mental functioning having been explained, mental disorders would in the future be understood as specific neural net malfunctions.
Pitts, alas, himself fell prey to mental illness. Both he and McCulloch wound up at MIT—Pitts, though he had never attended high school, as a graduate student for the pioneering cybernetician Norbert Wiener (the author of chapter 19). A fracture in the personal relationship between the three men sent Pitts into a spiral of depression and alcoholism from which he died at age 46. McCulloch, 25 years his senior, died a few months later (Gefter, 2015).
9.0 Abstract
BECAUSE of the “all-or-none” character of nervous activity, neural events and the relations among them can be treated by means of propositional logic. It is found that the behavior of every net can be described in these terms, with the addition of more complicated logical means for nets containing circles; and that for any logical expression satisfying certain conditions, one can find a net behaving in the fashion it describes. It is shown that many particular choices among possible neurophysiological assumptions are equivalent, in the sense that for every net behaving under one assumption, there exists another net which behaves under the other and gives the same results, although perhaps not in the same time. Various applications of the calculus are discussed.
9.1 Introduction
Theoretical neurophysiology rests on certain cardinal assumptions. The nervous system is a net of neurons, each having a soma and an axon. Their adjunctions, or synapses, are always between the axon of one neuron and the soma of another. At any instant a neuron has some threshold, which excitation must exceed to initiate an impulse. This, except for the fact and the time of its occurrence, is determined by the neuron, not by the excitation. From the point of excitation the impulse is propagated to all parts of the neuron. The velocity along the axon varies directly with its diameter, from < 1ms−1 in thin axons, which are usually short, to > 150ms−1 in thick axons, which are usually long. The time for axonal conduction is consequently of little importance in determining the time of arrival of impulses at points unequally remote from the same source. Excitation across synapses occurs predominantly from axonal terminations to somata. It is still a moot point whether this depends upon irreciprocity of individual synapses or merely upon prevalent anatomical configurations. To suppose the latter requires no hypothesis ad hoc and explains known exceptions, but any assumption as to cause is compatible with the calculus to come. No case is known in which excitation through a single synapse has elicited a nervous impulse in any neuron, whereas any neuron may be excited by impulses arriving at a sufficient number of neighboring synapses within the period of latent addition, which lasts < 0.25 ms. Observed temporal summation of impulses at greater intervals is impossible for single neurons and empirically depends upon structural properties of the net. Between the arrival of impulses upon a neuron and its own propagated impulse there is a synaptic delay of > 0.5 ms. During the first part of the nervous impulse the neuron is absolutely refractory to any stimulation. Thereafter its excitability returns rapidly, in some cases reaching a value above normal from which it sinks again to a subnormal value, whence it returns slowly to normal. Frequent activity augments this subnormality. Such specificity as is possessed by nervous impulses depends solely upon their time and place and not on any other specificity of nervous energies. Of late only inhibition has been seriously adduced to contravene this thesis. Inhibition is the termination or prevention of the activity of one group of neurons by concurrent or antecedent activity of a second group. Until recently this could be explained on the supposition that previous activity of neurons of the second group might so raise the thresholds of internuncial neurons that they could no longer be excited by neurons of the first group, whereas the impulses of the first group must sum with the impulses of these internuncials to excite the now inhibited neurons. Today, some inhibitions have been shown to consume < 1 ms. This excludes internuncials and requires synapses through which impulses inhibit that neuron which is being stimulated by impulses through other synapses. As yet experiment has not shown whether the refractoriness is relative or absolute. We will assume the latter and demonstrate that the difference is immaterial to our argument. Either variety of refractoriness can be accounted for in either of two ways. The “inhibitory synapse” may be of such a kind as to produce a substance which raises the threshold of the neuron, or it may be so placed that the local disturbance produced by its excitation opposes the alteration induced by the otherwise excitatory synapses. Inasmuch as position is already known to have such effects in the cases of electrical stimulation, the first hypothesis is to be excluded unless and until it be substantiated, for the second involves no new hypothesis. We have, then, two explanations of inhibition based on the same general premises, differing only in the assumed nervous nets and, consequently, in the time required for inhibition. Hereafter we shall refer to such nervous nets as equivalent in the extended sense. Since we are concerned with properties of nets which are invariant under equivalence, we may make the physical assumptions which are most convenient for the calculus.
Many years ago one of us, by considerations impertinent to this argument, was led to conceive of the response of any neuron as factually equivalent to a proposition which proposed its adequate stimulus. He therefore attempted to record the behavior of complicated nets in the notation of the symbolic logic of propositions. The “all-or-none” law of nervous activity is sufficient to insure that the activity of any neuron may be represented as a proposition. Physiological relations existing among nervous activities correspond, of course, to relations among the propositions; and the utility of the representation depends upon the identity of these relations with those of the logic of propositions. To each reaction of any neuron there is a corresponding assertion of a simple proposition. This, in turn, implies either some other simple proposition or the disjunction of the conjunction, with or without negation, of similar propositions, according to the configuration of the synapses upon and the threshold of the neuron in question. Two difficulties appeared. The first concerns facilitation and extinction, in which antecedent activity temporarily alters responsiveness to subsequent stimulation of one and the same part of the net. The second concerns learning, in which activities concurrent at some previous time have altered the net permanently, so that a stimulus which would previously have been inadequate is now adequate. But for nets undergoing both alterations, we can substitute equivalent fictitious nets composed of neurons whose connections and thresholds are unaltered. But one point must be made clear: neither of us conceives the formal equivalence to be a factual explanation. Per contra!—we regard facilitation and extinction as dependent upon continuous changes in threshold related to electrical and chemical variables, such as after-potentials and ionic concentrations; and learning as an enduring change which can survive sleep, anaesthesia, convulsions and coma. The importance of the formal equivalence lies in this: that the alterations actually underlying facilitation, extinction and learning in no way affect the conclusions which follow from the formal treatment of the activity of nervous nets, and the relations of the corresponding propositions remain those of the logic of propositions.
The nervous system contains many circular paths, whose activity so regenerates the excitation of any participant neuron that reference to time past becomes indefinite, although it still implies that afferent activity has realized one of a certain class of configurations over time. Precise specification of these implications by means of recursive functions, and determination of those that can be embodied in the activity of nervous nets, completes the theory.
9.2 The Theory: Nets without Circles
We shall make the following physical assumptions for our calculus.
1. The activity of the neuron is an “all-or-none” process.
2. A certain fixed number of synapses must be excited within the period of latent addition in order to excite a neuron at any time, and this number is independent of previous activity and position on the neuron.
3. The only significant delay within the nervous system is synaptic delay.
4. The activity of any inhibitory synapse absolutely prevents excitation of the neuron at that time.
5. The structure of the net does not change with time.
To present the theory, the most appropriate symbolism is that of Language II of Carnap (1937), augmented with various notations drawn from Whitehead and Russell (1910), including the Principia conventions for dots. Typographical necessity, however, will compel us to use the upright “E” for the existential operator instead of the inverted, and an arrow (→) for implication instead of the horseshoe. We shall also use the Carnap syntactical notations, but print them in boldface rather than German type; and we shall introduce a functor S, whose value for a property P is the property which holds of a number when P holds of its predecessor; it is defined by “S(P)(t) ▪ ≡ ▪ P(x) ▪ t = x′” [EDITOR: speculatively corrected from the original]; the brackets around its argument will often be omitted, in which case this is understood to be the nearest predicate-expression [Pr] on the right. Moreover, we shall write S2Pr for S(S(Pr)), etc.
The neurons of a given net 𝒩 may be assigned designations “c1,” “c2,” …, “cn.” This done, we shall denote the property of a number, that a neuron ci fires at a time which is that number of synaptic delays from the origin of time, by “N” with the numeral i as subscript, so that Ni(t) asserts that ci fires at the time t. Ni is called the action of ci. We shall sometimes regard the subscripted numeral of “N” as if it belonged to the object-language, and were in a place for a functoral argument, so that it might be replaced by a number-variable [z] and quantified; this enables us to abbreviate long but finite disjunctions and conjunctions by the use of an operator. We shall employ this locution quite generally for sequences of Pr; it may be secured formally by an obvious disjunctive definition. The predicates “N1,” “N2,” …, comprise the syntactical class “N.”
Let us define the peripheral afferents of 𝒩 as the neurons of 𝒩 with no axons synapsing upon them. Let N1, …, Np denote the actions of such neurons and Np+1, Np+2, …, Nn those of the rest. Then a solution of 𝒩 will be a class of sentences of the form Si: Np+1(z1) ▪ ≡ ▪ Pri(N1, N2, …, Np, z1), where Pri contains no free variable save z1 and no descriptive symbols save the N in the argument [Arg], and possibly some constant sentences [sa]; and such that each Si is true of 𝒩. Conversely, given a 
, containing no free variable save those in its Arg, we shall say that it is realizable in the narrow sense if there exists a net 𝒩 and a series of Ni in it such that N1(z1) ▪ ≡ ▪ Pr1(N1, N2, …, z1, sa1) is true of it, where sa1 has the form N (0). We shall call it realizable in the extended sense, or simply realizable, if for some n, Sn(Pr1)(p1, …, pp, z1, s) is realizable in the above sense. cpi is here the realizing neuron. We shall say of two laws of nervous excitation which are such that every S which is realizable in either sense upon one supposition is also realizable, perhaps by a different net, upon the other, that they are equivalent assumptions, in that sense.
The following theorems about realizability all refer to the extended sense. In some cases, sharper theorems about narrow realizability can be obtained; but in addition to greater complication in statement this were of little practical value, since our present neurophysiological knowledge determines the law of excitation only to extended equivalence, and the more precise theorems differ according to which possible assumption we make. Our less precise theorems, however, are invariant under equivalence, and are still sufficient for all purposes in which the exact time for impulses to pass through the whole net is not crucial.
Our central problems may now be stated exactly: first, to find an effective method of obtaining a set of computable S constituting a solution of any given net; and second, to characterize the class of realizable S in an effective fashion. Materially stated, the problems are to calculate the behavior of any net, and to find a net which will behave in a specified way, when such a net exists.
A net will be called cyclic if it contains a circle, i.e. if there exists a chain ci, ci+1, … of neurons on it, each member of the chain synapsing upon the next, with the same beginning and end. If a set of its neurons c1, c2, …, cp is such that its removal from 𝒩 leaves it without circles, and no smaller class of neurons has this property, the set is called a cyclic set, and its cardinality is the order of 𝒩. In an important sense, as we shall see, the order of a net is an index of the complexity of its behaviour. In particular, nets of zero order have especially simple properties; we shall discuss them first.
Let us define a temporal propositional expression (a TPE), designating a temporal propositional function (TPF), by the following recursion.
1. A 1p1[z1] is a TPE, where p1 is a predicate-variable.
2. If S1 and S2 are TPE containing the same free individual variable, so are SS1, S1 ∨S2, S1 ▪ S2, and S1 ▪ ∼ S2.
3. Nothing else is a TPE.
THEOREM 1. Every net of order 0 can be solved in terms of temporal propositional expressions.
Let ci be any neuron of 𝒩 with a threshold θi > 0, and let ci1, ci2, …, cip have respectively ni1, ni2, …, nip excitatory synapses upon it. Let cj1, cj2, …, cjq have inhibitory synapses upon it. Let κi be the set of the subclasses of {ni1, ni2, …, nip} such that the sum of their members exceeds θi. We shall then be able to write, in accordance with the assumptions mentioned above:
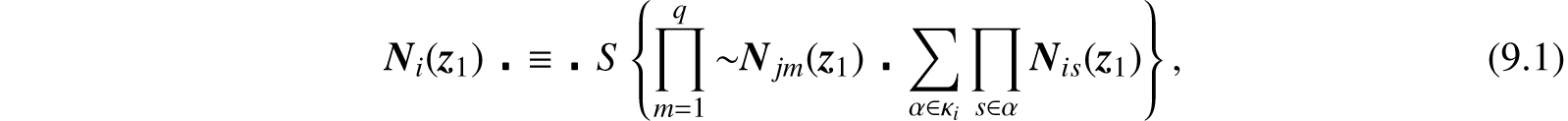
where the “∑” and “‘∏” are syntactical symbols for disjunctions and conjunctions which are finite in each case. Since an expression of this form can be written for each ci which is not a peripheral afferent, we can, by substituting the corresponding expression in (9.1) for each Njm or Nis whose neuron is not a peripheral afferent, and repeating the process on the result, ultimately come to an expression for Ni in terms solely of peripherally afferent N, since 𝒩 is without circles. Moreover, this expression will be a TPE, since obviously (9.1) is; and it follows immediately from the definition that the result of substituting a TPE for a constituent p(z) in a TPE is also one.
THEOREM 2. Every TPE is realizable by a net of order zero.
The functor S obviously commutes with disjunction, conjunction, and negation. It is obvious that the result of substituting any Si, realizable in the narrow sense (i.n.s.), for the p(z) in a realizable expression S1 is itself realizable i.n.s.; one constructs the realizing net by replacing the peripheral afferents in the net for S1 by the realizing neurons in the nets for the Si. The one neuron net realizes p1(z1) i.n.s., and Figure 9.1a shows a net that realizes Sp1(z1) and hence SS2, i.n.s., if S2 can be realized i.n.s. Now if S2 and S3 are realizable then SmS2 and SnS3 are realizable i.n.s., for suitable m and n. Hence so are Sm+nS2 and Sm+nS3. Now the nets of Figures 9.1b–d respectively realize S(p1(z1) ∨p2(z1)), S(p1(z1) ▪ p2(z1)), and S(p1(z1) ▪ ∼ p2(z1)) i.n.s. Hence Sm+n+1(S1 ∨S2), Sm+n+1(S1 ▪ S2), and Sm+n+1(S1 ▪ ∼ S2) are realizable i.n.s. Therefore S1 ∨S2, S1 ▪ S2, S1 ▪ ∼ S2 are realizable if S1 and S2 are. By complete induction, all TPE are realizable. In this way all nets may be regarded as built out of the fundamental elements of Figures 9.1a–d, precisely as the temporal propositional expressions are generated out of the operations of precession, disjunction, conjunction, and conjoined negation. In particular, corresponding to any description of state, or distribution of the values true and false for the actions of all the neurons of a net save that which makes them all false, a single neuron is constructible whose firing is a necessary and sufficient condition for the validity of that description. Moreover, there is always an indefinite number of topologically different nets realizing any TPE. …
The phenomena of learning, which are of a character persisting over most physiological changes in nervous activity, seem to require the possibility of permanent alterations in the structure of nets. The simplest such alteration is the formation of new synapses or equivalent local depressions of threshold. We suppose that some axonal terminations cannot at first excite the succeeding neuron; but if at any time the neuron fires, and the axonal terminations are simultaneously excited, they become synapses of the ordinary kind, henceforth capable of exciting the neuron. The loss of an inhibitory synapse gives an entirely equivalent result. We shall then have
THEOREM 7. Alterable synapses can be replaced by circles.
This is accomplished by the method of Figure 9.1i. It is also to be remarked that a neuron which becomes and remains spontaneously active can likewise be replaced by a circle, which is set into activity by a peripheral afferent when the activity commences, and inhibited by one when it ceases. [EDITOR: In Figure 9.1, the expression for top part of (f) has been corrected and the expression for top part of (i) is missing in the original. Part (g) is mysterious—the bottom diagram is a version of (d), but the expression for (g) matches neither part of the diagram for (g).]
9.3 The Theory: Nets with Circles
The treatment of nets which do not satisfy our previous assumption of freedom from circles is very much more difficult than that case. This is largely a consequence of the possibility that activity may be set up in a circuit and continue reverberating around it for an indefinite period of time, so that the realizable Pr may involve reference to past events of an indefinite degree of remoteness. …[EDITOR: The expression (Ex) t − 1 ▪ N1(x) ▪ N2(x) (in part (i) of Figure 9.1) means that there was a point x in time, no later than time t − 1, when N1(x) and N2(x) were both true. The unlabeled neuron—which feeds back on itself—will keep firing indefinitely.]
One more thing is to be remarked in conclusion. It is easily shown: first, that every net, if furnished with a tape, scanners connected to afferents, and suitable efferents to perform the necessary motor-operations, can compute only such numbers as can a Turing machine; second, that each of the latter numbers can be computed by such a net; and that nets with circles can be computed by such a net; and that nets with circles can compute, without scanners and a tape, some of the numbers the machine can, but no others, and not all of them. This is of interest as affording a psychological justification of the Turing definition of computability and its equivalents, Church’s λ-definability and Kleene’s primitive recursiveness: if any number can be computed by an organism, it is computable by these definitions, and conversely.
9.4 Consequences
Causality, which requires description of states and a law of necessary connection relating them, has appeared in several forms in several sciences, but never, except in statistics, has it been as irreciprocal as in this theory. Specification for any one time of afferent stimulation and of the activity of all constituent neurons, each an “all-or-none” affair, determines the state. Specification of the nervous net provides the law of necessary connection whereby one can compute from the description of any state that of the succeeding state, but the inclusion of disjunctive relations prevents complete determination of the one before. Moreover, the regenerative activity of constituent circles renders reference indefinite as to time past. Thus our knowledge of the world, including ourselves, is incomplete as to space and indefinite as to time. This ignorance, implicit in all our brains, is the counterpart of the abstraction which renders our knowledge useful. The role of brains in determining the epistemic relations of our theories to our observations and of these to the facts is all too clear, for it is apparent that every idea and every sensation is realized by activity within that net, and by no such activity are the actual afferents fully determined.
There is no theory we may hold and no observation we can make that will retain so much as its old defective reference to the facts if the net be altered. Tinitus, paraesthesias, hallucinations, delusions, confusions and disorientation intervene. Thus empiry confirms that if our nets are undefined, our facts are undefined, and to the “real” we can attribute not so much as one quality or “form.” With determination of the net, the unknowable object of knowledge, the “thing in itself,” ceases to be unknowable.
To psychology, however defined, specification of the net would contribute all that could be achieved in that field—even if the analysis were pushed to ultimate psychic units or “psychons,” for a psychon can be no less than the activity of a single neuron. Since that activity is inherently propositional, all psychic events have an intentional, or “semiotic,” character. The “all-or-none” law of these activities, and the conformity of their relations to those of the logic of propositions, insure that the relations of psychons are those of the two-valued logic of propositions. Thus in psychology, introspective, behavioristic or physiological, the fundamental relations are those of two-valued logic.
Hence arise constructional solutions of holistic problems involving the differentiated continuum of sense awareness and the normative, perfective and resolvent properties of perception and execution. From the irreciprocity of causality it follows that even if the net be known, though we may predict future from present activities, we can deduce neither afferent from central, nor central from efferent, nor past from present activities—conclusions which are reinforced by the contradictory testimony of eye-witnesses, by the difficulty of diagnosing differentially the organically diseased, the hysteric and the malingerer, and by comparing one’s own memories or recollections with his contemporaneous records. Moreover, systems which so respond to the difference between afferents to a regenerative net and certain activity within that net, as to reduce the difference, exhibit purposive behavior; and organisms are known to possess many such systems, subserving homeostasis, appetition and attention. Thus both the formal and the final aspects of that activity which we are wont to call mental are rigorously deducible from present neurophysiology. The psychiatrist may take comfort from the obvious conclusion concerning causality—that, for prognosis, history is never necessary. He can take little from the equally valid conclusion that his observables are explicable only in terms of nervous activities which, until recently, have been beyond his ken. The crux of this ignorance is that inference from any sample of overt behavior to nervous nets is not unique, whereas, of imaginable nets, only one in fact exists, and may, at any moment, exhibit some unpredictable activity. Certainly for the psychiatrist it is more to the point that in such systems “Mind” no longer “goes more ghostly than a ghost.” Instead, diseased mentality can be understood without loss of scope or rigor, in the scientific terms of neurophysiology. For neurology, the theory sharpens the distinction between nets necessary or merely sufficient for given activities, and so clarifies the relations of disturbed structure to disturbed function. In its own domain the difference between equivalent nets and nets equivalent in the narrow sense indicates the appropriate use and importance of temporal studies of nervous activity: and to mathematical biophysics the theory contributes a tool for rigorous symbolic treatment of known nets and an easy method of constructing hypothetical nets of required properties.
Reprinted from McCulloch and Pitts (1943), with permission from Springer.