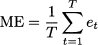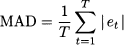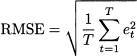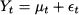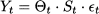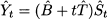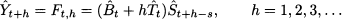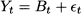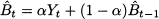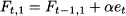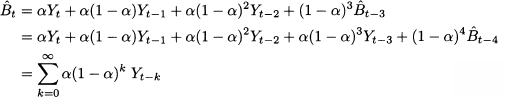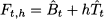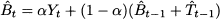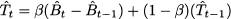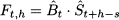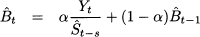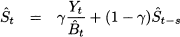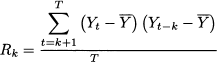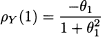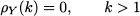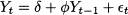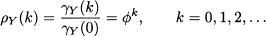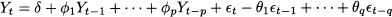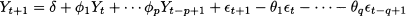Chapter 11
Time Series Models
Forecasting is a common task in business management. In Chapter 10, on simple linear regression models, we have met a kind of statistical model that can be used as a forecasting tool, provided that
- We are able to find potential explanatory variables
- We have enough data on all the relevant variables, in order to obtain reliable estimates of model parameters
Even though, strictly speaking, linear regression captures association and not causation, the idea behind such a model is that knowledge about explanatory variables is useful to predict the value of the explained variable. Unfortunately, there are many cases in which we are not able to find a convincing set of explanatory variables, or we lack data about them, possibly because they are too costly to collect. In some extreme cases, not only do we lack enough information about the explanatory variables, but we even lack information about the predicted variable. One common case is forecasting sales for a brand-new kind of product, with no past sales history. Then, we might have to settle for a qualitative, rather than quantitative forecasting approach. Qualitative forecasting may take advantage of qualified expert opinion; various experts may be pooled in order to obtain both a forecast and a measure of its uncertainty.1 Actually, these two families of methods can be and, in fact, are often integrated. Even when plenty of data are available, expert opinions are a valuable commodity, since statistical models are intrinsically backward-looking, whereas we should look forward in forecasting.
In this book, we stick to quantitative approaches, such as linear regression, leaving qualitative forecasting to the specialized literature. Within the class of quantitative forecasting methods, an alternative to regression models is the family of time series models. The distinguishing feature of time series models is that they aim at forecasting a variable of interest, based only on observations of the variable itself; no explanatory variable is considered.
Example 11.1 Stock trading on financial markets is one of those human endeavors in which good forecasts would have immense value. One possible approach is based on fundamental analysis. Given a firm, its financial and industrial performance is evaluated in order to assess the prospect for the price of its shares. In this kind of analysis, it is assumed that there is some rationality in financial markets, and we try to explain stock prices, at least partially, by a set underlying factors, which may also include macroeconomic factors such as inflation or oil price. On the contrary, technical analysis is based only on patterns and trends in the stock price itself. No explanatory variable is sought. The idea is that financial markets are mostly irrational, and that psychology should be used to explain observed behavior. In the first case, some statistical model, possibly a complicated linear regression model, could be arranged. In the second case, time series approaches are used.2
(Note: Time series models can be built to forecast a wide variety of variables, such as interest rates, electric power consumption, inflation, unemployment, etc. To be concrete, in most, if not all of our examples, we will deal with demand forecasting. Yet, the approaches we outline are much more general than it might seem.)
To illustrate the nature of time series models formally, let us introduce the fundamental notation, which is based on a discrete time representation in time buckets or periods (e.g., weeks) denoted by t:
- Yt is the realization of the variable of interest at time bucket t. If we are observing weekly demand for an item at a retail store, Yt is the demand observed at that store during time bucket t.
- Ft,h is the forecast generated at the end of time bucket t with horizon of h time buckets; hence, Ft,h is a prediction of demand at time t + h, where h = 1, 2, 3, … It is important to clarify the roles of subscripts t and h in our definition of forecast:
— t indicates when the forecast is made, and it defines the information set on the basis of which the forecast is built; for instance, at time t we have information about demand during all the time buckets up to and including t.
— h defines how many steps ahead in the future we want to forecast; the simplest case is h = 1, which implies that after observing demand in time bucket t, we are forecasting future demand in time bucket t + 1.
We should distinguish quite clearly when and for when the forecast is calculated. One might wonder why we should forecast with a horizon h > 1. The answer is that sometimes we have to plan actions in considerable advance. Consider, for instance, ordering an item from a supplier whose lead time is three time buckets; clearly, we cannot base our decision on a demand forecast with h = 1, since what we order now will not be delivered during the next time bucket.
In time series models, the information set consists only of observations of Yt; no explanatory variable is considered. Trivial examples of forecasting formulas could be

In the first case, we just use the last observation as a forecast for the next time bucket. In the second case, we take the average of all of the past t observations, from time bucket 1 up to time bucket t. In a sense, these are two extremes, because we either use a very tiny information set, or a set consisting of the whole past history. Maybe one observation is too prone to spikes and random shocks, which would probably add undesirable noise, rather than useful information, to our decision process; on the other hand, the choice of using all of them does not consider the fact that some observations far in the past could be hardly relevant. Furthermore, we are not considering the possibility of systematic variations due to trends or seasonality. In the following, we describe both heuristic and more formal approaches to forecasting.
There is an enormous variety of forecasting methods, and plenty of software packages implementing them. What is really important is to understand a few recurring and fundamental concepts, in order to properly evaluate competing approaches. However, there is an initial step that is even more important: framing the forecasting process within the overall business process. We insist on this in Section 11.1. The most sophisticated forecasting algorithm is utterly useless, if it is not in tune with the surrounding process. Whatever approach we take, it is imperative to monitor forecast errors; in Section 11.2 we define several error measures that can be used to choose among alternative models, to fine-tune coefficients governing their functioning, and to check and improve performance. Section 11.3 illustrates the fundamental ideas of time series decomposition, which highlights the possible presence of factors like trend and seasonality. Section 11.4 deals with a very simple approach, moving average, which has a limited domain of applicability but is quite useful in pointing out basic tradeoffs that we have to make when fine-tuning a forecasting algorithm. Section 11.5 is actually the core of the chapter, where we describe the widely used family of exponential smoothing methods; they are easy to use and quite flexible, as they can account for trend and seasonality in a straightforward and intuitive way. Finally, Section 11.6 takes a more formal route and deals with autoregressive and moving-average models within a proper statistical framework. This last section is aimed at more advanced readers and may be safely skipped.
11.1 BEFORE WE START: FRAMING THE FORECASTING PROCESS
When learning about forecasting algorithms, it is easy to get lost in technicalities and forget a few preliminary points.
Forecasting is not about a single number. We are already familiar with inferential statistics and confidence intervals. Hence, we should keep in mind that a single number, i.e., a point forecast, may be of quite little use without some measure of uncertainty. As far as possible, forecasting should be about building a whole probability distribution, not just a number to bet on.
Choose the right time bucket. Imagine that you order raw materials at the end of every week; should you bother about daily forecasting? Doing so, you add unnecessary complexity to your task, as weekly forecasts are what you really need. Indeed, it is tempting to use large time buckets in order to aggregate demand with respect to time and reduce forecast errors; this is not advisable if your business process requires forecasts with small time buckets.
What should we forecast? If this sounds like a dumb question, think again. Imagine that you are a producer of T-shirts, available in customary sizes and a wide array of colors. Forecasting sales of each single item may be a daunting task. As a general rule, forecasts are more reliable if we can aggregate items. Rather than forecasting demand for each combination of size and color, we could aggregate sizes and consider only forecasting for a set of colors. In fact, demand for a specific combination of color and size may be rather volatile, but the fraction of population corresponding to each size is much more stable. We may forecast aggregate sales for each T-shirt model, and then use common factors across mod els to disaggregate and obtain forecasts for each single combination. Of course, in the end, we want to forecast sales for each individual item, but in the process of building a forecast we use suitable aggregation and disaggregation strategies. This approach is also quite powerful in pooling demand data across items, thus improving the quality of estimates of common factors, but it must be applied to compatible product families. We cannot apply size factors that are standard for adults to T-shirts depicting cartoon characters (maybe).
Forecasts are a necessary evil. Common sense says that forecasts are always wrong, but we cannot do without them. This is pretty true, but sometimes we can do something to make our life easier and/or mitigate the effect of forecast errors. If our suppliers have a long delivery lead time, we must forecast material requirements well in advance. Since the larger the forecast horizon, the larger the uncertainty in forecasting, it is wise to try whatever we can to shorten lead time (possibly by choosing geographically closer suppliers). The same applies to manufacturing lead times. Sometimes, seemingly absurd approaches may improve forecasting. Consider the production process for sweaters. Just like with T-shirts, forecasting a specific combination of color, model, or size is quite hard. Two key steps in producing a sweater are dying the fabric with whatever color we like, and knitting. The commonsense approach is to dye first and knit later. However, the time needed to knit is much longer than the time needed to dye. This means that one has to forecast sales of a specific combination much in advance of sales, with a corresponding criticality. By swapping the two steps, knitting first, one may postpone the final decisions, and rely on more accurate forecasts. This is a typical postponement decision,3 whereby the impact on cost and quality must be traded off against the payoff from better matching of supply and demand.
The general point is that the forecasting process should support the surrounding business process and should help in making decisions. Forecast errors may be numerically large or small, but what really matters is their economic consequence.
As a last observation, let us consider another seemingly odd question: Can we observe what we are forecasting? To be concrete, let us consider demand again. Can we observe demand at a retail store? In an age of bar codes and point-of-sale data acquisition, the answer could be “yes.” Now imagine that you wish a pot of your favorite cherry yoghurt, but you find the shelf empty; what are you going to do? Depending on how picky you are, you might settle for a different packaging, a different flavor, or a different brand, or you could just go home quite angry. But unless you are very angry and start yelling at any clerk around, no one will know that potential demand has been lost. What we may easily measure are sales, not demand. Hence, we use sales as a proxy of demand, but this may result in underforecasting. If this looks like a peculiar case, consider a business-to-business setting. A potential customer phones and needs 10 electric motors now; your inventory level is down, but you will produce a new batch in 5 days. Unfortunately, the customer really needs those motors right now; so, he hangs up and phones a competitor. Chances are, this potential demand is never recorded anywhere in the information system. Again, we risk underestimating demand. Statistical techniques have been devised to correct for these effects, but sometimes it is more a matter of organization than sophisticated math.
11.2 MEASURING FORECAST ERRORS
Before we delve into forecasting algorithms, it is fundamental to understand how we may evaluate their performance. This issue is sometimes overlooked in practice: Once a forecast is calculated and used to make a decision, it is often thrown away for good. This is a mistake, as the performance of the forecasting process should be carefully monitored.
In the following, we will measure the quality of a forecast by a forecasting error, defined as
(11.1) 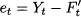
This is the forecast error for the variable at time t. The notation F’t refers to the forecast for time bucket t. It is not important when the forecast was made, but for when. If the horizon is h = 1, then F’t = F’t-1,1, whereas F’t = Ft-2,2 if h = 2. Also, notice that by this definition the error is positive when demand is larger than the forecast (i.e., we underforecasted), whereas the error is negative when demand is smaller than the forecast (i.e., we overforecasted). It is important to draw the line between two settings in which we may evaluate performance:
1. In historical simulation, we apply an algorithm on past data and check what the performance would have been, had we adopted that method. Of course, to make sense, historical simulation must be non-anticipative, and the information set that is used to compute Ft,h must not include any data after time bucket t. This may sound like a trivial remark, but, as we will see later, there might be an indirect way to violate this nonanticipativity principle.
2. In online monitoring, we gather errors at the end of each time bucket to possibly adjust some coefficients and fine-tune the forecasting algorithm. In fact, many forecasting methods depend on coefficients that can be set once and for all or dynamically adapted.
Whatever the case, performance is evaluated over a sample consisting of T time buckets, and of course we must aggregate errors by taking some form of average. The following list includes some of the most commonly used indicators:
- Mean error:
- Mean absolute deviation:
- Root-mean-square error:
- Mean percentage error:
(11.5)
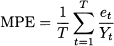
- Mean absolute percentage error:
(11.6)
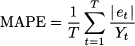
As clearly suggested by Eq. (11.2), ME is just the plain average of errors over the sample, so that positive and negative errors cancel each other. As a consequence, ME does not discriminate between quite different error patterns like those illustrated in Table 11.1; the average error is zero in both case (a) and (b), but we cannot say that the accuracy is the same. Indeed, ME measures systematic deviation or bias, but not the accuracy of forecasts. A significantly positive ME tells us that we are systematically underforecasting demand; a significantly negative ME means that we are systematically overstating demand forecasts. This is an important piece of information because it shows that we should definitely revise the forecasting process, whereas a very small ME does not necessarily imply that we are doing a good job. To measure accuracy, we should get rid of the error sign. This may be accomplished by taking the absolute value of errors or by squaring them. The first idea leads to MAD; the second one leads to RMSE, where the square root is taken in order to express error and demand in the same units. In case (a) of Table 11.1, MAD is 0; on the contrary, the reader is invited to verify that MAD is 40/6 = 6.67 in case (b), showing that MAD can tell the difference between the two sequences of errors. RMSE, with respect to MAD, tends to penalize large errors, as we may appreciate from Table 11.2. Cases (a) and (b) share the same ME and MAD, but RMSE is larger in case (b), which indeed features larger errors.
Table 11.1 Mean error measures bias, not accuracy.

Table 11.2 RMSE penalizes large errors more than MAD does.

The reader will certainly notice some similarity between RMSE and standard deviation. Comparing the definition in Eq. (11.4) and the familiar definition of sample variance and sample standard deviation in inferential statistics, one could even be tempted to divide by T - 1, rather than by T. This temptation should be resisted, however, since it misses a couple of important points.
- In inferential statistics we have a random sample consisting of independent observations of identically distributed variables. In forecasting there is no reason to think that the expected value of the variable we are observing is stationary. We might be chasing a moving target, and this has a profound impact on forecasting algorithms.
- Furthermore, in inferential statistics we use the whole sample to calculate the sample mean
 , which is then used to evaluate the sample standard deviation; a bias issue results, which must corrected. Here we use past demand information to generate the forecast F’t; then we evaluate the forecasting error with respect to a new demand observation Yt, which was not used to generate F’t.
, which is then used to evaluate the sample standard deviation; a bias issue results, which must corrected. Here we use past demand information to generate the forecast F’t; then we evaluate the forecasting error with respect to a new demand observation Yt, which was not used to generate F’t.
By the same token, MAD as defined in Eq. (11.3) should not be confused with MAD as defined in Eq. (4.4), where we consider deviations with respect to a sample mean. In fact, in forecasting literature the name mean absolute error (MAE) is sometimes used, rather than MAD, in order to avoid this ambiguity.
A common feature of ME, MAD, and RMSE is that they measure the forecast error using the same units of measurement as demand. Now imagine that MAD is 10; is that good or bad? Well, very hard to say: If MAD is 10 when demand per time bucket is something like 1000, this is pretty good. If MAD is 10 and demand is something like 10, this is pretty awful. This is why MPE and MAPE have been proposed. By dividing forecast errors by demand,4 we consider a relative error. Apparently, MPE and MAPE are quite sensible measures. In fact, they do have some weak spots:
- They cannot be adopted when demand during a time bucket can be zero. This may well be the case when the time bucket is small and/or demand is sporadic. In modern retail chains, replenishment occurs so often, and assortment variety is so high that this situation is far from being a rare occurrence.
- Even when demand is nonzero these indices can yield weird results if demand shows wide variations. A somewhat pathological example is shown in Table 11.3. The issue here is that forecast 1 is almost always perfect, and in one unlucky case it makes a big mistake, right when demand is low; the error is 9 when demand is 1, so percentage error is an astonishing 900%, which yields MAPE=90% when averaged over the 10 time buckets. Forecast 2, on the contrary, is systematically wrong, but it is just right at the right moment; the second MAPE is only 18%, suggesting that the second forecaster is better than the first one, which is highly debatable.
A possible remedy to the two difficulties above is to consider a ratio of averages, rather than an average of ratios. We may introduce the following performance measures:
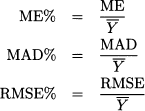
The idea is to take performance measures, expressed in absolute terms, and make them relative by dividing by the average demand
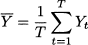
Table 11.3 Illustrating potential dangers in using MPE and MAPE.

In these measures, it is very unlikely that average demand over the T time buckets is zero; if this occurs, there is a big problem, but not with forecasting.
As we see, there is a certain variety of measures, and we must mention that others have been proposed. As common in management, we should keep several indicators under control, in order to get a complete picture. We close the section with a few additional remarks:
- Checking forecast accuracy is a way to gauge the inherent uncertainty in demand; this is helpful when we want to come up with something more than just a point forecast.
- We should never forget that a forecast is an input to a decision process. Hence, alternative measures might consider the effect of a wrong forecast, most notably from the economic perspective. However, how this is accomplished depends on the strategies used to hedge against forecast errors.
11.2.1 In- and out-of-sample checks
As will be clear from the following, when we want to apply certain forecasting algorithms, we might need to fit one or more parameters used to calculate a forecast. This is typically done by a proper initialization. When the algorithm depends on estimates of parameters, if we start from scratch, initial performance will be poor because the algorithm has to learn about the demand pattern first. However, we would like to ascertain how the algorithm performs in steady state, not in this initial transient phase.
If we are carrying out a historical simulation, based on a sample of past data, we may use a portion of available information to fit parameters. This portion of data that we use for fitting and initial learning is the fit sample. Arguably, the larger the fit sample, the better the initialization. However, this does not leave us with any data to test performance. In fact, it would be not quite correct to use knowledge of data to fit parameters, and then predict the very same data that we have used to initialize the algorithm. Performance evaluation should be carried out out-of-sample, i.e., predicting data that have not been used in any way for initialization purposes.5
This will be much clearer in the following, but it is important to state this principle right from the beginning. The available sample of data should be split into
1. A fit sample used for initialization
2. A test sample to evaluate performance in a realistic and sensible way
This approach is also known as data splitting, and it involves an obvious tradeoff, since a short fit sample would leave much data available for testing, but initial performance could be poor; on the other hand, a short test sample makes performance evaluation rather unreliable.
11.3 TIME SERIES DECOMPOSITION
The general idea behind time series models is that the data-generating process consists of two components:
1. A pattern, which is the “regular” component and may be quite variable over time, but in a fairly predictable way
2. An error, which is the “irregular” and unpredictable component6
Some smoothing mechanism should be designed in order to filter errors and expose the underlying pattern. The simplest decomposition scheme we may adopt is
(11.7) 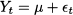
where  t is a random variable with expected value 0. Additional assumptions, for the sake of statistical tractability, may concern independence and normality of these random shocks. Faced with such a simple decomposition, we could just take an average of past observations in order to come up with an estimate of μ, which is the expected value of Yt. In real life, we do not have constant expected values, as market conditions may change over time. Hence, we could postulate a model like
t is a random variable with expected value 0. Additional assumptions, for the sake of statistical tractability, may concern independence and normality of these random shocks. Faced with such a simple decomposition, we could just take an average of past observations in order to come up with an estimate of μ, which is the expected value of Yt. In real life, we do not have constant expected values, as market conditions may change over time. Hence, we could postulate a model like
Here μt could be a “slowly” varying function of time, associated with market cycles, on which fast swings due to noise are superimposed. Alternatively, we could think of μt as a stochastic process whose sample paths are piecewise constant. In other words, every now and then a shock arrives, possibly due to the introduction or withdrawal of similar products by competitors (or ourselves), and μt jumps to a new value. Hence, we should not only filter random errors but also track the variation of μt, adapting our estimate. Equation (11.8) may look like a sort of catchall, which could fit any process. However, it is typically much better to try and see more structure in the demand process, discerning predictable and unpredictable variability. The elements of predictable variability that we will be concerned with in this chapter are7
- Trend, denoted by θt
- Seasonality, denoted by St
Trend is quite familiar from linear regression, and, strictly speaking, it is related to the slope of a line. Such a line represent a tendency of demand, on which random shocks and possibly seasonality are superimposed. In the following text, the intercept and slope of this line will be denoted as B (the level or baseline demand) and T (the trend in the strict sense), respectively; hence, the equation of the line is
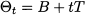
Seasonality is a form of predictable variability with precise regularity in timing. For instance, we know that in Italy more ice cream is consumed in summer than in winter, and that demand at a large retail store is larger on Saturdays than on Tuesdays. It is important to separate seasonality from the trend component of a time series; high sales of ice cream in July–August should not be mistaken for an increasing trend. An example of time series clearly featuring trend and seasonality is displayed in Fig. 11.1. There is an evident increasing trend, to which a periodic oscillatory pattern is superimposed. There is a little noise component, but we notice that demand peaks occur regularly in time, which makes this variability at least partially predictable.
Fig. 11.1 Time series featuring trend and seasonality.

Generally speaking, time series decomposition requires the specification of a functional form
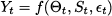
depending on each component: trend, seasonality, and noise. In principle, we may come up with weird functional forms, but the two most common patterns are as follows:
- The additive decomposition
(11.9)
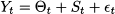
- The multiplicative decomposition
Within an additive decomposition, a possible assumption is that the noise term  t is normally distributed, with zero mean. This is not a harmless assumption for a multiplicative scheme, as it results in negative values that make no sense when modeling demand. A possible alternative is assuming that
t is normally distributed, with zero mean. This is not a harmless assumption for a multiplicative scheme, as it results in negative values that make no sense when modeling demand. A possible alternative is assuming that  t is lognormally distributed, with expected value 1. We recall from section 7.7.2 that a lognormal distribution results from taking the exponential of a normal variable, and it has positive support; hence, if we transform data by taking logarithms in Eq. (11.10), we obtain an additive decomposition with normal noise terms. It is also important to realize that the seasonal component is periodic
t is lognormally distributed, with expected value 1. We recall from section 7.7.2 that a lognormal distribution results from taking the exponential of a normal variable, and it has positive support; hence, if we transform data by taking logarithms in Eq. (11.10), we obtain an additive decomposition with normal noise terms. It is also important to realize that the seasonal component is periodic
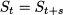
for some seasonality cycle s. If time buckets correspond to months, yearly seasonality corresponds to s = 12; if we partition a year in four quarters, then s = 4. The seasonal factor St in a multiplicative scheme tells us the extent to which the demand in time bucket t exceeds its long-run average, corrected by trend. For instance, if there is no trend, a multiplicative factors St = 1.2 tells that demand in time bucket t is 20% larger than the average. It is reasonable to normalize multiplicative seasonality factors in such a way that their average value is 1, so that they may be easily interpreted.
Example 11.2 Consider a year divided in four 3-month time buckets. We could associate S1 with winter, S2 with spring, S3 with summer, and S4 with autumn. Then, if things were completely static, we would have
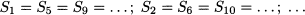
Now assume that, in a multiplicative model, we have
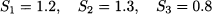
What should the value of S4 be? It is easy to see that we should have S4 = 0.7.
Example 11.3 (Additive vs. multiplicative seasonal factors) The kind of seasonality we have observed in Fig. 11.1 is additive. In fact, the width of the oscillatory pattern does not change over time. We are just adding and subtracting periodic factors. In Fig. 11.2 we can still see a trend with the superimposition of a seasonal pattern. However, we notice that the width of the oscillations is increasing. In fact, the two following conditions have a remarkably different effect:
Fig. 11.2 Time series featuring trend and multiplicative rather than additive seasonality.

- Demand in August is 20 items above normal (Fig. 11.1)
- Demand in August is 20% above normal (Fig. 11.2)
In the case of an additive seasonality term, the average of the seasonal factors in a whole cycle should be 0. With a multiplicative seasonality and an increasing trend, the absolute increase in August demand, measured by items, is itself increasing, leading to wider and wider swings.
The impact of noise differs as well, if we consider additive rather than multiplicative shocks. The most sensible model can often be inferred by visual inspection of data. To fix ideas and keep the treatment to a reasonable size, we will always refer to the following hybrid scheme, because of its simplicity:
(11.11) 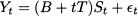
If there were no seasonality, the pattern would just be a line with intercept B and slope T. Since we assume E[ t] = 0, on the basis of estimates of parameters
t] = 0, on the basis of estimates of parameters 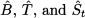 , our demand forecast is
, our demand forecast is
Here we use the notation 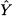 t, which is closer to the one used in linear regression, rather than Ft,h. We do so because, so far, it is not clear when and on the basis of which information the forecast is generated. Given a sample of demand observations, there are several ways to fit the parameters in this decomposition.
t, which is closer to the one used in linear regression, rather than Ft,h. We do so because, so far, it is not clear when and on the basis of which information the forecast is generated. Given a sample of demand observations, there are several ways to fit the parameters in this decomposition.
Example 11.4 Consider a sample of two seasonal cycles, consisting of four time buckets each; the seasonal cycle is s = 4, and we have demand observations Yt, t = 1, 2, …, 8. To decompose the time series, we could solve the following optimization model:
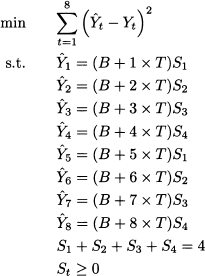
The optimization is carried out with respect to level B, trend T, and the four seasonal factors that repeat over time. Note that seasonal factors are normalized, so that their average value is 1; furthermore, either level or trend could be negative (but not both), whereas seasonal factors are restricted to nonnegative values, otherwise negative demand could be predicted.
The optimization problem in the example looks much like a least-squares problem, but, given the nonlinearity in the constraints, it is not as easy to solve as the ordinary least-squares problems we encounter in linear regression. Alternative procedures, much simpler and heuristic in nature, have been proposed to decompose a time series. We will not pursue these approaches in detail, as they are based on the unrealistic idea that the parameters in the demand model are constant over time.
In fact, market conditions do change, and we must track variations in the underlying unknown parameters, updating their estimates when new information is received. Hence, we should modify the static decomposition scheme of Eq. (11.12) as follows:
Since we update estimates dynamically, now we make the information set, i.e., demand observations up to and including time bucket t, and the forecast horizon h explicit. In this scheme we have three time-varying estimates:
- The estimate of the level component
 t at the end of time bucket t; if there were no trend or seasonality, the “true” parameter Bt would be an average demand, possibly subject to slow variations over time.
t at the end of time bucket t; if there were no trend or seasonality, the “true” parameter Bt would be an average demand, possibly subject to slow variations over time. - The estimate of the trend component
 t at the end of time bucket t, which is linked to the slope of a line. The slope can also change over time, as inversions in trend are a natural occurrence. Note that when forecasting demand Yt+h at the end of time bucket t, the estimate of trend at time t should be multiplied by the forecast horizon h.
t at the end of time bucket t, which is linked to the slope of a line. The slope can also change over time, as inversions in trend are a natural occurrence. Note that when forecasting demand Yt+h at the end of time bucket t, the estimate of trend at time t should be multiplied by the forecast horizon h. - The estimate of the multiplicative seasonality factor
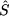 t + h - s, linked to percentage up- and downswings. This is the estimate at the end of time bucket t of the seasonal factor that applies to all time buckets similar to t + h, i.e., to a specific season within the seasonal cycle. We clarify in Section 11.5.4 that such an estimate is obtained at time bucket t + h - s, where s is the length of the seasonal cycle, but we may immediately notice that at the end time bucket t we cannot using anything like
t + h - s, linked to percentage up- and downswings. This is the estimate at the end of time bucket t of the seasonal factor that applies to all time buckets similar to t + h, i.e., to a specific season within the seasonal cycle. We clarify in Section 11.5.4 that such an estimate is obtained at time bucket t + h - s, where s is the length of the seasonal cycle, but we may immediately notice that at the end time bucket t we cannot using anything like 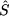 t+h, since this is a future estimate.
t+h, since this is a future estimate.
This dynamic decomposition leads to the heuristic time series approaches that are described in the following two sections.
11.4 MOVING AVERAGE
Moving average is a very simple algorithm, which serves well to illustrate some tradeoffs that we will face later. As a forecasting tool, it can be used when we assume that the underlying data generating process is simply
This is the model we obtain from (11.13) if we do not consider trend and seasonality.8 In plain words, the idea is that demand is stationary, with average Bt. In principle, the average should be constant over time. If so, we should just forecast demand by a plain average of all available observations. The average has the effect of filtering noise out and revealing the underlying “signal.” In practice, there are slow variations in the level Bt. Therefore, if we take the sample mean of all available data
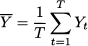
we may suffer from two drawbacks:
1. We might be considering data that do not carry any useful information, as they pertain to market conditions that no longer apply.
2. We assign the same weight 1/T to all demand observations, whereas more recent data should have larger weights; note that, in any case, weights must add up to 1.
A moving average includes only the most recent k observations:
(11.15) 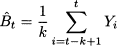
The coefficient k is a time window and characterizes the moving average. To get a grip of the sum, in particular of the +1 term in the lower limit, imagine that k = 2; then, at time t, after observing Yt, we would take the average

We see that the sum should start with time bucket t - 1, not t - 2. In a moving average with time window k, each observation within the last k ones has weight 1/k in the average. This is illustrated in Fig. 11.3. The estimate of the level is used to build a forecast. Since demand is assumed stationary, the horizon h plays no role at all, and we set
Fig. 11.3 Time window in a moving-average scheme.

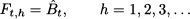
Example 11.5 Let us apply a moving average with time window k = 3 for the dataset
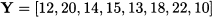
and compute MAD, assuming a forecast horizon of h = 1. We can make a first forecast only at the end of time bucket t = 3, after observing Y3 = 14:
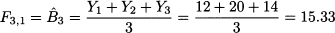
Here,  3 is the estimate of the level parameter Bt at the end of time bucket t = 3. Then, stepping forward, we drop Y1 = 12 from the information set and include Y4 = 15. Proceeding this way, we obtain the following sequence of estimates and forecasts:
3 is the estimate of the level parameter Bt at the end of time bucket t = 3. Then, stepping forward, we drop Y1 = 12 from the information set and include Y4 = 15. Proceeding this way, we obtain the following sequence of estimates and forecasts:
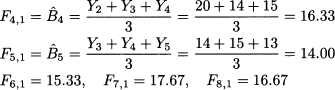
As we noticed, forecasts do not depend on the horizon; since demand is stationary, any forecast Ft,h based on the information set up to and including time bucket t will be the same for h = 1, 2, …. For instance, say that at the end of t = 5 we want to forecast demand during time bucket t = 10; the forecast would be simply
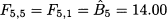
To compute MAD, we must match forecasts and observations properly. The first forecast error that we may compute is
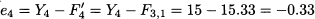
By averaging absolute errors over the sample, we obtain the following MAD:
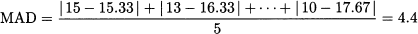
Note that we have a history of 8 time buckets, but errors should be averaged only over the 5 periods on which we may calculate an error. The last forecast F8,1 is not used to evaluate MAD, as the observation Y9 is not available.
A standard question asked by students after seeing an example like this is:
Should we round forecasts to integer values?
Since we are observing a demand process taking integer values, it is tempting to say that indeed we should round demand forecasts. Actually, there would be two mistakes in doing so:
- The point forecast is an estimate of the expected value of demand. The expected value of a discrete random variable may well be noninteger.
- We are confusing forecasts and decisions. True, we cannot purchase 17.33 items to meet demand; it must be either 17 or 18. However, what if items are purchased in boxes containing 5 items? What about making a robust decision hedging against demand uncertainty? What about existing inventory on hand? The final decision will depend on a lot of factors, and the forecast is just one of the many inputs needed.
11.4.1 Choice of time window
In choosing the time window k, we have to consider a tradeoff between
- The ability to smooth (filter) noise associated with occasionally large or small demand values
- The ability to adapt to changes in market conditions that shift average demand
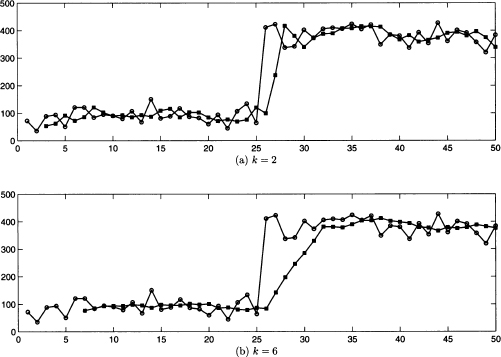
If k is large, the method has a lot of inertia and is not significantly influenced by occasional variability; however, it will be slow to adapt to systematic changes. On the contrary, if k is low, the algorithm will be very prompt, but also very nervous and prone to chase false signals. The difference in the behavior of a moving average as a function of time window length is illustrated in Fig. 11.4. The demand history is depicted by empty circles, whereas the squares show the corresponding forecasts (calculated one time bucket before; we assume h = 1). The demand history shows an abrupt jump, possibly due to opening another distribution channel. Two simulations are illustrated, with time windows k = 2 and k = 6, respectively. Note that, in plot (a), we start forecasting at the end of time bucket t = 2 for t = 3, since we assume h = 1, whereas in plot (b) we must wait for t = 6. We may also notice that, when k = 2, each forecast is just the vertical midpoint between the two last observations. We see that, with a shorter time window, the forecast tends to chase occasional swings; on the other hand, with a longer time window, the adaptation to the new regime is slower.
Fig. 11.4 Moving average with k = 2 and k = 6.
Moving average is a very simple approach, with plenty of applications beyond demand forecasting.9 However, this kind of average can be criticized because of its “all or nothing” character. As we see in Fig. 11.3, the most recent observations have the same weight, 1/k, which suddenly drops to 0. We could try a more gradual scheme in which
- Different weights are attributed to more recent observations
- A small but non-zero weight is associated with older observations
In other words, weights should decrease gradually to zero for older observations. This is exactly what the family of exponential smoothing algorithms accomplishes.
11.5 HEURISTIC EXPONENTIAL SMOOTHING
Exponential smoothing algorithms are a class of widely used forecasting methods that were born on the basis of heuristic insight. Originally, they lacked a proper statistical background, unlike the more sophisticated time series models that we outline in Section 11.6. More recently, attempts to justify exponential smoothing have been put forward, but the bottom line is that they proved their value over time. Indeed, there is no consistent evidence that more sophisticated methods have the upper hand, when it comes to real-life applications, at least in demand forecasting. However, heuristic approaches are less well suited to deal with other domains, such as financial markets, which indeed call for more sophistication. Apart from their practical relevance, exponential smoothing algorithms have great pedagogical value in learning the ropes of forecasting. Methods in this class have a nice intuitive appeal and, unlike moving averages, are readily adapted to situations involving trend and seasonality. One weak point that they suffer from is the need for ad hoc approaches to quantify uncertainty in forecasts; always keep in mind that a point forecast has very limited value in robust decision making, and we need to work with prediction intervals or, if possible, an estimate of a full-fledged probability distribution. In the next two sections, we illustrate the basic idea of exponential smoothing in the case of stationary demand. We also point out a fundamental issue with exponential smoothing: initialization. Then, we extend the idea to the cases of trend, multiplicative seasonality, and trend plus seasonality.
11.5.1 Stationary demand: three views of a smoother
In this section, we deal with the case of stationary demand, as represented by Eq. (11.14). In simple exponential smoothing we estimate the level parameter Bt by a mix of new and old information:
where α is a coefficient in the interval [0, 1]. In (11.16), the new information consists of the last observation of demand Yt, and the old information consists of the estimate  t-1, which was computed at the end of time bucket t - 1, after observing Yt - 1. The updated estimate
t-1, which was computed at the end of time bucket t - 1, after observing Yt - 1. The updated estimate  t is a weighted average of new and old information, depending on the smoothing coefficient α. To understand its effect, it is useful to examine the two extreme cases:
t is a weighted average of new and old information, depending on the smoothing coefficient α. To understand its effect, it is useful to examine the two extreme cases:
- If we set α = 1, we forget all of the past immediately, as the new estimate is just the last observation.10 If α is large, we are very fast to catch new trends, but we are also quite sensitive to noise and spikes in demand.
- If we set α = 0, new information is disregarded altogether; if α is very small, there is a lot of inertia and the learning speed is quite low.
We see that α plays a role similar to the time window k in a moving average. By increasing α we make the forecaster more responsive, but also more nervous and sensitive to noise; by decreasing α, we increase inertia, and noise is better smoothed. The tradeoff is illustrated in Fig. 11.5; a relatively small smoothing coefficient (α = 0.05) makes the adaptation to new market conditions very slow in case (a); by increasing α, the method is more responsive, as shown in case (b). In Fig. 11.6 we see the case of a sudden spike in demand. When α is small, on one hand the spike has a smaller effect; on the other hand the effect is more persistent, making the forecast a bit biased for a longer time period, as shown in plot (a). When α is large, there is an immediate effect on the forecast, which has a larger error and a larger bias, but this fades away quickly as the spike is rapidly forgotten, as shown in plot (b). In fact, the smoothing coefficient is also known as the forgetting factor.
Fig. 11.5 Effect of the smoothing coefficient α, when demand jumps to a new level.

Fig. 11.6 Effect of smoothing coefficient a, when demand has a spike.

Since we assume a stationary demand, the horizon h does not play any role and, just like with moving average, we have
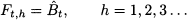
Equation (11.16) illustrates the way simple exponential smoothing should be implemented on a computer, but it does not shed much light on why this method earned such a name. Let us rewrite exponential smoothing in terms of forecasts for a time bucket, assuming that h = 1, so that
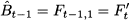
If we collect terms involving α, we get
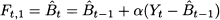
This shows that the new forecast is the old one, corrected by the last forecast error, which is smoothed by the coefficient α $le; 1. The larger is α, the stronger is the correction. This shows why this algorithm is a smoother: It dampens the correction induced by the error, which could be just the result of a transient spike. Note that the forecast is increased when the error is positive, i.e., we underforecasted demand, and decreased otherwise.
To understand where the term “exponential” comes from, we still need a third view, which is obtained by unfolding Eq. (11.16) recursively. Applying the equation at time t - 1, we obtain
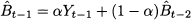
Plugging this equation into (11.16) yields
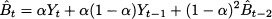
If we apply the same reasoning to  t - 2,
t - 2,  t - 3, etc., we find
t - 3, etc., we find
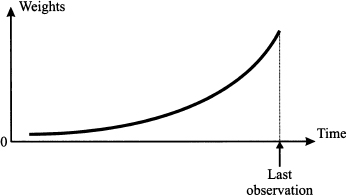
This third view clearly shows that exponential smoothing is just another average. We leave it as an exercise for the reader to prove that weights add up to one, but they are clearly an exponential function of k, with base (1 - α) < 1. The older the observation, the lower its weight. Figure 11.7 is a qualitative display of exponentially decaying weights, and it should be compared with the time window in Fig. 11.3. The exponential decay is faster when α is increased, as the base (1 - α) of the exponential function in Eq. (11.18) is smaller.
Fig. 11.7 Exponentially decaying weights in exponential smoothing.
11.5.2 Stationary demand: initialization and choice of α
One obviously weird feature of Eq. (11.18) is that it involves an infinite sequence of observations. However, in real life we do not have an infinite number of observations; the sum must be truncated somewhere in the past, right before we started collecting information. The oldest term in the average, in practice, corresponds to the initialization of the algorithm. To see this, let us assume that we have observations Y1, …, YT. If we apply Eq. (11.16) at time bucket t = 1, we have
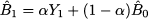
The term  0 is an initial estimate, or we should better say a guess, since it should be evaluated before the very first observation is collected. By applying the same idea that lead us to Eq. (11.18), we find
0 is an initial estimate, or we should better say a guess, since it should be evaluated before the very first observation is collected. By applying the same idea that lead us to Eq. (11.18), we find
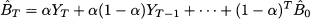
Hence, after collecting T observations, the weight of the initial estimate  0 in the average is (1 - α)T. If α is small, this initial term has a slowly decaying impact, for increasing T, and it may play a critical role, as a bad initialization will be forgotten too slowly.
0 in the average is (1 - α)T. If α is small, this initial term has a slowly decaying impact, for increasing T, and it may play a critical role, as a bad initialization will be forgotten too slowly.
To deal with initialization, we should clearly frame the problem:
1. If we are applying exponential smoothing online, to a brand-new product with no past sales history, we must make some educated guess, possibly depending on past sales of a similar product. Arguably, α should be larger at the beginning, since we must learn rapidly, and then it could be reduced when more and more information is collected.
2. If we are working online, but we are forecasting demand for an item with a significant past sales history, we may use old observations to initialize the smoother, but we should do it properly.
3. By the same token, initialization must be carried out properly when working offline and evaluating performance by historical simulation.
To see what “properly” means in case 2 above, imagine that we are at the end of time bucket t = T, and we have an information set consisting of T past observations:
We are working online and want to forecast demand for t = T + 1, and one possible way to initialize the smoother is to compute the sample mean of these observations, setting
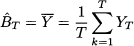
Then, our forecast for YT + 1 would be FT, 1 =  T. However, in doing so, we are forgetting the very nature of exponential smoothing, since the sample mean assigns the same weight to all of the observations. We should try to set up a situation as similar as possible to that of a forecasting algorithm that has been running forever. The way to do so is to apply exponential smoothing on the past data, from Y1 to YT, using the sample mean
T. However, in doing so, we are forgetting the very nature of exponential smoothing, since the sample mean assigns the same weight to all of the observations. We should try to set up a situation as similar as possible to that of a forecasting algorithm that has been running forever. The way to do so is to apply exponential smoothing on the past data, from Y1 to YT, using the sample mean  as an initialization of $BB0. Apparently, we are playing dirty here, since we use past data to come up with an initialization that is shifted back to the end of time bucket t = 0. However, there is nothing wrong with this, as long as we do not compute forecast errors to evaluate performance.
as an initialization of $BB0. Apparently, we are playing dirty here, since we use past data to come up with an initialization that is shifted back to the end of time bucket t = 0. However, there is nothing wrong with this, as long as we do not compute forecast errors to evaluate performance.
The last remark is also essential when carrying out historical simulation to evaluate performance. Assume again that we have a sample of T observations Yt, t = 1, …, T, and that the size of the fit sample is τ < T. We partition the sample as follows:
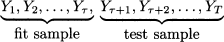
Then, the correct procedure is:
1. Use observations in the fit sample to initialize  0
0
2. Apply exponential smoothing on the fit sample, updating parameter estimates as prescribed, without calculating errors
3. Proceed on the test sample, collecting errors
4. Evaluate the selected forecast error measures
The reader could wonder why we should carry out step 2; a tempting shortcut is to proceed directly with the application of the smoother on the test sample. A good way to get the important message is by referring back to Monte Carlo simulation of a queueing system (Section 9.2.1). In that case, we should discard the initial part of the- simulation, which is just a transient phase, if the queueing system starts empty, and gather statistics only in steady state. The same consideration applies here. By running the smoother on the fit sample, we warm the system up and forget the initialization. We illustrate the idea in the example below.
Example 11.6 Consider a product whose unit purchase cost is $10, is sold for $13, and, if unsold within a shelf life of one week, is scrapped, with a salvage value of $5. We want to decide how many items to buy, based on the demand history reported in Table 11.4. If we were convinced that demand is stationary, i.e., its expected value and standard deviation do not change, we could just fit a probability distribution like the normal, based on sample mean and sample standard deviation. Then, the newsvendor model would provide us with the answer we need. However, if expected demand might shift in time, exponential smoothing can be applied. To see this, imagine taking the standard sample statistics when the demand shows an abrupt jump, like the demand history depicted in Fig. 11.5. We recall that the underlying demand model is
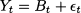
Imagine that, at some time bucket t = t*, the level jumps from value B’ to a larger value B". If we knew the “true” value of the level Bt at each time bucket, demand uncertainty would be related only to the standard deviation σ of the unpredictable component
of the unpredictable component  t. If we calculate sample mean and standard deviation mixing the two components, the jump in Bt would result in an estimate of σ
t. If we calculate sample mean and standard deviation mixing the two components, the jump in Bt would result in an estimate of σ that is much larger than true value; the sample mean would be halfway between two values B’ and B". In practice, we need to update dynamically the estimates of both expected value and standard deviation; hence, let us apply exponential smoothing, with α = 0.1 and a fit sample of 5 time buckets.
that is much larger than true value; the sample mean would be halfway between two values B’ and B". In practice, we need to update dynamically the estimates of both expected value and standard deviation; hence, let us apply exponential smoothing, with α = 0.1 and a fit sample of 5 time buckets.
Table 11.4 Application of exponential smoothing to a newsvendor problem.

The calculations are displayed in Table 11.4. On the basis of the fit sample, the initial estimate of level  0 is
0 is
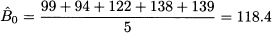
The first demand observation is used to update the estimate of level:
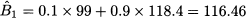
Note that we should not compute an error for the first time bucket, comparing Y1 = 99 against F0, 1 =  0 = 118.4, since the demand observation Y1 itself has been used to initialize the estimate; incidentally, using a fit sample of size 1, the first error would be zero. It would also be tempting to run the smoother starting from time bucket t = 6, the first time bucket in the test sample. However, it is better to “forget” the initialization and the consequent transient phase, by running the smoother through the full fit sample, without collecting errors. We proceed using the same mechanism and, after observing Y5 = 139, we update the estimate again:
0 = 118.4, since the demand observation Y1 itself has been used to initialize the estimate; incidentally, using a fit sample of size 1, the first error would be zero. It would also be tempting to run the smoother starting from time bucket t = 6, the first time bucket in the test sample. However, it is better to “forget” the initialization and the consequent transient phase, by running the smoother through the full fit sample, without collecting errors. We proceed using the same mechanism and, after observing Y5 = 139, we update the estimate again:
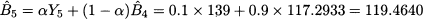
Now we may start forecasting and calculating errors:
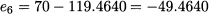
Please note that we should compare Y6 = 70 with the forecast in the line above in the table, F5,1 = 119.4640. Of course, you could arrange the table in such a way that each demand observation and the related forecast are on the same line. At the end of the test sample, the last forecast is
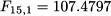
but this is not used in assessing performance, since observation Y16 is not available; however, we use it as an estimate 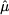 of the expected value of demand, valid for time bucket t = 16. In so doing, we implicitly assume that our estimates are unbiased.
of the expected value of demand, valid for time bucket t = 16. In so doing, we implicitly assume that our estimates are unbiased.
Now we also need an estimate  of the standard deviation. Since we cannot use sample standard deviation, we resort to using RMSE as an estimator. In order to evaluate RMSE, we square errors, as shown in the last column of Table 11.4. We obtain
of the standard deviation. Since we cannot use sample standard deviation, we resort to using RMSE as an estimator. In order to evaluate RMSE, we square errors, as shown in the last column of Table 11.4. We obtain

Hence, we assume that demand in time bucket t = 16 is normally distributed with the following expected value and standard deviation, respectively:

Now we apply the standard newsvendor model. The service level is calculated from the economics of the problem:11
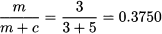
corresponding to a quantile z0.375 = -0.3186. The order quantity should be
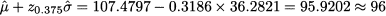
After collecting more observations, the above estimates would be revised; hence, the order quantity is not constant over time.
Apart from initialization, another issue in exponential smoothing is the choice of the smoothing coefficient α. The example suggests one possible approach, based on historical simulation: Choose the coefficient by minimizing a selected error measure. However, a possibly better strategy is dynamic adaptation. When dealing with a new product, we said that we could start with a larger α in order to forget a possibly bad initial guess rapidly; then, we could reduce α in order to shift emphasis toward noise filtering. Another element that we should take into consideration is bias. In Fig. 11.5 we have seen that the smoother can be slow to adapt to new market conditions, when an abrupt change occurs. The effect is that forecasts become systematically biased, which is detected by a mean error which is significantly different from zero. A strategy that has been proposed in the literature is to increase a when mean error is significantly different from zero. However, bias can also be the effect of a wrong demand model. Simple exponential smoothing assumes stationary demand, but a systematic error will result if, for instance, a strong upward or downward trend is present.
11.5.3 Smoothing with trend
Demand may exhibit additive trend components that, in a static case, could be represented by the following demand model
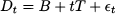
where B is the level and T is the trend. Looking at the demand model, linear regression seems a natural candidate to estimate these two parameters. However, level and trend might change over time, suggesting the opportunity of a dynamic demand model and an adaptation of exponential smoothing. Given estimates  t and
t and  t of level and trend, respectively, at the end of time bucket t, after observing Yt, the demand forecast with horizon h is
t of level and trend, respectively, at the end of time bucket t, after observing Yt, the demand forecast with horizon h is
Note that, unlike simple moving average and exponential smoothing, the forecast horizon does play a role here, as it multiplies trend. The following adaptation of exponential smoothing is known as Holt’s linear method:
Here α, β are two smoothing coefficients in the range [0,1]. Comparing Eq. (11.20) against simple exponential smoothing, we note that we cannot update  t solely on the basis of
t solely on the basis of  t-1 as the two values are not directly comparable when trend is involved. In fact, a forecast for Yt, based on the information set up to t - 1, would be
t-1 as the two values are not directly comparable when trend is involved. In fact, a forecast for Yt, based on the information set up to t - 1, would be
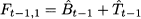
Then, by applying the same error correction logic of Eq. (11.17), we should adapt the estimate of level as follows:
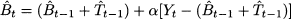
which leads to Eq. (11.20). Equation (11.21) uses a smoothing coefficient β to update the estimate of trend. In this case, the new information consists of the difference between the two last estimates of level,  t -
t -  t-1. We might wonder if we should not use the growth in demand, Yt - Yt-1, in updating trend estimates. Indeed, this is a possible alternative; however, the difference in demand might be oversensitive to noise, whereas the difference in estimated levels is more stable. This might be a disadvantage, however, when trend changes, since adaptation could be too slow. This can be countered by using a larger coefficient β, which is sensible since the level estimates are by themselves noise smoothers.
t-1. We might wonder if we should not use the growth in demand, Yt - Yt-1, in updating trend estimates. Indeed, this is a possible alternative; however, the difference in demand might be oversensitive to noise, whereas the difference in estimated levels is more stable. This might be a disadvantage, however, when trend changes, since adaptation could be too slow. This can be countered by using a larger coefficient β, which is sensible since the level estimates are by themselves noise smoothers.
We may appreciate the flexibility of the exponential smoothing framework, which can be easily and intuitively adapted to different demand models. However, a careful look at Eq. (11.19) suggests a potential danger when h is large: We should not extrapolate a trend too much in the future. In particular, with a negative trend, this could even result in a negative demand forecast. The above formulas apply to an additive trend, but when demand is low and trend is negative, a model with multiplicative trend should be adopted. In such a model, the demand forecast is
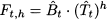
and a decreasing trend is represented by  t < 1; this corresponds to a percentage decrease in demand, and it prevents negative forecasts. We will not give update formulas for multiplicative trend, but they can be found in the specialized literature.
t < 1; this corresponds to a percentage decrease in demand, and it prevents negative forecasts. We will not give update formulas for multiplicative trend, but they can be found in the specialized literature.
Exponential smoothing with trend presents the same initialization issues that we have encountered with stationary demand. Given a fit sample, there are alternative initialization methods:
- Linear regression on the fit sample
- Heuristic approaches based on time series decomposition
Whatever approach we take, the minimal fit sample consists of two demand observations. From a mathematical perspective, it is impossible to estimate two parameters with just one observation; a simpler view is that with one observation there is no way to estimate a trend. Also note that, if we select this minimal fit sample, we will just fit a line passing through two points. On this fit sample, errors will be zero, because with two parameters and two observations we are able to find an exact fit. This reinforces the view that errors should not be computed on the fit sample.
11.5.4 Smoothing with multiplicative seasonality
In this section we consider the case of pure seasonality. Forecasts are based on the demand model of Eq. (11.13), in which the trend parameter is set to  t = 0:
t = 0:
where s is the length of the seasonal cycle, i.e., a whole cycle consists of s time buckets.12 To get a grip of this model, imagine a yearly cycle consisting of 12 monthly time buckets, and say that we are at the end of December of year X. Then, t = 0 is December of year X and time bucket t = 1 corresponds to January of year X + 1. On the basis of the estimate  0, how can we forecast demand in January? Of course, we cannot take
0, how can we forecast demand in January? Of course, we cannot take  0 ˙
0 ˙ 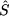 0, since this involves the seasonal factor of December. We should multiply
0, since this involves the seasonal factor of December. We should multiply  0 by the seasonal factor of January, but this is not
0 by the seasonal factor of January, but this is not 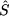 1, because
1, because 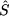 1 is the estimate of this seasonal factor after observing Y1. Since s = 12 and h = 1, the correct answer is
1 is the estimate of this seasonal factor after observing Y1. Since s = 12 and h = 1, the correct answer is
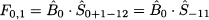
where 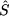 -11 is the estimate of the seasonal factor of January at the end of January in year X. We should use seasonal factors estimated one year ago! After observing Y1, i.e., January demand in year X + 1, we can update
-11 is the estimate of the seasonal factor of January at the end of January in year X. We should use seasonal factors estimated one year ago! After observing Y1, i.e., January demand in year X + 1, we can update 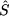 1, which will be used to forecast demand for January in year X + 2. It is easy to devise exponential smoothing formulas to update estimates of both level and seasonality factors:
1, which will be used to forecast demand for January in year X + 2. It is easy to devise exponential smoothing formulas to update estimates of both level and seasonality factors:
Here α and γ are familiar smoothing coefficients in the range [0, 1]. Equation (11.23) is an adaptation of simple exponential smoothing, in which demand Yt is deseasonalized by dividing it by the current estimate of the correct seasonal factor, 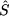 t-s. To see why this is needed, think of ice cream demand in summer; we should not increase the estimate of level after observing high sales, as this is just a seasonal effect. The need for deseasonalization is quite common in many application domains. Equation (11.24) takes care of updating the seasonal factor of time bucket t, based on the previous estimate
t-s. To see why this is needed, think of ice cream demand in summer; we should not increase the estimate of level after observing high sales, as this is just a seasonal effect. The need for deseasonalization is quite common in many application domains. Equation (11.24) takes care of updating the seasonal factor of time bucket t, based on the previous estimate 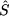 t-s, and the new information on the seasonal factor, which is obtained by dividing the last observation by the revised level estimate.
t-s, and the new information on the seasonal factor, which is obtained by dividing the last observation by the revised level estimate.
Initialization requires fitting the parameters  0 and
0 and 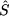 s-j, for j = 1, 2, …, s. We need s + 1 parameters, but actually the minimal fit sample consists of just s observations, i.e., a whole cycle. In fact, we lose one degree of freedom because the average value of multiplicative seasonality factors must be 1. Of course, the more cycles we use, the better the fit will be. Assuming that the fit sample consists of k full cycles, we have l = k ˙ s observations. A reasonable way to fit parameters in this case is the following:
s-j, for j = 1, 2, …, s. We need s + 1 parameters, but actually the minimal fit sample consists of just s observations, i.e., a whole cycle. In fact, we lose one degree of freedom because the average value of multiplicative seasonality factors must be 1. Of course, the more cycles we use, the better the fit will be. Assuming that the fit sample consists of k full cycles, we have l = k ˙ s observations. A reasonable way to fit parameters in this case is the following:
1. The initial estimate of level is set to average demand over the fit sample:
(11.25) 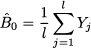
Note that we cannot take this plain average if the fit sample does not consist of full cycles; when doing so in such a case, we would overweight some seasons within the cycle.
2. Seasonal factors are estimated by dividing average demand of time buckets corresponding to each season within the fit sample, divided by the level estimate:
(11.26) 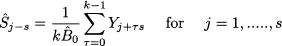
where k = l/s is the number of full cycles in the fit sample. To understand the sum above, say that we have k = 3 full cycles, each one consisting of s = 4 time buckets. Then, the seasonal factor for the first season within the cycle is estimated as
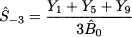
Example 11.7 Table 11.5 shows demand data for 6 time buckets. We assume s = 3, so what we see is a history consisting of two whole cycles. We want to initialize the smoother with a fit sample consisting of one cycle, and evaluate MAPE on a test sample consisting of the second cycle, applying exponential smoothing with coefficients α = 0.1 and γ = 0.2. Initialization yields the following parameters:

A useful check is
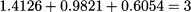
If we apply Eqs. (11.23) and (11.24) after the first observation, we obtain
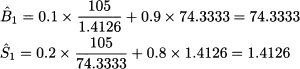
We note that estimates do not change! A closer look reveals that the first forecast would have been
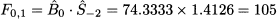
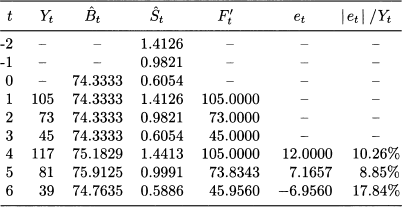
We do not update estimates, because the forecast was perfect. By a similar token, errors are zero and parameters are not updated for time buckets t = 2 and t = 3. On second thought, this is no surprise: We have used a model with four parameters, and actually 3 degrees of freedom, to match three observations. Of course, we obtain a perfect match, and errors are zero throughout the fit sample. All the good reasons for not calculating errors there! Things get interesting after observing Y4, and the calculations in Table 11.5 yield
Table 11.5 Applying exponential smoothing with multiplicative seasonality.
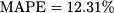
As a further exercise, let us compute forecasts F6,2 and F6,3:
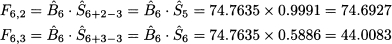
Once again, the example shows the danger of calculating errors within the fit sample; performance evaluation must always be carried out out-of-sample to be fair. Of course, we will not incur such a blatant mistake with a larger fit sample. In the literature, a backward initialization is often suggested. The idea is to run the smoother backward in time, starting from the last time bucket, in order to obtain initialized parameters. Doing so with a large data set will probably avoid gross errors, but a clean separation between fit and test samples is arguably the wisest idea.
11.5.5 Smoothing with trend and multiplicative seasonality
The last exponential smoothing approach we consider puts everything together and copes with additive trend and multiplicative seasonality. The Holt-Winter method is based on Eq. (11.13), which we repeat for convenience:
(11.27) 
The overall scheme uses three smoothing coefficients and it proceeds as follows
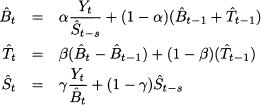
All of the remarks we have made about simpler versions of exponential smoothing apply here as well, including initialization. To initialize the method, we need s + 2 parameters, which must be estimated on the basis of at least s + 1 demand observations, since seasonal factors are not independent. Heuristic initialization approaches, based on time series decomposition, are described in the references at the end of the chapter. Alternatively, we could use a formal approach based on least-squares-like optimization models, as illustrated in Example 11.4.
11.6 A GLANCE AT ADVANCED TIME SERIES MODELING
The class of exponential smoothing methods was born out of heuristic intuition, even though methodological frameworks were later developed to provide them with a somewhat more solid justification. Despite these efforts, exponential smoothing methods do suffer from at least a couple of drawbacks:
- They are not able to cope with correlations between observations over time; for instance, we might have a demand process with positive or negative autocorrelation, formally defined below, and this must be considered by forecasting procedures.
- They do not offer a clear way to quantify uncertainty; using RMSE as an estimate of standard deviation, as we did in Example 11.6, may be a sensible heuristic, but again it may be inadequate when autocorrelation is an issue.
It is also worth noting that simple linear regression models share some of the limitations above, as standard OLS estimates do assume uncorrelated errors. If necessary, we may resort to an alternative body of statistical theory that deals with formal time series models. In this section we give a flavor of the theory, by outlining the two basic classes of such models: moving-average and autoregressive processes. They can be integrated in the more general class of ARIMA (autoregressive integrated moving average) processes, also known as Box–Jenkins models. As we shall see, time series modeling offers many degrees of freedom, maybe too many; when observing a time series, it may be difficult to figure out which type of model is best-suited to capture the essence of the underlying process. Applying time series requires the following steps:
1. Model identification. We should first select a model structure, i.e., its type and its order.
2. Parameter estimation. Given the qualitative model structure, we must fit numerical values for its parameters. We will not delve into the technicalities of parameter estimation for time series models, but this step relies on the statistical tools that we have developed in Section 9.9.
3. Forecasting and decision making. In the last step, we must make good use of the model to come up with a forecast and a quantification of its uncertainty, in order to find a suitably robust decision.
All of the above complexity must be justified by the application at hand. Time series models are definitely needed in quantitative finance, maybe not in demand forecasting. We should also mention that, quite often, a quantitative forecast must be integrated with qualitative insights and pieces of information; if so, a simpler and more intuitive model might be easier to twist as needed.
In its basic form, time series theory deals with weakly stationary processes, i.e., time series Yt with the following properties, related to first- and second-order moments:
1. The expected value of Yt does not change in time: E[Yt] = μ.
2. The covariance between Yt and Yt+k depends only on time lag k.
The second condition deserves some elaboration.
DEFINITION 11.1 (Autocovariance and autocorrelation) Given a weakly stationary stochastic process Yt, the function

is called autocovariance of the process with time lag k. The function
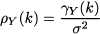
is called the autocorrelation function (ACF).
The definition of autocorrelation relies on the fact that variance is constant as well:
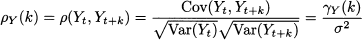
In practice, autocorrelation may be estimated by the sample autocorrelation function (SACF), given a sample path Yt, t = 1, …, T:
where  is the sample mean of Yt. The expression in Eq. (11.28) may not look quite convincing, since the numerator and the denominator are sums involving a different number of terms. In particular, the number of terms in the numerator is decreasing in the time lag k. Thus, the estimator looks biased and, for a large value of k, Rk will vanish. However, this is what one expects in real life. Furthermore, although we could account for the true number of terms involved in the numerator, for large k the sum involves very few terms and is not reliable. Indeed, the form of sample autocorrelation in Eq. (11.28) is what is commonly used in statistical software packages, even though alternatives have been proposed.13 If T is large enough, under the null hypothesis that the true autocorrelations ρk are zero, for k ≥ 1, the statistic
is the sample mean of Yt. The expression in Eq. (11.28) may not look quite convincing, since the numerator and the denominator are sums involving a different number of terms. In particular, the number of terms in the numerator is decreasing in the time lag k. Thus, the estimator looks biased and, for a large value of k, Rk will vanish. However, this is what one expects in real life. Furthermore, although we could account for the true number of terms involved in the numerator, for large k the sum involves very few terms and is not reliable. Indeed, the form of sample autocorrelation in Eq. (11.28) is what is commonly used in statistical software packages, even though alternatives have been proposed.13 If T is large enough, under the null hypothesis that the true autocorrelations ρk are zero, for k ≥ 1, the statistic  is approximately normal standard. Since z0.99 = 1.96 ≊ 2, a commonly used approximate rule states that if
is approximately normal standard. Since z0.99 = 1.96 ≊ 2, a commonly used approximate rule states that if
the sample autocorrelation at lag k is statistically significant. For instance, if T = 100, autocorrelations outside the interval [-0.2, 0.2] are significant. We should keep in mind that this is an approximate result, holding for a large number T of observations. We may plot the sample autocorrelation function at different lags, obtaining an autocorrelogram that can be most useful in pointing out hidden patterns in data.
Fig. 11.8 A seasonal time series (left) and its autocorrelogram (right).

Example 11.8 (Detecting seasonality with autocorrelograms) Consider the time series displayed in figure 11.8. A cursory look at the plot may not suggest much structure in the data, but the autocorrelogram does. The autocorrelogram displays two horizontal lines defining a band, outside which autocorrelation is statistically significant; notice that T = 100 and the two horizontal lines are set at -0.2 and 0.2, respectively; this is consistent with Eq. (11.29). We notice that sample autocorrelation is stronger at time lags 5, 10, 15, and 20. This suggests that there is some pattern in the data. In fact, the time series was generated by sampling the following process:
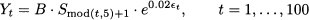
where:
 t is a sequence of independent, standard normal variables; taking the exponential of
t is a sequence of independent, standard normal variables; taking the exponential of  t makes sure that we have positive values.
t makes sure that we have positive values.- mod(t, 5) denotes the remainder of integer division of t by 5; actually, this is just a process with a seasonal cycle of length 5, with parameters corresponding to the following level and seasonal factors:
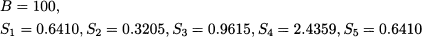
We see that an autocorrelogram is a useful tool to spot seasonality and other hidden patterns in data.
Another important building block in time series modeling is white noise, denoted by  t in the following. This is just a sequence of i.i.d. random variables. If they are normal, we have a Gaussian white noise. As we have mentioned, the first step in modeling a time series is the identification of the model structure. In the following we outline a few basic ideas that are used to this aim, pointing out the role of autocorrelation in the analysis.
t in the following. This is just a sequence of i.i.d. random variables. If they are normal, we have a Gaussian white noise. As we have mentioned, the first step in modeling a time series is the identification of the model structure. In the following we outline a few basic ideas that are used to this aim, pointing out the role of autocorrelation in the analysis.
11.6.1 Moving-average processes
A finite-order moving-average process of order q, denoted by MA(q), can be expressed as
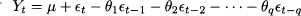
where random variables  t are white noise, with E[
t are white noise, with E[ t] = 0 and Var(
t] = 0 and Var( t) = σ2. These variables play the role of random shocks and drive the process. It is fairly easy to see that the process is weakly stationary. A first observation is that expected value and variance are constant:
t) = σ2. These variables play the role of random shocks and drive the process. It is fairly easy to see that the process is weakly stationary. A first observation is that expected value and variance are constant:
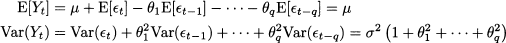
The calculation of autocovariance is a bit more involved, but we may take advantage of the uncorrelation of white noise:
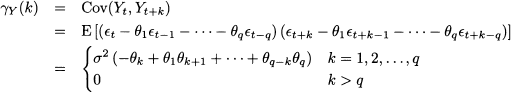
As a consequence, the autocorrelation function is
Thus, the autocorrelation function depends only on the lag k. We also notice that the autocorrelation function cuts off for lags larger than the order of the process. This makes sense, since the process Yt is a moving average of the driving process  t. Hence, by checking whether the sample autocorrelation function cuts off after a time lag, we may figure out whether a time series can be modeled as a moving average, as well as its order q. Of course, the sample autocorrelation will not be exactly zero for k > q; nevertheless, by using the autocorrelogram and its significance bands, we may get some clue.
t. Hence, by checking whether the sample autocorrelation function cuts off after a time lag, we may figure out whether a time series can be modeled as a moving average, as well as its order q. Of course, the sample autocorrelation will not be exactly zero for k > q; nevertheless, by using the autocorrelogram and its significance bands, we may get some clue.
Example 11.9 Let us consider a simple MA(1) process
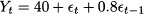
where  t is a sequence of uncorrelated standard normal variables (Gaussian white noise). In Fig. 11.9 we show a sample path obtained by Monte Carlo simulation, and the corresponding sample autocorrelogram. The sample autocorrelation looks significant at time lag 1, which is expected, given the nature of the process. Note that, by applying Eq. (11.30), we find that the autocorrelation function, for a MA(1) process Yt = μ +
t is a sequence of uncorrelated standard normal variables (Gaussian white noise). In Fig. 11.9 we show a sample path obtained by Monte Carlo simulation, and the corresponding sample autocorrelogram. The sample autocorrelation looks significant at time lag 1, which is expected, given the nature of the process. Note that, by applying Eq. (11.30), we find that the autocorrelation function, for a MA(1) process Yt = μ +  t - θ1
t - θ1 t -1, is
t -1, is
Fig. 11.9 Sample path and corresponding SACF for the moving-average process Yt = 40 +  t + 0.8
t + 0.8 t-1.
t-1.
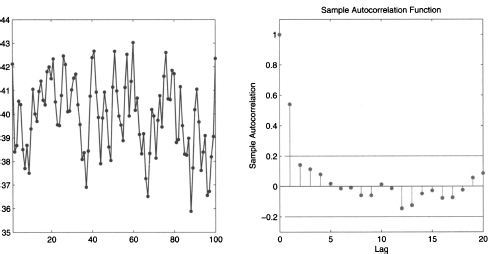
Figure 11.10 shows the sample path and autocorrelogram of a slightly different MA(1) process:
Fig. 11.10 Sample path and corresponding SACF for the moving-average process Yt = 40 +  t - 0.8
t - 0.8 t-1.
t-1.
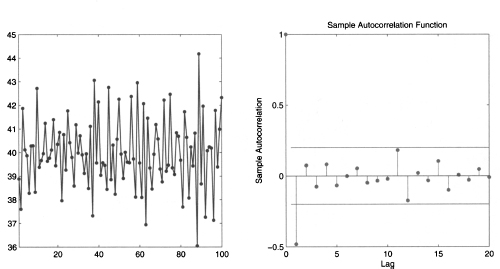
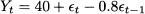
The change in sign in θ1 has an effect on the sample path; an upswing tends to be followed by a downswing, and vice versa. The autocorrelogram shows a cutoff after time lag 1, and a negative autocorrelation.
If we increase the order of the process, we should expect more significant autocorrelations. In Fig. 11.11, we repeat the exercise for the MA(2) process
Fig. 11.11 Sample path and corresponding SACF for the moving-average process Yt = 40 +  t + 0.9
t + 0.9 t-1 + 0.5
t-1 + 0.5 t-2.
t-2.

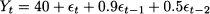
We notice that, in this case, the autocorrelation function cuts off after time lag k = 2.
We should mention that sample autocorrelograms are a statistical tool. It may well be the case that, for the moving-average processes in the example, we get a different picture. This is a useful experiment to carry out with the help of statistical software.
11.6.2 Autoregressive processes
In finite-order moving-average processes, only a finite number of past realizations of white noise influence the value of Yt. This may be a limitation for those processes in which all of the previous realizations have an effect, even though this possibly fades in time. This consideration led us from forecasting using simple moving averages to exponential smoothing. In principle, we could consider an infinite-order moving-average process, but having to do with an infinite sequence of θt-k coefficients does not sound quite practical. Luckily, under some technical conditions, such a process may be rewritten in a compact form involving time-lagged realizations of the Yt itself. This leads us to the definition of an autoregressive process of a given order. The simplest such process is the autoregressive process of order 1, AR(1):
One could wonder under which conditions this process is stationary, since we cannot use the same arguments as in the moving-average case. A heuristic argument to find the expected value μ = E[Yt] is based on taking expectations and dropping the time subscript in Eq. (11.33):
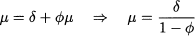
The argument is not quite correct, as it leads to a sensible result if the process is indeed stationary, which is the case if |φ| < 1. Otherwise, intuition suggests that the process will grow without bounds. The reasoning can be made precise by using the infinite-term representation of Yt, which is beyond the scope of this book. Using the correct line of reasoning, we may also prove that
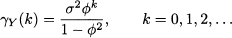
In particular
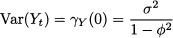
and we may also observe that, for a stationary AR(1) process,
We notice that autocorrelation is decreasing, but it fades away with no sharp cutoff.
Example 11.10 In Figs. 11.12 and 11.13, we show a sample path and the corresponding sample autocorrelogram for the two AR(1) processes
Fig. 11.12 Sample path and corresponding SACF for the autoregressive process Yt = 8 + 0.8Yt-1 +  t.
t.

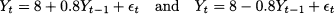
respectively. Notice that the change in sign in the φ coefficient has a significant effect on the sample path, as well as on autocorrelations. In the first case, autocorrelation goes to zero along a relatively smooth path.14 The sample path of the second process features evident up- and downswings; we also notice an oscillatory pattern in the autocorrelation.
The autocorrelation behavior of AR processes does not present the cutoff properties that help us determine the order of a MA process. The tool that has been developed for AR process identification is the partial autocorrelation function (PACF). The rationale behind PACF is to measure the degree of association between Yt and Yt-k, removing the effects of intermediate lags, i.e., Yt-1, …, Yt-k+1. We cannot dwell too much on PACF, but we may at least get a better intuitive feeling as follows.
Fig. 11.13 Sample path and corresponding SACF for the autoregressive process Yt = 8 - 0.8Yt-1 +  t.
t.
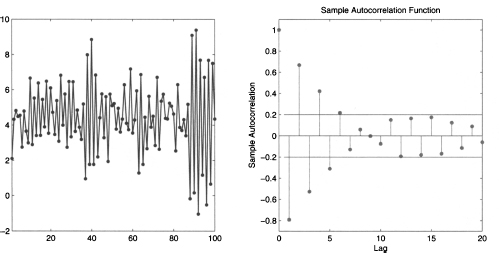
Example 11.11 (Partial correlation) Consider three random variables X, Y, and Z, and imagine regressing X and Y on Z:
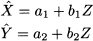
Note that we are considering a probabilistic regression, not a sample-based regression. From Section 10.6, we know that
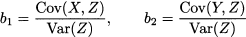
Furthermore, we have regression errors

which may be regarded as the random variables X and Y, after the effect of Z is removed. The correlation ρ(X, Y) may be large because of the common factor Z (the “lurking” variable). If we want to get rid of it, we may consider the partial correlation ρ(X*, Y*).
Following the intuition provided by the example, we might consider estimating the partial autocorrelation between Yt and Yt-k by the following linear regression:

By including intermediate lagged variables Yt-1, ˙ ˙ ˙, Yt-k+1, we capture their effect by the regression coefficients b1, …, bk-1. Then, we could use bk as an estimate of partial autocorrelation. Actually, this need not be the sounder approach, but software packages provide us with ready-to-use functions to estimate the PACF by its sample counterpart (SPACF). In Fig. 11.14 we show the SPACF for the two AR(1) processes of Example 11.10. We see that the SPACF cuts off after lag 1, even though statistical sampling errors suggest that there is a significant value at larger lags in the first case. SPACF can be used to assess the order of an AR model.
Fig. 11.14 Sample partial autocorrelation function for the autoregressive processes of Example 11.10.

11.6.3 ARMA and ARIMA processes
Autoregressive and moving-average processes may be merged into ARMA (autoregressive moving-average) processes like:
The model above is referred to as ARMA(p, q) process, for self-explanatory reasons. Conditions ensuring stationarity have been developed for ARMA processes, as well as identification and estimation procedures. Clearly, the ARMA modeling framework affords us plenty of opportunities to fit historical data. However, it applies only to stationary data. It is not too difficult to find real-life examples of data processes that are nonstationary. Just think of stock market indices; most investors really wish that the process is not stationary.
Fig. 11.15 A sample path and the corresponding SACF for the random walk Yt = Yt-1 + 0.05ζt.

Example 11.12 (A nonstationary random walk) A quite common building block in many financial models is the random walk. An example of random walk is
where ζt is a sequence of independent and standard normal random variables. This is actually an AR process, but from Section 11.6.2 we know that it is nonstationary, as φ = 1. A sample path of the process is shown in Fig. 11.15. In this figure, the nonstationarity of the process is pretty evident, but this need not always be the case. In figure 11.16 we show another sample path for the same process. A subjective comparison of the two sample paths would not suggest that they are just two realizations of the same stochastic process. However, the two autocorrelograms show a common pattern: Autocorrelation fades out slowly. Indeed, this is a common feature of nonstationary processes. Figure 11.17 shows the SPACF for the second sample path. We see a very strong partial autocorrelation at lag 1, which cuts off immediately. Again, this is a pattern corresponding to the process described by Eq. 11.36.
Since the theory of stationary MA and AR processes is well developed, it would be nice to find a way to apply it to nonstationary processes as well. A commonly used trick to remove nonstationarity in a time series is differencing, by which we consider the time series
Applying differencing to the sample path of Fig. 11.15 results in the sample path and SACF illustrated in figure 11.18. The shape of the SACF is not surprising, since the differenced process is just white noise.
Fig. 11.16 Another sample path and the corresponding SACF for the random walk Yt = Yt-1 + 0.05ζt.
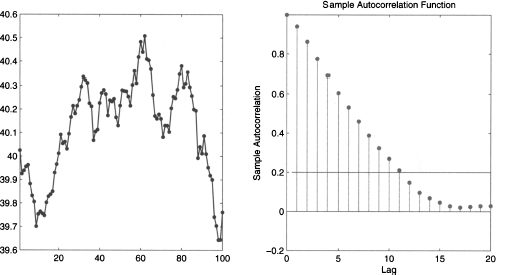
Fig. 11.17 Sample partial autocorrelation function for the random walk Yt = Yt-1 + 0.05ζt.

Fig. 11.18 The effect of differencing on the sample random walk of Fig. 11.15.

Example 11.13 (What is nonstationarity, anyway?) A time series with trend
where  t is white noise, is clearly nonstationary and features a deterministic trend. A little digression is in order to clarify the nature of nonstationarity
t is white noise, is clearly nonstationary and features a deterministic trend. A little digression is in order to clarify the nature of nonstationarity
in a random walk
The sample paths in Example 11.12 show that in the random walk does not feature a deterministic trend. Recursive unfolding of Eq. (11.39) results in
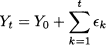
Therefore
Hence, we must have a different kind of nonstationarity in the random walk of Eq. (11.39) than in the process described by Eq. (11.38). To investigate the matter, let us consider the expected value of the increment Y’t = Yt - Yt-1, conditional on Yt-1:
Therefore, given the last observation Yt-1, we cannot predict whether the time series will move up or down. Now, let us consider a stationary AR(1) process
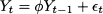
where φ  (-1, 1). The increment in this case is
(-1, 1). The increment in this case is
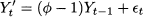
Since (φ - 1) < 0, we have
This suggests that a stationary AR(1) process is mean reverting, in the sense that the process tends to return to its expected value; the nonstationary random walk does not enjoy this property.
If we introduce the backshift operator B, defined by
we may express the first difference in Eq. (11.37) as
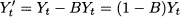
Sometimes, differencing must be repeated in order to obtain a stationary time series. We obtain second-order differencing by repeated application of (first-order) differencing:

This suggests that we may formally apply the algebra of polynomials to the backshift operator, in order to find differences of arbitrary order. By introducing polynomials

we may rewrite the ARMA model of Eq. (11.35) in the compact form
(11.40) 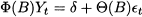
We may extend the class of stationary ARMA models, in order to allow for nonstationarity. We find the more general class of ARIMA (autoregressive integrated moving average) processes, also known as Box–Jenkins models. An ARIMA (p, d, q) process can be represented as follows:15
(11.41) 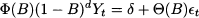
where φ(B) and  (B) are polynomials of order p and q, respectively, and d is a differencing order such that the process Yt is stationary, whereas, if we take differences of order (d - 1), the process is still nonstationary. The name “integrated” stems from the fact that we obtain the nonstationary process by integrating a stationary one, i.e., by undoing differencing. In most business applications the order d is 0 or 1. A full account of this class of models is beyond the scope of this book; we refer the reader to the bibliography provided at the end of this chapter, where it is also shown how Box-Jenkins models can be extended to cope with seasonality.
(B) are polynomials of order p and q, respectively, and d is a differencing order such that the process Yt is stationary, whereas, if we take differences of order (d - 1), the process is still nonstationary. The name “integrated” stems from the fact that we obtain the nonstationary process by integrating a stationary one, i.e., by undoing differencing. In most business applications the order d is 0 or 1. A full account of this class of models is beyond the scope of this book; we refer the reader to the bibliography provided at the end of this chapter, where it is also shown how Box-Jenkins models can be extended to cope with seasonality.
11.6.4 Using time series models for forecasting
Time series models may be used for forecasting purposes. As usual, we should find not only a point forecast, but also a prediction interval. Given an information set consisting of observations up to Yt, we wish to find a forecast Ft,h = 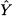 t+h(t), at time t, with horizon h ≥ 1, that is “best” in some well specified sense. A reasonable criterion is the minimization of the mean squared error
t+h(t), at time t, with horizon h ≥ 1, that is “best” in some well specified sense. A reasonable criterion is the minimization of the mean squared error
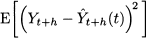
It can be shown that this is obtained by the conditional expectation

To be concrete, assume that we have estimated the parameters of a model like
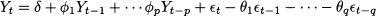
If we want to forecast with horizon h = 1, we should step forward to
To build a point forecast, we note the following:
- If all of the observations Yt - p+1, …, Yt are available,16 we should just plug their values into Eq. (11.42).
- Of course we do not know the future random shock
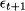 ; however, if random shocks are uncorrelated, we may just plug its expected value E[
; however, if random shocks are uncorrelated, we may just plug its expected value E[ t+1] = 0 into the equation.
t+1] = 0 into the equation. - Unfortunately, we cannot directly observe the past shocks
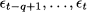 . In chapter 10 on simple linear regression, we faced a similar issue related to the difference between unobservable errors and observable residuals. We have to estimate
. In chapter 10 on simple linear regression, we faced a similar issue related to the difference between unobservable errors and observable residuals. We have to estimate  Bt - q+1, …,
Bt - q+1, …,  Bt on the basis of prediction errors.
Bt on the basis of prediction errors.
Example 11.14 Consider the model
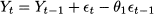
In order to forecast Yt+1, we write
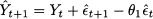
where the prediction of the future shock is  , and the past shock is estimated by the observed forecast error
, and the past shock is estimated by the observed forecast error
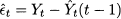
If we want to forecast with horizon h > 1, we should rewrite Eq. (11.42) for the appropriate time subscript, and run a multistep forecasting procedure, whereby successive forecasts are generated and used. As the reader can imagine, when the moving-average order q is large, things are not as simple as in the example above. Indeed, forecasting based on ARIMA models is by no way a trivial business, and alternative approaches have been proposed. One possibility is to rewrite the model as an infinite-order moving average
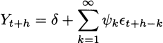
and plug estimates of random shocks. The procedures to accomplish all of this are beyond the scope of this book;17 luckily, statistical software packages are available to carry out model estimation and forecasting. These software tools also provide the user with a prediction interval, using procedures which are not unlike those we used to find confidence intervals. The idea is surrounding the point forecast with an interval related to some standard prediction error, using quantiles from t or standard normal distributions. When using these procedures, we should keep in mind the following:
- Typically, it is assumed that random shocks are normal and uncorrelated.
- Since the mathematics of time series is quite involved, the only source of uncertainty accounted for is the realization of the future random shock. However, we have seen in Section 10.4 that uncertainty in parameter estimates also plays a role. Unfortunately, simple linear regression is a simple problem with an analytical solution, which lends itself to an accurate analysis; often, to estimate parameters of time series models, numerical optimization is required, which makes a formal analysis quite difficult.
As a result, the forecast uncertainty could be underestimated. Hence, it is good practice to split available data into a fit and a test sample, and assess forecast errors out-of-sample before applying a model in a business setting.
Problems
11.1 Consider the demand data in the table below:

We want to apply exponential smoothing with trend:
- Using a fit sample of size 3, initialize the smoother using linear regression.
- Choose smoothing coefficients and evaluate MAPE and RMSE on the test sample.
- After observing demand in the last time bucket, calculate forecasts with horizons h = 2 and h = 3.
11.2 The following table shows quarterly demand data for 3 consecutive years:

Choose smoothing coefficients and apply exponential smoothing with seasonality:
- Initial parameters are estimated using a fit sample consisting of two whole cycles.
- Evaluate MAD and MPE on the test sample, with h = 1.
- • What is F5,3?
11.3 In the table below, “–” indicates missing information and “??” is a placeholder for a future and unknown demand:

Initialize a smoother with multiplicative seasonality by using a fit sample of size 7.
11.4 We want to apply the Holt–Winter method, assuming a cycle of one year and a quarterly time bucket, corresponding to ordinary seasons. We are at the beginning of summer and the current parameter estimates are
- Level 80
- Trend 10
- Seasonality factors: winter 0.8, spring 0.9, summer 1.1, autumn 1.2
On the basis of these estimates, what is your forecast for next summer? If the demand scenario (summer 88, autumn 121, winter 110) is realized, what are MAD and MAD%?
11.5 Prove that the weights in Eq. (11.18) add up to one. (Hint: Use the geometric series.)
11.6 Prove Eqs. (11.31) and (11.32).
11.7 Consider a moving-average algorithm with time window n. Assume that the observed values are i.i.d. variables. Show that the autocorrelation function for two forecasts that are k time buckets apart is
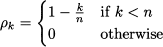
For further reading
- A classical reference on forecasting is the book by Makridakis et al. [6], which covers both regression and time series models, illustrating them with a vast array of applications. Among other things, the interested reader may find details on static time series decomposition approaches.
- Another general reference worth looking at is the text by Bowerman et al. [1], which offers a succinct treatment, without dwelling too much on technicalities. The text by Heij et al. [5], from which Example 11.13 was taken, offers a good compromise between theory and applications.
- There are quite advanced books on time series modeling, like the monumental text by Hamilton [4]. For a gentler treatment, a possible reference is that by Montgomery et al. [7], whose Chapter 5 has influenced the presentation in Section 11.6 above.
- We have dealt mostly with demand forecasting, but we did not cover many important issues, such as forecasting for brand-new products; interested readers may consult Chapter 3 of Ref. [2], which has influenced much of the presentation here.
- For further listening, the title of Section 11.5.1 is a homage to Jaco Pastorius’ Three Views of a Secret.
REFERENCES
1. B.L. Bowerman, R.T. O’Connell, and A.B. Koehler, Forecasting, Time Series, and Regression, Brooks/Cole, Pacific Grove, CA, 2005.
2. P. Brandimarte and G. Zotteri, Introduction to Distribution Logistics, Wiley, New York, 2007.
3. P.J. Brockwell and R.A. Davis, Time Series: Theory and Methods, 2nd ed., Springer, New York, 1991.
4. J.D. Hamilton, Time Series Analysis, Princeton University Press, Princeton, NJ, 1994.
5. C. Heij, P. de Boer, P.H. Franses, T. Kloek, and H.K. van Dijk, Econometric Methods with Applications in Business and Economics, Oxford University Press, New York, 2004.
6. S. Makridakis, S.C. Wheelwright, and R.J. Hyndman, Forecasting: Methods and Applications, 3rd ed., Wiley, New York, 1998.
7. D.C. Montgomery, C.L. Jennings, and M. Kulahci, Introduction to Time Series Analysis and Forecasting, Wiley, New York, 2008.
1 Some qualitative forecasting methods, like the Delphi method, have been developed to manage the judgmental forecasts of a pool of experts. If poorly applied, these methods may lead to a consensus forecast destroying valuable information; in fact, the disagreement between experts may be leveraged to find a measure of inherent uncertainty.
2 For the sake of simplicity, we have stated the two approaches in a somewhat extreme and overly simplistic manner. In practice, we may well build a statistical model in which behavioral factors are accounted for by suitable explanatory variables; in fact, quantitative models of this kind have been proposed for active portfolio management.
3 The case we are outlining is well known: Benetton reversed the sequence of manufacturing steps in order to ease severe difficulties with forecasting. Hewlett-Packard is another company that has successfully adopted product design for postponement, in order to improve supply chain performance.
4 It is important to keep in mind that errors should be divided by demand Yt, and not by forecast F’t. This second choice may lead to forecast manipulations when a forecaster’s wages are tied to forecast errors.
5 We should mention that out-of-sample testing should also be carried out with a regression model.
6 The term “unpredictable” should be better qualified. This component is unpredictable conditional on our knowledge. Actually, some components of the observed process could be predictable, if we had better information. As a concrete example, consider demand spikes due to trade promotions, as observed by a manufacturer who is not informed in advance by retailers.
7 It is also standard procedure to include a cycle component, which we will formally disregard, as it can be subsumed by other components. The name “cycle” stems from its link with economic cycles.
8 We should mention that moving averages are also used in some static decomposition algorithms, as a preliminary step to smooth data and expose trend and seasonality components.
9 Moving averages of stock prices are used in many trading strategies based on technical analysis, whether you believe in them or not.
10 In fact, exponential smoothing with α = 1 is equivalent to moving average with k = 1.
11 See Section 7.4.4.
12 To be precise, Eq. (11.22) applies only if the forecast horizon does not exceed the cycle length, i.e., if h ≤ s; a more general formulation is  , where [x] is the “floor” operator, rounding down x to the nearest integer.
, where [x] is the “floor” operator, rounding down x to the nearest integer.
13 The denominator in Eq. (11.28) is related to the estimate of autocovariance. In the literature, sample autocovariance is typically obtained by dividing the sum by T, even though this results in a biased estimator. If we divide by T - k, we might obtain an autocovariance matrix which is not positive semidefinite; see pp. 220–221 of Brockwell and Davis [3].
14 This need not be the case, as we are working with sample autocorrelations. Nevertheless, at least for significant values, we observe a monotonic behavior consistent with Eq. (11.34).
15 To be precise, this representation requires that the two polynomials φ(B) and θ(B) satisfy some additional technical conditions that are beyond the scope of this book.
16 In principle, with a high-order model and a small fit sample, we could lack some observation in the past; however, in this case, the real trouble comes from poor parameter estimates.
17 See, e.g., chapter 5 of Brockwell and Davis [3], where the recursive nature of time series forecasting is aptly illustrated.