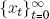. Table 21.1 lists the main parameters of the model and their units.The Model
In a small country there lives an immortal representative household that gets utility from two nonstorable consumption goods. The household faces cash-in-advance constraints.1 “Cash” consists of a large and a small denomination coin, each produced by a government-regulated mint that stands ready to coin any silver brought to it by household-owned firms. The government specifies the amounts of silver in large and small coins, and also collects a flat-rate seigniorage tax on the volume of newly minted coins; it rebates the revenues in a lump sum. Coins are the only storable good available to the household. The firm can transform either of two consumption goods into the other one-for-one and can trade either consumption good for silver at a fixed international price. After describing these components of the economy in greater detail, we shall define an equilibrium. For any variable, we let {x} denote the infinite sequence 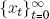. Table 21.1 lists the main parameters of the model and their units.
The household
The representative household maximizes
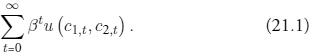
We assume that the one-period utility function is of the form u(c1,t, c2,t) = v[g(c1,t)]+v(c2,t) where v(·) is strictly increasing, twice continuously differentiable, strictly concave, and satisfies the Inada condition limx→0 v′(x) = +∞. For illustrative purposes we will sometimes use v(·) = log(·). The function g is monotonic, twice continuously differentiable, and satisfies g(0) = 0 and g(x) = x + α with α > 0 for x greater than some small number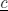 
.2 We use consumption of good 1, c1, to represent “small” purchases, and c2 to stand for “large” purchases.
| Variable | Meaning | Units |
| ϕ | world price of silver | oz silver / cons good |
| b1 | intrinsic content of penny | oz silver / penny |
| b2 | intrinsic content of dollar | oz silver / dollar |
| γ1 | melting point of penny | pence / cons good |
| γ2 | melting point of dollar | dollars / cons good |
| σi | seigniorage rate | (none) |
| b1−1 | mint equivalent of penny | pence / oz silver |
| b2−1 | mint equivalent of dollar | dollars / oz silver |
| m1 | stock of pennies | pence |
| m2 | stock of dollars | dollars |
| e | exchange rate | pence / dollar |
| p | price of cons goods | pence / cons good |
There are two kinds of cash: pennies, whose stock is m1, and dollars, whose stock is m2. Each stock is measured in number of coins, pennies or dollars. Both coins can be used for large purchases, but only pennies can be used for small purchases.3 A dollar exchanges for et pennies. Thus, the cash-in-advance constraints are:
where pt is the penny price of good i. We call (21.3) the “penny-in-advance” constraint. The household’s budget constraint, expressed in pence, is
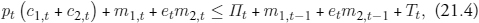
where Πt denotes the firm’s profits measured in pence, and Tt denotes lump sum transfers from the government, both items that will be described shortly.
The household faces given sequences {p}, {e}, {Π}, {T}, begins life with initial conditions m1,−1, m2,−1, and chooses sequences {c1}, {c2}, {m1}, {m2} to maximize (21.1) subject to (21.2), (21.3), and (21.4).
Production
A household-owned, profit-maximizing firm carries out two activities: it sells consumption goods to the household, and also makes decisions about minting and melting.
Production of goods
The firm owns an exogenous sequence of an endowment {ξ} from which goods can be produced. Furthermore, one unit of either consumption good can be traded in the international market for ϕ > 0 units of silver,4 leading to the following restrictions on feasible allocations:
where c1,t ≥ 0, c2t ≥ 0 and St stands for the net exports of silver from the country. 5
Production of coins
Stocks of coins evolve according to
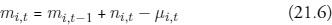
where ni,t ≥ 0, μi,t ≥ 0 are rates of minting and melting of pennies, i = 1, and dollars, i = 2. These rates are chosen by the firm. The absence of any upper bound on the rate of minting embodies “free” or “unlimited” minting.
Coins are melted or minted to finance net exports of silver in the amount
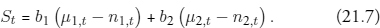
Net exports of silver St correspond to net imports of φ–1St of consumption goods.
Government
The government sets bi, the number of ounces of silver in a penny, i = 1, and in a dollar, i = 2. It also levies a seigniorage tax on minting: for every new coin of type i minted, the government charges a flat tax at rate σi > 0.
The quantities 1/b1 and et/b2 (measured in number of pence per minted ounce of silver) are called by Redish (1990) “mint equivalents.” The quantities (1 − σ1)/b1, et(1 − σ2)/b2 are called “mint prices,” and equal the number of pennies paid out by the mint per ounce of silver.
Depending on citizens’ minting decisions, the government collects revenues Tt in the amount
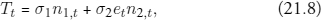
which are rebated in lump-sum fashion to the household. Below we shall describe other interpretations of σi partly in terms of the mint’s costs of production. The only modification that these alternative interpretations require would be to alter (21.8).
Timing
The firm receives the endowment, sells it, mints and melts, pays seigniorage, and pays all earnings to the household at the end of each period.
We adapt the usual shopper-worker decomposition of the household to support the following within-period timing of events at t. We use a small country interpretation of the “technology” for transforming consumption goods from and into silver. First, the household separates into a shopper and a worker. The worker owns the firm, which receives the endowment ξt and net imports of goods ϕ−1 St. The firm converts ξt + ϕ−1 St into c1,t and c2,t subject to equation (21.5), and sells the goods subject to the cash-in-advance constraints to the shopper. The firm then mints and melts coins and uses the net proceeds of metal to settle its import account. The firm pays the seigniorage tax to the government, which immediately transfers the proceeds to the household as Tt. Finally, the firm pays its net nominal proceeds (m1,t and m2,t) to the “worker.” At the end of the period, the firm has nothing, while the household gets the goods that it consumes and money stocks that it will carry into period t+1.
The firm’s profit measured in pence is
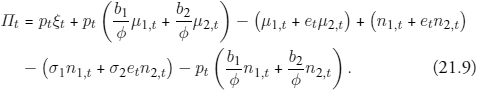
The first term measures revenues from the sale of the endowment. The next terms are melting revenues (the value of the silver in the melted coins), followed by melting expenses (the number of coins melted), minting revenues (the number of coins minted), seigniorage payments on new minting, and minting expenses (the value of the silver turned into coins).
In every period t, the firm takes the prices (pt,et)as given and chooses minting and melting n1,t, n2,t, μ1,t, μ2,t to maximize (21.9) subject to (21.6).
Equilibrium
A feasible allocation is a triple of sequences {c1}, {c2}, {S} satisfying (21.5). A price system is a pair of sequences {p}, {e}. A money supply is a pair of sequences {m1}, {m2} satisfying the initial conditions (m1,−1, m2,−1). An equilibrium is a price system, a feasible allocation, and a money supply such that given the price system, the allocation and the money supply solve the household’s problem and the firm’s problem.
Analytical strategy
We proceed sequentially to extract restrictions that our model places on co-movements of the price level and the money supply. The firm’s problem puts some restrictions on these co-movements, and the household’s problem adds more.
The firm’s problem
The firm’s problem puts restrictions on the price level in the form of two intervals. Define γi = ϕ/bi and rearrange (21.9):
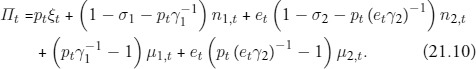
Each period, the firm chooses ni,t, μi,t to maximize Πt subject to non-negativity constraints ni,t ≥ 0, μi,t ≥ 0 and to the upper bound on melting: mi,t−1 ≥ μi,t, for i = 1, 2. The form of (21.10) immediately implies the following no-arbitrage conditions:6
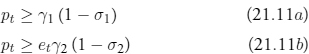
and the following first-order conditions:
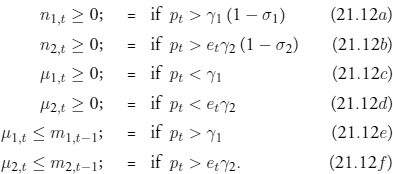
Implications of the arbitrage conditions for monetary policy
The no-arbitrage conditions (21.11) place a lower bound on the price level. Furthermore, the first-order conditions constrain the mint’s policy if both coins are to exist.7 The constraints put pt within both of two intervals, [γ1(1 − σ1), γ1] (corresponding to pennies) and [etγ2(1 − σ2), etγ2] (corresponding to dollars), as illustrated in figure 21.1. Only when the price level pt is at the lower end of either interval might the associated coin be minted. Only when the price is at the upper end might that coin be melted.
Thus, if the lower ends of the intervals do not coincide (i.e., if γ1(1 − σ1) ≠ etγ2(1 − σ2)), then only one type of coin can ever be minted. Equating the lower ends of the intervals (by the government’s choice of (bi, σi)) makes the mint stand ready to buy silver for the same price, whether it pays in pennies or dollars. If the upper ends of the intervals don’t coincide, then one type of coin will be melted before the other. Equating the upper ends of the intervals makes the ratio of metal contents in the two coins equal the exchange rate: e = b2/b1. In such a case, pennies are said to be “full-bodied.”
Figure 21.1 Constraints on the price level imposed by the arbitrage conditions.
Household preferences and equations (21.2) and (21.3) imply that pt ≤ max{etγ2, γ1} (both monies cannot disappear) and etγ2 ≤ γ1 (pennies cannot disappear). If this last inequality is strict, the intrinsic content of pennies is less than proportionate to their value in dollars, in which case pennies are “light” or “overvalued.”
Thus, if pennies are not full-bodied, a sufficient rise in the price level will make large coins disappear. If the mint prices differ, a sufficient fall in prices will prompt minting of only one of the two coins. The perpetual coexistence of both coins in the face of price fluctuations requires that pennies be full-bodied and that equal mint prices prevail for both coins; that is, the intervals must coincide, and therefore the seigniorage rates must be equal. This is not possible if we reinterpret the σi ’s in terms of the production costs for the two types of coins, because per unit of value it is cheaper to produce large than small denomination coins.
Interpretations of σi
In using (21.8), we have interpreted σi as a flat tax rate on minting of coins of type i. But so far as concerns the firm’s problem and the arbitrage pricing restrictions, σi can be regarded as measuring all costs of production borne by the mint, including the seigniorage it must pay to the government. On this interpretation, in setting σi, the government names the sum of the seigniorage tax rate and the mint’s costs of production. If a government were unwilling to subsidize production of coins, then the costs of production would serve as a lower bound on σi.
The government could decide to set gross seigniorage σi to 0, by subsidizing the mint. In this circumstance, our two coins could coexist only if pennies were full-weight (their intrinsic content being proportional to their face values), and if the price level never deviated from γ1 = eγ2.
We discussed earlier the attitudes of medieval writers as well as the actual policies followed by governments. One tradition of thought advocated setting σi = 0, but it was not followed in practice until the seventeenth century; other jurists thought that σi should remain close to production costs, except in cases of clearly established fiscal emergency.
On the other side, restraints were placed on the government’s freedom to set σi by potential competitors to the mint, such as counterfeiters or foreign mints, and by the government’s ability to enforce laws against counterfeiting and the circulation of foreign coins. Let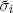 
be the production costs for counterfeiters, or for arbitrageurs taking metal to foreign mints and bringing back coins (inclusive of transport costs). A wide gap between σi and 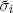was difficult to maintain unless a government’s enforcement powers were strong. If they were not, 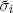placed an upper bound on σi. 8
A government could maintain positive seigniorage if the costs of production of licensed mints were smaller than those of competitors. For example, Montanari ([1683] 1804, 114) argued that the death penalty for counterfeiting, while impossible to enforce strictly, adds a risk premium to counterfeiters’ wage bill, thereby increasing 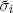when the same technology is used by all. Furthermore, if a government were able to restrict access to the mint’s technology, or if it could secure the exclusive use of a better technology, it could set seigniorage above the mint’s production costs, up to the level of competitors’ costs.
Per coin production costs differed between small and large denomination coins. The medieval technology made it significantly more expensive to produce smaller denomination coins.9 In situations that tied the σi ’s to the costs of production, different production costs implied different widths of our no-arbitrage intervals. This meant either that pennies had to be less than full-bodied or that the mint prices differed. In either case, price level fluctuations could arrest production or, by stimulating melting, cause the disappearance of one coin.
Full-weight and underweight coins
So far, our model assumes that all coins of a given denomination are of the same weight. Actual coins deteriorated over time. One cause was wear and tear, that is, physical and chemical alteration inevitably resulting from handling in trade. A coin owner could purposefully make a coin deteriorate through sweating, clipping, or shaving. Sweating is an artificial form of abrasion in which the losses are collected, while clipping and shaving are outright removal of pieces of metal from the edges of the coin.
Wear and tear can, by itself, be consequential. Figure 21.2 plots estimates of wear for coins in nineteenth-century Britain, France, Canada, and the United States. Estimates for medieval abrasion on English silver coinage are from 0.2 to 0.3% per annum (estimates of Grierson and Mayhew cited in Lane and Mueller 1985, 24 n1), a rate comparable to those observed in the nineteenth century. Such rates of abrasion deprive coins of 10 to 20% of their weight after 30 years.
Figure 21.2 Annual rate of loss for various denominations, based on coin surveys in Britain (1833, 1868, 1881), France (1868, 1884), Canada (1914), and the United States (1886). The coin denominations are converted to British shillings. Sources: Nanteuil (1928) for France; Grierson (1963) for Britain; U.S. Mint (1886, 119) for the United States; U.K. Mint (1914, 168) for Canada.
We can incorporate the presence of underweight coins in our model, following Sargent and Smith (1997). Assume that, at any time t, the stock of small coins m1,0 is composed of coins containing their legal weight in silver b1, and of coins containing δb1, with δ ∈ (0, 1). The stock of full-weight coins is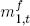 
and that of underweight coins is 
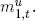Only full-weight coins can be minted. Both coins can be melted for their respective silver contents. In the cash-in-advance and penny-in-advance constraints (21.2) and (21.3), only the total stock 
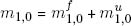enters as before, with no distinction made in the purchases of goods between the two types of coins.
The only required modification to the model occurs in the firm’s profit function and its first-order conditions. Let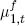 
and 
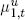be the number of full-weight and underweight coins melted, respectively: then (21.12c) is replaced by:
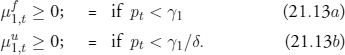
The interval for small coins is modified: it now has two melting points, one for full-weight coins at γ1, the other for underweight coins at γ1/δ. The price level can now rise above γ1 without leading to a complete disappearance of small coins: but the heaviest coins are melted down first. The result is a broader interval, as if σ1 were larger, but with possible changes in the stock of small coins within the broader interval.
Below, we shall typically assume that only full-weight coins exist. We shall make it clear when we do admit underweight coins in order to use our model to shed light on British monetary controversies of about 1695.
The household’s problem
We have extracted the preceding restrictions from the requirement that equilibrium prices should not leave the firm arbitrage opportunities. We now turn to additional restrictions that the household’s optimum problem imposes on equilibrium prices and quantities.
The household chooses sequences {c1}, {c2}, {m1}, {m2} to maximize (21.1) subject to (21.4), (21.2) and (21.3), as well as the constraints mi,t ≥ 0 for i = 1, 2. Attach Lagrange multipliers λt, ηt, θt and νi,t, respectively, to these constraints. Using the notation ui,t = ∂u(c1,t, c2,t)/∂ci, the first-order conditions are:
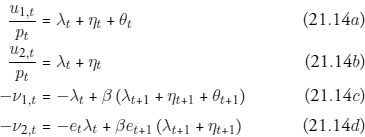
with corresponding relaxation conditions. Conditions (21.14a–c) lead to the following:
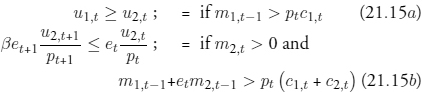
Multiplying (21.14c) by et+1, subtracting it from (21.14d), rearranging, and imposing that ν1,t = 0 (because of the Inada conditions on u), we find:
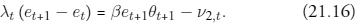
Suppose θt+1 > 0 and ν2,t = 0: this implies that et+1 > et. In words, if the penny-in-advance constraint is binding and positive holdings of dollars are carried over from t to t + 1, dollars must appreciate in terms of pennies from t to t +1.
The intuition for this paradoxical result is as follows. The household holds money from t to t + 1, and also wishes at t + 1 that it had held a higher proportion of pennies (i.e., if [21.3] is binding at t + 1), yet it chose not to. It must be that pennies were dominated in rate of return by dollars, that is, et+1 > et. Thus shortages of pennies occur only after dollars dominate pennies in rate of return.
To describe the rate of return on pennies further, write (21.14c) and (21.14d) at t, and (21.14a) and (21.14b) at t +1, and make the necessary substitutions (recalling that ν1,t = 0) to find that, if m2,t > 0:
In models with only one cash-in-advance constraint but two currencies, this equation holds with equality. Inequality (21.17) embodies a form of one-sided exchange rate indeterminacy and makes possible a class of equilibrium exchange rate paths along which the small change is not appreciating relative to large coins.
Having set out the equilibrium conditions, in the next chapter we use back-solving to create some equilibrium examples.
1 The model modifies Sargent and Smith (1997), which in turn modified Lucas (1982) and Lucas and Stokey (1987). See Barro (1979), Sargent and Wallace (1983), and McCallum (1989) for other models of commodity money.
2 The composition with the function g makes preferences nonhomothetic and assures that Inada conditions hold for both c1 and c2. Such restrictions on preferences could also be represented in a variety of alternative ways. The behavior of g in the interval (0,
) accounts for the curvature of the expansion paths in Figures 22.1 and 22.3. We shall typically assume that equilibrium outcomes occur at consumption allocations for which g(x) = x + a, for example, in the the arguments on pages 353, 357, and 362.
3 The assumption that pennies can be used for the same purchases as dollars is motivated by several episodes in history during which small denominations overtook the monetary functions of large denominations with great ease (see for example chapter 14).
4 Alternatively, there is a reversible linear technology for converting consumption goods into silver.
5 Equation (21.5) can be recovered from the budget constraints holding at equilibrium prices, as usual. By substituting IIt = ptξt, (21.8), and (21.6) into (21.4) we obtain
pt (c1,t + c2,t) ≤ ptξt + μ1,t + etμ2,t − (1 − σ1) n1,t − et (1 − σ2) n2,t.
Using the no-arbitrage conditions (21.12) in this expression and rearranging leads to
c1,t + c2,t ≤ ξt + [γ1−1 (μ1,t − n1,t) + γ2−1 (μ2,t − n2,t)],
where γi = ϕ/bi. The term in square braces equals net imports of consumption goods.
6 These restrictions must hold if the right side of (21.10) is to be bounded (which it must be in any equilibrium); their violation would imply that the firm could earn unbounded profits.
7 See the related discussion in Usher (1943, 197–201).
8 See Usher (1943, 201): “Seigniorage presented no special problem unless the amount exceeded the average rate of profit attractive to gold and silversmiths, or to mints in neighboring jurisdictions. Beyond this limit, the effective monopoly of coinage might be impaired by illegal coinage of essentially sound coins, or by the more extensive use of foreign coin.”
9 This was true of competitors’ costs as well: Montanari notes that the risk premium induced by the death penalty is the same across denominations. For arbitrageurs taking metal to foreign mints, transportation costs made the operation worthwhile only for the larger coins; the near-uniformity of medieval seigniorage rates on gold coins, contrasted with much greater variation on smaller coinage, bears this out.
