1
The Complete Guide to Quantum Mechanics (Abridged)
Everything You’ve Ever Wanted to Know, and a Few Things You Didn’t
Here’s what I’ve learned over the past forty years or so.
Nature is lumpy, not smooth and continuous
We now know that all matter is composed of atoms. And each atom is in turn made up of light, negatively charged electrons ‘orbiting’ a nucleus consisting of heavy, positively charged protons (two up quarks and a down quark), and electrically neutral neutrons (one up quark and two down quarks).* Atoms are discrete. We can say that they are ‘localized’. Atoms are ‘here’ or ‘there’. In itself this is not particularly revelatory.
But despite what a few ancient Greek philosophers had argued, two and a half thousand years before, towards the end of the nineteenth century atoms were really rather controversial. After all, why believe in the existence of atoms when you can never hope to see them or gain any kind of evidence for them?
In fact, it was a determination to refute the existence of atoms that led Max Planck to study the properties and behaviour of so-called ‘black-body’ radiation trapped inside cylindrical vessels made from platinum and porcelain.* When such a vessel is heated, its interior glows like a furnace. As the temperature rises, the light radiation released inside glows red, orange-yellow, bright yellow, and ultimately brilliant white. Planck was interested in finding a theory to describe the variations in the pattern and intensities of different frequencies (or wavelengths, or colours) of the radiation as the temperature is raised.
What Planck found in an ‘act of desperation’ in 1900 turned him into a committed atomist, but it took a few more years for the real significance of his discovery to sink in. Planck had concluded that the radiation inside the cavity is absorbed and emitted by its walls as though it is composed of discrete bits which he called quanta. This is summarized in an equation now known as the Planck–Einstein relation:
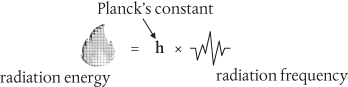
This might not seem very profound. But think about it. Radiation frequency is smoothly and continuously variable—there are no sudden jumps or breaks in the rainbow spectrum of colours: instead they blend seamlessly from one colour to another. If energy = radiation frequency, then this would imply that energy too must be smooth and continuous. But this is not what Planck had found. For any given frequency Planck’s constant (represented by the letter h) represents the smallest amount of energy that can be absorbed or emitted by an object. Energy isn’t taken up or given out smoothly and continuously by the object, but rather in discrete bits determined by h. Planck’s constant is the telltale sign of all things quantum.
Planck initially attributed this behaviour to the atomic nature of the material that formed the walls of the vessels. But it was Einstein who really launched the quantum revolution when in 1905 he rather outrageously suggested that the radiation itself is ‘quantized’ in localized, discrete bits or lumps of energy. This is Einstein’s ‘light-quantum’ hypothesis, and it is the reason why we refer to the above relation today using both Planck and Einstein’s names. He was right, of course. We now know these lumps of light-energy as photons.
So it’s not only matter that comes in lumps, but also radiation. Put more and more energy into an electron inside an atom and it will ‘orbit’ the nucleus at greater and greater average distances until it is ripped out of the atom completely. But you can’t increase this energy smoothly and continuously. The electron will absorb energy only at very discrete intervals organized in an atomic spectrum (see Figure 1).
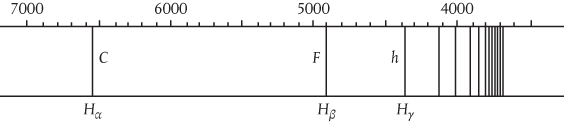
Figure 1 This picture shows a series of lines in the atomic spectrum of hydrogen, which consists of a single proton orbited by a single electron. Energy increases from left to right, and the spectrum shows that energy is not absorbed or emitted continuously, but only in discrete amounts. This spectrum appears in a 1910 textbook Lærebog i Physik, by Christian Christiansen, who taught Niels Bohr at the University of Copenhagen. Wavelengths are recorded in ångstroms (tenths of a nanometre or billionth of a metre) along the top, with the characteristic spectral lines Hα (656.3 nanometres—red), Hβ (486.1 nanometres—blue) and Hγ (434.0 nanometres—violet) clearly marked.
These intervals form a ladder with rungs in a distinctive pattern. It was Niels Bohr in 1913 who figured out that this pattern is characterized by one or more quantum numbers and, unlike a real ladder, the quantum rungs get closer and closer together the higher in energy you go. Pump just the right amount of energy into an electron in an atom, sufficient to climb from one rung to the next, and the electron’s orbit appears to change discontinuously, in a ‘quantum jump’.
So far as we know, there is nothing in reality that isn’t quantized, possibly including space and time.
Waves are particles and particles are waves
I have to admit that French physicist Louis de Broglie is a bit of a hero of mine. He seems to have had little impact on science after winning the Nobel Prize in 1929, but his contribution six years earlier was more than enough to leave a lasting mark on human history.
Einstein’s light-quantum hypothesis was greeted with considerable scepticism at the time. When he was recommended for membership in the prestigious Prussian Academy of Sciences in 1913, its leading members—Planck among them—acknowledged his remarkable contributions to physics, which by this time included his special theory of relativity (the general theory would follow a few years later). In accepting his nomination, they were prepared to forgive his lapses of judgement: ‘That he may sometimes have missed the target in his speculations, as, for example, in his hypothesis of light-quanta, cannot be really held too much against him, for it is not possible to introduce really new ideas even in the most exact sciences without sometimes taking a risk.’1
But in his short paper, Einstein had suggested that it might be possible to gain evidence for the quantum nature of light by studying the photoelectric effect. Shine light on metal surfaces of a certain frequency and intensity and electrons will get kicked out. Now, the energy of a classical wave is related to its amplitude—the height of its peaks and depths of its troughs—think of the difference between gently rolling surf and a tsunami. This energy is reflected in the intensity of the wave or, if you prefer, its brightness. If, as everybody believed, light is described purely in terms of waves, then increasing the light intensity increases the energy and should therefore smoothly increase the number and energies of the electrons ejected from the surface.
But this is not what was observed in early experiments. The Planck–Einstein relation suggests that it is the light frequency—not the intensity—that is all important. Light of the wrong frequency, no matter how intense, just won’t cut it. Only light-quanta (photons) with sufficient energy will knock the electrons from the surface. Increasing the intensity of the light simply increases the number (but not the energies) of the ejected electrons.
At the time this kind of behaviour was very counterintuitive, but it was nevertheless shown to be correct in further experiments performed about ten years later, and led to the award of the Nobel Prize in Physics to Einstein in 1921.
This was a great achievement, but it also posed a big problem. There was an already well-established body of evidence in favour of a wave theory of light. Push light of a single colour through a narrow aperture or slit, cut with dimensions of the order of the wavelength of the light, and it will squeeze through, bend around at the edges and spread out beyond. It ‘diffracts’. A photographic plate exposed a short distance away will reveal a diffuse band, rather than a narrow line with the same dimensions as the slit.*
Cut two slits side by side and we get interference—evidenced by alternating bright and dark bands called interference fringes. As the waves from both slits spread out and run into each other, where wave peak meets wave peak we get a bigger peak (which we call constructive interference), and where peak meets trough we get cancellation (destructive interference)—see Figure 2a. Constructive interference gives rise to the bright fringes. Destructive interference gives rise to the dark fringes. This kind of behaviour is not limited to light—such wave interference is fairly easily demonstrated using water waves, Figure 2b.

Figure 2 (a) When passed through two narrow, closely spaced slits, light of a single wavelength produces a pattern of alternating light and dark fringes. These can be readily explained in terms of a wave theory of light in which overlapping waves interfere constructively (giving rise to a bright fringe) and destructively (dark fringe). (b) Such interference is not restricted to light, and can be fairly easily demonstrated with water waves.2
But waves are inherently delocalized: they are here and there. Einstein’s light-quantum hypothesis didn’t negate all the evidence for the delocalized wave-like properties of light. What he was suggesting is that a complete description somehow needs to take account of its localized particle-like properties, too. He had some ideas about how this might be done, and we’ll come to consider these later on in this book.
Okay, so light exhibits some peculiar behaviours, but matter must surely be different. It’s fairly straightforward to show that material particles such as electrons behave pretty much how we would expect. For example, we observe distinct tracks in a device called a cloud chamber—see Figure 3a.† This picture shows a bright track left by a positively charged alpha particle (the nucleus of a helium atom, consisting of two protons and two neutrons), and a series of fainter tracks left by negatively charged electrons, their curved motions caused by the application of a magnetic field.

Figure 3 (a) Tracks caused by the motions of an alpha particle and electrons ejected from a rod of radioactive thorium inside a cloud chamber. (b) A two-slit interference pattern generated using electrons.
The simplest explanation for such tracks is that they trace the paths or trajectories of individual particles as they pass through the chamber.
And here we come to de Broglie’s historically profound insight. Why force a distinction? If light waves can also be particles (photons, though this name hadn’t yet been coined), could particles like electrons also be waves? The idea seems completely absurd and, indeed, some physicists dismissed it as ‘la Comédie Française’. We’re so used to thinking of elementary particles like electrons as small, localized bits of charged matter that to imagine them any other way requires some considerable mental effort.
Readers familiar with televisions in the days before plasma and LCD screens may recall that these consisted of one or more electron or ‘cathode ray’ guns, each of which would produce a beam of electrons. The beams were then accelerated and modulated to produce broadcast images on a phosphorescent screen.
So, imagine we pass a narrow beam of electrons through a plate in which we’ve cut two small, closely spaced holes or slits.
Our instinct might be to imagine that in a two-slit experiment, the electrons in the beam will follow paths through either one slit or the other, like machine-gun bullets, producing two bright lines on the screen marking where the electrons have passed through. We would expect each line to be brightest in the centre, showing where most of the electrons have passed straight through the corresponding slit unimpeded, becoming a little more diffuse as we move away, signalling electrons that have caught the edges of the slit and scattered on their way through. But these experiments have been done, and this is not what we see. Instead of two bright lines characteristic of particles following straight paths through the slits, we get a two-slit interference pattern—Figure 3b.
Electrons can also be waves.
De Broglie’s idea was just that—an idea. He was able to develop a direct mathematical relationship between a wave-like quantity—wavelength—and a particle-like quantity—linear momentum*—such that

But this was not a fully fledged wave theory of matter. That challenge fell to Erwin Schrödinger, whose formulation—first published early in 1926 and called wave mechanics—is still taught to science students today.
Everything we think we know about a quantum system is supposed to be summarized in its wavefunction
Schrödinger’s theory is really the classical theory of waves in which we make use of the de Broglie relation to substitute wavelength for linear momentum. This requires a bit of mathematical sleight of hand and some assumptions that prove to be unjustified. Although Schrödinger published a much more obscure derivation, this is what it really boils down to. The result is Schrödinger’s wave equation.
It’s helpful to stop and think about this for a minute. The classical wave equation features a wavefunction, which you can think of as describing a familiar sine wave, oscillating smoothly and continuously between peak and trough. The wave equation then describes the motion of this wave in space and time. Into this, we’ve now injected Planck’s constant and linear momentum, a very particle-like property. If we adopt the classical expression for momentum as mass × velocity, you can see that this is now a wave equation that features something that has a mass, and this gets incorporated into the solutions of the equation—the wavefunctions.
How can a wave have mass? This is just one mind-bending consequence of wave–particle duality. And we’re just getting started.
What’s quite fascinating about all this is that, right from the very beginning, physicists were scratching their heads about Schrödinger’s wavefunction. It’s pretty obvious how the wavefunction should be interpreted in classical wave theory but, aside from now featuring particle-like properties such as mass and momentum, in Schrödinger’s wave mechanics the wavefunction had taken on an altogether different significance.
In classical mechanics, there are no real issues with the way we interpret the concepts represented in the theory. We think we know what mass is. We know what velocity and acceleration are. These are things we observe directly—by simple observation we can tell the difference between something moving slowly and something moving fast. When we put our foot down and go from nought to sixty in some incredibly short time, or when we loop the loop on a rollercoaster, we feel the acceleration. We can calculate linear momentum and we know what this means. These things, called physical ‘observables’, sit right on the surface of the classical equations of motion. We don’t have to dig any deeper for some kind of hidden meaning for them. It’s obvious what they are and how they should be interpreted.
But now look at what Schrödinger’s wave mechanics asks us to do. You want to know the linear momentum of an electron moving freely through a vacuum? Then you need to solve the wave equation and identify the relevant wavefunction, determine the rate of change of this wavefunction in space, and multiply the result by minus the square root of minus 1 times Planck’s constant divided by 2π.* This procedure returns the linear momentum multiplied by the wavefunction, from which we can then deduce the momentum.
In Schrödinger’s wave mechanics (and, more generally, in quantum mechanics), we calculate observables such as momentum and energy by performing specific mathematical operations on the relevant wavefunction. Such manipulations are then summarized collectively as operators for the observables. The operators are mathematical recipes, which we can think of as ‘keys’ which unlock the wavefunction (depicted below as a box), releasing the observable before closing again. The logic is as follows:
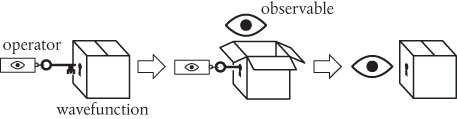
The description given in the paragraph above summarizes the mathematical operator (the key) for linear momentum in quantum mechanics. There’s one further small step. I won’t give the details here, but it is quite straightforward to deduce something called the expectation value of the operator, which is a kind of average value. It has the helpful property that
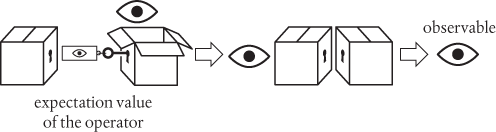
When two identical boxes face off against each other as ‘mirror images’, as shown above, and if everything is being done properly, then these combine together to produce the result 1. This leaves us with just the observable, so the expectation value provides a useful recipe for calculating the values of observables such as momentum and energy.
Whoa. You don’t need to be a rocket scientist to realize that something has fundamentally changed. It’s as though nature has chosen to hide its secrets in the quantum wavefunction, hence the locked box pictogram. To discover the value of an observable, we need to open the box with the right key (the operator). Opening the box with one kind of key gives us one kind of observable, such as momentum. A different observable will require a different key.
We never had to do anything like this in classical mechanics. The observables were always right there, in front of us, staring us in the face.
No, seriously, electrons really do behave like waves
At this point I want to bring you back to the electron interference pattern shown in Figure 3b. We might shrug our shoulders at this, and acknowledge the wave nature of electrons without thinking too deeply about what this might mean. But let’s push the experiment a stage further. Let’s wind down the intensity of the electron beam so that, on average, only one electron passes through the slits at a time. What then?
What we see is at first quite comforting. Each electron passing through the slits registers as a single bright dot on the phosphorescent screen, telling us that ‘an electron struck here’. This is perfectly consistent with our prejudices about electrons as particles, as it seems they pass—one by one—through one or other of the slits and hit the screen in a seemingly random pattern—see Figure 4a.

Figure 4 We can observe electrons as they pass, one at a time, through a two-slit apparatus by recording where they strike a piece of photographic film. Photographs (a) to (e) show the resulting images when, respectively, 10, 100, 3,000, 20,000, and 70,000 electrons have been detected.
But wait. The pattern isn’t random. As more and more electrons pass through the slits we cross a threshold. We begin to see individual dots group together, overlap, and merge. Eventually we get a two-slit interference pattern of alternating bright and dark fringes, Figure 4e.
We can quickly discover that if we close one or the other slit or try to discover which slit each individual electron passes through then we will lose the interference pattern. We just get behaviour characteristic of particles following straight-line paths. If we try to look to see how we get wave behaviour, we get particle behaviour. If we don’t look to see how we get wave behaviour, we get wave behaviour. Left to itself, it seems that the behaviour of each electron must somehow depend on the existence of the slit through which it does not pass, which is decidedly odd.
Alternatively, we conclude that the wave nature of the electron is an intrinsic behaviour. Each individual electron behaves as a wave, described by a wavefunction, passing through both slits simultaneously and interfering with itself before striking the screen.
So, how are we supposed to know precisely where the next electron will appear?
The wavefunction gives us only probabilities: in quantum mechanics we can only know what might happen, not what will happen
A wave alternates between positive amplitude, largest at a peak, and negative amplitude, largest at a trough. We calculate the intensity of the wave as the square of its amplitude, which is always a positive number. So, in two-slit interference described purely in terms of waves we imagine a resulting wave which, when squared, produces a pattern which alternates between regions of high intensity (bright fringes) and zero intensity (dark fringes), as shown in Figure 5a.
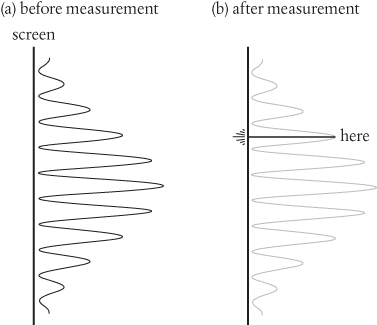
Figure 5 (a) Before measurement, the square of the electron wavefunction predicts a distribution of probabilities for where the electron might be found, spread across the screen. (b) After measurement, the electron is recorded to be found in one, and only one, location on the screen.
But, by its very nature, this pattern of intensity is spread across the screen. It is distributed through space, or delocalized. And yet we know that in the experiment with electrons, as illustrated in Figure 4, we see electrons detected one at a time, as single bright spots, in only one location on the screen. Each electron hitting the screen is localized.
How does this work?
Schrödinger had wanted to interpret the wavefunction literally, as the theoretical representation of a ‘matter wave’. He argued that atoms are simply the diffraction patterns of electron waves captured and wrapped around atomic nuclei. But to make sense of one-electron interference we must reach for an alternative interpretation suggested later in 1926 by Max Born.
Born reasoned that in quantum mechanics the square of the wavefunction is a measure not of the intensity of the electron wave, but of the probability of ‘finding’ its associated electron.* The alternating peaks and troughs of the electron wave translate into a pattern of quantum probabilities—in this location (which will become a bright fringe) there’s a higher probability of finding the next electron, and in this other location (which will become a dark fringe) there’s a very low or zero probability of finding the next electron.
Just think about what’s happening here. Before an electron strikes the screen, it has a probability of being found ‘here’, ‘there’, and ‘most anywhere’ where the square of the wavefunction is bigger than zero.
Does this mean that an individual electron can be in more than one place at a time? No, not really. It is true to say that it has a probability of being found in more than one place at a time and there is definitely a sense in which we think of the electron wavefunction as delocalized or distributed. But if by ‘individual electron’ we’re referring to an electron as a particle, then there is a sense in which this doesn’t exist as such until the wavefunction interacts with the screen, at which point it appears ‘here’, in only one place, as shown in Figure 5b.
That this might be a bit of a problem was recognized in the late 1920s/early 1930s by John von Neumann. If ‘measurement’ is just another kind of quantum process or transition, then von Neumann argued that this suggests a need for a ‘measurement operator’, such that
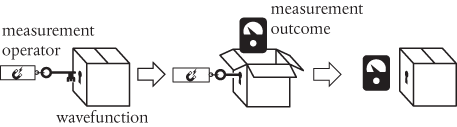
The measurement outcome is then just the expectation value of the measurement operator.
Just like the distributed interference pattern shown in Figure 5a, the wavefunction in question may consist of different measurement possibilities, such as the pointer of the gauge above pointing to the left or to the right. Von Neumann realized that there is nothing in the mathematical structure of quantum mechanics that explains how we get from many possible outcomes to just one actual outcome. So, to ensure that the structure is mathematically robust and consistent, he had no choice but to postulate a discontinuous transition or jump which gets us from the possible to the actual. This postulate is generally known today as the ‘collapse of the wavefunction’. It is absolutely central to the ongoing debate about how quantum theory is to be interpreted.
Quantum probability is not like classical probability
One more thing. That there’s a 50% probability that a tossed coin will land ‘heads’ simply means that it has two sides and we have no way of knowing (or easily predicting) which way up it will land. This is a classical probability born of ignorance. We can be confident that the coin continues to have two sides—heads and tails—as it spins through the air, but we’re ignorant of the exact details of its motion so we can’t predict with certainty which side will land face up.
Quantum probability is thought to be very different. When we toss a quantum coin* we might actually be quite knowledgeable about most of the details of its motion, but we can’t assume that ‘heads’ and ‘tails’ exists before the coin has landed, and we look.
Einstein deplored this seeming element of pure chance in quantum mechanics. He famously declared that ‘God does not play dice’.3
For a specific physical system or situation, there is no such thing as the ‘right’ wavefunction
Physics is a so-called ‘hard’ or ‘exact’ science. I take this to mean that its principal theoretical descriptions are based on rigorous mathematics, not on words or phrases that can often be ambiguous and misleading. But mathematics is still a language, and although we might marvel at its incredible fertility and ‘unreasonable effectiveness’,4 if not applied with sufficient care it is still all too capable of ambiguity and misdirection.
Centuries of very highly successful, mathematically based physics have led us to the belief that this is all about getting the right answer. Nature behaves a certain way. We do this, and that happens. Every time. If the mathematics doesn’t predict that with certainty every time we do this, then we’re inclined to accept that the mathematical description isn’t adequate, and we need a better theory.
In quantum mechanics, we’re confronted with a few things that might seem counterintuitive. But this is still a mathematically based theory. Sure, we’ve swopped the old classical observables such as momentum and energy for mathematical operators which we use to unlock their quantum equivalents from the box we call the wavefunction. But—to take one example—the frequencies (and hence the energies) of the lines in an atomic spectrum are incredibly precise—just look back at Figure 1. If quantum mechanics is to predict what these should be, then surely this must mean discovering the precise expression for the wavefunction of the electron involved?
And it is here that we trip over another of quantum mechanics’ dirty little secrets. There is really no such thing as the ‘right’ wavefunction. All we need is a function that is a valid solution of the wave equation. Isn’t this enough to define the ‘right’ one? No, not really. Whilst there are some mathematical rules we need to respect, we can take any number of different solutions and combine them in what’s known as a superposition. The result is also a perfectly acceptable solution of the wave equation.
I want to illustrate this with an example from the quantum theory of the hydrogen atom, consisting of a nucleus formed by a single proton, ‘orbited’ by a single electron. In fact, this was the problem that Schrödinger addressed in his 1926 paper with such spectacular success. The wavefunctions of lowest energy form spherical patterns around the central nucleus. But there are wavefunctions of modest energy that are shaped like dumbbells. There are three of these.
All three of these solutions of the wave equation are characterized by a set of quantum numbers. Two of these are the same for each of the dumbbell-shaped functions, but the third differs from one to the other, taking values of –1, 0, and +1, as shown in Figure 6a. For now it doesn’t really matter what these quantum numbers represent. Here’s the thing. Whilst these are the ‘natural’ solutions of the wave equation, they’re not the most helpful when we come to think about combining atoms in three-dimensional space to form molecules which, after all, is what chemistry is all about.
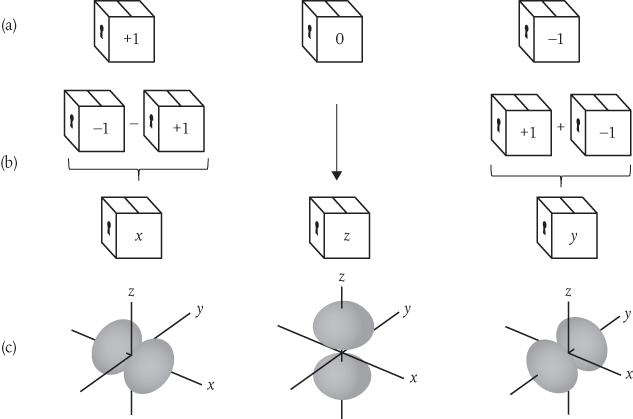
Figure 6 The ‘natural’ solutions of the Schrödinger wave equation for the hydrogen atom include a set of wavefunctions characterized by quantum numbers with values +1, 0, and –1. But it’s often more helpful to combine these in the way shown here, which produces three wavefunctions directed along the three spatial dimensions characterized by Cartesian coordinates x, y, and z. So, which are the ‘right’ wavefunctions?
It’s much easier to deal with wavefunctions defined in three spatial dimensions, using Cartesian x, y, and z coordinates. This is okay for the function characterized by the quantum number 0, as we can simply define this to lie along the z coordinate. But what of the others? Well, this turns out to be relatively easy. To get a wavefunction directed along the y coordinate we form a superposition in which we add the functions corresponding to +1 and –1, as shown in Figure 6b. To get a wavefunction directed along the x coordinate we form a superposition in which we subtract the function corresponding to +1 from the function corresponding to –1. Because we’re combining functions that are known to be solutions of the wave equation, and provided we follow the rules, we can be confident that the superpositions represent valid solutions, too. The resulting functions are shown mapped along the three coordinates in Figure 6c.
But which then are the ‘right’ wavefunctions? Students learn fairly quickly that there really isn’t a straightforward answer to this question. The ‘right’ wavefunction obviously depends on what kind of system we’re dealing with, but we’re free to choose the form that’s most appropriate for the specific problem we’re trying to solve.
Delocalized waves can be combined together in ways that localized particles simply can’t, and we can take full advantage of this in quantum mechanics.
Heisenberg’s uncertainty principle is about what we can know. It is not about what we can only hope to measure
Werner Heisenberg hated Schrödinger’s wave mechanics. Not because the mathematics was dodgy, but because Schrödinger insisted that the wavefunction be taken literally as the physical description of the electron as a matter wave. The trouble is that waves flow smoothly and continuously, and there is no room in this picture for sudden quantum jumps of the kind needed to interpret the transitions that form an atomic spectrum. Schrödinger simply doubled down and denied that the jumps happened at all, proclaiming: ‘If all this damned quantum jumping were really here to stay, I should be sorry I ever got involved with quantum theory.’5
In 1927, Heisenberg realized that the essential discontinuity—the ‘jumpiness’—at the heart of quantum mechanics implies a fundamental limit on what we can discover about the values of pairs of physical observables, such as position and linear momentum. At first, he believed that this limit arises because of an inevitable ‘clumsiness’ involved in making measurements on delicate quantum systems with our large-scale, laboratory-sized instruments. For example, Heisenberg argued, if we want to determine the precise position of an electron in space we need to locate it by hitting it with photons of such high energy that we must forgo any hope of determining the electron’s precise momentum. Any attempt to ‘see’ where the electron is (or, at least, was) will just knock it for six, preventing us from seeing to where and how fast it was going.
But Bohr disagreed, and the two argued, bitterly. Bohr insisted that the uncertainty principle has nothing to do with the clumsiness or otherwise of our measurements. Instead it implies a fundamental limit on what we can know about a quantum system.
Perhaps the simplest way of explaining Bohr’s point relies on the essential duality of waves and particles in quantum mechanics. Think about how we might measure the wavelength of a wave. We could infer the wavelength by counting the numbers of peaks and troughs in a certain fixed region of space. Each wave cycle consists of one peak and one trough, and the wavelength is the distance from the start to the finish of the cycle. So we sum the numbers of peaks and troughs, and divide by two. This tells us the number of cycles in our spatial region. The wavelength is then the length of this region divided by the number of cycles.
Obviously, we will struggle to make any kind of precise measurement if our sample region is shorter than the wavelength. We quickly realize that we can increase the precision by making the region large enough to include lots and lots of cycles. Now, from the de Broglie relation, a precise wavelength gives us a precise measure of linear momentum for the associated particle. But, of course, we’ve deliberately made our sample region large, so we’ve lost any hope of measuring a precise position for the associated particle. It could be anywhere in there.
The opposite is also true. It’s possible to add together a large number of waves in a superposition, each with a different wavelength, such that the wave has a single peak located at a very precise position. Such a superposition is called a ‘wavepacket’. This gives us a fix on the precise position, but now we’ve lost any hope of measuring a precise momentum, because our wavepacket consists of a broad range of wavelengths, implying a broad range of momenta.
Bohr’s view prevailed, and we now write Heisenberg’s uncertainty relation as*
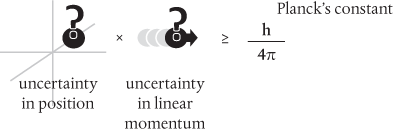
Note that nowhere does this say that measurements of position and momentum are somehow mutually exclusive. We can in principle measure the position with absolute precision (zero uncertainty), but then the momentum would be completely undetermined: it would have infinite uncertainty. There’s nothing preventing us from determining both position and momentum with more modest precision within the bounds of the uncertainty principle.
The principle is not limited to position and momentum. It applies to other pairs of observables. Perhaps the best known relates to energy and time, which we will meet again in Chapter 4. Now, there’s a caveat. There are arguments that the energy–time uncertainty relation actually doesn’t exist except as a variation of that for position and momentum. Early attempts to derive the energy–time relation from first principles proved rather unsatisfactory. To my knowledge, the most widely accepted derivation, published in 1945 by Leonid Mandelstam and Igor Tamm, clearly specifies the interpretation of ‘time’ in the relation as a time interval.
I think this is enough for now. I want you to be clear that what I’ve described so far is based on the ‘authorized’ or ‘official’ version of quantum mechanics taught to science students all around the world. We’ll see in Part II that as the search for meaning has unfolded in the past 90 years or so, some physicists and philosophers have happily challenged this authority, and we shouldn’t assume that the version taught today will still be taught in another 90 years’ time.
Eager readers will also note that I’ve deliberately held back some of the more infamous examples of quantum weirdness—such as Schrödinger’s cat and the Einstein–Podolsky–Rosen experiment. Please be patient: we will come to these in Chapter 4. I first want to give you some context in which to think about them.
To summarize, we’ve seen that experimental discoveries in the first decades of the twentieth century led to the realization that physical reality is inherently lumpy. In the classical mechanics of everyday life, we can safely ignore Planck’s constant and the lumpiness it implies, and assume everything is smooth and continuous. But at the level of molecules, atoms, and subatomic particles, from which everything in the visible universe is constructed, Planck’s constant comes into its own and we can no longer ignore the duality of waves and particles.
De Broglie opened Pandora’s Box in 1923. Schrödinger gave us his wave equation and his wavefunctions a few years later. The all-too-familiar observables of classical mechanics became locked away inside the quantum wavefunction, requiring mathematical operators to liberate them from their prison. Born said that the wavefunctions are utterly inscrutable; they tell us only about quantum probabilities. Heisenberg (and Bohr) explained that the heart of quantum mechanics beats uncertainly. Nature suffers a peculiar arrhythmia.
And then the debates began. What is quantum mechanics telling us about the nature of physical reality? And just what is this thing called reality, anyway?