4
When Einstein Came Down to Breakfast
Because You Can’t Write a Book About Quantum Mechanics without a Chapter on the Bohr–Einstein Debate
Armed with this perspective on the business of scientific theorizing, let’s return to 1927.
Bohr’s debates with both Schrödinger and Heisenberg prompted a period of deep introspection. As we saw in Chapter 1, Schrödinger argued for a realistic interpretation of the wavefunction, in the sense of Proposition #3. For him the wavefunction was something physically meaningful and tangible; it was something that could be easily visualized, a base concept. Heisenberg favoured a much more positivist, or anti-realist interpretation of quantum mechanics. He rejected any suggestion of some kind of underlying wave nature of matter that could be easily visualized, preferring to focus instead only on what can be observed, such as the lines in an atomic spectrum, and the inherent discontinuity and uncertainty that such measurements implied. Bohr hovered between these extremes, perceiving the validity of both descriptions yet puzzled by the fact that he could find no words of his own.
After some reflection, he eventually concluded that the language of classical physics, the language of waves and particles, of causality and continuity, is quite inadequate for describing quantum phenomena. And yet, as intelligent beings experiencing a classical world, this is the only language we have.
Whatever the true nature of the electron-in-itself, the behaviour it exhibits is conditioned by the kinds of experiments we choose to perform. These, by definition, are experiments requiring apparatus of classical dimensions, resulting in effects sufficiently substantial to be observed and recorded in the laboratory, perhaps in the form of tracks in a cloud chamber, or the series of spots on an exposed photographic plate which build up to an interference pattern, as we saw in Figure 4.
So, a certain kind of experiment will yield effects that we interpret, using the language of classical physics, as electron diffraction and interference. We conclude that in this experiment the electron is a wave. Another kind of experiment will yield effects which we interpret in terms of the trajectories and collisions of localized electrons. We conclude that in this experiment the electron is a particle. Bohr reasoned that these experiments are mutually exclusive. We cannot conceive an experiment to demonstrate both types of behaviour simultaneously, not because we lack the ingenuity, but because such an experiment is simply inconceivable.
What we get is a quantum world composed of shadows cast by our classical apparatus (think Plato’s cave). We can see the electron’s wave shadows or we can see its particle shadows. But because we are unable to construct apparatus in anything other than classical dimensions we cannot see what the electron really is: we can never discover anything about the electron-in-itself. What we are left to deal with is a fundamental wave–particle duality, a quantum world whose shadows are consistently different when we choose to cast them in different ways, using different classical apparatus.
Bohr sought to resolve this dilemma by declaring that these very different, mutually exclusive behaviours are not contradictory, they are instead complementary. They are different shadow projections of the same objectively real things-in-themselves.
So, where does this leave Bohr on Proposition #3? This is a good question. Although Bohr was infamously obscure in many of his writings on the subject, and he was much less staunchly empiricist than Heisenberg, on balance I believe it is fair to conclude that Bohr adopted a generally anti-realist interpretation of the wavefunction. Although it’s a bit of a stretch to provide only one Bohr quote in support of this conclusion (especially as this is not even a direct quote), I’ve nevertheless always found this rather telling. He is quoted as saying:1
There is no quantum world. There is only an abstract quantum physical description. It is wrong to think that the task of physics is to find out how nature is. Physics concerns what we can say about nature.
If indeed he ever said it, much has been written about Bohr’s quoted use of the phrase ‘There is no quantum world’, as it seems to suggest that he denied the existence of an objective reality (Proposition #1). I believe this is nonsense, and entirely characteristic of a debate that oversimplifies questions concerning ‘reality’. I attach much greater significance to ‘Physics concerns what we can say about nature’. Bohr’s quote is all about the representation.
This kind of anti-realism is quite subtle. What Bohr is actually saying is that we’re fundamentally limited by the classical nature of our apparatus and our measurements, and the language of classical waves and particles we use to describe what we see. It’s therefore pretty pointless to speculate about the reality or otherwise of elements of the ‘abstract quantum physical description’, including the wavefunction, as we have absolutely no way of discovering anything about them.2
Heisenberg was initially resistant to Bohr’s notion of complementarity, as it gave equal validity to the wave description associated with his rival Schrödinger. As their debate became more bitter and personalized, Wolfgang Pauli was called to Bohr’s institute in Copenhagen in early June 1927 to calm things down and broker a peace. With Pauli’s help, Bohr and Heisenberg agreed to an uneasy reconciliation.
Among the key ingredients in the resulting interpretation of quantum mechanics are Bohr’s notion of wave–particle complementarity, the uncertainty principle, and Born’s quantum probability. It goes without saying that, as far as these physicists were concerned, by 1927 quantum mechanics was already a complete theory, and there was nothing more to be added.
What was remarkable was the zeal with which the disciples of this new quantum orthodoxy embraced and preached the new gospel. Heisenberg spoke and wrote of the ‘Kopenhagener Geist der Quantentheorie’; the ‘Copenhagen spirit’ of quantum theory.3 This has become known as the Copenhagen interpretation although, strictly speaking, there was never really a single ‘interpretation’ that all its advocates bought into. Like scripture, everybody had their own personal views on what it meant.
Einstein didn’t like it at all.
The stage was set for a great debate about the quantum representation of reality. This commenced at the fifth Solvay congress in Brussels, part of a series of invitation-only international conferences on physics supported by the wealthy Belgian industrialist and philanthropist Ernest Solvay. This was the first time the protagonists had an opportunity to gather together, face to face. Born and Heisenberg delivered a joint lecture, declaring that quantum mechanics is a complete theory, ‘whose fundamental physical and mathematical assumptions are no longer susceptible of any modification’.4 Schrödinger then delivered a lecture on wave mechanics. And, following an interruption to allow participants the opportunity to attend a competing conference that had been organized in Paris, Bohr presented a lecture on complementarity.
Then Einstein stood to raise an objection. He was concerned by the implications of physical events which we would now interpret as the collapse of the wavefunction. Look back at Figure 5. Before measurement, the electron wavefunction is distributed across the screen, with a probability of being found in any location where the square of the wavefunction is non-zero—Figure 5a. After measurement, we learn that the electron is ‘here’, in a single location—Figure 5b. However, Einstein now pointed out, we also learn simultaneously that the electron is definitely not ‘there’, where ‘there’ can be any location on the screen where we might have expected to find it.
Einstein argued that this ‘assumes an entirely peculiar mechanism of action at a distance, which prevents the wave continually distributed in space from producing an action in two places on the screen’.5 This would later become widely known as ‘spooky action at a distance’. The particle, which according to the wavefunction is somehow distributed over a large region of space, becomes localized instantaneously, the act of measurement appearing to change the physical state of the system far from the point where the measurement is actually recorded. Einstein felt that this kind of action at a distance violates one of the key postulates of his special theory of relativity: no physical action, or information resulting in physical action, can be communicated at a speed faster than light. Any physical process that happens instantaneously over substantial distances violates this postulate.
We should note right away that all this talk about physical action betrays the fact that these concerns are based on a realistic interpretation of the wavefunction, in the spirit of Proposition #3. This is not to say that Einstein wanted to ascribe reality to the wavefunction in the same way that Schrödinger did (we will see shortly that their views were quite different). But it’s important to realize that, from the outset, the Bohr–Einstein debate involved a clash of philosophical positions. At great risk of oversimplifying, it was a confrontation between realism and anti-realism, between acceptance and rejection of Proposition #3.
What I find quite fascinating is that Einstein was attacking a position that Bohr wasn’t actually defending. But by teasing out the physical consequences of his realist assumptions, Einstein sought to expose inconsistencies with what was fast becoming the standard or default interpretation.
As far as Bohr himself was concerned, the Copenhagen interpretation obliges us to resist the temptation to ask: But how does nature actually do that? Like emergency services personnel at the scene of a tragic accident, Bohr advises us to move along, as there’s nothing to see here. And there lies the rub: for what is the purpose of a scientific theory if not to aid our understanding of the physical world? We want to rubberneck at reality. The only way to do this in quantum mechanics is to take the wavefunction more literally and realistically.
The discussion continued in the dining room of the Hôtel Britannique, where the conference participants were staying. Otto Stern described what happened next:6
Einstein came down to breakfast and expressed his misgivings about the new quantum theory, every time [he] had invented some beautiful experiment from which one saw that [the theory] did not work…. Pauli and Heisenberg, who were there, did not pay much attention, ‘ach was, das stimmt schon, das stimmt schon’ [ah well, it will be all right, it will be all right]. Bohr, on the other hand, reflected on it with care and in the evening, at dinner, we were all together and he cleared up the matter in detail.
Einstein developed a series of hypothetical tests, or gedankenexperiments (thought experiments), based on the presumption of Proposition #3. These were about matters of principle; they were not meant to be taken too literally as practical experiments that could be carried out in the laboratory.
He began by attempting to show up inconsistencies in the interpretation of the uncertainty principle, but each challenge was deftly rebutted by Bohr. However, under pressure from Einstein’s insistent probing, the basis of Bohr’s counterarguments underwent a subtle shift. Bohr was obliged to fall back on the notion that measurements using classical apparatus are just too ‘clumsy’, implying limits on what can be measured, rather than limits on what we can know. This was precisely the position for which he had criticized Heisenberg earlier in the year.
In the eyes of the majority of physicists gathered in Brussels, Bohr won the day. But Einstein remained stubbornly unconvinced, and the seeds of a much more substantial challenge were sown.
‘At the next meeting with Einstein at the Solvay Conference in 1930,’ wrote Bohr some years later, ‘our discussions took quite a dramatic turn.’7
Suppose, said Einstein, we build an apparatus consisting of a box which contains a clock connected to a shutter. The shutter covers a small hole in the side. We fill the box with photons and weigh it. At a predetermined and precisely known time, the clock triggers the shutter to open for a short time interval sufficient to allow a single photon to escape. The shutter closes. We reweigh the box and, from the mass difference and E = mc2, we determine the precise energy of the photon that escaped. By this means, we have measured both the energy and the time interval within which a photon has been released from the box, with a precision that contradicts the energy–time uncertainty relation. This is Einstein’s ‘photon box’ experiment.
Bohr was quite shocked, and he didn’t see the solution right away. He had a sleepless night, searching for the flaw in Einstein’s argument that he was convinced must exist. By breakfast the following morning he had an answer.
On the blackboard Bohr drew a rough, pseudo-realistic sketch of the apparatus that would be required to make the measurements in the way Einstein had described them (Figure 9). In this sketch the whole box is imagined to be suspended by a spring and fitted with a pointer so that its position can be read on a scale affixed to the support. A small weight is added to align the pointer with the zero reading on the scale. The clock mechanism is shown inside the box, connected to the shutter.
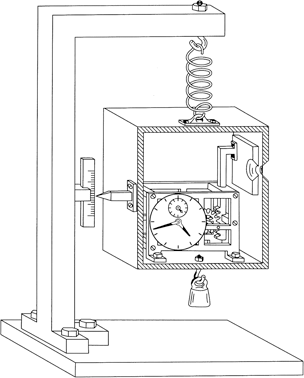
Figure 9 Einstein’s ‘photon box’ gedankenexperiment.
After the release of one photon, the small weight is replaced by another, slightly heavier weight. This compensates for the weight lost through release of the photon so that the pointer returns to the zero of the scale. We suppose that the weight required to do this can be determined independently with unlimited precision. The difference in the two weights required to balance the box gives the mass, and hence the energy, of the photon that was released, as Einstein had argued.
So far, so good.
Bohr now drew attention to the first weighing, before the photon escapes. Obviously, the clock is set to trigger the shutter at some predetermined time and the box is sealed. We can’t look at the clock because this would involve an exchange of photons—and hence energy—between the box and the outside world.
To weigh the box, a weight must be selected that sets the pointer to the zero of the scale. However, to make a precise position measurement, the pointer and scale will need to be illuminated—we need to be able to see it. But this apparatus is required to be extremely sensitive—the position of the box must change on the release of a single photon. So, as photons bounce off the scale, the box can be expected to jump about unpredictably. We can increase the precision of the measurement of the average position of the pointer by allowing ourselves a long time in which to perform the balancing procedure. This will give us the necessary precision in the weight of the box and, since we can anticipate the need for this, the clock can be set so that it opens the shutter only after this balancing procedure has been completed.
Now comes Bohr’s coup de grâce.
According to Einstein’s own general theory of relativity, a clock moving in a gravitational field is subject to time dilation effects. The very act of weighing a clock changes the way it keeps time. As the box bounces upwards, time slows down. As it bounces downwards, time speeds up. So, because the box is jumping about unpredictably in a gravitational field (owing to the act of balancing the weight of the box by measuring the position of the pointer), the rate of the clock is changed in a similarly unpredictable manner. This introduces an uncertainty in the exact timing of the opening of the shutter which depends on the length of time needed to complete the balancing procedure. The longer we make this procedure (the greater the ultimate precision in the measurement of the energy of the photon), the greater the uncertainty in its exact moment of release.
Bohr was able to show that the product of the uncertainties in energy and time for the photon box apparatus is entirely consistent with the uncertainty principle.
Although the photon box experiment would go on to spawn a number of research papers arguing both for and against the validity of Bohr’s counterargument, Einstein conceded that Bohr’s response appeared to be ‘free of contradictions’, but in his view it still contained ‘a certain unreasonableness’.8 At the time this was hailed as a triumph for Bohr and for the Copenhagen interpretation. Bohr had used Einstein’s own general theory of relativity against him.
But note that, once again, Bohr had been obliged to defend the integrity of the uncertainty principle using arguments based on an inevitable and sizeable disturbance of the observed quantum system. At first sight, there seems to be no way around this. Surely, measurement of any kind will always involve interactions that are at least as big as the quantum system being measured. How can a clumsy disturbance possibly be avoided?
Einstein chose to shift the focus of his challenge. Instead of arguing that quantum mechanics—and particularly the uncertainty principle—is inconsistent, he now sought to derive a logical paradox arising from what he saw to be the theory’s incompleteness. Although another five years would elapse, Bohr was quite unprepared for Einstein’s next move.
Despite its seeming impossibility, Einstein needed to find a way to render Bohr’s disturbance defence either irrelevant or inadmissible. This meant contriving a physical situation in which it is indeed possible in principle to acquire knowledge of the physical state of a quantum system without disturbing it in any way. Working with two young theorists, Boris Podolsky and Nathan Rosen, Einstein devised a new challenge that was extraordinarily cunning. They had found a way to do the seemingly impossible.
Imagine a situation in which two quantum particles interact and move apart. These particles may be photons, for example, emitted in rapid succession from an atom, or they could be electrons or atoms. For convenience, we’ll label these particles as A and B. For our purposes, we just need to suppose that, as a result of the operation of some law of conservation, the two particles are produced in a pair of physical states that are opposed. It really doesn’t matter what these states are, so let’s just call them ‘up’, which we denote as ↑, and ‘down’, denoted ↓. So, we imagine a physical process which produces a pair of quantum particles—A and B—in ↑ and ↓ states, such that if A is ↑, B must be ↓, and if A is ↓, B must be ↑.
Here’s the thing. According to quantum mechanics, the correct way to describe this kind of situation is by using a single wavefunction which encompasses both particles and both possible outcomes. Such a pair of particles are said to be entangled.
We follow the mathematical rules and write down an expression for this ‘total wavefunction’ which we express as a superposition of the contributions from the wavefunctions for both possible situations. In doing this we are obliged to include contributions in which A is ↑ and A is ↓, and B is ↑ and B is ↓. But our law of conservation explicitly excludes the possibility of observing pairs in which A and B are either both ↑ or both ↓. We’re therefore left with something like this:

Let’s now suppose that particles A and B separate and move a large distance apart. We make a measurement on either particle to discover its state. As this is a measurement on a two-particle total wavefunction, we are obliged to represent this in terms of the expectation value of the measurement operator acting on the total wavefunction:
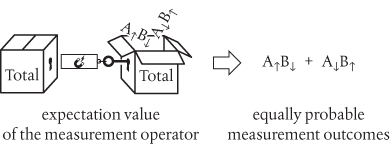
And we see that the outcomes A↑B↓ and A↓B↑ are equally probable. But, of course, for each measurement we will only ever see one outcome, analogous to detecting a single spot as each electron passes, one at a time, through two slits. In a realistic interpretation we must therefore presume that the total wavefunction collapses to deliver only one outcome, either A↑B↓ or A↓B↑, such that in a series of repeated measurements on identically prepared systems we will get A↑B↓ 50% of the time, and A↓B↑ 50% of the time.
Now suppose we make a measurement on A and discover that it is ↑. This must mean that the total wavefunction has collapsed to leave B in a ↓ state. Likewise, if we discover that A is ↓, this must mean that the total wavefunction has collapsed to leave B in an ↑ state. There are no other possible outcomes.
The total wavefunction relates only the probability of getting one outcome or the other, so in principle we have no way of knowing in advance whether A will be measured to be ↑ or ↓. But this really doesn’t matter, for once we know the state of A, we also know the state of B with certainty, even though we may not have measured it. In other words, we can discover the state of particle B with certainty without disturbing it in any way. All we have to assume is that any measurement we make on particle A in no way affects or disturbs B, which could be an arbitrarily long distance away, say halfway across the Universe. We conclude that the state of particle B (and by inference, the state of particle A) must surely have been defined all along.
Devilish, isn’t it?
In their 1935 paper, which was titled ‘Can Quantum-Mechanical Description of Physical Reality be Considered Complete?’, Einstein, Podolsky, and Rosen (EPR) offered a philosophically loaded definition of physical reality:9
If, without in any way disturbing a system, we can predict with certainty (i.e. with a probability equal to unity) the value of a physical quantity, then there exists an element of physical reality corresponding to this physical quantity.
It’s easy to see what they were trying to do. If the wavefunction is interpreted realistically, in accordance with Proposition #3, then it ought to account for the reality of the properties—the physical states of particles A and B—that it purports to describe. It clearly doesn’t. There is nothing in the formulation that describes what these states are before we make a measurement on A, so the theory cannot be complete.
The alternative is to accept that the reality of the state of particle B is determined by the nature of a measurement we choose to make on a completely different particle an arbitrarily long distance away. Whatever we think might be going on, this seems to imply ‘spooky action at a distance’ which is at odds with the special theory of relativity. EPR argued that: ‘No reasonable definition of reality could be expected to permit this.’10
Details of this latest challenge were reported in The New York Times before the EPR paper was published, in a news article titled ‘Einstein Attacks Quantum Theory’. This provided a non-technical summary of the main arguments, with extensive quotations from Podolsky who, it seems, had been the principal author of the paper.
There is much in the language and nature of the arguments employed in the EPR paper that Einstein appears later to have regretted, especially the reality criterion. All the more disappointing, perhaps, as the main challenge presented by EPR does not require this (or any) criterion, though it does rest on the presumption that, whatever we make of reality, it is assumed to be local, meaning that as particles A and B move apart, they are assumed to exist independently of each other. Einstein deplored The New York Times article and the publicity surrounding it.
Nevertheless, this new challenge from Einstein sent shockwaves through the small community of quantum physicists. It hit Bohr like a ‘bolt from the blue’.11 Pauli was furious. Paul Dirac exclaimed: ‘Now we have to start all over again, because Einstein proved that it does not work.’12
Bohr’s response, when it came a short time later, inevitably targeted the reality criterion as the principal weakness. He argued that the stipulation ‘without in any way disturbing a system’ is essentially ambiguous, since the quantum system is influenced by the very conditions which define its future behaviour. In other words, we have to deal with elements of an empirical reality defined not by the quantum system in abstract, but by the quantum system in the context of the measurements we make on it and the apparatus we use. These dictate what we can expect to observe. EPR’s error lies in their presumption that the wavefunction should be interpreted realistically, and the ‘spooky action at a distance’ is simply a consequence of this error. Just don’t ask how nature actually does this, as there really is nothing to see here.
Einstein was, at least, successful in pushing Bohr to give up his clumsiness defence, and to adopt a more firmly anti-realist position. Those in the physics community who cared about these things seemed to accept that Bohr’s response had put the record straight.
Schrödinger wrote to congratulate Einstein shortly after the EPR paper appeared in print. In his letter he highlighted what is, in fact, the principal challenge. When interpreted realistically, the total two-particle wavefunction is necessarily ‘non-local’; it is distributed in just the same way that the electron wavefunction is distributed across the screen in the two-slit experiment. Our instinct is to imagine that, after moving a long distance apart, particles A and B are separated. They are distinct, independently existing, or ‘locally real’ particles. Quantum mechanics has absolutely no explanation for how we get from one situation to the other.
Einstein replied with enthusiasm, and as their correspondence continued through the summer of 1935 a further challenge to what had by now become the orthodox Copenhagen interpretation gradually emerged.
First, Einstein had to deal with Schrödinger’s insistence that the wavefunction be interpreted as a description of a real ‘matter wave’. Although he couldn’t be clear on the details, Einstein preferred to think of the wavefunction in terms of statistics. We describe the properties of an atomic gas in terms of physical quantities such as temperature and pressure. But if we consider the gas as a collection of atoms, we can use the classical theories developed by Ludwig Boltzmann and James Clerk Maxwell to deduce expressions for temperature and pressure as the result of statistical averaging over a range of atomic motions. In this case, we deal with statistics and probabilities only because we have no way of following the motions of each individual atom in the gas. Of course, we might not be able to account for such motions except in terms of statistics, but this doesn’t mean that atoms (or their motions) aren’t real.
Einstein’s realist interpretation of the wavefunction was very different to Schrödinger’s. If quantum probability is, after all, a statistical probability born of ignorance, then there must exist a further underlying reality that we are ignorant of, just as atomic motions underlie the temperature and pressure of a gas. This was Einstein’s point: as this underlying reality makes no appearance in quantum mechanics, then the theory cannot be considered to be complete. Einstein wouldn’t be drawn on precisely what he thought this underlying reality might be, and the EPR paper concludes with the comment ‘we left open the question of whether or not such a description exists. We believe, however, that such a theory is possible.’13 I’ll have more to say about this in a later chapter.
Schrödinger’s interpretation of the wavefunction couldn’t possibly be right, and Einstein sought to persuade him of this in a letter dated 8 August 1935. In this letter Einstein asked him to imagine a charge of gunpowder that, at any time over a year, may spontaneously explode. At the beginning of the year, the gunpowder is described by a wavefunction. But how should we describe the situation through the course of the year? Until we look to see what’s happened, we would have to regard the wavefunction as a superposition of the wavefunctions corresponding to an explosion, and to a non-explosion. He wrote:14
Through no art of interpretation can this [wavefunction] be turned into an adequate description of a real state of affairs; [for] in reality there is just no intermediary between exploded and not-exploded.
Schrödinger eventually relented, and came to share Einstein’s views. But the gunpowder experiment had set him thinking. As there is nothing in the mathematical formulation of quantum mechanics that accounts for the collapse of the wavefunction, then why assume this happens at the quantum level? Why not imagine that entanglement reaches all the way up the measurement chain, to the classical apparatus itself? In a reply dated 19 August he outlined another thought experiment that would become eternally enduring:15
Contained in a steel chamber is a Geigercounter prepared with a tiny amount of uranium, so small that in the next hour it is just as probable to expect one atomic decay as none. An amplified relay provides that the first atomic decay shatters a small bottle of prussic acid. This and—cruelly—a cat is also trapped in the steel chamber. According to the [wavefunction] for the total system, after an hour, sit venia verbo [pardon the phrase], the living and dead cat are smeared out in equal measure.
This is the famous paradox of Schrödinger’s cat.
Einstein was in complete agreement. A total wavefunction consisting of contributions from the wavefunctions of a live and dead cat is surely a fiction. Better to try to interpret the wavefunction realistically in terms of statistics. If the experiment is duplicated, the laboratory filled with hundreds of chambers each containing a cat, then after an hour we predict that in a certain number of these (predicted as a probability derived from the wavefunction), the cat will be dead.* The Geiger counter in each box clicks or doesn’t click. If it clicks, the relay is activated, the prussic acid is released and the cat is killed. If it doesn’t click, the cat survives. Nowhere in this experiment is a cat ever suspended in some kind of peculiar purgatory.
Schrödinger intended the cat paradox as a rather tongue-in-cheek dig at the apparent incompleteness of quantum mechanics, rather than a direct challenge to the Copenhagen interpretation. It does not seem to have elicited any kind of formal response from Bohr. Schrödinger wrote to Bohr on 13 October 1935 to tell him that he found his response to the challenge posed by EPR to be somewhat unsatisfactory. Surely, he argued, Bohr was overlooking the possibility that future scientific developments might undermine the assertion that the measuring apparatus must always be treated using classical physics. Bohr replied briefly that, if they were to serve as measuring instruments, then they simply could not be of quantum dimensions.
The community of physicists had in any case moved on by this time, and probably had little appetite for an endless philosophical debate that, in the view of the majority, had already been satisfactorily addressed by Bohr.
In the meantime, the ‘Copenhagener Geist’ had become formalized and enshrined in the very mathematical structure of quantum mechanics. The theory had emerged from a profoundly messy sequence of discoveries that had involved underlying violence to the mathematics, more than a few unjustified assumptions, and occasional conceptual leaps of faith. In its early years, the passage across the Sea of Representation had been difficult. Then there was the challenge of reconciling the two distinctly different approaches to quantum mechanics that had been developed by Heisenberg and by Schrödinger, which Schrödinger himself had demonstrated to be entirely mathematically equivalent.
In the late 1920s, Paul Dirac and John von Neumann separately sought to put the theory into some sort of order by establishing a single, formally consistent mathematical structure for quantum mechanics. Their approaches were summarized in two books: Dirac’s The Principles of Quantum Mechanics was first published in 1930, and von Neumann’s Mathematical Foundations of Quantum Mechanics was published in German in 1932. Their approaches were somewhat different, and von Neumann was critical of some aspects of Dirac’s mathematics, but from these emerged the structure that is taught to students today.
Von Neumann had been a student of the great mathematician David Hilbert who, in a lecture delivered to the International Congress of Mathematicians in Paris in 1900, had outlined a long list of key problems that he believed would occupy the next generation of leading mathematicians. This list has become known as Hilbert’s problems. The sixth of these concerns the mathematical treatment of physics. Hilbert argued that an important goal for future mathematicians would be to treat the physical sciences in the same manner as geometry. This means grounding physics in a set of axioms.
Axioms are self-evident truths that are assumed without proof, and represent the foundations of the mathematical structure that is derived from them. The proof of the axioms then lies in the consistency of the structure and the truth of the theorems that can be deduced from it. Hilbert’s axiomatic method represented an almost pathological drive to eliminate any form of intuitive reasoning from the mathematics, arguing that the subject was far too important for its truths to be anything less than ‘hard-wired’. Applied to physics, this demand for mathematical rigour and consistency inevitably resulted in a rather disconcerting increase in obscure symbolism and abstraction. In his review of Dirac’s Principles, Pauli warned that Dirac’s abstract formalism and focus on mathematics at the expense of physics held ‘a certain danger that the theory will escape from reality’.16 It became nearly impossible for anyone of average intelligence but without formal training in mathematics or logic fully to comprehend aspects of modern physics.
Actually, you’re already quite familiar with the first few of the axioms of quantum mechanics from your reading of Chapter 1. We start with:
Axiom #1: The state of a quantum mechanical system is completely defined by its wavefunction.
In other words, quantum mechanics is mathematically complete, as indeed it must be if it is to serve its purpose as a foundational theory of physics. So much for Einstein. I call this the ‘nothing to see here’ axiom.
Axiom #2: Observables are represented in quantum theory by a specific class of mathematical operators.
Again, I don’t propose to give you the details of what is meant here by ‘specific class’. All you really need to know is that these operators are particularly suited to the task of extracting the values of observables from the wavefunction. I think of this as the ‘right set of keys’ axiom. To get at the observables, such as momentum and energy, we need to unlock the box represented by the wavefunction. Different observables require different keys drawn from the right set.
Axiom #3: The average value of an observable is given by the expectation value of its corresponding operator.
This tells us how to use the keys. I think of it as the ‘open the box’ axiom. It is the recipe we use to get at the observables themselves.
If quantum mechanics is to be a useful predictive theory of physics, we obviously need to know how to use it:
Axiom #4: The probability that a measurement will yield a particular outcome is derived from the square of the corresponding wavefunction.*
This is known as the ‘Born rule’.† Or, if you prefer, you can think of this as the ‘What might we get?’ axiom. Note that when we apply this to a quantum superposition with two or more possible outcomes, it doesn’t say what we will get in any individual measurement.
There is one further axiom in the main framework, related to the way we anticipate that the wavefunction will change in time:
Axiom #5: In a closed system with no external influences, the wavefunction evolves in time according to the time-dependent Schrödinger equation.
This means that, once established, the wavefunction evolves in a predictably deterministic and continuous manner, its properties at one moment determined entirely by its properties the moment before. Think of the electron wavefunction evolving smoothly in time as it passes through two slits, forming a ‘wavefront’ which alternates between high and low or zero amplitude as a result of interference, as shown in Figure 5a. This is the ‘how it gets from here to there’ axiom.
There is no place here for the kind of discontinuity we associate with the process of measurement. As von Neumann understood, accepting Axiom #5 forces us to adopt a further (but related) axiom in which we assume that a wavefunction representing a superposition of many measurement possibilities collapses to give a single outcome.
Of course, we never had to do anything like this in classical mechanics.
Now, Euclid’s geometric axioms are concerned with the properties of straight lines, circles, and right angles and, I would contend, meet the criterion of self-evident truth. But there’s nothing particularly self-evident about the axioms of quantum mechanics. I guess this is hardly surprising. The formulation of quantum mechanics is as abstract and obscure as Euclidean geometry is familiar.
These axioms leave entirely open the question of the reality or otherwise of the wavefunction—after all, this is mathematics, not philosophy. But I think it’s helpful to note just how many of the Copenhagen interpretation’s basic tenets became absorbed into the axiomatic structure of quantum mechanics. Just as empirical facts can never be free of some theory needed to interpret them, so theory can never be completely free of the metaphysical preconceptions that assisted at its birth. The standard mathematical formulation of quantum mechanics is not an entirely neutral witness to the debate that would follow.
This is the great game of theories. Let’s now see how physicists have played this game for the past ninety years or so.