Bridging the Two Cultures: Paul Valéry

PHILIP J. DAVIS

The conjunction of mathematics and poetry is alive and well. Thus, e.g., Strange Attractors, a stimulating anthology of poems that allude to mathematics (often very superficially) has just appeared.¹ Quite by accident I learned that Paul Valéry (1871–1945), the famous French poet, essayist, philosopher and aphorist, had left in his extensive notebooks many observations, impressions, ruminations and thoughts about mathematics. As opposed to the material in Strange Attractors, Valéry created no poems specifically about mathematics. What is remarkable in his case is the depth of his infatuation with the deepest aspects of mathematics, and his struggle to come to grips with them through his own poetic imagination and intuition.²

What, I wondered, was the significance of Valéry’s innumerable jottings about mathematics? He is not mentioned in any history or philosophy of mathematics of which I am aware; his name attaches to no mathematical ideas, constructions, theorems, processes. Was he then, merely expressing, as a private citizen so to speak, his feelings about a subject for which he had a deep attraction; or was he putting forward a claim as having given birth to a unique vision as to what mathematics was all about? The question is relevant because Valéry’s work has been the subject of thousands of articles and theses, and though he is known now in France to the general public largely as a university (Montpellier–Valéry), his writings are the object of continued studies by specialists. Thus, the University of Newcastle upon Tyne houses a Centre for Valéry Studies headed up by Prof. Brian Stimson.

Valéry’s notebooks (Cahiers) have all been published. I opened one at random (Vol. V) and found strewn among the author’s jottings on innumerable topics, mathematical equations, notations, computations, figures, together with animadversions on the same. Are these, I wondered, simply mathematical graffiti? Was he trying to play the mathematician and floundering around with difficult problems (e.g., the four color problem) or was he merely a commentator looking down with love and admiration from the Olympian heights on a topic that seems to have engaged his thoughts continually? To appreciate and make sense of this material is not easy; one must go into the author’s head and language, get under his skin. A knowledge of his total oeuvre is really required.

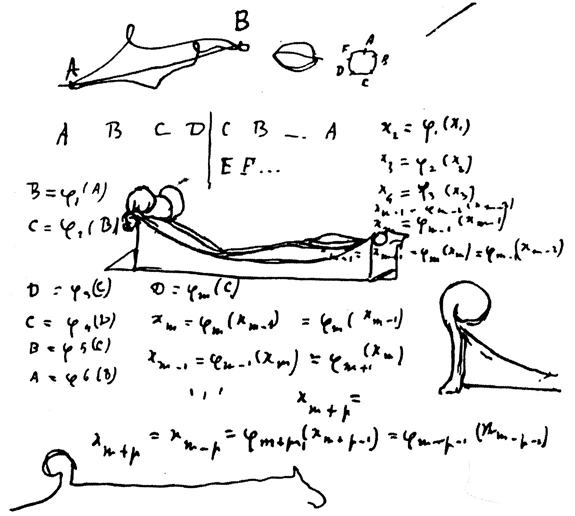
FIGURE 1. Jottings extracted from Cahier V, p. 200.

To help me arrive at an answer, I turn to a lengthy article by Judith Robinson, a scholar of French literature and a specialist on Valéry which treats the mathematical jottings in his Cahiers in some depth. Robinson boned up on mathematical ideas and was able to connect the dots of the dispersed jottings, figures, computations, into a continuous narrative. In what follows, when I use the name Valéry, I really mean the Valéry as seen principally through the imaginative eyes of Robinson.

Valéry was much concerned with mathematics and physics and in his mind the two are almost inextricable. He read extensively; he knew the mathematician Emile Borel and the physicists Jean Perrin and Paul Langevin. He corresponded with Jacques Hadamard. He admired Riemann and Cantor and his admiration of Poincaré was unbounded. He kept Poincaré’s books beside his bed, rereading them constantly. Mathematics, he wrote, became his opium. Valéry was “greatly influenced in his thinking” by the developments relativity, in atomic and quantum physics, in particular by Heisenberg’s Uncertainty Principle. He has many references to the ideas of mathematics and physics which he comprehended in an intuitive, impressionistic way and often employed metaphorically. His understanding was, according to Robinson, not superficial, not that of the mere amateur.

As befits a poet and a littérateur Valéry was much concerned with language. He questioned “ready-made” language, considered it impure, vague, imprecise, ambiguous, a stumbling block in perceiving and apprehending reality. He believed that our (natural) languages were responsible for the raising of stupid, meaningless, undefined, or often false questions such as “who created the world ?,” “what is the purpose of life ?,” “what is the relationship between mind and matter” or “the distinction between the knower and the known.” On the other hand, he admired mathematics as the only precise, coherent, rigorous, and unambiguous intellectual language devised by humans.

Perhaps the greatest virtue of mathematics as Valéry sees it is that it enables us not only to define our terms but also to relate them to one another in a logical and coherent way. Now this is exactly what ordinary language has great difficulty in doing.

Valéry’s concern with language reminded me, by way of contrast, of the Neapolitan philosopher of language and anti-Cartesian Giambattista Vico (1668–1744.) My source for Vico is the book of Sir Isaiah Berlin.³ Vico’s ideas, when applied to mathematics, presage today’s social constructivism.

[Vico] concedes that mathematical knowledge is indeed wholly valid and its propositions are certain. But the reasons for this are only too clear: ‘We demonstrate geometry because we make it’.

His catch phrase, often quoted, is “Verum esse ipse factum” (Truth itself is constructed).

I do not know whether Valéry read Vico; nonetheless, a remark of Valéry that he begins

to inquire by what sign we recognize that a given object is or is not made by man (Man and the Sea Shell)

leads me to think that a study comparing and contrasting the ideas of Vico and those of Valéry would be of significance. I myself am sympathetic towards Vico’s ideas, for while admitting the precise, coherent, rigorous, and unambiguous nature of mathematical language, such language lies totally embedded in natural languages (e.g., English) with all their impurities. Strip mathematical texts of all descriptions, explications, instructions given in natural language, and a page of naked mathematical symbols would be incomprehensible.

Berlin also remarks that

Political courage was no more characteristic of Vico than of Leibniz or a good many other scholars and philosophers of the age . . .⁴

These men were above the fray, and to this list we may safely add Valéry. Even as Leibniz dreamed of a formal language—a characteristica universalis—within which calculations of mathematical, scientific, legal and metaphysical concepts could be expressed and related problems solved, Valéry dreamed of a language, an “algebra de l’esprit,” an arithmetica universalis that would be a useful instrument in the study of brain function, a language in which “the physical and the psychological could be compared”; a language into which “propositions of every kind could be translated.” Turning to the influence of other contemporaries, Valéry admired the logic of Russell, and one can see the relationship between Valéry’s thought and that of Wittgenstein. What interested him primarily was not the object, but the relationship between objects, and in the flexibility and generality of such relationships that he discovered in various geometries and in the ideas of Riemann. These were ideas that he hoped could be expressed in notational terms. Despite these perceptions, I do not believe Valéry could be termed a logicist. I would call him a formalist.

Valéry did not go public with these thoughts; he committed them to his notebooks, perhaps in the hope that they would be interpreted by later scholars. The aspects of mathematics that he admired so much are today simply part of the working knowledge and attitudes of today’s mathematicians. He did not contribute anything either to mathematics or physics or to their philosophy. But what is absolutely remarkable in this story is that a person so devoted to language and literature should have immersed himself deeply and knowingly and arrived at individual insights into questions of mathematics and physics. Valéry was called by some a new Leonardo; by others a philosopher for old ladies. Whatever.

The importance of Valéry for me is that his notebooks are proof positive that the “Two Cultures” of C.P. Snow, the literary and the scientific, often thought to be unbridgeable, can indeed be bridged if only in one direction. The American philosopher William James wrote “The union of the mathematician with the poet, fervor with measure, passion with correctness, this surely is the ideal.” While the thoughts of Valéry are as close as have been come to the realization of this ideal in measure and passion, the bridge he constructed was personal and cannot easily be transmitted to the general readership.

Acknowledgements

I wish to thank Brian Stimpson for supplying me with valuable information and Charlotte Maday and Vera Steiner for their encouragement.

Notes

1. Strange Attractors, AK Peters, 2008.

2. A 2006 Stanford University thesis by Rima Joseph, Paul Valéry parmi la mathematique, considers the influence that Valéry’s knowledge of mathematics may have had on his poetry: “The elucidation of such [mathematical] models used in metaphors by Valéry reveal mathematics as an aesthetic object ultimately forming his poetics.”

3. Vico and Herder, Viking.

4. Loc. cit. p. 5.

References

Sir Isaiah Berlin, Vico and Herder, Viking, 1976.

J. M. Cocking, Duchesne-Guillemin on Valéry, Modern Language Review, 62, 1967, pp. 55–60.

Jaques Duchesne-Guillemin, Etudes pour un Paul Valéry, La Baconnière, Neuchatel, 1964.

Rima Joseph, Paul Valéry parmi la mathematique, Doctoral thesis, Stanford University, 2006.

Walter Putnam, Paul Valéry Revisited, Twayne Publishers, 1995.

Judith Robinson, Language Physics and Mathematics in Valéry’s Cahiers. Modern Language Review, Oct 1960, pp. 519–536.

Judith Robinson: L’Analyse de l’esprit dans les Cahiers de Valéry, Paris, Corti, 1963.

Judith Robinson (ed.), Fonctions de l’esprit: 13 savants redécouvrent Valéry, Paris, Hermann, 1983. (Contributions by Jean Dieudonné, René Thom, André Lichnerowicz, Pierre Auger, Bernard d’Espagnat, Jacques Bouveress and Ily Prigogine.)

Michel Sirvent, Chiffrement, déchiffrement: de Paul Valéry à Jean Ricardou, French Review 66:2 December 1992, pp. 255–266.

Paul Valéry, History and Politics, Vol 10, Bollingen, Pantheon, 1962.

Paul Valéry, Cahiers 1894–1914, V, Gallimard, 1994. Translations of various volumes forthcoming.