Exploring Curvature with Paper Models
HOWARD T. ISERI
Curvature is a fundamental concept in modern geometry, and yet the topic is often neglected in the high school and undergraduate curriculum. A concept of curvature dating to Carl Friedrich Gauss (1777–1855) is used by differential geometers to study both Euclidean geometry and the non-Euclidean geometries discovered by Janos Bolyai (1802–1860), Nikolai Lobachevsky (1792–1856), and Bernhard Riemann (1826–1866) as curved surfaces. Although a formal investigation of the curvature of surfaces requires advanced multivariate calculus, the underlying concept can be explored using only basic plane geometry. The origin of this idea can be traced to Rene Descartes (1596–1650.) By measuring angles on polyhedral surfaces, Descartes measured the same quantities that Gauss would measure two centuries later and, at the same time, gave us a simple way to explore non-Euclidean geometry in terms of curvature.
Although curvature originates in mathematics, popular interest in the topic is due mostly to scientists. Einstein’s discovery of the general theory of relativity (1915) introduced the notion that the behavior of gravity can be explained by equating the presence of matter in space with curvature. This curvature of space would allow a photon (with no mass, and hence no gravitational attraction) to travel in a straight line but also to appear to change direction when passing a massive object. This phenomenon was observed in the famous experiment that brought general relativity to the public’s attention, when in 1919 Arthur Eddington, during a solar eclipse, observed that a distant star appeared to have changed position because the light coming from the star had traveled close to the sun. Today, the curvature and geometry of our universe are at the center of the debate concerning whether the universe contains enough matter to keep it from expanding forever.
The first part of this article examines how the curvature of curves and surfaces is related to the angles of polygons or polygonal curves and “solid” angles at the vertices of polyhedra. We examine the theorem at the center of Descartes’ work in this area to give us a simple measure of the sharpness of a solid angle and then show how Descartes’ theorem can be proved from the seemingly unrelated Euler theorem. The second part of the article presents examples of paper models that use Descartes’ version of curvature to explore hyperbolic and elliptic figures in a precise and accessible way.
The Curvature of Curves
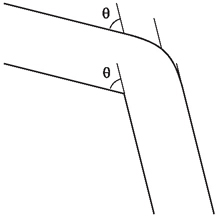
Figure 1 shows two paths, one polygonal and one smoothly curved. Following each from bottom to top, we see that the beginning direction and the ending direction are the same for both curves. The change in direction, therefore, is measured in both instances by the same angle, θ. For the polygonal curve, we call this angle the exterior angle. The interior angle, the one we typically measure, is supplementary to the exterior angle, so they sum to 180 degrees, or π radians, and we can easily find one from the other on a polygonal curve.
If we interpret a curve as a path that we travel along, an external angle on a polygonal path measures an abrupt change in direction. On a smooth curve, this change in direction occurs gradually, and we have, in some sense, infinitely many, infinitesimally small external angles. So although we can measure the change in direction between two points on the same curve, another concept is needed to adequately describe how this change in direction takes place. This concept, called curvature, is defined to be the rate at which the direction changes with respect to arc length. From point A to point B on a curve, for example, the direction will change by some angle Δθ, and the arc length along the curve between these two points will be a distance Δs. This notation gives us an average curvature of Δθ/Δs. Taking shorter sections of the curve and a limit, we arrive at the curvature at each point, which is an instantaneous rate of rotation.
In figure 2, we have a circle of radius r. The arc between points A and B is a quarter of the circle and has length 2πr/4 = πr/2. The change in direction between points A and B is π/2 radians. Dividing the change in direction by the arc length gives an average rate of change in direction (curvature) of 1/r radians per unit distance. The average curvature, not surprisingly, is the same for any arc of the circle, so in the limit, the curvature (denoted by the Greek letter κ, “kappa”) at every point on a circle of radius r is κ = 1/r radians per unit distance. Note that small circles will have more curvature, which should make sense. In general, if a curve has curvature κ at some point, then the part of the curve near that point will look like part of a circle of radius 1/κ.
The significance of curvature to geometry becomes clearer in higher dimensions, and Descartes’ theorem allows us to explore that significance. Before discussing surfaces, however, we will be helped by considering a lower-dimensional version of Descartes’ theorem.
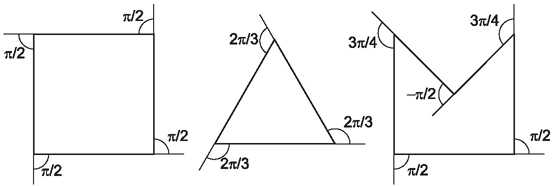
Imagine an ant walking around each shape in figure 3 in a counter-clockwise direction. To do so it must turn as indicated by the shapes’ exterior angles. The first figure is a square, and the four exterior angles each measure π/2 radians. The sum of the exterior angles in this instance is 2π radians. The sum is the same for the triangle. The figure on the right has one turn to the right, which we define to be negative, and with that, the exterior angles again sum to 2π radians.
One-dimensional Descartes’ theorem: Given any simple, closed polygonal curve in the plane, the exterior angles will sum to 2π radians.
This theorem holds true for smooth curves. Imagine a circle painted on the floor. If you walk around it once, your body will make one complete rotation. If you face north initially, you will turn gradually until you face west, then south, and then north again. That is, you will make a 2π radian rotation. On a polygonal curve, the only difference is that the turns happen abruptly, but the net rotation is still 2π radians. For smooth curves, because curvature is essentially a derivative of the direction function with respect to the arc length, integrating the curvature around a simple, closed curve will give the net rotation, 2π radians. For this reason, an accumulated amount of curvature is called total curvature, and so total curvature is the same as a net change in direction. That is, the sum of the external angles measures total curvature.
In Euclidean (plane) geometry this sum of angle measures around a closed figure is 2π radians, and we will see that deviations from the number 2π serve as measures of how much a non-Euclidean geometry differs from the Euclidean model.
The Curvature of Surfaces
We have seen that the total curvature around a simple closed curve in the plane is always the same. As we turn to surfaces, the situation is similar, as long as we choose a suitable measure of curvature. Gaussian curvature is the standard measure of curvature for a smoothly curving surface, and it nicely ties the standard non-Euclidean geometries together as surfaces with constant Gaussian curvature. In particular, Gaussian curvature is 0 for the Euclidean plane, –1 for the hyperbolic “plane,” and 1 for the elliptic and spherical “planes.” Furthermore, we can show that integrating Gaussian curvature over any surface that is a smooth deformation of a sphere always yields the number 4π, which should remind us of the fact that the net rotation for a simple closed curve in the Euclidean plane is always 2π. Here, as with curves, an accumulated amount of Gaussian curvature is called total curvature. We can say, therefore, that closed curves (which are deformations of a circle) in the Euclidean plane always have total curvature 2π, and closed surfaces in Euclidean space that are deformations of a sphere always have total (Gaussian) curvature 4π. Being a deformation of a sphere here is important, because deformations of a torus, for example, always have total curvature 0.
Unfortunately, the definition of Gaussian curvature is somewhat involved, and calculating it for a typical surface is impractical. As with the curvature of curves, however, Gaussian curvature has an angular analog, which Descartes described in a manuscript with a tenuous existence. This manuscript was apparently not published during Descartes’ lifetime. After Descartes died in 1650, when his papers were collected, it was accidentally dropped in a river, fished out, and hung to dry. Gottfried Leibniz (1646–1716), the coinventor of calculus, was given the opportunity to copy some of these papers including the manuscript containing our theorem. Leibniz’ copy was then lost, found, and published in 1860 (Federico 1982; Phillips 1999).
FIGURE 4. The angles around points E and F sum to 2π. The angles around vertex V sum to 3π/2. To construct the model, remove shaded regions and tape them together so that the vertices labeled with 1 come together, the vertices labeled 2 come together, and so on.
Descartes’ work focused on the angles of polyhedra. The external angle at a vertex of a polyhedral surface measures how much that vertex is “not flat,” just as the external angle on a polygonal curve measures how much the curve is not straight. To see how this measure can be accomplished, consider a point in the plane. If we were to fit a collection of angles around this point, their measures would sum to 2π radians. Compare this result with the surface of a cube, a polyhedral surface with eight vertices. Each point on a face of the cube is surrounded by 2π radians. For example, on the one hand the point F shown in figure 4 has four right angles around it. Each point on the edge of the cube also is surrounded by 2π radians, as illustrated by the point E in figure 4. On the other hand, each vertex point, such as the point V, is surrounded by only three right angles, which total 3π/2 radians.
Compared with a point in the plane, therefore, each vertex comes up short by π/2 radians. Descartes called this deviation from 2π the angulum externum, or external angle. Since the eight vertices of the cube each have an external angle of π/2, the total external angle is 4π, or as Descartes says, “eight right angles” (Federico 1982). This is the same number that differential geometers find for the total amount of Gaussian curvature (i.e., the total curvature) on a sphere or any figure that can be deformed to a sphere.
Let us try this same computation with another simple polyhedron, a tetrahedron with four equilateral triangular faces. Each vertex is surrounded by three π/3-radian angles for a total of π radians. We are left with an external angle of 2π – π = π radians. Since four vertices are involved, we have an external angle sum of 4π. The result will be the same for any convex polyhedron, as we will prove. This outcome is Descartes’ theorem.
(Two-dimensional) Descartes’ theorem: For any polyhedron the sum of the external angles is 4π.
This theorem is relatively easy to prove from Euler’s formula,
(1)f – e + v = 2,
where, for a given polyhedron, f is the number of faces, e the number of edges, and v the number of vertices. For simplicity, each of the faces can be subdivided into triangles by inserting diagonals, so we can assume that all the faces are triangles, although not necessarily on distinct planes. Each face now contributes three edges, each of which are shared by two faces. In other words, 3f = 2e. Multiplying equation (1) on both sides by 2 and substituting 3f for 2e gives us
(2)–f + 2v = 4.
Multiplying by π on both sides gives us
(3)πv – πf = 4π.
We can now interpret equation (3). The (interior) angle sum of each of the f triangular faces is π, so the sum of all the angles of all the faces must be πf, which is also the sum of the angles at all the vertices. At each vertex the external angle is equal to 2π minus the angle sum. For all v vertices the sum of the external angles must be 2πv minus the sum of all the angles, which we already know is πf. Therefore, if we let C be the sum of all the external angles, we get
(4)C = 2πv – πf = 4π.
Note that if we were to allow an angle excess (i.e., angles surrounding a vertex that sum to more than 2π radians) to be a negative external angle, no modification to these computations is necessary. As a result, equation (4) applies to nonconvex as well as to convex polyhedra.
As an aside, we should note that Descartes considered only those polyhedra that were deformable to a sphere. However, both Euler’s formula and Descartes’ theorem can be extended to other surfaces. The external angles of a polyhedral torus, for example, sum to 0.
For curves in the Euclidean plane, we saw that the change in direction measured by the external angle occurs gradually for a smoothly curving curve, and the amount of change per unit arc length is called curvature. The external angle on a surface measures the “sharpness” at a vertex where the inclination of the faces abruptly changes. But again, on a smooth surface, this change occurs gradually. Therefore, to define Gaussian curvature as the amount of change per unit surface area makes sense. In fact, as noted earlier, integrating Gaussian curvature over a region on a surface yields a quantity called total curvature, and this phenomenon is what the sum of the external angles measures on a polyhedral surface. For both curves and surfaces, therefore, external angles provide a way to measure total curvature. Virtually any theorem about a smooth surface involving total curvature can be transformed into a theorem about polyhedral surfaces by replacing the words total curvature with the words sum of the measures of the external angles. The paper models discussed subsequently, therefore, are legitimate approximations for the geometry of curved surfaces.
The Geometry of Geodesics
Lines in the plane minimize distance in the sense that given two points, the shortest distance between them is measured along a line. For measurements taken along a surface, those curves that minimize distance are called geodesics. The lines on a plane are nothing more than the geodesics of a flat surface, and Euclidean geometry is just a particular example of the geometry of geodesics on surfaces.
We have already seen that the sum of the external angles is 4π for a cube, and coincidentally, the total (Gaussian) curvature for a sphere is also 4π. The geodesics on these two surfaces, as we shall see, also behave in a similar way.
On the sphere, the geodesics are the great circles, and on the sphere, a triangle with geodesic sides has an angle sum greater than 180 degrees, or π radians. The particular angle sum turns out to be directly related to the total curvature contained in the triangle.
For example, on a sphere a triangle can have three right angles. We can put one vertex at the north pole and two on the equator as in figure 5. This triangle contains one-eighth of the surface area of the sphere, and so it also must contain one-eighth of the total curvature, in particular, C = 4π/8 = π/2. The angle sum of the triangle is 3π/2, which is π/2 greater than the Euclidean angle sum of π radians. The agreement between the angle sum excess and the curvature contained within the triangle is not a coincidence.

FIGURE 5. A triangle on a sphere can have three right angles.
FIGURE 6. A triangle on a cube. The triangle has three right angles, an angle sum of 270 degrees, and an angle-sum excess of 90 degrees, or π/2 radians.
In fact, the angle sum of a triangle is always π + C, where C is the curvature contained in the triangle. This outcome is the spherical version of the fundamental theorem of surface geometry, the Gauss-Bonnet theorem.
On the cube, a geodesic must be as straight as possible and, equivalently, must minimize distance. Plans for a paper model of a cube are shown in figure 6. Four straight-line segments are also drawn. Since folding along the edges will not change the length of the segments, nor will it change any small measurements taken along the surface, these segments will become geodesics on the cube after being folded and taped. Note also that after the edges are taped together, the segments AD and DC come together just as AE and EB do. The fact that AB, BC, and CA are each geodesic segments follows, and we have a triangle with three right angles. We again have a triangle with an angle sum π/2 more than the Euclidean angle sum of π radians. Furthermore, this triangle contains one vertex with an external angle of C = 2π – 3π/2 = π/2. In other words, the excess angle sum equals the curvature contained within.
Note, however, that for triangles on a sphere or a cube, the notion of “interior” is somewhat ambiguous. The three edges, in fact, separate the cube’s surface into two regions. If we consider the larger region as the “interior” of the triangle, then the triangle’s three “interior” angles each measure 3π/2 radians for an angle sum of 9π/2 radians. The angle sum excess, therefore, is 7π/2, which is equal to the sum of the seven external angles of the cube, each measuring π/2 radians, that lie in the larger region. This result again matches the total curvature contained within this interpretation of the triangle, and so both interpretations of the triangle have this property. In general, for any triangle, we have
(5)Σ = π + C,
where Σ is the angle sum of a triangle and C is the total curvature contained in the triangle.
The sphere is an example of an elliptic geometry, in which we see triangles with angle sums greater than π radians. A differential geometer would equate elliptic geometry with positive Gaussian curvature. In hyperbolic geometry, we see triangle angle sums that are less than π radians, and negative Gaussian curvatures characterize hyperbolic geometries. As we shall see, the corresponding solid angles have more than 2π radians surrounding them, and so extra radian measure beyond 2π can naturally be viewed as a negative external angle.
In his book The Shape of Space, Jeffrey Weeks (1985) presents a visualization of the hyperbolic plane, and therefore negative curvature, with something he calls hyperbolic paper, which he attributes to the well-known geometer William Thurston. The idea is based on the fact that equilateral triangles tile the plane with six triangles coming together at each vertex and each contributing an angle measuring π/3 radians around that vertex. These six angles total 2π radians around each of these vertex points. Hyperbolic paper, in contrast, squeezes seven equilateral triangles around each vertex, creating a very wavy surface and an approximation to the hyperbolic plane.
In figure 7 the seven equilateral triangles, when taped together, create a small piece of hyperbolic paper. As in the cube example, several line segments are drawn in this figure, and after the seven triangles are taped together, the lines come together to form geodesic ΔABC with angle sum 2π/3 radians. In constructing geodesics across “cuts,” one must make sure that vertical angles formed by the cut and the geodesic are equal. The photograph shows what the paper looks like after being taped together. Note that the paper takes a saddle shape, which is characteristic of a hyperbolic surface with negative curvature. The triangle in this figure has an angle sum that is less than π radians; in particular, the angle sum “excess” is –π/3 radians. This result agrees with the fact that the external angle at the central vertex of the surface is –π/3 radians. Again the deviation of the angle sum of a triangle from π radians equals the total curvature contained in the triangle.
FIGURE 7. A triangle on hyperbolic paper. The angle at the top is 30 degrees, at the bottom is 40 degrees, and on the right is 50 degrees, for an angle sum of 120 degrees and an angle-sum deficit of 60 degrees, or π/3 radians.
Exploring Euclidean and Non-Euclidean Geometry
Virtually all the phenomena observed in Euclidean and non-Euclidean geometry can be explored concretely on our paper models. For example, Euclid’s fifth postulate states that given a figure like that shown in figure 8 with α < π/2, the lines l and m must intersect. In hyperbolic geometry, however, the two lines might not intersect. In Euclidean geometry the distance between the lines decreases linearly, but in hyperbolic geometry this rate of decrease may get smaller. Negative curvature between the lines lessens the rate of decrease in the distance between l and m. In fact, total curvature equal to –α between the lines stops this decrease completely. The ability to contain this amount of curvature in a small region helps make this phenomenon easier to see.
FIGURE 9. Two lines cut by a transversal near a point with negative curvature. The interior angles below the transversal measure 90 degrees and 45 degrees, but the two lines do not intersect.
If α = π/4, then curvature totaling –π/4 can prevent these lines from intersecting, and we can build a model that illustrates this outcome. Adding a π/4-radian wedge gives us the necessary Cartesian curvature, and we can construct a model as in figure 9. Note that since the edges on a polyhedral surface do not affect the geometry, we have no need to crease edges in the paper models. With the introduction of negative curvature, the lines l and m diverge in one part of the model and remain equidistant in another. Also notice that ABCD has three right angles and one acute angle. A quadrilateral with three right angles is called a Lambert quadrilateral after one of the mathematicians whose work paved the way for the development of non-Euclidean geometry. In Euclidean geometry the fourth angle of a Lambert quadrilateral is necessarily a right angle, but in hyperbolic geometry it is always acute. This outcome illustrates how the history of non-Euclidean geometry can be investigated with these paper models by building counterexamples to Euclidean objects.
FIGURE 10. Two lines cut by a transversal near an “elliptic” vertex. The interior angles, ∠A and ∠B, measure 90 degrees and 135 degrees, respectively, but the two lines still intersect on that side of the transversal.
Elliptic comparisons with Euclid’s fifth postulate can be made just as easily. In figure 8, if α > π/2, then the lines l and m can still intersect on the right if enough positive curvature occurs between the lines. For example, when α = 3π/4 radians, in a Euclidean plane l and m diverge on that side of the transversal. Positive curvature of C = π/4 is sufficient to stop that divergence, and more curvature forces the lines to intersect. In figure 10, positive curvature of C = π/2 is introduced between l and m by removing a π/2-radian wedge. This removal results in the two lines’ intersecting on the side of the transversal with interior angles summing to more than π radians. In this instance, the lines l and m have two points of intersection. Here we can see why in elliptic geometry we can have “2-gons,” which are impossible in Euclidean geometry.
Summary
Through all these examples, we see that a direct relationship exists between the curvature of a surface and such properties as the angle sum of a triangle.
We have seen how total curvature on paper models can be used to complement and contrast with the phenomena encountered in the usual Euclidean and non-Euclidean geometries. These polyhedral models make possible the construction of explicit, concrete models with precise specifications, and with these come the ability to explore isolated properties by comparing and contrasting spaces with and without these properties. This ability to play with and manipulate geometric spaces is crucial to reaching a deep understanding of geometry.
References
Federico, Pasquales J. Descartes on Polyhedra. New York: Springer Verlag, 1982.
Phillips, Tony. “Descartes’s Lost Theorem.” American Mathematical Society Web Site Feature Column, September 1999. www.ams.org/featurecolumn/archive/descartesl.html.
Weeks, Jeffrey. The Shape of Space. New York: Marcel Dekker, 1985.