Circle Packing: A Personal Reminiscence
PHILIP L. BOWERS
The Prehistory of Circle Packing
Two important stories in the recent history of mathematics are those of the geometrization of topology and the discretization of geometry. The first of these begins at a time when the mathematical world is entrapped by abstraction. Bourbaki reigns and generalization is the cry of the day. Coxeter is a curious doddering uncle, at best tolerated, at worst vilified as a practitioner of the unsophisticated mathematics of the nineteenth century.
THE GEOMETRIZATION OF TOPOLOGY
It is 1978 and I have just begun my graduate studies in mathematics in geometric topology. By my second year of study, there is some excitement in the air over ideas of Bill Thurston that purport to offer a way to resolve the Poincaré conjecture by using nineteenth century mathematics—specifically, the noneuclidean geometry of Lobachevski and Bolyai—to classify all 3-manifolds. These ideas appear in a set of notes from Princeton, and the notes are both fascinating and infuriating—theorems are left unstated and often unproved, chapters are missing never to be seen, the particular dominates—but the notes are bulging with beautiful and exciting ideas, often with but sketches of intricate arguments to support the landscape that Thurston sees as he surveys the topology of 3-manifolds. Thurston’s vision is a throwback to the previous century, having much in common with the highly geometric, highly particular landscape that inspired Felix Klein and Max Dehn. These geometers walked around and within Riemann surfaces, one of the hot topics of the day, knew them intimately, and understood them in their particularity, not from the rarified heights that captured the mathematical world in general, and topology in particular, in the period from the 1930’s until the 1970’s. The influence of Thurston’s Princeton notes on the development of topology over the next 30 years would be pervasive, not only in its mathematical content, but even more so in its vision of how to do mathematics. It gave a generation of topologists permission to get their collective hands dirty with the particular and to delve deeply into the study of specific structures on specific examples.
What has geometry to do with topology? Thurston reminded us what Klein had known, that the topology of manifolds is closely related to the geometric structures they support. Just as surfaces may be classified and categorized using the mundane geometry of triangles and lines, Thurston suggested that the infinitely richer, more intricate world of 3-manifolds could, just possibly, be classified using the natural 3-dimensional geometries, which he classified and of which there are eight. And if he was right, the resolution of the most celebrated puzzle of topology—the Poincaré Conjecture—would be but a corollary to this geometric classification.
The Thurston Geometrization Conjecture dominated the discipline of geometric topology over the next three decades. Even after its recent resolution by Hamilton and Perelman, its imprint remains embedded in the working methodology of topologists, who have geometrized not only the topology of manifolds, but the fundamental groups attached to these manifolds. Thus we have as legacy the young and very active field of geometric group theory that avers that the algebraic and combinatorial properties of groups are closely related to the geometries on which they act. This seems to be a candidate for the next organizing principle in topology.
The decade of the eighties was an especially exciting and fertile time for topology as the geometric influence seemed to permeate everything. In the early part of the decade, Jim Cannon, inspired by Thurston, took up a careful study of the combinatorial structure of fundamental groups of surfaces and 3-manifolds, principally cocompact Fuchsian and Kleinian groups, constructing by hand on huge pieces of paper the Cayley graphs of example after example. He has relayed to me that the graphs of the groups associated to hyperbolic manifolds began to construct themselves, in the sense that he gained an immediate understanding of the rest of the graph, after he had constructed a large enough neighborhood of the identity. There was something automatic that took over in the construction and, after a visit with Thurston at Princeton, automatic group theory emerged as a new idea that has found currency among topologists studying fundamental groups. In this work, Cannon anticipated the thin triangle condition as the sine qua non of negative curvature, itself the principal organizing feature of Thurston’s classification scheme. He studied negatively curved groups, rather than negatively curved manifolds, and showed that the resulting geometric structure on the Cayley graphs of such groups provides combinatorial tools that make the structure of the group amenable to computer computations. This was a marriage of group theory with both geometry and computer science, and had immediate ramifications in the topology of manifolds.
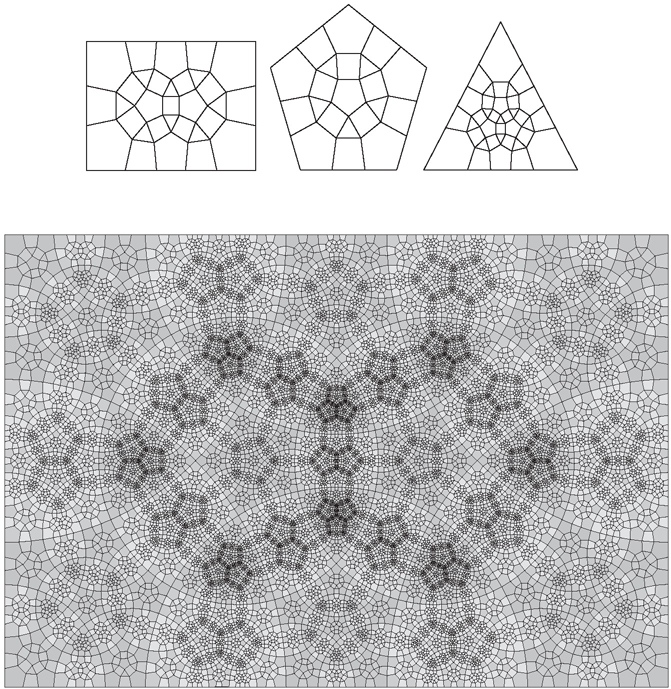
Ultimately these ideas led to one of the most beautiful conjectures left still unresolved by Perelman’s final resolution of the Geometrization Conjecture, namely, that a negatively curved group with 2-sphere boundary is, essentially, a cocompact Kleinian group, the fundamental group of a compact hyperbolic 3-manifold.1,2 Cannon’s attempt to resolve this conjecture in collaboration with his colleagues, Bill Floyd and Walter Parry, has produced some of the most elegant geometric results in recent memory, especially in their elucidation of finite subdivision rules and their use as combinatorial constructs in producing conformal structures on surfaces; see Fig. 1. Activity surrounding Cannon’s program led in the nineties to two discretizations of the classical Riemann Mapping Theorem, the Discrete Riemann Mapping Theorem of Cannon-Floyd-Parry [10] that offers a discrete analogue, proved independently by Schramm [19], and the Combinatorial Riemann Mapping Theorem of Cannon [9] that constructs a classical conformal structure on a space that carries an appropriate combinatorial superstructure. We will return to this development later, but we first mention another strand of the story.
In 1987, Mikhail Gromov increased the excitement and accelerated this project in geometrizing topology and group theory with the publication of his essay Hyperbolic Groups [12] in which he presents his grand, but rather sparsely argued, view of negative curvature in group theory. He followed this in 1993 with the influential Asymptotic Invariants of Infinite Groups [13] accomplishing a similar task for nonpositive curvature. Almost immediately after the respective publications of these two works, groups of mathematicians offered detailed proofs elucidating the big ideas of Gromov, and graduate students in succeeding years wrote theses whose geneses lay in these essays, sometimes explaining, with detailed proofs, a remark of a single sentence from one of the essays. I recall sometime in the mid-nineties at an AMS conference a conversation between two graduate students about their soon to be submitted dissertations. Both acknowledged their debt to Gromov, one stating something along the lines that “yea, mine is based on a secondary comment to a question Gromov posed on page 89 of Asymptotic . . . ,” this in response to the other’s explanation that his was based on an unproved claim in Gromov’s Hyperbolic. . . .”
Finally, it is interesting that the resolution of the Geometrization Conjecture in the past five years relies less on the spirit of nineteenth century hyperbolic geometry, which lies at the heart of Thurston’s original insights, and more on the modern theory of differential equations. Thurston had proved the conjecture for large classes of manifolds, including Haken manifolds, for which he received the Fields Medal in 1982. That same year, Richard Hamilton proposed a method for solving part of the conjecture using Riemannian geometry and the flow of Ricci curvature [14], and later generalized this to a proposal for proving the general conjecture. Hamilton pushed his program forward over the next two decades, but it took the insights of Grigori Perelman to overcome difficulties that arose from singularities of the Ricci flow, in which the principal ingredient is the modern theory of differential equations and global analysis. Perelman famously turned down the offer of a Fields Medal for this work in 2006.
FIGURE 1. Examples of circle packing-generated embeddings of expansion complexes of Cannon-Floyd-Parry that tile the complex plane and are generated by finite subdivision rules with pentagonal combinatorics. The upper left tiling is particularly interesting as it is regular in the sense that each of the pentagons the eye sees at every level of scaling is conformally regular—conformally equivalent to a regular pentagon preserving vertices. Moreover, the whole infinite tiling can be generated from any single elementary tile, just by repeated anti-conformal reflections across edges. See [8].
CIRCLE PACKING: THE BEGINNING
It was into and from this setting that circle packing was born. Its antecedents lay in Koebe’s Theorem [17] of 1936 and Andre’ev’s Theorems [1, 2] of 1970. The analyst Paul Koebe had proved that every triangulation of a disk produces a circle packing of the unit disk in C, a pattern of circles within the unit disk, each corresponding to a vertex of the triangulation, with circles tangent when the corresponding vertices are adjacent, and boundary circles internally tangent to the boundary of the unit disk. Moreover, this pattern is unique up to Möbius transformations of the disk or, what is the same, up to isometries of the disk realized as a model of the hyperbolic geometry of Lobachevski and Bolyai. This seeming novelty was promptly forgotten and it did not emerge among the circle packing community that Koebe had proved this until sometime in the early nineties. From a completely different direction, the geometer E.M. Andre’ev in a first paper of 1970 gave a description of the cusped 3-dimensional hyperbolic polyhedra, and in a second described more general hyperbolic polyhedra, ultimately giving a description of certain 3-dimensional finite-volume hyperbolic polyhedra.
In the late seventies, Thurston, unaware of both the Koebe and Andre’ev results, proved a generalization of Koebe’s Theorem that allowed for specified overlaps among the circles rather than tangency, gave a proof subject to computations, and generalized to surfaces of arbitrary genus. He then observed that the results on 3-dimensional hyperbolic polyhedra discovered by Andre’ev follow from the generalized Koebe results. The connection with hyperbolic 3-space is made by realizing the complex plane as the boundary of the upper half-space of C × R a model of 3-dimensional hyperbolic geometry, augmenting the circle packing with a dual pattern of circles mutually perpendicular to the given ones, and taking the intersection of the appropriate hyperbolic half-spaces bounded by these circles to yield a convex hyperbolic polyhedron with cusps. The generalization to prescribed overlap angles among circles allowed Thurston to include the finite-volume results of Andre’ev in his scheme. Thurston has reported that he proved this theorem one morning, and later that afternoon found the Andre’ev results. It took another fifteen years for Koebe’s contribution to be recognized. These results were not peripheral to his program for classifying 3-manifolds, but were a central ingredient to a part of the program. The now-called Koebe-Andre’ev-Thurston Theorem has been generalized further to include cases where the objects being packed are not circles, but other convex figures, to cases where circles wrap around themselves multiple times, to infinite triangulations of open disks, and even to cases where adjacent vertices represent circles that ‘overlap’ with imaginary angles.
Though Thurston included his circle packing results in the infamous Chapter 13 of the Princeton notes—infamous because many copies sent out omitted Chapter 13—the topic did not generate any heat until 1985 when Thurston suggested in a lecture at Purdue University that the original Koebe Theorem could be used to give an effective computational algorithm for approximating the Riemann mapping of a proper simply-connected domain of C to the unit disk. In the audience sat the analyst Ken Stephenson, now author of the definitive text on circle paking3 and one of the current leaders in the field, then a circle packing novice astonished and intrigued by Thurston’s conjectural association of Koebe’s Theorem with one of the most important results of complex analysis. Stephenson had been trained as a complex analyst, but always had sympathies for the more geometric aspects of the theory. Thurston’s talk, and the subsequent verification of Thurston’s suggestion by Burt Rodin and Dennis Sullivan [18], began the transformation of Stephenson from classical complex analyst to discrete conformal geometer. It led to a flurry of research by several groups and individuals in the geometry of circle packings, their existence and uniqueness, connection to conformal and analytic mappings, applications to solving open mathematical problems, amenability to computations, and relationships to random walks and other discrete phenomena.
Circle packing as a discipline quickly attracted the interest of researchers in analysis, combinatorics, geometry, and topology, and initially developed along “two not disparate branches. The one branch may be characterized broadly as analytic and combinatorial in style with particular attention focused on the topic of Thurston’s Purdue talk; namely, the relationship of circle packing to the approximation of conformal mappings. The emphasis is on the connections of circle packing to classical complex analysis, which motivates and legitimizes its study, and in particular on the construction of both discrete analogs and proofs of some classical theorems of complex analysis. . . . The other branch may be characterized broadly as geometric and topological in style with particular interest in the pure geometry of circle packing. It needs no other motivation or justification than the pleasing interplay between geometry, topology, and combinatorics that exposes a certain rigidity of circle packing that is reminiscent of the rigidity so characteristic of complex analytic functions. The results are often beautiful and sometimes surprising, reminding the authors of their first encounters as graduate students with the surprising rigidity and striking inevitability that permeates this world of complex analytic functions.” 4 This quote of the writer and his colleague Ken Stephenson was written in 1991 and gives a broad sense of the early directions of the subject.
THE DISCRETIZATION OF GEOMETRY
The initial work in circle packing, from 1985 through the mid-nineties, took place in the atmosphere of the geometrizing influence of the topologists. It was not central to their theme of classifying manifolds and understanding the geometric structure of groups, but it did offer an unexplored tributary open to the interested researcher. It was, in addition, amenable to computer exploration and, in fact, not a few mathematicians have been drawn into the subject by the beautifully intricate computer-generated pictures of circle packings and patterns that adorn many publications. Circle-Pack is the most extensive and sophisticated software package available for generating these pictures and is continuously updated by its author and the chief proselytizer of computer experimentation in circle packing—the analyst turned geometer, Ken Stephenson. This software has grown up hand-in-hand with theory, sometimes suggesting routes of theoretical inquiry, other times building intuition and displaying ideas graphically.
The computational tractability of circle packing has placed it squarely in the midst of our second important story in the recent history of mathematics, that of the discretization of geometry that has occured with increasing sophistication over the past decade and a half. Whereas our first story, and circle packing as one of its chapters, has its roots in theoretical, pure mathematics, our second has its in applied computational science, particularly in the various sorts of 2- and 3-dimensional imaging problems that have become accessible only recently with the advent of powerful desktop computers. These imaging problems led to challenging mathematical problems in collecting, representing, manipulating, and deforming representations of embedded surfaces and solids in R3. This ultimately meant that tesselations of 2- and 3-dimensional objects, sometimes triangulations, sometimes quadragulations, needed to be represented and manipulated as data in computations. The worry was to preserve as much as possible in the combinatorial data that encoded the geometry of these objects the original metric data—distances, intrinsic geodesics, angles, and intrinsic and extrinsic curvature. Often this meant calculating geodesics and curvature on combinatorial objects rather than on the original smooth ones, and the usual tools of Riemannian geometry are rendered ineffective in this combinatorial setting.
This story is so unlike the first story with its few prominent protagonists (Thurston, Cannon, Gromov), guided by an overarching paradigm (the Geometrization Conjecture and negative curvature), with revered texts as blueprints (Thurston’s Princeton Notes and Gromov’s Hyperbolic Groups). Discretization of geometry was and is driven by the habitual need to see and manipulate images, and its impetus came from a varied assortment of sources, from the pure mathematics of minimal surfaces and their images, to computer vision and target recognition, from medical imaging of anatomical data to surface manipulation in manufacturing design. It became obvious to several groups of mathematical and computer scientists that the problems they faced were not going to be solved by mere approximation. What was needed was a discrete version of Riemannian geometry faithful in its domain to the spirit of the classical field, representing the continuous objects whose properties they mirrored in some faithful way, but whose computational tools stand on their own and not as approximation to the continuous. This led to the identification of natural analogues in the discrete setting of the usual tools of differential geometry—polyhedral surfaces and spaces, discrete normal vector fields, discrete curvature operators, discrete Laplace-Beltrami operators, discrete geodesics, discrete Gauss maps. One of the interesting features of this effort is that often there are several discrete analogues of the same continuous tool, each of which approximates the continuous appropriately in terms of convergence as mesh size shrinks, but that capture different properties of the discrete objects of study. The paradigm though is different from that of classical numerical approximation where the raison d’être of the discrete operations and calculations is the approximation of the continuous. Rather, the standard in this emerging field of discrete differential geometry is that the discrete theory is a self-contained whole, with natural, exact tools leading to exact calculations, not approximations. Though the classical theory emerges in the limit of small mesh size, this often is not the overriding interest.
Boris Springborn, Peter Schröder, and Ulrich Pinkall state the paradigm this way: “instead of viewing discretization as a means of making the smooth problem amenable to numerical methods, we seek to develop on the discrete level a geometric theory that is as rich as the analogous theory for the smooth problem. The aim is to discretize the whole theory, not just the equations. Instead of asking for an approximation of the smooth problem, we are thus guided by questions like: What corresponds to a Riemannian metric and Gaussian curvature in an analogous theory for triangle meshes?”5
This effort has progressed through the work of many research teams with a variety of expertise—expertise in the pure mathematics of Riemannian geometry, including geometry on infinite-dimensional manifolds, in combinatorial topology and metric geometry, in computer science, symbolic computations, databases and programming, in statistics and engineering, and in a variety of scientific fields. The effort is really vast and multifaceted, and its story does not lend itself to a linear telling, so I am content to name a sampling of notable groups with whom I have some personal familiarity and from which the interested reader may gain a sense of the scope and power of these new ideas in discrete differential geometry. Each of the following groups maintains extensive web archives that explain and detail their considerable work in this emerging field: the Multi-Res Modeling Group at Caltech under the direction of Peter Schröder, the Mathematical Geometry Processing Group at Freie Universität Berlin under the direction of Konrad Polthier, the German Matheon Research Center and particularly its Polyhedral Surfaces Unit under the coordination of Alexander Bobenko, the Discrete Geometry Group at Technische Universität Berlin under the direction of Günter Ziegler, and the Computer Vision Lab at Florida State University under the direction of Xiuwen Liu and Washington Mio.
Circle Packing Comes of Age
Though the origin of circle packing lies in topology, it began to emerge as a separate discipline in the mid-nineties and only recently has found its natural home in the setting of discrete differential geometry. That part of discrete differential geometry that concerns the discretization, in the sense already articulated, of classical complex analysis and conformal geometry is now subsumed under the heading of discrete conformal geometry. Circle packing is one approach to discretizing parts of these classical disciplines and has both advantages and disadvantages when compared to others. Its greatest success is in providing a faithful discrete analogue of classical complex analytic function theory in the complex plane, with discrete versions of classical analytic mappings that in their particularities share essential features and qualities of their classical counterparts. Many of the classical theorems of complex analysis have circle packing analogues that actually imply the truth of the classical theorems in the limit as circle radii approach zero. This is not a two way street as the truth of the classical rarely implies that of the discrete. It is as if the discrete is more fundamental, more primitive, with the classical theory derivative of the discrete. These comments apply as well to other subdisciplines within discrete differential geometry.
A fitting metaphor comes from physics. The discrete theory—circle packing and discrete analytic functions—is the quantum theory from which the classical theory of analytic functions emerges. Classical analytic functions are continuous deformations of the classical complex plane and can be very complicated, but when viewed at the atomic scale, i.e., from the tangent plane, they are local complex dilations that preserve infinitesimal circles. Discrete analytic functions preserve actual circles and locally model the behavior of their classical counterparts. The salient large scale features of the continuous classical functions arise from this atomic scale circle-preserving property of the discrete functions. When we look closely enough at what we thought was the continuous, we find lurking underneath the discrete.
CIRCLE PACKING AS DISCRETE GEOMETRY
To indicate how discrete combinatorial data can carry continuous geometric information, even without any metric or angular data decorating the combinatorics, consider an arbitrary triangulation K of a genus g compact oriented surface S. I stress that S carries no metric structure, it is merely a topological surface. Then there is a unique S conformal structure on and, in that conformal structure, a circle packing C={Cv :v ∈V (K)} , a collection of circles in S indexed by the vertex set V(K) of K, unique up to Möbius transformations, with Cv tangent to Cw whenever the vertices v and w of K are adjacent. To unwrap this a bit, when the genus g = 0, S is a topological 2-sphere and up to equivalence there is only one conformal structure on S, the one identifying S as the Riemann sphere .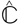 
The circles Cv are then usual circles in the Riemann sphere and this can be seen as a restatement of Koebe’s Theorem. When the genus is g = 1, then S is a topological torus, and there is a continuous 2-dimensional family of pairwise nonequivalent conformal structures available for S. The triangulation K chooses exactly one such structure, and it carries with it an essentially unique flat metric, and the circles Cv are circles with respect to this metric. The generic case is when g ≥ 2. Then there is a continuous (6g – 6)-dimensional family of pairwise nonequivalent conformal structures available for S and the combinatorics of K chooses exactly one such structure. This structure carries a unique metric of constant curvature –1, a hyperbolic metric, and the circles Cv are hyperbolic circles. The packing C is unique up to hyperbolic isometry. I emphasize the fact that none of the other uncountably many conformal structures with their hyperbolic metrics supports a circle packing whose tangencies are encoded in the combinatorics of K.
This is a striking example of discrete combinatorial data encoding continuous geometric information. The result may be proved by several different methods and was one of the key theorems that stimulated early research in circle packing. It is also one of the facts buried in Chapter 13 of Thurston’s Princeton Notes and has been rediscovered and reworked and generalized by several mathematicians. The early years were very active in exploring and generalizing from this result and articulating a background theory of circle packing surfaces. The subject becomes more difficult and intricate when the surfaces or packings are more general—noncompact surfaces with nonempty boundary, or packings that overlap, or wrap around singularities, or infinite packings—but the interplay between combinatorics and geometry remains the organizing principle.
Circle packing has advanced to the point that it offers a discrete theory of general complex analytic mappings of planar domains, and a theory of polynomial mappings of the sphere. Discrete rational mappings of the sphere and discrete conformal mappings of Riemann surfaces are areas of current research. A new direction is in circle packing of surfaces with more general structures than conformal ones; for example, circle packing of projective surfaces has enjoyed recent attention.
SOME MATHEMATICAL CONTRIBUTIONS
Koebe’s Theorem was derived by Koebe as a corollary of his uniformization theorem that says that every finitely connected planar domain is conformally equivalent to the complement in C of a finite number of disks and points, unique up to Möbius transformations. This Koebe Uniformization Theorem is a generalization of the Riemann Mapping Theorem and gives supporting evidence for the very seductive Koebe Conjecture, which avers that every domain in the Riemann sphere is conformally equivalent to a circle domain, defined as the complement in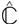 
of a closed set, each component of which is either a point or a round disk, and this is unique up to Möbius transformations.
Despite concerted attempts to prove the Koebe Conjecture over the previous sixty years, not a great deal of success had been recorded until Zheng-Xu He and Oded Schramm in their 1993 Annals of Mathematics paper [15] offered an intricate proof based on circle packing that applied to all domains with countably many complementary components. The general conjecture remains unresolved a decade and a half later, and the He-Schramm result is still the state of the art on the conjecture.
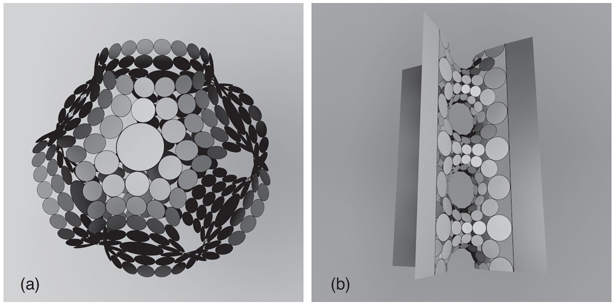
Returning now to Cannon’s Conjecture described earlier, that a negatively curved group with 2-sphere boundary is, essentially, a cocompact Kleinien group, circle packing has been instrumental as an experimental tool in Cannon, Floyd, and Parry’s program. Their program uses combinatorial data on the 2-sphere boundary that arise as the ‘shadows’ of half-spaces to attempt to construct a conformal structure in which these ‘shadows’ are almost round, which they have shown is sufficient to guarantee the conjectured result. They have given conditions that would guarantee the existence of such conformal structures and have modeled the combinatorics-to-conformal-structure procedure by finite subdivision rules, a purely discrete, combinatorial construct. Circle packing techniques have been used as an experimental probe for suggesting this requirement of almost roundness in several important cases in their program. Fig. 2 shows the results of circle packing techniques applied to the dodecahedral subdivision rule that demonstrate how ‘roundness’ emerges from combinatorial data. The underlying combinatorial structure recognized in the example is purely a product of the iteration of the simple subdivision rules illustrated in the top of Fig. 2. Circle packing is then used to place a natural geometric structure on the combinatorics in which the roundness—the pattern of circles that the eye sees—miraculously appears at multiple scales of resolution. Mario Bonk and Bruce Kleiner [5, 6] have offered another approach to Cannon’s Conjecture using analysis on metric spaces that, in at least one place, uses the Koebe-Andre’ev-Thurston Theorem.
FIGURE 2. The figure is generated by applying the dodecahedral subdivision rule to a rectangle three times in succession [original in color]. At each application, the rectangles are subdivided according to the pattern shown in the upper left, the pentagons according to that of the upper middle, and the triangles according to that of the upper right. Circle packing generates the embedding, in which the almost roundness at multiple scales emerges. This is an approximate view of the shadows cast on the sphere at infinity by the first, second, and third generation hyperbolic half-spaces determined by the dodecahedral tiling of hyperbolic 3-space. (Cannon-Floyd-Parry)
I mention one last example where circle packing has made an impact in pure mathematics, and that is in offering new tools as well as new settings in which to study types of graphs. Infinite graphs offer a discrete setting in which to study random walks. Plane triangulation graphs are infinite graphs that offer not only the transient-recurrent dichotomy of random walks, but also the hyperbolic-parabolic dichotomy of circle packing. This hyperbolic-parabolic dichotomy arises since each plane triangulation graph encodes the tangency combinatorics of a circle packing in either the hyperbolic plane or the euclidean plane, but never both. How the circle packing type—hyperbolic or parabolic—compares with the random walk type—transient or recurrent—has led to fruitful interplay between circle packing and classical random walks, which has enriched both fields.
SOME APPLICATIONS
One of the interesting applications of circle packing and pattern theory is in discrete conformal flattening where a smooth surface in R3 is represented by a planar surface in a way that preserves, as much as possible, the conformal structure of the original. Though there are flattening algorithms based on classical numerical analysis that provide quick, accurate conformal maps, the advantage the circle packing algorithms bring is that, once flattened, the full range of the discrete theory of analytic and conformal mappings is available. Stephenson’s software package has been used in anatomical flattenings in several studies; see, for example, [16].
Bobenko and Springborn [3] have initiated exploration recently of new algorithms based on circle patterns whose tangencies are encoded using square, rather than triangular, combinatorics. The inspiration for this comes from the physics of integrable systems, and has been successful, not only at conformal flattening, but in an elegant discrete representation of minimal embedded surfaces in R3 by Bobenko, Hoffmann, and Springborn [4], as in Fig. 3.
Finally, I mention the modest appearance of circle packing in the recently articulated mathematical theory of origami used to design and fold incredibly intricate origami figures, and their use in engineering design. I highly recommend Robert Lang’s recent TED lecture of February 2008 found on the TED website at http://www.ted.com/.
Epilogue
This story began in an era of rarified abstraction in mathematics. The influence of mathematicians like Thurston and Cannon and Gromov brought a relaxation of that abstraction in geometry and topology and gave us permission to practice geometry again with our hands in the way of the great Felix Klein and his contemporaries. Circle packing represents one example of this more hands on approach to geometry, and its success is a testament to the power of the particular in mathematics. The elegant complexity that arises from the simplicity of elementary geometry—for what is more elementary than the circle—has fascinated a generation of circle packers, and promises to continue to fascinate new generations as the theory is extended and applied. All this from the humble circle!
Acknowledgments
This article is dedicated to the memory of Oded Schramm, who worked in circle packing before his discovery of stochastic Loewner evolution and its applications to critical phenomena. This extraordinary mathematician’s untimely death on 01 September 2008 in a hiking accident was a great loss for our community.
Notes
1. Precisely, the group acts properly discontinuously, cocompactly, and isometrically on hyperbolic 3-space.
2. For a beautifully presented description of this work, see [11].
3. [21], Introduction to Circle Packing: the Theory of Discrete Analytic Functions, published in 2005 by Cambridge University Press.
4. [7], pp. 157–8.
5. [20], p. 77:1.
References
[1]E.M. Andre’ev, Convex polyhedra in Lobacevskii space, Math. USSR Sbornik 10 (1970), pp. 413–440.
[2]E.M. Andre’ev, Convex polyhedra of finite volume in Lobacevskii space, Math. USSR Sbornik 12 (1970), pp. 255–259.
[3]A.I. Bobenko and B.A. Springborn, Variational principles for circle patterns and Koebe’s theorem, Trans. AMS 356 (2003), pp. 659–689.
[4]A.I. Bobenko, T. Hoffmann, and B.A. Springborn, Minimal surfaces from circle patterns: geometry from combinatorics, Annals of Math. 164:1 (2006), pp. 231–264.
[5]M. Bonk and B. Kleiner, Quasisymmetric parametrizations of two-dimensional metric spheres, Invent. Math. 150 (2002), no. 1, pp. 127–183.
[6]M. Bonk and B. Kleiner, Conformal dimension and Gromov hyperbolic groups with 2-sphere boundary, Geometry & Topology 9 (2005), pp. 219–246.
[7]P.L. Bowers and K. Stephenson, Circle packings in surfaces of finite type: An in situ approach with applications to moduli, Topology 32 (1993), pp. 157–183.
[8]P.L. Bowers and K. Stephenson, A “regular” pentagonal tiling of the plane, Con. Geom. and Dynamics 1 (1997), pp. 58–86.
[9]J.W. Cannon, The combinatorial Riemann mapping theorem, Acta. Math. 173 (1994), 155–234.
[10]J.W. Cannon, W.J. Floyd, and W.R. Parry, Squaring rectangles: the finite Riemann mapping theorem, in The Mathematical Heritage of Wilhelm Magnus—Groups, Geometry, and Special Functions, Contemporary Mathematics, vol. 169, Amer. Math. Soc., Providence, 1994, pp. 133–212.
[11]J.W. Cannon, W.J. Floyd, and W.R. Parry, The length-area method and discrete Riemann mappings, unpublished manuscript available from Bill Floyd that is based on a talk given by J. Cannon at the Ahlfors Celebration at Stanford University in September, 1997 (1998).
[12]M. Gromov, Hyperbolic Groups, in Essays in Group Theory, G.M. Gersten, ed., MSRI Publ. 8, 1987, pp. 75–263.
[13]M. Gromov, Asymptotic invariants of infinite groups, in Geometric Group Theory, Vol. 2 (Sussex, 1991), LMS Lecture Note Series, 182, Cambridge University Press, Cambridge, 1993, pp. 1–295.
[14]R. Hamilton, Three-manifolds with positive Ricci curvature, J. Diff. Geom. 17 (1982), pp. 255–306.
[15]Z-X. He and O. Schramm, Fixed points, Koebe uniformization and circle packings, Annals of Math. 137 (1993), pp. 369–406.
[16]M.K. Hurdal and K. Stephenson, Cortical cartography using the discrete conformal approach of circle packings, NeuroImage 23 (2004), Supplement 1, pp. S119–S128.
[17]P. Koebe, Kontaktprobleme der Konformen Abbildung, Ber. Sächs. Akad. Wiss. Leipzig, Math.-Phys. Kl. 88 (1936), pp. 141–164.
[18]B. Rodin and D. Sullivan, The convergence of circle packings to the Riemann mapping, J. Diff. Geom. 26 (1987), pp. 349–360.
[19]O. Schramm, Square tilings with prescribed combinatorics, Israel J. Math. 84 (1993), 97–118.
[20]B. Springborn, P. Schröder, and U. Pinkall, Conformal equivalence of triangle meshes, ACM Transactions on Graphics 27:3 [Proceedings of ACM SIGGRAPH 2008], Article 77, 2008.
[21]K. Stephenson, Introduction to Circle Packing: the Theory of Discrete Analytic Functions, Cambridge Univ. Press, 2005.