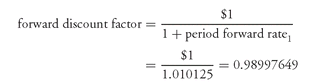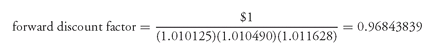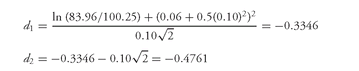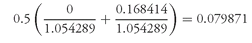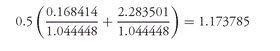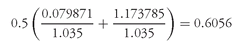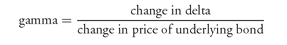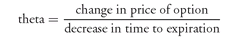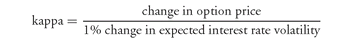CHAPTER 14
VALUATION OF INTEREST RATE DERIVATIVE INSTRUMENTS
I. INTRODUCTION
In the previous chapter, we described interest rate derivative instruments—futures, forwards, options, swaps, caps, and floors. In this chapter, we focus on the valuation of these instruments. Later, we will see how they can be used by portfolio managers to control interest rate risk.
II. INTEREST RATE FUTURES CONTRACTS
In this section we will use an illustration to show how a futures contract is valued. Suppose that a 20-year, $100 par value bond with a coupon rate of 8% is selling at par and that the next coupon payment is six months from now. Also suppose that this bond is the deliverable for a futures contract that settles in three months. If the current 3-month interest rate at which funds can be loaned or borrowed is 4% per year, what should be the price of this futures contract?
Suppose the price of the futures contract is 105. Consider the following strategy:
Sell the futures contract that settles in three months at $105.
Borrow $100 for three months at 4% per year.
With the borrowed funds, purchase the underlying bond for the futures contract.
Notice that, ignoring initial margin and other transaction costs, there is no cash outlay for this strategy because the borrowed funds are used to purchase the bond. Three months from now, the following must be done:
Deliver the purchased bond to settle the futures contract.
Repay the loan.
When the bond is delivered to settle the futures contract three months from now, the amount received is the futures price of $105 plus the accrued interest. Since the coupon rate is 8% for the bond delivered and the bond is held for three months, the accrued interest is $2[(8% × $100)
/4]. Thus, the amount received is $107 ($105 + $2). The amount that must be paid to repay the loan is the $100 principal plus the interest. Since the interest rate for the loan is 4% per year and the loan is for three months, the interest cost is $1. Thus, the amount paid is $101 ($100 + $1).
184 To summarize, at the end of three months the cash flow will be:
| Cash inflow from delivery of the bond | = | $107 |
| Cash outflow from repayment of the loan | = | -$101 |
| Profit | = | $6 |
This strategy guarantees a profit of $6. Moreover, the profit is generated with no initial outlay because the funds used to purchase the bond are borrowed. The profit will be realized regardless of the futures price at the settlement date. Obviously, in a well-functioning market, arbitrageurs would buy the bond and sell the futures, forcing the futures price down and bidding up the bond price so as to eliminate this profit.
This strategy of purchasing a bond with borrowed funds and simultaneously selling a futures contract is called a cash and carry trade.
In contrast, suppose that the futures price is $96 instead of $105. Consider the strategy below and which is depicted in
Exhibit 2:
Buy the futures contract that settles in three months at $96.
Sell (short) the bond underlying the futures contract for $100.
Invest (lend) the $100 proceeds from the short sale for three months at 4% per year.
Once again, there is no cash outlay if we ignore the initial margin for the futures contract and other transaction costs. Three months from now when the futures contract must be settled, the following must be done:
Purchase the underlying bond to settle the futures contract.
Receive proceeds from repayment of the loan.
When the bond is delivered to settle the futures contract three months from now, the amount paid is the futures price of $96 plus the accrued interest of $2, or $98. The amount that will be received from the proceeds invested (lent) for three months is $101, or $100 principal plus interest of $1.
185 To summarize, at the end of three months the cash flow will be:
| Cash inflow from the amount invested (lent) | = | $101 |
| Cash outflow to purchase the bond | = | −$98 |
| Profit | = | $3 |
A profit of $3 will be realized. This is an arbitrage profit because it requires no initial cash outlay and will be realized regardless of the futures price at the settlement date.
Because this strategy involves initially selling the underlying bond, it is called a reverse cash and carry trade.
There is a futures price that eliminates any arbitrage profit. There will be no arbitrage profit if the futures price is $99. Let’s look at what would happen if each of the two previous strategies is followed when the futures price is $99. First, consider the cash and carry trade:
Sell the futures contract that settles in three months at $99.
Borrow $100 for three months at 4% per year.
With the borrowed funds purchase the underlying bond for the futures contract.
When the bond is delivered to settle the futures contract three months from now, the amount received is the futures price of $99 plus the accrued interest of $2, or $101. The amount required to repay the loan is the $100 principal plus the interest of $1. Thus, the amount paid is $101. To summarize, at the end of three months the cash flow will be:
| Cash inflow from delivery of the bond | = | $101 |
| Cash outflow from repayment of the loan | = | −$101 |
| Profit | = | $0 |
Thus, there is no arbitrage profit if the futures price is $99.
Next, consider the reverse cash and carry trade. In this trade the following is done today:
Buy the futures contract that settles in three months at $99.
Sell the bond underlying the futures contract for $100.
Invest (lend) the $100 proceeds from the short sale for three months at 4% per year.
Three months from now when the futures contract must be settled, the amount to be paid is the futures price of $99 plus the accrued interest of $2, or $101. The amount that will be received from the proceeds of the three month loan is $101, $100 plus interest of $1. At the end of three months the cash flow will be:
| Cash inflow from the amount invested (lent) | = | $101 |
| Cash outflow to purchase the bond | = | X−$101 |
| Profit | = | $0 |
Thus, neither strategy results in a profit or loss. Hence, the futures price of $99 is the equilibrium or theoretical price, because any higher or lower futures price will permit arbitrage profits.
A. Theoretical Futures Price Based on Arbitrage Model
Considering the arbitrage arguments (based on the cash and carry trade) just presented, the theoretical futures price can be determined from the following information:
1. The price of the underlying bond in the cash market. (In our example, the price of the bond is $100.)
2. The coupon rate on the bond. (In our example, the coupon rate is 8% per year.)
3. The interest rate for borrowing and lending until the settlement date. The borrowing and lending rate is referred to as the financing rate. (In our example, the financing rate is 4% per year.)
We will let
r = financing rate (in decimal)
c = current yield, or annual dollar coupon divided by the cash market price (in decimal)
P = cash market price
F = futures price
t = time, in years, to the futures delivery date
Given an assumption of no interim cash flows and no transaction costs, the equation below gives the theoretical futures price that produces a zero profit (i.e., no arbitrage profit) using either the cash and carry trade or the reverse cash and carry trade:
Let’s apply
equation (1) to our previous example in which
r = 0.04 c = 0.08 P = 100 t = 0.25
Then the theoretical futures price is
F = 100 + 100 × 0.25 × (0.04 − 0.08) = 100 − 1 = 99
This agrees with the theoretical futures price we derived earlier.
It is important to note that c is the current yield, found by dividing the coupon interest payment by the cash market price. In our illustration above, since the cash market price of the bond is 100, the coupon rate is equal to the current yield. If the cash market price is not the par value, the coupon rate is not equal to the current yield.
The theoretical futures price may be at a premium to the cash market price (higher than the cash market price) or at a discount from the cash market price (lower than the cash market price), depending on (
r −
c). The term (
r −
c) is called the
net financing cost because it adjusts the financing rate for the coupon interest earned. The net financing cost is more commonly called the
cost of carry, or simply
carry. Positive carry means that the current yield earned is greater than the financing cost;
negative carry means that the financing cost exceeds the current yield. The relationships can be expressed as follows:
| Carry | Futures price |
|---|
| Positive (c > r) | At a discount to cash price (F < P) |
| Negative (c < r) | At a premium to cash price (F > P) |
| Zero (c = r) | Equal to cash price(F = P) |
In the case of interest rate futures, carry depends on the shape of the yield curve. When the yield curve is upward sloping, the short-term financing rate is lower than the current yield on the bond, resulting in positive carry. The futures contract then sells at a discount to the cash price for the bond. The opposite is true when the yield curve is inverted.
Earlier we explained how the cash and carry trade or the reverse cash and carry trade can be used to exploit any mispricing of the futures contract. Let’s review when each trade is implemented based on the actual futures price relative to the theoretical futures price. In our illustration when the theoretical futures price was 99 but the actual futures price was 105, the arbitrage profit due to the futures contract being overpriced was captured using the cash and carry trade. Alternatively, when the cash market price was assumed to be 96, the arbitrage profit resulting from the cheapness of the futures contract was captured by the reverse cash and carry trade. To summarize:
| Relationship between theoretical futures price and cash market price | Implement the following trade to capture the arbitrage profit |
|---|
| theoretical futures price > cash market price | cash and carry trade |
| theoretical futures price < cash market price | reverse cash and carry trade |
B. A Closer Look at the Theoretical Futures Price
To derive the theoretical futures price using the arbitrage argument, we made several assumptions. Below we look at the implications of these assumptions.
1. Interim Cash Flows In the model we assumed no interim cash flows due to variation margin or coupon interest payments. However, we know that interim cash flows can occur for both of these reasons. Because we assumed no initial margin or variation margin, the price derived is technically the theoretical price for a forward contract that is not marked to market. Incorporating interim coupon payments into the pricing model is not difficult. However, the value of the coupon payments at the settlement date will depend on the interest rate at which they can be reinvested. The shorter the maturity of the futures contract and the lower the coupon rate, the less important the reinvestment income is in determining the futures price.
2. The Short-Term Interest Rate (Financing Rate) In presenting the theoretical futures price in
equation (1), we assumed that the borrowing and lending rates are equal. Typically, however, the borrowing rate is higher than the lending rate. If we will let
rB = borrowing rate and rL = lending rate
and continue with our assumption of no interim cash flows and no transaction costs, then the futures price that would produce no cash and carry arbitrage profit is
and the futures price that would produce no reverse cash and carry arbitrage profit is
Equations (2) and (3) together provide boundaries for the theoretical futures price.
Equation (2) provides the upper boundary and
equation (3) the lower boundary. For example, assume that the borrowing rate is 4% per year, while the lending rate is 3.2% per year. Then using
equation (2) and the previous example, the upper boundary is
F (upper boundary) = 100 + 100 × 0.25 × (0.04 − 0.08) = 99
The lower boundary, using
equation (3), is
F(lower boundary) = 100 + 100 × 0.25 × (0.032 − 0.08) = 98.8
In calculating these boundaries, we assume no transaction costs are involved in taking the position. In actuality, the transaction costs of entering into and closing the cash position as well as the round-trip transaction costs for the futures contract must be considered because these transaction costs affect the boundaries for the futures contract.
3. Deliverable Bond Is Not Known The arbitrage arguments used to derive
equation (1) assumed that only one instrument is deliverable. But as explained in the previous chapter, the futures contracts on Treasury bonds and Treasury notes are designed to allow the short the choice of delivering any one of a number of deliverable issues (the quality or swap option
186). Because there may be more than one deliverable, market participants track the price of each deliverable bond and determine which bond is the cheapest to deliver. The futures price will then trade in relation to the cheapest-to-deliver issue.
There is the risk that while an issue may be the cheapest to deliver at the time a position in the futures contract is taken, it may not be the cheapest to deliver after that time. A change in the cheapest-to-deliver can dramatically alter the futures price. What are the implications of the quality (swap) option on the futures price? Because the swap option is an option granted by the long to the short, the long will want to pay
less for the futures contract than indicated by
equation (1). Therefore, as a result of the quality option, the theoretical futures price as given by
equation (1) must be adjusted as follows:
(4)
Market participants have employed theoretical models to estimate the fair value of the quality option. A discussion of these models is beyond the scope of this chapter.
4. Delivery Date Is Not Known In the pricing model based on arbitrage arguments, a known delivery date is assumed. For Treasury bond and note futures contracts, the short has a timing option and a wild card option, so the long does not know when the security will be delivered. The effect of the timing and wild card options
187 on the theoretical futures price is the same as with the quality option. These delivery options result in a theoretical futures price that is lower than the one suggested by
equation (1), as shown below:
(5)
or alternatively,
Market participants attempt to value the delivery options in order to apply
equation (6). A discussion of these models is a specialist topic.
5. Putting It Altogether To summarize, there is not one theoretical futures price that would eliminate any arbitrage profit, but a range for the theoretical futures prices based on borrowing and lending rates. Consequently, the futures price can fluctuate within this range and there will be no arbitrage profit. Once recognition is given to the delivery options granted to the short in the futures contract, the theoretical futures price is lower. Specifically, it is reduced by the value of the delivery options. This means that the lower boundary for the theoretical futures price shifts down by an amount equal to the value of the delivery options and the upper boundary for the theoretical futures price shifts down by the same amount.
III. INTEREST RATE SWAPS
In an interest rate swap, the counterparties agree to exchange periodic interest payments. The dollar amount of the interest payments exchanged is based on the notional principal. In the most common type of swap, there is a fixed-rate payer and a fixed-rate receiver. The convention for quoting swap rates is that a swap dealer sets the floating rate equal to the reference rate (i.e., the interest rate used to determine the floating-rate in a swap) and then quotes the fixed rate that will apply.
A. Computing the Payments for a Swap
In the previous chapter on interest rate derivative instruments, we described the basic features of an interest rate swap using rough calculations for the payments and explained how the parties to a swap either gain or lose when interest rates change. For valuation, however. we need more details. To value a swap it is necessary to determine the present value of the fixed-rate payments and the present value of the floating-rate payments. The difference between these two present values is the value of a swap. As will be explained below, whether the value is positive (i.e., an asset) or negative (i.e., a liability) depends on whether the party is the fixed-rate payer or the fixed-rate receiver.
We are interested in how the swap rate is determined at the inception of the swap. At the inception of the swap, the terms of the swap are such that the present value of the floating-rate payments is equal to the present value of the fixed-rate payments. At inception the value of the swap is equal to zero. This is the fundamental principle in determining the swap rate (i.e., the fixed rate that the fixed-rate payer will pay).
Here is a roadmap of the presentation. First we will look at how to compute the floating-rate payments. We will see how the future values of the reference rate are determined to obtain the floating rate for the period. From the future values of the reference rate we will then see how to compute the floating-rate payments, taking into account the number of days in the payment period. Next we will see how to calculate the fixed-rate payments given the swap rate. Before we look at how to calculate the value of a swap, we will see how to calculate the swap rate. This will require an explanation of how the present value of any cash flow in an interest rate swap is computed. Given the floating-rate payments and the present value of the floating-rate payments, the swap rate can be determined by using the principle that the swap rate is the fixed rate that makes the present value of the fixed-rate payments equal to the present value of the floating-rate payments. Finally, we will see how the value of a swap is determined after the inception of a swap.
1. Calculating the Floating-Rate Payments For the first floating-rate payment, the amount is known because the floating-rate is known at the beginning of the period even though it is paid at the end of the period (i.e., payment is made in arrears). For all subsequent payments, the floating-rate payment depends on the value of the reference rate when the floating rate is determined. To illustrate the issues associated with calculating the floating-rate payment, we assume that:
• swap starts today, January 1 of year 1
• the floating-rate payments are made quarterly based on “actual/360” (“actual” means the actual number of days in the quarter)
• the reference rate is 3-month LIBOR (London interbank offered rate)
• the notional amount of the swap is $100 million
• the term of the swap is three years
The quarterly floating-rate payments are based on an “actual/360” day count convention. This convention means that we assume 360 days in a year and that, in computing the interest for the quarter, the actual number of days in the quarter is used. The floating-rate payment is set at the beginning of the quarter but paid at the end of the quarter—that is, the floating-rate payments are made in arrears.
Suppose that today 3-month LIBOR is 4.05%. Let’s look at what the fixed-rate payer will receive on March 31 of year 1—the date when the first quarterly swap payment is made. There is no uncertainty about what the floating-rate payment will be. In general, the floating-rate payment is determined as follows:
In our illustration, assuming a non-leap year, the number of days from January 1 of year 1 to March 31 of year 1 (the first quarter) is 90. If 3-month LIBOR is 4.05%, then the fixed-rate payer will receive a floating-rate payment on March 31 of year 1 equal to:
Now the difficulty is in determining the floating-rate payments after the first quarterly payment. While the first quarterly payment is known, the next 11 are not. However, there is a way to hedge the next 11 floating-rate payments by using a futures contract. The futures contract equivalent to the future floating-rate payments in a swap whose reference rate is 3-month LIBOR is the Eurodollar CD futures contract. In effect then, the remaining swap payments are equivalent to a package of futures contracts. We will digress to discuss this contract.
a.
The Eurodollar CD Futures Contract As explained in the previous chapter, a swap position can be interpreted as a package of forward/futures contracts or a package of cash flows from buying and selling cash market instruments. It is the former interpretation that will be used as the basis for valuing a swap.
Eurodollar certificates of deposit (CDs) are denominated in dollars but represent the liabilities of banks outside the United States. The contracts are traded on both the International Monetary Market of the Chicago Mercantile Exchange and the London International Financial Futures Exchange. The rate paid on Eurodollar CDs is LIBOR.
The 3-month Eurodollar CD is the underlying instrument for the Eurodollar CD futures contract. The contract is for $1 million of face value and is traded on an index price basis. The index price basis is equal to 100 minus the product of the annualized LIBOR futures rate in decimal and 100. For example, a Eurodollar CD futures price of 94.00 means a 3-month LIBOR futures rate of 6% [100 minus (0.06 × 100)].
The Eurodollar CD futures contract is a cash settlement contract. That is, the parties settle in cash for the value of a Eurodollar CD based on LIBOR at the settlement date.
The Eurodollar CD futures contract allows the buyer of the contract to lock in the rate on 3-month LIBOR today for a future 3-month period. For example, suppose that on February 1 in Year 1 an investor purchases a Eurodollar CD futures contract that settles in March of Year 1. Assume that the LIBOR futures rate for this contract is 5%. This means that the investor has agreed to invest in a 3-month Eurodollar CD that pays a rate of 5%. Specifically, the investor has locked in a 3-month rate of 5% beginning March of Year 1. If on February 1 of Year 1 this investor purchased a contract that settles in September of Year 2 and the LIBOR futures rate is 5.4%, the investor has locked in the rate on a 3-month investment beginning September of Year 2.
The seller of a Eurodollar CD futures contract is agreeing to lend funds for three months at some future date at the LIBOR futures rate. For example, suppose that on February 1 of Year 1 a bank sells a Eurodollar CD futures contract that settles in March of Year 1 and the LIBOR futures rate is 5%. The bank locks in a borrowing rate of 5% for three months beginning in March of Year 1. If the settlement date is September of Year 2 and the LIBOR futures rate is 5.4%, the bank is locking in a borrowing rate of 5.4% for the 3-month period beginning September of Year 2.
The key point here is that the Eurodollar CD futures contract allows a participant in the financial market to lock in a 3-month rate on an investment or a 3-month borrowing rate. The 3-month period begins in the month that the contract settles.
b.
Determining Future Floating-Rate Payments Now let’s return to our objective of determining the future floating-rate payments. These payments can be locked in over the life of the swap using the Eurodollar CD futures contract. We will show how these floating-rate payments are computed using this contract.
We will begin with the next quarterly payment—for the quarter that runs from April 1 of year 1 to June 30 of year 1. This quarter has 91 days. The floating-rate payment will be determined by 3-month LIBOR on April 1 of year 1 and paid on June 30 of year 1. There is a 3-month Eurodollar CD futures contract for settlement on March 31 of year 1. The price of that futures contract will reflect the market’s expectation of 3-month LIBOR on April 1 of year 1. For example, if the futures price for the 3-month Eurodollar CD futures contract that settles on March 31 of year 1 is 95.85, then as explained above, the 3-month Eurodollar futures rate is 4.15%. We will refer to that rate for 3-month LIBOR as the “forward rate.”
188 Therefore, if the fixed-rate payer bought 100 of these 3-month Eurodollar CD futures contracts on January 1 of year 1 (the inception of the swap) that settle on March 31 of year 1, then the payment that will be locked in for the quarter (April 1 to June 30 of year 1) is
(Note that each futures contract is for $1 million and hence 100 contracts have a notional amount of $100 million.) Similarly, the Eurodollar CD futures contract can be used to lock in a floating-rate payment for each of the next 10 quarters. Once again, it is important to emphasize that the reference rate at the beginning of period t determines the floating-rate that will be paid for the period. However, the floating-rate payment is not made until the end of period t .
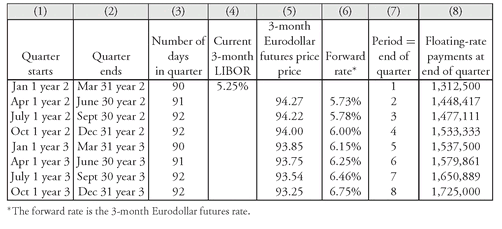
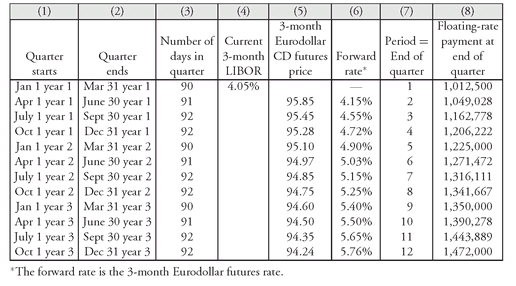
Exhibit 3 shows this for the 3-year swap. Shown in Column (1) is when the quarter begins and in Column (2) when the quarter ends. The payment of $1,012,500 will be received at the end of the first quarter (March 31 of year 1). That is the known floating-rate payment as explained earlier. It is the only payment that is known. The information used to compute the first payment is in Column (4) which shows the current 3-month LIBOR (4.05%). The payment is shown in the last column, Column (8).
Notice that Column (7) numbers the quarters from 1 through 12. Look at the heading for Column (7). It identifies each quarter in terms of the end of the quarter. This is important because we will eventually be discounting the payments (cash flows). We must take care to understand when the payments are to be exchanged in order to discount properly. So, the first payment of $1,012,500 is going to be received at the end of quarter 1. When we refer to the time period for any payment, the reference is to the end of quarter. So, the fifth payment of $1,225,000 would be identified as the payment for period 5, where period 5 means that it will be exchanged at the end of the fifth quarter.
2. Calculating the Fixed-Rate Payments The swap specifies the frequency of settlement for the fixed-rate payments. The frequency need not be the same for the floating-rate payments. For example, in the 3-year swap we have been using to illustrate the calculation of the floating-rate payments, the frequency is quarterly. The frequency of the fixed-rate payments could be semiannual rather than quarterly.
EXHIBIT 3 Floating-Rate Payments Based on Initial LIBOR and Eurodollar CD Futures
In our illustration we will assume that the frequency of settlement is quarterly for the fixed-rate payments, the same as for the floating-rate payments. The day count convention is the same as for the floating-rate payment, “actual/360”. The equation for determining the dollar amount of the fixed-rate payment for the period is:
This is the same equation used for determining the floating-rate payment except that the swap rate is used instead of the reference rate (3-month LIBOR in our illustration).
For example, suppose that the swap rate is 4.98% and that the quarter has 90 days. Then the fixed-rate payment for the quarter is:
If there are 92 days in a quarter, the fixed-rate payment for the quarter is:
Note that the rate is fixed for each quarter but the dollar amount of the payment depends on the number of days in the period.
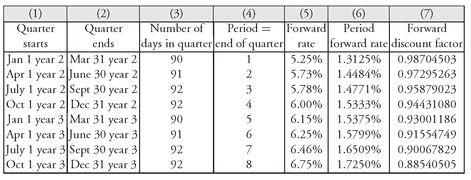
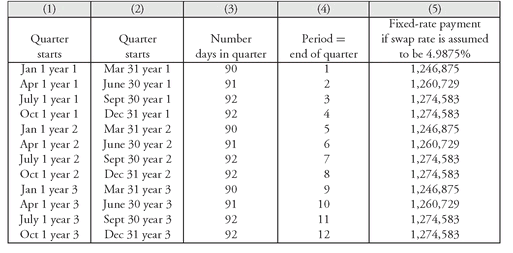
Exhibit 4 shows the fixed-rate payments based on an
assumed swap rate of 4.9875%. (Later we will see how the swap rate is determined.) The first three columns of the exhibit show the same information as in
Exhibit 3—the beginning and end of the quarter and the number of days in the quarter. Column (4) simply uses the notation for the period. That is, period 1 means the end of the first quarter, period 2 means the end of the second quarter, and so on. Column (5) shows the fixed value payments for each period based on a swap rate of 4.9875%.
EXHIBIT 4 Fixed-Rate Payments Assuming a Swap Rate of 4.9875%
B. Calculation of the Swap Rate
Now that we know how to calculate the payments for the fixed-rate and floating-rate sides of a swap where the reference rate is 3-month LIBOR given (1) the current value for 3-month LIBOR, (2) a series for 3-month LIBOR in the future from the Eurodollar CD futures contract, and (3) the assumed swap rate, we can demonstrate how to compute the swap rate.
At the initiation of an interest rate swap, the counterparties are agreeing to exchange future payments. No upfront payments are made by either party. This means that the swap terms must be such that the present value of the payments to be made by the counterparties must be at least equal to the present value of the payments that will be received. In fact, to eliminate arbitrage opportunities, the present value of the payments made by a party will be equal to the present value of the payments received by that same party. The equivalence of the present value of the payments (or no arbitrage) is the key principle in calculating the swap rate.
Since we will have to calculate the present value of the payments, let’s show how this is done.
1. Calculating the Present Value of the Floating-Rate Payments As explained earlier, we must be careful about how we compute the present value of payments. In particular, we must carefully specify (1) the timing of the payments and (2) the interest rates used to discount the payments. We already addressed the first issue. In constructing the exhibit for the payments, we indicated that the payments are made at the end of the quarter. So, we denoted the timing of the payments with respect to the end of the quarter.
Now let’s turn to the interest rates that should be used for discounting. Earlier we emphasized two points. First, every cash flow should be discounted at its own discount rate using the relevant spot rate. So, if we discounted a cash flow of $1 using the spot rate for period
t, the present value would be:
The second point we emphasized is that forward rates are derived from spot rates so that if we discount a cash flow using forward rates rather than a spot rate, we would arrive at the same value. That is, the present value of $1 to be received in period
t can be rewritten as:
We will refer to the present value of $1 to be received in period
t as the
forward discount factor. In our calculations involving swaps, we will compute the forward discount factor for a period using the forward rates. These are the same forward rates that are used to compute the floating-rate payments—those obtained from the Eurodollar CD futures contract. We must make just one more adjustment. We must adjust the forward rates used in the formula for the number of days in the period (i.e., the quarter in our illustrations) in the same way that we made this adjustment to compute the payments. Specifically, the forward rate for a period, which we will refer to as the
period forward rate, is computed using the following equation:
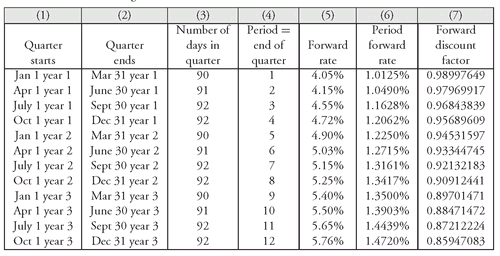
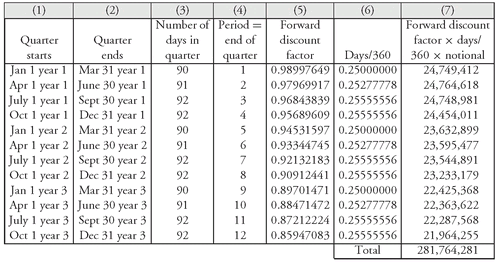
For example, look at
Exhibit 3. The annual forward rate for period 4 is 4.72%. The period forward rate for period 4 is:
Column (5) in
Exhibit 5 shows the annual forward rate for each of the 12 periods (reproduced from
Exhibit 3) and Column (6) shows the period forward rate for each of the 12 periods. Note that the period forward rate for period 1 is
4.05%, which is
of the known rate for 3-month LIBOR.
EXHIBIT 5 Calculating the Forward Discount Factor
Also shown in
Exhibit 5 is the forward discount factor for each of the 12 periods. These values are shown in the last column. Let’s show how the forward discount factor is computed for periods 1, 2, and 3. For period 1, the forward discount factor is:
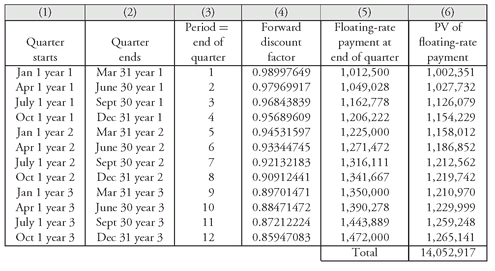
Given the floating-rate payment for a period and the forward discount factor for the period, the present value of the payment can be computed. For example, from
Exhibit 3 we see that the floating-rate payment for period 4 is $1,206,222. From
Exhibit 5, the forward discount factor for period 4 is 0.95689609. Therefore, the present value of the payment is:
present value of period 4 payment = $1,206,222 × 0.95689609 = $1,154,229
Exhibit 6 shows the present value for each payment. The total present value of the 12 floating-rate payments is $14,052,917. Thus, the present value of the payments that the fixed-rate payer will receive is $14,052,917 and the present value of the payments that the fixed-rate receiver will pay is $14,052,917.
EXHIBIT 6 Present Value of the Floating-Rate Payments
2. Determination of the Swap Rate The fixed-rate payer will require that the present value of the fixed-rate payments that must be made based on the swap rate not exceed the $14,052,917 present value of the floating-rate payments to be received. The fixed-rate receiver will require that the present value of the fixed-rate payments to received be at least as great as the $14,052,917 that must be paid. This means that both parties will require the present value of the fixed-rate payments to be $14,052,917. If that is the case, the present value of the fixed-rate payments is equal to the present value of the floating-rate payments and therefore the value of the swap is zero for both parties at the inception of the swap. The interest rates used to compute the present value of the fixed-rate payments are the same as those used to discount the floating-rate payments.
Beginning with the basic relationship for no arbitrage to exist:
PV of floating-rate payments = PV of fixed-rate payments
it can be shown that the formula for the swap rate is:
189
where
Note that all the values needed to compute the swap rate are known.
EXHIBIT 7 Calculating the Denominator for the Swap Rate Formula
Let’s apply the formula to determine the swap rate for our 3-year swap.
Exhibit 7 shows the calculation of the denominator of the formula. The forward discount factor for each period shown in Column (5) is obtained from Column (4) of
Exhibit 6. The sum of the last column in
Exhibit 7 shows that the denominator of the swap rate formula is $281,764,281. We know from
Exhibit 6 that the present value of the floating-rate payments is $14,052,917. Therefore, the swap rate is
Given the swap rate, the swap spread can be determined. For example, since this is a 3-year swap, the convention is to use the 3-year on-the-run Treasury rate as the benchmark. If the yield on that issue is 4.5875%, the swap spread is 40 basis points (4.9875% − 4.5875%).
The calculation of the swap rate for all swaps follows the same principle: equating the present value of the fixed-rate payments to that of the floating-rate payments.
C. Valuing a Swap
Once the swap transaction is completed, changes in market interest rates will change the payments for the floating-rate side of the swap. The value of an interest rate swap is the difference between the present values of the payments for the two sides of the swap. The 3-month LIBOR forward rates from the current Eurodollar CD futures contracts are used to (1) calculate the floating-rate payments and (2) determine the discount factors used to calculate the present value of the payments.
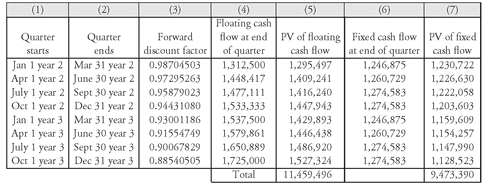
To illustrate this, consider the 3-year swap used to demonstrate how to calculate the swap rate. Suppose that one year later, interest rates change as shown in Columns (4) and (6) in
Exhibit 8. Column (4) shows the current 3-month LIBOR. In Column (5) are the Eurodollar CD futures prices for each period. These rates are used to compute the forward rates in Column (6). Note that interest rates have increased one year later since the rates in
Exhibit 8 are greater than those in
Exhibit 3. As in
Exhibit 3, the current 3-month LIBOR and the forward rates are used to compute the floating-rate payments. These payments are shown in Column (8) of
Exhibit 8.
EXHIBIT 8 Rates and Floating-Rate Payments One Year Later if Rates Increase
EXHIBIT 9 Period Forward Rates and Forward Discount Factors One Year Later if Rates Increase
In
Exhibit 9, the forward discount factor is computed for each period, in the same way as it was calculated in
Exhibit 5. The forward discount factor for each period is shown in the last column of
Exhibit 9.
In
Exhibit 10 the forward discount factor (from
Exhibit 9) and the floating-rate payments (from
Exhibit 8) are shown. The fixed-rate payments need not be recomputed. They are the payments shown in Column (8) of
Exhibit 4. These are the fixed-rate payments for the swap rate of 4.9875% and they are reproduced in
Exhibit 10. Now the two payment streams must be discounted using the new forward discount factors. As shown at the bottom of
Exhibit 10, the two present values are as follows:
Present value of floating rate payments $11,459,496 Present value of fixed rate payments $9,473,390
The two present values are not equal and therefore for one party the value of the swap increased, and for the other party the value of the swap decreased. Let’s look at which party gained and which party lost.
EXHIBIT 10 Valuing the Swap One Year Later if Rates Increase
| Summary | Fixed-rate payer | Fixed-rate receiver |
|---|
| PV of payments received | 11,459,496 | 9,473,390 |
| PV of payments made | 9,473,390 | 11,459,496 |
| Value of swap | 1,986,106 | -1,986,104 |
The fixed-rate payer will receive the floating-rate payments, which have a present value of $11,459,496. The present value of the payments that must be made by the fixed-rate payer is $9,473,390. Thus, the swap has a positive value for the fixed-rate payer equal to the difference in the two present values of $1,986,106. This is the value of the swap to the fixed-rate payer. Notice that, consistent with what we said in the previous chapter, when interest rates increase (as they did in the illustration analyzed), the fixed-rate payer benefits because the value of the swap increases.
In contrast, the fixed-rate receiver must make payments with a present value of $11,459,496 but will only receive fixed-rate payments with a present value equal to $9,473,390. Thus, the value of the swap for the fixed-rate receiver is −$1,986,106. Again, as explained in the previous chapter, the fixed-rate receiver is adversely affected by a rise in interest rates because of the resulting decline in the value of a swap.
The same valuation principle applies to more complicated swaps. For example, there are swaps whose notional amount changes in a predetermined way over the life of the swap. These include amortizing swaps, accreting swaps, and roller coaster swaps. Once the payments are specified, the present value is calculated as described above by simply adjusting the payment amounts for the changing notional amounts—the methodology does
not change.
190
IV. OPTIONS
An option grants the buyer of the option the right, but not the obligation, to purchase from or sell to the contract writer an asset (the underlying) at a specified price (the strike price) within a specified period of time (or at a specified date). The compensation that the option buyer pays to acquire the option from the option writer is the option price. (The option price is also referred to as the option premium.) A call option grants the buyer the right to purchase the underlying from the writer (seller); a put option gives the buyer the right to sell the underlying to the writer. An American option allows the buyer to exercise the option at any time up to and including the expiration date. A European option allows the buyer to exercise the option only on the expiration date.
The maximum amount that an option buyer can lose is the option price. The maximum profit that the option writer can realize is the option price. The option buyer has substantial upside return potential, while the option writer has substantial downside risk.
A. Components of the Option Price
The option price can be decomposed into two parts: the intrinsic value and the time value. We describe each below.
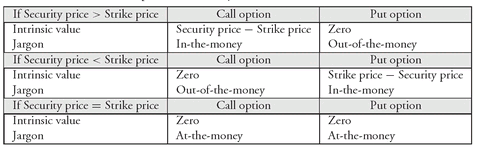
1. Intrinsic Value The option value is a reflection of the option’s intrinsic value and its time value. The intrinsic value of an option is its economic value if it is exercised immediately. If no positive economic value would result from exercising the option immediately, then the intrinsic value is zero.
For a call option, the intrinsic value is positive if the current market price of the underlying security is greater than the strike price. The intrinsic value is then the difference between the current market price of the underlying security and the strike price. If the strike price of a call option is greater than or equal to the current market price of the security, the intrinsic value is zero. For example, if the strike price for a call option is $100 and the current market price of the security is $105, the intrinsic value is $5. That is, an option buyer exercising the option and simultaneously selling the underlying security would realize $105 from the sale of the security, which would be covered by acquiring the security from the option writer for $100, thereby netting a $5 gain.
When an option has intrinsic value, it is said to be in the money. When the strike price of a call option exceeds the current price of the security, the call option is said to be out of the money; it has no intrinsic value. An option for which the strike price is equal to the current price of the security is said to be at the money. Both at-the-money and out-of-the-money options have an intrinsic value of zero because they are not profitable to exercise.
For a put option, the intrinsic value is equal to the amount by which the current price of the security is below the strike price. For example, if the strike price of a put option is $100 and the current price of the security is $92, the intrinsic value is $8. The owner of the put option who simultaneously buys the underlying security and exercises the put will net $8 since by exercising the option the security will be sold to the writer for $100, while the security is purchased in the market for $92. The intrinsic value is zero if the strike price is less than or equal to the current market price.
Our put option with a strike price of $100 would be: (1) in the money when the security’s price is less than $100, (2) out of the money when the security’s price exceeds $100, and (3) at the money when the security’s price is equal to $100.
The relationships above are summarized in
Exhibit 11.
2. Time Value The time value of an option is the amount by which the option price exceeds its intrinsic value. The option buyer hopes that at some time up to the expiration date, changes in the market price of the underlying security will increase the value of the rights conveyed by the option. For this prospect, the option buyer is willing to pay a premium above the intrinsic value.
EXHIBIT 11 Relationship Between Security Price, Strike Price, and Intrinsic Value
EXHIBIT 12 Summary of Factors that Affect the Price of an American Option on a Fixed Income Instrument
| General effect of an increase of factor on: |
|---|
| Factor | Call price | Put price |
|---|
| Price of underlying security | increase | decrease |
| Strike price | decrease | increase |
| Time to expiration | increase | increase |
| Expected interest rate volatility | increase | increase |
| Short-term risk-free rate | increase | decrease |
| Coupon payments | decrease | increase |
For example, if the price of a call option with a strike price of $100 is $9 when the current price of the security is $105, the time value of this option is $4 ($9 minus its intrinsic value of $5). Had the current price of the security been $90 instead of $105, then the time value of this option would be $9 because the option has no intrinsic value.
B. Factors that Influence the Value of an Option on a Fixed Income Instrument
There are six factors that influence the value of an option when the
underlying security is a fixed income instrument:
1. current market price of the underlying security
2. strike price of the option
3. time to expiration of the option
4. expected interest rate volatility over the life of the option
5. short-term risk-free interest rate over the life of the option
6. coupon interest payment over the life of the option
The impact of each of these factors may depend on whether (1) the option is a call or a put, and (2) the option is an American option or a European option. A summary of the effect of each factor on American put and call option prices is presented in
Exhibit 12.
1. Price of the Underlying Security The option price changes as the price of the underlying security changes. For a call option, as the price of the underlying security increases (holding all other factors constant), the option price increases. This is because the intrinsic value of a call option increases when the price of the underlying security increases. The opposite holds for a put option: as the price of the underlying security increases, the price of a put option decreases. This is because the intrinsic value of a put option decreases when the price of the underlying security increases.
2. Strike Price All other factors equal, the lower the strike price, the higher the price of a call option. For put options, the higher the strike price, the higher the option price.
3. Time to Expiration of the Option An option is a “wasting asset.” That is, after the expiration date passes the option has no value. Holding all other factors equal, the longer the time to expiration of the option, the greater the option price. As the time to expiration decreases, less time remains for the underlying security’s price to rise (for a call buyer) or to fall (for a put buyer)—to compensate the option buyer for any time value paid—and, therefore, the probability of a favorable price movement decreases. Consequently, for American options, as the time remaining until expiration decreases, the option price approaches its intrinsic value.
4. Expected Interest Rate Volatility Over the Life of the Option All other factors equal, the greater the expected interest rate volatility or yield volatility, the more an investor would be willing to pay for the option, and the more an option writer would demand for it. This is because the greater the volatility, the greater the probability that the price of the underlying security will move in favor of the option buyer at some time before expiration. The procedure for estimating interest rate volatility is explained in Chapter 8.
5. Short-Term Risk-Free Rate Over the Life of the Option Buying the underlying security ties up one’s money. Buying an option on the dollar amount of the underlying security makes available for investment the difference between the security price and the option price at the risk-free rate. All other factors constant, the higher the short-term risk-free rate, the greater the cost of buying the underlying security and carrying it to the expiration date of the call option. Hence, the higher the short-term risk-free rate, the more attractive the call option is relative to the direct purchase of the underlying security. As a result, the higher the short-term risk-free rate, the greater the price of a call option. In the case of a put option, the alternative to buying a put is shorting the security. When the security is shorted, the proceeds received can be invested at the short-term risk-free rate. When the short-term risk-free rate increases, this makes it more attractive to short the security relative to buying a put option. Consequently, the value of a put option declines when the short-term risk-free rate increases.
6. Coupon Payments Over the Life of the Option Coupon interest payments on the underlying security tend to decrease the price of a call option because they make it more attractive to hold the underlying security than to hold the option. That is, the owner of the security receives the coupon payments but the buyer of the call option does not. The higher the coupon payment received by the owner of the security, the more attractive it is to own the security and the less attractive it is to own the call option. So, the value of a call option declines the higher the coupon payment.
The opposite is true for the put option. Coupon interest payments on the underlying security tend to increase the price of a put option. The buyer of a put option compares the position to a short position in the security. When shorting the security, the coupon payment must be paid by the short seller. So, the higher the coupon payment the less attractive it is to short the security and the more attractive it is to buy the put option. As a result, the value of a put option increases the higher the coupon payment.
C. Factors that Influence the Value of a Futures Option
There are five factors that influence the value of an option in which the underlying is a futures contract:
1. current futures price
2. strike price of the option
3. time to expiration of the option
4. expected interest rate volatility over the life of the option
5. short-term risk-free rate over the life of the option
These are the same factors that affect the value of an option on a fixed income instrument. Notice that the coupon payment is not a factor since the underlying is a futures contract.
D. Pricing Models for Options and Options on Futures
At any time, the intrinsic value of an option can be determined. The question is, what is an approximate time value for an option? To answer this question, option pricing models have been developed. Two models used to value options on a fixed income instrument are the Black-Scholes model and the arbitrage-free binomial model. For options on futures, the most common model is the Black model, a version of the Black-Scholes model. We will discuss the two common models for options on fixed income instruments before discussing the Black model for options on futures for fixed income instruments.
1. The Black-Scholes Model The most common model for the pricing of options is the Black-Scholes option pricing model. Although this model was developed for options on stocks, it has been applied to options on bonds as well. Such applications are fraught with problems. We will discuss the model for stocks first and then discuss the limitations of applying the model to bonds.
The model was developed for valuing European style call options on a non-dividend-paying common stock.
191 To derive the option pricing model based on arbitrage arguments, certain assumptions are imposed. There have been a good number of extensions of the Black-Scholes option pricing that have been formulated by relaxing the assumptions. While the model was developed for common stock, it has been applied to value options on fixed income instruments. With the exception of the coupon payment, the factors that we explained earlier that determine the value of an option of a fixed income instrument are included in the Black-Scholes formula. As we will see, because of the assumptions imposed the Black-Scholes option pricing model does not necessarily produce reasonable values for options on bonds.
The option price derived from the Black-Scholes option pricing model is “fair” in the sense that if any other price existed, it would be possible to earn riskless arbitrage profits by taking an offsetting position in the underlying stock. If the price of the call option in the market is higher than that derived from the Black-Scholes option pricing model, an investor could sell the call option and buy a certain number of shares in the underlying stock. If the reverse is true and the market price of the call option is less than the “fair” price derived from the model, the investor could buy the call option and sell short a certain number of shares in the underlying stock. This process of hedging by taking a position in the underlying stock allows the investor to lock in the riskless arbitrage profit. The number of shares necessary to hedge the position changes as the factors that affect the option price change, so the hedged position must be changed constantly.
To understand the limitations of applying the model to bonds, let’s look at the values that would be derived in a couple of examples. We know that there are coupon-paying bonds and zero-coupon bonds. In our illustration we will use a zero-coupon bond. The reason is that the original Black-Scholes model was for common stock that did not pay a dividend and so a zero-coupon bond would be the equivalent type of instrument. Specifically, we will look at how the Black-Scholes option pricing model would value a zero-coupon bond with three years to maturity assuming the following:
Strike price = $88.00
Time remaining to expiration = 2 years
Current bond price = $83.96 (assuming for simplicity annual compounding)
Expected return volatility = standard deviation = 10%
Risk-free rate = 6%
The Black-Scholes formula gives a value of $ 8.116.
192 There is no reason to suspect that this estimated value is incorrect. However, let’s change the problem slightly. Instead of a strike price of $88, let’s make the strike price $100.25.
10 The Black-Scholes option pricing model would give a fair value of $2.79. Is there any reason to believe this is incorrect? Well, consider that this is a call option on a zero-coupon bond that will never have a value greater than its maturity value of $100. Consequently, a call option with a strike price of $100.25 must have a value of zero. Yet, the Black-Scholes option pricing model tells us that the value is $2.79! In fact, if we assume a higher volatility, the model would give an even greater value for the call option.
Why is the Black-Scholes model off by so much in our illustration? The answer is that there are three assumptions underlying the Black-Scholes model that limit its use in pricing options on fixed income instruments.
The first assumption is that the probability distribution for the underlying security’s prices assumed by the Black-Scholes model permits some probability—no matter how small—that the price can take on any positive value. But in the case of a zero-coupon bond, the price cannot take on a value above $100. In the case of a coupon bond, we know that the price cannot exceed the sum of the coupon payments plus the maturity value. For example, for a 5-year 10% coupon bond with a maturity value of $100, the price cannot be greater than $150 (five coupon payments of $10 plus the maturity value of $100). Thus, unlike stock prices, bond prices have a maximum value. The only way that a bond’s price can exceed the maximum value is if negative interest rates are permitted. While there have been instances where negative interest rates have occurred outside the United States, users of option pricing models assume that this is outcome cannot occur. Consequently, any probability distribution for prices assumed by an option pricing model that permits bond prices to be higher than the maximum bond value could generate nonsensical option prices. The Black-Scholes model does allow bond prices to exceed the maximum bond value (or, equivalently, assumes that interest rates can be negative).
The second assumption of the Black-Scholes model is that the short-term interest rate is constant over the life of the option. Yet the price of an interest rate option will change as interest rates change. A change in the short-term interest rate changes the rates along the yield curve. Therefore, for interest rate options it is inappropriate to assume that the short-term rate will be constant. The third assumption is that the variance of returns is constant over the life of the option. As a bond moves closer to maturity its price volatility declines and therefore its From a normal distribution table it can be determined that
N(0
.5869) = 0
.7214 and
N (0
.4455) = 0
.6720. Then
C = 83.96(0.7214) − 88[e−(0.06)(2)(0.6720)] = $8.116.
Substituting the new strike price, we get
From a normal distribution table
N (−0
.3346) = 0
.3689 and
N(−0
.4761) = 0
.3170. Then
C = 83.96(0.3689) − 100.25[e−(0.06)(2)(0.3170)] = $2.79.
return volatility declines. (We discussed this in Chapter 5 where we demonstrated the “pull to par” characteristic of a bond.) Therefore, the assumption that variance of returns is constant over the life of the option is inappropriate.
193The limitations of the Black-Scholes model in pricing options on bonds are summarized below:
| Assumptions | Bond characteristics |
|---|
| 1. | The price of the underlying has some possibility of rising to any price. | There is a maximum price for a bond and any higher price implies that a negative interest rate is possible. |
| 2. | Short-term rates remain constant. | Changes in short-term rates occur which cause bond price to change. |
| 3. | Volatility (variance) of returns is constant over the life of the option. | Bond return volatility decreases as the bond approaches maturity. |
2. Arbitrage-Free Binomial Model The proper way to value options on bonds is to use an arbitrage-free model that takes into account the yield curve. This model can incorporate different volatility assumptions along the yield curve. The most common model employed by dealer firms is the Black-Derman-Toy model.12
We have already developed the basic principles for employing this model. In the chapter on valuing bonds with embedded options, Chapter 9, we explained how to construct a binomial interest rate tree such that the tree would be arbitrage free. We used the interest rate tree to value bonds (both option-free bonds and bonds with embedded options). The same tree can be used to value a stand-alone option on a bond.
To illustrate how this is done, let’s consider a 2-year European call option on a 4-year Treasury bond with a 6.5% coupon rate and a strike price of 100.25. That is, if the call option is exercised at the option expiration date, the option buyer has the right to purchase a 6.5% coupon Treasury bond with two years remaining to maturity at a price of 100.25. We will assume that the estimated par Treasury yield curve for maturities up to four years is as follows:
| Maturity | Yield to maturity | Market price |
|---|
| 1 year | 3.5% | 100 |
| 2 years | 4.2% | 100 |
| 3 years | 4.7% | 100 |
| 4 years | 5.2% | 100 |
For purposes of this illustration, we will assume annual-pay bonds as we did in our illustrations in Chapter 9.
The next step is to construct an arbitrage-free binomial interest rate tree. We explained the general principles of constructing the tree in Chapter 9.
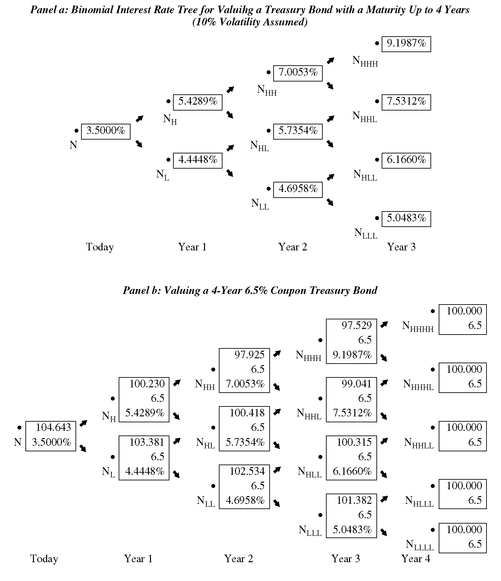
Exhibit 13a shows the binomial interest rate tree assuming interest rate volatility of 10%;
194 as noted earlier in our discussion of the factors that affect the value of an option, the volatility assumption is critical.
Exhibit 13b uses the interest rate tree in
Exhibit 13a to value the underlying for our option: the 4-year Treasury bond with a 6.5% coupon rate. The boxes at each node and the backward induction method for valuation using the interest rate tree were described in Chapter 9. The valuation of our 4-year Treasury bond using the binomial interest rate tree using the backward induction method is as follows. Begin in Year 4 (the bond’s maturity). We know that regardless of the path taken by interest rates, at Year 4 our 4-year Treasury bond will have a value of $100 and there will be a coupon payment of $6.5. That is why each box at Year 4 shows a value of $100 and $6.5. Working backwards to Year 3, recall from Chapter 9 that the present value of the cash flow shown at each of the two nodes to the right (Year 4 in our illustration) are discounted at the interest rate shown in the box at Year 3 and the present values are then averaged because we are assuming the two cash flows have an equal probability of occurring. For example, look at the N
HHH. The situation is simple in this case. The two nodes to the right (N
HHHH and N
HHHL) both have a cash flow of $106.50. Discounting at the interest rate of 9.1987% shown in the box at N
HHH, the present value is $97.529 which is also shown in the box at N
HHH.
Let’s do one more calculation to show the backward induction procedure. Look at NHH. The two nodes to the right of NHH are NHHH and NHHL . The value shown at NHH is found by (a) calculating the present value of ($97.529 + $6.5) at 7.0053%, (b) calculating the present value of ($99.041 + $6.5) at 7.0053%, and (c) averaging the two present values. The result of this calculation is $97.925 and it is this value that is shown in the box at at NHH.
Applying the backward induction method to “Today” in
Exhibit 13, the value of $104.643 is shown. This is the arbitrage-free value of the 4-year 6.5% Treasury bond.
Our objective is not to show how to value the arbitrage-free bond. We demonstrated how this in done in Chapter 9. Our objective is to show how to value a 2-year European call option on the 4-year Treasury bond with a coupon rate of 6.5%. To do so, we use a portion of
Exhibit 13b. Specifically,
Exhibit 14 shows the value of our hypothetical Treasury bond (excluding coupon interest) at each node at the end of Year 2.
The same backward induction procedure used for valuing a bond is used for valuing an option on a bond. Now we start at the end of the tree, Year 2 for our option. It is the end of the tree because our option is a 2-year European option so it can only be exercised at the end of Year 2. Hence, we will not be concerned with Year 3 and Year 4. The decision rule at a node for determining the value of an option on a bond depends on whether or not the option being valued is in the money. (The exercise decision is only applied at the option’s expiration date because we are valuing a European option.) That is, a call option will be exercised at one of the nodes at the option’s expiration date if the bond’s price at the node is greater than the strike price (i.e., if the call option is in the money). In the case of a put option, the option will be exercised at one of the nodes at the option’s expiration date if the strike price at the node is greater than the bond’s price (i.e., if the put option is in the money).
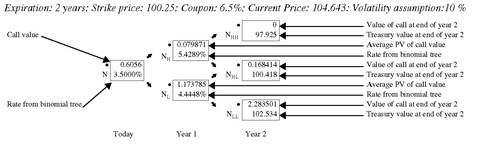
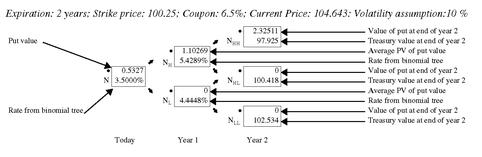
Start at the end of the tree, Year 2 (the expiration date of the option). Three values are shown in
Exhibit 14: 97.925, 100.418, and 102.534. Given these three values, the value of a call option with a strike price of 100.25 can be determined at each node. For example, if in Year 2 the price of this Treasury bond is 97.925, then since the strike price is 100.25, the value of the call option would be zero. In the other two cases, since the price in Year 2 is greater than the strike price, the value of the call option is the difference between the price of the bond at the node and 100.25.
EXHIBIT 13 Valuing a 4-Year 6.5% Coupon Treasury Bond Using a Binomial Interest Rate Tree
EXHIBIT 14 Valuing a European Call Option Using the Arbitrage-Free Binomial Method
Exhibit 14 shows the value of the call option two years from now (the option expiration date) at each of the three nodes. Given these values, the binomial interest rate tree is used to find the present value of the call option using the backward induction procedure. The discount rates are those from the binomial interest rate tree and are shown as the second number at each node. The first number at each node for Year 1 is the average present value found by discounting the call option value at the two nodes to the right using the discount rate at the node. (It is the average because it is assumed that each present value has an equal probability of occurring.) Now let’s move back one year to “Today.” The value of the option is the first number shown at the root (i.e., Today) of the tree, $0.6056. The calculations to obtain this value are explained below.
To obtain the value for the option at N
H, the values of 0 and 0.168414 are discounted and then averaged. The discount rate is the rate shown at N
H of 5.4289%. That is,
The multiplication by 0.5 in the above formula is because we are taking the average of the two present values.
To obtain the value for option at N
L , the values of 0.168414 and 2.283501 are discounted at 4.4448% and then averaged (i.e., multiplied by one half):
The value at the root, N, is found by discounting at 3.5% the value at N
H of 0.079871 and the value at N
L of 1.173785 and then averaging the values to get the value of 0.6056 as shown below:
The same procedure is used to value a European put option. This is illustrated in
Exhibit 15 assuming that the buyer of the put option has the right to put the current 4-year 6.5% coupon Treasury bond in two years and the strike price is 100.25. The value of the put option two years from now is shown at each of the three nodes in Year 2.
3. Black Model The most commonly used model for futures options is the one developed by Black.
195 The model was initially developed for valuing European options on forward contracts.
EXHIBIT 15 Valuing a European Put Option Using the Arbitrage-Free Binomial Method
There are two problems with this model. First, the Black model does not overcome the problems cited earlier for the Black-Scholes model. Failing to recognize the yield curve means that there will not be consistency between pricing Treasury futures and pricing options on Treasury futures. Second, the Black model was developed for pricing European options on futures contracts. Treasury futures options, however, are American options. Despite its limitations, the Black model is the most common model for pricing short-dated options on Treasury futures.
E. Sensitivity of Option Price to Change in Factors
In employing options in an investment strategy, a money manager would like to know how sensitive the price of an option is to a change in any one of the factors that affects its price. These measures are commonly referred to as the “Greeks.” Here we look at the sensitivity of a call option’s price to changes in the price of the underlying bond, the time to expiration, and expected interest rate volatility. The same measures apply when the underlying is a Treasury bond futures contract.
1. The Call Option Price and the Price of the Underlying Bond The sensitivity of an option to a change in the price of the underlying bond is called the
delta of the option. Specifically,
For a call option, the delta is positive since as we noted earlier, the higher the price of the underlying bond, the higher the option price. For a put option, delta is negative because the higher the price of the underlying bond, the lower the option price.
Let’s interpret the delta. Suppose that the delta of a call option is 0.4. This means that if the price of the underlying bond increases by $1, the price of the call option will increase by approximately $0.40. Suppose that the delta of a put option is −0.2. This means that if the price of the underlying bond increases by $1 the price of the put option will decrease by approximately $0.20. The delta of an option changes as the price of the underlying moves closer to or away from the strike price.
For an option where the intrinsic value is zero and the price of the underlying is very far from the strike price (i.e., an option that is said to be deep out of the money), the delta is close to 0. For example, consider a call option that expires in one year and has a strike price of $100. Suppose that the current price of the underlying bond is $45. Then an increase in the price of the underlying bond by $1 (from $45 to $46) would not be expected to change the value of the call option.
For an option that is deep in the money, the delta of a call option is close to 1 and the delta of a put option is close to −1. This is because the change in the option’s price will closely mirror the change in the price of the underlying bond.
Delta plays the same role in approximating the sensitivity of the option’s price to changes in the price of the underlying bond as duration does for measuring the sensitivity of the bond’s price to changes in interest rates. In both cases, the changes are approximations. For bonds, the approximation can be improved by using the convexity measure. For an option, the approximation can be improved by calculating the
gamma of an option. The gamma for an option is:
2. The Call Option Price and Time to Expiration All other factors constant, the longer the time to expiration, the greater the option price. Since each day the option moves closer to the expiration date, the time to expiration decreases. The
theta of an option measures the change in the option price as the time to expiration decreases, or equivalently, it is a measure of time decay. Theta is measured as follows:
Assuming that the price of the underlying bond does not change (which means that the intrinsic value of the option does not change), theta measures how quickly the time value of the option changes as the option moves towards expiration.
Buyers of options prefer a low theta so that the option price does not decline quickly as it moves toward the expiration date. An option writer benefits from an option that has a high theta. This is because a high theta means that as the option moves closer to the expiration date, the option price falls faster than an option with a low theta. The option writer wants the option price to fall quickly as the option moves toward the expiration date because the option can then be bought back at a lower price.
3. The Call Option Price and Expected Interest Rate Volatility All other factors constant, a change in the expected interest rate volatility will change the option price. The
kappa of an option measures the change in the price of the option for a 1% change in expected interest rate volatility. (An option’s kappa is also referred to as its
vega.) That is,
The kappa of an option is positive because, as explained earlier, the option price increases when expected interest rate volatility increases.
V. CAPS AND FLOORS
In applying the backward induction methodology to valuing caps and floors, the decision to exercise at a node will depend on whether or not the cap or the floor is in the money. Remember that a cap and a floor are nothing more than a package or strip of options. More specifically, they are a strip of European options on interest rates. Thus, to value a cap, the value of each period’s cap, called a caplet, is found and the values of all the caplets are then summed. The same can be done for a floor.
To illustrate how this is done, we will use the binomial tree given in
Exhibit 13a. We will simplify the analysis by ignoring the difference in the timing of the payments for caps and floors. Specifically, the settlement payment for caps and floors is in arrears. Allowing for that would require complicating the presentation and revising the binomial tree.
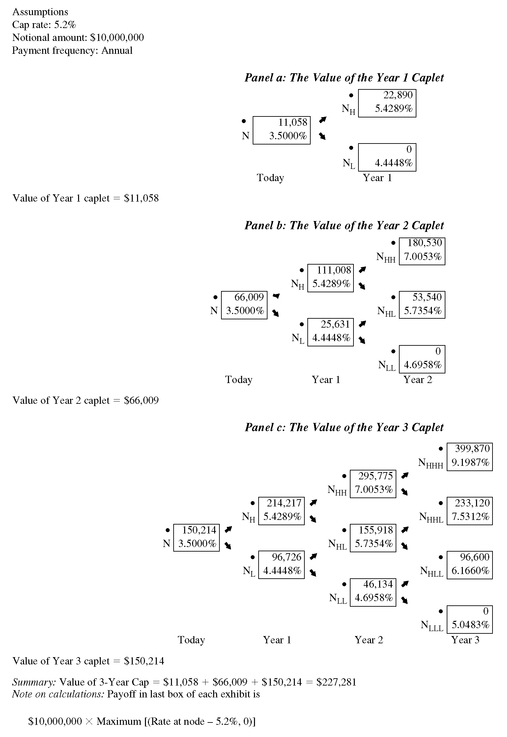
196 Consider first a 5.2% 3-year cap with a notional amount of $10 million. The reference rate is the 1-year rate in the binomial tree. The payoff for the cap is annual.
Exhibits 16a,
16b, and
16c show how this cap is valued by valuing the three caplets. The value for the caplet for any year, say Year X, is found as follows. First, calculate the payoff in Year X at each node as either:
16 1. zero if the 1-year rate at the node is less than or equal to 5.2%, or
2. the notional principal amount of $10 million times the difference between the l-year rate at the node and 5.2% if the 1-year rate at the node is greater than 5.2%.
Then, the backward induction method is used to determine the value of the Year X caplet.
For example, consider the Year 3 caplet. At the top node in Year 3 of
Exhibit 16c, the 1-year rate is 9.1987%. Since the 1-year rate at this node exceeds 5.2%, the payoff in Year 3 is:
$10, 000, 000 × (0.091987 − 0.052) = $399,870
Let’s show how the values shown at the nodes N
HH, N
H, and the root of the tree, N, are determined. For node N
HH we look at the value for the cap at the two nodes to its right, N
HHH and N
HHL. The backward induction method involves discounting the values at these nodes, $399,870 and $233,120, by the interest rate from the binomial tree at node N
HH, 7.0053%, and computing the average present value. That is,
EXHIBIT 16 Valuation of a 3-Year 5.2% Cap (10% Volatility Assumed)
Value at NHH = [$399,870/(1.070053) + $233,120/(1.070053)]/2 = $295,775
This is the value reported at NHH.
Now let’s see how the value at node N
H is determined. Using the backward induction method, the values at nodes N
HH and N
HL are discounted at the interest rate from the binomial tree at node N
H, 5.4289%, and then the present value is averaged. That is,
Value at NH = [$295,775/(1.054289) + $155,918/(1.054289)]/2 = $214,217
This is the value reported at NH.
Finally, we get the value at the root, node N, which is the value of the Year 3 caplet found by discounting the value at N
H and N
L by 3.5% (the interest rate at node N) and then averaging the two present values. Doing so gives:
Value at N = [$214,217/(1.035) + $96,726/(1.035)]/2 = $150,214
This is the value reported at N.
Following the same procedure, the value of the Year 2 caplet is found to be $66,009 and the value of the Year 1 caplet is $11,058. The value of the cap is then the sum of the values of the three caplets. That is,
value of cap = value of Year 1 caplet + value of Year 2 caplet + value of Year 3 caplet
Thus, the value of the cap is $227,281, found by adding $11,058, $66,009, and $150,214.
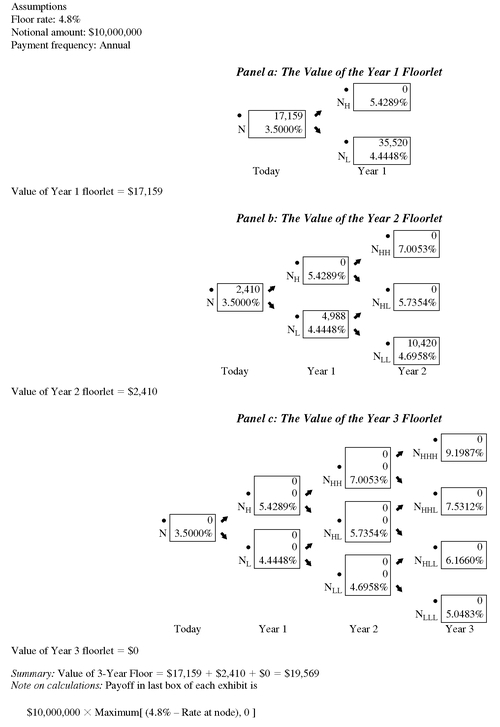
Similarly, an interest rate floor can be valued.
Exhibit 17 shows how for a 4.8% 3-year floor with a notional amount of $10 million. Again, the reference rate is the 1-year rate in the binomial tree and the payoff for the floor is annual. The value for the floor for any year, called a
floorlet, say Year X, is found as follows. First, calculate the payoff in Year X at each node as either
197 1. zero if the 1-year rate at the node is greater than or equal to 4.8%, or
2. the notional amount of $10 million times the difference between 4.8% and the 1-year rate at the node if the 1-year rate at the node is less than 4.8%.
Let’s see how the value of the Year 2 floorlet is determined using the backward induction method. Specifically, we will see how to compute the values at nodes N
LL, N
L., and N (the root of the tree and the value of the Year 2 floorlet). Look first at N
LL. Since the rate of 4.6958% is less than the floor rate of 4.8%, there is a payoff equal to
$10, 000, 000 × (0.048 − 0.046958) = $10,420
EXHIBIT 17 Valuation of a 3-Year 4.8% Floor (10% Volatility Assumed)
This is the value shown at node N
LL. Now we use the backward induction method to compute the value at N
L. We use the values at N
LL and N
HL to get the value at N
L. The two values are discounted at 4.4448% (the interest rate at node N
L) and then averaged. That is,
Value at NL = [0/(1.044448) + $10,420/(1.044448)]/2 = $4,988
This is the value reported at NL.
Finally, we compute the value for the Year 2 floorlet by discounting the values at N
H and N
L at 3.5% and then averaging, as shown below:
Value at N = [0/(1.035) + $4,988/(1.035)]/2 = $2,410
This is the value shown at the root of the tree and is the value of the Year 2 floorlet.
Adding the Year 1 floorlet, Year 2 floorlet, and Year 3 floorlet shown in
Exhibit 17 gives the value of the 3-year floor: $17,159 + $2, 410 + $0 = $19,569.


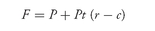
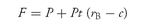
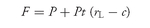
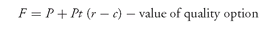



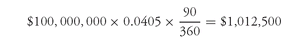
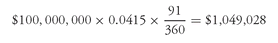

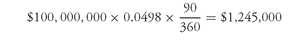
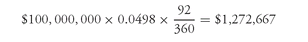
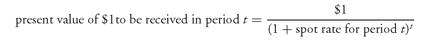


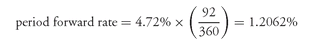
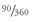 4.05%, which is
4.05%, which is 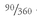 of the known rate for 3-month LIBOR.
of the known rate for 3-month LIBOR.