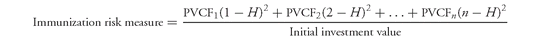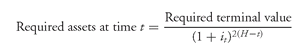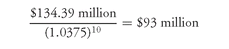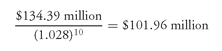CHAPTER 19
PORTFOLIO IMMUNIZATION AND CASH FLOW MATCHING
I. INTRODUCTION
In this chapter we will explain strategies for managing bond portfolios to satisfy predetermined liabilities. The two strategies we will discuss are immunization and cash flow matching. Immunization is a hybrid strategy having elements of both active and passive strategies. It is used to minimize reinvestment risk over a specified investment horizon. Immunization can be employed to structure a portfolio designed to fund a single liability or multiple liabilities. Cash flow matching is used to construct a portfolio that will fund a schedule of liabilities from a portfolio’s cash flows, with the portfolio’s value diminishing to zero after payment of the last liability.
II. IMMUNIZATION STRATEGY FOR A SINGLE LIABILITY
Classical immunization can be defined as the process by which a bond portfolio is created to have an assured return for a specific time horizon irrespective of interest rate changes.
295 The fundamental principle underlying immunization is to structure a portfolio that balances the change in the value of the portfolio at the end of the investment horizon with the return from the reinvestment of portfolio cash flows (both coupon and principal payments). That is, immunization offsets interest rate risk and reinvestment risk. The general principle of immunization is summarized in
Exhibit 1.
To accomplish this balancing requires controlling portfolio duration. By setting the portfolio duration equal to the desired portfolio time horizon, positive and negative incremental return sources offset one another. This is a necessary condition for effectively immunized portfolios.
EXHIBIT 1 General Principle of Classical Immunization
A. Illustration
To demonstrate the principle of immunization, consider the situation faced by a life insurance company that sells a guaranteed investment contract (GIC). This policy specifies that a life insurance company guarantees that a specified dollar amount will be paid to the policyholder at a specified future date. Or, equivalently, the life insurance company guarantees a specified rate of return on the payment date (referred to as the “crediting rate”).
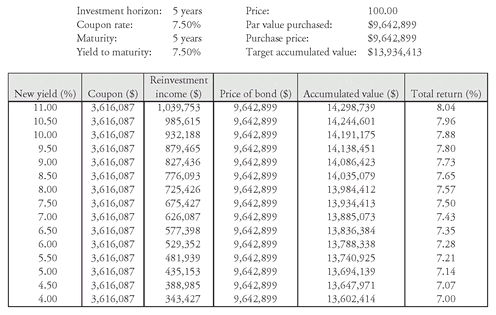
For example, suppose that a life insurance company sells a 5-year GIC that guarantees an interest rate of 7.5% per year on a bond-equivalent yield basis (or, equivalently, 3.75% every six months for the next ten 6-month periods). Suppose that the payment made by the policyholder to purchase the GIC is $9,642,899. Then the value that the life insurance company has guaranteed to the policyholder five years from now is $13,934,413. When investing the $9,642,899, the target accumulated value for the life insurance company is $13,934,413 after five years, which is the same as a target yield of 7.5% on a bond-equivalent basis.
EXHIBIT 2 Total Accumulated Value and Total Return After Five Years for a 5-Year 7.5% Bond Selling to Yield 7.5%
Suppose the life insurance company buys $9,642,899 par value of a bond selling at par with a 7.5% yield to maturity that matures in five years. The life insurance company will not be assured of realizing a total return at least equal to the target return of 7.5% because to realize 7.5% the coupon interest payments must be reinvested at a minimum rate of 3.75% every six months. That is, the accumulated value will depend on the reinvestment rate.
To demonstrate this, assume that immediately after investing the $9,642,899 in the 7.5% 5-year bond, yields in the market change and stay at the new level for the remainder of the five years.
Exhibit 2 illustrates what happens at the end of five years. The first column shows the new yield level. The second column shows the total coupon payments. The third column gives the reinvestment earned over the five years if the coupon payments are reinvested at the new yield level shown in the first column. The price of the bond at the end of five years shown in the fourth column is the par value. The fifth column is the accumulated value from all three sources: coupon interest, reinvestment income, and bond price. The total return is shown in the last column.
296If yields do not change so that the coupon payments can be reinvested at 7.5% (3.75% every six months), the life insurance company will achieve the target accumulated value. If market yields rise, an accumulated value (total return) higher than the target accumulated value (target yield) will be achieved. This is because the coupon payments can be reinvested at a higher rate than the initial yield to maturity. Contrast this with what happens when the yield declines. The accumulated value (total return) will be less than the target accumulated value (target yield). Therefore investing in a coupon bond with a yield to maturity equal to the target yield and a maturity equal to the investment horizon does not assure that the target accumulated value will be achieved.
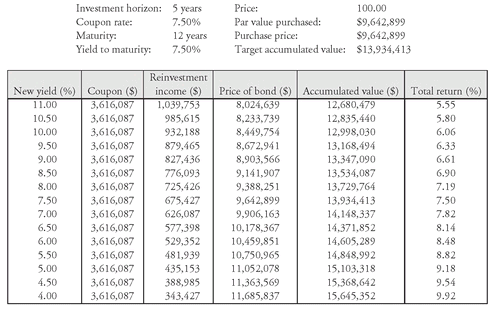
Suppose that instead of investing in a bond maturing in five years the life insurance company invests in a 12-year bond with a coupon rate of 7.5% selling at par to yield 7.5%.
Exhibit 3 presents the accumulated value and total return in five years if the market yield changes immediately after the bond is purchased and remains at the new yield level. The fourth column of the exhibit is the market price of a 7.5% 7-year bond (since five years have passed at the horizon date). If the market yield increases, the portfolio will fail to achieve the target accumulated value; if the market yield decreases, the accumulated value (total return) will exceed the target accumulated value (target yield).
EXHIBIT 3 Total Accumulated Value and Total Return After Five Years for a 12-Year 7.5% Bond Selling to Yield 7.5%
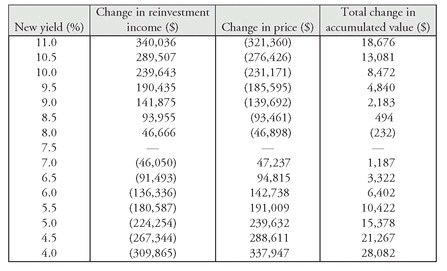
EXHIBIT 4 Change in Reinvestment Income and Price Due to Interest Rate Change After Five Years for a 12-Year 7.5% Bond Selling to Yield 7.5%
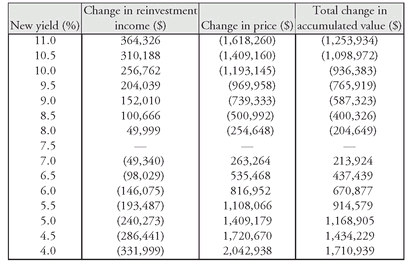
The reason for this result can be seen in
Exhibit 4 that summarizes the change in reinvestment income and the change in price resulting from a change in the market yield. For example, if the market yield rises instantaneously by 200 basis points, from 7.5% to 9.5%, reinvestment income will be $204,039 greater; however, the market price of the bond will decrease by $969,958. The net effect is that the accumulated value will be $765,919 less than the target accumulated value. The reverse will be true if the market yield decreases. The change in the price of the bond will more than offset the decline in reinvestment income, resulting in an accumulated value that exceeds the target accumulated value. Now we can see what is happening to the accumulated value. There is a trade-off between interest rate (or price) risk and reinvestment risk. For this 12-year bond, the target accumulated value will be realized only if the market yield does not increase.
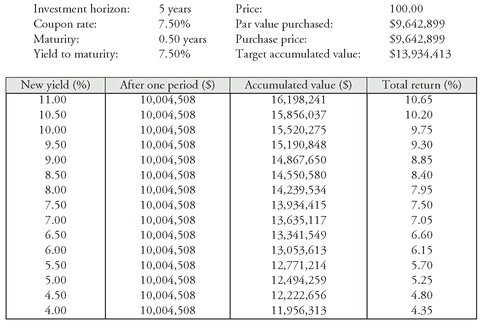
EXHIBIT 5 Total Accumulated Value and Total Return After Five Years for a 6-Month 7.5% Bond Selling to Yield 7.5%
Because neither a coupon bond with the same maturity nor a bond with a longer maturity provides the target accumulated value, maybe a bond with a maturity shorter than five years will. Consider a 7.5% bond with six months remaining to maturity selling at par.
Exhibit 5 shows the accumulated value and total return over the 5-year investment horizon. The second column shows the accumulated value after six months. The third column shows the accumulated value after five years by reinvesting the value accumulated after six months at the yield shown in the first column.
297By investing in this 6-month bond, the manager incurs no price risk, although there is reinvestment risk. The target accumulated value will be achieved only if the market yield remains at 7.5% or rises. Once again, the life insurance company is not assured of achieving the target accumulated value.
If we assume there is a one-time instantaneous change in the market yield, is there a coupon bond that the life insurance company can purchase to equal the target accumulated value whether the market yield rises or falls? The life insurance company should look for a coupon bond so that regardless of how the market yield changes, the change in reinvestment income will offset the change in price.
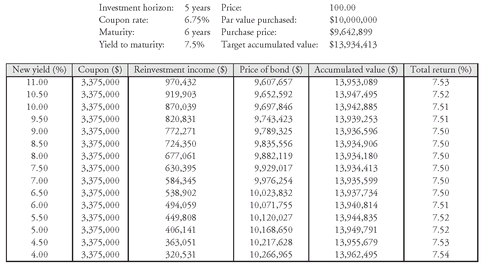
Consider a 6-year 6.75% bond selling at $96.42899 to yield 7.5%. Suppose $10 million of par value of this bond is purchased for $9,642,899.
Exhibit 6 provides the same information for this bond as
Exhibits 2,
3, and
5 do for the previous bonds considered for purchase. Looking at the last two columns, we see that the accumulated value and the total return are never less than the target accumulated value and target yield.
298 Thus, the target accumulated value is assured regardless of what happens to the market yield.
Exhibit 7 shows why. When the market yield rises, the change in the reinvestment income more than offsets the decline in price. When the market yield declines, the increase in price exceeds the decline in reinvestment income. What characteristic of this bond assures that the target accumulated value will be realized regardless of how the market yield changes? The duration for each of the four bonds is shown in
Exhibit 8.
The duration of the liability is 4.82.5 Notice that the 6-year 6.75% bond which equals the target accumulated value regardless of what happens to the market yield, has a duration equal to the duration of the liability, 4.82. This is the key. To immunize a portfolio’s target accumulated value (target yield) against a change in the market yield, the life insurance company must invest in a bond (or a bond portfolio) such that (1) the portfolio’s duration is equal to the liability’s duration, and (2) the initial present value of the cash flows from the bond (or bond portfolio) equals the present value of the future liability.
The two bonds with a duration shorter than the duration of the liability expose the portfolio to reinvestment risk. The one bond with a duration greater than the investment horizon exposes the portfolio to price risk.
When bonds with embedded options are included in an immunized portfolio, it is the effective duration that is the appropriate duration measure. The effective duration of the liability is the same as the modified duration of the liability. Thus, the requirements for immunization can be restated in more general terms as: (1) the portfolio’s effective duration is equal to the liability’s effective duration and (2) the initial present value of the projected cash flows from the bond (or bond portfolio) equals the present value of the future liability.
EXHIBIT 6 Total Accumulated Value and Total Return After Five Years for a 6-Year 6.75% Bond Selling to Yield 7.5%
EXHIBIT 7 Change in Reinvestment Income and Price Due to Interest Rate Change after Five Years for a 6-Year 6.75% Bond Selling to Yield 7.5%
EXHIBIT 8 Duration for the Four Bonds Analyzed as Potential Candidates for Immunization
| Bond | Duration | Risk |
|---|
| 5-year, 7.5% coupon at par | 4.11 | Reinvestment |
| 12-year, 7.5% coupon at par | 7.83 | Price |
| 6-month, 7.5% coupon at par | 0.48 | Reinvestment |
| 6-year, 6.75% coupon at 96.42899 | 4.82 | |
B. Rebalancing an Immunized Portfolio
Our illustration of the principles underlying immunization assumes a one-time instantaneous change in the market yield. In practice, the market yield will fluctuate over the investment horizon. As a result, the duration of the portfolio will change as the market yield changes. In addition, the duration will change simply because of the passage of time. In any interest rate environment different from a flat term structure, the duration of a portfolio will change at a different rate than time.
Even in the face of changing market yields, a portfolio can be immunized if it is rebalanced periodically so that its duration is readjusted to the duration of the liability. For example, if the investment horizon is initially five years and the yield is 7.5%, the initial portfolio should have a duration of 4.82. After six months the investment horizon will be 4.5 years and the liability’s duration will be 4.34 (= 4.5/1.0375). However, the duration of the portfolio will probably be different from 4.34. Thus, the portfolio must be rebalanced so that its duration is equal to 4.34. Six months later the portfolio must be rebalanced again so that its duration will equal the duration of a liability due in four years.
How often should the portfolio be rebalanced to adjust its duration? On one hand, more frequent rebalancing increases transaction costs, thereby reducing the likelihood of achieving the target return. On the other hand, less frequent rebalancing will result in the portfolio’s duration wandering from the target duration (i.e., the duration of the liability), which will also reduce the likelihood of achieving the target return. Thus, a manager faces a trade-off: some transaction costs must be accepted to prevent the portfolio duration from wandering too far from its target; but some misalignment in the portfolio duration must be tolerated, or transaction costs will become prohibitively high.
C. Application Considerations
In the actual process of constructing an immunized portfolio, the selection of the universe is extremely important. The lower the credit quality of the securities considered, the higher the potential risk and return. Immunization theory assumes there will be no defaults and that securities will be responsive only to overall changes in interest rates. The lower the credit quality, the greater the possibility these assumptions will not be met. Further, securities with embedded options such as call features or mortgage-backed prepayments complicate and may even prevent the accurate measure of cash flows and hence duration, frustrating the basic requirements of immunization. Finally, liquidity is a consideration for an immunized portfolio because, as noted above, the portfolio must be rebalanced over time and principal liquidated on the target investment horizon to pay the liability.
Optimization procedures can be used to construct an immunized portfolio. Typically, immunization takes the form of minimizing the initial portfolio cost subject to the constraint of having sufficient cash to satisfy the liability at the horizon date. Further considerations such as average credit quality, minimum and maximum concentration constraints, and, perhaps, issuer constraints may also be included. Throughout this process the need to establish realistic guidelines and objectives is critical. In addition, because the optimization is very sensitive to the pricing of the universe being considered, accurate pricing and the interface of an experienced trader are valuable. Because of the many inputs and variations that are typically available, the optimization process should be approached in an iterative manner where the final solution is the result of a number of trials.
Transaction costs are important in meeting the target rate for an immunized portfolio. Transaction costs must be considered not only in the initial immunization (i.e., when the immunized portfolio is first created), but also in the periodic rebalancing necessary to avoid duration drift. The manager does not want to get into a situation where the portfolio will incur a substantial number of trades and enjoy only marginal benefits from risk minimization. Fortunately, transaction costs can be included in the optimization framework such that a trade-off between transaction costs and risk minimization can be evaluated.
D. Extensions of Classical Immunization Theory
The sufficient condition for classical immunization is that the duration of the portfolio match the duration of the liability. Classical theory is based on the following assumptions:
Assumption 1. Any changes in the yield curve are parallel changes, (i.e., interest rates move either up or down by the same amount for all maturities).
Assumption 2. The portfolio is valued at a fixed horizon date and there are no cash inflows or outflows during the time horizon except for coupon income and reinvestment income.
Assumption 3. The target value of the investment is defined as the portfolio value at the horizon date if the interest rate structure does not change (i.e., no change in forward rates).
Perhaps the most critical assumption of classical immunization techniques concerns Assumption 1—the type of interest rate change anticipated. A property of a classically immunized portfolio is that the target value of the investment is the lower limit of the value of the portfolio at the horizon date if there are parallel interest rate changes.
299 This would appear to be an unrealistic assumption since such interest rate behavior is rarely, if ever, experienced in reality. According to the theory, if there is a change in interest rates that does not correspond to this shape preserving shift, matching the duration of the portfolio to the duration of the liability no longer assures immunization.
300A natural extension of classical immunization theory is a technique for modifying the assumption of parallel shifts in interest rates. One approach is to develop a strategy to handle an arbitrary interest rate change so that it is not necessary to specify an alternative duration measure. The approach, developed by Gifford Fong and Oldrich Vasicek, establishes an
immunization risk measure against an arbitrary interest rate change.
301 The immunization risk measure can then be minimized subject to the constraint that the portfolio duration be equal to the investment horizon resulting in a portfolio with minimum exposure to any interest rate movements.
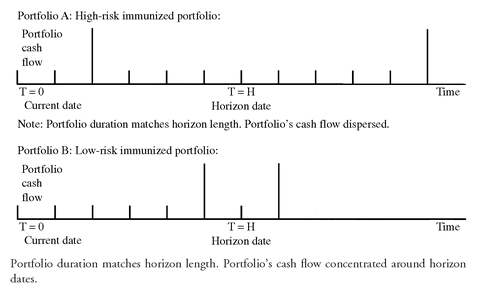
One way of minimizing immunization risk is shown in
Exhibit 9. The spikes in the two panels of
Exhibit 9 represent actual portfolio cash flows. The taller spikes depict the actual cash flows generated by principal payments while the smaller spikes represent coupon payments. Both portfolio A and portfolio B are composed of two bonds whose weighted durations equal the investment horizon. Portfolio A is, in effect, a “barbell” portfolio—a portfolio comprised of short and long maturities and interim coupon payments. For portfolio B, the two bonds mature very close to the investment horizon and the coupon payments are nominal over the investment horizon. When a portfolio has the characteristics of portfolio B it is called a “bullet” portfolio.
It is not difficult to see why the barbell portfolio should have greater immunization risk than the bullet portfolio. Assume that both portfolios have durations equal to the liability’s duration, so that both portfolios are immune to parallel rate changes. This immunity is attained as a consequence of balancing the effect of changes in reinvestment rates on payments received during the investment horizon against the effect of changes in capital value of the portion of the portfolio still outstanding at the end of the investment horizon. When interest rates change in an arbitrary nonparallel way, however, the effect on the two portfolios is very different. Suppose, for instance, that short rates decline while long rates go up. Both portfolios would realize a decline of the portfolio’s value at the end of the investment horizon below the target accumulated value, since they experience a capital loss in addition to lower reinvestment rates. The decline, however, would be substantially higher for the barbell portfolio for two reasons. First, the lower reinvestment rates are experienced for the bonds in the barbell portfolio for the shorter maturities than on the bullet portfolio, so that the reinvestment risk is much greater. Second, the longer maturity bond in the barbell portfolio at the end of the investment horizon is much longer than the longer maturity bond in the bullet portfolio, which means that the same rate increase generates a greater capital loss. Thus, the bullet portfolio has less exposure to the change in the interest rate term structure than the barbell portfolio.
EXHIBIT 9 Illustration of Immunization Risk Measure
It should be clear from the foregoing discussion that immunization risk is reinvestment risk. The portfolio that has the least reinvestment risk will have the least immunization risk. When there is a high dispersion of cash flows around the horizon date, as in the barbell portfolio, the portfolio is exposed to higher reinvestment risk. In contrast, when the cash flows are concentrated around the horizon date, as in the bullet portfolio, the portfolio is subject to minimum reinvestment risk.
An example of a zero immunization risk portfolio is a portfolio consisting of zero-coupon bonds maturing at the investment horizon. This is because there is no reinvestment risk. Moving from these bonds to coupon-paying bonds, the portfolio manager encounters the problem of how to select coupon-paying bonds that provide the best protection against immunization risk. The foregoing discussion indicates that the manager should select bonds which have most of their cash flow payments around the horizon date. Therefore, if the manager can construct a portfolio that replicates zero-coupon bonds that mature at the investment horizon, that portfolio will be the lowest immunization risk portfolio.
Now let us formalize the measure of immunization risk. As explained earlier, the target accumulated value of an immunized portfolio is a lower bound on the terminal value of the portfolio at the investment horizon if yields on all maturities change by the same amount. If yields of different maturities change by different amounts, then the target accumulated value is not necessarily the lower bound on the investment value. Fong and Vasicek demonstrate that if the yield curve changes in any arbitrary way, the relative change in the portfolio value depends on the product of two terms.
302 The first term depends solely on the structure of the investment portfolio while the second term is a function of interest rate movement only. The second term characterizes the nature of the yield curve shift. Since this shift can be arbitrary, this term is an uncertain quantity and therefore outside of the control of the manager. However, the first term is under the control of the manager since it depends solely on the composition of the portfolio. This first term is thus a measure of risk for immunized portfolios and defined as follows:
where
The immunization risk measure agrees with the intuitive interpretation of risk discussed earlier. For portfolio A in
Exhibit 9, the barbell portfolio, the portfolio payments are widely dispersed in time and the immunization risk measure would be high. The portfolio payments occur close to the investment horizon for portfolio B in
Exhibit 9, the bullet portfolio, so that the immunization risk measure is low.
Given the measure of immunization risk that is to be minimized and the constraint that the duration of the portfolio equals the duration of the liability as well as any other applicable investment constraints, the optimal immunized portfolio can be found using optimization models.
303
III. CONTINGENT IMMUNIZATION
Contingent immunization consists of identifying both the available immunization target rate and a lower
safety net level return with which a client would be minimally satisfied or is a minimum required rate of return.
304 The manager can continue to pursue an active strategy until an adverse investment experience drives the then available potential return—combined active return (from actual past experience) and immunized return (from expected future experience)—down to the safety net level; at such time the manager would be obligated to completely immunize the portfolio and lock in the safety net level return. As long as this safety net return is not violated, the manager can continue to actively manage the portfolio. Once the immunization mode is activated because the safety net return is violated, the manager can no longer return to the active mode unless the contingent immunization plan is abandoned.
A. Key Considerations
The key considerations in implementing a contingent immunization strategy are:
1. establishing well defined immunized initial and ongoing available target returns
2. identifying a suitable and immunizable safety net
3. implementing an effective monitoring procedure to ensure that the safety net return is not violated
B. An Illustration
To illustrate the basic principles of the contingent immunization strategy suppose a plan sponsor is willing to accept a 6% return over a 5-year investment horizon at a time when the possible immunized rate of return is 7.5%. The 6% rate of return is called the safety net (or minimum target or floor) return. The difference between the possible immunized rate of 7.5% and the safety net return is called the cushion spread or excess achievable return. It is this cushion spread of 150 basis points in our example that offers the manager latitude in pursuing an active strategy. The greater the cushion spread the more scope the manager has for an active management policy.
Assuming an initial portfolio of $100 million, the required terminal asset value when the safety net return is 6% is $134.39 million. The general formula for the required terminal value assuming semiannual compounding is:
Required terminal value = I (1 + s/2)2H
where
I = initial portfolio value
s = safety net rate
H = number of years in the investment horizon
In our example, the initial portfolio value is $100 million,
s is 6%, and
H is five years. Therefore, the required terminal value is:
$100 million(1.03)10 = $134.39 million
Since the current available return is assumed to be 7.5%, the assets required at the inception of the plan in order to generate the required terminal value of $134.39 million are $93 million. This is found as follows assuming semiannual compounding. The required assets at any given point in time,
t , necessary to achieve the required terminal value are:
where
it = the immunized semiannual yield available at time t
The other variables were defined earlier.
Since in our example the required terminal value is $134.39 million and the market yield that can be realized if the immunization mode is activated is 7.5%, the required assets are:
Consequently, the safety cushion of 150 basis points translates into an initial dollar safety margin of $7 million ($100 million − $93 million).
Now suppose that the portfolio manager invested the initial $100 million in a portfolio of 30-year par bonds with a coupon of 7.5%. Let’s look at what happens if there is a change in the yield level immediately following the purchase of these bonds.
First assume the yield level decreases to 5.6% from 7.5%. The value of the portfolio of 30-year bonds would increase to $127.46 million. However, the asset value required to achieve the required terminal value if the portfolio is immunized at a 5.6% rate is $102 million. This is found by using the previous formula. The required terminal value is $134.39 million and the market yield for immunizing (following the yield change) is 5.6%, therefore:
The amount by which the $127.46 million exceeds the required asset value (i.e., the dollar safety margin) in this case is $25.5 million ($127.46 million − $101.96 million). This amount is $18.46 million greater than the initial dollar safety margin of $7 million and therefore allows the manager more freedom to pursue active management.
Suppose instead of a decline in the yield level the immediate change is an increase in the yield level to 8.6%. At that yield level the portfolio of 30-year bonds would decline in value to $88.23 million. The required asset value to achieve the terminal value of $134.39 million is $88.21 million. Consequently, an immediate rise in the yield by 110 basis points to 8.6% will decrease the dollar safety margin to zero. At this yield level the immunization mode would be triggered with an immunization target rate of 8.6% to ensure that the required terminal value will be realized. If this were not followed, further adverse movements of interest rates would jeopardize the required terminal value for the portfolio of $134.39 million. The yield level at which the immunization mode becomes necessary is called the trigger point.
C. Controlling and Monitoring the Strategy
For purposes of monitoring a contingent immunization plan, it is useful to recast the dollar safety margin in terms of the potential return. This return, also called the return achievable with an immunization strategy, measures the yield that would be realized if, at any given point in time, the current value of the portfolio is immunized at the prevailing market yield.
Since duration approximates the price sensitivity of a portfolio to changes in market yields, trigger yields can be computed for portfolios of different durations so that the manager would know how much leeway there is for a given risk position with respect to an adverse movement in the market yield; that is, how much of an adverse movement in the market yield can be tolerated before the immunization mode must be activated. However, when using duration to compute trigger points it is important to remember the limitation of duration—it assumes a small parallel shift in the yield curve. In practice, the specific rate movements need to be monitored because the skewness of any particular movement should be expected to change the portfolio’s trigger point.
The key to a contingent immunization plan is the ability to control and monitor the performance of the portfolio over time so that the manager knows how much leeway he has to actively manage the portfolio, and when the portfolio should be immunized in order to achieve the minimum target return.
An accurate immunization target is critical in determining not only the basis for the initial problem set-up (e.g., the safety net return will usually be a certain basis point difference from the target over a specified time period), but also in determining what immunization levels are available over the investment horizon. A safety net return too close to the initial target return makes triggering the immunization process highly likely, while too low a safety net defeats the purpose of the process since the very low satisfactory minimum return would probably never trigger immunization. Finally, without an adequate monitoring procedure, the benefits of the strategy may be lost because of the inability to know when action is appropriate.
In spite of good control and monitoring procedures, attainment of the minimum target return may not be realized due to factors beyond the control of the manager. There are two reasons for this.
305 The first is that there is the possibility of a rapid adverse large movement in market yields that the manager does not have enough time to shift from an active to an immunization strategy at the rate needed to achieve the minimum target return. Frequent jumps of market yields of several hundred basis points would hinder the effective implementation of a contingent immunization strategy. The second reason why the minimum target return may not be attained is that, if the immunization strategy is implemented, there is no guarantee that the immunized rate will be achieved even if the portfolio is reconstructed at the required rate.
IV. IMMUNIZATION FOR MULTIPLE LIABILITIES
Immunization with respect to a single investment horizon is applicable to situations where the objective of the investment is to preserve the value of the investment at the horizon date. This may be the case when a single given liability is payable at the horizon date or a target investment value is to be attained at that date. More often, however, investment funds pay a number of liabilities and no single horizon corresponds to the schedule of liabilities (i.e., multiple liabilities). Examples of such liabilities are pension fund payments, insurance policy annuity payments, and contractual payments under a structured settlement in a legal case.
Two strategies can be employed in seeking to satisfy these liabilities. The first is an extension of the single-period immunization strategy discussed earlier. The second is a cash flow matching strategy. We discuss the immunization strategy first.
A portfolio is said to be immunized with respect to a given liability stream if there are enough funds to pay all of the liabilities when due even if interest rates change by a parallel shift. However having the portfolio duration match the liabilities duration is not sufficient for immunizing multiple liabilities.
306
A. Conditions for Immunizing Multiple Liabilities
The necessary and sufficient conditions to assure multiple liability immunization in the case of parallel rate shifts are as follows:
307 • The first condition is that the present value of the assets must equal the present value of the liabilities.
• The
second condition is that the (composite) portfolio duration must equal the (composite) liabilities duration.
The composite liabilities duration is a weighted average, found as follows:
• The third condition is that the distribution of durations of individual assets in the portfolio must have a wider range than the distribution of the liabilities.
An implication of the second condition is that if there are liabilities beyond 30 years, it is not necessary to have a duration for the portfolio that is 30 years in order to immunize the entire liability stream. The condition requires the manager construct a portfolio so the portfolio duration matches the weighted average of the liability durations. This is important because in any reasonable interest rate environment it is unlikely that a portfolio of investment-grade coupon bonds can be constructed with a duration in excess of 15 years. However, in a corporate pension fund situation, the liability stream is typically a diminishing amount liability stream. That is, liabilities in the earlier years are the greatest and liabilities further out toward the 30-year end are generally lower. By taking a weighted average duration of the liabilities, the manager can usually construct the portfolio duration at something that is more manageable, say, 8 or 9.
The third condition requires that when selecting securities to be included in a portfolio, the manager not only has to keep track of matching assets and liabilities duration, but also must track the specified distribution of portfolio assets.
The three conditions for multiple liability immunization assure immunity against parallel rate shifts only. In a series of articles, Reitano has explored the limitations of the parallel shift assumption.
308 He has also developed models that generalize the immunization of multiple liabilities to arbitrary yield curve shifts. His research makes it clear that classical multiple-period immunization can disguise the risks associated with nonparallel yield curve shifts and that a model that protects against one type of yield curve shift may introduce reinvestment and price risk to other interest rate shifts.
B. Acceptable Universe of Securities and the Cost of Immunizing
When discussing the actual process to construct a single-period immunization strategy, several factors affecting portfolio return were reviewed. Effectively, the greater the credit risk the manager is willing to accept, the higher the potential yield that can be locked in when immunizing a single liability. Equivalently, the higher the potential yield, the lower the cost of immunizing a single-period liability (i.e., the lower the present value of the liability).
The situation is the same when seeking to immunize multiple liabilities. However, a portfolio manager does not think in terms of a single “yield” that can be locked in via immunization since there are multiple liabilities. Instead, a portfolio manager thinks in terms of the cost of creating the initial immunized portfolio. Again, the greater the credit risk that the portfolio manager/client is willing to accept, the lower the cost of the immunized portfolio. In fact, it is not simply credit risk where the portfolio manager can pick up additional potential yield. If a portfolio manager/client is willing to accept call risk or prepayment risk, for example, there is potential to create a lower cost immunized portfolio.
C. Immunizing Defined Benefit Obligations
Sponsors of defined benefit plans represent the major potential users of the multiple liability immunization strategy.
309 As just explained, a plan sponsor will work with a portfolio manager in deciding the universe of securities that are permitted in the immunized portfolio. In turn, this depends on the degree of risk the plan sponsor is willing to accept.
A special case of immunization for multiple liabilities is when the plan sponsor wants to immunize the surplus of the defined benefit plan against an adverse movement in interest rates. Recall that surplus is the difference between the present value of the plan assets and the present value of the liabilities. When interest rates change, this will affect the value of the plan assets and the plan liabilities. To determine the value of the liabilities of a defined benefit plan a suitable interest rate or interest rates must be employed. Let’s look at this issue of valuing liabilities.
First, it should be clear that the liabilities should not be discounted at a single interest rate for the same reason that it is inappropriate to discount cash inflows for an asset using a single interest rate. Each liability is unique in terms of when it is paid in the future and therefore requires its own interest rate-the spot rate. There is no controversy in the finance literature about the use of spot rates for discounting liabilities. Where there is a controversy is the spot rates that should be used.
Historically, in determining the value of liabilities actuaries would somehow figure out what single interest rate they believe that a plan sponsor could earn on plan assets. That single interest rate would then be used to determine the present value of the plan liabilities. Not only is the valuation of liabilities using a single interest rate wrong, but the interest rate was subjectively determined (i.e., it was not market determined). This approach to determining the value of plan liabilities is unacceptable.
There are two yield curves that have been proposed for valuing liabilities based on market yields and multiple interest rates: (1) the Treasury spot rate curve and (2) the Treasury yield curve plus a spread. In the United States, this issue is unresolved as of year-end 2003. Advocates of the Treasury spot rate curve approach to valuing liabilities argue that liabilities should be reported for financial reporting purposes based on how much it would cost the plan sponsor to pay them off today by buying a portfolio of zero-coupon Treasuries.
310 That is, if a corporate sponsor of a defined benefit pension plan became bankrupt and the liabilities had to be paid off, this would be the cost to pay off those liabilities without any risk that they would not be satisfied.
Those who advocate a spread over the Treasury yield curve—an approach that has been advocated by the U.S. Department of the Treasury—argue that it is reasonable to expect a return could be earned on plan assets greater than that offered on Treasury securities in the long run. More specifically, an investment-grade rated corporate bond index yield curve is mentioned as the appropriate interest rates at which to discount liabilities. There are at least three problems with this approach. First, the yields are for coupon-bearing instruments and therefore are not spot rates. Second, using a corporate bond index yield curve means that as corporate credit spreads in the market increase (assuming Treasury yields do not decline to offset this), the value of plan liabilities will decrease. This does not make economic sense. Third, there is credit risk and therefore no assurance that the liabilities will be satisfied.
311
V. CASH FLOW MATCHING FOR MULTIPLE LIABILITIES
Cash flow matching is an alternative to immunizing portfolio to match liabilities. It is an intuitively appealing strategy because the manager need only select securities to match liabilities.
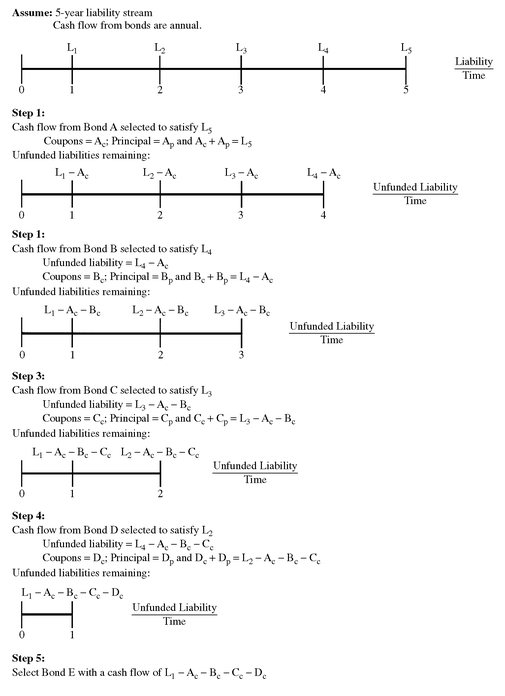
Cash flow matching can be described intuitively as follows. A bond is selected with a maturity that matches the last liability. The amount invested in this bond is such that the principal plus final coupon payment is equal to the last liability. The remaining elements of the liability stream are then reduced by the coupon payments on this bond, and another bond is chosen for the next to last liability, adjusted for any coupon payments of the first bond selected. Going backward in time, this sequence is continued until all liabilities have been matched by payments on the securities selected for the portfolio.
Exhibit 10 provides a simple illustration of this process for a 5-year liability stream. Linear programming techniques can be employed to construct a least-cost cash flow matching portfolio from an acceptable universe of bonds.
A. Cash Flow Matching Versus Multiple Liability Immunization
In the special case where all of the liability flows were perfectly matched by the asset flows of the portfolio, the resulting portfolio would have no reinvestment risk and, therefore, no immunization or cash flow matching risk. However, given typical liability schedules and bonds available for cash flow matching, perfect matching is unlikely. Under such conditions, a minimum immunization risk approach would, at worst, be equal to cash flow matching and would probably be better, because an immunization strategy is less costly to fund liabilities. This is due to two factors.
EXHIBIT 10 Illustration of Cash Flow Matching Process
First, a relatively conservative rate of return assumption for short-term cash, which may occasionally be substantial, must be made throughout the life of the plan in cash flow matching, whereas an immunized portfolio is essentially fully invested at the remaining horizon duration. Second, funds from a cash flow matched portfolio must be available when each liability is due and, because of the difficulty in perfect matching, usually before. An immunized portfolio need only have sufficient value on the date of each liability because funding is achieved by a rebalancing of the portfolio. Because the reinvestment assumption for excess cash for cash flow matching is for many years into the future, a conservative assumption is appropriate.
Thus, even with the sophisticated linear programming techniques used in cash flow matching, in most cases it will be more costly than immunization. However, cash flow matching is easier to understand than multiple liability immunization, and this has occasionally led to its selection as the strategy for meeting liabilities (i.e., called dedicated portfolio strategies).
B. Extensions of Basic Cash Flow Matching
In the basic cash flow matching technique described above, only asset cash flows occurring prior to a liability date can be used to satisfy the liability. The technique can be extended to handle situations in which cash flows occurring both before and after the liability date can be used to meet a liability.
A popular variation of multiple liability immunization and cash flow matching to fund liabilities is one that combines the two strategies. This strategy, referred to as combination matching or horizon matching, creates a portfolio that is duration-matched with the added constraint that it be cash matched in the first few years, usually five years. The advantage of combination matching over multiple liability immunization is that liquidity needs are provided for in the initial cash flow matched period. Also, most of the positive slope or inversion of a yield curve tends to take place in the first few years. Cash flow matching the initial portion of the liability stream reduces the risk associated with nonparallel shifts of the yield curve. The disadvantage of combination matching over multiple liability immunization is that the cost is greater.