

This book is an attempt to derive the simplest structures of social interaction that develop spontaneously, and to do so by extrapolating the structural implications of the content of relationships. For the purposes of this initial study, I have argued that we may simply group contents into those that are symmetric, those that are asymmetric (but possibly reciprocated), and those that are antisymmetric. Of these three, symmetric relationships are simplest in their structural implications, for they do not imply any intrinsic differentiation of persons.1 That is, a symmetric relationship does not establish one interactant as the giver, and the other as the receiver, one as the dominant, the other as the subordinate, or anything like that. Instead, the relationship is intrinsically an equal one. Perhaps the simplest such relationship is mere copresence—if I am with you at some time, you must be with me at this time. But the more interesting relationships tend to have a content that highlights the mutuality. The one that sociologists examine most frequently is often called “friendship.” This notion of friendship (which is not the same thing as wished-for friendship) is fundamentally similar to the notion of alliance, which is the subject of much anthropological research. For both friendship and alliance, the relationship requires reciprocation if it is to be real. When taken extremely seriously, these relationships go beyond equality and establish a sort of equivalence—what you do to my ally or my friend you do to me.
We begin our examination of the tendency of certain relationships to take on structural forms by examining relationships of equivalence. We will also find that at least in some situations, thinking in terms of equivalence implies the opposite, antiequivalence. Depending on what they are trying to do, actors may focus on equivalence, on antiequivalence, or on both. It seems natural that such relationships should lead to clear structural forms. But as we shall see, this is rarely the case.
Let us begin with the simple mutual relationships of friendship. Such relationships were the first sorts of interpersonal ties used by social scientists to derive structure, and they remain what most analysts assume when they imagine “ties” or other unspecified relations—they are the default for structural analysis. Since they impose no particular claims on the nature of persons (no role implications), we might imagine that they are the best material for composing building blocks that can be the basis for large structures. On the contrary, I shall argue, the structures that tend to arise from mutual relationships cannot be concatenated without some sort of fundamental transformation or weakening, and both transformation and weakening tend to undermine the relationships themselves. Thus we will begin with the nature of the relationship, derive structural forms, and then—just as Simmel would have appreciated—see how these forms cut against the nature of the relationship itself.
By the “nature” of the mutual relationship I mean the tendency to make connected persons equivalent. Such a tendency allows for clear structural forms to emerge—instead of many persons, each different from the other, a pattern emerges with a much smaller number of distinct positions. One such form of equivalence that social analysts continually rediscover for the case of mutual relationships is the clique. The clique, at least in the purest form, is generally considered to be a subset of persons, each of whom is tied to every other; here we will think in terms of sets of persons all of whom interact with one another. This interaction by definition does not distinguish between persons; indeed, in the clique, all members are “equivalent” in a technical sense. (If we denote “a has relationship R with b” by aRb, we say that a relationship R establishes equivalence classes if it is symmetric in that aRb implies bRa, reflexive in that aRa for all a, and transitive, in that aRb and bRc implies aRc.)
For example, below (figure 2.1) we see two cliques of five persons each. Within each clique, all possible interactions occur, while none occur between members of the different cliques. Because all members are equivalent, and all tied to one another, members are truly indistinguishable, and we may see the structure as only “horizontal.”2
The simplest (“pure”) clique structure as illustrated below places every person in one and only one clique. Sociologists have often wondered why such structures would arise. One answer in purely structural terms is that the clique will arise when people consider themselves equivalent. Such equivalence might be expressed as follows: “If you have a relationship with A, well then so will I. But if you do not have a relationship with B, I will not either.” Such equivalence and resultant clique-formation might reasonably result when the relationship in question is that of alliance, since to be an ally means to say, “I will take an attack on you as an attack on me.”
Figure 2.1. Two cliques
And indeed, there is intriguing evidence of clique formations appearing in alliance relations between groups. For example, K. E. Read (1954) studied political relations among the Highland New Guinea groups making up the larger unit of the Gahuku-Gama and provided a chart showing relations of alliance and enmity between the “subtribes.” Although Read, unlike the later analyst Hage (1973; cf. Hage and Harary 1983: 59), did not notice this, inspection demonstrates that there are three cliques present.3 Within any clique, all relations are positive relations of alliance. The relations between members of any two different cliques, however, are likely to be actively hostile, although in some cases they seem to be indifferent.
Similar clique-formation might reasonably occur between individuals when the relationship of “close friendship” is considered. For example, it may be extremely uncomfortable to befriend your close friend’s enemy; an insult to your good friend must be an insult to you. Further, the existence of such cliques among schoolchildren is a well-known, or at least, well-believed-to-be-known, fact of American life.4 Indeed, the recurrence of such cliques in schools is a reasonable supposition, but the reason for the structural tendency may be somewhat different from what is commonly assumed. Much of the interaction between children at school takes place in relatively short periods of time—the group may be (partially) together during lunch or recess, but not throughout the day. If child A wishes to eat lunch with B, and B is going to eat lunch with C, A has no choice but to accept C along with B. Ties of “lunching together” with other children must be forsaken. It is then, the institutional structure—in this case and many others, the simple act of setting out separate lunch tables—that leads any regularity in interactions to take on a clique form (this point has also been made by Anderson 1979: 459).5
Structures produced by such institutional scaffolding cannot be said to have formed “spontaneously” and are thus poor material for us to use in understanding the emergence of structure from relationships. Still, this process whereby A and C, both of whom are friends with B, encounter one another more frequently and hence are more likely to establish a positive relationship, may be similar inside and outside such institutional forms. Most simply, as Homans (1950; 1974) has suggested, we should expect a positive feedback loop between the time people spend together and their degree of agreement across a host of measures. Those who find themselves in agreement will tend to like each other, and hence spend more time together. What is important is that such a process leads the relationship of friendship to become transitive: if A is friends with B and B with C, we can expect A and C to also become friends simply because of the increased likelihood of their spending time together.
Let us return to the definition of an equivalence relation R being (i) symmetric (aRb implies bRa), (ii) reflexive (aRa for all a), and (iii) transitive (aRb and bRc implies aRc). It will be seen that the first condition follows from the definition of mutual relations, and the second is trivial (all persons interact with themselves). The essence of the partitioning of some group up into cliques, then, turns on whether relations are transitive or intransitive, with transitive relations leading to equivalence relations and hence cliques. We shall investigate such transitivity below and find that despite the plausibility of Homans’s idea, the evidence for the production of transitive friendship cliques is slight. But even should such a structural tendency exist, it is an inherently limited basis for the production of larger structures.
To demonstrate this limitation, let us imagine that a number of cliques exist. Can these be the basis for the construction of some larger structure with clear formal principles? The answer is, not without fundamental disruption to the structural tendencies inherent in cliques.
If transitivity is to be preserved, the connection of two cliques requires all pairs of persons to establish relations. That is, using our example of the two five-person cliques above, if person A1 in clique A establishes a relation between B1 in clique B, then all other 24 (= 5 × 5 −1) relationships must also be established. But it is probably the difficulty of sustaining so many relationships that has led to the small size of the various cliques in the first place.
We may call this the problem of “completion”—the very nature of the relationship (one that is egalitarian and transitive) puts too heavy a burden on interactants. We require all persons to have relationships with one another (thus the structure is “complete”) if the structure is not to be degraded or transformed. Putting cliques together to make larger structures, then, is simply unworkable unless something is changed.
There are, then, two options for facilitating structure formation via the aggregation of cliques. The first is to introduce a second or perhaps also third type of relationship. Thus we may have a different type of interaction, “bridging,” which is done by some but not all clique members. Such bridging is illustrated in the figure below (figure 2.2, top); the double line indicates a bridge, and the nodes connected to it can now be differentiated from the other nodes. In this case, we may say that within a clique relationships remain transitive, but we introduce a second type of relationship, the bridge, and therefore move to what I have called a complex structure, one that involves more than one type of relationship.
The second is to abandon the rigid transitivity requirement. Thus we allow some person(s) to be in more than one clique at a time. Once again, differentiation is introduced into what was an equivalence relation, as there are some nodes (we may call them “welds”) at which transitivity stops. An example is given in figure 2.2, bottom, of our two cliques joined by one person. You will note the absence of transitivity, as (for example) a5 and b2 each have a relationship with the welding node, but not with one another.
Given this relaxation, it is possible for cliques to concatenate to form larger structures, although these structures lack the kind of absolute principles that might guide subjective action via clear heuristics. In particular, you cannot assume that your ally’s ally will be your ally.
Let us concentrate on welds, which do not involve introducing a second relationship. (Most network analysts tend to assume the case of welds because they only have data on a single relationship.) Allowing for welds not only requires a sacrifice of strict transitivity, but of strict equality as well: we see the transformation of a wholly horizontal to a potentially vertical structure. The verticality comes in the fact that welds are qualitatively different, and where there is difference, there may be inequality. This point has been made most clearly by Burt (1992; 2004); looking at managers, he finds that welds get promoted faster, make more money, get better evaluations, and so on. In other cases, being a weld may be unfortunate—welds may have more work to do—but good or bad, they are different in a way that introduces inequality. The equivalence that was the essence of the relationship has been lost. Thus by solving the problem of completion (allowing some pairs of persons not to have relationships), we introduce the problem of inequality. Although the relationships are supposed to be equal, we introduce a vertical differentiation between the persons.
Figure 2.2. Bridge and weld
In this simple example of a single weld, this verticality can be expressed as a categorical distinction between welds and regular nodes. But as we attempt to build a larger structure, we are likely to find this clear distinction dissolving into a differentiation that is only a matter of degree, not of kind. At the same time, we find that the structural components (the two five-person cliques in this case) lose their clear identity. Instead of a clear structure, we have only some degree of tendency toward structure—some degree along a continuum stretching from total randomness at one end to separate cliques at the other. This tendency, however—one toward “clumpiness”—is still fundamentally related to that which we saw underlying the clique. We may term such sets of relationships “webs” and see to what extent their organization can reflect this structural tendency (also see, e.g., White and Harary 2001).
We may define webs in network terms as sets of symmetrical ties with low variance of degree and low density but a significant tendency toward transitivity or clustering—groups of three, all of whom are tied to one another. Two seemingly similar relationships that fit this bill are “friendship” and “acquaintance.” For friendship, the low variance criterion means that although some people have only one really good friend, and some have close to one hundred, most have around ten, and no one has a thousand. The density criterion means that if you pick any two people randomly, the chances are low that they are friends. Acquaintance may initially seem very similar to friendship, only “less so”—it may be seen as an attenuated form of friendship. But acquaintance may have particular structural attributes. In particular, it may well be that a set of acquaintance relationships forms a “small world.”
The “small world” is a set of relationships, envisioned as a network, in which the overall network is large and sparse, yet any two points are connected by a surprisingly small number of intermediaries (at least, surprising given the tendency toward transitivity and hence “clumpiness” of the web). This idea was introduced by Milgram (1967) with the finding that most Americans seemed to be connected by no more than “six degrees of separation”—six intermediaries could be found between A and H so that A knows B, B knows C, C knows D, D knows E, E knows F, F knows G, and G knows H.6
Such networks are important for communication (and hence for influence and social change), since they allow one to spread a message (or a disease) throughout a large population, and communication is not easily impeded by the removal of some relationships. While there actually is very little reliable evidence on the matter, for the sake of argument, I will assume that the web of acquaintance relationships does in fact have small-world properties. (It is worth emphasizing that acquaintance is not the same thing as friendship: for reasons we will uncover, it is unlikely that the small-world property holds for friendship relations.) Because most randomly generated networks of similar density and distribution of degree lack small-world properties (also see Strogatz 2001), we may ask what is it that might lead our social world to be a small one?
One likely contender is movement. The following is sufficient to produce a small world. First, be born. Second, establish one hundred connections to the first people you see. Third, go to some new environment (this may or may not require geographical separation, but some such movements are necessary). Fourth, drop twenty old attachments (as long as the probability of retention is not too highly associated in a positive direction with age of the attachment), and form twenty new ones to people around you. Repeat steps three and four at intervals of approximately ten years until you are retired.7 As long as a few people do this, they will bring the rest of us together in a relatively small world (compare the argument of Robins, Pattison, and Woolcock 2005: 921ff, and the discussion of chapter 5 in this book).
More technically, Watts (1999: 67, 241) has demonstrated that a small amount of random rewiring of a simple type of graph is sufficient to produce small-world graphs. In particular, consider the two separate cliques in figure 2.1 of this chapter—Watts considers this a “caveman” world in that people establish relationships with the few in their cave but have no relationships with those in other caves. Consider a process in which one tie is changed from a “within” cave to a “between” cave tie such that all caves are connected to those that are “near” them. This network is now connected, but does not necessarily possess small-world properties, and this is because the connection has happened according a spatial logic, and not a “relational” one.
A relational graph is one in which the probability of two nodes (e.g., persons) being tied is proportional only to the number (or proportion) of ties they have to nodes in common. Thus those with mutual friends are more likely to become friends. In a spatial graph, all the nodes are embedded in a space (whether a physical one or merely an analytic one), and the probability of a tie between two nodes is a (decreasing) function of their distance in this space.
This second type of graph would seem a natural model for social relations, since persons actually do occupy a position in a (nearly) two-dimensional space, and it is reasonable to expect that they are more likely to establish relations with those near them than with those far. Indeed, even within the local scale (that is, ignoring the attenuated probability of intercontinental friendships and so on), there is persuasive evidence that this is the case. In a wonderful study of relationships between adult graduate students in a student housing complex, Festinger, Schachter, and Back (1963) demonstrated that the probability of two persons or families being friends depended greatly not only on their general location, but the paths they would take on their daily entrances and exits from their apartments. Those who shared a staircase were more likely to become friends than those equally close but tending to use different stairwells.
As if there weren’t sufficient reason to expect a spatial component to social networks, researchers have been in recent years greatly enamored of techniques (especially multidimensional scaling, but also correspondence analysis) that more or less create an analytic space to explain the pattern of relations. Thus a complex pattern of relationships among many persons is simplified by placing each person in a three- or four-dimensional analytic space (as opposed to a geographical space), and proposing that people form ties to those close to them in this space. The dimensions of this space might not have any intuitively accessible explanation, but they might also resolve to familiar social attributes such as education and income. Yet these efforts may be in the wrong direction if spatial analysis is false to the principles of social networks.
And false the spatial model must be (if the relationship in question is the small-world relationship of acquaintance): after the fact, the point that spatial graphs cannot be small-world graphs seems quite obvious, but I am not aware of anyone who saw its importance before Watts. The particular assumptions used by Watts may be problematic for direct application to certain social relationships, but the point should stand: a spatial organization leads the “big world” to stay a big world because by definition the areas of this space cannot come any closer together (see Watts 1999: 241). While random rewiring in a relational graph can produce a small world, any randomization added to a spatial model simply moves the graph more toward a random graph, without the clustering characteristic of small-world graphs.8
Yet given the well-known importance of spatial metaphors for understanding social life (such as the “social space” of Bourdieu [1984]), should we conclude that social networks are not spatial but are relational? The answer will depend on whether we are interested in strong ties like friendship or weak ties like acquaintance. I will argue shortly that strong ties probably follow a spatial logic. Weak ties do not, but it is not because this notion of social space is irrelevant; it is that it is not necessarily the case that all spaces are isotropic. It is this point, that weak ties are likely to defy the closure implicit in spatial logic, that was the important contribution of Granovetter’s (1973, especially 1268) widely cited and widely misused article on the strength of weak ties.9 Among other things Granovetter argued on theoretical and empirical grounds that it is only weak ties that should show evidence of a small world.
There may indeed be a social space in which we can position persons so that those near-by are more likely to form ties to one another than those far away. We do not need to specify in advance whether this space can be identified with dimensions such as “capitals,” or whether, after the fashion of Friedkin (1998) it should simply be considered a reparameterization of relational patterns. But in addition to this analytic space, plain old everyday geographic space also influences the probability of relationship formation and survival. As Watts (1999: 133) has argued, it seems highly likely that interpersonal relations will be affected by distance in two spaces, geographic space and social space. But precisely because two different spaces are involved, we cannot describe the formation of acquaintanceship by embedding all persons in a single analytic space and predicting that those close will form relationships.
Figure 2.3. “OR” logic of acquaintance
For example, imagine a simpler two-dimensional space in which one dimension is “geographical” distance and the other is “social” distance (see figure 2.3). Denote the first distance g and the second s; the normal Cartesian distance between any two points i and j in this space would be
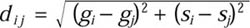
There are, of course, other ways of calculating distance, but this is as good as any for illustrating the point that, according to normal spatial principles, you are basically only as close as you are far apart on the dimension most separating you. But it seems very likely that one will form at least a weak friendship with a next door neighbor who is not at all close in social space, and that similarly one may maintain a tie to one with whom one has a great deal in common even when that person is separated geographically (perhaps a school friend that one sees only at annual reunions or trade meetings). Hence we can imagine ties traversing this analytic space connecting persons who are very close on one but not both dimensions. Weak ties “tunnel” through the joint geographic-social space, since they operate on an OR logic: A is likely to know B if the two are close in geographic space or social space. (Thus in the figure above, the ties that are wholly horizontal or wholly vertical connect people who are very close on one dimension but far apart on the other, connections that are extremely unlikely if the overall logic in this two-space space is spatial.) Such a network probably has small-world properties (this point has recently been made in more rigorous terms by Watts, Dodds, and Newman 2002).10 In other words, the overall set of acquaintances is such that everyone is reasonably close to everyone else.
Figure 2.4. Wheel
But people can also be reasonably close if some special persons have structural positions that facilitate the indirect connections of others. In the simplest such structure, there are as few ties as is compatible with a connected structure—all persons except the special person have ties only to this special person. This person (located at the center of figure 2.4) may be termed the “hub” of the structure, and the others may be called the “spokes.”11 A hub and its spokes may be called (what else) a “wheel.”
We often see hub structures when a group has gelled around a particular charismatic individual. The group only exists so long as the hub person retains his or her charisma or activity. Of course, many charismatic leaders show a marked disinclination to have anything to do with one another, and hence their structures do not form the building blocks for larger structures. But in other cases, hubs establish relationships not only with their own spokes but also with other hubs, thereby bringing their spokes into indirect connection, as shown in figure 2.5.
Figure 2.5. Multihub structure
We shall explore such multihub structures in chapter 5 in terms of their properties for spreading information and influence. Here, we can imagine successively introducing “noise”—some random rewiring, allowing some spokes to have connections to other spokes, or some spokes to be attached to more than one hub—and moving from this structurally simple graph to one that would appear more or less indistinguishable from the small worlds we have seen above.
Indeed, a multihub structure might have small-world properties, in terms of having the characteristic path length of a random graph, but more clustering than a random graph (for a mathematical demonstration, see Yamaguchi 2002). And yet it would not be a small world as derived by Watts, for the reason that here there is, at least in principle, a qualitative distinction between two classes of persons. They may be considered hubs and spokes, central and peripheral, cosmopolitans and locals, but they are different and it should give us analytic purchase to describe the typical characteristics of each class.
Judith Kleinfeld (2002) has recently emphasized that merely on a priori grounds it is reasonable to imagine that much of the supposed small-world phenomenon is actually due to such a two-class structure. Some people (we can call them “locals”) are embedded in cavelike cliques and have no ties outside their caves, while others (we can call them “cosmopolitans”) have ties both to locals in their cave and to other cosmopolitans. Locals can only communicate outside of their cave by the good graces of the cosmopolitans. (She compares this to a bowl of oatmeal, with some parts lumpier than others.)
There must be some truth to this; it seems much easier for Milgram-type chains to be completed if the target is prominent.12 I can get a message to our president with only five intermediaries under the relationship of “face-to-face acquaintance” (mayor, state political party chair, governor, senator, president), but my odds of successfully completing a transmission to someone less prominent are far lower.13 Kleinfeld suggests that small-world studies have been skewed because they relied on a subset of unusually well-connected participants (almost all studies use volunteers), and completely skirt around the many ethnic enclaves that may be small worlds in themselves, but are not well tied to the rest of the world.
Certainly Kleinfeld’s images are appealing—perhaps especially so to someone in a more remote area (Kleinfeld herself is a professor in Fairbanks, Alaska). Although there is nothing about a “lumpy” world that is necessarily incompatible with small-world properties, this derivation demonstrates something generally overlooked about acquaintanceship as a relation, and this is that it is not strictly symmetric. We are acquainted with those whom we remember, and we tend to remember more prominent people and forget the less prominent. People seem to remember their more successful distant kin and forget the unsuccessful (cf. Smith 1983: 67); I remember that I knew the mayor but she has probably forgotten all about me.
In sum, the set of “acquaintance” relationships may tend to have small-world properties, and this may indeed have something to do with the “random rewiring” that occurs when we pick up and move. It certainly has a great deal to do with the fact that we can be acquainted with those to whom we are close in either geographical or social space. But it also has to do with the fact that acquaintance turns out not to be an inherently symmetric relationship. There is both more and less equality in such relationships than we assume. There is less equality in that those whom we know do not necessarily know us. In some cases this has to do with a stratification of persons into more and less prominent, with the limiting case being a two-class world of cosmopolitans and locals. But it need not have to do with prominence: new students enter a college or a school with a largely empty set of acquaintances, and they busily begin adding to this set the moment they unpack. The upperclassmen and women they meet, on the other hand, have already largely filled their set of available acquaintances and may well forget the new ones they meet simply because they have less room to store names.
Thus there is more equality than we might think. When we ask “whom do you know?” we may find great inequality—some prominent people are “known” over and over again. But there is less inequality in terms of the number of acquaintances that people have. Precisely because prominent people do not know all those who know them, they are more like the less-prominent in their number of acquaintances.
We shall return to the complications that arise when we allow for nominations to be unreciprocated at the conclusion of this chapter. But we set out to investigate specifically mutual relationships revolving around equivalence. Weak relationships of acquaintance turned out not to fit the bill; we now turn to stronger relationships of friendship.
Men are conjoined by a vast network of acquaintanceship. Brown knows Jones, Jones knows Robinson, etc.; and by choosing your farther intermediaries rightly you may carry a message from Jones to the Empress of China, or the Chief of the African Pigmies, or to anyone else in the world. . . . What may be called love-systems are grafted on the acquaintance-system. A loves (or hates) B; B loves (or hates) C, etc. But these systems are smaller than the great acquaintance systems that they presuppose.
—WILLIAM JAMES, Pragmatism
In this largely overlooked anticipation of the small-world problem, James posits that there are two networks spanning humanity, one of weak acquaintance ties, and the other of stronger ties. He also proposes that the latter is a proper subset of the former, which is eminently reasonable, since in order to love or hate someone, we must know them, but the reverse is not true. We have been concerned with the former type of relationship; let us now turn our attention to the latter. I propose that in contrast to acquaintanceship, close friendship satisfies the Cartesian AND formula in which A and B have to be close both in geographical space and in social space to become close friends. And this is why it is doubtful that sets of these relationships have small-world properties: they are probably a bit more like connected cavemen worlds, in which the caves are distributed in some space. (Somewhat loosely, two spaces that jointly affect relationship-formation via AND can produce a single space.)
Although Americans may be more likely to have friendship relationships that cross boundaries of social space than the French who formed Bourdieu’s reference world (see Varenne 1977), it is still probably the case that the stronger the tie underlying the relationship, the greater the tendencies toward transitivity and hence closure. Louch (2000) points out that even if one has a will to retain ties with those in different sections of social space, it may be more difficult to do this with those from whom we differ considerably. I see my sociologist friends from California every year or so at a convention; my friends who were janitors or body therapists, never. It does not seem to be the case that truly close friendships weather separations that would break weaker ones—people are unlikely to retain close ties with those from whom they become geographically separated (Martin and Yeung 2006).
But for this very reason (i.e., spatialization), strong friendship relations are unlikely to rigorously follow rules of transitivity and lead to cliques, and it is worthwhile to consider why not. Winship (1977) generalized this transitivity criterion to be expressed in terms of social distance as follows: if the distance between persons X and Y is dxy, and that between persons Y and Z is dyz, then the distance between X and Z will be no more than the sum of dxy and dyz. This is called the “triangle” inequality because all triangles in a simple space satisfy the requirement. According to this light, it is entirely possible for people to be tied by weaker-than-transitively-implied ties. That is, if X and Y are “close” in this space (say, they are good friends), and Y and Z are also close (good friends), X and Z need not be good friends. But they are acquaintances on good terms. If X and W are also acquaintances on good terms, W and Z need not be friendly at all (see figure 2.6).
In sum, spatial models may be roughly appropriate to strong friendships; indeed, Watts’s “connected caves” model may be roughly appropriate. One phenomenon supporting such a spatial model of connected small worlds is pluralistic ignorance (Allport 1924; O’Gorman 1986), or when everyone shares an incorrect belief, especially about what everyone believes. Such pluralistic ignorance easily arises when people only check the beliefs of those in their “cave” and conclude that “everyone” shares their beliefs. Thus pollsters report irate calls from members of the public demanding to know “who [the pollsters] were talking to” when the pollsters present results that seem obviously wrong to the callers (see, for example, Kagay 1999). Small worlds should be extremely good for spreading information robustly, yet the relationships that are used for political conversation—probably relatively close relationships—evidently do not communicate to around one-third of Americans that the other two-thirds still supported President Clinton around the time of his impeachment. A small world indeed!14
Figure 2.6. Spatial intransitivities
We began with the simple relationship of friendship as a starting point to witness the emergence of social structure. Making a distinction between friendship and acquaintance, we saw two different versions of a similar structural tendency—a tendency toward clumpiness. In both cases, this can be understood as a tendency toward transitivity. There are many ways in which this tendency can be understood, but the most intuitively reasonable one has to do with the exclusivity of copresence at any time: if C is often with B, it is difficult for A to be with B without sometimes being with C as well. This gives A more opportunity to form a relationship with C than with some otherwise equivalent D, and, if Homans (1950) is correct, probably goes further and actually encourages the formation of an attachment.
But we have found limitations to this tendency that forestall the emergence of clear structure—that is, sets with clear formal properties that are available on inspection both to analysts and to actors. In the case of mutual relationships it seemed that the expected structures would be pure cliques. For the case of the weak ties of acquaintanceship, clique formation is hindered by three things. First, there is the mobility of persons who retain some old ties and hence produce a small world. Second, since people make or retain weak ties when they are close in geographic or social space, there is a block to transitivity when we switch from closeness based on one space to closeness based on another.15 Thus my neighbor knows my other neighbors, and my colleagues know my other colleagues, but my neighbors do not know my colleagues. Third, there is the fact that acquaintanceship is not strictly mutual.
For the case of stronger ties of friendship, the pressure toward transitivity is only strong enough to lead to clumpiness and not the development of clear-cut cliques. And the reason seems to be that strong ties form according to distance in a compound social space, and so relationships lack strong transitivity—a web of close connections may span a large distance, and thus if a is close to b, b close to c, c close to d, d need not be close to a—a violation of transitivity. People may form clumps in webs that can be distributed across social space, but these clumps seem destined to fall short of clear structure. While we can imagine these as one-time cliques that have been welded together, to the extent that they take on a spatial logic, we may expect it to be difficult to uncover bounded, exclusive structural units.
In sum, the heuristics that seem to lie behind the formation of acquaintanceship and friendship do not seem to lead to structure. These heuristics may well be architectonic—that is, of the nature to lead to structural consequences—but they are not absolute. Most important, a mere tendency toward transitivity does not, in itself, lead to structure. “Likeness” is not the same thing as equivalence. But that does not mean that there may not be cases where actors take a relationship pertaining to equivalence and approach it with heuristics with clear structural import. Such a structural logic was proposed by balance theorists, who basically started the rigorous analysis of the emergence of structure from interpersonal relationships. These theorists began from an elegant and strong set of axioms about human reasoning that had testable structural implications. We can see that these axioms turned on the nature of the equivalence established by a mutual relation. But as theorists tried to apply the resulting claims to actual data, they were forced to successively relax the stringent structural assumptions made; tracing out this process takes us from the nature of equivalence to the nature of ranking.
Ch’u and Chin shall not go to war with each other. In their likings and dislikings they shall be the same. . . . if any would injure Ch’u, Chin shall attack them, and for Chin, Ch’u shall do the same.
—from Chinese alliance covenant, 576 BC, quoted in Frank Kierman, “Phases and Modes of Combat in Early China,” in Chinese Ways in Warfare
Above we considered the exemplars of a mutual relationship to be alliance or friendship, since they establish a kind of implicit equivalence between the parties in question. We examined friendship relationships to see whether they tended to take on structural forms that would allow actors to internalize simple and absolute heuristics; now we turn things around and see what the heuristics that might be applied to these relationships imply in structural terms. Perhaps alliance is a simpler case than friendship because it may be less multivalent and should be more rational. Those who make irrational alliances, we might guess, get selected out.
Alliances differ, but the strongest form is one that stresses the equivalence of the parties. Those making the alliance may swear that, as the old Anglo-Saxon oath of commendation went, “Thy friends will be my friends, thy enemies, my enemies” (Bloch 1961 [1940]: 232). Let us return to this case but make the additional simplifying assumption that those who are not allies or friends are enemies. Alliance can be considered a positive relation (indeed, given a value +1) and enmity considered a negative one (-1); for purposes of brevity I shall call these “love” and “hate.”
Taking this setup seriously, the psychologist Fritz Heider (1946; 1958: 212) turned to Spinoza’s arguments (1930 [1677]: 125–34) in propositions 22, 24, and 31 of the third part of his Ethics regarding the relation between our own loves and hates and those of others. “If we imagine that a person affects with joy a thing which we love, we shall be affected with love towards him. If, on the contrary, we imagine that he affects it with sorrow, we shall also be affected with hatred towards him.”16 Taking these reasonable ideas and converting them into all-or-nothing choices allows us to derive very strong predictions for the class of possible structures (Harary 1955).
Indeed, from this Heider developed what is now known as “balance theory” by noting that this implies that we want the signs of any chain of associations or relations to make a positive when they multiply together (Heider 1946; 1958: 206). According to this reasonable model, even if two wrongs do not make a right, two hates make a love, in that learning that someone hates someone you hate is enough to make you immediately like this person, or at least choose him or her as an ally. All in all, four rules of action can be derived: you will love anyone your friend loves, you will hate anyone your friend hates, hate anyone your enemy loves, and love anyone your enemy hates (see Davis 1963: 450; Johnsen 1986: 278).
Quite simply, when applied to sets of relationships that can be either positive or negative, balance theory implies that any social whole splits into two mutually hostile cliques or, even more improbably, one happy camp of universal love (see Cartwright and Harary 1956: 286). Also, hopefully less improbably, self-hatred was also ruled out, and so all relations had to be mutually hostile or mutually friendly (otherwise they would contradict balance if A loved B and B hated A, since A would have to hate herself to hate her friend’s enemy).
Empirical adequacy aside for the moment, we see here a perfect example of the duality of heuristic and structure—the empirical pattern can either be described in formal terms (either in terms of an equivalence relation and an antiequivalence relation or in terms of multiplication of sign) or in the subjective terms of the four rules discussed above.17 To return now to the issue of empirical adequacy—there wasn’t any. Cases of such clear bifurcation, or the presence of all four laws of action, were stunningly rare (see Abell 1968 for a discussion).18 It does seem that in friendship many people will understand the force of the first heuristic, my friend’s friend is my friend (Davis 1977: 58)—at least to notice violations as problematic. Thus Rousseau (1928 [1782]: 733) complained of the fact that while he gave all his friends to Friedrich Grimm, none of Grimm’s friends became Rousseau’s friends. There is even some evidence that people may be influenced by the rule that “an enemy of a friend is an enemy.” But the other two heuristics do not seem to be recognized as structural laws in friendship (see Doreian and Krackhardt 2001: 60). Such laws have been followed in history, but they generally arise where two large opponents draw smaller allies among themselves (for some references to the use of balance theory for international relations, see Doreian 1971: 85).
A perfect example is the conflict between Sparta and Athens in the fifth century BC, in which almost all smaller cities had to ally with one in order to be protected from the other, though this alliance was also sure to bring down the wrath of the second (for a description of this taking of sides, see Thucydides VII: 57, p. 514). One way to choose sides was to use the rule “the enemy of my enemy is my friend.” For one wonderful example, the Corcyraeans chose to ally themselves with Athens, even though they were Dorians and closely connected to the Peloponnesian party, because of their hatred of Corinth, which was allied with Sparta. Other examples occur in criminal gang conflict, where rival gangs will use the same principle to affiliate with two overarching alliance systems such as Bloods and Crips or People and Folks (for examples, see Venkatesh and Levitt 2000: 435; Hagedorn 1988: 67f).19
Now it is possible for the equivalent of the four laws (and consequently the bifurcation of the population) to arise in the absence of two major powers. In one interesting case, when traveling Polopa of Highland New Guinea (see Brown 1979: 727ff) come upon strangers, they immediately attempt to find either enemies in common or friends in common. Since they assume that there is no such thing as neutrality and hence “he who is not with me is against me,” failure to establish alliance via one of these two rules (my enemy’s enemy is my friend; my friend’s friend is my friend) establishes a prejudice of enmity. Consequently, it seems that the alliance structure is “two colorable” (indeed, Brown actually referred to the alliance clusters as colors) in that there are two groups, with all intergroup relations negative and all intragroup relations positive (Hage and Harary 1983: 40).20 But such cases of balance are the exception, not the rule, and in this case seems to be due to the exceptional vulnerability of the traveler.
Indeed, we shall see that even given only two states (love and hatred) and extremely rational participants, there must be rather strong institutional supports for the balanced structure to emerge, for the simple reason that the “laws” of balance assume a type of reactivity that is the opposite of what we would consider rational. Take the principle, “my enemy’s friend is my enemy.” It is a poor sort of enemy who allows himself to be guided by this maxim. Consider two enemies, A and B, the former of whom decides, balance theory be hanged, to attempt to make friends with B’s friend C. If successful, B will have no choice (assuming he does not also abandon balance theory) but to turn C into an enemy. By assiduously courting all of B’s friends, A should be able to leave B completely isolated.21
To conclude, there are cases in which the relationship of alliance—intrinsically a relationship of equivalence—leads to the production of perfectly balanced structures, which are bifurcations into two hostile groups. Yet such cases are an exception, even when we have a relation of alliance as opposed to hostility. This is not because the people in question are cognitively incapable of reaching the logical conclusions implied by balance theory, but because they are reasonable enough to avoid them.
Further, it turns out not to be correct that the subjective possession of balancelike rules necessarily leads to bifurcations. As Levi-Strauss (1963: 161) emphasized, despite the duality of heuristic and structure, heuristics of bifurcation do not necessarily lead to bifurcated structures. Indeed, in the one case in which there is a repeated tendency toward the production of balanced bifurcations from the point of view of any particular actor, we see an inverse relationship between the existence of exhaustive subjective heuristics for allocating persons into two categories, and the existence of stable bifurcations in the population. That is, where we see actors struggling to systemize ideas of equivalence and antiequivalence, we see them reproduce the outlines of balance theory. Yet in these very cases in which people hold a set of subjective principles seemingly compatible with balance theory, we are least likely to see the stable division of persons into classes that balance theory predicts.
This case—one found in traditional societies from North America to Africa to Australia—involves the division of all possible kinsmen into “joking” partners or “avoidance” partners.22 The former are treated with familiarity (the jokes frequently involve sexual innuendo and teasing), and the latter with deferential respect (sexual matters never raised or alluded to). Such a system seems to have generated independently in a wide variety of geographically disparate areas. Hage (1976; cf. Hage and Harary 1983: 47) takes the G/wi Khoisan of the Kalahari as an example (as originally discussed by Silberbauer 1961; 1972) and demonstrates the strong tendency toward balance. G/wi informants explicitly only discuss two of the four laws of balance: the joking partner of my joking partner is my joking partner, and the avoidance partner of my joking partner is my avoidance partner (Hage and Harary 1983: 47).
If the G/wi interpreted these rules as referring to triads, they would be sufficient to produce a balanced bifurcation of the society. That is, they might say to themselves, “that the avoidance partner of my joking partner is my avoidance partner implies that the avoidance partner of my avoidance partner is my joking partner too.” But they do not—and note that the rules they emphasize are those that studies of American friendship have also found being used—my equivalent’s equivalent is my equivalent and my equivalent’s antiequivalent is my antiequivalent.
As a result of their selective interest (and contrary to Hage and Harary’s reasonable attempt to emphasize this as a case of balance), the G/wi system does not lead to two supercliques of joking partners. First of all, contrary to implication, the G/wi do not find anything anomalous in three people all being mutual avoidance partners (Hage 1976: 41), which would imply a possibility of multiple cliques of joking partners. But this is also not what occurs—instead, the system is closer to a bifurcation, but one that is different for each person.
Figure 2.7. Bifurcations and two-colorings
Perhaps a simpler way of deriving such a structure than Hage’s (1976) emphasis on balance is to start with the fact that, as Hage and Harary (1983) mention, the resulting graph of a balanced structure is “two-colorable,” meaning that any person can be assigned to one of two colors or cliques. Topology demonstrates that a map is two colorable if the boundaries of all regions are lines that do not stop within the area and the intersections of these lines occur at single points (as opposed to two lines overlapping for a while). The example in figure 2.7 is of a spherical area with a number of curves all of which reach to the perimeter of the area (left); the middle diagram shows that this is in fact two-colorable.
You will note that if a new line is drawn across the surface, the map will remain two-colorable: one only has to “flip” all colors on one side of the line. In the third panel, a new vertical line is added through the center—all the colors to the right are inverted, but the figure remains two-colorable. In a very close analogy, consider a set of distinctions that can be made between all persons. Between any two people who are alike in all other ways, being different on one distinction makes them antiequivalent. But adding a second distinction makes them anti-antiequivalent, which turns out to be the same as equivalent. Each distinction made is then like one of the lines in the above figure. The resulting set of social categories can then also be made two-colorable, so that whenever we cross one of these distinction-lines, we switch from one color to the other.
Joking/avoidance relationships seem to arise where there are such sets of distinctions, usually oriented around sex and parentage. These distinctions are put together to get at a more fundamental distinction, namely those who are equivalent to ego, and those who are antiequivalent (this corresponds to the distinction between black and white in the above diagrams).
It seems that in cultures that dichotomize all persons into joking and avoidance partners, the essential logic is closely related to the selection of possible marriage partners in a kinship system, which does not permit of division into exogamous moieties (the bifurcation underlying the restricted exchange examined in more detail in the next chapter). When there are moieties, people (taking ego as male) reason “I cannot marry X, because she is like me—a member of moiety A.” In joking/avoidance systems, ego reasons, “I cannot marry X, because she is unlike me—an avoidance partner.”23 This logic is structured with distinctions that cut through all persons (as opposed to only being applicable to a subset of persons). These distinctions establish both equivalence and difference or, as I have called it here, antiequivalence. The term antiequivalence highlights the ways in which the transitive logic works—someone who is the opposite of someone who is opposite to me is the same as me. We can therefore simplify the sort of patchwork two-color graph above by constructing a two-portion graph with a single border—relations of antiequivalence imply a crossing of this border, while relations of equivalence do not.
For the G/wi, relations of equivalence are “marriage” and “same-sex sibling.”24 Relations of antiequivalence are “parent-child” and “opposite sex sibling.” We can actually assimilate this system to the “two-colorable” graphs above by ignoring the equivalence relations and focusing on those of antiequivalence. So we may make two lines indicating “boundary crossings” to those who are antiequivalent. One is that of an alternate-sex sibling (the vertical line on the diagram in figure 2.8), and the other is that of an adjacent generation (the horizontal line). The fact that same-sex siblingship and marriage are equivalence relations need not appear—we only know that if we are traversing one of these relationships we do not move from whatever area we are in.
Figure 2.8. Equivalence and anti-equivalence
First, our male ego can empirically confirm that -1 × -1 = +1 for either of these relationships considered individually. If he crosses the vertical line (and hence thinks of his sister), and then “standing” there, crosses the line again to his sister’s opposite-sex sibling, he ends up with his brother, an equivalence relationship. One can go back and forth over this line as many times as one wants, and multiplying negatives will not steer us in the wrong direction.
So too when it comes to the relationship of antiequivalence of adjacent generation (see figure 2.9). Ego must avoid his parents (and his children). But if he goes to his father and then to his father’s father, he finds someone equivalent to himself. Both have to avoid ego’s father. From this, one can imagine a chain of alternating generations—two-colorable—ascending upward and downward infinitely.
So for either of the single relations of avoidance, we find the balance theoretic approach works admirably. We can treat antiequivalence as a negative relation and allow relations to multiply. And we can then build on this for other cases. Relations of marriage equate the husband and wife, so that each must assume the avoidance and joking relations of the other, but since one should only marry a joking partner, confusions do not necessarily result (though there are exceptions discussed below). For this reason, one’s father’s brother’s wife is an avoidance partner.
For the G/wi case, there are two complications. One is relatively minor and pertains to the way that cousins are treated—as in many cultures, parallel and cross-cousins are differentiated and here treated opposite to how we might expect. This seeming violation is easily explained by the nature of cousin-marriage.25
Figure 2.9. Equivalence of grandfather
But there is an even more glaring inconsistency, at least from the perspective of balance theory. Hage (1976) correctly points out that the G/wi system gives rise to the intransitive triad of two joking and one avoidance relation between a brother, sister, and their grandfather. That is, a male ego “correctly” jokes with his grandfather (since the avoidance partner of his father, an avoidance partner, must be a joking partner); the same is true for a female ego. The transitivity of joking should lead to the brother and sister joking, but of course they do not. It is accurate to say both that this apparent inconsistency only appears as an inconsistency because of a misunderstanding of the joking system, and that this inconsistency reveals a more fundamental tension that arises in all such systems, and leads all resolutions to possess some sort of inconsistency.
Figure 2.10. Contradiction of joking-avoidance system
Turning to the first response, note that the “problem” can more simply be stated by pointing to the unbalanced triad containing a brother, a sister, and a parent, all of whom will be avoidance partners (see figure 2.10). While the logic of antiequivalence should make this impossible (as the avoidance partner of my avoidance partner should be my joking partner), it is worth remembering that G/wi informants themselves saw nothing anomalous in such a triad. Further, they simply do not consider their sisters (or brothers) their parent’s daughters (sons); they are sisters or brothers. As Goody (1977) stressed, Western anthropologists tended to approach oral cultures with their own cultural tools such as “tables” and imposed these on a different form of reasoning. The table became a sort of cognitive procrustean bed, whereby those parts of practical logic that did not fit were simply lopped off. In this case, the “inconsistency” does not arise in actual practice because of the way in which people traverse their relational tasks.
Put another way, while these boundary crossings (from equivalence into nonequivalence) do indeed concatenate according to the antitransitive logic that should produce balanced relationships (in the way that −1 × −1 = 1, and not −1), not all possible “walks” through the set of boundaries are reasonable. One’s sister, after all, is one’s sister, and not one’s father’s father’s son’s son’s daughter, and one’s father’s father is one’s father’s father, and not one’s father’s sister’s father. Recall that we found that in American friendships, people tend to follow the balance rules that the friend of a friend should be a friend and that the enemy of a friend should be an enemy, but not that the friend of an enemy should be an enemy or that the enemy of an enemy should be a friend. In both cases, people have an order whereby they traverse relationships. They first go to the equivalent, and then to the nonequivalent.
At the same time, the inconsistency is real and comes from a readily identifiable source, namely the prohibition on sibling marriage. The joking/avoidance system is essentially a way of adding two types of relationships, one having to do with opposite-sexness and the other having to do with adjacent generations. In general, the idea of two negatives making a positive works quite well, not only for generations, but for same-sex siblings (that is, the opposite-sex sibling of an opposite-sex sibling is a same-sex sibling). The problem is that these two cannot be wedded without some unmooring. This is not simply because one’s opposite sex sibling’s grandfather is one’s own grandfather, but more fundamentally, because siblings are both similar (vis-à-vis common descent) and different (vis-à-vis prohibition on incestuous unions).
Put somewhat differently, in contrast to the simple incest taboo on all nuclear family relations, which may be seen as simply saying “all these people are too much like you,” joking/avoidance systems attempt to use these taboos to determine a new sense of equivalence and hence a positive determination of marriage partners without recourse to marriage classes. Let us make the conventional distinction between “affines” (those related to one through marriage) and “cognates” (those related to one via common descent). The joking system thus introduces a notion of equivalence-as-affines that cuts across the notion of equivalence-as-cognate used in the kinship structure.26 Indeed, in many systems it is clear that the important relationship is not so much equivalence with one’s self as it is equivalence with one’s spouse (e.g., see the Mossi case discussed by Hammond 1964: 262). In such cases, siblings of one’s spouse are considered potential marriage partners (as second wives or replacement husbands), and sexual banter (in some cases sexual contact during carnivallike festivals) is appropriate (for example, the North Mexican Tarahumara [Kennedy 1970: 38]).
Similarly, in such groups we are also likely to see a subjective heuristic emphasizing the equivalence of same-sex siblings.27 The wife’s sister and the brother’s wife are both seen as potential wives. The Cheyenne say, “The sister-in-law is like a wife” (Eggan 1970 [1955]: 57, 78f), and indeed may be taken as a second wife in a few cases, as a man may marry his brother’s widow. Thus the chain of equivalences (spouse and same-sex sibling) point to potential spouses. You may also compete freely with these partners, leading to the playful—but often violent—joking behavior between brothers-in-law (see Kennedy 1970).28
The taboo on brother-sister incest, when coupled with the idea that marriage connects equivalents, makes it a natural conclusion that this relationship is one of antiequivalence. But the idea of alternating generations—that one jokes with grandparents and grandchildren but not parents, children, great-grandparents or great-grandchildren—is also reasonably widespread.29 Thus it is not surprising that people repeatedly come up with the idea of antiequivalence: that is, the principle that two wrongs make a right, or that −1 ××1 = +1.
The G/wi system is an unusually detailed version of a more widespread attempt to use logic to systematize relations of sameness and difference (for another example, see Marshall [1957] on the !Kung). In many kinship systems where we see a division into joking and avoidance partners we find that marriage, rather than being a relationship of equivalence, indicates antiequivalence. Here the logic is applied to the family or lineage, and not the individual. Others are divided up into “those I may marry” as opposed to “those I may not marry.” One may not marry cognates, but one also may not marry those who have married those whom your family has married (coaffines).30 An example here includes the Cheyenne, who also have institutionalized joking/avoidance relations. The same term is used for spouse’s siblings and sibling’s spouse (akin to our “brother/sister in law”), but the spouses of the spouses’ siblings are treated as siblings (Eggan 1970 [1955]: 42ff).31
In sum, we have seen examples of people systematizing the relationships of equivalence and antiequivalence. In some cases such as the G/wi, this bifurcation is expressed in rules nearly akin to those of balance theory. Despite this, we do not see the structures that seem dual to these heuristics arising; the subjective understanding is not architectonic—compatible with structure.32 I have stressed that this is because of the order in which heuristics are applied as people carry out their tasks at hand. Each ego can think from his or her own perspective without needing to see from the top down; each ego can compile a division of the population without these divisions needing to be compatible with one another.
Significantly, nearly all societies with exclusive divisions based on joking and avoidance relationships tend to have bilateral reckoning of descent—that is, they pay attention both to father’s and mother’s bloodlines.33 As we shall see in chapter 5, while unilineal descent naturally leads people to conceive of their relations in terms compatible with nested equivalence classes (for my cousin’s cousin is my cousin), bilateral kinship does not. My cousin’s cousin may be my second-cousin. Each person has a view of the social structure that is related to, but not reducible to, the views of all others. As a result, each person can use a logic that implies a division of all others into two classes without there being any two classes on which all can agree. Indeed, were this possible, there would be little reason for the subjective heuristics required by joking and avoidance relationships.
Thus we have seen two ways in which equivalence and antiequivalence may be systematized. There is the simple architectonic solution of cliques; within a clique all are equivalent, and across cliques there are no relations at all. If we assume hostility between all, we have the puzzle of whether to consider my enemy’s friend my friend or my enemy, and the need for strategic thinking. But strategic thinking is famously incompatible with simple structures (Bourdieu 1977). The strategic actor cannot have her hands tied by “logic” or “rules,” and the agonistically oriented strategist will often seek to frustrate those who attempt to predict her action by doing the opposite of what these others expect.
It is possible, however, for people to begin with relations of both equivalence and antiequivalence, as long as they use these relations not in an architectonic sense but in a “local” or ego-centered sense. Equivalence ripples through the population but does not lead to the emergence of stable cliques—that sort of rampant mechanical solidarity that some of the anthropologists imagined would destroy the larger society. There is another way to think about equivalence and antiequivalence without destroying society, and this is to moderate the transitivity; we close this section with an examination of the best known case.
Here we can consider the avoidance categories of the ancient Israelites codified in Leviticus 18 (ego, the recipient of the command, is assumed to be male). The transitive logic is explicit: “You shall not uncover the nakedness of your father, which is the nakedness of your mother; she is your mother, you shall not uncover her nakedness. You shall not uncover the nakedness of your father’s wife; it is your father’s nakedness. You shall not uncover the nakedness of your sister, the daughter of your father or the daughter of your mother, whether born at home or born abroad. You shall not uncover the nakedness of your son’s daughter or of your daughter’s daughter, for their nakedness is your own nakedness. You shall not uncover the nakedness of your father’s wife’s daughter, begotten by your father, since she is your sister. You shall not uncover the nakedness of your father’s near kinswoman; she is your father’s near kinswoman. You shall not uncover the nakedness of your mother’s sister; she is your mother’s near kinswoman. You shall not uncover the nakedness of your father’s brother, that is, you shall not approach his wife; she is your aunt. You shall not uncover the nakedness of your daughter-in-law; she is your son’s wife, you shall not uncover her nakedness. You shall not uncover the nakedness of your brother’s wife; she is your brother’s nakedness”34 (further limitations on uncovering nakedness follow, but they are not about ego’s kin but about the kin of the naked in question).
So we see here that starting with the essential taboo on uncovering the mother’s nakedness, the father and other husbands of the mother are considered equivalent (as least for purposes of assessing nakedness-quality) with her and hence taboo. We can consider “mother” to be a many-to-one function of ego M(ego); because we always look from the perspective of some ego, we can more simply denote M(ego) = M. If we now denote spouse as a function S(), S(M) denotes the spouse of the mother; according to Leviticus S(M) ≡ M and hence S is an identity relation in that it does not change the avoidance status of a person. Consistently, we find S (S(M)) = S(M) = M with the prohibition on the father’s wife.
To continue, since the sister (or half-sister, as emphasized in the sentence after the next) is the daughter of either father or mother, she also falls into the avoidance category. (So if C = M−1 denotes the relation child, C(M) ≡ M and C(S(M)) = C(M) = M.) We know that there is a taboo on relationships with children, for it is the inverse of the taboo on relationships with parents. We also find the children’s children taboo because of their relation to ego through their parents (C(C(M)) = C(M) = M and C(S(S(M))) = C(S(M)) = M. From there, kinswomen of one’s father are ruled out, and then mother’s sister (C(M(M)) = M(M) = M), the relation “sister” establishing equivalence with the mother. Since the father is equivalent to his brother, the father’s brother’s wife is off limits (or if B=brother, S(B(S(M))) = S(C(M((S(M))))) = S(C(M(M))) = S(C(M)) = S(M) = M; similarly, since children are off limits, the son’s wife is off limits (S(C) = C). Denoting males as triangles, females as circles, marriages as double horizontal lines, descent as a vertical line, and siblingship as a single horizontal line, and making ego the recognizable male, this translates to the following prohibitions, where a female “no” sign indicates one whose nakedness ego is forbidden to uncover (figure 2.11).
These prohibitions work on a transitive contagion logic—if you are to avoid uncovering your mother’s nakedness, then also avoid uncovering her daughter’s or her sister’s nakedness.35 If you avoid your daughter’s nakedness, avoid your daughter’s daughter’s nakedness. But there is an inherent problem to the logic of these relationships, and this is that like all forms of logic, it tends to go too far. The problem of transitivity, then, is that the heuristic dual to some set of relationships may, if taken seriously, have perverse results whereby we must establish relationships with those with whom we would prefer not to, or with those who will refuse to establish relationships with us. In the case of Leviticus, where the relationship is “forbidden union,” we might find ourselves successively eliminating one potential partner after another.
Figure 2.11. Contagion of equivalence
But actually, this system of prohibitions does not explode, since the taboos die out in practice as one gets a few relationships past ego. That is, while I called the relations implicit in the account of Leviticus “equivalence,” it is understood that they do not concatenate forever without attenuation. Although one’s mother’s daughter is prohibited because there is a sense that the nakedness of children is the same as the nakedness of their parents, this does not imply that one’s mother’s mother’s daughter’s daughter is necessarily prohibited, even though we could use similar substitution to derive this.36 And this is because although your mother’s sister’s nakedness is your mother’s nakedness, your mother’s sister isn’t your mother. We know this because you are not prohibited from your mother’s sister’s daughter’s nakedness in the way that you are your mother’s daughter’s nakedness.
But if kinship is understood in terms of a set of qualitative classes with equivalences, so that all persons are in a fixed number of classes and any person is equivalent to one of your near kin, even such limited transitivity would instantly make for a nation of bachelors. Not surprisingly, it is in societies in which such repeating kin classes are fundamental—and, just as significantly, often where possessing of a common name indicates not only a spiritual identity, but a fundamental social identity—avoidance has to be antitransitive to prevent all potential marriage partners from being avoidance partners.37
It is not that avoidance in Leviticus is transitive; rather, it is that while for the G/wi, avoidance is about unlikeness and two unlikenesses can make a likeness (while two likenesses also make a likeness), for Leviticus, there is only likeness, and one avoids the like. Thus here we start from ego and move out locally, allowing for the transitivity of identity to fade away eventually. In the G/wi system (as reconstituted here), however, there is no attenuation of identity and anti-identity, no matter how far from ego we go.
In sum, kinship relations tend to establish ideas of equivalence; for reasons that are still debated, there is a near-universal human tendency to establish relations of marriage preferentially to those who are different in at least some respects. But this does not always lead to a structure of classes (which we examine in the next chapter). When relations of equivalence are emphasized in the absence of classes, there is a fork in the road. One fork takes us down the road to Leviticus: one cannot marry the like; the relations of likeness are transitive but attenuate rather quickly and hence lead to strong local prohibitions but little overall structure. The other fork takes us to joking-avoidance structures: here one must marry the like; the relations of unlikeness concatenate eternally without any attenuation in strength, but they must be antitransitive so that there are some possible marriage partners uncontaminated with the sacred.
This antitransitivity seems, at first blush, to imply the formation of large-scale structure—a bifurcation along the lines of balance theory. But this is not at all what we have found; indeed, it is the absence of such a bifurcation, despite the general equation of cognates with coaffines, that seems to lead to the joking system itself. This case then casts light on the questions posed in the first chapter pertaining to the relationship between heuristics, small structures, and big structures. Without the benefit of close empirical examination, it would seem obvious on a priori grounds that persons holding certain heuristics will produce the analogous structures, and these structures will be indifferent to scale. Balance is balance. But instead we find that these heuristics are applied in a certain order to relatively local problems, and even here, do not produce a particular structure. Local structures do not seem to arise from subjective ways of putting together relationships; if anything, the reverse is true.
We have seen that balance theory implied the bifurcation of interactants into two groups. Despite a fondness for bifurcations on the part of the species, and indeed a tendency for some societies to take a dual form (division into “moieties” or “phratries”), actual cases satisfying the original theory were few and far between. Clearly, there was something too stringent about balance theory. In part, it came from the assumption that those who are not allies are enemies—and those who had enemies were least likely to follow the ascribed heuristics. Perhaps the biggest breakthrough in balance theory came largely as a result of an indirect change due to computerization—more and more of mathematical psychology and sociology was conducted in matrix notation (as opposed to graph theory). While it takes a bit of cognitive flexibility to conceive of “a” graph that is not connected (or has two separate components), matrices are full of zeros and no one thinks twice about it. Thus people tended more and more to allow for indifference (relations that were neither positive nor negative) and for “unconnected” graphs. Researchers stopped thinking about their relations as (+1/-1), and thought of them as either present or absent (1/0).
This change in turn facilitated a focus on the transitivity of ties, as opposed to balance.38 We saw that the clearest examples of relationships that highlight mutuality, friendship, and alliance imply some sort of equivalence between the parties involved. Equivalence is an inherently transitive thing: if A = B and B = C, we know that A = C. (Recall that a relation R is transitive if whenever aRb and bRc, aRc). Balance may be understood as an extremely strong type of transitivity—so strong it is not realistic as a description of social formations. In Kurt Vonnegut’s wacky novel Cat’s Cradle, a scientist forms a variety of ice that has a freezing point considerably above room temperature. It also has the property of transitivity: if it comes in contact with regular water, it transforms this substance into the liquid form of itself, and hence it freezes. Consequently, dropping a single piece of this ice into a stream leads, willy-nilly, to the stream freezing, the river into which it flows freezing, all other streams flowing into this river freezing, the ocean into which the river empties freezing, all oceans freezing, all rivers freezing, and then all naturally occurring water freezing. Strong transitivity in social relations is similar: were it to exist (and thank goodness, like Vonnegut’s ice, it does not), it would instantly ripple through social networks and destroy society.
But could there be a weaker form of transitivity inherent in relationships such as friendship, one that might not lead to the complete bifurcation of balance theory, but still toward separate clusters? As we shall see, as researchers progressively tried to weaken the strong sense of transitivity inherent in balance theory, so as to better describe actual data, they found themselves abandoning the premise that the relationships they were learning about were horizontal relationships of equivalence. Instead—I suppose saying they were dragged kicking and screaming is an overstatement, but certainly this was not a planned result—they formulated models of an intrinsically hierarchical world. Every step toward more accurate description inexorably involved the introduction of more inequality.
Davis (1967) began by suggesting a relaxation that allowed for multiple cliques between which there were no relations (as opposed to hostile relations). These new type of cliques he called “clusters,” which correspond somewhat better to the common-sense understanding of cliques. (These are identical to Watts’s [1999: 43] “cavemen” graphs discussed above.) What is important is that thinking in terms of transitivity for binary relations (0/1) allowed for more than two clumps, since there were only friends, and no enemies.39 Only one rule was maintained, namely, my friend’s friend is my friend. If friendship is considered intrinsically symmetric, as is necessarily the case for clique formation, the individuals split into a set of cliques among whom there are wholly loving relations and between whom there is total indifference.
The researchers pursuing the nature of these clusters (especially Holland, Leinhardt, and Davis) realized that the structural implications could be studied on the triadic level: a classic balance structure (in which 0 could be treated as −1) would arise if for any three persons, either two were connected by mutual ties and the third was not, or all three were connected by mutual ties. A cluster model (one that allowed more than two cliques) would also allow for triads in which no persons were connected by ties.
Both the cluster and the clique model rule out asymmetric relations, since if two people are in the same clique or cluster, each will choose the other. Yet respondents asked to name their friends often produced asymmetric data. That is, just because A “likes” or “chooses” B there is no reason to assume that B likes or chooses A. Now it must be emphasized that we are here talking about relations and not necessary relationships, that is, patterns of interaction. Yet the results reached by a study of these relations can inform the study of relationships. The cluster model simply was wrong for relations of choice, so how could the actual structure of these relations be portrayed?
To account for the asymmetric relations, researchers then proposed the “ranked clusters” model. In this model, there are still cliques or clusters, but it is possible for members of one cluster to try to form relations with those of a “higher” cluster (thus the clusters can be ranked). Within a cluster, all relations are mutual; between clusters relations are either not present (if the clusters are of equivalent rank), or are asymmetric (if one cluster is of higher rank than the other). The following diagram (figure 2.12, after Davis and Leinhardt 1972) indicates an example of the structure proposed: within a clique, all relations are mutual. Between cliques on the same level, there are no ties (hence no one from clique 2 chooses anyone from clique 3, or vice versa; this also holds for cliques 4 and 5). The double arrows indicate that this relation connects all members of one clique to all members of another clique. Members of cliques are still equivalent to one another. But their equality in large part comes from their inequality vis-à-vis the larger group. The population itself is fundamentally structured by inequality.
This understanding implied that the law of transitivity would hold for all relations. But because it was assumed that members of a “lower” cluster would always attempt to form relations with those of a higher cluster, one should not see triads with a single asymmetric relation and two null relations. That is, let the single asymmetric relation connect a to b. Since there is no relation between a and c, a and c must be in different cliques, neither of which is “better” than the other. The same logic must hold for b and c. But by equivalence, this would imply that a and b belong to cliques at the same “level,” in which case there should be no asymmetric relation between the two.
Unfortunately for the model, triads with one and only one asymmetric relation are in fact very common—in certain environments (Holland and Leinhardt 1970). Most of the sociometric data available come from children choosing which other children they would like to interact with (sit next to, etc.). Where boys and girls are in the same classroom, and the data are pooled, these triads with a single choice tend to abound. This is because, as Leinhardt (1968) had earlier pointed out, there is a tendency for boys and girls to form independent hierarchies (Davis 1979: 56). Permitting these triads still leads to a specification in which the relation in question is transitive: any triads compatible with transitivity are allowed. This resulting class of structures (which Holland and Leinhardt [1971] called “t-graphs”) not only includes the ranked clusters model as a special case, but all the other models we have examined in this section.
Figure 2.12. Ranked clusters
It is worth remembering that we have followed analysts in examining relations that are not necessarily translated into relationships of actual interaction. If indeed it “takes two to tango,” then it might well be that the asymmetric betweenclique relations are unlikely to translate into patterns of interaction. All interaction will take place among within-clique subsets (and note that it is not necessarily the case that all members of the clique ever interact as part of a group).
Thus if we are interested in patterns of interaction, we may actually see symmetric (mutual) relations as being a wholly different type of beast from asymmetric relations—the former are an equivalence relation that partition the members into sets of possible interactants, while the latter express relations of longing that indicate the relative popularity of the cliques.40 The “transitivity” of the graph, then, breaks down into two types of transitivity—the transitivity of a mutual relation that leads to clumping, and the transitivity of antisymmetric relations that leads to what we will call a “popularity tournament,” namely the vertical differentiation of previously undifferentiated persons on the basis of the sociometrie choice of other persons.41
The final relaxation to the t-graph model was made by Johnsen (1985), who started with the anomalous presence of forbidden triads with two mutual relations and one asymmetric. These triads had frustrated Davis (1979) because they violate the fundamental transitivity of equivalence. That is, we find that A seems equivalent to B (since they have a mutual relation), and B equivalent to C, but while A chooses C, C does not reciprocate. Johnsen showed that such triads arise because although there is a tendency toward cliquing in these structures, one cannot equate the equivalence relation leading to cliques with mutual choices. Although we can still define cliques in terms of their relations with one another, we must now allow for nonmutual relations within cliques.
To some extent, we have rediscovered something we already stumbled across when we first considered strong friendships. These friendships seem to have a spatial logic, which means that while there are necessarily tendencies toward transitivity, they will generally fall quite short of the absolute transitivity necessary to form clear structures. And this is because, although A is close to B and B close to C, A is not necessarily close to C. Then we were assuming that such relationships were mutual, at least in distinction to relationships of acquaintanceship. Now we find that relationships stronger than those of acquaintance also fall short of true mutuality, and again have more of a spatial logic than one of strict transitivity.
Let us imagine that people are to some degree rankable, that they know one another’s rank, and that those of higher rank are more attractive as friends. Let us also assume that people will tend to reciprocate choices unless the person offering them the choice is too far below them in rank. In this case, we will see these anomalous triads. Imagine that in rank C is highest, then B and then A. A will choose B and C, and B will choose C. B will reciprocate A’s choice, and C will reciprocate B’s choice, but C will not reciprocate A’s choice–A is too far below C to merit such attention. Thus the problematic triad emerges.42
In sum, we have traced the evolution of an understanding of structural tendencies that began looking at balance, a structural tendency assumed to flow from the nature of equivalence, and was progressively forced to make room for more and more asymmetry and ranking. This increased focus on asymmetry and ranking came, as is clear in retrospect, from the reliance on questionnaire data on “choices” of favored others (e.g., with whom would you like to sit?). The relation of the resulting data to interaction is not immediately clear. But if there is in some case at hand a hierarchical structure of persons in terms of their “attractiveness,” it would be difficult to analyze interaction patterns without an understanding of this hierarchical structure. Indeed, this might be a good place to begin our investigation of intrinsically antisymmetric relationships. We will briefly look at the popularity tournament and in the next chapter continue examining the tensions between equality and inequality.
As we have seen, simply asking “whom would you choose among the other group members to do X with?” can induce a vertical differentiation among otherwise undifferentiated persons, as some group members are more frequently chosen. The simplest measure of the vertical position of any person is the number of choices received, also known as the “in-degree” of the graph of the network in question (because it is the degree of arrows pointing “in” to that node). If we wanted to determine each person’s overall attractiveness, we could standardize this by dividing by the total number of choices or something like that, but there is a complication due to patterns of nonreciprocation. We might imagine two people, each with an in-degree of four. The first reciprocates all four of her choices (and makes no other choices, having an “out-degree” of four), while the second only has an out-degree of one. If, as is generally the case, we interpret the process of choosing and being chosen as a latently agonistic one, in which one’s status position is higher when one is chosen by others but does not choose them in return, we might see the vertical position of the second as higher than that of the first (also see the discussion of Coleman 1960: 86).
We shall not re-create the evolution of methods of disentangling the various aspects of such graphs, since the solution proposed by Holland and Leinhardt (1981) is so immediately interpretable and elegant. Since this model will be used to analyze data in the next chapter, we might as well introduce it here in a technically accurate form. The probability of person i choosing person j (as opposed to not choosing) can be seen as a function of three quantities: the “expansiveness” of person i (how likely person i is to choose others in general), the “attractiveness” of person j (how likely person j is to attract those choices which are made), and the tendency toward reciprocity in this group.43 This “attractiveness” can be seen as akin to a location in a one-dimensional space that is oriented vertically.
Now if the value for each person’s “attractiveness” references an intrinsic property of that person, the resulting structure is rather easy to explain, yet sociological analyses have almost never been able to defend such a simple interpretation. Instead, there is a recurrent sense that there is no attractiveness outside of the pattern of choices itself. The pattern of choosing generates the inequality as much as if not more than some inequality generates the pattern of choosing. Each person’s attractiveness or, more generally, status in some hierarchy, must be considered an endogenous result of the tournament itself.
If so, there is a delicious instability to such processes, for they follow Merton’s (1968) “Matthew Effect,” namely, that to them who have more shall be given. Each additional choice person j garners increases his or her attractiveness, and thus increases the pressures on others to choose j. This logic was laid out for the case of heterosexual dating in college campuses by Willard Waller (1937: especially 730). Waller argued that for women, at least, the most important factor determining desirability as a date was popularity, “for the girl’s prestige depends upon dating more than anything else; here as nowhere else nothing succeeds like success. Therefore the clever coed contrives to give the impression of being much sought after even if she is not.” Thus if a woman successfully gave the impression of being sought-after as a date, this would jump-start the actual process of being asked on dates, and would then be (to take another of Merton’s famous phrases), a self-fulfilling prophecy.
In other words, a popularity tournament in this substantively important sense is more than simply the variance in degree that arises when we relax the assumption that all choices must be reciprocated. It is a particular social dynamic that arises in situations where two important conditions hold. The first is that each person has some information about the popularity of others. This condition of publicity is not given sufficient attention: in many of the most familiar examples of the popularity tournament, such as generic (friendship) popularity among children, it is simply assumed, and not always for very good reason, that such perceptions of popularity are widespread and accurate on the part of the children. (For evidence supporting such social knowledge of rank among school children, see Ausubel, Schiff, and Gasser 1952). In other cases, there are specific institutional structures to distribute such knowledge. The sociology of science quantifies the number of references made to any article as an indicator of that article’s dominance in its field; in a wonderful bit of reflexivity, these procedures can now be used to deny tenure or promotion to sociologists for writing articles that are too dull to cite (perhaps including ones involving analyses of meticulous counts of citations to other scientists’ papers).
The second condition for a popularity tournament to arise is that any additional choice received by a person increases that person’s attractiveness. Popular children are more desirable as friends than nonpopular children (for whatever reason). If possible, a child will tend to drop a friendship with a nonpopular child and initiate one with a popular child.44 One needs to cite frequently cited articles to avoid seeming ignorant (see Latour 1987 for a charming exposition of the logic of citation), although one can afford to ignore those that are ignored by others.45
Given these conditions, the popularity tournament tends to increase any preexisting differentiation. Further, there need be no preexisting differentiation at all for a final state to be reached with high differentiation, so long as each person revises his or her choices on the basis of the current popularity of each other person (i.e., A’s estimate of B’s “attractiveness” is a function of the choices currently received by B from all other persons: see Orléan 1988, 110; Gould 2002). In other words, if there is a good reason for actors to be oriented to one another’s choices, then there is a strong probability of increasing vertical differentiation of the objects of their choices. Even if the initial choice received by B is a mistake, B is now more attractive and likely to get more choices.
We have seen the conditions that lead to a popularity tournament, but why on earth would people modify their preferences in such a fashion? We can understand why such modification might take place when people are choosing objects that they can later alienate (especially sell). This type of action is usually called “speculation,” because people are not actually concerned with the popularity of this object when they buy it, but with its future popularity.46 Unfortunately, they usually take current popularity as a good indicator of future popularity, and since people tend to have a limited ability to foresee anything but steady increases or decreases in popularity over time, there is a tendency for purely speculative action to have feedback to a destabilizing extent, for example, in the famous tulip craze in Holland in the early seventeenth century (see the account of Mackay 1852).
But in other cases, it is possible for some of the popularity of the object to accrue to the possessor without the possessor alienating it. In such cases, the object is generally known as a “status symbol.” (According to Veblen [1912: 128ff], it is necessary also that these objects be acquired only at considerable expense, but this is more or less the same as saying that they are in great demand.) Something similar can inspire persons to participate in a popularity tournament—their own status depends on their ability to establish ties with others. It is interesting that this understanding of the reason for enthusiastically taking part in the popularity tournament has been a consistent plank in the sociological understanding of heterosexual pairing, from the analyses of Waller (1937) discussed above to Rubin (1985). That is, for a male, “going with” a popular female increases the popularity of the male in question; for a female, “going with” a popular male increases the popularity of the female in question. For homosexual pairing, the idea is analogous but formally closer to the traditional (one-class) popularity tournament.
One may analyze this as a two-sided matching game (here see Roth and Sotomayor 1990): this is the sort of open-air choice situation in which persons try to get the “best” match they can in vertically ranked others, given that they are vertically rankable themselves. Such a situation is generally handled through trial and error—multiple iterations known as “dating” when it comes to heterosexual pairing—though there is a famous matching system of medical students and hospitals for residency that is accomplished through a single-iteration game. Such two-sided matching can lead to what is known as a Nash equilibrium—no one person has any good reason to change given that all others do not change (see Mortensen 1988). This does not mean that no one could be happier, nor that all matches are equal (one of the two parties may consistently get a better deal than the other, since equal rank does not imply equal value), but it is still a stable outcome. Emphasis on the stability of this outcome, however, can be misleading, for it leads us to assume that the choice process has solved the problem of inequality. Instead, as we have seen, it may generate it.
Mutual relationships such as alliance or close friendship seem the perfect building blocks for large structure. The nature of the relationship is such as to clearly imply a set of subjective heuristics associated with equivalence—your friends are my friends, your enemies are my enemies. This implies a form of transitivity that leads to equivalence classes. And indeed, aggregating these classes should lead to larger and larger clumps. It would seem quite plausible that large-scale social structures would form through such an agglomerative process—different “tribes,” say, forming alliances, and then alliances emerging between these first alliances, and so on.
But we have found inherent limits to such agglomeration. Transitivity cannot be maintained if only because we cannot keep track of thousands of close friends. Weakening transitivity leads to heuristics that are probabilistic or tendential, and not absolute. The correlative forms that sets of relationships take on are webs that lack the clarity of simple structures. Further, the vagaries of relationship formation in webs introduce differentiation and hence inequality between persons, splitting up equivalence classes into ranked orders.
Thus instead of seeing a clear path toward the formation of structure from mutual relationships, we have seen three different heuristics that can be used to guide tie formation. One (reciprocity) has to do with the level of the dyad: ego is likely to choose alter if alter chooses ego. This maintains the equality of the relationship but does not necessarily lead to larger structure. There are relationships which seem to be formed in accordance with such a heuristic. Most important, there is strong friendship, which is all about “closeness.” The spatial component of the overall organization of these relationships leads to only a mild tendency toward transitivity. A second heuristic (preferential attachment) has to do with the individual level: ego is likely to choose those alters who are disproportionately chosen by others. The example here is the popularity tournament. While transitivity will arise, this is wholly a side-effect of the organization in terms of individual variability.47 The third heuristic (transitivity) has to do with the level of the network or group. Technically we might argue that is has to do with the level of the triad, but substantively, this structural principle involves the linkage of dyads and the flow of characteristics of organization across the set of relationships. An example here is the set of acquaintances that might form a small world.
Consider the degree to which the subjective process of relationship formation can emphasize any of these heuristics—something that might run from “not at all” to “exclusive concern.” We might then consider charting the analytic space in which relationships might be placed in terms of their mix of concern. Further, because there is a limit to the amount of concern one may have with the logic of relationships, if we restrict our attention to these three heuristics, we may treat them all as summing to the total degree of structural imperative present. Consequently, we can chart the importance of these different levels of structure in figure 2.13 (here one may compare the very similar diagram of Feld and Elmore 1982: 82). This sort of figure arises when we have three different dimensions that cannot vary independently—maximizing the value of any one involves minimizing the value on the others. We can imagine lines parallel to any side and moving toward the opposing corner as indicating values of the dimension that is “high” at that corner and “low” at the side. Thus the side running between the points “dyadic level” and “individual level” represents the lowest point for degree of group organization—if we were to construct successive parallel lines moving toward the right and somewhat downward, these would indicate higher and higher degrees of attention to transitive closure. Any position indicates a particular mix—say, X% emphasis on reciprocity, Y% on preferential attachment and Z% on transitivity, where X+ Y + Z = 100.
Figure 2.13. Heuristics for structure
It is worth emphasizing that in this case I do not mean in any technical sense that increasing the tendencies toward reciprocity and/or preferential attachment would decrease the degree of measurable transitivity in any set of relationships. In fact, the reverse is true (Feld and Elmore 1982: 82). The poles of the figure mean not “degree of” this structural principle in some group, but “degree of concern with” this principle among a set of actors.
In part as a result of this limitation, the figure adds very little to a simple verbal statement—to the degree that individual level structure is of paramount importance, group level and dyadic level structure cannot be important, and so on. This figure is placed here because similar figures will be of importance in elucidating structure in further sections. Although there is only a rough degree of parallelism across the figures, it is worth emphasizing that we may attach a substantive (and not merely a formal) significance to each of these poles.48
Let us anticipate somewhat and propose that the presence or absence of reciprocity is fundamentally about the equality of relationships. The degree of transitivity is about the internal organization of some set of relationships. And the degree of preferential attachment is about the degree to which individuals become differentiated from one another within the group.
It is tempting to imagine that we can draw a simple correspondence between each of these structural principles and some overall structure. For example, perhaps emphasizing equality and dyadic relations leads to markets, emphasizing transitivity leads to command hierarchies and trees, and emphasizing preferential attachment leads to dominance orders. But because the structural imperatives of relationships are in large part a function of their content, much of the difference between structures such as trees as opposed to orders is inherent in the nature of the relationship itself. These different principles, then, are best understood as moments that are relevant for the differentiation of possible structures given any particular relational content. Rather than find a direct mapping between these positions and naturally occurring social structures, we are likely to find a similarity of the trade-offs involved in concatenating different types of relationships into structures.
For an example, let us return once more to mutual relationships, which are those that by definition imply the same action profile for ego and for alter (as opposed to relationships that may or may not be reciprocated). If such mutuality is interpreted in terms of equivalence, then we conclude that your friends are my friends, and to say this is to make transitivity—particularly, triadic closure—a heuristic guiding the formation of relationships. The principle of triadic closure states that A is more likely to establish a relationship with B if B and A are both tied to some C. But this means that, all other things being unequal, as they always are, those alters with more ties are likely to garner further ties. (Thus if D has no friends, the law of transitive closure will not persuade A to form a tie with D no matter what.) Here the tendency toward inequality is not due to an actual tendency toward preferential attachment (all other things being equal). But the effect is, in some ways, the same—the relationship of equality has induced a new relation of inequality among persons.
What happens if they act on this new relation? It probably means that they try to establish relationships with those who already have many relationships, which pushes the structure toward a popularity tournament. Second, it probably means that relationships are not mutual or symmetric. The popular have neither time nor inclination to befriend all of the hordes of the unpopular. The resulting set of relations will then be asymmetric or, at the extreme, antisymmetric. Thus there are different paths open for a reformulation of the fundamental structural principles guiding interaction.
One path involves an affirmation of the principle of hierarchy—a rejection of the equality implicit in mutual relationships. While analysts often mistake the existence of a mere popularity tournament for an order of domination—a “pecking order”—there is indeed an affinity between the two, since one way of dealing with the destabilization inherent in allowing the nonreciprocation of relations is to cement the vertical inequalities into a hierarchy. But not every vertical stratification requires an a repudiation of the principles of equality—indeed, it may be the grounds for the emergence of a new structural tendency toward equality.
Consider a hierarchy resulting from a popularity tournament in which the degree to which people want to interact with others is an increasing function of these others’ position in this hierarchy. If everyone must interact with some number of people, we will find those close in rank tending to interact. (This is the result of the successful matching game discussed above.) The fact that those at the bottom wish to interact with those at the top has no observable effects. The resulting structure is easily compatible with a unidimensional “spatial” model of relations, in which position on the dimension indicates position in the hierarchy, and people choose those close to them in this space.49 In other words, equivalence (or near-equivalence) is established in the structure of relationships, though the people remain starkly unequal.
Because of this, people may understand the inequality that arises when we allow for a nonreciprocation of relationships in terms of a “market” or at least in terms of “exchange.” Of course, a matching game is not only not a market in the conventional sense, it is not even a barter market. As a result, none of the interesting properties of markets are relevant, and we gain nothing from assimilating the formation of structure to such a template. Thus if such structures are to handle the inherent inequality in the relationships, they must take a particular form. We go on to explore such “exchange” structures that negate this inequality, before going on and exploring those pecking orders that enforce inequality.
1 For purposes of explication, we shall restrict attention to cases in which not only is the relationship mutual, but we are unable to distinguish between the people in any way relevant for the establishment of their relationship (thus we ignore cases in which one person chooses to interact with another who is not in turn free to decline).
2 This fundamental insight was later generalized to nonclique forms of equivalence, first the structural equivalence of White, Boorman, and Breiger (1976) and later the regular equivalence of Everett and Borgatti (1994). As our exploration progresses we shall see reasons why the latter more mathematically elegant understandings are probably less useful for social structures than is the original idea of structural equivalence.
3 Hage (1973) actually concluded that there were two violations present, but I believe that this came from a poor drawing of the original graph by Read; one group (the Masilakidzuha) is placed at the intersection of a number of lines and appears to be the endpoint of two lines, while I am confident that this line connects two other groups (the Uheto and Nagamiza, who are in the same clique) that straddle the Masilakidzuha; the two errors as seen by Hage are a supposed positive relation from the Uheto to the Masilakidzuha and again from the Nagamiza to the Masilakidzuha.
4 Schoolchildren most probably are organized in groups that tend to but fall short of pure cliques in that not all within-clique relations are present (or the density < 1), though betweenclique relations are never or rarely present (density << 1).
5 Even further, institutions go beyond setting up structures that channel choices into cliques—they also imperatively require persons to interact with one another (e.g., members of a work team). While this cuts against the intuitive understanding of what we mean by “clique,” from the perspective of structural constraints on interaction, we must admit that such situations of imperatively coordinated association are probably the most common form of cliquelike interaction. The children who whisper to one another about those whom they will exclude—often taken as the model for cliques—are interactionally less likely to form a clique than are a group of workers at the same position on the shop floor. These workers are likely to all interact with one another, and not with the other workers in the building who are simultaneously engaged in work-related interaction in a different area of the workplace. The paradox, then, is that while cliques have been assumed to result from the free choice of individuals who like to exclude, people rarely voluntarily form cliques. Instead, they more often are forced to.
6 So the source A and target H are here not considered the degrees of separation. Milgram found a mean length of 5, but some chains were never finished, suggesting 6 as a better median. Actually, as McCue (2002) emphasizes, these are too many links given the average person’s numbers of acquaintances, if we assume that acquaintanceship is random. The “smallness” in question is best seen in terms of the size of a world with random connections that would have the same length connecting paths as does our far-from-random world. Technically, we can follow Watts (1999: 114) and define a small-world graph as one that has a characteristic path length that is similar to that of a random graph but is much more clustered than is a random graph.
7 This also helps answer the mathematically more confusing question of how people can know the operating principles of their small world (see Kleinberg 2000).
8 One may, however, produce a small world in a spatial graph by adding error that leads to tunneling through space, as in Wong, Pattison and Robins (2006). Spatial graphs may have strong tendencies toward clustering; in fact, a two-dimensional space can lead to the rigid clustering of the Davis-Leinhardt model discussed below (Davis 1979: 57, n5).
9 Here also see Hammer (1979–80: 168).
10 Indeed, Travers and Milgram (1969: 432f) found that the two ways people made connections to the target in their classic experiments was through geographical likeness or occupational likeness (that is, to reach a doctor in Boston, a mechanic in Nebraska might make a connection to a doctor in Nebraska or a mechanic in Boston). Also see Killworth and Bernard (1979: 480ff) for a detailed exposition.
11 Technically, a spoke should be seen as the relationship itself, which connects the hub to the rim via a nipple, but hubs and nipples doesn’t sound quite so theoretically impressive as hubs and spokes.
12 This is discussed in terms of “contractions” by Watts (1999: 118, 146). Jane Jacobs (1989 [1961]: 134f) as a child invented the small world idea in playing a game “messages” with her sister, where they tried to think of the shortest way two “wildly dissimilar” persons could transmit information by word of mouth. The game was ruined once they thought of Eleanor Roosevelt, who might well know anyone.
13 It is important to emphasize that there is as of yet no evidence that the length of completed chains increases when less prominent targets are chosen; it is that the probability of success decreases. I should also emphasize that I lived in a smallish town when I wrote this, and the mayor lived on the next street.
14 Further, Watts (1999: 211) shows that in small worlds, the local context increasingly mirrors the global context, which can make it hard for groups to create islands of prosocial cooperation. But such islands repeatedly form. Indeed, Kurzman (2004: 135) reports that in the preliminaries to the Iranian revolution, people deliberately tried to use the weakest possible ties they had to gauge the mood of the nation, understanding that to stay within their cave might lead them to get the sucker’s payoff due to overestimating the general support for anti-Shah protest.
15 In a fascinating recent piece of research, Sorenson and Stuart (2001) find venture capitalist firms also having this dual-logic to tie formation—generally they are limited by geographical space, but network position that flows from a relational logic can be used to tunnel through spatial barriers.
16 On the influence from Spinoza, see Heider (1983: 150). Spinoza (proposition 33) also posited a tendency for reciprocity stemming from ego’s attempt to win the favor of a favored alter, as well (Axiom 1, fifth part). I have somewhat to my sorrow recently discovered not only that Ronald Breiger anticipated me in drawing attention to Spinoza’s relevance to balance theory but provided a much more sophisticated treatment of these issues. (Of course, despite my sorrow, in accordance with Spinoza’s arguments, my appreciation of Breiger must increase to learn that he appreciates what I appreciate.) See Breiger (2010).
17 Cartwright and Harary (1956: 291) reasonably pointed out that in addition to positive and negative relations, it was also possible for relations to simply be absent. When balance theorists began to allow for this possibility, it first seemed not to make very much of a difference—the set still seemed to have to split into two mutually hostile groups. Null relations were only possible within the relatively friendly group (Doreian 1971: 76f). But this was simply because the analysts were only looking at “graphs”—sets of relationships between persons that hung together—and the substantively reasonable case in which there were a set of groups that ignored each other was just out of the ballpark by definition, as it would lead to an unconnected set of graphs. More important for substantive purposes, it was still understood that balance involved the adherence to the four laws given above.
18 Davis (1963) emphasized that these laws should not be considered as the rules of all social organization and reasonably suggested that they were akin to the rules of mechanical solidarity, in contrast to the structure of exchange theory a la Levi-Strauss, in which positive ties must unite groups, since the structure is held together by organic solidarity.
19 Interestingly, the leaders of the official gangs in larger cities in may incorrectly assume that they have thus acquired authority over these affiliates, when the “joining” was not intended to imply any acceptance of central direction (Hagedorn 1988: 72) but merely to form alliances against local enemies. We will return to this when we examine party formation in chapter 8.
20 Even more interesting is Hage and Harary’s (1983: 56) noting that there are other groups in the area in which the enemy of an enemy can be either friend or enemy; in this case, the structure that develops is a different one that we shall examine in the next section.
21 For evidence that this does occur, see Doreian and Krackhardt (2001: 57). Leinhardt (1972: 204) noted that there could be good reasons for maintaining relations that defied the dictates of transitivity, though I do not know anyone before Doreian (2002: 106; also Doreian and Krackhardt 2001: 61) to point out that individual-level effects can destroy balance—if some person C is truly hateful, it is a bit much to criticize B for not liking C just because B dislikes A and A hates C. Finally, there is an important way in which the truest friendship cannot be bound to the dictates of balance theory (here see Silver 2002: 13).
22 Radcliffe-Brown (1940) was the first to emphasize the commonalities in joking/avoidance systems, though his theoretical explanation, influential as it may have been, is untenable and based on unsupported functionalist assumptions.
23 At the same time, it is equally possible for these systems to be based on the fact that one cannot marry into lineages that are “like” one’s own; as we shall see, the same cognitive heuristics can be used for this task.
24 Similarly, Eggan (1970 [1955]: 70, 75) says that “the principle of the ‘equivalence of siblings’ is one of the basic principles for kinship systems of the Cheyenne and Arapaho type,” two other societies with avoidance/joking relationships whereby one treats parents and opposite-sex siblings with avoidance/respect, grandparents and siblings-in-law with joking hilarity. Father’s sisters and mother’s brothers may be joked with, as can unspecified distant relatives. Where bilateral cross-cousin marriage is prescribed, this may lead one to joke with one’s spouse’s parents, because they are father’s sister and mother’s brother. Thus Chagnon (1968b: 70) reports a Makiritare informant explaining, “When you marry this way, you are. . . . good friends with [i.e. can play and joke with] your wodöma [father-in-law]. If you marry a different way, you must be careful around your wodöma and respect him.” Thus we may hypothesize that despite the seeming similarity of the G/wi division of all persons into joking and avoidance partners to the dual organization compatible with cross-cousin marriage (see next chapter), the two systems cannot exist together (for if you joke with your father-in-law because he is your father’s sister, you must avoid his daughter). In another case (the Nyakyusa of Tanganyika), the joking relationship is assimilated to cross-cousinship and also to rivalry (Wilson 1957); while cross-cousin marriage is generally forbidden, this still seems to be a way of designating potential affines.
25 First, parallel cousins are given special treatment and considered siblings. Thus a male ego treats an opposite sex parallel cousin (say, father’s brother’s daughter) as his sister, and hence avoids her, as opposed to following the logic father = cross (to avoidance); brother = stay; daughter = cross (joking). Second, both mother’s brother’s son and mother’s brother’s daughter are treated as joking partners. Silberbauer (1961: 357) notes this “slight difficulty,” but cannot explain it. This exception becomes explicable if there is a need to consider cross-cousin marriage as preferable over parallel cousin marriage; Hammel (1973) has demonstrated that such a preference is likely to occur in a polygamous society where men tend to be significantly older than the women they marry. Since the G/wi are indeed polygamous, it is reasonable to propose that the identification of cross-cousins as future marriage partners explains what seems to be a lapse of logic. The polarities of cross-cousins and parallel-cousins are reversed to facilitate marriages more in keeping with age differences between prospective spouses; cognitively, this is accomplished by seeing these cousins as cases in themselves. Thus just as a sister is a sister (and not a father’s daughter), a male’s cross-cousin is here not seen as “mother’s brother’s daughter” (which would be –1 × –1 × –1 = –1 = avoidance), but is seen (immediately) as “wife” (and hence joking).
In contrast, the Tikopia also have large classes of joking and avoidance partners (tautau laui and tautau pariki), with joking between grandparent-grandchild and between same-sex siblings and avoidance between parent-child and between opposite-sex siblings. Further, they stress the equivalence of spouses and same-sex siblings (hence a man jokes suggestively with his brother’s wife). Yet the cousin polarity is reversed, as there is avoidance between cross cousins and not between parallel cousins. But in this case, cross-cousin marriage is seriously discouraged and is less common than parallel cousin marriage. Here the seeming anomaly is that a man jokes with his mother’s brother, but respects his father’s sister and her offspring. Firth (1963 [1936]: 195, 199, 207f, 231, 285).
Despite the complexity of Hage’s presentation of the G/wi case, he leaves out or misreports crucial information reported by Silberbauer pertaining to the relation of a male ego to his father’s sister’s children, and of ego to ego’s nephews and nieces, both of which support my interpretation here. Thus a male ego’s brother’s daughter is avoidance and his sister’s daughter a joking partner. This last is interesting because, since joking partners are potential wives, this implies the possibility of male-ego’s marriage with sister’s daughter. This type of marriage is compatible with a polygamous society in which age of husband significantly exceeds age of wife.
26 Viveiros de Castro (1998: 347, 360f) has emphasized the ambiguity of relationships to opposite-sex kin in systems that emphasize the affine/cognate bifurcation and has a beautiful discussion of different ways of conceiving of the logical relations between equivalence and antiequivalence.
27 See note 24 on the equivalence of siblings in Cheyenne and Arapaho systems. In contrast, kinship systems that divide people into opposing categories but emphasize a connection between the cross-sex siblings, such as the Palauan studied by Smith (1983: 4f, 74f, 86, 312), do not lead to the joking system, even though there may be a principle of generational equivalence. In this case, the crucial concatenation of relationships happens by linking a cross-sex siblingship with a marriage (e.g., male ego, ego’s sister, ego’s sister’s husband).
28 In other societies which do not equate coaffines (those who have married into lineages into which one has married) and cognates, joking and avoidance relationships may simply map on to affines and cognates respectively. Thus among the Yanomamö, says Chagnon (1968b: 58f, 66), a man jokes with his brothers-in-law but treats cognates of his age with coolness, because the former are allies, while the latter are competitors (and indeed, the most enmity occurs between those who are classificatory cognates). This may be seen as one relaxation of the well-defined joking relationship of the G/wi (to emphasize the cognate/affine distinction); the other is to simply emphasize the generational classes, which is also common.
29 A good example here is the Juang of central India, who divide all people into cognates (kutumb) and potential marriage partners (bondhu) (see Parkin 1993). Basically, all cognates are “avoidance” partners, though the degree of avoidance is not always very high. The principal of alternating generations then divides the bondhu into joking and avoidance partners, with the former potential spouses and the latter not.
30 Interestingly, Wikmunkan joking relationships seem to be based on the same structure—a division into kinsmen and affines—but reverse the polarity, as one jokes with those who do not give one wives and avoids those who do (Jackes 1969).
31 This is a special case of the more general arrangement that Houseman and White (1998a, 1988b) call “sidedness.” See their wonderful treatment for an exposition of such structures that are clear from the point of view of any ego but do not lead to classes. This sort of arrangement is also generally implied by Dravidian kinship systems that distinguish between parallel and cross relatives, identifying these with cognates and affines respectively (Ives 1998: 99).
32 As Bo Anderson (1979) has argued, in the balance theoretic tradition there was too much attention to formal properties of graphs and not enough attention to human action (also see Opp 1984: 38; Doreian 2002; Hummon and Doreian 2003: 20). An exemplary attempt to disentangle different types of intransitivity, and predict which forms would be psychologically unpleasant and hence more unstable, was carried out by Hallinan and Hutchins (1980).
33 Where there is unilineal descent, as among the Kiga of Rwanda studied by Freedman (1977), joking is likely to take place with the clan that gives one one’s spouse, but not with all other clans, leading to selective joking but not the same bifurcated structure. Thus people here all agree as to the classes of equivalents (the clans), but do not make a bifurcation.
34 RSV Lev 18: 1–17.
35 Now certain categories are not mentioned here, for example, the mother’s brother’s daughter’s nakedness, but almost certainly because these are considered too far away to be worthy of discussion, not because of a preferential logic.
36 C(C(M(M)))) = C(M(M))) = M(M) = M.
37 An example here is the !Kung, among whom a man may not marry a woman with the name of a prohibited female relative such as mother, sister, daughter, mother-in-law, etc. (see Lee 1972: 356f). Interestingly, among the Tikopia, siblings are distinguished not as male and female (as in our “brother” and “sister” but as “same sex as me” and “other sex,” and these distinctions—with their implicit avoidances—transferred to their children, but not their grandchildren, leading Firth (1963 [1936]: 229) to comment that “there is thus a mechanism inherent in the kinship system for the continual conversion of certain restrained into free relationships.”
38 See for example Harary and Kommel’s (1979) formulation of indices of the total degree of transitivity for −1, 0, 1 relational graphs. In addition to the mathematical elegance, there were good reasons to focus on transitivity coming from theories of cognitive development. Piaget privileged transitivity as a key element in deriving a mature and scientific understanding of the relationships inherent in the physical world. In an extremely important piece of research, Leinhardt (1972) analyzed children’s groups across a number of grades to see whether (as Piagetians might expect) there was an increase in the tendency for choices to be transitive over time. There is, in fact, evidence of such an increase, although it is not necessarily continuous (he found jumps in transitivity at the kindergarten as opposed to prekindergarten level and at grade 5 as opposed to 4 for boys). But Leinhardt realized that some of this change might be due not to a more developed cognitive sense of transitive implications, but to the vertical differentiation of children—there would be a tendency toward transitivity simply arising from some children being more popular than others (Leinhardt 1972: 210).
39 It is eminently possible to derive clusters from signed graphs, as do Hage and Harary (1983) (in particular, see their interesting application to Young’s data on food-giving friendships and enmities, 4). In this case, one can generalize to “colorings” of signed graphs, given the key theorem that absence of any cycle with one and only one negative line allows for the graph to be divided up into a number of clusters such that all intercolor ties are negative or null, and all intracolor ties are positive or null. I simply follow the historical progression here.
40 Interestingly, early on Heider (1946; 1958: 183. 200–202) emphasized the important distinction between mutual relations of equivalence (“unit”) and asymmetric relations of “liking.”
41 Because of their paramount focus on individual-level transitivity, the simple model in which the cliques formed a single linear order (in which all cliques can be ranked on a single dimension such that given any two different cliques A and B, we may say A < B or A < B) was not originally considered. But Holland and Leinhardt (1971: 115) did note that if null relations are prohibited, then the graph must form a quasi series, in which the cliques are ordered (as opposed to partially ordered). This may also be seen as a popularity tournament in which people only reciprocate to (and probably only interact with) their exact equivalents; it may hence be seen as a linear ordering with a tendency toward equivalence. It is worth noting (as we will examine such structures in the next chapter) that there is no evidence of such a structure emerging in social data.
42 Further exploration (e.g., Eder and Hallinan 1978: 242, 244f, though see Lubbers 2003) also suggests that girls have a stronger tendency to form isolated dyads than do boys, and this affects the evolution of the network as a whole.
43 If we denote a choice from i to j as xij= 1 with xij= 0 if the choice is not made, and we call the expansiveness of person i αi, the attractiveness of person j βj, and the tendency to mutuality ρ, we may write this model as follows:
ln (Pr[xij = 1] / Pr [xij = 0]) = αi + βj + ρxji
In many cases the data gathering instrument is such that αi is some constant c for all i (such as when people are asked to give three choices). If βj = β for all j, there is no vertical differentiation, and we have a simple web type structure. If ρ = 0, there is no tendency toward reciprocity, and this is a pure popularity tournament. If αi = − βj and ρ=0, we have a model for a ranking process that will be described in chapter 4. It will be noted that the ρ parameter captures some horizontal tendencies (tendencies toward mutualism and therefore equality), while the other parameters capture vertical differentiation.
44 Because there may be reasons for participants in the popularity tournament to have a certain number of relationships, they may not drop all relations with the unpopular.
45 There certainly may be some persons who play popularity tournaments in a contrarian manner, choosing what is unpopular and dropping choices to items or persons that turn out to be popular. The presence of such contrarians leads to a tendency toward equalization, and such contrarianism is probably found in cultural fields in which certain aficionados are unable to enjoy anything that turns out to be popular (cf. Bourdieu 1984 [1979]). Interestingly, there are few good examples of such contrarianism for popularity tournaments in which it is other persons, and not objects chosen by other persons, that are being vertically differentiated. As Gould (2002: 1149f) suggests, the “contrary” choices that serve to put a brake on the feedback of popularity probably come from (1) the decreased availability of the popular and (2) the tendency toward reciprocity.
46 More exactly, they are concerned with the change in the popularity of one thing relative to the change in the popularity of other things.
47 Boyd and Jonas (2001) demonstrate for the specific case of regular equivalence that allowing for such popularity effects does destroy the mathematical regularities of equivalence: unless there is a good reason why people stop adding relationships (their example of a relationship with a decreasing return to number of ties is the doctor-patient relation: past a certain number, doctors want no more patients), the logic of popularity—vertical differentiation—begins to replace the horizontal logic of equivalence.
48 Interestingly, Bergman (1988) argues that the key algebraic forms tend to have three properties, one having to do with each element considered singularly (such as reflexivity), one having to do with pairs of elements (such as symmetry) and one having to do with triads (such as transitivity). The investigations here reach largely similar conclusions for the case of spontaneously formed social structures.
49 This fact, that popularity tournaments coupled with a disinclination to interact with those far below one in status leads to matching of near equals for interaction, can easily be generalized to the case of two different groups and two different statuses. This fits the case of heterosexual pairing discussed by Waller (1937) and leads to the frequent confusion of such pairing structures with a price-making market (see Martin and George 2006). But the restrictive conditions necessary for a pure market need not be invoked when we simply see interaction follow a spatial logic induced by a popularity tournament.