Heads I win, tails you lose.
Often said in children’s games
ALL OF THE PREVIOUS WORK on probabilities pales into insignificance compared to Jakob Bernoulli’s epic Ars conjectandi (The Art of Conjecture), which he wrote between 1684 and 1689. It was published posthumously in 1713 by his nephew Nicolaus Bernoulli. Jakob, who had already published extensively on probability, collected together the main ideas and results then known, and added many more of his own. The book is generally considered to mark the arrival of probability theory as a branch of mathematics in its own right. It begins with the combinatorial properties of permutations and combinations, which we’ll revisit shortly in modern notation. Next, he reworked Huygens’s ideas on expectation.
Coin tossing is staple fodder for probability texts. It’s familiar, simple, and illustrates many fundamental ideas well. Heads/tails is the most basic alternative in games of chance. Bernoulli analysed what’s now called a Bernoulli trial. This models repeatedly playing a game with two outcomes, such as a coin toss with either H or T. The coin can be biased: H might have probability 2/3 so that T has probability 1/3, for instance. The two probabilities must add up to 1, because each toss is either a head or a tail. He asked questions like ‘What’s the probability of getting at least 20 Hs in 30 tosses?’, and answered them using counting formulas known as permutations and combinations. Having established the relevance of these combinatorial ideas, he then developed their mathematics in considerable depth. He related them to the binomial theorem, an algebraic result expanding powers of the ‘binomial’ (two-term expression) x + y; for example,
(x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4
The third portion of the book applies the previous results to games of cards and dice that were common at that period. The fourth and last continues the emphasis on applications, but now to decision-making in social contexts, including law and finance. Bernoulli’s big contribution here is the law of large numbers, which states that over a large number of trials, the number of times that any specific event H or T occurs is usually very close to the number of trials multiplied by the probability of that event. Bernoulli called this his golden theorem, ‘a problem in which I’ve engaged myself for twenty years’. This result can be viewed as a justification of the frequentist definition of probability: ‘proportion of times a given event happens’. Bernoulli saw it differently: it provided a theoretical justification for using proportions in experiments to deduce the underlying probabilities. This is close to the modern axiomatic view of probability theory.
Bernoulli set the standard for all who followed, but he left several important questions open. One was practical. Calculations using Bernoulli trials became very complicated when the number of trials is large. For example, what is the probability of getting 600 or more Hs in 1000 tosses of a fair coin? The formula involves multiplying 600 whole numbers together and dividing by another 600. In the absence of electronic computers, performing the sums by hand was at best tedious and time-consuming, and at worst beyond human abilities. Solving questions like this constituted the next big step in the human understanding of uncertainty via probability theory.
DESCRIBING THE MATHEMATICS OF PROBABILITY theory in historical terms becomes confusing after a while, because the notation, terms, and even concepts changed repeatedly as mathematicians groped their way towards a better understanding. So at this point I want to explain some of the main ideas that came out of the historical development in more modern terms. This will clarify and organise some concepts we need for the rest of the book.
It seems intuitively clear that a fair coin will, in the long run, produce about the same number of heads as tails. Each individual toss is unpredictable, but cumulative results over a series of tosses are predictable on average. So although we can’t be certain about the outcome of any particular toss, we can place limits on the amount of uncertainty in the long run.
I tossed a coin ten times, and got this sequence of heads and tails:
T H T T T H T H H T
There are 4 heads and 6 tails – nearly an equal split, but not quite. How likely are those proportions?
I’ll work up to the answer gradually. The first toss is either H or T, with equal probabilities of 1/2. The first two tosses could have been any of HH, HT, TH, or TT. There are four possibilities, all equally likely, so each has probability 1/4. The first three tosses could have been any of HHH, HHT, HTH, HTT, THH, THT, TTH, or TTT. There are eight possibilities, all equally likely, so each has probability 1/8. Finally, let’s look at the first four tosses. There are 16 sequences, each with probability 1/16, and I’ll list them according to how many times H occurs:
0 times |
1 sequence (TTTT) |
1 time |
4 sequences (HTTT, THTT, TTHT, TTTH) |
2 times |
6 sequences (HHTT, HTHT, HTTH, THHT, THTH, TTHH) |
3 times |
4 sequences (HHHT, HHTH, HTHH, THHH) |
4 times |
1 sequence (HHHH) |
The sequence I tossed began THTT, with only one head. That number of heads occurs 4 times out of 16 possibilities: probability 4/16 = 1/4. For comparison, two heads and two tails occurs 6 times out of 16 possibilities: probability 4/16 = 3/8. So although heads and tails are equally likely, the probability of getting the same number of each isn’t 1/2; it’s smaller. On the other hand, the probability of getting close to two heads – here 1, 2, or 3 – is (4 + 6 + 4)/16 = 14/16, which is 87.5%.
With ten tosses there are 210 = 1024 sequences of Hs and Ts. Similar sums (there are short cuts) show that the numbers of sequences with a given number of Hs go like this:
1 sequence |
probability 0·001 |
|
1 time |
10 sequences |
probability 0·01 |
2 times |
45 sequences |
probability 0·04 |
3 times |
120 sequences |
probability 0·12 |
4 times |
210 sequences |
probability 0·21 |
5 times |
252 sequences |
probability 0·25 |
6 times |
210 sequences |
probability 0·21 |
7 times |
120 sequences |
probability 0·12 |
8 times |
45 sequences |
probability 0·04 |
9 times |
10 sequences |
probability 0·01 |
10 times |
1 sequence |
probability 0·001 |
My sequence has 4 heads and 6 tails, an event with probability 0·21. The most probable number of heads is 5, with probability only 0·25. Picking a particular number of heads isn’t terribly informative. A more interesting question is: What is the probability of getting a number of heads and tails in some range, such as somewhere between 4 and 6? The answer is 0·21 + 0·25 + 0·21 = 0·66. In other words, if we toss a coin ten times, we can expect either a 5:5 or 6:4 split two times out of three. The flipside is that we can expect a greater disparity one time out of three. So a certain amount of fluctuation around the theoretical average is not only possible, but quite likely.
If we look for a larger fluctuation, say a split of 5:5, 6:4, or 7:3 (either way), the probability of staying within those limits becomes 0·12 + 0·21 + 0·25 + 0·21 + 0·12 = 0·9. Now the chance of getting a worse imbalance is about 0·1 – one in ten. This is small, but not ridiculously so. It’s surprising that when you toss a coin ten times, the chance of getting two or fewer heads, or two or fewer tails, is as big as 1/10. It will happen, on average, once every ten trials.
AS THESE EXAMPLES ILLUSTRATE, EARLY work in probability mainly focused on counting methods for equally likely cases. The branch of mathematics that counts things is known as combinatorics, and the concepts that dominated the earliest work were permutations and combinations.
A permutation is a way to arrange a number of symbols or objects in order. For example, the symbols A B C can be ordered in six ways:
Similar lists show that there are 24 ways to arrange four symbols, 120 ways to arrange five, 720 ways to arrange six, and so on. The general rule is simple. For instance, suppose we want to arrange six letters A B C D E F in some order. We can select the first letter in six different ways: it’s either A or B or C or D or E or F. Having chosen the first letter, we’re left with five others to continue the ordering process. So there are five ways to choose the second letter. Each of those can be appended to the initial choice, so overall we can choose the first two letters in
6 × 5 = 30
ways. There are four choices for the next letter, three choices for the next letter, two choices for the next letter, and the sixth letter is the only one left. So the total number of arrangements is
6 × 5 × 4 × 3 × 2 × 1 = 720
The standard symbol for this calculation is 6!, read as ‘six factorial’ (or more properly as ‘factorial six’, but hardly anyone ever says that).
By the same reasoning, the number of ways to arrange a pack of 52 cards in order is
52! = 52 × 51 × 50 × ··· × 3 × 2 × 1
which my faithful computer tells me, with impressive speed, is
80,658,175,170,943,878,571,660,636,856,403,766,975,289,505,440, 883,277,824,000,000,000,000
This answer is exact, gigantic, and not something you could find by listing all the possibilities.
More generally, we can count how many ways there are to arrange in order any four letters from the six letters A B C D E F. These arrangements are called permutations (of four letters from six). The sums are similar, but we stop after choosing four letters. So we get
6 × 5 × 4 × 3 = 360
ways to arrange four letters. The neatest way to say this mathematically is to think of it as
(6 × 5 × 4 × 3 × 2 × 1)/(2 × 1) = 6!/2! = 720/2 = 360.
Here we divide by 2! to get rid of the unwanted ×2×1 at the end of 6!. By the same reasoning, the number of ways to arrange 13 cards out of 52 in order is
52!/39! = 3,954, 242, 643, 911, 239, 680, 000
Combinations are very similar, but now we count not the number of arrangements, but the number of different choices, ignoring order. For instance, how many different hands of 13 cards are there? The trick is to count the number of permutations first, and then ask how many of them are the same except for the ordering. We’ve already seen that every set of 13 cards can be ordered in 13! ways. That means that each (unordered) set of 13 cards appears 13! times in the (hypothetical) list of all 3,954,242,643,911,239,680,000 ordered lists of 13 cards. So the number of unordered lists is
3; 954; 242; 643; 911; 239; 680; 000=13! ¼ 635; 013; 559; 600
and that’s the number of different hands.
In a probability calculation, we might want the probability of getting a particular set of 13 cards – say, all the spades. That’s exactly one set out of those 635 billion hands, so the probability of being dealt that hand is
1/635, 013, 559, 600 = 0·000000000001574 ...
which is 1·5 trillionths. Across the planet, it should happen once in about 635 billion hands, on average.
There’s an informative way to write this answer. The number of ways to choose 13 cards out of 52 (the number of combinations of 13 out of 52) is
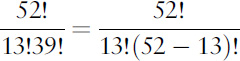
Algebraically, the number of ways to choose r objects from a set of n objects is
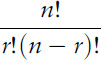
So we can calculate this number in terms of factorials. It is often spoken informally as ‘n choose r’; the fancy term is binomial coefficient, written symbolically as
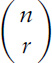
This name arises because of a connection with the binomial theorem in algebra. Look at my formula for (x + y)4 a few pages back. The coefficients are 1, 4, 6, 4, 1. The same numbers occur when we count how many ways a given numbers of heads arises in four consecutive tossings. The same goes if you replace 4 by any whole number.
THUS ARMED, LET’S TAKE ANOTHER look at the list of 1024 sequences of Hs and Ts. I said that there are 210 sequences in which H appears four times. We can calculate this number using combinations, though how to do it isn’t immediately obvious since it’s related to ordered sequences in which the symbols can repeat, which looks like a very different animal. The trick is to ask at which positions the four Hs appear. Well, they might be in positions 1, 2, 3, 4 – HHHH followed by six Ts. Or they might be in positions 1, 2, 3, 5 – HHHTH followed by five Ts. Or... Whatever the positions may be, the list of those positions at which the four Hs appear is a list of four numbers from the full set 1, 2, 3, ..., 10. That is, it’s the number of combinations of 4 numbers out of 10. But we know how to find that: we just work out
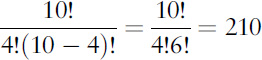
Binomial distribution for ten trials, H and T equally likely. Divide the numbers on the vertical scale by 1024 to get probabilities.
Magic! Repeating this kind of calculation, we get the entire list:
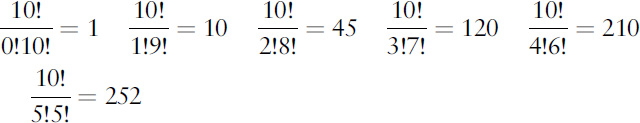
after which the numbers repeat in reverse order. You can see this symbolically, or argue that (for instance) six Hs is the same as four Ts, and the number of ways to get four Ts is obviously the same as the number of ways to get four Hs.
The general ‘shape’ of the numbers is that they start small, rise to a peak in the middle, and then decrease again, with the entire list being symmetric about the middle. When we graph the number of sequences against the number of heads, as a bar chart, or histogram if you want to be posh, we see this pattern very clearly.
A measurement made at random from some range of possible events is called a random variable. The mathematical rule that associates each value of the random variable to its probability is called a probability distribution. Here the random variable is ‘number of heads’, and the probability distribution looks much like the bar chart, except that the numbers labelling the vertical scale must be divided by 1024 to represent probabilities. This particular probability distribution is called a binomial distribution because of the link to binomial coefficients.
Distributions with different shapes occur when we ask different questions. For example, with one dice, the the throw is either 1, 2, 3, 4, 5 or 6, and each is equally likely. This is called a uniform distribution.
If we throw two dice and add the resulting numbers together, the totals from 2 to 12 occur in different numbers of ways:
2 = 1 = 1 |
1 way |
3 = 1 + 2, 1 + 1 |
2 ways |
4 = 1 + 3, 2 + 2, 3 + 1 |
3 ways |
5 = 1 + 4, 2 + 3, 3 + 2, 4 + 1 |
4 way |
6 = 1 + 5, 2 + 4, 3 + 3, 4 + 2, 5 + 1 |
5 ways |
7 = 1 + 6, 2 + 5, 3 + 4, 4 + 3, 5 + 2, 6 + 1 |
6 ways |
increasing by 1 at each step, but then the numbers of ways start to decrease because throws of 1, 2, 3, 4 and 5 are successively eliminated:
8 = 2 + 6, 3 + 5, 4 + 4, 5 + 3, 6 + 2 |
5 ways |
9 = 3 + 6, 4 + 5, 5 + 4, 6 + 3 |
4 ways |
10 = 4 + 6, 5 + 5, 6 + 4 |
3 ways |
11 = 5 + 6, 6 + 5 |
2 ways |
12 = 6 + 6 |
1 way |
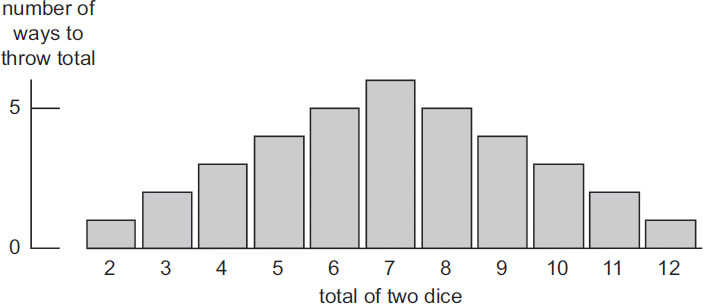
Distribution for the total of two dice. Divide the vertical scale by 36 to get probabilities.
Distribution for the total of three dice. Divide the numbers on the vertical scale by 216 to get probabilities.
The probability distribution for these totals is therefore shaped like a triangle. The numbers are graphed in the figure; the corresponding probabilities are these numbers divided by their total, which is 36.
If we throw three dice and add up the resulting numbers, the shape rounds off and starts to look more like a binomial distribution, although it’s not quite the same. It turns out that the more dice we throw, the closer the total gets to a binomial distribution. The central limit theorem in Chapter 5 explains why this happens.
COINS AND DICE ARE COMMON metaphors for randomness. Einstein’s remark that God does not play dice with the universe is widely known. It’s less widely known that he didn’t use those exact words, but what he did say made the same point: he didn’t think the laws of nature involve randomness. It’s therefore sobering to discover that he may have chosen the wrong metaphor. Coins and dice have a dirty secret. They’re not as random as we imagine.
In 2007 Persi Diaconis, Susan Holmes, and Richard Montgomery investigated the dynamics of coin tossing.13 They started with the physics, building a coin-tossing machine that flips the coin into the air, so that it rotates freely until it lands on a flat receptive surface, without bouncing. They set up the machine to perform the flip in a very controlled way. So controlled that, as long as you place the coin heads up in the machine, it always lands heads – despite turning over many times in mid-air. Place it tails up, and it always lands tails. This experiment demonstrates very clearly that coin tossing is a predetermined mechanical process, not a random one.
Joseph Keller, an applied mathematician, had previously analysed a special case: a coin that spins around a perfectly horizontal axis, turning over and over until it’s caught in a human hand. His mathematical model showed that provided the coin spins fast enough, and stays in the air long enough, only a small amount of variability in the initial conditions leads to equal proportions of heads and tails. That is, the probability that the coin comes down heads is very close to the expected value 1/2, and so is that of tails. Moreover, those figures still apply even if you always start it heads up, or tails up. So a really vigorous flip does a good job of randomisation, provided the coin spins in the special way Keller’s model assumes.
At the other extreme, we can imagine a flip that is just as vigorous, but makes the coin spin around a vertical axis, like a turntable for playing vinyl records. The coin goes up, comes down again, but never flips right over, so it always lands exactly the same way up as it was when it left the hand. A realistic coin toss lies somewhere in between, with a spin axis that’s neither horizontal nor vertical. If you don’t cheat, it’s probably close to horizontal.
Suppose for definiteness we always start the toss with heads on top. Diaconis’s team showed that unless the coin obeys Keller’s assumptions exactly, and flips about a precisely horizontal axis (which in practice is impossible) it will land with heads on top more than half the time. In experiments with people tossing it in the usual manner, it lands heads about 51% of the time and tails 49% of the time.
Before we get too worried about ‘fair’ coins not being fair, we must take three other factors into account. Humans can’t toss the coin with the same precision as a machine. More significantly, people don’t toss coins by always starting heads up. They start with heads or tails, at random. This evens out the probabilities for ending up heads or tails, so the outcome is (very close to) fifty-fifty. It’s not the toss that creates the equal probabilities; it’s the unconscious randomisation performed by the person tossing the coin when they place it on their thumb before flipping it. If you wanted to gain a slight edge, you could practise precision tossing until you got really good, and always start the coin the same way up that you want it to land. The usual procedure neatly avoids this possibility by introducing yet another element of randomness: one person tosses, and the other one calls ‘heads’ or ‘tails’ while the coin is in the air. Since the person tossing doesn’t know in advance what the other person will call, they can’t affect the chances by choosing which way up to start the coin.
THE ROLL OF A DICE is more complicated, with more possible outcomes. But it seems reasonable to examine the same issue. When you roll a dice, what’s the most important factor in determining which face ends up on top?
There are plenty of possibilities. How fast it spins in the air? How many times it bounces? In 2012 Marcin Kapitaniak and colleagues developed a detailed mathematical model of a rolling dice, including factors like air resistance and friction.14 They modelled the dice as a perfect mathematical cube with sharp corners. To test the model, they made high-speed movies of rolling dice. It turned out that none of the above factors is as important as something far simpler: the initial position of the dice. If you hold the dice with face 1 on top, it rolls 1 slightly more often than anything else. By symmetry, the same goes for any other number.
The traditional ‘fair dice’ assumption is that each face has probability 1=6 ¼ 0 167 of being thrown. The theoretical model shows that in an extreme case where the table is soft and the coin doesn’t bounce, the face on top at the start ends up on top with probability 0·558 – much larger. With the more realistic assumption of four or five bounces, this becomes 0·199 – still significantly bigger. Only when the dice rotates very fast, or bounces about twenty times, does the predicted probability become close to 0·167. Experiments using a special mechanical device to toss the dice with a very precise speed, direction, and initial position showed similar behaviour.