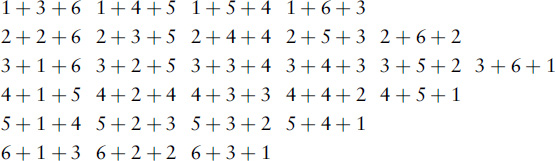
1 The quote probably has nothing to do with Berra, and may come from an old Danish proverb:
https://quoteinvestigator.com/2013/10/20/no-predict/
2 Ezekiel 21:21.
3 Ray Hyman. Cold reading: how to convince strangers that you know all about them, Zetetic 1 (1976/77) 18–37.
4 I’m not sure exactly what’s meant by ‘lighted carbon’ – maybe charcoal? – but several sources mention it in this connection, including:
John G. Robertson, Robertson’s Words for a Modern Age (reprint edition), Senior Scribe Publications, Eugene, Oregon, 1991.
http://www.occultopedia.com/c/cephalomancy.htm
5 If ‘beat the odds’ means ‘improve your chance of getting the winning numbers’, then probability theory predicts that no such system works except by accident. If it means ‘maximise your winnings if you do win’, you can take some simple precautions. The main one is: avoid choosing numbers that a lot of other people will also be likely to choose. If your numbers come up (just as likely as any other set of numbers) you’ll share the winnings with fewer people.
6 A good example is the wave equation, originally deduced from a model of a violin string as a line segment vibrating in the plane. This model paved the way for more realistic ones, used today for everything from analysing the vibrations of a Stradivarius to calculating the internal structure of the Earth from seismic recordings.
7 I’m aware that the singular is technically ‘die’, but nowadays pretty much everyone uses ‘dice’ in the singular as well. The word ‘die’ is old-fashioned and easily misinterpreted; many people are unaware that ‘dice’ is its plural. So in this book I’ll write ‘a dice’.
8 We ditched fate to make dice fairer, New Scientist, 27 January 2018, page 14.
9 If you’re happy about the red/blue dice, but not convinced this is right when the dice look identical, two things may help. First, how do the coloured dice ‘know’ to produce twice as many combinations as they would have done if they had the same colour? That is, how can the colours affect the throws to that extent? Second: take two dice so similar that even you can’t tell which is which, throw them a lot of times, and count the proportion of times you get two 4s. If unordered pairs decide the result, you’ll get something close to 1/21. If it’s ordered pairs, it should be close to 1/36.
If you’re not convinced even about coloured dice, the same considerations apply, but you should do the experiment with coloured dice.
10 The 27 ways to total 10 are:
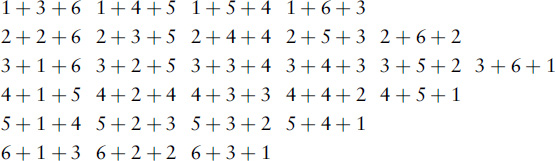
The 25 ways to total 9 are:
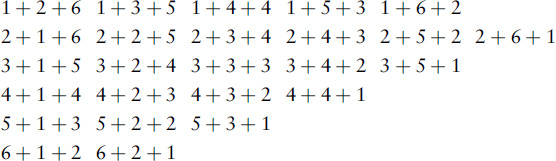
11 https://www.york.ac.uk/depts/maths/histstat/pascal.pdf
12 The ratio in which the stakes should be divided is
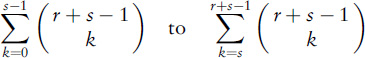
where player 1 needs r more rounds to win, player 2 needs s more. In this case, the ratio is:
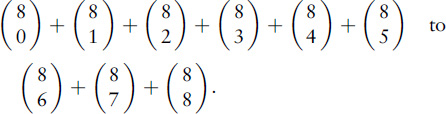
13 Persi Diaconis, Susan Holmes, and Richard Montgomery. Dynamical bias in the coin toss, SIAM Review 49 (2007) 211–235.
14 M. Kapitaniak, J. Strzalko, J. Grabski, and T. Kapitaniak. The three-dimensional dynamics of the die throw, Chaos 22 (2012) 047504.
15 Stephen M. Stigler, The History of Statistics, Harvard University Press, Cambridge, Massachusetts, 1986, page 28.
16 We want to minimise (x – 2)2 + (x 3)2 + (x – 7)2. This is quadratic in x and the coefficient of x2 is 3, which is positive, so the expression has a unique minimum. This occurs when the derivative is zero, that is, 2(x – 2) + 2(x – 3)+2(x – 7) = 0. So x = (2 + 3 + 7)/3, the mean. A similar calculation leads to the mean for any finite set of data.
17 The formula is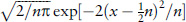 
considered as an approximation to the probability of getting x heads in n tosses.
18 Think of people entering the room one at a time. After k people have entered, the probability that all their birthdays are different is
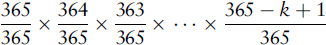
because each new arrival has to avoid the previous k – 1 birthdays. This is 1 minus the probability of at least one common birthday, so we want the smallest k for which this expression is less than 1/2. This turns out to be k = 23. More details are at:
https://en.wikipedia.org/wiki/Birthday_problem
19 Non-uniform distributions are discussed in: M. Klamkin and D. Newman. Extensions of the birthday surprise, Journal of Combinatorial Theory 3 (1967) 279–282.
A proof that the probability of two matching birthdays is least for a uniform distribution is given in:
D. Bloom. A birthday problem, American Mathematical Monthly 80 (1973) 1141–1142.
20 The diagram looks similar but now each quadrant is divided into a 365 × 365 grid. The dark strips in each quadrant contain 365 squares each. But there is an overlap of 1 inside the target region. So this contains 365 + 365 – 1 = 729 dark squares, there are 365 + 365 = 730 dark squares outside the target, so the total number of dark squares is 729 + 730 = 1459. The conditional probability of hitting the target is 729/1459, which is 0·4996.
21 For calculations, Quetelet used a binomial distribution for 1000 coin tosses, which he found more convenient, but he emphasised the normal distribution in his theoretical work.
22 Stephen Stigler, The History of Statistics, Harvard University Press, Cambridge, Massachusetts, 1986, page 171.
23 This isn’t necessarily true. It assumes all distributions are obtained by combining bell curves. But it was good enough for Galton’s purposes.
24 The word ‘regression’ came from Galton’s work on heredity. He used the normal distribution to explain why, on the whole, children with either two tall parents or two short parents tend to be somewhere in between, calling this ‘regression to the mean’.
25 Another figure deserving mention is Francis Ysidro Edgeworth. He lacked Galton’s vision but was a far better technician, and put Galton’s ideas on a sound mathematical basis. However, his story is too technical to include.
26 In symbols:
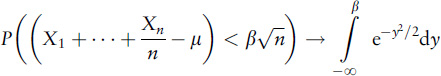
where the right-hand side is the cumulative normal distribution for mean 0 and variance 1.
27 We have P(A|B) = P(A&B)/P(B) and also P(B|A) = P(B&A)/P(A). But the event A&B is the same as B&A. Dividing one equation by the other, we have P(A|B)/P(B|A) = P(A)/P(B). Now multiply both sides by P(B|A).
28 Frank Drake introduced his equation in 1961 to summarise some of the key factors that affect the likelihood of alien life, as part of the first meeting of SETI (Search for ExtraTerrestrial Intelligence). It’s often used to estimate the number of alien civilisations in the Galaxy, but many of the variables are difficult to estimate and it’s not suitable for that purpose. It also involves some unimaginative modelling assumptions. See:
https://en.wikipedia.org/wiki/Drake_equation
29 N. Fenton and M. Neil. Risk Assessment and Decision Analysis with Bayesian Networks, CRC Press, Boca Raton, Florida, 2012.
30 N. Fenton and M. Neil. Bayes and the law, Annual Review of Statistics and Its Application 3 (2016) 51–77.
https://en.wikipedia.org/wiki/Lucia_de_Berk
31 Ronald Meester, Michiel van Lambalgen, Marieke Collins, and Richard Gil. On the (ab)use of statistics in the legal case against the nurse Lucia de B. arXiv:math/0607340 [math.ST] (2005).
32 The science historian Clifford Truesdell is reputed to have said: ‘Every physicist knows what the first and the second law [of thermodynamics] mean, but the problem is that no two agree about them.’ See: Karl Popper. Against the philosophy of meaning, in: German 20th Century Philosophical Writings (ed. W. Schirmacher), Continuum, New York, 2003, page 208.
33 You can find the rest at:
https://lyricsplayground.com/alpha/songs/f/firstandsecondlaw.html.
34 N. Simanyi and D. Szasz. Hard ball systems are completely hyperbolic, Annals of Mathematics 149 (1999) 35–96.
N. Simanyi. Proof of the ergodic hypothesis for typical hard ball systems, Annales Henri Poincaré 5 (2004) 203–233.
N. Simanyi. Conditional proof of the Boltzmann–Sinai ergodic hypothesis. Inventiones Mathematicae 177 (2009) 381–413. There is also a 2010 preprint, which seems not to have been published:
N. Simanyi. The Boltzmann–Sinai ergodic hypothesis in full generality:
https://arxiv.org/abs/1007.1206
35 Carlo Rovelli. The Order of Time, Penguin, London 2018.
36 The figure is a computer calculation, also subject to the same errors. Warwick Tucker found a computer-aided but rigorous proof that the Lorenz system has a chaotic attractor. The complexity is real, not some numerical artefact. W. Tucker. The Lorenz attractor exists. C.R. Acad. Sci. Paris 328 (1999) 1197–1202.
37 Technically, the existence of invariant measures that give the right probabilities has been proved only for special classes of attractors. Tucker proved the Lorenz attractor has one, in the same paper. But extensive numerical evidence suggests they’re common.
38 J. Kennedy and J.A. Yorke. Basins of Wada, Physica D 51 (1991) 213–225.
39 P. Lynch. The Emergence of Numerical Weather Prediction, Cambridge University Press, Cambridge, 2006.
40 Fish later said that the caller was referring to a hurricane in Florida.
41 T.N. Palmer, A. Döring, and G. Seregin. The real butterfly effect, Nonlinearity 27 (2014) R123–R141.
42 E.N. Lorenz. The predictability of a flow which possesses many scales of motion. Tellus 3 (1969) 290–307.
43 T.N. Palmer. A nonlinear dynamic perspective on climate prediction. Journal of Climate 12 (1999) 575–591.
44 D. Crommelin. Nonlinear dynamics of atmospheric regime transitions, PhD Thesis, University of Utrecht, 2003.
D. Crommelin. Homoclinic dynamics: a scenario for atmospheric ultralow-frequency variability, Journal of the Atmospheric Sciences 59 (2002) 1533–1549.
45 The sums go like this:
total over 90 days |
90 × 16 = 1440 |
total over 10 days |
10 × 30 = 300 |
total over all 100 days |
1740 |
average |
1740=100 ¼ 17 4 |
46 For the 800,000-year record:
E.J. Brook and C. Buizert. Antarctic and global climate history viewed from ice cores, Nature 558 (2018) 200–208.
47 This quotation appeared in Reader’s Digest in July 1977, with no documentation. The New York Times published an article ‘How a “difficult” composer gets that way’ by the composer Roger Sessions on 8 January 1950. It included: ‘I also remember a remark of Albert Einstein, which certainly applies to music. He said, in effect, that everything should be as simple as it can be, but not simpler!’
48 Data from the U.S. Geological Survey show that the world’s volcanoes produce about 200 million tons of CO2 per year. Human transportation and industry emit 24 billion tons, 120 times as big.
https://www.scientificamerican.com/article/earthtalks-volcanoes-or-humans/
49 The IMBIE team (Andrew Shepherd, Erik Ivins, and 78 others). Mass balance of the Antarctic Ice Sheet from 1992 to 2017, Nature 558 (2018) 219–222.
50 S.R. Rintoul and 8 others. Choosing the future of Antarctica, Nature 558 (2018) 233–241.
51 J. Schwartz. Underwater, Scientific American (August 2018) 44–55.
52 E.S. Yudkowsky. An intuitive explanation of Bayes’ theorem:
http://yudkowsky.net/rational/bayes/
53 W. Casscells, A. Schoenberger, and T. Grayboys. Interpretation by physicians of clinical laboratory results, New England Journal of Medicine 299 (1978) 999–1001.
D.M. Eddy. Probabilistic reasoning in clinical medicine: Problems and opportunities, in: (D. Kahneman, P. Slovic, and A. Tversky, eds.), Judgement Under Uncertainty: Heuristics and Biases, Cambridge University Press, Cambridge, 1982.
G. Gigerenzer and U. Hoffrage. How to improve Bayesian reasoning without instruction: frequency formats, Psychological Review 102 (1995) 684–704.
54 The Kaplan–Meier estimator deserves mention, but it would interrupt the story. It’s the most widely used method for estimating survival rates from data in which some subjects may leave the trial before the full time period – either through death or other causes. It’s non-parametric and second on the list of highly cited mathematics papers. See: E.L. Kaplan and P. Meier. Nonparametric estimation from incomplete observations, Journal of the American Statistical Association 53 (1958) 457–481.
https://en.wikipedia.org/wiki/Kaplan%E2%80%93Meier_estimator
55 B. Efron. Bootstrap methods: another look at the jackknife, Annals of Statistics 7 B (1979) 1–26.
56 Alexander Viktorin, Stephen Z. Levine, Margret Altemus, Abraham Reichenberg, and Sven Sandin. Paternal use of antidepressants and offspring outcomes in Sweden: Nationwide prospective cohort study, British Medical Journal 316 (2018); doi: 10.1136/bmj.k2233.
57 Confidence intervals are confusing and widely misunderstood. Technically, the 95% confidence interval has the property that the true value of the statistic lies inside that interval for 95% of the times a confidence interval is calculated from a sample. It does not mean ‘the probability that the true statistic lies in the interval is 95%.’
58 A corporate euphemism for ‘these people will never be able to pay us back’.
59 Technically it was the Swedish National Bank’s Prize in Economic Sciences in Memory of Alfred Nobel, set up in 1968, not one of the prize categories Nobel established in his 1895 will.
60 Technically, a distribution f(x) has fat tails if it decays like a power law; that is, f(x) ~ x -(1+a) as x tends to infinity, for a > 0.
61 Warren Buffett. Letter to the shareholders of Berkshire Hathaway, 2008:
http://www.berkshirehathaway.com/letters/2008ltr.pdf
62 A.G. Haldane and R.M. May. Systemic risk in banking ecosystems, Nature 469 (2011) 351–355.
63 W.A. Brock, C.H. Hommes, and F.O.O. Wagner. More hedging instruments may destabilise markets, Journal of Economic Dynamics and Control 33 (2008) 1912–1928.
64 P. Gai and S. Kapadia. Liquidity hoarding, network externalities, and interbank market collapse, Proceedings of the Royal Society A (2010) 466, 2401–2423.
65 For a long time it was thought that the human brain contains ten times as many glial cells as neurons. Credible internet sources still say about four times. But a 2016 review of the topic concludes that there are slightly fewer glial cells than neurons in the human brain. Christopher S. von Bartheld, Jami Bahney, and Suzana Herculano-Houze, The search for true numbers of neurons and glial cells in the human brain: A review of 150 years of cell counting, Journal of Comparative Neurology, Research in Systems Neuroscience 524 (2016) 3865–3895.
66 D. Benson. Life in the game of Go, Information Sciences 10 (1976) 17–29.
67 Elwyn Berlekamp and David Wolfe. Mathematical Go Endgames: Nightmares for Professional Go Players, Ishi Press, New York 2012.
68 David Silver and 19 others. Mastering the game of Go with deep neural networks and tree search, Nature 529 (1016) 484–489.
69 L.A. Necker. Observations on some remarkable optical phaenomena seen in Switzerland; and on an optical phaenomenon which occurs on viewing a figure of a crystal or geometrical solid, London and Edinburgh Philosophical Magazine and Journal of Science 1 (1832) 329–337. J. Jastrow. The mind’s eye, Popular Science Monthly 54 (1899) 299–312.
70 I. Kovács, T.V. Papathomas, M. Yang, and A. Fehér. When the brain changes its mind: Interocular grouping during binocular rivalry. Proceedings of the National Academy of Sciences of the USA 93 (1996) 15508–15511.
71 C. Diekman and M. Golubitsky. Network symmetry and binocular rivalry experiments, Journal of Mathematical Neuroscience 4 (2014) 12; doi: 10.1186/2190-8567-4-12.
72 Richard Feynman, in a lecture: ‘The Character of Physical Law’. Earlier Niels Bohr said ‘Anyone who is not shocked by quantum theory has not understood it,’ but that’s not quite the same message.
73 Richard P. Feynman, Robert B. Leighton, and Matthew Sands. The Feynman Lectures on Physics, Volume 3, Addison-Wesley, New York, 1965, pages 1.1–1.8.
74 Roger Penrose. Uncertainty in quantum mechanics: Faith or fantasy? Philosophical Transactions of the Royal Society A 369 (2011) 4864–4890.
75 https://en.wikipedia.org/wiki/Complex_number
76 François Hénault. Quantum physics and the beam splitter mystery:
https://arxiv.org/ftp/arxiv/papers/1509/1509.00393.
77 If the spin quantum number is n, the spin angular momentum is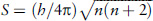 
where h is Planck’s constant.
78 Electron spin is curious. A superposition of two spin states ↑ and ↓ that point in opposite directions can be interpreted as a single spin state with an axis whose direction is related to the proportions in which the original states are superposed. However, a measurement about any axis yields either 1/2 or –1/2. This is explained in Penrose’s paper cited in Note 74.
79 An unexamined assumption here is that if a classical cause produces a classical effect, then a quantum fraction of that cause (in some superposed state) produces a quantum fraction of the same effect. A half-decayed atom creates a half-dead cat. It makes some sort of sense in terms of probabilities, but if it were true in general, a half-photon wave in a Mach–Zehnder interferometer would create half a beam-splitter when it hits one. So this kind of superposition of classical narratives can’t be how the quantum world behaves.
80 I discussed Schrödinger’s cat at length in Calculating the Cosmos, Profile, London, 2017.
81 Tim Folger. Crossing the quantum divide, Scientific American 319 (July 2018) 30–35.
82 Jacqueline Erhart, Stephan Sponar, Georg Sulyok, Gerald Badurek, Masanao Ozawa, and Yuji Hasegawa. Experimental demonstration of a universally valid error-disturbance uncertainty relation in spin measurements, Nature Physics 8 (2012) 185–189.
83 Lee A. Rozema, Ardavan Darabi, Dylan H. Mahler, Alex Hayat, Yasaman Soudagar, and Aephraim M. Steinberg. Violation of Heisenberg’s measurement-disturbance relationship by weak measurements, Physics Review Letters 109 (2012) 100404. Erratum: Physics Review Letters 109 (2012) 189902.
84 If you generate a pair of particles, each having nonzero spin, in such a way that the total spin is zero, then the principle of conservation of angular momentum (another term for spin) implies that their spins will remain perfectly anticorrelated if they are then separated – as long as they’re not disturbed. That is, their spins always point in opposite directions along the same axis. If you now measure one, and collapse its wave function, it acquires a definite spin in a definite direction. So the other one must also collapse, and give the opposite result. It sounds mad, but it seems to work. It’s also a variation on my pair of spies; they’ve just antisynchronised their watches.
85 See Note 74.
86 Even male insects feel pleasure when they ‘orgasm’, New Scientist, 28 April 2018, page 20.
87 J.S. Bell. On the Einstein Podolsky Rosen paradox, Physics 1 (1964) 195–200.
88 Jeffrey Bub has argued that Bell and Hermann misconstrued von Neumann’s proof, and that it does not aim to prove that hidden variables are completely impossible. Jeffrey Bub. Von Neumann’s ‘no hidden variables’ proof: A reappraisal, Foundations of Physics 40 (2010) 1333–1340.
89 Adam Becker, What is Real?, Basic Books, New York 2018.
90 Strictly speaking, Bell’s original version also requires the outcomes on both sides of the experiment to be exactly anticorrelated whenever the detectors are parallel.
91 E. Fort and Y. Couder. Single-particle diffraction and interference at a macroscopic scale, Physical Review Letters 97 (2006) 154101.
92 Sacha Kocsis, Boris Braverman, Sylvain Ravets, Martin J. Stevens, Richard P. Mirin, L. Krister Shalm, and Aephraim M. Steinberg. Observing the average trajectories of single photons in a two-slit interferometer, Science 332 (2011) 1170–1173.
93 This section is based on Anil Anathaswamy, Perfect disharmony, New Scientist, 14 April 2018, pages 35–37.
94 It can’t just be size, can it? Consider the effect of a beam-splitter (a 1/4 phase shift) and a particle detector (scramble the wave function). Both are comfortably macroscopic. The first thinks it’s quantum, the second knows it’s not.
95 D. Frauchiger and R. Renner. Quantum theory cannot consistently describe the use of itself, Nature Communications (2018) 9:3711; doi: 10.1038/S41467-018-05739-8.
96 A. Sudbery. Quantum Mechanics and the Particles of Nature, Cambridge University Press, Cambridge, 1986, page 178.
97 Adam Becker, What is Real?, Basic Books, New York, 2018.
98 Peter Bierhorst and 11 others. Experimentally generated randomness certified by the impossibility of superluminal signals, Nature 223 (2018) 223–226.
99 E. Ott, C. Grebogi, and J.A. Yorke. Controlling chaos, Physics Review Letters 64 (1990) 1196.
100 The occurrence of chaos in heart failure, rather than just randomness, has been detected in humans:
Guo-Qiang Wu and 7 others, Chaotic signatures of heart rate variability and its power spectrum in health, aging and heart failure, PLos Online (2009) 4(2): e4323; doi: 10.1371/journal.pone.0004323.
101 A. Garfinkel, M.L. Spano, W.L. Ditto, and J.N. Weiss. Controlling cardiac chaos, Science 257 (1992) 1230–1235. A more recent article on chaos control of a model heart is in: B.B. Ferreira, A.S. de Paula, and M.A. Savi. Chaos control applied to heart rhythm dynamics, Chaos, Solitons and Fractals 44 (2011) 587–599.
102 At the time, President George W. Bush decided not to attack Iraq in response to 9/11. But soon after, the USA and its allies did invade, citing Saddam Hussein’s ‘support for terrorism’ as a reason. The Guardian newspaper for 7 September 2003 reported a poll showing that ‘seven out of ten Americans continue to believe that Saddam Hussein had a role’ in the attacks, despite there being no evidence for this.
https://www.theguardian.com/world/2003/sep/07/usa.theobserver