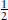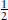2. However, those programs used brute force algorithms rather than the artificial intelligence algorithms used to win at Go.I used to be indecisive,
But now I’m not so sure.
Message on a T-shirt
IN CHAPTER 2 I ASKED why human beings so easily accept sweeping claims when there’s no serious evidence to support them, and why they so readily embrace irrational beliefs even when there’s clear evidence against them. Naturally, each of us has his or her own view on which beliefs are, or are not, irrational, but we can all ask those questions about everybody else.
Part of the answer may lie in how our brains evolved, over millions of years, to make rapid decisions about uncertain but life-threatening possibilities. These evolutionary explanations are guesses – it’s difficult to see how they could be tested, since brains don’t fossilise and there’s no way to find out for certain what went on in our ancestors’ minds – but they seem plausible. We can be more certain about how modern human brains work, because it’s possible to perform experiments that relate brain structure to brain function, and both to genetics.
It would be foolish to underestimate the difficulties of understanding a brain – even that of a fruit fly, let alone a highly complex human being. The fruit fly Drosophila melanogaster is a staple of genetic research; its brain contains about 135,000 neurons, linked together by synapses which transmit electrical signals between them. Scientists are currently investigating the structure of this network, known as the fruit fly connectome. At the moment, only two regions out of the 76 main subdivisions of the brain have been mapped. So right now we don’t even know the structure of the fruit fly’s connectome, let alone how it works. Mathematicians know that even a network of eight or ten neurons can do very puzzling things, because the simplest realistic models of such networks are nonlinear dynamical systems. Networks have special features that aren’t typical of general dynamical systems; this may be why nature uses them so much.
The human brain contains about 100 billion neurons, and more than a hundred trillion synapses. Other brain cells may also be involved in its workings, notably glial cells, which occur in roughly the same numbers as neurons, but whose functions remain mysterious.65 Research is also under way to map the human connectome, not because that will let us simulate a brain, but because it will provide a reliable database for all future brain research.
If mathematicians can’t understand a ten-neuron ‘brain’, what hope is there of understanding a 100-billion-neuron one? Like weather versus climate, it all depends on what questions you ask. Some ten-neuron networks can be understood in considerable detail. Some parts of the brain can be understood even if the whole thing remains bafflingly complex. Some of the general principles upon which the brain is organised can be teased out. In any case, this kind of ‘bottom-up’ approach, listing the components and how they’re linked, and then working our way up towards a description of what the entire system does, isn’t the only way to proceed. ‘Top-down’ analysis, based on the large-scale features of the brain and its behaviour, is the most obvious alternative. In practice, we can mix both together in quite complicated ways. In fact, our understanding of our own brains is growing rapidly, thanks to technological advances that reveal how a network of neurons is connected and what it’s doing, and to new mathematical ideas about how such networks behave.
MANY ASPECTS OF BRAIN FUNCTION can be viewed as forms of decision-making. When we look at the external world, our visual system has to figure out which objects it’s seeing, guess how they will behave, assess their potential for threat or reward, and make us act in accordance with those assessments. Psychologists, behavioural scientists, and workers in artificial intelligence have come to the conclusion that in some vital respects, the brain seems to function as a Bayesian decision machine. It embodies beliefs about the world, temporarily or permanently wired into its structure, which lead it to make decisions that closely resemble what would emerge from a Bayesian probability model. (Earlier, I said that our intuition for probability is generally rather poor. That’s not in conflict with what I’ve just said, because the inner workings of these probability models aren’t consciously accessible.)
The Bayesian view of the brain explains many other features of human attitudes to uncertainty. In particular, it helps to explain why superstitions took root so readily. The main interpretation of Bayesian statistics is that probabilities are degrees of belief. When we assess a probability as fifty-fifty, we’re effectively saying we’re as willing to believe it as we are to disbelieve it. So our brains have evolved to embody beliefs about the world, and these are temporarily or permanently wired into its structure.
It’s not just human brains that work this way. Our brain structure goes back into the distant past, to mammalian and even reptilian evolutionary ancestors. Those brains, too, embodied ‘beliefs’. Not the kind of beliefs we now articulate verbally, such as ‘breaking a mirror brings seven years’ bad luck’. Most of our own brain-beliefs aren’t like that either. I mean beliefs such as ‘if I flick my tongue out this way then I’m more likely to catch a fly’, encoded in the wiring of the region of the brain that activates the muscles involved. Human speech added an extra layer to beliefs, making it possible to express them, and more importantly, to pass them on to others.
To set the scene for a simple but informative model, imagine a region of the brain containing a number of neurons. They can be linked together by synapses, which have a ‘connection strength’. Some send weak signals, some send strong signals. Some don’t exist at all, so they send no signals. The stronger the signal, the greater is the response of the neuron receiving it. We can even put numbers to the strength, which is useful when specifying a mathematical model: in appropriate units, maybe a weak connection has strength 0·2, a strong one 3·5, and a non-existent one 0.
A neuron responds to an incoming signal by producing a rapid change in its electrical state: it ‘fires’. This creates a pulse of electricity that can be transmitted to other neurons. Which ones depends on the connections in the network. Incoming signals cause a neuron to fire when they push its state above some threshold value. Moreover, there are two distinct types of signal: excitatory ones, which tend to make the neuron fire, and inhibitory ones, which tend to stop it firing. It’s as though the neuron adds up the strengths of the incoming signals, counting excitatory ones as positive and inhibitory ones as negative, and fires only if the total is big enough.
In new-born infants, many neurons are randomly connected, but as time passes some synapses change their strengths. Some may be removed altogether, and new ones can grow. Donald Hebb discovered a form of ‘learning’ in neural networks, now called Hebbian learning. ‘Nerve cells that fire together wire together’. That is, if two neurons fire in approximate synchrony, then the connection strength between them gets bigger. In our Bayesian-belief metaphor, the strength of a connection represents the brain’s degree of belief that when one of them fires, so should the other one. Hebbian learning reinforces the brain’s belief structure.
PSYCHOLOGISTS HAVE OBSERVED THAT WHEN: a person is told some new information, they don’t just file it away in memory. That would be a disaster in evolutionary terms, because it’s not a good idea to believe everything you’re told. People tell lies, and they try to mislead others, often as part of a process aimed at bringing the others under their control. Nature tells lies too: that waving leopard tail may, on closer analysis, turn out to be a dangling vine or a fruit; stick insects pretend to be sticks. So when we receive new information, we assess it against our existing beliefs. If we’re smart, we also assess the credibility of the information. If it comes from a trusted source, we’re more likely to believe it; if not, less likely. Whether we accept the new information, and modify our beliefs accordingly, is the outcome of an internal struggle between what we already believe, how the new information relates to what we already believe, and how much confidence we have that the new information is true. Often this struggle is subconscious, but we can also reason consciously about the information.
In a bottom-up description, what’s happening is that complex arrays of neurons are all firing and sending signals to each other. How those signals cancel each other out, or reinforce each other, determines whether the new information sticks, and the connection strengths change to accommodate it. This already explains why it’s very hard to convince ‘true believers’ that they’re wrong, even when the evidence seems overwhelming to everyone else. If someone has a strong belief in UFOs and the United States government puts out a press release explaining that an apparent sighting was actually a balloon experiment, the believer’s Bayesian brain will almost certainly discount the explanation as propaganda. The press release will very possibly reinforce their belief that they don’t trust the government on this issue, and they’ll congratulate themselves on not being so gullible as to believe government lies. Beliefs cut both ways, so someone who doesn’t believe in UFOs will accept the explanation as fact, often without independent verification, and the information will reinforce their belief that they don’t trust UFO nuts. They’ll congratulate themselves on not being so gullible as to believe in UFOs.
Human culture and language have made it possible for the belief systems of one brain to be transferred into another. The process is neither perfectly accurate nor reliable, but it’s effective. Depending on the beliefs concerned and whoever is analysing the process, it goes by many names: education, brainwashing, bringing up the kids to be good people, the One True Religion. The brains of young children are malleable, and their ability to assess evidence is still developing: consider Santa Claus, the Tooth Fairy, and the Easter Bunny – though children are quite shrewd and many understand they have to play the game to get the reward. The Jesuit maxim ‘Give me a child until he is seven and I will give you the man’ has two possible meanings. One is that what you learn when you’re young lasts longest; the other is that brainwashing innocent children to accept a belief system fixes it in their minds throughout adult life. Both are likely true, and from some viewpoints they’re identical.
THE BAYESIAN BRAIN THEORY EMERGED from a variety of scientific areas: Bayesian statistics, obviously, but also machine intelligence and psychology. In the 1860s Hermann Helmholtz, a pioneer in the physics and psychology of human perception, suggested that the brain organises its perceptions by building probabilistic models of the external world. In 1983 Geoffrey Hinton, working in artificial intelligence, proposed that the human brain is a machine that makes decisions about the uncertainties it encounters when observing the outside world. In the 1990s this idea was turned into mathematical models based on probability theory, embodied in the notion of a Helmholtz machine. This isn’t a mechanical device, but a mathematical abstraction, comprising two related networks of mathematically modelled ‘neurons’. One, the recognition network, works from the bottom up; it’s trained on real data and represents them in terms of a set of hidden variables. The other, a top-down ‘generative’ network, generates values of those hidden variables and hence of the data. The training process uses a learning algorithm to modify the structure of the two networks so that they classify the data accurately. The two networks are modified alternately, a procedure known as a wake–sleep algorithm.
Similar structures with many more layers, referred to as ‘deep learning’, are currently achieving considerable success in artificial intelligence. Applications include the recognition of natural speech by a computer, and computer victories in the oriental board game Go. Computers had previously been used to prove that the board game draughts is always a draw with perfect play. IBM’s Deep Blue beat chess grandmaster and world champion Garry Kasparov in 1996, but lost the six-game series 4–2. After a major upgrade, it won the next series 3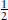 2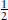. However, those programs used brute force algorithms rather than the artificial intelligence algorithms used to win at Go.
Go is an apparently simple game with endless depths of subtlety, invented in China over 2500 years ago, and played on a 19 × 19 grid. One player has white stones, the other black; they place their stones in turn, capturing any they surround. Whoever surrounds the most territory wins. Rigorous mathematical analysis is very limited. An algorithm devised by David Benson can determine when a chain of stones can’t be captured no matter what the other player does.66 Elwyn Berlekamp and David Wolfe have analysed the intricate mathematics of endgames, when much of the board is captured and the range of available moves is even more bewildering than usual.67 At that stage, the game has effectively split into a number of regions that scarcely interact with each other, and players have to decide which region to play in next. Their mathematical techniques associate a number, or a more esoteric structure, with each position, and provide rules for how to win by combining these values.
In 2015 the Google company DeepMind tested a Go-playing algorithm AlphaGo, based on two deep-learning networks: a value network that decides how favourable a board position is, and a policy network that chooses the next move. These networks were trained using a combination of games played by human experts, and games where the algorithm played against itself.68 AlphaGo then pitted its electronic wits against Lee Sedol, a top professional Go player, and beat him, four games to one. The programmers found out why it had lost one game and corrected its strategy. In 2017 AlphaGo beat Ke Jie, ranked number one in the world, in a three-game match. One interesting feature, showing that deep-learning algorithms need not function like a human brain, was AlphaGo’s style of play. It often did things that no human player would have considered – and won. Ke Jie remarked: ‘After humanity spent thousands of years improving our tactics, computers tell us that humans are completely wrong... I would go as far as to say not a single human has touched the edge of the truth of Go.’
There’s no logical reason why artificial intelligence should work in the same way as human intelligence: one reason for the adjective ‘artificial’. However, these mathematical structures, embodied in electronic circuits, bear some similarity to the cognitive models of the brain developed by neuroscientists. So a creative feedback loop between artificial intelligence and cognitive science has emerged, each borrowing ideas from the other. And it’s starting to look as though our brains and artificial ones do in fact work, sometimes and to some extent, by implementing similar structural principles. Down at the level of the materials they’re made from, and how their signalling processes function, they’re of course very different.
TO ILLUSTRATE THESE IDEAS IN A concrete setting, though with a more dynamic mathematical structure, consider visual illusions. Visual perception involves puzzling phenomena when ambiguous or incomplete information is presented to one or both eyes. Ambiguity is one type of uncertainty: we’re not sure exactly what we’re seeing. I’ll take a quick look at two distinct types.
The first type was discovered by Giambattista della Porta in 1593, and included in his De refractione (On Refraction), a treatise on optics. della Porta put one book in front of one eye, and another in front of the other. He reported that he could read from one book at a time, and he could change from one to the other by withdrawing the ‘visual virtue’ from one eye and moving it to the other. This effect is now called binocular rivalry. It occurs when two different images, presented one to each eye, lead to alternating percepts – what the brain believes it’s seeing – possibly of neither image separately.
Left: Necker cube. Right: Jastrow’s rabbit/duck.
The second type is illusions, or multistable figures. These occur when a single image, either static or moving, can be perceived in several ways. Standard examples are the Necker cube, introduced by the Swiss crystallographer Louis Necker in 1832, which appears to flip between two different orientations, and the rabbit/duck illusion invented by the American psychologist Joseph Jastrow in 1900, which flips between a not very convincing rabbit and an only slightly more convincing duck.69
A simple model of the perception of the Necker cube is a network with just two nodes. These represent neurons, or small networks of neurons, but the model is intended only for schematic purposes. One node corresponds to (and is assumed to have been trained to respond to) one perceived orientation of the cube, the other to the opposite orientation. These two nodes are linked to each other by inhibitory connections. This ‘winner-takes-all’ structure is important, because the inhibitory connections ensure that if one node is active, the other isn’t. So the network comes to an unambiguous decision at any given time. Another modelling assumption is that this decision is determined by whichever node is most active.
Initially both nodes are inactive. Then, when the eyes are shown the Necker cube image, the nodes receive inputs that trigger activity. However, the winner-takes-all structure means that both nodes can’t be active at the same time. In the mathematical model they take turns: first one is more active, then the other. Theoretically these alternatives repeat at regular intervals, which isn’t quite what’s observed. Subjects report similar changes of percept, but they occur at irregular intervals. The fluctuations are usually explained as random influences coming from the rest of the brain, but this is open to debate.
The same network also models binocular rivalry. Now the two nodes correspond to the two images shown to the subject: one to the left eye, the other to the right eye. People don’t perceive the two images superimposed on each other; instead, they alternate between seeing one of them and seeing the other. Again, this is what happens in the model, though with more regular timing of the switches between percepts.
If the mathematical model predicted only a switch between the two known possibilities, it wouldn’t be terribly interesting. But in slightly more complicated circumstances, analogous networks behave in more surprising ways. A classic example is the monkey/text experiment of Ilona Kovács and colleagues.70 A picture of a monkey (it looks suspiciously like a young orangutan, which is an ape, but everyone calls it a monkey) is cut into six pieces. A picture of blue text on a green background is cut into six similarly shaped pieces. Then three of the pieces in each image are swapped with the corresponding pieces in the other one to create two mixed images. These are then shown separately to the subject’s left and right eyes.
What do they see? Most report seeing the two mixed images, alternating. This makes good sense: it’s what happened with Porta’s two books. It’s as if one eye wins, then the other, and so on. But some subjects report alternation between a complete monkey image and complete text. There’s a handwaving explanation of that: their brain ‘knows’ what a complete monkey and complete text should look like, so it fits suitable pieces together. But since it’s seeing both mixtures, it still can’t decide which one it’s looking at, so it flips between them. However, this isn’t very satisfactory, and it doesn’t really explain why some subjects see one pair of images and others see a different pair.
A mathematical model sheds more light. It’s based on a network model for high-level decision-making in the brain, proposed by the neuroscientist Hugh Wilson. I’ll call models of this type Wilson networks. In its simplest form, an (untrained) Wilson network is a rectangular array of nodes. These can be thought of as model neurons, or populations of neurons, but for modelling purposes they need not be given any specific physiological interpretation. In the rivalry setting, each column of the array corresponds to an ‘attribute’ of the image presented to the eye: a feature such as colour or orientation. Each attribute has a range of alternatives: for example, colour could be red, blue, or green; orientation could be vertical, horizontal, or diagonal. These discrete possibilities are the ‘levels’ of that attribute. Each level corresponds to a node in that attribute column.
If the first two ‘mixed’ images are shown to each eye separately, some subjects see alternation between the last two complete images.
Any specific image can be viewed as a combination of choices of levels, one for each relevant attribute. A red horizontal image combines the ‘red’ level of the colour column with the ‘horizontal’ level of the orientation column, for instance. The architecture of a Wilson network is designed to detect patterns by responding more strongly to ‘learned’ combinations of specific levels, one for each attribute. In each column, all pairs of distinct nodes are connected to each other by inhibitory couplings. Without further input or modification, this structure creates a winner-takes-all dynamic in the column, so that usually only one node is dynamically the most active. The column then detects the corresponding level of its attribute. Training by the images presented to the eyes is modelled by adding excitatory connections between the nodes corresponding to the appropriate combination of levels. In a rivalry model, such connections are added for both images.
Casey Diekman and Martin Golubitsky have shown that a Wilson network model of rivalry can sometimes have unexpected implications.71 For the monkey/text experiment, the dynamics of the network predicts that it can oscillate in two distinct ways. As we’d expect, it can alternate between the two learned patterns – the mixed images shown to the eye. But it can also alternate between a complete monkey and complete text. Which pair occurs depends on the connection strengths, suggesting that the difference between subjects is related to how strongly or weakly the corresponding populations of neurons are connected in the subject’s brain. It’s striking that the simplest Wilson network representing the experiment predicts exactly what’s observed in experiments.
Left: Untrained Wilson network with five attributes, each having three levels. Dashed lines are inhibitory connections. Right: A pattern (shaded level for each attribute) is represented by excitatory connections (solid arrows) between those nodes. Adding these connections to the original network trains it to recognise that pattern.
WILSON NETWORKS ARE SCHEMATIC MATHEMATICAL models, intended to shed light on how simple dynamic networks can in principle make decisions based on information received from the outside world. More strongly, some regions in the brain have a very similar structure to a Wilson network, and they seem to make their decisions in much the same way. The visual cortex, which processes signals from the eyes to decide what we’re looking at, is a case in point.
Human vision doesn’t work like a camera, whatever the school textbooks say. To be fair, the way the eye detects images is rather like a camera, with a lens that focuses incoming light on to the retina at the back. The retina is more like a charge-coupled device in a modern digital camera than an old-fashioned film. It has a large number of discrete receptors, called rods and cones: special light-sensitive neurons that respond to incoming light. There are three types of cone, and each is more sensitive to light in a specific range of wavelengths, that is, light of (roughly) a specific colour. The colours, in general terms, are red, green, and blue. Rods respond to low light levels. They respond most strongly to light around the ‘light blue’ or cyan wavelengths, but our visual system interprets these signals as shades of grey, which is why we don’t see much colour at night.
Where human vision starts to differ significantly from a camera is what happens next. These incoming signals are transmitted along the optic nerves to a region of the brain called the visual cortex. The cortex can be thought of as a series of thin layers of neurons, and its job is to process the patterns of signals received from the eyes so that other regions of the brain can identify what they’re seeing. Each layer responds dynamically to the incoming signals, much as a Wilson network responds to a Necker cube or the monkey/text pair of images. Those responses are transmitted down to the next layer, whose structure causes it to respond to different features, and so on. Signals also pass from the deeper layers to the surface ones, affecting how they respond to the next batch of signals. Eventually somewhere along this cascade of signals, something decides ‘it’s granny’, or whatever. It might perhaps be one specific neuron, often referred to as a grandmother cell, or it might do this in a more sophisticated way. We don’t yet know. Once the brain has recognised granny, it can pull up other information from other regions, such as ‘help her off with her coat’, or ‘she always likes a cup of tea when she arrives’, or ‘she’s looking a bit worried today’.
Cameras, when hooked up to computers, are starting to perform some tasks like this too, such as using facial recognition algorithms to tag your photos with the names of the people in them. So although the visual system isn’t like a camera, a camera is becoming more and more like the visual system.
Neuroscientists have studied the wiring diagram of the visual cortex in some detail, and new methods of detecting connections in the brain will doubtless lead to an explosion of more refined results. Using special dyes that are sensitive to electrical voltages, they’ve mapped out the general nature of connections in the top layer V1 of the visual cortex in animals. Roughly speaking, V1 detects segments of straight lines in whatever the eyes are looking at, and it also works out in which direction the lines point. This is important for finding the boundaries of objects. It turns out that V1 is structured much like a Wilson network that has been trained using straight lines in various orientations. Each column in the network corresponds to a ‘hypercolumn’ in V1, whose attribute is ‘direction of a line seen at this location’. The levels of that attribute are a coarse-grained set of directions that the line might point in.
The really clever part is the analogue of the learned patterns in a Wilson network. In V1, these patterns are longer straight lines, crossing the visual fields of many hypercolumns. Suppose a single hypercolumn detects a short piece of line somewhere at an angle of 60°, so the neuron for this ‘level’ fires. It then sends excitatory signals to neurons in neighbouring hypercolumns, but only to those at the same 60° level. Moreover, these connections link only to those hypercolumns that lie along the continuation of that line segment in V1. It’s not quite that precise, and there are other weaker connections, but the strongest ones are pretty close to what I’ve described. The architecture of V1 predisposes it to detect straight lines and the direction in which they point. If it sees a piece of such a line, it ‘assumes’ that line will continue, so it fills in gaps. But it doesn’t do this slavishly. If sufficiently strong signals from other hypercolumns contradict this assumption, they win instead. At a corner, say, where two edges of an object meet, the directions conflict. Send that information to the next layer down and you now have a system to detect corners as well as lines. Eventually, somewhere along this cascade of data, your brain recognises granny.
A FORM OF UNCERTAINTY THAT most of us have experienced at some point is: ‘Where am I?’ Neuroscientists Edvard and May-Britt Moser and their students discovered in 2005 that rat brains have special neurons, known as grid cells, that model their location in space. Grid cells live in a part of the brain whose name is a bit of a mouthful: the dorsocaudal medial entorhinal cortex. It’s a central processing unit for location and memory. Like the visual cortex, it has a layered structure, but the pattern of firing differs from layer to layer.
The scientists placed electrodes in the brains of rats and then let them run around freely in an open space. When a rat was moving, they monitored which cells in its brain fired. It turned out that particular cells fire whenever the rat is in one of a number of tiny patches of the space (‘firing fields’). These patches form a hexagonal grid. The researchers deduced that these nerve cells constitute a mental representation of space, a cognitive map that provides a kind of coordinate system, telling the rat’s brain where the animal is. The activity of grid cells is updated continuously as the animal moves. Some cells fire whichever direction the rat is heading in; others depend on the direction and are therefore responsive to it.
We don’t yet understand exactly how grid cells tell the rat where it is. Curiously, the geometric arrangement of the grid cells in its brain is irregular. Somehow, these layers of grid cells ‘compute’ the rat’s location by integrating tiny movements as it wanders around. Mathematically, this process can be realised using vector calculations, in which the position of a moving object is determined by adding together lots of small changes, each with its own magnitude and direction. It’s basically how sailors navigated by ‘dead reckoning’ before better navigational instruments were devised.
We know the network of grid cells can function without any visual input, because the firing patterns remain unchanged even in total darkness. However, it also responds quite strongly to any visual input. For example, suppose the rat runs inside a cylindrical enclosure, and there’s a card on the wall to act as a reference point. Choose a particular grid neuron, and measure its grid of spatial patches. Then rotate the cylinder and repeat: the grid rotates through the same amount. The grids and their spacings don’t change when the rat is placed in a new environment. However the grid cells compute location, the system is very robust.
In 2018 Andrea Banino and coworkers reported using deep-learning networks to carry out a similar navigational task. Their network had lots of feedback loops, because navigation seems to depend on using the output of one processing step as the input for the next – in effect a discrete dynamical system with the network as the function being iterated. They trained the network using recorded patterns of the paths that various rodents (such as rats and mice) had used when foraging, and provided it with the kind of information that the rest of the brain might send to grid neurons.
The network learned to navigate effectively in a variety of environments, and it could be transferred to a new environment without losing performance. The team tested its abilities by giving it specific goals, and in a more advanced setting by running it (in simulation, since the entire set-up is inside a computer) through mazes. They assessed its performance for statistical significance using Bayesian methods, fitting the data to mixtures of three distinct normal distributions.
One remarkable result was that as the learning process progressed, one of the middle layers of the deep-learning network developed similar patterns of activity to those observed in grid neurons, becoming active when the animal was in some member of a grid of spatial patches. Detailed mathematical analysis of the structure of the network suggested that it was simulating vector calculations. There’s no reason to suppose it was doing that the way a mathematician would, writing down the vectors and adding them together. Nonetheless, their results support the theory that grid cells are critical for vector-based navigation.
MORE GENERALLY, THE CIRCUITS THAT the brain uses to understand the outside world are to some extent modelled on the outside world. The structure of the brain has evolved over hundreds of thousands of years, ‘wiring in’ information about our environment. It also changes over much shorter periods as we learn. Learning ‘fine tunes’ the wired-in structures. What we learn is conditioned by what we’re taught. So if we’re taught certain beliefs from a very early age, they tend to become wired into our brains. This can be seen as a neuroscientific verification of the Jesuit maxim mentioned earlier.
Our cultural beliefs, then, are strongly conditioned by the culture we grow up in. We identify our place in the world and our relations to those around us by which hymns we know, which football teams we support, what music we play. Any ‘beliefs’ encoded in our brain wiring that are common to most people, or which can be debated rationally in terms of evidence, are less contentious. But the beliefs we hold that don’t have such support can be problematic unless we recognise the difference. Unfortunately those beliefs play an important role in our culture, which is one reason they exist at all. Beliefs based on faith, not evidence, are very effective for distinguishing Us from Them. Yes we all ‘believe’ that 2 + 2 = 4, so that doesn’t make me any different from you. But do you pray to the cat-goddess every Wednesday? I thought not. You’re not One of Us.
This worked quite well when we lived in small groups, because nearly everyone we met did pray to the cat-goddess, and it was a good idea to be warned if not. But even when extended to tribes it became a source of friction, often leading to violence. In today’s connected world, it’s becoming a major disaster.
Today’s populist politics has given us a new phrase for what used to be called ‘lies’ or ‘propaganda’. Namely, Fake News. It’s getting increasingly difficult to distinguish real news from fake. Vast computing power is placed in the hands of anyone with a few hundred dollars to spare. The widespread availability of sophisticated software democratises the planet, which in principle is good, but it often compounds the problem of differentiating truth from lies.
Because users can tailor what kind of information they see so that it reinforces their own preferences, it’s increasingly easy to live in an information bubble, where the only news you get is what you want to be told. China Miéville parodied this tendency by taking it to extremes in The City & the City, a science-fiction/crime mash-up in which Inspector Borlú, a detective in the Extreme Crime Squad of the city of Besźel, is investigating a murder. He makes repeated visits to its twin city of Ul Qoma to work with the police there, crossing the border between them. At first, the picture you get is rather like Berlin before the wall came down, divided into East and West, but you slowly come to realise that the two halves of the city occupy the same geographical space. Citizens of each are trained from birth not to notice the other, even as they walk among its buildings and people. Today, many of us are doing the same on the internet, wallowing in confirmation bias, so that all of the information we receive reinforces the view that we’re right.
Why are we so easily manipulated by fake news? It’s that age-old Bayesian brain, running on embodied beliefs. Our beliefs aren’t like files in a computer, which can be deleted or replaced at the twitch of a mouse. They’re more like the hardware, wired in. Changing wired-in patterns is hard. The more strongly we believe, or even just want to believe, the harder it gets. Each item of fake news that we believe, because it suits us to, reinforces the strength of those wired-in connections. Each item that we don’t want to believe is ignored.
I don’t know a good way to prevent this. Education? What happens if a child goes to a special school that promotes a particular set of beliefs? What happens when it’s forbidden to teach subjects whose factual status is clear, but which contradict beliefs? Science is the best route humanity has yet devised for sorting fact from fiction, but what happens if a government decides to deal with inconvenient facts by cutting funding for research on them? Federal funding for research on the effects of gun ownership is already illegal in the USA, and the Trump administration is considering doing the same for climate change.
It won’t go away, guys.
One suggestion is that we need new gatekeepers. But an atheist’s trusted website is anathema to a true believer, and vice versa. What happens if an evil corporation gets control of a website we trust? As always, this isn’t a new problem. As the Roman poet Juvenal wrote in his Satires around 100 AD, Quis custodiet ipsos custodes? Who will guard the guards themselves? But the problem today is worse, because a single tweet can span the entire planet.
Perhaps I’m too pessimistic. On the whole, better education makes people more rational. But our Bayesian brains, whose quick-and-dirty survival algorithms served us so well when we lived in caves and trees, may no longer be fit for purpose in the misinformation age.
