I have seen men, ardently desirous of having a son, who could learn only with anxiety of the births of boys in the month when they expected to become fathers. Imagining that the ratio of these births to those of girls ought to be the same at the end of each month they judged that the boys already born would render more probable the births next of girls.
Pierre-Simon de Laplace, A Philosophical Essay on Probabilities
HUMAN INTUITION FOR PROBABILITY IS hopeless.
When we’re asked to give a rapid estimate of the odds of chance events, we often get them completely wrong. We can train ourselves to improve, as professional gamblers and mathematicians have done, but that takes time and effort. When we make a snap judgement of how probable something is, likely as not we get it wrong.
I suggested in Chapter 2 that this happens because evolution favours ‘quick and dirty’ methods when a more reasoned response could be dangerous. Evolution prefers false positives to false negatives. When the choice is between a half-hidden brown thing being either a leopard or a rock, even a single false negative can prove deadly.
Classic probability paradoxes (in the sense of ‘giving a surprising result’, rather than self-contradictory logic) support this view. Consider the birthday paradox: how many people have to be in a room before it becomes more likely than not that two of them have the same birthday? Assume 365 days in the year (no 29 February dates), and all of them equally likely (which isn’t quite true, but hey). Unless people have come across this one before, they go for quite large numbers: 100, perhaps, or 180 on the grounds that this is roughly half of 365. The correct answer is 23. If you want to know why, I’ve put the reasoning in the Notes at the back.18 If the distribution of births isn’t uniform, the answer can be smaller than 23, but not larger.19
Here’s another puzzle that people often find confusing. The Smiths have exactly two children, and at least one is a girl. Assume for simplicity that boys and girls are equally likely (actually boys are slightly more likely, but this is a puzzle, not a scholarly paper on demography) and that children are one or the other (gender and unusual chromosome issues ignored). Assume also that the sexes of the children are independent random variables (true for most couples but not all). What is the probability that the Smiths have two girls? No, it’s not 1/2. It’s 1/3.
Now suppose that the elder child is a girl. What is the probability that they have two girls? This time, it really is 1/2.
Finally, suppose that at least one is a girl born on a Tuesday. What is the probability that they have two girls? (Assume all days of the week are equally likely – also not true in reality, but not too far off.) I’ll leave that one for you to think about for a while.
The rest of this chapter examines some other examples of paradoxical conclusions and faulty reasoning in probability. I’ve included some old favourites, and some less well-known examples. Their main purposes is to drive home the message that when it comes to uncertainty, we need to think very carefully and not make snap judgements. Even when effective methods exist to deal with uncertainties, we have to be aware that they can mislead us if misused. The key concept here, conditional probability, is a running theme in the book.
A COMMON ERROR, WHEN FACED with a choice between two alternatives, is to make the natural default human assumption that the chances are even – fifty-fifty. We talk blithely of events being ‘random’, but we seldom examine what that means. We often equate it with things being just as likely to happen as not: fifty-fifty odds. Like tossing a fair coin. I made just this assumption at the end of the second paragraph of this chapter, when I wrote: ‘likely as not’. Actually, what’s likely, and what’s not, seldom occur with equal probabilities. If you think about what the words in the phrase mean, this becomes obvious. ‘Not likely’ means low probability, ‘likely’ means higher. So even our standard phrase is confused.
Those time-honoured probability puzzles show that getting it wrong can be a lot more likely than not. In Chapter 8 we’ll see that our poor understanding of probabilities can lead us astray when it really matters, such as deciding guilt or innocence in a court of law.
Here’s a clear-cut case where we can do the sums. If you’re presented with two cards lying on a table and are told (truthfully!) that one is the ace of spades, and the other isn’t, it seems obvious that your chance of picking the ace of spades is 1/2. That’s true for that scenario. But in very similar situations, the default fifty-fifty assumption that evolution has wired into our brains is completely wrong. The classic example is the Monty Hall problem, much beloved of probability theorists. It’s almost a cliché nowadays, but some aspects often get overlooked. Additionally, it’s a perfect route into the counterintuitive territory of conditional probability, which is where we’re heading. This is the probability of some event occurring, given that some other event has already happened. And it’s fair to say that when it comes to conditional probabilities, the default assumptions that evolution has equipped our brains with are woefully inadequate.
Monty Hall was the original host of the American TV game show Let’s Make a Deal. In 1975 the biostatistician Steve Selvin published a paper on a version of the show’s strategy; it was popularised (amid huge and largely misplaced controversy) by Marilyn vos Savant in her column in Parade magazine in 1990. The puzzle goes like this. You’re presented with three closed doors. One conceals the star prize of a Ferrari; each of the others conceals the booby prize of a goat. You choose one door; when it’s opened you’ll win whatever is behind it. However, the host (who knows where the car is) then opens one of the other two doors, which he knows reveals a goat, and offers you the opportunity to change your mind. Assuming you prefer a Ferrari to a goat, what should you do?
This question is an exercise in modelling as well as in probability theory. A lot depends on whether the host always offers such a choice. Let’s start with the simplest case: he always does, and everyone knows that. If so, you double your chances of winning the car if you switch.
This statement immediately conflicts with our default fifty-fifty brain. You’re now looking at two doors. One hides a goat; the other a car. The odds must surely be fifty-fifty. However, they’re not, because what the host did is conditional on which door you chose. Specifically, he didn’t open that door. The probability that a door hides the car, given that it’s the one you chose, is 1/3. That’s because you chose from three doors, and the car is equally likely to be behind each of them because you had a free choice. In the long run, your choice will win the car one time in three – so it will not win the car two times in three.
Since another door has been eliminated, the conditional probability that the car is behind a door, given that this is not the one you chose, is 1 – 1/3 = 2/3, because there’s only one such door, and we’ve just seen that two times out of three your door is the wrong one. Therefore, two times out of three, changing to the other door wins the car. That’s what Steve said, it’s what Marilyn said, and a lot of her correspondents didn’t believe it. But it’s true, with the stated conditions on what the host does.
If you’re sceptical, read on.
One psychological quirk is fascinating: people who argue that the odds must be fifty-fifty (so either door is equally likely to win the car) generally prefer not to change their minds, even though fifty-fifty odds imply that swapping won’t do any harm. I suspect this is related to the modelling aspect of the problem, which involves the sneaking suspicion – very possibly correct – that the host is out to fool you. Or maybe it’s the Bayesian brain, believing it’s being fooled.
If we abandon the condition that the host always offers you the opportunity to change your mind, the calculation changes completely. At one extreme, suppose the host offers you the opportunity to change doors only when your choice would win the car. Conditional on him offering that choice, your door wins with probability 1, and the other one wins with probability 0. At the other extreme, if the host offers you the opportunity to change doors only when your choice would not win the car, the conditional probabilities are the other way round. It seems plausible that if the host mixes up these two situations in suitable proportions, your chance of winning by staying with your original choice can be anything, and so can your chance of losing. Calculations show that this conclusion is correct.
Another way to see that fifty-fifty can’t be right is to generalise the problem and consider a more extreme example. A stage magician spreads out a pack of cards face down (an ordinary pack with 52 different cards, nothing rigged) and offers you a prize if you can pick the ace of spades. You choose a card and slide it out, still face down. The magician picks up the other 51 cards, looks at them all while hiding them from you, and starts placing them face up on the table, none being the ace of spades. He keeps going for some time, then puts one card face down next to yours, then resumes placing cards that aren’t the ace of spades face up until the whole pack has been dealt with. Now there are 50 cards face up, none the ace of spades, and two face down: the one you chose initially, and the one he placed next to it.
Assuming he didn’t cheat – which is perhaps silly if he’s a stage magician, but I assure you that on this occasion he didn’t – which card is more likely to be the ace of spades? Are they equally likely? Hardly. Your card was chosen at random from the 52 in the pack, so it will be the ace of spades one time out of 52. The ace of spades will be in the rest of the pack 51 times out of 52. If it is, the magician’s card must be the ace of spades. On the rare occasion that it’s not – one time out of 52 – your card is the ace of spades, and the magician’s card is whatever was left after he discarded 50 cards. So the probability your card is the ace of spades is 1/52; the probability the magician’s card is the ace of spades is 51/52.
The fifty-fifty scenario does arise, however, under suitable conditions. If someone who has not seen what has transpired is brought on stage, shown those two cards, and asked to pick which of them is the ace of spades, their chance of succeeding is 1/2. The difference is that you chose your card at the start of the proceedings, and what the magician did was conditional on that choice. The newcomer turns up after the process is complete, so the magician can’t do anything conditional on their choice.
To drive the point home, suppose we repeat the procedure but this time you turn your card face up before the magician starts discarding cards. If your card isn’t the ace of spades, his card has to be (again assuming no sleight of hand). And this happens 51 times out of 52 in the long run. If your card is the ace of spades, then his can’t be; this happens one time out of 52 in the long run.
The same argument works with the car and goats if you open the door you chose. One time in three you’ll see the car. The other two times, you’ll see two open doors with goats and one closed door. Where do you think the car is?
BACK TO THE SMITHS AND their children, a simpler puzzle but just as deceptive. Recall the two versions:
1 The Smiths have exactly two children, and you’re told that at least one is a girl. Assuming boys and girls are equally likely, along with the other conditions I mentioned, what is the probability that they have two girls?
2 Now suppose you’re told that the elder child is a girl. What is the probability that they have two girls?
The default reaction to the first question is to think: ‘One is a girl. The other one is equally likely to be a boy or a girl.’ That leads to the answer 1/2. The flaw is that they might have two girls (after all, that’s the event whose chances we’re being asked to estimate), in which case ‘the other one’ isn’t uniquely defined. Think of the two births happening in order (even with twins, one is born first). The possibilities are
GG GB BG BB
We assumed the sex of the second child is independent of that of the first, so these four possibilities are equally likely. If all cases can occur, each has probability 1/4. However, the extra information rules out BB. We’re left with three cases, and they’re still equally likely. Only one of them is GG, so the probability of that is 1/3.
It looks as though the probabilities here have changed. Initially, GG has probability 1/4; suddenly it’s 1/3. How come?
What’s changed is the context. These puzzles are all about the appropriate sample spaces. The extra information ‘not BB’ cuts the sample space down from four possibilities to three. The real-world sample space now consists not of all families with two children, but of families with two children, not both boys. The corresponding model sample space consists of GG, GB, BG. These are all equally likely, so their probability in that sample space is 1/3, not 1/4. BB is irrelevant because in this case it can’t occur.
It’s not paradoxical that extra information changes the relevant probabilities. If you’re betting on Galloping Girolamo, and you get a hot tip that the favourite Barnstorming Bernoulli has some mystery illness that slows it down, your chance of winning has definitely increased.
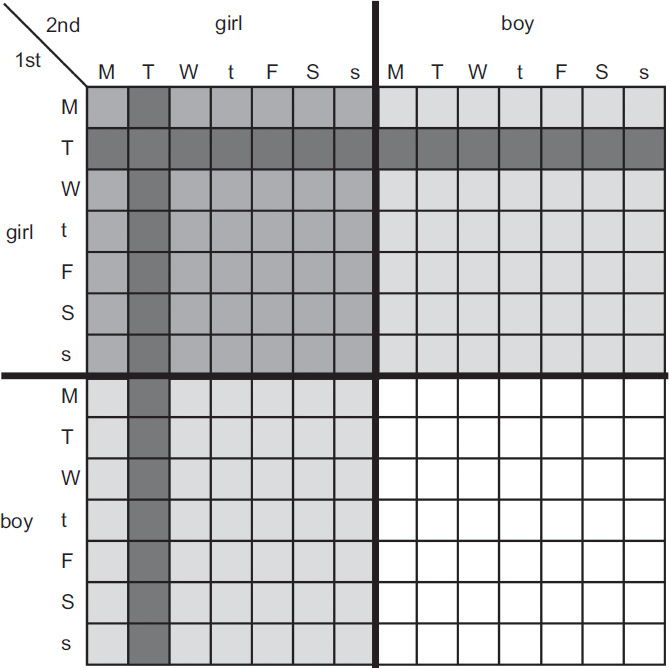
Sample spaces for the Tuesday girl. Grey shading: ‘at least one girl’. Medium grey shading: ‘both are girls’. Dark grey shading: ‘at least one girl born on Tuesday’.
This puzzle is another example of conditional probability. Mathematically, the way to calculate a conditional probability is to cut the sample space down by including only the events that still might occur. In order to make the total probability for the smaller sample space equal to 1, the previous probabilities must all be multiplied by a suitable constant. We’ll see which constant shortly.
In the third version of the puzzle, we know that at least one child is a girl born on a Tuesday. As before, the question is: What is the probability that the Smiths have two girls? I’ll call this the target event. The probability we want is the chance that the Smiths hit the target. As I said, we’ll assume all days of the week are equally likely, to keep the account simple.
At first sight, the new information seems irrelevant. What does it matter which day she’s born on? They’re all equally likely! But before leaping to conclusions, let’s look at the appropriate sample spaces. The picture shows all possible combinations of sex and day for both the first and second child. This is the full sample space, and each of its 196 squares (14 × 14) is equally likely, probability 1/196. The top left-hand quadrant, shaded light grey except where overlapped by a dark square, contains 49 squares. This corresponds to the event ‘both are girls’; the probability of that on its own is 49/196 = 1/4, as expected.
The new information ‘at least one is a girl born on a Tuesday’ cuts the sample space down to the two dark stripes. In total these contain 27 squares: 14 horizontal, plus 14 vertical, minus 1 for the overlap because we mustn’t count the same event twice. In our new cut-down sample space, these events are still all equally likely, so the conditional probability of each is 1/27. Count how many dark squares lie in the ‘both girls’ target region: the answer is 13 (7 + 7, minus 1 for the overlap). The other 14 lie in regions where the Smiths have at least one boy, so they miss the target. All small squares are equally likely, so the conditional probability that the Smiths have two girls, given that at least one is a girl born on Tuesday, is 13/27.
The birth day does matter!
I doubt anyone would be likely to guess this answer, except by sheer accident, unless they’re a statistician who’s good at mental arithmetic. You have to do the sums.
However, if instead we’d been told that at least one child is a girl born on Wednesday, or Friday, we’d have got the same conditional probability, using different stripes in the picture. In that sense, the day doesn’t matter. So what’s going on?
Sometimes telling people a counterintuitive piece of mathematics leads them to conclude that the mathematics is useless, not to embrace its surprising power. There’s a danger of this occurring here, because some people instinctively reject this answer. It just doesn’t make sense to them that the day she’s born can change the probabilities. The calculation alone doesn’t help much if you feel that way; you strongly suspect that there’s a mistake. So some kind of intuitive explanation is needed to reinforce the sums.
The underlying error in the reasoning ‘the day she’s born can’t change anything’ is subtle but crucial. The choice of day is irrelevant, but picking some specific day does matter, because there might not be a specific she. For all we know – indeed, this is the point of the puzzle – the Smiths might have two girls. If so, we know that one of them is born on Tuesday, but not which one. The two simpler puzzles show that extra information that improves the chance of distinguishing between the two children, such as which one is born first, changes the conditional probability of two girls. If the elder is a girl, that probability is what we expect: 1/2. (The same would also be true if the younger were a girl.) But if we don’t know which child is the girl, the conditional probability decreases to 1/3.
These two simpler puzzles illustrate the importance of extra information, but the precise effect isn’t terribly intuitive. In the current version, it’s not clear that the extra information does distinguish the children: we don’t know which child was born on Tuesday. To see what happens, we count squares in the diagram.
The grid has three grey quadrants corresponding to ‘at least one girl’. The medium-grey quadrant corresponds to ‘both are girls’, the pale-grey quadrants to ‘the elder is a girl’ and ‘the younger is a girl’, and the white quadrant corresponds to ‘both are boys’. Each quadrant contains 49 smaller squares.
The information ‘at least one girl’ eliminates the white quadrant. If that’s all we know, the target event ‘both girls’ occupies 49 squares out of 147, a probability of 49/147 = 1/3. However, if we have the extra information ‘the elder is a girl’ then the sample space comprises only the top two quadrants, with 98 squares. Now the target event has probability 49/98 = 1/2. These are the numbers I got before.
In these cases, the extra information increases the conditional probability of two girls. It does so because it reduces the sample space, but also because the extra information is consistent with the target event. This is the medium-grey region, and it lies inside both of the cut-down sample spaces. So the proportion of the sample space that it occupies goes up when the size of the sample space goes down.
The proportion can also go down. If the extra information was ‘the elder child is a boy’, the sample space becomes the bottom two quadrants, and the entire target event has been eliminated: its conditional probability decreases to 0. But whenever the extra information is consistent with the target event, it makes that event more likely, as measured by conditional probability.
The more specific the extra information is, the smaller the sample space becomes. However, depending on what that information is, it can also reduce the size of the target event. The outcome is decided by the interplay between these two effects: the first increases the conditional probability of the target, but the second decreases it. The general rule is simple:

In the complicated version of the puzzle, the new information is ‘at least one child is a girl born on Tuesday’. This is neither consistent with the target event nor inconsistent. Some dark-grey regions are in the top left quadrant, some are not. So we have to do the sums. The sample space is cut down to 27 squares, of which 13 hit the target and the other 14 don’t. The overall effect is a conditional probability of 13/27, which is a good bit smaller than the 1/3 that we get without the extra information.
Let’s check this result is consistent with the rule I just stated. ‘Extra information’ occurs in 27 squares out of 196, probability 27/196. ‘Hitting target and agreeing with information’ occurs in 13 squares out of 196, probability 13/196. My rule says that the conditional probability we want is
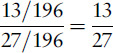
which is what we got by square counting. The 196s cancel, so the rule just expresses the square-counting procedure in terms of probabilities defined on the full sample space.
Notice that 13/27 is close to 1/2, which is what we would have got if we’d been told that the elder child is a girl. And this brings me back to the main point, and the reason why the conditional probability changes. Because it’s possible for both children to be girls, it makes a big difference whether what we know is likely to distinguish between them. This is why ‘one is a girl born on Tuesday’ matters: the ambiguity when this information is true of both children has less effect. Why? Because even when the other child is a girl too, most of the time she will be born on a different day. Only 1/7 of the time is she born the same day. As we increase the chance of distinguishing between the two children, we move away from the 1/3 case (no distinction) to the 1/2 (we know exactly which one we’re talking about).
The reason the answer here isn’t exactly 1/2 is that in the target region, the two dark stripes, each with 7 squares, overlap by one square. Outside the target, the other two stripes don’t overlap. So we get 13 stripes inside, 14 outside. The smaller this overlap, the closer the conditional probability gets to 1/2.
So here’s a final version of the puzzle for you. All conditions as before, except that instead of the day of the week, we’re told that one child is a girl, born on Christmas day. Assume all days of the year are equally likely (as always, not true in the real world) and that 29 February never happens (ditto). What is the conditional probability that both children are girls?
Would you believe 729/1459? See the Notes for the sums.20
Is this kind of hair-splitting about conditional probabilities important? In puzzles, no, unless you’re a puzzle fan. In the real world, it can literally be a matter of life and death. We’ll see why in Chapters 8 and 12.
IN EVERYDAY LANGUAGE, PEOPLE OFTEN talk of the ‘law of averages’. This phrase may have arisen as a simplified statement of Bernoulli’s law of large numbers, but in everyday usage it amounts to a dangerous fallacy, which is why you won’t find mathematicians or statisticians using it. Let’s see what’s involved, and why they don’t like it.
Suppose you toss a fair coin repeatedly, and keep a running count of how many times H and T turn up. There’s a definite possibility of random fluctuations, so that at some stage the cumulative totals might give different numbers of heads and tails – say 50 more Hs than Ts. Part of the intuition behind the law of averages is that such an excess of heads ought to disappear if you keep going. That’s correct, if suitably interpreted, but even so the situation is delicate. The mistake is to imagine that this excess of heads makes tails become more likely. However, it’s not totally unreasonable to imagine that they must; after all, how else can the proportions eventually balance out?
This kind of belief is encouraged by tables showing how often any particular number has come up in a lottery. Data for the UK’s National Lottery can be found online. They’re complicated by a change that increased the range of numbers that might be drawn. Between November 1994 and October 2015, when there were 49 numbers, the lottery machine spat out a ball bearing the number 12 on 252 occasions, whereas 13 turned up only 215 times. That was the least frequent number, in fact. The most frequent was 23, which was drawn 282 times. These results are open to many interpretations. Are the lottery machines unfair, so that some numbers are more likely to occur than others? Does 13 come up less often because, as we all know, it’s unlucky? Or should we bet on 13 in future because it’s got behind, and the law of averages says it has to catch up?
It’s mildly curious that the worst number is 13, but whoever writes the script for the universe has a habit of using clichés. As it happens, 20 was also drawn 215 times, and I don’t know of any superstitions about that number. Statistical analyses, based on Bernoulli’s original principles, show that fluctuations of this magnitude are to be expected when the machines draw each number with equal probability. So there’s no scientific reason to conclude that the machines aren’t fair. Moreover, it’s hard to see how the machine can ‘know’ what number is written on any particular ball, in the sense that the numbers don’t influence the mechanics. The simple and obvious probability model of 49 equally likely numbers is almost certainly applicable, and the probability of 13 being drawn in the future is not influenced by what’s happened in the past. It’s no more or less likely than any other number, even if it’s been a bit neglected.
The same goes for coins, for the same reason: if the coin is fair, a temporary excess of heads does not make tails become more likely. The probability of heads or tails is still 1/2. Above, I asked a rhetorical question: How else can the proportions balance out? The answer is that there’s another way that can happen. Although an excess of heads has no effect on the subsequent probability of getting a tail, the law of large numbers implies that in the long term, the numbers of heads and tails do tend to even out. But it doesn’t imply they have to become equal; just that their ratio gets closer to 1.
Suppose that initially we tossed 1000 times, getting 525 heads and 475 tails: an excess of 50 heads, and a ratio of 525/475 = 1·105. Now suppose we toss the coin another two million times. On average we expect about one million heads and an equal number of tails. Suppose this happens, exactly. Now the cumulative scores are 1,000,525 heads and 1,000,475 tails. There are still 50 more heads. However, the ratio is now 1,000,525/1,000,475, which is 1·00005. This is much closer to 1.
AT THIS POINT, I’M FORCED to admit that probability theory tells us something stronger, and it sounds just like what people think of as the law of averages. Namely, whatever the initial imbalance may be, if you keep tossing for long enough then the probability that at some stage tails will catch up, and give exactly the same number as heads, is 1. Essentially, this is certain, but since we’re talking of a potentially infinite process it’s better to say ‘almost certain’. Even if heads get a million throws ahead, tails will almost certainly catch up. You just have to keep tossing for long enough – though it will be very long indeed.
Mathematicians often visualise this process as a random walk. Imagine a pointer moving along the number line (positive and negative integers in order), starting at 0. At each toss of the coin, move it one step to the right if it’s heads, one step to the left if it’s tails. Then the position at any stage tells us the excess of Hs over Ts. For instance, if the tosses start HH it ends up two steps to the right at the number 2; if it’s HT it goes one step right, one left, and ends up back at 0. If we graph the number it sits on against time, so left/right becomes down/up, we get a random-looking zigzag curve. For instance, the sequence
TTTTHTHHHHHHTTTHTTTH
(which I got by actually tossing a coin) gives the picture shown. There are 11 Ts and 9 Hs.
The mathematics of random walks tells us that the probability that the pointer never returns to zero is 0. Therefore the probability that eventually the numbers even out again is 1 – almost certain. But the theory also tells us some more surprising things. First, these statements are true even if we give H or T a big head start. Whatever the initial imbalance may be, it will almost certainly disappear if we keep tossing. However, the average time required for this to happen is infinite. That may seem paradoxical, but what it means is this. If we wait for the first return to 0, it takes some particular time. Keep going. Eventually it almost certainly makes a second return. This might take fewer steps than the first one, or it might take more. Every so often, it’s a lot longer; indeed, if you choose any very large number you want, then almost certainly some return will take at least that long. If you average infinitely many arbitrarily large numbers, it’s reasonable that you can get an infinite average.
First 20 steps of a typical random walk.
This habit of repeatedly returning to 0 looks as if it conflicts with my statement that a coin has no memory. However, it doesn’t. The reason is that despite everything I’ve said, there’s also a sense in which coin tosses do not tend to even out in the long run. We’ve seen that the cumulative total is almost certain to be as large (negative or positive) as we wish, if we wait long enough. By the same token, it must eventually cancel out any initial imbalance.
Anyway, back to that tendency to even out if we wait long enough. Doesn’t that prove the law of averages? No, because random walk theory has no implications for the probability of H or T turning up. Yes, they even out ‘in the long run’ – but we have no idea exactly how long that will be in any particular instance. If we stop at that precise moment, it looks like the law of averages is true. But that’s cheating: we stopped when we reached the result we wanted. Most of the time, the proportions weren’t in balance. If we specify a fixed number of tosses in advance, there’s no reason for heads and tails to even out after that number. In fact, on average, after any specific number of tosses, the discrepancy will be exactly the same as it was at the beginning.