 The probability that a woman with breast cancer has a positive mammography
The probability that a woman with breast cancer has a positive mammographyA natural death is where you die by yourself without a doctor’s help. Unknown schoolboy, Examination script
IN 1957 A NEW WONDER DRUG became available in Germany. You could get it without a doctor’s prescription. Initially it was sold as a cure for anxiety, but later it was recommended to counteract nausea in pregnant women. Its proprietary name was Contergan, but the generic term is thalidomide. After a time, doctors noticed a big increase in the number of babies born with phocomelia – partially formed limbs, leading to death in a proportion of cases – and realised that the drug was responsible. About 10,000 children were affected, with 2000 deaths. Pregnant women were advised not to use the drug, and it was withdrawn in 1959 after it was discovered that prolonged use could cause nerve damage. However, it was later approved for some specific diseases: a form of leprosy and multiple myeloma (cancer of the plasma cells in the blood).
The thalidomide tragedy is a reminder of the uncertain nature of medical treatments. The drug had been extensively tested. The conventional wisdom was that thalidomide would be unable to cross the placental barrier between mother and child, so it could have no effect on the foetus. Nevertheless, the researchers carried out standard tests to detect teratogenic effects – malformations in the foetus – using small laboratory animals. These showed nothing harmful. Later it became clear that humans are unusual in this respect. The medical profession, the pharmaceutical companies that manufacture drugs, the makers of other medical equipment such a replacement hip joints, or just doctors testing different versions of some procedure (such as how best to administer radiotherapy to a cancer patient) have developed methods for testing whether treatments are effective, and reducing risk to patients. As thalidomide shows, these methods aren’t foolproof, but they provide a rational way to mitigate the uncertainties. The main tool is statistics, and we can understand several basic statistical concepts and techniques by seeing how they’re used in medicine. The methods are constantly being refined as statisticians come up with new ideas.
All such investigations have an ethical dimension, because at some point a new drug, treatment, or treatment protocol has to be tried out on human subjects. In the past, medical experiments were sometimes performed on criminals, unwitting members of the armed forces, the poor and destitute, or slaves, often without their knowledge or consent. Today’s ethical standards are more stringent. Unethical experiments still happen, but in most parts of the world they’re a rare exception, leading to criminal prosecution if discovered.
The three main types of medical uncertainty concern drugs, equipment, and treatment protocols. All three are developed in the laboratory, and tested before trying them out on humans. The tests sometimes involve animals, opening up new ethical considerations. Animals shouldn’t be used unless there’s no other way to obtain the required information, and then only under strict safeguards. Some people want animal experiments outlawed altogether.
The later stages of these tests, which are needed to make the drug, device, or treatment regime available for doctors to use on patients, usually involve clinical trials: experiments performed on humans. Government regulators sanction such tests based on an assessment of the risks and potential benefits. Allowing a trial to be carried out need not imply that it’s considered safe, so the statistical concept of risk is deeply involved in the entire process.
Different types of trial are used in different circumstances – the whole area is extraordinarily complex – but it’s common to start with pilot trials on a small number of people, who may be volunteers or existing patients. Statistically, conclusions based on small samples are less reliable than those involving larger numbers of individuals, but pilot trials give useful information about the risks, leading to improved experimental designs for later trials. For example, if the treatment produces severe side effects, the trial is terminated. If nothing particularly nasty happens, the trial can be extended to larger groups of people, at which stage statistical methods provide a more trustworthy assessment of how effective the treatment concerned is.
If it passes enough tests of this kind, the treatment becomes available for doctors to use, very possibly with restrictions on the type of patient for whom it’s considered suitable. Researchers continue to collect data on the outcomes of the treatment, and these data can give increased confidence in its use, or reveal new problems that didn’t show up in the original trials.
ASIDE FROM PRACTICAL AND ETHICAL problems, the way a clinical trial is set up centres around two related issues. One is the statistical analysis of the data generated by the trial. The other is the experimental design of the trial: how to structure it so that the data are useful, informative, and as reliable as possible. The techniques chosen for the data analysis affect what data are collected, and how. The experimental design affects the range of data that can be collected, and the reliability of the numbers.
Similar considerations apply to all scientific experiments, so clinicians can borrow techniques from experimental science, and their work also contributes to scientific understanding in general.
Clinical trials have two main objectives: does the treatment work, and is it safe? In practice, neither factor is absolute. Drinking small amounts of water is close to 100% safe (not exactly: you might choke on it), but it won’t cure measles. Childhood vaccination against measles is almost 100% effective, but it’s not totally safe. Rarely, a child may experience a severe reaction to the vaccine. These are extreme cases, and many treatments are riskier than water and less effective than vaccination. So there may have to be a trade-off. This is where risk enters the picture. The risk associated with an adverse event is the probability it will happen multiplied by the damage it would do.
Even at the design stage, experimenters try to take these factors into account. If there’s evidence that people have taken some drug to treat a different condition without suffering severe side effects, the safety issue is to some extent settled. If not, the size of the trial must be kept small, at least until early results come in. One important feature of experimental design is the use of a control group – people who are not given the drug or treatment. Comparing the two groups tells us more than just testing the people in the trial on their own. Another important feature is the conditions under which the trial is carried out. Is it structured so that the result is reliable? The thalidomide trial underestimated the potential risk to a foetus; with hindsight, trials on pregnant women should have been given more weight. In practice, the structure of clinical trials evolves as new lessons are learned.
A subtler problem concerns the influence that the experimenter has on the data they collect. Unconscious bias can creep in. Indeed, conscious bias can creep in, as someone sets out to ‘prove’ some favourite hypothesis and cherry-picks data that fit it. Three important features are common to most clinical trials nowadays. For definiteness, suppose we’re testing a new drug. Some subjects will receive the drug; a control group will be given a placebo, a pill that as far as possible appears to be indistinguishable from the drug, but has no significant effect.
The first feature is randomisation. Which patients get the drug, and which get the placebo, should be decided by a random process.
The second is blindness. Subjects should not know whether they got the drug or the placebo. If they knew, they might report their symptoms differently. In a double-blind set-up, the researchers are also unaware of which subjects got the drug or the placebo. This prevents unconscious bias, either in the interpretation of data, its collection, or such things as removing statistical outliers. Going to greater lengths still, a double-dummy design is one that gives each subject both drug and placebo, alternating them.
Thirdly, the use of a placebo as control lets researchers account for the now well known placebo effect, in which patients feel better merely because the doctor has given them a pill. This effect can kick in even when they know the pill is a placebo.
The nature of the trial – the disease it aims to cure, or mitigate, and the condition of the subject – may rule out some of these techniques. Giving a placebo to a patient, instead of the drug, can be unethical if it’s done without their consent. But with their consent, the trial can’t be blind. One way round this, when the trial concerns a new treatment and the aim is to compare it to an existing one that is known to be relatively effective, is to use an ‘active control’ trial in which some patients get the old treatment and some get the new. You can even tell them what’s going on, and get their consent to a random use of the two treatments. The trial can still be blind in such circumstances. Not quite so satisfactory scientifically, perhaps, but ethical considerations override most others.
THE TRADITIONAL STATISTICAL METHODS EMPLOYED in clinical trials were developed in the 1920s at the Rothamsted experimental station, an agricultural research centre. This may seem a far cry from medicine, but similar issues of experimental design and data analysis show up. The most influential figure was Ronald Fisher, who worked at Rothamsted. His Principles of Experimental Design laid down many of the central ideas, and included many of the basic statistical tools still in widespread use today. Other pioneers of this period added to the toolkit, among them Karl Pearson and William Gosset (who used the pseudonym ‘Student’). They tended to name statistical tests and probability distributions after the symbols representing them, so we now have things like the t-test, chi-squared (X2), and the gamma-distribution (Γ).
There are two main ways to analyse statistical data. Parametric statistics models the data using specific families of probability distributions (binomial, normal, and so on) that involve numerical parameters (such as mean and variance). The aim is to find the parameter values for which the model best fits the data, and to estimate the likely range of errors and how significant the fit is. The alternative, non-parametric statistics, avoids explicit models, and relies solely on the data. A histogram, presenting the data without further comment, is a simple example. Parametric methods are better if the fit is very good. Non-parametric ones are more flexible, and don’t make assumptions that might be unwarranted. Both types exist in profusion.
Perhaps the most widespread of all these techniques is Fisher’s method for testing the significance of data in support (or not) of a scientific hypothesis. This is a parametric method, usually based on the normal distribution. In the 1770s Laplace analysed the sex distribution of nearly half a million births. The data indicated an excess of boys, and he wanted to find out how significant that excess was. He set up a model: equal probabilities of boys and girls, given by a binomial distribution. Then he asked how likely the observed figures are if this model applies. His calculated probability was very small, so he concluded that the observations were highly unlikely to occur if the chances of boys and girls are actually fifty-fifty.
This kind of probability is now known as a p-value, and Fisher formalised the procedure. His method compares two opposite hypotheses. One, the null hypothesis, states that the observations arise by pure chance. The other, the alternative hypothesis, states that they don’t, and that’s the one we’re really interested in. Assuming the null hypothesis, we calculate the probability of obtaining the given data (or data in an appropriate range, since the specific numbers obtained have probability zero). This probability is usually denoted by p, leading to the term p-value.
For example, suppose we count the number of boys and girls in a sample of 1000 births, and we get 526 boys, 474 girls. We want to understand whether the excess of boys is significant. So we formulate the null hypothesis that these figures arise by chance. The alternative hypothesis is that they don’t. We’re not really interested in the probability of exactly these values occurring by chance. We’re interested in how extreme the data are: the existence of more boys than girls. If the number of boys had been 527, or 528, or any larger number, we would also have had evidence that might indicate an unusual excess. So what matters is the probability of getting 526 or more boys by chance. The appropriate null hypothesis is: this figure or an even greater excess of boys arises by chance.
Now we calculate the probability of the null hypothesis happening. At this point it becomes clear that I’ve missed out a vital ingredient from my statement of the null hypothesis: the theoretical probability distribution that’s assumed. Here, it seems reasonable to follow Laplace and choose a binomial distribution with fifty-fifty probabilities of boys and girls, but whichever distribution we choose, it’s tacitly built into the null hypothesis. Because we’re working with a large number of births, we can approximate Laplace’s choice of a binomial distribution by the appropriate normal distribution. The upshot here is that p = 0·5, so there’s only a 5% probability that such extreme values arise by chance. We therefore, in Fisher’s jargon, reject the null hypothesis at the 95% level. This means that we’re 95% confident that the null hypothesis is wrong, and we accept the alternative hypothesis.
Does that mean we’re 95% confident that the observed figures are statistically significant – that they don’t arise by chance? No. What it means is hedged about with weasel words: we’re 95% confident that the observed figures don’t arise by chance, as specified by a fifty-fifty binomial distribution (or the corresponding normal approximation). In other words, we’re 95% confident that either the observed figures don’t arise by chance, or the assumed distribution is wrong.
One consequence of Fisher’s convoluted terminology is that this final phrase can easily be forgotten. If so, the hypothesis we think we’re testing isn’t quite the same as the alternative hypothesis. The latter comes with extra baggage, the possibility that we chose the wrong statistical model in the first place. In this example, that’s not too worrying, because a binomial or normal distribution is very plausible, but there’s a tendency to assume a normal distribution by default, even though it’s sometimes unsuitable. Students are generally warned about this when they’re introduced to the method, but after a while it can fade from view. Even published papers get it wrong.
In recent years, a second problem with p-values has been gaining prominence. This is the difference between statistical significance and clinical significance. For example, a genetic test for the risk of developing cancer might be statistically significant at the 99% level, which sounds pretty good. But in practice it might detect only one extra cancer case in every 100,000 people, while giving a ‘false positive’ – what appears to be a detection of cancer, but turns out not to be – 1000 times in every 100,000 people. That would render it clinically worthless, despite its high statistical significance.
SOME QUESTIONS ABOUT PROBABILITIES IN medicine can be sorted out using Bayes’s theorem. Here’s a typical example52. A standard method for detecting potential breast cancers in women is to take a mammogram, a low-intensity X-ray image of the breast. The incidence of breast cancer in women aged 40 is about 1%. (Over their entire lifetime it’s more like 10%, and rising.) Suppose women of that age are screened using this method. About 80% of women with breast cancer will test positive, and 10% of women without breast cancer will also test positive (a ‘false positive’). Suppose that a woman tests positive. What is the probability that she will develop breast cancer?
In 1995 Gerd Gigerenzer and Ulrich Hoffrage discovered that when doctors are asked this question, only 15% of them get the answer right.53 Most of them go for 70–80%.
We can calculate the probability using Bayes’s theorem. Alternatively, we can use the same reasoning as in Chapter 8, as follows. For definiteness, consider a sample of 1000 women in this age group. The size of the sample doesn’t matter, because we’re looking at proportions. We assume the numbers concerned are exactly as specified by the probabilities – this wouldn’t be the case in a real sample, but we’re using a hypothetical sample to compute the probabilities, so this assumption is sensible. Of those 1000 women, 10 have cancer, and 8 of those will be picked up by the test. Of the remaining 990 women, 99 will test positive. The total number of positives is therefore 107. Of these, 8 have cancer, a probability of 8/107, which is about 7·5%.
This is about one tenth of what most doctors think when asked to estimate the probability in controlled studies. When dealing with an actual patient, they might take more care than when asked for an estimate off the top of their head. Let’s hope so, or better still, equip them with suitable software to save them the trouble. The main error in reasoning is to ignore the false positives, leading to the 80% estimate, or to assume they have a small effect, reducing this figure to 70% or so. That way of thinking fails here because the number of women who don’t have cancer is much bigger than the number that do. Even though a false positive is less likely than a genuine positive, the sheer number of women without cancer overwhelms the figures for those who have the condition.
This is yet another instance of fallacious reasoning about conditional probabilities. The doctors are in effect thinking about:
 The probability that a woman with breast cancer has a positive mammography
The probability that a woman with breast cancer has a positive mammography
when they should be thinking about:
 The probability that a woman with a positive mammography has breast cancer.
The probability that a woman with a positive mammography has breast cancer.
Interestingly, Gigerenzer and Hoffrage showed that doctors estimate this probability more accurately if they’re told the figures in a verbal narrative. If ‘probability of 1%’ is replaced by ‘one woman in a hundred’ and so on, they mentally visualise something more like the calculation we’ve just done. Psychological studies show that people are often more able to solve a mathematical or logic question if it’s presented as a story, especially in a familiar social setting. Historically, gamblers intuited many basic features of probability long before the mathematicians got to work on it.
IN A MOMENT I’M GOING to take a look at a modern medical trial, which used more sophisticated statistical methods. To prepare for that, I’ll start with the methods themselves. Two follow the traditional lines of least squares and Fisher’s approach to hypothesis testing, but in less traditional settings. The third is more modern.
Sometimes the only data available are a binary yes/no choice, such as pass/fail in a driving test. You want to find out whether something influences the results, for example whether the number of driving lessons someone takes affects their chances of passing. You can plot the outcome (say 0 for fail, 1 for pass) against the number of hours of lessons. If the outcome were closer to a continuous range, you’d use regression analysis, fit the best straight line, calculate the correlation coefficient, and test how significant it is. With only two data values, however, a straight line model doesn’t make a lot of sense.
In 1958 David Cox proposed using logistic regression. A logistic curve is a smooth curve that increases slowly from 0, speeds up, and then slows down again as it approaches 1. The steepness of the rise in the middle, and its location, are two parameters that give a family of such curves. You can think of this curve as a guess about the examiner’s opinion of the driver on a scale from poor to excellent, or a guess about the actual scores he or she assigned if that’s how the test worked. Logistic regression attempts to match this presumed distribution of opinions or scores using only the pass/fail data. It does this by estimating the parameters for which the curve best fits the data, according to whatever definition of ‘best fit’ we wish. Instead of trying to fit the best straight line, we fit the best logistic curve. The main parameter is usually expressed as the corresponding odds ratio, which gives the relative probabilities of the two possible results.
The second method, Cox regression, was also developed by Cox, and dates from 1972. It’s a ‘proportional hazards’ model, able to deal with events that change over time.54 For example, does taking some drug make the occurrence of a stroke less likely, and if so, by how much? The hazard rate is a number that tells us how likely a stroke is over a given period of time; doubling the hazard rate halves the average time to a stroke. The underlying statistical model assumes a specific form for the hazard function – how the hazard depends on time. It includes numerical parameters, which model how the hazard function depends on other factors such as medical treatment. The aim is to estimate those parameters and use their values to decide how significantly they affect the likelihood of a stroke, or whatever other outcome is being studied.
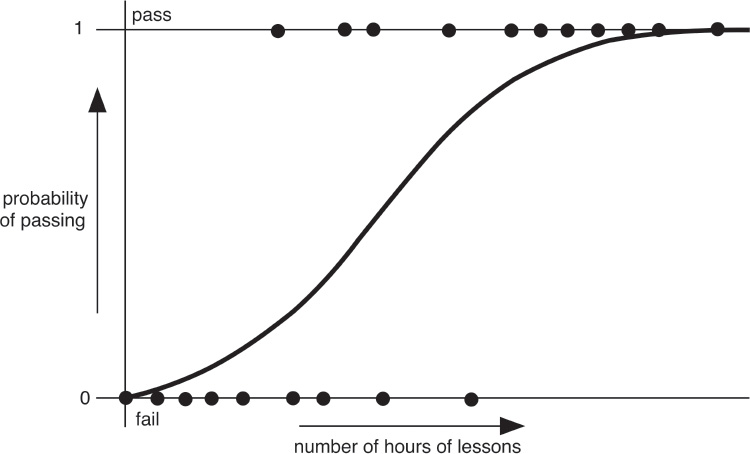
Hypothetical driving-test data (dots) and fitted logistic curve.
The third method is used to estimate the reliability of a statistic calculated from a sample, such as the sample mean. The issue goes back to Laplace, and in astronomy it can be dealt with by measuring the same things many times and applying the central limit theorem. In medical trials and many other areas of science, this may not be possible. In 1979 Bradley Efron suggested a way to proceed without collecting more data, in a paper ‘Bootstrap methods: another look at the jackknife’.55 The first term comes from the saying ‘pull yourself up by your bootstraps’; the jackknife was an earlier attempt of a similar kind. Bootstrapping is based on ‘resampling’ the same data. That is, taking a series of random samples from the existing data, calculating their means (or whatever statistic you’re interested in), and finding the resulting distribution of values. If the variance of this resampled distribution is small, the original mean is likely to be close to the true mean of the original population.
For instance, suppose we have data on the heights of a sample of 20 people and want to infer the average height of everyone on the globe. This is a rather small sample so the reliability of the sample mean is questionable. The simplest version of the bootstrap selects 20 of those people at random and calculates the mean for that sample. (The same person can be selected more than once when you resample; statisticians call this ‘resampling with replacement’. That way, you don’t get the same mean every time.) You resample the data a large number of times, say 10,000. Then you calculate statistics, such as the variance of these 10,000 resampled data points. Or draw a histogram of them. This is easy with computers, but it was impractical before the modern era, so nobody suggested doing it. Strange as it may seem, bootstrapping gives better results than the traditional assumption of a normal distribution or calculating the variance of the original sample.
WE’RE NOW READY TO TAKE a look at a well-designed modern medical trial. I’ve chosen a research paper from the medical literature, by Alexander Viktorin and coworkers, which appeared in 2018.56 Their study was about existing drugs, already in widespread use, and they were looking for unintended effects. Specifically, the aim was to examine what happens when a father is using antidepressants at the time a child is conceived. Is there evidence of any harmful effects on the child? They looked at four possibilities: preterm (premature) births, malformations, autism, and intellectual disability.
The study worked with a very large sample of 170,508 children – all children conceived in Sweden between 29 July 2005 and 31 December 2007, as given by the Swedish Medical Birth Register, which covers about 99% of births there. This database includes information that can be used to calculate the date of conception to within a week. Fathers were identified using the Multi-Generation Register provided by Statistics Sweden, which distinguishes between biological and adoptive parents; only biological fathers should be included. If the required data were unavailable, that child was excluded. The regional ethics committee in Stockholm approved the study, and its nature meant that in Swedish law individuals did not have to be asked for consent. As an extra precaution to ensure confidentiality, all data were anonymised: not associated with specific names. The data were collected until 2014, when the child reached the age of 8 or 9.
It turned out that the father had used antidepressants during conception in 3983 cases. A control group of 164,492 children had fathers who had not used them. A third ‘negative control group’ of 2033 children had fathers who didn’t use antidepressants at the time of conception, but did use them later, while the mother was pregnant. (If the drug is harmful, that should show up in the first group, but not in the second. Moreover, we wouldn’t expect it to show up in the third group either, because the main way a drug or its effects could pass from father to child would be at conception. Testing that expectation is a useful check.)
The study reported that none of the four conditions investigated are caused by the father taking antidepressants during the period around conception. Let’s see how the team arrived at these conclusions.
To make the data objective, the investigators used standard clinical classifications to detect and quantify the four adverse conditions. Their statistical analysis used a variety of techniques, each appropriate for the condition and data concerned. For hypothesis testing, the investigators chose the 95% significance level. For two conditions, preterm birth and malformations, the available data were binary: either the child had the condition, or not. An appropriate technique is logistic regression, which provided estimated odds ratios for preterm birth and malformations, quantified using 95% confidence intervals. These define a range of values such that we’re 95% confident that the statistic lies inside that range.57
The other two conditions, autism spectrum disorder and intellectual disability, are psychiatric disorders. In children, these become more common as the child ages, so the data depend on time. They were corrected for such effects using Cox regression models, providing estimates for hazard ratios. Because data for siblings from the same parents can introduce spurious correlations in the data, the team also used bootstrapping to perform sensitivity analyses to assess the reliability of the statistical results.
Their conclusions supplied statistical evidence to quantify possible associations of antidepressants with the four types of condition. For three conditions, there was no evidence of any association. A second strand was to compare the first group (father used drug during conception) with the third group (father didn’t use it during conception, but did during the mother’s pregnancy). For the first three conditions again there were no significant differences. For the fourth, intellectual disability, there was a slight difference. If it had indicated a greater risk of intellectual disability for the first group, that might have hinted that the drug was having some effect at conception – the only time when it was likely to affect the eventual foetus. But in fact, the first group had a marginally lower risk of intellectual disability than the third.
This is an impressive study. It shows careful design of experiments and correct ethical procedures, and applies a range of statistical techniques that goes well beyond Fisher’s style of hypothesis testing. It used traditional ideas such as confidence intervals to indicate the level of confidence in the results, but tailored them to the methods used and the type of data.