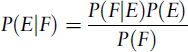
Absurdity, n. A statement or belief manifestly inconsistent with one’s own opinion. Ambrose Bierce, The Devil’s Dictionary
WHEN NEWTON PUBLISHED THE CALCULUS Bishop George Berkeley was moved to respond with a pamphlet: The Analyst, subtitled ‘A discourse addressed to an infidel mathematician. Wherein it is examined whether the object, principles, and inferences of the modern analysis are more distinctly conceived, or more evidently deduced, than religious mysteries and points of faith.’ The title page has a biblical epigram: ‘First cast out the beam out of thine own Eye; and then shalt thou see clearly to cast out the mote out of thy brother’s eye.—Matt. vii:5’
You don’t need to be terribly sensitive to deduce that the bishop wasn’t a calculus fan. When his pamphlet appeared in 1734, science was making big advances, and many scholars and philosophers were starting to argue that evidence-based science was superior to faith as a way to understand the natural world. The place of Christian beliefs, previously considered to be absolute truths by virtue of the authority of God, was being usurped by mathematics, which was not only true, but necessarily true, and it could prove it.
Of course mathematics is no such thing, but then neither is religion. However, at the time, the bishop had every reason to be sensitive about challenges to faith, and he set out to rectify matters by pointing out some logical difficulties in calculus. His not-very-hidden agenda was to convince the world that mathematicians weren’t as logical as they claimed to be, demolishing their claim to be sole guardians of absolute truths. He had a point, but outright attack is a bad way to convince people they’re wrong; mathematicians get upset when outsiders try to tell them how to do mathematics. Ultimately Berkeley had missed the point, and the experts could see that, even if at the time they couldn’t quite lay down rigorous logical foundations.
THIS ISN’T A BOOK ABOUT calculus, but I’m telling the story because it leads directly to one of the great unappreciated heroes of mathematics, a man whose scientific reputation at the time of his death was very ordinary, but has gone from strength to strength ever since. His name was Thomas Bayes, and he created a revolution in statistics that has never been more relevant than it is today.
Bayes was born in 1701, perhaps in Hertfordshire. His father Joshua was a Presbyterian minister, and Thomas followed in his footsteps. He took a degree in logic and theology at Edinburgh University, assisted his father for a short period, and then became minister of the Mount Sion Chapel in Tunbridge Wells. He is the author of two very different books. The first, in 1731, was Divine Benevolence, or an Attempt to Prove That the Principal End of the Divine Providence and Government is the Happiness of His Creatures. Exactly what we might expect of a nonconformist man of the cloth. The other, in 1736, was An Introduction to the Doctrine of Fluxions, and Defence of the Mathematicians against the Objections of the Author of the Analyst. Which was most definitely not what we might expect. The minister Bayes was defending the scientist Newton against an attack by a bishop. The reason was simple: Bayes disagreed with Berkeley’s mathematics.
When Bayes died, his friend Richard Price received some of his papers, and published two mathematical articles extracted from them. One was on asymptotic series – formulas approximating some important quantity by adding large numbers of simpler terms together, with a specific technical meaning for ‘approximate’. The other bore the title ‘Essay towards solving a problem in the doctrine of chances’, and appeared in 1763. It was about conditional probability.
Bayes’s key insight occurs early in the paper. Proposition 2 begins: ‘If a person has an expectation depending on the happening of an event, the probability of the event is [in the ratio] to the probability of its failure as his loss if it fails [is in the ratio] to his gain if it happens.’ This is a bit of a mouthful, but Bayes explains it in more detail. I’ll recast what he wrote in modern terms, but it’s all there in his paper.
If E and F are events, write the conditional probability that E occurs, given that F has occurred, as P(E|F) (read as ‘the probability of E given F’). Assume the two events E and F are independent of each other. Then the formula that we now call Bayes’s theorem states that
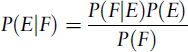
This follows easily27 from what is now considered to be the definition of conditional probability:
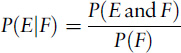
Let’s check the second formula out on the two-girl puzzle, in the first case where we’re told that at least one of the Smiths’ children is a girl. The full sample space has four events GG, GB, BG, BB, each with probability 1/4. Let E be ‘two girls’, that is, GG. Let F be ‘not two boys’, which is the subset {GG, GB, BG}, probability 3/4. The event ‘E and F’ is GG, the same as event E. According to the formula, the probability that they have two girls, given that at least one child is a girl, is
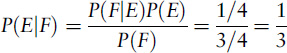
This is the result we got before.
Bayes went on to consider more complicated combinations of conditions and their associated conditional probabilities. These results, and more extensive modern generalisations, are also referred to as Bayes’s theorem.
BAYES’S THEOREM HAS IMPORTANT PRACTICAL consequences, for example to quality control in manufacturing. There it provides answers to questions such as: ‘Given that the wheels fell off one of our toy cars, what is the probability that it was manufactured at our Wormingham factory?’ But over the years, it morphed into an entire philosophy about what probability is, and how to deal with it.
The classical definition of probability – ‘interpretation’ is perhaps a better word – is the frequentist one: the frequency with which an event occurs when an experiment is repeated many times. As we’ve seen, this interpretation goes right back to the early pioneers. But it has several defects. It’s not clear exactly what ‘many times’ means. In some (rare) series of trials, the frequency need not converge to any well-defined number. But the main one is that it relies on being able to perform the identical experiment as many times as we wish. If that’s not possible, it’s unclear whether ‘probability’ has any meaning, and if it does, we don’t know how to find it.
For example, what is the probability that we will discover intelligent aliens by the year 3000 AD? By definition, this is an experiment we can run only once. Yet most of us intuitively feel that this probability ought to have a meaning – even if we disagree entirely on its value. Some will insist the probability is 0, others 0·99999, and wishy-washy fence-sitters will go for 0·5 (the fifty-fifty default, almost certainly wrong). A few will trot out the Drake equation, whose variables are too imprecise to help much.28
The main alternative to frequentism is the Bayesian approach. Whether the good Reverend would recognise it as his brainchild is not totally clear, but he certainly set himself up for getting the (in some eyes dubious) credit. The approach actually goes back further, to Laplace, who discussed questions such as: ‘How likely is it that the Sun will rise tomorrow?’. But we’re stuck with the term now, if only for historical reasons.
Here’s how Bayes defines probability in his paper: ‘The probability of any event is the ratio between the value at which an expectation depending on the happening of the event ought to be computed, and the chance of the thing expected upon its happening.’ This statement is somewhat ambiguous. What is our ‘expectation’? What does ‘ought to be’ mean? One reasonable interpretation is that the probability of some event can be interpreted as our degree of belief that it will happen. How confident we are in it as a hypothesis; what odds would persuade us to gamble on it; how strongly we believe in it.
This interpretation has advantages. In particular, it lets us assign probabilities to events that can occur only once. My question about aliens could reasonably be answered ‘The probability of intelligent aliens visiting us by the year 3018 is 0·316.’ This statement doesn’t mean ‘If we run that period of history repeatedly a thousand times, aliens will turn up in 316 of the runs.’ Even if we owned a time machine, and its use didn’t change history, we’d get either 0 occasions of alien invasions, or 1000. No: the 0·316 means that our confidence that they’ll turn up is moderate.
The interpretation of probability as degree of belief also has evident disadvantages. As George Boole wrote in An Investigation into the Laws of Thought in 1854, ‘It would be unphilosophical to affirm that the strength of expectation, viewed as an emotion of the mind, is capable of being referred to any numerical standard. The man of sanguine temperament builds high hopes where the timid despair, and the irresolute are lost in doubt.’ In other words, if you disagree with my assessment, and say that the probability of an alien invasion is only 0·003, there’s no way to work out who’s right. If anyone. That’s true even if the aliens turn up. If they don’t, your estimate is better than mine; if they do, mine is better than yours. But neither of us is demonstrably correct, and other figures would have performed better than either – depending on what happens.
Bayesians have a kind of answer to that objection. It reintroduces the possibility of repeating the experiment, though not under the exact selfsame conditions. Instead, we wait another thousand years, and see if another bunch of aliens turns up. But before doing that, we revise our degrees of belief.
Suppose, for the sake of argument, that an expedition from Apellobetnees III turns up in the year 2735. Then my 0·316 performed better than your 0·003. So, when it comes to the following millennium, we both revise our degrees of belief. Yours definitely needs revising upwards; maybe mine does too. Perhaps we agree to compromise on 0 718.
We can stop there. The exact event is not repeatable. We still have a better estimate of whatever it is we’re estimating. If we’re more ambitious, we can revise the question to ‘probability of aliens arriving within a period of 1000 years’, and do the experiment again. This time, oh dear, no new aliens arrive. So we revise our degree of belief down again, say to 0·584, and wait another thousand years.
That all sounds a bit arbitrary, and as stated it is. The Bayesian version is more systematic. The idea is that we start out with an initial degree of belief – the prior probability. We do the experiment (wait for aliens), observe the outcome, and use Bayes’s theorem to calculate a posterior probability – our improved, better informed degree of belief. No longer just a guess, it’s based on some limited evidence. Even if we stop there, we’ve achieved something useful. But where appropriate, we can reinterpret that posterior probability as a new prior one. Then we can do a second experiment to get a second posterior probability, which in some sense ought to be better still. Using that as a new prior, we experiment again, get an even better posterior ... and so it goes.
It still sounds subjective, which it is. Remarkably, however, it often works amazingly well. It gives results, and suggests methods, that aren’t available in a frequentist model. Those results and methods can solve important problems. So the world of statistics has now fragmented into two distinct sects, Frequentists v. Bayesians, with two distinct ideologies: Frequentism and Bayesianism.
A pragmatic view would be that we don’t have to choose. Two heads are better than one, two interpretations are better than one, and two philosophies are better than one. If one’s no good, try the other. Gradually that view is prevailing, but right now a lot of people insist that only one sect is right. Scientists in many areas are entirely happy to go along with both, and Bayesian methods are widespread because they’re more adaptable.
A COURT OF LAW MIGHT SEEM an unlikely test ground for mathematical theorems, but Bayes’s theorem has important applications to criminal prosecutions. Unfortunately, the legal profession largely ignores this, and trials abound with fallacious statistical reasoning. It’s ironic – but highly predictable – that in an area of human activity where the reduction of uncertainty is vital, and where well-developed mathematical tools exist to achieve just that, both prosecution and defence prefer to resort to reasoning that is archaic and fallacious. Worse, the legal system itself discourages the use of the mathematics. You might think that applications of probability theory in the courts should be no more controversial than using arithmetic to decide how much faster than the speed limit someone is driving. The main problem is that statistical inference is open to misinterpretation, creating loopholes that both prosecution and defence lawyers can exploit.
An especially devastating judgement against the use of Bayes’s theorem in legal cases was delivered in the 1998 appeal of Regina v. Adams, a rape case where the sole evidence of guilt was a DNA match to a swab taken from the victim. The defendant had an alibi, and didn’t resemble the victim’s description of her attacker, but he was convicted because of this match. On appeal, the defence countered the prosecution’s contention that the match probability was one in 200 million with testimony from an expert witness, who explained that any statistical argument must take account of the defence’s evidence as well, and that Bayes’s theorem was the correct approach. The appeal succeeded, but the judge condemned all statistical reasoning: ‘The task of the jury is ... to evaluate evidence and reach a conclusion not by means of a formula, mathematical or otherwise, but by the joint application of their individual common sense and knowledge of the world to the evidence before them.’ All very well, but Chapter 6 shows how useless ‘common sense’ can be in such circumstances.
Nulty & Ors v. Milton Keynes Borough Council in 2013 was a civil case about a fire at a recycling centre near Milton Keynes. The judge concluded that the cause was a discarded cigarette, because the alternative explanation – electrical arcing – was even less likely. The company insuring the engineer who allegedly threw away the cigarette lost the case and was told to pay £2 million compensation. The Appeal Court rejected the judge’s reasoning, but disallowed the appeal. The judgement threw out the entire basis of Bayesian statistics: ‘Sometimes the “balance of probability” standard is expressed mathematically as “50+ % probability”, but this can carry with it a danger of pseudo-mathematics... To express the probability of some event having happened in percentage terms is illusory.’
Norma Fenton and Martin Neil29 report a lawyer saying: ‘Look, the guy either did it or he didn’t do it. If he did then he is 100% guilty and if he didn’t then he is 0% guilty; so giving the chances of guilt as a probability somewhere in between makes no sense and has no place in the law.’ It’s unreasonable to assign probabilities to events you know have (or have not) happened. But it’s entirely sensible to assign probabilities when you don’t know, and Bayesianism is about how to do this rationally. For instance, suppose someone tosses a coin; they look at it, you don’t. To them, the outcome is known and its probability is 1. But to you, the probability is 1/2 for each of heads and tails, because you’re not assessing what happened, you’re assessing how likely your guess is to be right. In every court case, the defendant is either guilty or not – but that information has no bearing on the court, whose job to find out which. Rejecting a useful tool because it might bamboozle juries is a bit silly if you allow them to be bamboozled in the time-honoured manner by lawyers talking rubbish.
MATHEMATICAL NOTATION CONFUSES MANY PEOPLE, and it certainly doesn’t help that our intuition for conditional probabilities is so poor. But those aren’t good reasons to reject a valuable statistical tool. Judges and juries routinely deal with highly complex circumstances. The traditional safeguards are things like expert witnesses – though as we’ll see, their advice is not infallible – and careful direction of the jury by the judge. In the two cases I mentioned, it was, perhaps, reasonable to rule that the lawyers hadn’t presented a sufficiently compelling statistical case. But ruling against the future use of anything remotely related was, in the eyes of many commentators, a step too far, making it much harder to convict the guilty, thereby reducing the protection of the innocent. So a brilliant and fundamentally simple discovery that had proved to be a very useful tool for reducing uncertainty went begging, because the legal profession either didn’t understand it, or was willing to abuse it.
Unfortunately, it’s all too easy to abuse probabilistic reasoning, especially about conditional probabilities. We saw in Chapter 6 how easily our intuition can be led astray, and that’s when the mathematics is clear and precise. Imagine you’re in court, accused of murder. A speck of blood on the victim’s clothing has been DNA-fingerprinted, and there’s a close match to your DNA. The prosecution argues that the match is so close that the chances of it occurring for a randomly chosen person are one in a million – which may well be true, let’s assume it is – and concludes that the chance you are innocent is also one in a million. This, in its simplest form, is the prosecutor’s fallacy. It’s total nonsense.
Your defence counsel springs into action. There are sixty million people in the United Kingdom. Even with those one-in-a-million odds, 60 of them are equally likely to be guilty. Your chance of guilt is 1/60, or about 1·6%. This is the defence lawyer’s fallacy, and it’s also nonsense.
These examples are invented, but there are plenty of cases in which something along those lines has been put to the court, among them Regina v. Adams, where the prosecution highlighted an irrelevant DNA match probability. There are clear examples where innocent people have been convicted on the basis of the prosecutor’s fallacy, as the courts themselves have acknowledged by reversing the conviction on appeal. Experts in statistics believe that many comparable miscarriages of justice, caused by fallacious statistical reasoning, have not been reversed. It seems likely, though harder to prove, that criminals have been found not guilty because the court fell for the defence lawyer’s fallacy. It’s easy enough, however, to explain why both lines of reasoning are fallacious.
For present purposes, let’s leave aside the issue of whether probabilistic calculations should be allowed in trials at all. Trials are, after all, supposed to assess guilt or innocence, not to convict you on the grounds that you probably did the dirty deed. The topic under discussion is what we need to be careful about when the use of statistics is allowed. As it happens, there’s nothing to stop probabilities being presented as evidence in British or American law. Clearly the prosecution and the defence in my DNA scenario can’t both be right, since their assessments disagree wildly. So what’s wrong?
The plot of Conan Doyle’s short story ‘Silver Blaze’ hinges on Sherlock Holmes drawing attention to ‘the curious incident of the dog in the night-time’. ‘The dog did nothing in the night-time,’ protests Scotland Yard’s Inspector Gregory. To which Holmes, enigmatic as ever, replies, ‘That was the curious incident.’ There’s a dog doing nothing in the two arguments above. What is it? There’s no reference to any other evidence that might indicate guilt or innocence. But additional evidence has a strong effect on the a priori probability that you’re guilty, and it changes the calculations.
Here’s another scenario that may help to make the problem clear. You get a phone call telling you you’ve won the National Lottery, a cool 10 million pounds. It’s genuine, and you pick up your winner’s cheque. But when you present it to your bank, you feel a heavy hand on your shoulder: it’s a policeman, and he arrests you for theft. In court, the prosecution argues that you almost certainly cheated, defrauding the lottery company of the prize money. The reason is simple: the chance of any randomly chosen person winning the lottery is one in 20 million. By the prosecutor’s fallacy, that’s the probability that you’re innocent.
In this case it’s obvious what’s wrong. Tens of millions of people play the lottery every week; someone is very likely to win. You haven’t been selected at random beforehand; you’ve been selected after the event because you won.
AN ESPECIALLY DISTURBING LEGAL CASE involving statistical evidence occurred in the trial of Sally Clark, a British lawyer who lost two children to cot deaths (SIDS, sudden infant death syndrome). The prosecution’s expert witness testified that the probability of this double tragedy occurring by accident was one in 73 million. He also said that the actual rate observed was more frequent, and he explained this discrepancy by offering the opinion that many double cot deaths weren’t accidental, but resulted from Munchausen syndrome by proxy, his own special area of expertise. Despite the absence of any significant corroborating evidence other than the statistics, Clark was convicted of murdering her children, widely reviled in the media, and sentenced to life imprisonment.
Serious flaws in the prosecution’s case were evident from the outset, to the alarm of the Royal Statistical Society, which pointed them out in a press release after the conviction. After more than three years in prison Clark was released on appeal, but not because of any of those flaws: because the pathologist who had examined the babies after the deaths had withheld possible evidence of her innocence. Clark never recovered from this miscarriage of justice. She developed psychiatric problems and died of alcohol poisoning four years later.
The flaws are of several kinds. There’s clear evidence that SIDS has a genetic element, so one cot death in a family makes a second one more likely. You can’t sensibly estimate the chances of two successive deaths by multiplying the chance of one such death by itself. The two events are not independent. The claim that most double deaths are the result of Munchausen syndrome by proxy is open to challenge. Munchausen syndrome is a form of self-harm. Munchausen syndrome by proxy is self-harm inflicted by harming someone else. (Whether this makes sense is controversial.) The court seemed unaware that the higher rate of double deaths reported by their expert witness might, in fact, just be the actual rate of accidental ones. With, no doubt, a few rare cases where the children really had been murdered.
But all this is beside the point. Whatever probability is used for accidental double cot deaths, it has to be compared with the possible alternatives. Moreover, everything has to be conditional on the other evidence: two deaths have occurred. So there are three possible explanations: both deaths were accidents; both were murders; something else entirely (such as one murder, one natural death). All three events are extremely unlikely: if anything probabilistic matters, it’s how unlikely each is compared with the others. And even if either death was a murder, there also remains the question: Who did it? It’s not automatically the mother.
So the court focused on:
 The probability that a randomly chosen family suffers two cot deaths
The probability that a randomly chosen family suffers two cot deaths
when it should have been thinking about:
 The probability that the mother is a double murderer, given that two cot deaths have occurred.
The probability that the mother is a double murderer, given that two cot deaths have occurred.
It then confused the two, while using incorrect figures.
Ray Hill, a mathematician, carried out a statistical analysis of cot deaths, using real data, and found that it’s between 4·5 and 9 times as likely that there will be two SIDS accidents in one family as it is that there will be two murders. In other words, on statistical grounds alone, the likelihood of Clark being guilty was only 10–20%.
Again, the dog didn’t bark. In this kind of case, statistical evidence alone is totally unreliable unless supported by other lines of evidence. For example, it would have improved the prosecution’s case if it could have been established, independently, that the accused had a track record of abusing her children, but no such track record existed. And it would have improved the defence’s case to argue that there had been no signs of such abuse. Ultimately, the sole ‘evidence’ of her guilt was that two children had died, apparently from SIDS.
Fenton and Neil discuss a large number of other cases in which statistical reasoning may have been misapplied.30 In 2003 Lucia de Berk, a Dutch children’s nurse, was accused of four murders and three attempted murders. An unusually high number of patients had died while she was on duty in the same hospital, and the prosecution put together circumstantial evidence, claiming that the probability of this happening by chance was one in 342 million. This calculation referred to the probability of the evidence existing, given that the accused is not guilty. What should have been calculated was the probability of guilt, given the evidence. De Berk was convicted and sentenced to life imprisonment. On appeal, the verdict was upheld, even though alleged evidence of her guilt was retracted during the appeal by a witness who admitted: ‘I made it up.’ (This witness was being detained in a criminal psychology unit at the time.) The press, not surprisingly, disputed the conviction, a public petition was organised, and in 2006 the Netherlands Supreme Court sent the case back to the Amsterdam Court, which again upheld the conviction. In 2008, after much bad publicity, the Supreme Court reopened the case. In 2010 a retrial found that all of the deaths had been due to natural causes and that the nurses involved had saved several lives. The court quashed the conviction.
It ought to be obvious that with large numbers of deaths in hospitals, and large numbers of nurses, unusually strong associations between some deaths and a particular nurse are likely. Ronald Meester and colleagues31 suggest that the ‘one in 342 million’ figure is a case of double-dipping (see Chapter 7). They show that more appropriate statistical methods lead to figure of about one in 300, or even one in 50. These values are not statistically significant as evidence of guilt.
IN 2016 FENTON, NEIL, AND Daniel Berger published a review of Bayesian reasoning in legal cases. They analysed why the legal profession is suspicious of such arguments and reviewed their potential. They began by pointing out that the use of statistics in legal proceedings has increased considerably over the past four decades, but that most such uses involve classical statistics, even though the Bayesian approach avoids many of the pitfalls associated with classical methods, and is more widely applicable. Their main conclusions were that the lack of impact stems from ‘misconceptions by the legal community about Bayes’s theorem ... and the lack of adoption of modern computational methods’. And they advocated the use of a new technique, Bayesian networks, which could automate the calculations required in a way that would ‘address most concerns about using Bayes in the law’.
Classical statistics, with its rather rigid assumptions and longstanding traditions, is open to misinterpretation. An emphasis on statistical significance tests can lead to the prosecutor’s fallacy, because the probability of the evidence given guilt can be misrepresented as the probability of guilt given the evidence. More technical concepts such as confidence intervals, which define the range of values in which we can confidently assume some number lies, are ‘almost invariably misinterpreted since their proper definition is both complex and counterintuitive (indeed it is not properly understood even by many trained statisticians).’ These difficulties, and the poor track record of classical statistics, made lawyers unhappy about all forms of statistical reasoning.
This may be one reason for resisting Bayesian methods. Fenton and colleagues suggest another, more interesting one: too many of the Bayesian models presented in court are oversimplified. These models are used because of the assumption that the calculations involved should be sufficiently simple that they can be done by hand, so the judge and jury can follow them.
In the computer age, this restriction isn’t necessary. It’s sensible to be concerned about incomprehensible computer algorithms; as an extreme case we can imagine an artificially intelligent Justice Computer that silently weights the evidence and declares either ‘guilty’ or ‘not guilty’, without explanation. But when the algorithm is entirely comprehensible, and the sums are straightforward, it ought not to be hard to safeguard against the more obvious potential issues.
The toy models of Bayesian reasoning that I’ve discussed involve a very small number of statements, and all we’ve done is think about how probable one statement is, given some other statement. But a legal case involves all sorts of evidence, along with the statements associated with them, such as ‘the suspect was at the crime scene’, ‘the subject’s DNA matches the traces of blood on the victim’, or ‘a silver car was seen in the vicinity’. A Bayesian network represents all of these factors, and how they influence each other, as a directed graph: a collection of boxes joined by arrows. There’s one box for each factor and one arrow for each influence. Moreover, associated with each arrow is a number, the conditional probability of the factor at its head, given the factor at its tail. A generalisation of Bayes’s theorem then makes it possible to compute the probability of any particular factor occurring, given any other, or even given everything else that’s known.
Fenton and colleagues suggest that Bayesian networks, suitably implemented, developed, and tested, could become an important legal tool, able to ‘model the correct relevant hypotheses and the full causal context of the evidence’. Certainly there are plenty of issues about what types of evidence can be deemed suitable for such treatment, and those issues need to be debated and agreed. That said, the main obstacles preventing such a debate are the strong cultural barriers between science and the law that currently exist.