Heat won’t pass from a cooler to a hotter, You can try it if you like but you far better notter. Michael Flanders and Donald Swann, First and Second Law (lyrics)
FROM LAW AND ORDER TO law and disorder. From human affairs to physics.
One of the very few scientific principles to have become a household name, or at least to have come close, is the second law of thermodynamics. In his notorious ‘two cultures’ Rede lectures of 1959, and the subsequent book, the novelist C.P. Snow said that no one should consider themselves cultured if they don’t know what this law says:
A good many times I have been present at gatherings of people who, by the standards of the traditional culture, are thought highly educated and who have with considerable gusto been expressing their incredulity at the illiteracy of scientists. Once or twice I have been provoked and have asked the company how many of them could describe the Second Law of Thermodynamics. The response was cold: it was also negative. Yet I was asking something which is the scientific equivalent of: Have you read a work of Shakespeare’s?
He was making a sensible point: basic science is at least as much a part of human culture as, say, knowing Latin quotations from Horace, or being able to quote verse by Byron or Coleridge. On the other hand, he really ought to have chosen a better example, because plenty of scientists don’t have the second law of thermodynamics at their fingertips.32
To be fair, Snow went on to suggest that no more than one in ten educated people would be able to explain the meaning of simpler concepts such as mass or acceleration, the scientific equivalent of asking ‘Can you read?’ Literary critic F.R. (Frank Raymond) Leavis replied that there was only one culture, his – inadvertently making Snow’s point for him.
In a more positive response, Michael Flanders and Donald Swann wrote one of the much-loved comic songs that they performed in their touring revues At the Drop of a Hat and At the Drop of Another Hat between 1956 and 1967, two lines of which appear as an epigram at the start of this chapter.33 The scientific statement of the second law is phrased in terms of a rather slippery concept, which occurs towards the end of the Flanders & Swann song: ‘Yeah, that’s entropy, man.’
Thermodynamics is the science of heat, and how it can be transferred from one object or system to another. Examples are boiling a kettle, or holding a balloon over a candle. The most familiar thermodynamic variables are temperature, pressure, and volume. The ideal gas law tells us how they’re related: pressure times volume is proportional to absolute temperature. So, for instance, if we heat the air in a balloon, the temperature increases, so either it has to occupy a greater volume (the balloon expands), or the pressure inside has to increase (eventually bursting the balloon), or a bit of both. Here I’m ignoring the obvious point that the heat may also burn or melt the balloon, which is outside the scope of the ideal gas law.
Another thermodynamic variable is heat, which is distinct from, and in many respects simpler than, temperature. Far subtler than either is entropy, which is often described informally as a measure of how disordered a thermodynamic system is. According to the second law, in any system not affected by external factors, entropy always increases. In this context, ‘disorder’ is not a definition but a metaphor, and one that’s easily misinterpreted.
The second law of thermodynamics has important implications for the scientific understanding of the world around us. Some are cosmic in scale: the heat death of the universe, in which aeons into the future everything has become a uniform lukewarm soup. Some are misunderstandings, such as the claim that the second law makes evolution impossible because more complex organisms are more ordered. And some are very puzzling and paradoxical: the ‘arrow of time’, in which entropy seems to single out a specific forward direction for the flow of time, even though the equations from which the second law is derived are the same, in whichever direction time flows.
The theoretical basis for the second law is kinetic theory, introduced by the Austrian physicist Ludwig Boltzmann in the 1870s. This is a simple mathematical model of the motion of molecules in a gas, which are represented as tiny hard spheres that bounce off each other if they collide. The molecules are assumed to be very far apart, on average, compared to their size – not packed tightly as in a liquid or, even more so, a solid. At the time, most leading physicists didn’t believe in molecules. In fact, they didn’t believe that matter is made of atoms, which combine to make molecules, so they gave Boltzmann a hard time. Scepticism towards his ideas continued throughout his career, and in 1906 he hanged himself while on holiday. Whether resistance to his ideas was the cause, it’s difficult to say, but it was certainly misguided.
A central feature of kinetic theory is that in practice the motion of the molecules looks random. This is why a chapter on the second law of thermodynamics appears in a book on uncertainty. However, the bouncing spheres model is deterministic, and the motion is chaotic. But it took over a century for mathematicians to prove that.34
THE HISTORY OF THERMODYNAMICS AND kinetic theory is complicated, so I’ll omit points of fine detail and limit the discussion to gases, where the issues are simpler. This area of physics went through two major phases. In the first, classical thermodynamics, the important features of a gas were macroscopic variables describing its overall state: the aforementioned temperature, pressure, volume, and so on. Scientists were aware that a gas is composed of molecules (although this remained controversial until the early 1900s), but the precise positions and speeds of these molecules were not considered as long as the overall state was unaffected. Heat, for example, is the total kinetic energy of the molecules. If collisions cause some to speed up, but others to slow down, the total energy stays the same, so such changes have no effect on these macroscopic variables. The mathematical issue was to describe how the macroscopic variables are related to each other, and to use the resulting equations (‘laws’) to deduce how the gas behaves. Initially, the main practical application was to the design of steam engines and similar industrial machinery. In fact, the analysis of theoretical limits to the efficiency of steam engines motivated the concept of entropy.
In the second phase, microscopic variables such as the position and velocity of the individual molecules of the gas took precedence. The first main theoretical problem was to describe how these variables change as the molecules bounce around inside the container; the second was to deduce classical thermodynamics from this more detailed microscopic picture. Later, quantum effects were taken into consideration as well with the advent of quantum thermodynamics, which incorporates new concepts such as ‘information’ and provides detailed underpinnings for the classical version of the theory.
In the classical approach, the entropy of a system was defined indirectly. First, we define how this variable changes when the system itself changes; then we add up all those tiny changes to get the entropy itself. If the system undergoes a small change of state, the change in entropy is the change in heat divided by the temperature. (If the state change is sufficiently small, the temperature can be considered to be constant during the change.) A big change of state can be considered as a large number of small changes in succession, and the corresponding change in the entropy is the sum of all the small changes for each step. More rigorously, it’s the integral of those changes in the sense of calculus.
That tells us the change in entropy, but what about the entropy itself? Mathematically, the change in entropy doesn’t define entropy uniquely: it defines it except for an added constant. We can fix this constant by making a specific choice for the entropy at some well-defined state. The standard choice is based on the idea of absolute temperature. Most of the familiar scales for measuring temperature, such as degrees Celsius (commonly used in Europe) or Fahrenheit (America), involve arbitrary choices. For Celsius, 0°C is defined to be the melting point of ice, and 100°C is the boiling point of water. On the Fahrenheit scale, the corresponding temperatures are 32°F and 212°F. Originally Daniel Fahrenheit used the temperature of the human body for 100°F, and the coldest thing he could get as 0°F. Such definitions are hostages to fortune, whence the 32 and 212. In principle, you could assign any numbers you like to these two temperatures, or use something totally different, such as the boiling points of nitrogen and lead.
As scientists tried to create lower and lower temperatures, they discovered that there’s a definite limit to how cold matter can become. It’s roughly 273°C, a temperature called ‘absolute zero’ at which all thermal motion ceases in the classical description of thermodynamics. However hard you try, you can’t make anything colder than that. The Kelvin temperature scale, named after the Irish-born Scots physicist Lord Kelvin, is a thermodynamic temperature scale that uses absolute zero as its zero point; its unit of temperature is the kelvin (symbol: K). The scale is just like Celsius, except that 273 is added to every temperature. Now ice melts at 273K, water boils at 373K, and absolute zero is 0K. The entropy of a system is now defined (up to choice of units) by choosing the arbitrary added constant so that the entropy is zero when the absolute temperature is zero.
That’s the classical definition of entropy. The modern statistical mechanics definition is in some respects simpler. It boils down to the same thing for gases, though that’s not immediately obvious, so there’s no harm in using the same word in both cases. The modern definition works in terms of the microscopic states: microstates for short. The recipe is simple: if the system can exist in any of N microstates, all equally likely, then the entropy S is
S = kB log N
where kB is a constant called Boltzmann’s constant. Numerically, it’s 1·38065 × 10-23 joules per kelvin. Here log is the natural logarithm, the logarithm to base e = 2·71828::: . In other words, the entropy of the system is proportional to the logarithm of the number of microstates that in principle it could occupy.
For illustrative purposes, suppose that the system is a pack of cards, and a microstate is any of the orders into which the pack can be shuffled. From Chapter 4 the number of microstates is 52!, a rather large number starting with 80,658 and having 68 digits. The entropy can be calculated by taking the logarithm and multiplying by Boltzmann’s constant, which gives
S = 2·15879 × 10-21
If we now take a second pack, it has the same entropy S. But if we combine the two packs, and shuffle the resulting larger pack, the number of microstates is now N = 104!, which is a much larger number starting 10,299 with 167 digits. The entropy of the combined system is now
T = 5·27765 × 10-21
The sum of the entropies of the two subsystems (packs) before they were combined is
2S = 4·31758 × 10-21
Since T is bigger than 2S, the entropy of the combined system is larger than the sum of the entropies of the two subsystems.
Metaphorically, the combined pack represents all possible interactions between the cards in the two separate packs. Not only can we shuffle each pack separately; we can get extra arrangements by mixing them together. So the entropy of the system when interactions are permitted is bigger than the sum of the entropies of the two systems when they don’t interact. The probabilist Mark Kac used to describe this effect in terms of two cats, each with a number of fleas. When the cats are separate, the fleas can move around, but only on ‘their’ cat. If the cats meet up, they can exchange fleas, and the number of possible arrangements increases.
Because the logarithm of a product is the sum of the logarithms of the factors, entropy increases whenever the number of microstates for the combined system is bigger than the product of the numbers of microstates of the individual systems. This is usually the case, because the product is the number of microstates of the combined system when the two subsystems are not allowed to mix together. Mixing allows more microstates.
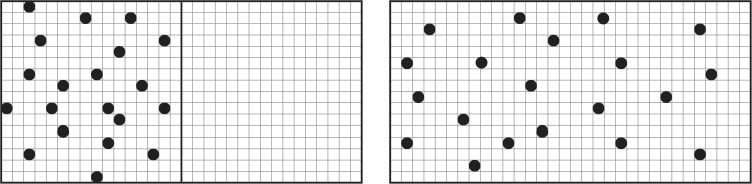
Now imagine a box with a partition, a lot of oxygen molecules on one side, and a vacuum on the other. Each of these two separate subsystems has a particular entropy. Microstates can be thought of as the number of ways to arrange the positions of the separate molecules, provided we ‘coarse-grain’ space into a large but finite number of very tiny boxes, and use them to say where the molecules are. When the partition is removed, all the old microststates of the molecules still exist. But there are lots of new microstates, because molecules can go into the other half of the box. The new ways greatly outnumber the old ways, and with overwhelming probability the gas ends up filling the whole box with uniform density.

Left: With partition. Right: When the partition is removed, many new microstates are possible. Coarse-grained boxes in grey.
More briefly: the number of available microstates increases when the partition is removed, so the entropy – the logarithm of that number – also increases.
Physicists say that the state when the partition is still present is ordered, in the sense that the set of oxygen molecules in one part is kept separate from the vacuum in the other. When we remove the partition, this separation ceases, so the state becomes more disordered. This is the sense in which entropy can be interpreted as the amount of disorder. It’s not a terribly helpful metaphor.
NOW WE COME TO THE vexed issue of the arrow of time.
The detailed mathematical model for a gas is a finite number of very tiny hard spherical balls, bouncing around inside a box. Each ball represents one molecule. It’s assumed that collisions between molecules are perfectly elastic, which means that no energy is lost or gained in the collision. It’s also assumed that when a ball collides with the walls it bounces like an idealised billiard ball hitting a cushion: it comes off at the same angle that it hit (no spin), but measured in the opposite direction, and it moves with exactly the same speed that it had before it hit the wall (perfectly elastic cushion). Again, energy is conserved.
The behaviour of those little balls is governed by Newton’s laws of motion. The important one here is the second law: the force acting on a body equals its acceleration times its mass. (The first law says the body moves at uniform speed in a straight line unless a force acts on it; the third says that to every action there is an equal and opposite reaction.) When thinking about mechanical systems, we usually know the forces and want to find out how the particle moves. The law implies that at any given instant the acceleration equals the force divided by the mass. It applies to every one of those little balls, so in principle we can find out how all of them move.
The equation that arises when we apply Newton’s laws of motion takes the form of a differential equation: it tells us the rate at which certain quantities change as time passes. Usually we want to know the quantities themselves, rather than how rapidly they’re changing, but we can work out the quantities from their rates of change using integral calculus. Acceleration is the rate of change of velocity, and velocity is the rate of change of position. To find out where the balls are at any given instant, we find all the accelerations using Newton’s law, then apply calculus to get their velocities, and apply calculus again to get their positions.
Two further ingredients are needed. The first is initial conditions. These specify where all the balls are at a given moment (say time t = 0) and how fast they’re moving (and in which direction). This information pins down a unique solution of the equations, telling us what happens to that initial arrangement as time passes. For colliding balls, it all boils down to geometry. Each ball moves at a constant speed along a straight line (the direction of its initial velocity) until it hits another ball. The second ingredient is a rule for what happens then: they bounce off each other, acquiring new speeds and directions, and continue again in a straight line until the next collision, and so on. These rules determine the kinetic theory of gases, and the gas laws and suchlike can be deduced from them.
Newton’s laws of motion for any system of moving bodies lead to equations that are time-reversible. If we take any solution of the equations, and run time backwards (change the time variable t to its negative –t) we also get a solution of the equations. It’s usually not the same solution, though sometimes it can be. Intuitively, if you make a movie of a solution and run it backwards, the result is also a solution. For example, suppose you throw a ball vertically into the air. It starts quite fast, slows down as gravity pulls it, becomes stationary for an instant, and then falls, speeding up until you catch it again. Run the movie backwards and the same description applies. Or strike a pool ball with the cue so that it hits the cushion and bounces off; reverse the movie and again you see a ball hitting the cushion and bouncing off. As this example shows, allowing spheres to bounce doesn’t affect reversibility, provided the bouncing rule works the same way when it’s run backwards.
This is all very reasonable, but we’ve all seen reverse-time movies where weird things happen. Egg white and a yolk in a bowl suddenly rise into the air, are caught between two halves of a broken eggshell, which join together to leave an intact egg in the cook’s hand. Shards of glass on the floor mysteriously move towards each other and assemble into an intact bottle, which jumps into the air. A waterfall flows up the cliff instead of falling down it. Wine rises up from a glass, back into the bottle. If it’s champagne, the bubbles shrink and go back along with the wine; the cork appears mysteriously from some distance away and slams itself back into the neck of the bottle, trapping the wine inside. Reverse movies of people eating slices of cake are distinctly revolting – you can figure out what they look like.
Most processes in real life don’t make much sense if you reverse time. A few do, but they’re exceptional. Time, it seems, flows in only one direction: the arrow of time points from the past towards the future.
Of itself, that’s not a puzzle. Running a movie backwards doesn’t actually run time backwards. It just gives us an impression of what would happen if we could do that. But thermodynamics reinforces the irreversibility of time’s arrow. The second law says that entropy increases as time passes. Run that backwards and you get something where entropy decreases, breaking the second law. Again, it makes sense; you can even define the arrow of time to be the direction in which entropy increases.
Things start to get tricky when you think about how this meshes with kinetic theory. The second law of Newton says the system is time-reversible; the second law of thermodynamics says it’s not. But the laws of thermodynamics are a consequence of Newton’s laws. Clearly something is screwy; as Shakespeare put it, ‘the time is out of joint’.
The literature on this paradox is enormous, and much of it is highly erudite. Boltzmann worried about it when he first thought about the kinetic theory. Part of the answer is that the laws of thermodynamics are statistical. They don’t apply to every single solution of Newton’s equations for a million bouncing balls. In principle, all the oxygen molecules in a box could move into one half. Get that partition in, fast! But mostly, they don’t; the probability that they do would be something like 0·000000..., with so many zeros before you reach the first nonzero digit that the planet is too small to hold them.
However, that’s not the end of the story. For every solution such that entropy increases as time passes, there’s a corresponding time-reversed solution in which entropy decreases as time passes. Very rarely, the reversed solution is the same as the original (the thrown ball, provided initial conditions are taken when it reaches to peak of its trajectory; the billiard ball, provided initial conditions are taken when it hits the cushion). Ignoring these exceptions, solutions come in pairs: one with entropy increasing; the other with entropy decreasing. It makes no sense to maintain that statistical effects select only one half. It’s like claiming that a fair coin always lands heads.
Another partial resolution involves symmetry-breaking. I was very careful to say that when you time-reverse a solution of Newton’s laws, you always get a solution, but not necessarily the same one. The time-reversal symmetry of the laws does not imply time-reversal symmetry of any given solution. That’s true, but not terribly helpful, because solutions still come in pairs, and the same issue arises.
So why does time’s arrow point only one way? I have a feeling that the answer lies in something that tends to get ignored. Everyone focuses on the time-reversal symmetry of the laws. I think we should consider the time-reversal asymmetry of the initial conditions.
That phrase alone is a warning. When time is reversed, initial conditions aren’t initial. They’re final. If we specify what happens at time zero, and deduce the motion for positive time, we’ve already fixed a direction for the arrow. That may sound a silly thing to say when the mathematics also lets us deduce what happens for negative time, but hear me out. Let’s compare the bottle being dropped and smashed with the time-reversal: the broken fragments of bottle unsmash and reassemble.
In the ‘smash’ scenario, the initial conditions are simple: an intact bottle, held in the air. Then you let go. As time passes, the bottle falls, smashes, and thousands of tiny pieces scatter. The final conditions are very complicated, the ordered bottle has turned into a disordered mess on the floor, entropy has increased, and the second law is obeyed.
The ‘unsmash’ scenario is rather different. The initial conditions are complicated: lots of tiny shards of glass. They may seem to be stationary, but actually they’re all moving very slowly. (Remember, we’re ignoring friction.) As time passes, the shards move together and unsmash, to form an intact bottle that leaps into the air. The final conditions are very simple, the disordered mess on the floor has turned into the ordered bottle, entropy has decreased, and the second law is disobeyed.
The difference here has nothing to do with Newton’s law, or its reversibility. Neither is it governed by entropy. Both scenarios are consistent with Newton’s law; the difference comes from the choice of initial conditions. The ‘smash’ scenario is easy to produce experimentally, because the initial condition is easy to arrange: get a bottle, hold it up, let go. The ‘unsmash’ scenario is impossible to produce experimentally, because the initial condition is too complicated, and too delicate, to set up. In principle it exists, because we can solve the equations for the falling bottle until some moment after it has smashed. Then we take that state as initial condition, but with all velocities reversed, and the symmetry of the mathematics means that the bottle would indeed unsmash – but only if we realised those impossibly complicated ‘initial’ conditions exactly.
Our ability to solve for negative time also starts with the intact bottle. It calculates how it got to that state. Most likely, someone put it there. But if you run Newton’s laws backwards in time, you don’t deduce the mysterious appearance of a hand. The particles that made up the hand are absent from the model you’re solving. What you get is a hypothetical past that is mathematically consistent with the chosen ‘initial’ state. In fact, since tossing a bottle into the air is its own time-reversal, the backwards solution would also involve the bottle falling to the ground, and ‘by symmetry’ it would also smash. But in reverse time. The full story of the bottle – not what actually happened, because the Hand of God at time zero isn’t part of the model – consists of thousands of shards of glass, which start to converge, unsmash, rise in the air as an intact bottle, reach the peak of their trajectory at time zero, then fall, smash, and scatter into thousands of shards. Initially, entropy decreases; then it increases again.
In The Order of Time, Carlo Rovelli says something very similar.35 The entropy of a system is defined by agreeing not to distinguish between certain configurations (what I called coarse-graining). So entropy depends on what information about the system we can access. In his view, we don’t experience an arrow of time because that’s the direction along which entropy increases. Instead, we think entropy increases because to us the past seems to have lower entropy than the present.
I SAID THAT SETTING UP INITIAL conditions to smash a bottle is easy, but there’s a sense in which that’s untrue. It’s true if I can go down to the supermarket, buy a bottle of wine, drink it, and then use the empty bottle. But where did the bottle come from? If we trace its history, its constituent molecules probably went through many cycles of being recycled and melted down; they came from many different bottles, often smashed before or during recycling. But all of the glass involved must eventually trace back to sand grains, which were melted to form glass. The actual ‘initial conditions’ decades or centuries ago were at least as complicated as the ones I declared to be impossible for unsmashing the bottle.
Yet, miraculously, the bottle was made.
Does this disprove the second law of thermodynamics?
Not at all. The kinetic theory of gases – indeed, the whole of thermodynamics – involves simplifying assumptions. It models certain common scenarios, and the models are good when those scenarios apply.
One such assumption is that the system is ‘closed’. This is usually stated as ‘no external energy input is allowed’, but really what we need is ‘no external influence not built into the model is allowed’. The manufacture of a bottle from sand involves huge numbers of influences that are not accounted for if you track only the molecules in the bottle.
The traditional scenarios in the thermodynamics texts all involve this simplification. The text will discuss a box with a partition, containing gas molecules in one half (or some variant of this set-up). It will explain that if you then remove the partition, entropy increases. But what it doesn’t discuss is how the gas got into the box in that initial arrangement. Which had lower entropy than the gas did when it was part of the Earth’s atmosphere. Agreed, that’s no longer a closed system. But what really matters here is the type of system, or, more specifically, the initial conditions assumed. The mathematics doesn’t tell us how those conditions were actually realised. Running the smashing-bottle model backwards doesn’t lead to sand. So the model really only applies to forward time. I italicised two words in the above description: then and initial. In backward time, these have to change to before and final. The reason that time has a unique arrow in thermodynamics, despite the equations being time-reversible, is that the scenarios envisaged have an arrow of time built in: the use of initial conditions.
It’s an old story, repeated throughout human history. Everyone is so focused on the content that they ignore the context. Here, the content is reversible, but the context isn’t. That’s why thermodynamics doesn’t contradict Newton. But there’s another message. Discussing a concept as subtle as entropy using vague words like ‘disorder’ is likely to lead to confusion.