We demand rigidly defined areas of doubt and uncertainty! Douglas Adams, The Hitchhiker’s Guide to the Galaxy
IN THE 16TH AND 17TH centuries, two great figures of science noticed mathematical patterns in the natural world. Galileo Galilei observed them down on the ground, in the motion of rolling balls and falling bodies. Johannes Kepler discovered them in the heavens, in the orbital motion of the planet Mars. In 1687, building on their work, Newton’s Principia changed how we think about nature by uncovering deep mathematical laws that govern nature’s uncertainties. Almost overnight, many phenomena, from the tides to planets and comets, became predictable. European mathematicians quickly recast Newton’s discoveries in the language of calculus, and applied similar methods to heat, light, sound, waves, fluids, electricity, and magnetism. Mathematical physics was born.
The most important message from the Principia was that instead of concentrating on how nature behaves, we should seek the deeper laws that govern its behaviour. Knowing the laws, we can deduce the behaviour, gaining power over our environment and reducing uncertainty. Many of those laws take a very specific form: they are differential equations, which express the state of a system at any given moment in terms of the rate at which the state is changing. The equation specifies the laws, or the rules of the game. Its solution specifies the behaviour, or how the game plays out, at all instants of time: past, present, and future. Armed with Newton’s equations, astronomers could predict, with great accuracy, the motion of the Moon and planets, the timing of eclipses, and the orbits of asteroids. The uncertain and erratic motions of the heavens, guided by the whims of gods, were replaced by a vast cosmic clockwork machine, whose actions were entirely determined by its structure and its mode of operation.
Humanity had learned to predict the unpredictable.
In 1812 Laplace, in his Essai philosophique sur les probabilités (Philosophical Essay on Probabilities) asserted that in principle the universe is entirely deterministic. If a sufficiently intelligent being knew the present state of every particle in the universe, it would be able to deduce the entire course of events, both past and future, with exquisite detail. ‘For such an intellect,’ he wrote, ‘nothing would be uncertain, and the future just like the past would be present before its eyes.’ This view is parodied in Douglas Adams’s The Hitchhiker’s Guide to the Galaxy as the supercomputer Deep Thought, which ponders the Ultimate Question of Life, the Universe, and Everything, and after seven and a half million years gives the answer: 42.
For the astronomers of his era, Laplace was pretty much right. Deep Thought would have obtained excellent answers, as its real-world counterparts do today. But when astronomers started to ask more difficult questions, it became clear that although Laplace might be right in principle, there was a loophole. Sometimes predicting the future of some system, even just a few days ahead, required impossibly accurate data on the system’s state now. This effect is called chaos, and it has totally changed our view of the relation between determinism and predictability. We can know the laws of a deterministic system perfectly but still be unable to predict it. Paradoxically, the problem doesn’t arise from the future. It’s because we can’t know the present accurately enough.
SOME DIFFERENTIAL EQUATIONS ARE EASY to solve, with well-behaved answers. These are the linear equations, which roughly means that effects are proportional to causes. Such equations often apply to nature when changes are small, and the early mathematical physicists accepted this restriction in order to make headway. Nonlinear equations are difficult – often impossible to solve before fast computers appeared – but they’re usually better models of nature. In the late 19th century, the French mathematician Henri Poincaré introduced a new way to think about nonlinear differential equations, based on geometry instead of numbers. His idea, the ‘qualitative theory of differential equations’, triggered a slow revolution in our ability to handle nonlinearity.
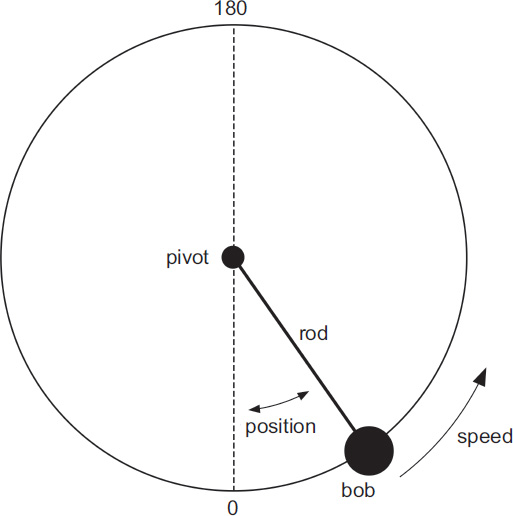
A pendulum, and the two variables specifying its state: position, measured as an angle anticlockwise, and speed, also measured anticlockwise (angular velocity).
To understand what he did, let’s look at a simple physical system, the pendulum. The simplest model is a rod with a heavy bob on the end, pivoted at a fixed point and swinging in a vertical plane. The force of gravity pulls the bob downwards, and initially we assume no other forces are acting, not even friction. In a pendulum clock, such as an antique grandfather clock, we all know what happens: the pendulum moves to and fro in a regular manner. (A spring or a weight on a pulley compensates for any energy lost through friction.) Legend has it that Galileo got the idea for a pendulum clock when he was watching a lamp swinging in a church and noticed that the timing was the same whatever angle it swung through. A linear model confirms this, as long as the swings are very small, but a more accurate nonlinear model shows that this isn’t true for larger swings.
The traditional way to model the motion is to write down a differential equation based on Newton’s laws. The acceleration of the bob depends on how the force of gravity acts in the direction the bob is moving: tangent to the circle at the position of the bob. The speed at any time can be found from the acceleration, and the corresponding position found from that. The dynamical state of the pendulum depends on those two variables: position and speed. For example, if it starts hanging vertically downwards at zero speed, it just stays there, but if the initial speed isn’t zero it starts to swing.
Solving the resulting nonlinear model is hard; so hard that to do it exactly you have to invent new mathematical gadgets called elliptic functions. Poincaré’s innovation was to think geometrically. The two variables of position and speed are coordinates on a so-called ‘state space’, which represents all possible combinations of the two variables – all possible dynamic states. Position is an angle; the usual choice is the angle measured anticlockwise from the bottom. Since 360° is the same angle as 0°, this coordinate wraps round into a circle, as shown in the diagram. Speed is really angular velocity, which can be any real number: positive for anticlockwise motion, negative for clockwise. State space (also called phase space for reasons I can’t fathom) is therefore a cylinder, infinitely long with circular cross-section. The position along it represents the speed, the angle round it represents the position.
If we start the pendulum swinging at some initial combination of position and speed, which is some point on the cylinder, those two numbers change as time passes, obeying the differential equation. The point moves across the surface of the cylinder, tracing out a curve (occasionally it stays fixed, tracing a single point). This curve is the trajectory of that initial state, and it tells us how the pendulum moves. Different initial states give different curves. If we plot a representative selection of these, we get an elegant diagram, called the phase portrait. In the picture I’ve sliced the cylinder vertically at 270° and opened it flat to make the geometry clear.
Most of the trajectories are smooth curves. Any that go off the right-hand edge come back in at the left-hand edge, because they join up on the cylinder, so most of the curves close up into loops. These smooth trajectories are all periodic: the pendulum repeats the same motions over and over again, forever. The trajectories surrounding point A are like the grandfather clock; the pendulum swings to and fro, never passing through the vertical position at 180°. The other trajectories, above and below the thick lines, represent the pendulum swinging round and round like a propeller, either anticlockwise (above the dark line) or clockwise (below).
Phase portrait of pendulum. Left- and right-hand sides of the rectangle are identified, because position is an angle. A: centre. B: saddle. C: homoclinic trajectory. D: another homoclinic trajectory.
Point A is the state where the pendulum is stationary, hanging down vertically. Point B is more interesting (and not found in a grandfather clock): the pendulum is stationary, pointing vertically upwards. Theoretically, it can balance there forever, but in practice the upward state is unstable. The slightest disturbance and the pendulum will fall off and head downwards. Point A is stable: slight disturbances just push the pendulum on to a tiny nearby closed curve, so it wobbles a little.
The thick curves C and D are especially interesting. Curve C is what happens if we start the pendulum very close to vertical, and give it a very tiny push so that it rotates anticlockwise. It then swings back up until it’s nearly vertical. If we give it just the right push, it rises ever more slowly and tends to the vertical position as time tends to infinity. Run time backwards, and it also approaches the vertical, but from the other side. This trajectory is said to be homoclinic: it limits on the same (homo) steady state for both forward and backward infinite time. There’s a second homoclinic trajectory D, where the rotation is clockwise.
We’ve now described all possible trajectories. Two steady states: stable at A, unstable at B. Two kinds of periodic state: grandfather clock and propeller. Two homoclinic trajectories: anticlockwise C and clockwise D. Moreover, the features A, B, C, and D organise all of these together in a consistent package. A lot of information is missing, however; in particular the timing. The diagram doesn’t tell us the period of the periodic trajectories, for instance. (The arrows show some timing information: the direction in which the trajectory is traversed as time passes.) However, it takes an infinite amount of time to traverse an entire homoclinic trajectory, because the pendulum moves ever more slowly as it nears the vertical position. So the period of any nearby closed trajectory is very large, and the closer it comes to C or D, the longer the period becomes. This is why Galileo was right for small swings, but not for bigger ones.
A stationary point (or equilibrium) like A is called a centre. One like B is a saddle, and near it the thick curves form a cross shape. Two of them, opposite each other, point towards B; the other two point away from it. These I’ll call the in-set and out-set of B. (They’re called stable and unstable manifolds in the technical literature, which I think is a bit confusing. The idea is that points on the in-set move towards B, so that’s the ‘stable’ direction. Points on the out-set move away, the ‘unstable’ direction.)
Point A is surrounded by closed curves. This happens because we ignored friction, so energy is conserved. Each curve corresponds to a particular value of the energy, which is the sum of kinetic energy (related to the speed) and potential energy (arising from gravity and depending on position). If there’s a small amount of friction, we have a ‘damped’ pendulum, and the picture changes. The closed trajectories turn into spirals, and the centre A becomes a sink, meaning all nearby states move towards it. The saddle B remains a saddle, but the out-set C splits into two pieces, both of which spiral towards A. This is a heteroclinic trajectory, connecting B to a different (hetero) steady state A. The in-set D also splits, and each half winds round and round the cylinder, never getting near A.
Phase portrait of a damped pendulum. A: sink. B: saddle. C: two branches of the out-set of the saddle, forming heteroclinic connections to the sink. D: two branches of the in-set of the saddle.
These two examples, the frictionless and damped pendulums, illustrate all of the main features of phase portraits when the state space is two-dimensional, that is, the state is determined by two variables. One caveat is that, as well as sinks, there can be sources: stationary points from which trajectories lead outwards. If you reverse all the arrows, A becomes a source. The other is that closed trajectories can still occur when energy isn’t conserved, though not in a mechanical model governed by friction. When they do, they’re usually isolated – there are no other closed trajectories nearby. Such a closed trajectory occurs, for example, in a standard model of the heartbeat, and it represents a normally beating heart. Any initial point nearby spirals ever closer to the closed trajectory, so the heartbeat is stable.
Poincaré and Ivar Bendixson proved a famous theorem, which basically says that any typical differential equation in two dimensions can have various numbers of sinks, sources, saddles, and closed cycles, which may be separated by homoclinic and heteroclinic trajectories, but nothing else. It’s all fairly simple, and we know all the main ingredients. That changes dramatically when there are three or more state variables, as we’ll now see.
IN 1961 THE METEOROLOGIST EDWARD LORENZ was working on a simplified model of convection in the atmosphere. He was using a computer to solve his equations numerically, but he had to stop in the middle of a run. So he entered the numbers again by hand to restart the calculation, with some overlap to check all was well. After a time, the results diverged from his previous calculations, and he wondered whether he’d made a mistake when he typed the numbers in again. But when he checked, the numbers were correct. Eventually he discovered that the computer held numbers internally to more digits than it printed out. This tiny difference somehow ‘blew up’ and affected the digits that it did print out. Lorenz wrote: ‘One meteorologist remarked that if the theory were correct, one flap of a seagull’s wings could change the course of weather forever.’
The remark was intended as a put-down, but Lorenz was right. The seagull quickly morphed into the more poetic butterfly, and his discovery became known as the ‘butterfly effect’. To investigate it, Lorenz applied Poincaré’s geometric method. His equations have three variables, so state space is three-dimensional space. The picture shows a typical trajectory, starting from lower right. It rapidly approaches a shape rather like a mask, with the left half pointing out of the page towards us, and the right half pointing away from us. The trajectory spirals around inside one half for a while, then switches to the other half, and keeps doing this. But the timing of the switches is irregular – apparently random – and the trajectory isn’t periodic.
If you start somewhere else, you get a different trajectory, but it ends up spiralling around the same mask-like shape. That shape is therefore called an attractor. It looks like two flat surfaces, one for each half, which come together at top centre and merge. However, a basic theorem about differential equations says that trajectories never merge. So the two separate surfaces must lie on top of each other, very close together. However, this implies that the single surface at the bottom actually has two layers. But then the merging surfaces also have two layers, so the single surface at the bottom actually has four layers. And...

Typical trajectory of the Lorenz equations in three-dimensional space, converging on to a chaotic attractor.
The only way out is that all the apparent surfaces have infinitely many layers, closely sandwiched together in a complicated way. This is one example of a fractal, the name coined by Benoit Mandelbrot for any shape that has detailed structure however much you magnify it.
Lorenz realised that this strange shape explains why his second run on the computer diverged from the first. Imagine two trajectories, starting very close together. They both head off to one half of the attractor, say the left half, and they both spiral round inside it. But as they continue, they start to separate – the spiral paths stay on the attractor, but diverge. When they get near the middle, where the surfaces merge, it’s then possible for one to head off to the right half while the other makes a few more spirals round the left half. By the time that one crosses over into the right half, the other one has got so far away that it’s moving pretty much independently.
This divergence is what drives the butterfly effect. On this kind of attractor, trajectories that start close together move apart and become essentially independent – even though they’re both obeying the same differential equation. This means that you can’t predict the future state exactly, because any tiny initial error will grow ever faster until it’s comparable in size to the whole attractor. This type of dynamics is called chaos, and it explains why some features of the dynamics look completely random. However, the system is completely deterministic, with no explicit random features in the equations.36
Lorenz called this behaviour ‘unstable’, but we now see it as a new type of stability, associated with an attractor. Informally, an attractor is a region of state space such that any initial condition starting near that region converges towards a trajectory that lies in the region. Unlike the traditional attractors of classical mathematics, points and closed loops, chaotic attractors have more complex topology – they’re fractal.
An attractor can be a point or a closed loop, which correspond to a steady state or a periodic one. But in three or more dimensions it can be far more complicated. The attractor itself is a stable object, and the dynamics on it is robust: if the system is subjected to a small disturbance, the trajectory can change dramatically; however, it still lies on the same attractor. In fact, almost any trajectory on the attractor explores the whole attractor, in the sense that it eventually gets as near as we wish to any point of the attractor. Over infinite time, nearly all trajectories fill the attractor densely.
Stability of this kind implies that chaotic behaviour is physically feasible, unlike the usual notion of instability, where unstable states are usually not found in reality – for example, a pencil balancing on its point. But in this more general notion of stability, the details are not repeatable, only the overall ‘texture’. The technical name for Lorenz’s observation reflects this situation: not ‘butterfly effect’, but ‘sensitivity to initial conditions’.
LORENZ’S PAPER BAFFLED MOST METEOROLOGISTS, who were worried that the strange behaviour arose because his model was oversimplified. It didn’t occur to them that if a simple model led to such strange behaviour, a complicated one might be even stranger. Their ‘physical intuition’ told them that a more realistic model would be better behaved. We’ll see in Chapter 11 that they were wrong. Mathematicians didn’t notice Lorenz’s paper for a long time because they weren’t reading meteorology journals. Eventually they did, but only because the American Stephen Smale had been following up an even older hint in the mathematical literature, discovered by Poincaré in 1887–90.
Poincaré had applied his geometric methods to the infamous three-body problem: how does a system of three bodies – such as the Earth, Moon and Sun – behave under Newtonian gravitation? His eventual answer, once he corrected a significant mistake, was that the behaviour can be extraordinarily complex. ‘One is struck with the complexity of this figure that I am not even attempting to draw,’ he wrote. In the 1960s Smale, the Russian Vladimir Arnold, and colleagues extended Poincaré’s approach and developed a systematic and powerful theory of nonlinear dynamical systems, based on topology – a flexible kind of geometry that Poincaré had also pioneered. Topology is about any geometric property that remains unchanged by any continuous deformation, such as when a closed curve forms a knot, or whether some shape falls apart into disconnected pieces. Smale hoped to classify all possible qualitative types of dynamic behaviour. In the end this proved too ambitious, but along the way he discovered chaos in some simple models, and realised that it ought to be very common. Then the mathematicians dug out Lorenz’s paper and realised his attractor is another, rather fascinating, example of chaos.
Some of the basic geometry we encountered in the pendulum carries over to more general systems. The state space now has to be multidimensional, with one dimension for each dynamic variable. (‘Multidimensional’ isn’t mysterious; it just means that algebraically you have a long list of variables. But you can apply geometric thinking by analogy with two and three dimensions.) Trajectories are still curves; the phase portrait is a system of curves in a higher-dimensional space. There are steady states, closed trajectories representing periodic states, and homoclinic and heteroclinic connections. There are generalisations of in-sets and out-sets, like those of the saddle point in the pendulum model. The main extra ingredient is that in three or more dimensions, there can be chaotic attractors.
The appearance of fast, powerful computers gave the whole subject a boost, making it much easier to study nonlinear dynamics by approximating the behaviour of the system numerically. This option had always been available in principle, but performing billions or trillions of calculations by hand wasn’t a viable option. Now, a machine could do the task, and unlike a human calculator, it didn’t make arithmetical mistakes.
Synergy among these three driving forces – topological insight, the needs of applications, and raw computer power – created a revolution in our understanding of nonlinear systems, the natural world, and the world of human concerns. The butterfly effect, in particular, implies that chaotic systems are predictable only for a period of time up to some ‘prediction horizon’. After that, the prediction inevitably becomes too inaccurate to be useful. For weather, the horizon is a few days. For tides, many months. For the planets of the solar system, tens of millions of years. But if we try to predict where our own planet will be in 200 million years’ time, we can be fairly confident that its orbit won’t have changed much, but we have no idea whereabouts in that orbit it will be.
However, we can still say a lot about the long-term behaviour in a statistical sense. The mean values of the variables along a trajectory, for example, are the same for all trajectories on the attractor, ignoring rare things such as unstable periodic trajectories, which can coexist inside the attractor. This happens because almost every trajectory explores every region of the attractor, so the mean values depend only on the attractor. The most significant feature of this kind is known as an invariant measure, and we’ll need to know about that when discussing the relation between weather and climate in Chapter 11, and speculating on quantum uncertainty in Chapter 16.
We already know what a measure is. It’s a generalisation of things like ‘area’, and it gives a numerical value to suitable subsets of some space, much like a probability distribution does. Here, the relevant space is the attractor. The simplest way to describe the associated measure is to take any dense trajectory on the attractor – one that comes as close as we wish to any point as long as we wait long enough. Given any region of the attractor, we assign a measure to it by following this trajectory for a very long time and counting the proportion of time that it spends inside that region. Let the time become very large, and you’ve found the measure of that region. Because the trajectory is dense, this in effect defines the probability that a randomly chosen point of the attractor lies in that region.37
There are many ways to define a measure on an attractor. The one we want has a special feature: it’s dynamically invariant. If we take some region, and let all of its points flow along their trajectories for some specific time, then in effect the entire region flows. Invariance means that as the region flows, its measure stays the same. All of the important statistical features of an attractor can be deduced from the invariant measure. So despite the chaos we can make statistical predictions, giving our best guesses about the future, with estimates of how reliable they are.
DYNAMICAL SYSTEMS, THEIR TOPOLOGICAL FEATURES, AND invariant measures will turn up repeatedly from now on. So we may as well clear up a few more points now, while we’re clued in on that topic.
There are two distinct types of differential equation. An ordinary differential equation specifies how a finite number of variables change as time passes. For example, the variables might be the positions of the planets of the solar system. A partial differential equation applies to a quantity that depends on both space and time. It relates rates of change in time to rates of change in space. For example, waves on the ocean have both spatial and temporal structure: they form shapes, and the shapes move. A partial differential equation relates how fast the water moves, at a given location, to how the overall shape is changing. Most of the equations of mathematical physics are partial differential equations.
Today, any system of ordinary differential equations is called a ‘dynamical system’, and it’s convenient to extend that term metaphorically to partial differential equations, which can be viewed as differential equations in infinitely many variables. So, in broad terms, I’ll use the term ‘dynamical system’ for any collection of mathematical rules that determines the future behaviour of some system in terms of its state – the values of its variables – at any instant.
Mathematicians distinguish two basic types of dynamical system: discrete and continuous. In a discrete system, time ticks in whole numbers, like the second hand of a clock. The rules tell us what the current state will become, one tick into the future. Apply the rule again, and we deduce the state two ticks into the future, and so on. To find out what happens in a million ticks’ time, apply the rule a million times. It’s obvious that such a system is deterministic: given the initial state, all subsequent states are uniquely determined by the mathematical rule. If the rule is reversible, all past states are also determined.
In a continuous system, time is a continuous variable. The rule becomes a differential equation, specifying how rapidly the variables change at any moment. Subject to technical conditions that are almost always valid, given any initial state, it’s possible in principle to deduce the state at any other time, past or future.
THE BUTTERFLY EFFECT IS FAMOUS enough to be lampooned in Terry Pratchett’s Discworld books Interesting Times and Feet of Clay as the quantum weather butterfly. It’s less well known that there are many other sources of uncertainty in deterministic dynamics. Suppose there are several attractors. A basic question is: For given initial conditions, which attractor does the system converge towards? The answer depends on the geometry of ‘basins of attraction’. The basin of an attractor is the set of initial conditions in state space whose trajectories converge to that attractor. This just restates the question, but the basins divide state space into regions, one for each attractor, and we can work out where these regions are. Often, the basins have simple boundaries, like frontiers between countries on a map. The main uncertainty about the final destination arises only for initial states very near these boundaries. However, the topology of the basins can be much more complicated, creating uncertainty for a wide range of initial conditions.
If state space is a plane, and the shapes of the regions are fairly simple, two of them can share a common boundary curve, but three or more can’t. The best they can do is to share a common boundary point. But in 1917 Kunizo Yoneyama proved that three sufficiently complicated regions can have a common boundary that doesn’t consist of isolated points. He credited the idea to his teacher Takeo Wada, and his construction is called the Lakes of Wada.

The first few stages in constructing the Lakes of Wada. Each disc puts out ever-finer protuberances that wind between the others. This process continues forever, filling the gaps between the regions.
A dynamical system can have basins of attraction that behave like the Lakes of Wada. An important example arises naturally in numerical analysis, in the Newton–Raphson method. This is a time-honoured numerical scheme for finding the solutions of an algebraic equation by a sequence of successive approximations, making it a discrete dynamical system, in which time moves one tick forward for each iteration. Wada basins also occur in physical systems, such as when light is reflected in four equal spheres that touch each other. The basins correspond to the four openings between spheres, through which the light ray eventually exits.
Riddled basins – like a colander, full of holes – are a more extreme version of Wada basins. Now we know exactly which attractors can occur, but their basins are so intricately intertwined that we have no idea which attractor the system will home in on. In any region of state space, however small, there exist initial points that end up on different attractors. If we knew the initial conditions exactly, to infinite precision, we could predict the eventual attractor, but the slightest error makes the final destination unpredictable. The best we can do is to estimate the probability of converging to a given attractor.
Riddled basins aren’t just mathematical oddities. They occur in many standard and important physical systems. An example is a pendulum driven by a periodically varying force at its pivot, subject to a small amount of friction; the attractors are various periodic states. Judy Kennedy and James Yorke have shown that their basins of attraction are riddled.38