![]()
3! − 2! = 4
The Magic of CountingThe Magic of Counting
Math with an Exclamation Point!
We began this book with the problem of adding the numbers from 1 to 100. We discovered the total of 5050 and found a nice formula for the sum of the first n numbers. Now suppose we were interested in finding the product of the numbers from 1 to 100; what would we get? A really big number! If you’re curious, it’s the 158-digit number given below:
9332621544394415268169923885626670049071596826438162146
8592963895217599993229915608941463976156518286253697920
827223758251185210916864000000000000000000000000
In this chapter, we will see how numbers like this are the foundation of counting problems. These numbers will enable us to determine such things as the number of ways to arrange a dozen books on a bookshelf (nearly half a billion), your chance of being dealt at least one pair in poker (not bad), and your chance of winning the lottery (not good).
When we multiply the numbers from 1 to n together, we denote the product as n!, which is pronounced “n factorial.” In other words,
n! = n × (n − 1) × (n − 2) × · · · × 3 × 2 × 1
For example,
5! = 5 × 4 × 3 × 2 × 1 = 120
I think the exclamation point is the appropriate notation since the number n! grows very quickly and, as we’ll see, it has many exciting and surprising applications. For convenience, mathematicians define 0! = 1, and n! is not defined when n is a negative number.
Aside
From its definition, many people expect that 0! should be equal to 0. But let me try to convince you why 0! = 1 makes sense. Notice that for n ≥ 2, n! = n × (n − 1)!, and so
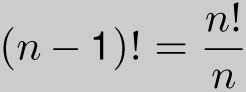
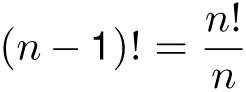
If we want that statement to remain true when n = 1, this would require that

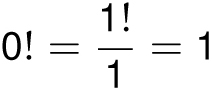
As seen below, factorials grow surprisingly quickly:


How big are these numbers? It’s been estimated that there are about 1022 grains of sand in the world and about 1080 atoms in the universe. If you thoroughly mix up a deck of 52 cards, which we’ll see can be done 52! ways, there is a very good chance that the order you obtained has never been seen before and will never be seen again, even if every person on earth produced a new shuffled deck every minute for the next million years!
Aside
At the beginning of this chapter, you probably noticed that 100! ended with lots of zeros. Where did all the zeros come from? When multiplying the numbers from 1 to 100 we obtain a 0 every time a multiple of 5 is multiplied by a multiple of 2. Among the numbers from 1 to 100 there are 20 multiples of 5 and 50 even numbers, which might suggest that we should have 20 zeros at the end. But the numbers 25, 50, 75, and 100 each contribute an additional factor of 5, so 100! will end with 24 zeros.
Just like in Chapter 1, there are many beautiful number patterns using factorials. Here is one my favorites.
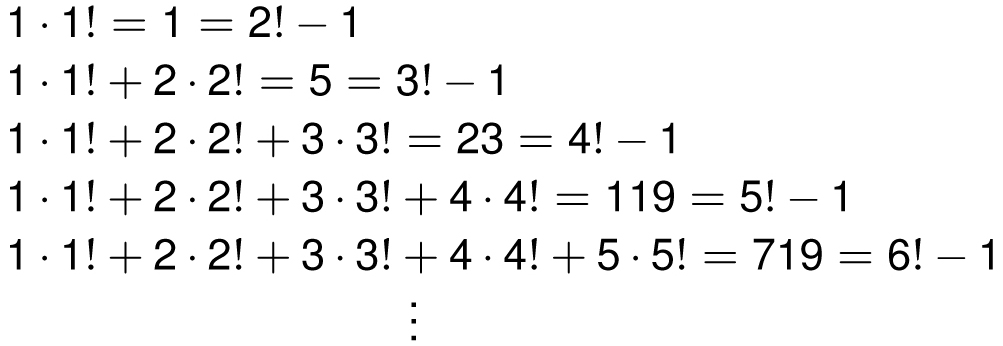
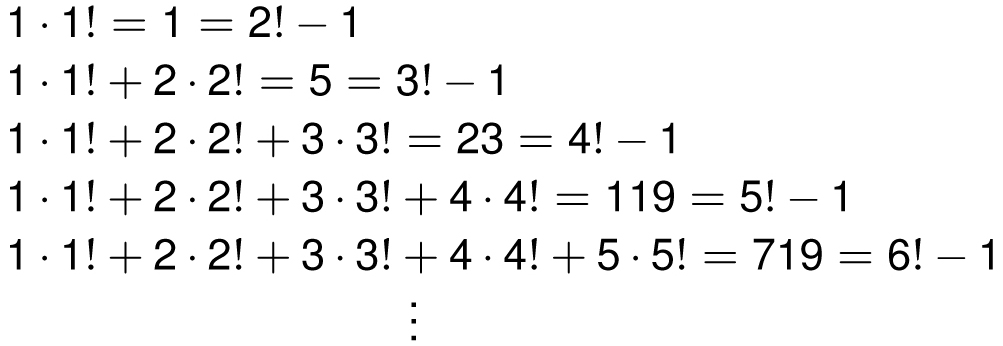
A factorial number pattern
The Rule of Sum and Product
Most counting problems essentially boil down to two rules: The rule of sum and the rule of product. The rule of sum is used when you want to count the total number of options you have when you have different types of choices. For example, if you had 3 short-sleeved shirts and 5 long-sleeved shirts, then you have 8 different choices for which shirt to wear. In general, if you have two types of objects, where there are a choices for the first type and b choices for the second type, then there are a + b different objects (assuming that none of the b choices are the same as any of the a choices).
Aside
The rule of sum, as stated, assumes that the two types of objects have no objects in common. But if there are c objects that belong to both types, then those objects would be counted twice. Hence the number of different objects would be a + b − c. For example, if a class of students has 12 dog owners, 19 cat owners, and 7 students who own both dogs and cats, then the number of students who own a cat or a dog would be 12 + 19 − 7 = 24. For a more mathematical example, among the numbers from 1 to 100 there are 50 multiples of 2, 33 multiples of 3, and 16 numbers that are multiples of 2 and 3 (namely the multiples of 6). Hence the number of numbers between 1 and 100 that are multiples of 2 or 3 is 50 + 33 − 16 = 67.
The rule of product says that if an action consists of two parts, and there are a ways to do the first part and then b ways to do the second part, then the action can be completed in a × b ways. For instance, if I own 5 different pairs of pants and 8 different shirts, and if I don’t care about color coordination (which I’m afraid applies to most mathematicians), then the number of different outfits is 5 × 8 = 40. If I own 10 ties and an outfit consists of shirt, pants, and tie, then there would be 40 × 10 = 400 outfits.
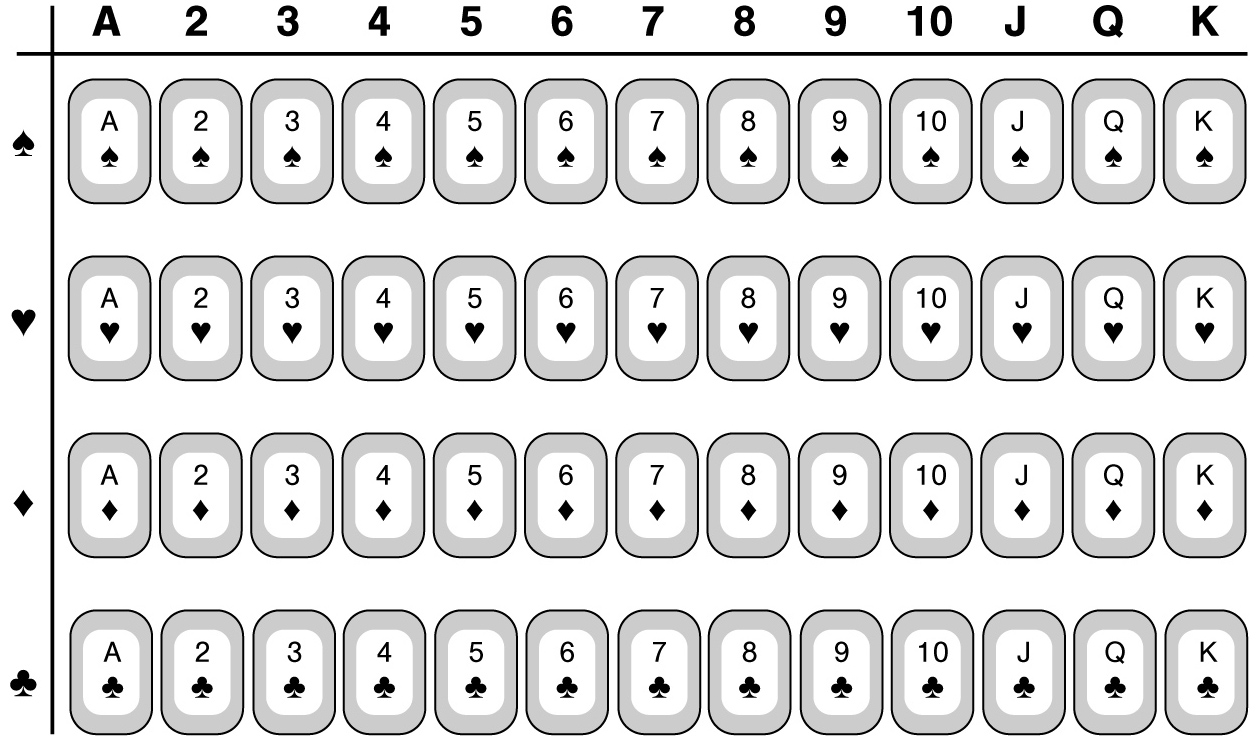
In a typical deck of cards, each card is assigned one of 4 suits (spades, hearts, diamonds, or clubs) and one of 13 values (A, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, or K). Hence the number of cards in a deck is 4 × 13 = 52. If we wanted to, we could deal out all 52 cards in a 4-by-13 rectangle, which is another way of seeing that there are 52 cards.

Let’s apply the rule of product to count zip codes. How many five-digit zip codes are theoretically possible? Each digit of a zip code can be any number from 0 to 9, so the smallest zip code could be 00000 and the largest would be 99999; hence there are 100,000 possibilities. But you can also see this by the rule of product. You have 10 choices for the first digit (0 through 9) then 10 choices for the second digit, 10 choices for the third, 10 choices for the fourth, and 10 choices for the fifth. Hence there are 105 = 100,000 possible zip codes.
When counting zip codes, numbers were allowed to be repeated. Now let’s look at the situation where objects can’t be repeated, such as when you are arranging objects in a row. It’s easy to see that two objects can be arranged 2 ways. For instance, letters A and B can be arranged either as AB or as BA. And three objects can be arranged 6 ways: ABC, ACB, BAC, BCA, CAB, CBA. Now can you see how four objects can be arranged in 24 ways without explicitly writing them down? There are 4 choices for which letter goes first (either A or B or C or D). Once that letter has been chosen, there will be 3 choices for the next letter, then 2 choices for the next letter, and finally there is only 1 possibility for the last letter. Altogether, there are 4 × 3 × 2 × 1 = 4! = 24 possibilities. In general, there are n! ways to arrange n different objects.
We combine the rules of sum and product in this next example. Suppose a state manufactures license plates of two varieties. Type I license plates consist of 3 letters followed by 3 digits. Type II license plates consist of 2 letters followed by 4 digits. How many license plates are possible? (We allow all 26 letters and all 10 digits, ignoring the confusion that can occur with similar characters like O and 0.) From the rule of product, the number of Type I plates is:
26 × 26 × 26 × 10 × 10 × 10 = 17,576,000
The number of Type II plates is
26 × 26 × 10 × 10 × 10 × 10 = 6,760,000
Since every plate is either Type I or Type II (not both), then the rule of sum says that the number of possibilities is their total: 24,336,000.
One of the pleasures of doing counting problems (mathematicians call this branch of mathematics combinatorics) is that quite often you can solve the same problem in more than one way. (We saw this was true with mental arithmetic problems too.) The last problem can actually be done in one step. The number of license plates is
26 × 26 × 36 × 10 × 10 × 10 = 24,336,000
since the first two characters of the plate can each be chosen 26 ways, the last 3 characters can each be chosen 10 ways, and the third character, depending on whether it was a letter or a digit, can be chosen 26 + 10 = 36 ways.
Lotteries and Poker Hands
In this section, we’ll apply our new counting skills to determine the chance of winning the lottery or being dealt various types of poker hands. But first let’s relax with a little bit of ice cream.
Suppose an ice cream shop offers 10 flavors of ice cream. How many ways can you create a triple cone? When creating a cone, the order of the flavors matters (of course!). If the flavors are allowed to be repeated, then since we have 10 choices for each of the three scoops, there would be 103 = 1000 possible cones. If we insist that all three flavors be different, then the number of cones is 10 × 9 × 8 = 720, as illustrated opposite.
But now for the real question. How many ways can you put three different flavors in a cup, where order does not matter? Since order doesn’t matter, there are fewer possibilities. In fact, there are 1/6th as many ways. Why is that? For any choice of three different flavors in a cup (say chocolate, vanilla, and mint chip), there are 3! = 6 ways that they can be arranged on a cone. Hence there would be 6 times as many cones as cups. Consequently, the number of cups is


Another way to write 10 × 9 × 8 is 10!/7! (although the first expression is easier to calculate). Hence the number of cups can be expressed as 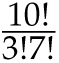
![]() . We call this expression “10 choose 3,” and it is denoted by the symbol
. We call this expression “10 choose 3,” and it is denoted by the symbol 
![]() , which equals 120. In general, the number of ways to choose different objects where order does not matter from a collection of n different objects is pronounced “n choose k” and has the formula
, which equals 120. In general, the number of ways to choose different objects where order does not matter from a collection of n different objects is pronounced “n choose k” and has the formula
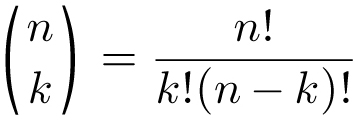
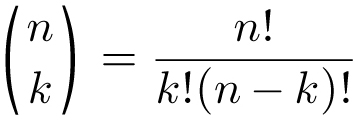
Mathematicians refer to these counting problems as combinations, and numbers of the form 
![]() are called binomial coefficients. Counting problems where the order does matter are called permutations. It’s easy to mix these terms up—for example, we often refer to a “combination lock” when we really should be saying “permutation lock,” since the order that the numbers are used is important.
are called binomial coefficients. Counting problems where the order does matter are called permutations. It’s easy to mix these terms up—for example, we often refer to a “combination lock” when we really should be saying “permutation lock,” since the order that the numbers are used is important.
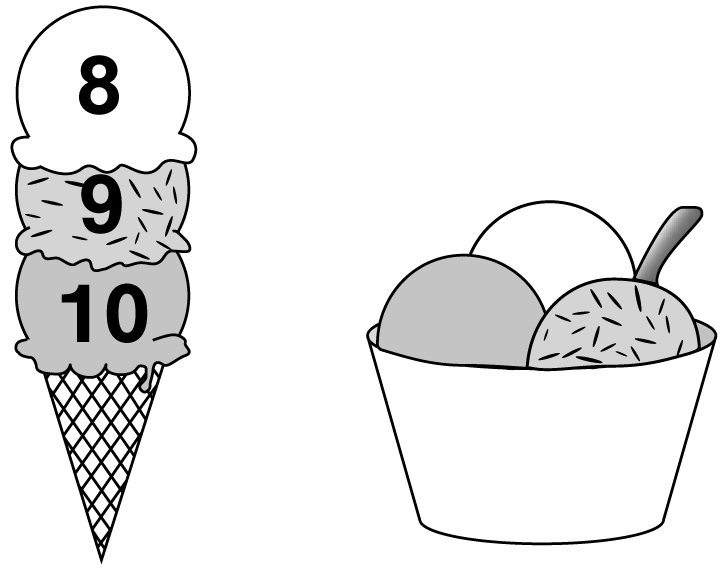
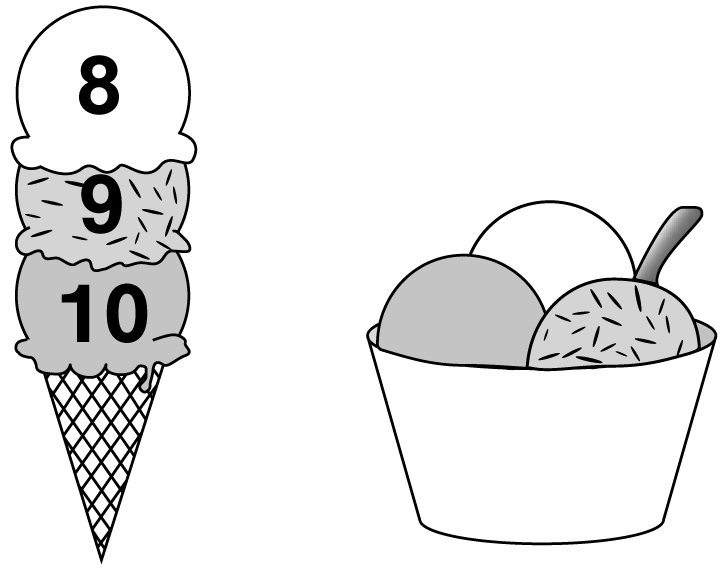
For every cup with 3 flavors, there are 3! = 6 ways to arrange them on a cone
If the ice cream shop offered 20 flavors and you wish to fill a bucket with 5 scoops consisting of all different flavors (where order is not important), then there would be
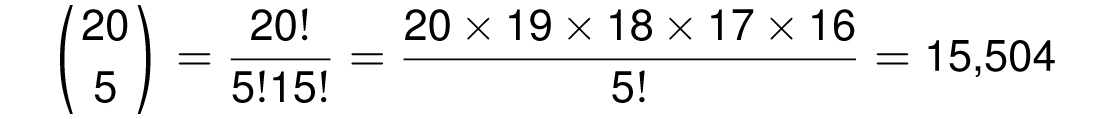
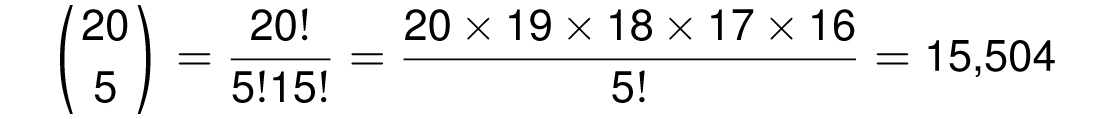
possibilities. By the way, if your calculator does not have a button that computes 
![]() , you can just type the words “20 choose 5” into your favorite search engine and it will probably display a calculator with the answer.
, you can just type the words “20 choose 5” into your favorite search engine and it will probably display a calculator with the answer.
Binomial coefficients sometimes appear in problems where order seems to matter. If we flip a coin 10 times, how many possible sequences are there (like HTHTTHHTTT or HHHHHHHHHH)? Since there are 2 possible outcomes for each flip, then the rule of product tells us that there are 210 = 1024 sequences, each of which has the same probability of occurring. (Some people are initially surprised by this, since the second sequence in our example may seem less probable than the first one, but they each have probability of 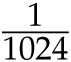
![]() .) On the other hand, it is way more likely for ten flips of a coin to produce 4 heads than 10 heads. There is just one way to achieve 10 heads, so that has probability
.) On the other hand, it is way more likely for ten flips of a coin to produce 4 heads than 10 heads. There is just one way to achieve 10 heads, so that has probability 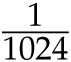
![]() . But how many ways can we get 4 heads out of 10? Such a sequence is determined by picking 4 of the 10 flips to be heads, and the rest are forced to be tails. The number of ways to determine which 4 of the 10 flips are to be heads is
. But how many ways can we get 4 heads out of 10? Such a sequence is determined by picking 4 of the 10 flips to be heads, and the rest are forced to be tails. The number of ways to determine which 4 of the 10 flips are to be heads is 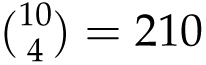
![]() . (It’s like picking 4 different scoops of ice cream among 10 possible flavors.) Hence when a fair coin is flipped 10 times, the probability that we get exactly 4 heads is
. (It’s like picking 4 different scoops of ice cream among 10 possible flavors.) Hence when a fair coin is flipped 10 times, the probability that we get exactly 4 heads is
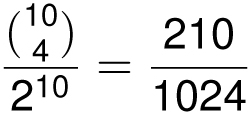
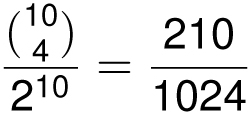
which is about 20 percent of the time.
Aside
It’s natural to ask, from 10 possible flavors, how many cups with 3 scoops can be made if repetition of flavors is allowed? (The answer is not 103/6, which is not even a whole number!) The direct approach would be to consider three cases, depending on the number of different flavors in the cup. Naturally there are 10 cups that use just one flavor and, from the above discussion, there are 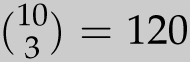
![]() cups that use three flavors. There are
cups that use three flavors. There are 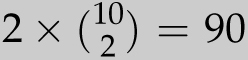
![]() cups that use two flavors, since we can choose the two flavors in
cups that use two flavors, since we can choose the two flavors in 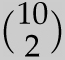
![]() ways, then decide which of the flavors gets two scoops. Adding all three cases together, the number of cups is 10 + 120 + 90 = 220.
ways, then decide which of the flavors gets two scoops. Adding all three cases together, the number of cups is 10 + 120 + 90 = 220.
There is another way to get this answer without breaking it into three cases. Any cup can be represented using 3 stars and 9 bars. For example, choosing flavors 1, 2, and 2 can be represented by the star-bar arrangement
* | ** | | | | | | | |
Picking flavors 2, 2, and 7 would look like
| ** | | | | | * | | |
and the star-bar arrangement
| | * | | * | | | | | *
would be a cup with flavors 3, 5, and 10. Every arrangement of 3 stars and 9 bars corresponds to a different cup. Together the stars and bars occupy 12 spaces, 3 of which are occupied by stars. Hence, the stars and bars can be arranged in 
![]() ways. More generally, the number of ways to choose k objects out of n where order is not important, but repetition is allowed, is the number of ways to arrange k stars and n − 1 bars, which can be done in
ways. More generally, the number of ways to choose k objects out of n where order is not important, but repetition is allowed, is the number of ways to arrange k stars and n − 1 bars, which can be done in 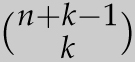
![]() ways.
ways.


Many problems involving games of chance involve combinations. For example, in the California Lottery, you pick 5 different numbers between 1 and 47. Additionally, you choose a MEGA number between 1 and 27 (which is allowed to be a repeat of one of your 5 chosen numbers). There are 27 choices for the MEGA number and the other 5 numbers can be chosen 
![]() ways. Hence the number of possibilities is
ways. Hence the number of possibilities is
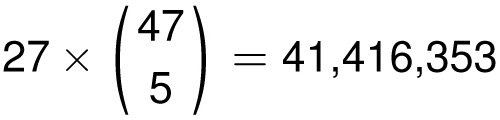
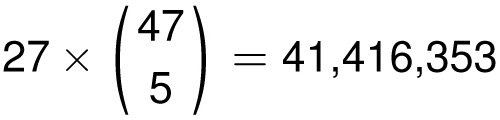
Thus your chance of winning the lottery grand prize is about 1 in 40 million.
Now let’s switch gears and consider the game of poker. A typical poker hand consists of 5 different cards chosen from 52 different cards, where the order of the 5 cards is unimportant. Hence the number of poker hands is
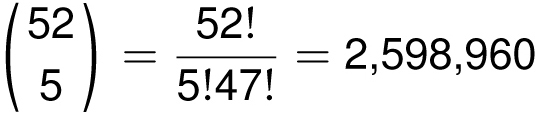
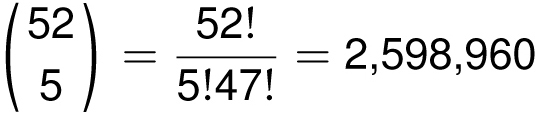
In poker, five cards of the same suit, such as
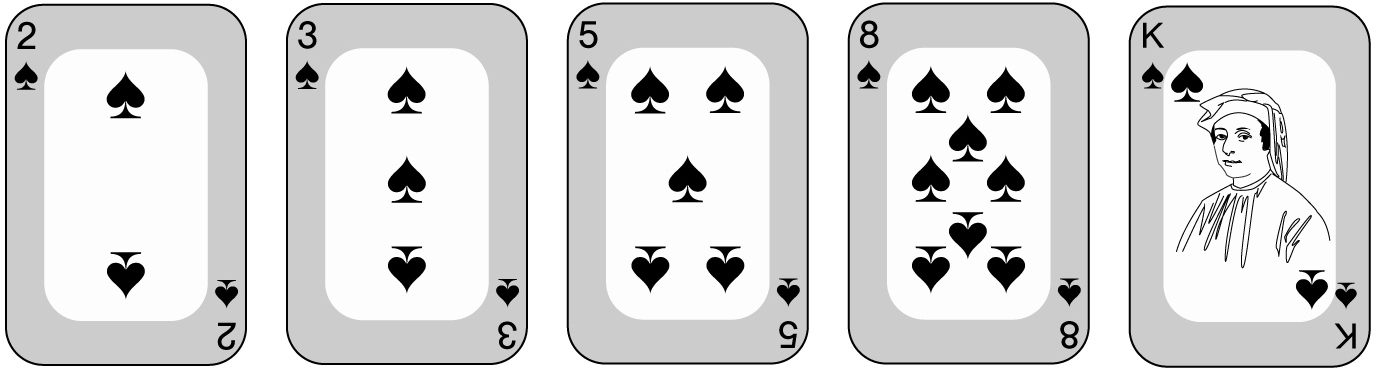

is called a flush. How many flushes are there? To create a flush, first choose your suit, which can be done in 4 ways. (Mentally, I like to commit to a definite choice, say spades.) Now how many ways can you choose 5 cards of that suit? From the 13 spades in a deck, 5 of them can be chosen in 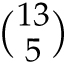
![]() ways. Hence the number of flushes is
ways. Hence the number of flushes is


Hence the chance of being dealt a flush in poker is 5148/2,598,960, which is approximately 1 in 500. For poker purists, you can subtract 4 × 10 = 40 hands from the 5148 for straight flushes, when the flush uses five consecutive cards.
A straight in poker consists of 5 cards of consecutive values, such as A2345 or 23456 or . . . or 10JQKA, like the one below.


There are 10 different types of straights (defined by the lowest card), and once we choose its type (say 34567) then each of the 5 cards can be assigned one of 4 suits. Hence the number of straights is
10 × 45 = 10,240
which is nearly twice as many as flushes. So the probability of being dealt a straight is about 1 in 250. That’s the reason flushes are worth more than straights in poker: they are harder to get.
An even more valuable hand is the full house, consisting of 3 cards of one value and 2 cards of a different value. A typical hand might look like this:


To construct a full house, we first need to choose a value to be tripled (13 ways), then a value to be doubled (12 ways). (Say we’ve decided on using three queens and two 7s.) Then we need to assign suits. We can decide which three queens to use in 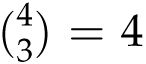
![]() ways and which two 7s in
ways and which two 7s in 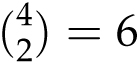
![]() ways. Altogether the number of full houses is
ways. Altogether the number of full houses is
13 × 12 × 4 × 6 = 3744
So the probability of being dealt a full house is 3744/2,598,960, which is about 1 in 700.
Let’s contrast the full house with getting exactly two pair. Such hands have two cards of one value, two cards of a different value, and another card of a third value, like


Many people mistakenly start counting the paired values with 13 × 12, but this double-counts, since first picking queens followed by 7s is the same as first picking 7s followed by queens. The correct way to start is 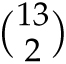
![]() (say picking queens and 7s together), then choosing a new value for the unpaired card (like 5), then assign suits. The number of two-pair hands is
(say picking queens and 7s together), then choosing a new value for the unpaired card (like 5), then assign suits. The number of two-pair hands is
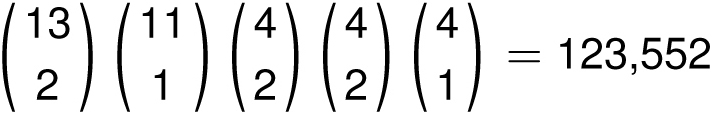
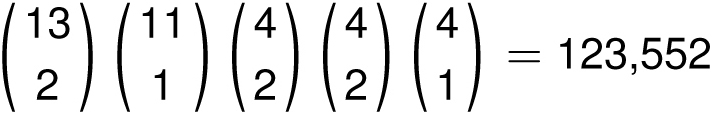
which occurs about 5 percent of the time.
We won’t go through all of the rest of the poker hands in detail, but see if you can verify the following. The number of poker hands that are four of a kind, like 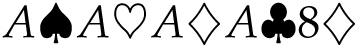
![]() , is
, is


A poker hand like 
![]() is called three of a kind. The number of these is
is called three of a kind. The number of these is
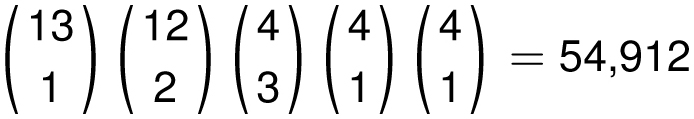
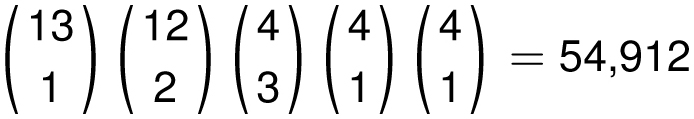
The number of poker hands with exactly one pair, like 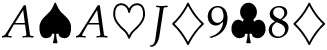
![]() , is
, is


about 42 percent of all hands.
Aside
So how many hands might be classified as junk, containing no pairs, no straight, and no flush? You could carefully add up the cases above and subtract from 
![]() , but here is a direct answer:
, but here is a direct answer:
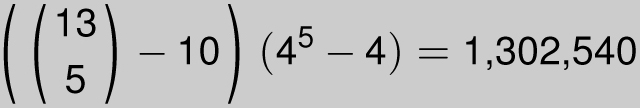
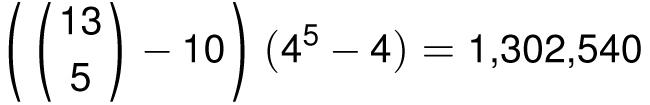
The first term counts the ways to choose any 5 different values (preventing two or more cards of the same value) with the exception of the 10 ways of picking five consecutive values like 34567. Then the next term assigns a suit to each of these five different values; there are 4 choices for each value, but we have to throw away the 4 possibilities that they were all assigned the same suit. The upshot is that about 50.1 percent of all hands are worth less than one pair. But that means 49.9 percent are worth one pair or better.
Here’s a question that has three interesting answers, two of which are actually correct! How many five-card hands contain at least one ace? A tempting wrong answer is simply 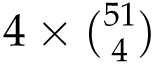
![]() . The (faulty) reasoning is that you pick an ace 4 ways, and then the other 4 cards can be chosen freely among the remaining 51 cards (including other aces). The problem with this reasoning is that some hands (those with more than one ace) get counted more than once. For instance, the hand
. The (faulty) reasoning is that you pick an ace 4 ways, and then the other 4 cards can be chosen freely among the remaining 51 cards (including other aces). The problem with this reasoning is that some hands (those with more than one ace) get counted more than once. For instance, the hand 
![]() would get counted when we first choose
would get counted when we first choose 
![]() (then the other 4 cards) as well as when we first choose the
(then the other 4 cards) as well as when we first choose the 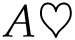
![]() (then the other 4 cards). A correct way to handle this problem is to break the problem into four cases, depending on the number of aces in the hand. For instance, the number of hands with exactly one ace is
(then the other 4 cards). A correct way to handle this problem is to break the problem into four cases, depending on the number of aces in the hand. For instance, the number of hands with exactly one ace is 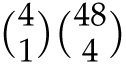
![]() (by picking one ace, then four non-aces). If we continue this way, and count hands with two, three, or four aces, the total number of hands with at least one ace is
(by picking one ace, then four non-aces). If we continue this way, and count hands with two, three, or four aces, the total number of hands with at least one ace is


But a quicker calculation can be done by addressing the opposite question. The number of hands with no aces is simply 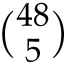
![]() . Hence the number of hands with at least one ace is
. Hence the number of hands with at least one ace is
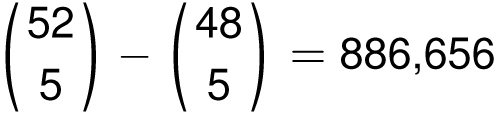
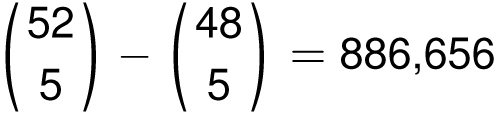
We noted earlier that poker hands are ranked according to how rare they are. For example, since there are more ways to be a single pair than two pair, one pair is worth less than two pair. The order of poker hands, from lowest to highest, is:
One pair
Two pair
Three of a kind
Straight
Flush
Full house
Four of a kind
Straight flush
A simple way to remember this is “One, two, three, straight, flush; two-three, four, straight-flush.” (“Two-three” is the full house.)
Now suppose we play poker with jokers (cards, not people). Here we have 54 cards where the two jokers are wild and can be assigned any value that gives you the best hand. So, for example, if you end up with 
![]() and joker, you would choose to make the joker an ace to give yourself three aces. If you turn the joker into a king, then your hand would be two pair, which is an inferior hand.
and joker, you would choose to make the joker an ace to give yourself three aces. If you turn the joker into a king, then your hand would be two pair, which is an inferior hand.


What card should we assign the joker to achieve the best hand?
But here’s where things get interesting. Under the traditional ordering of hands, if you are presented with hands like the one above that could be assigned two pair or three of a kind, then you would count it as three of a kind instead of two pair. But the consequence of this is that there will be more hands that would count as three of a kind than as two pair, so two pair would become the rarer hand. But if we try to fix that problem by making the two-pair hand more valuable, then the same problem occurs and we wind up with more hands that would count as two pair than as three of a kind. The surprising conclusion, discovered in 1996 by mathematician Steve Gadbois, is that when you play poker with jokers, there is no consistent way to rank the hands in order of frequency.
Patterns in Pascal’s Triangle
Behold Pascal’s triangle:


Pascal’s triangle with symbols
In Chapter 1, we saw interesting patterns arise when we put numbers in triangles. The numbers 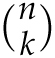
![]() that we’ve just been studying contain their own beautiful patterns when viewed in a triangle, called Pascal’s triangle, as displayed above. Using our formula
that we’ve just been studying contain their own beautiful patterns when viewed in a triangle, called Pascal’s triangle, as displayed above. Using our formula 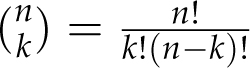
![]() , let’s turn these symbols into numbers and look for patterns (see next page). We will explain most of these patterns in this chapter, but feel free to skip the explanations on first reading and just enjoy the patterns.
, let’s turn these symbols into numbers and look for patterns (see next page). We will explain most of these patterns in this chapter, but feel free to skip the explanations on first reading and just enjoy the patterns.
The top row (called row 0) has just one term, namely 
![]() . (Remember 0! = 1.) Every row will begin and end with 1 since
. (Remember 0! = 1.) Every row will begin and end with 1 since


Have a look at row 5.
Row 5: 15 10 10 5 1
Notice that the second entry is 5, and in general, the second entry of row n is n. This makes sense because 
![]() , the number of ways to choose one object from n objects, is equal to n. Notice also that each row is
, the number of ways to choose one object from n objects, is equal to n. Notice also that each row is


Pascal’s triangle with numbers
symmetric: it reads the same backward as it does forward. For example, in row 5, we have
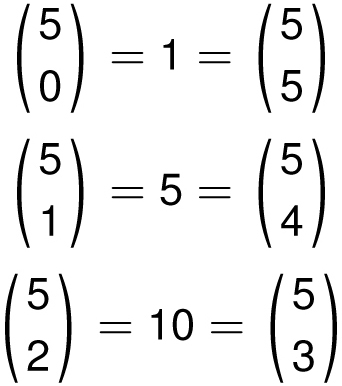
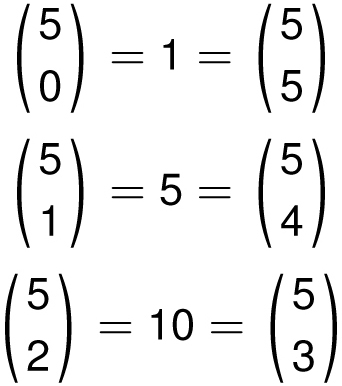
In general, the pattern says that
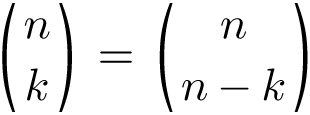
Aside
This symmetry relationship can be justified two ways. From the formula, we can algebraically show that
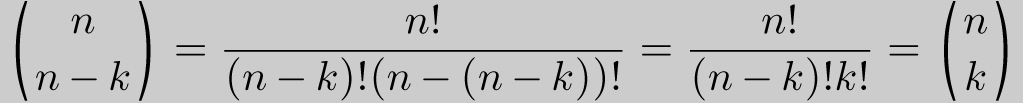
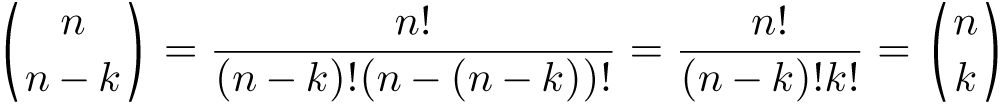
But you don’t really need the formula to see why it is true. For example, why should 
![]() The number
The number 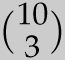
![]() counts the ways to choose 3 ice cream flavors (from 10 possibilities) to put in a cup. But this is the same as choosing 7 flavors to not put in the cup.
counts the ways to choose 3 ice cream flavors (from 10 possibilities) to put in a cup. But this is the same as choosing 7 flavors to not put in the cup.
The next pattern that you might notice is that, except for the 1s at the beginning and end of the row, every number is the sum of the two numbers above it. This relationship is so striking that we call it Pascal’s identity. For example, look at rows 9 and 10 in Pascal’s triangle.


Each number is the sum of the two numbers above it
Now why should that be? When we see that 120 = 36 + 84, this is a statement about the counting numbers
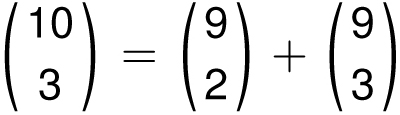
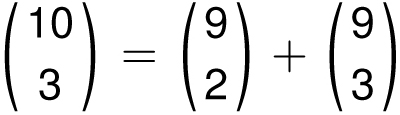
To see why this is true, let’s ask the question: If an ice cream store sells 10 flavors of ice cream, how many ways can you choose 3 different flavors of ice cream for a cup (where order is not important)? The first answer, as we have already noted, is 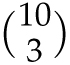
![]() . But there is another way to answer the question. Assuming that one of the possible flavors is vanilla, how many of the cups do not contain vanilla? That would be
. But there is another way to answer the question. Assuming that one of the possible flavors is vanilla, how many of the cups do not contain vanilla? That would be 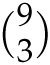
![]() , since we can choose any 3 flavors from the remaining 9 flavors. How many cups do contain vanilla? If vanilla is required to be one of the flavors, then there are just
, since we can choose any 3 flavors from the remaining 9 flavors. How many cups do contain vanilla? If vanilla is required to be one of the flavors, then there are just 
![]() ways to choose the remaining two flavors in the cup. Hence the number of possible cups is
ways to choose the remaining two flavors in the cup. Hence the number of possible cups is 
![]() . Which answer is right? Our logic was correct both times, so they are both right, and hence the two quantities are equal. By the same logic (or algebra, if you prefer), it follows that for any number k between 0 and n,
. Which answer is right? Our logic was correct both times, so they are both right, and hence the two quantities are equal. By the same logic (or algebra, if you prefer), it follows that for any number k between 0 and n,
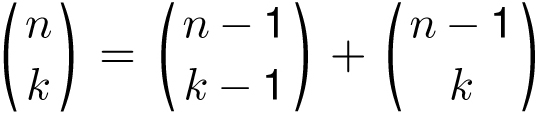
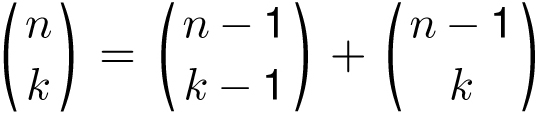
Now let’s see what happens when we add all of the numbers in each row of Pascal’s triangle, as seen on the opposite page.
The pattern suggests that the sum of the numbers in each row is always a power of 2. Specifically row n will add up to 2n. Why should that be? Another way to describe the pattern is that the first row sums to 1, and then the sum doubles with each new row. This makes sense if you think of Pascal’s identity, which we just proved. For instance, when we add the numbers in row 5, and rewrite them in terms of the numbers in row 4, we get
1 + 5 + 10 + 10 + 5 + 1
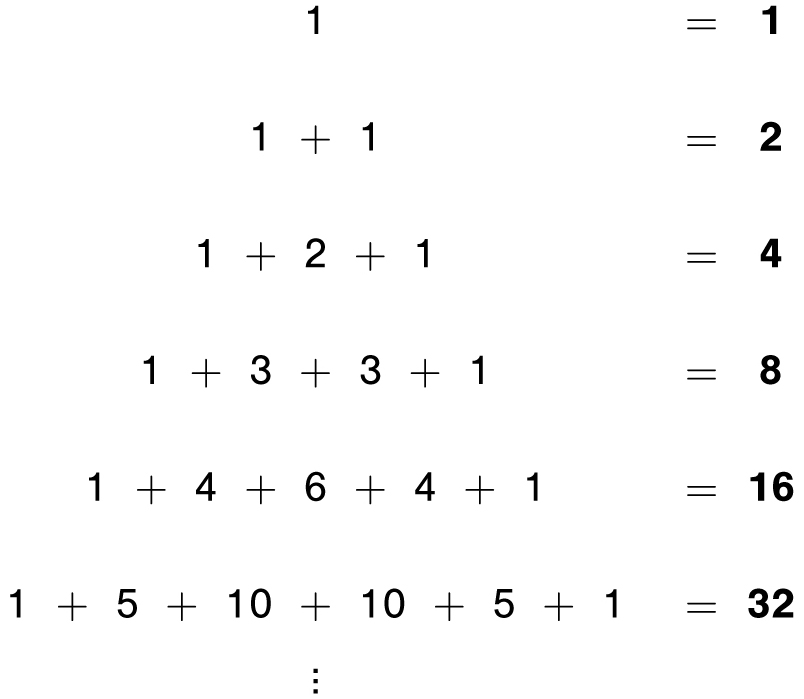
In Pascal’s triangle, the row sums are powers of 2
= 1 + (1 + 4) + (4 + 6) + (6 + 4) + (4 + 1) + 1
= (1 + 1) + (4 + 4) + (6 + 6) + (4 + 4) + (1 + 1)
which is literally twice the sum of the numbers in row 4. And by the same reasoning, this doubling pattern will continue forever.
In terms of the binomial coefficients, this identity says that when we sum the numbers in row n:
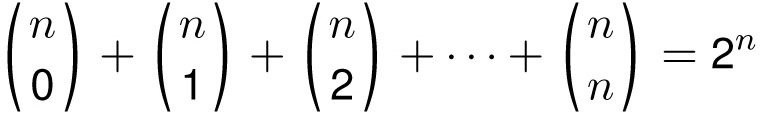
which is somewhat surprising, since the individual terms are evaluated with factorials, and are often divisible by many different numbers. And yet the grand total has 2 as its only prime factor.
Another way to explain this pattern is through counting. We call such an explanation a combinatorial proof. To explain the sum of the numbers in row 5, let’s go to an ice cream store that offers 5 flavors. (The argument for row n is similar.) How many ways can we put different scoops of ice cream in our cup with the restriction that no flavor is allowed to be repeated? Our cup is allowed to have 0 or 1 or 2 or 3 or 4 or 5 different flavors, and the order of the scoops in the cup is not important. How many ways can it have exactly 2 scoops? As we’ve seen before, this can be done 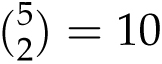
![]() different ways. Altogether, depending
different ways. Altogether, depending
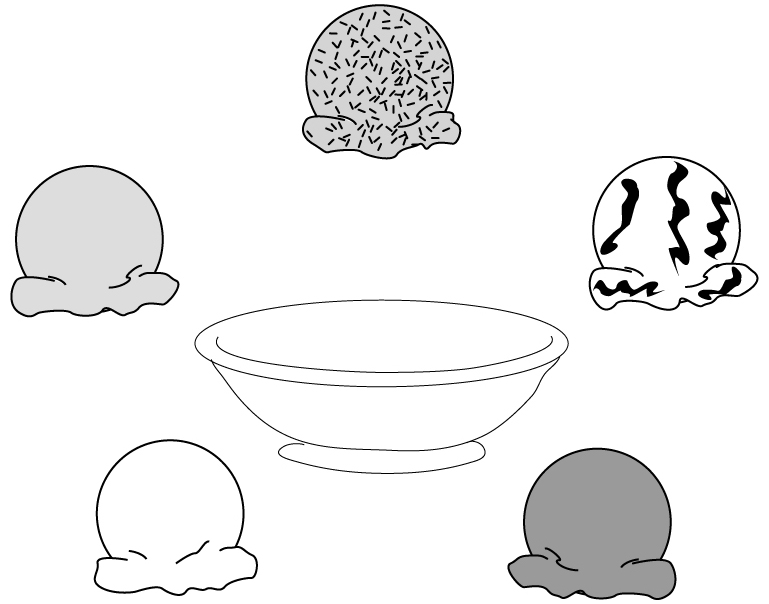

How many ways can we put different scoops of ice cream in our cup?
on the number of scoops in the cup, the rule of sum tells us that there are


ways, which simplifies to 1 + 5 + 10 + 10 + 5 + 1. On the other hand, we can also answer our question with the rule of product. Instead of deciding in advance how many scoops will be in our cup, we can look at each flavor and decide, yes or no, whether it will be in the cup. For instance, we have 2 choices for chocolate (yes or no), then 2 choices for vanilla (yes or no), and so on down to the fifth flavor. (Notice that if we decide “no” on each flavor, then we have an empty cup, which is permissible.) Hence the number of ways we can make our decision is
2 × 2 × 2 × 2 × 2 = 25
Since our reasoning was correct both times, it follows that


as predicted.
Aside
A similar combinatorial argument shows that if we sum every other number in row n, we get a total of 2n–1. This is no surprise in odd-numbered rows like row 5, since the numbers we are adding, 1 + 10 + 5, are the same as the numbers we are excluding, 5 + 10 + 1, so we get half of the 2n grand total. But it also works in even-numbered rows as well. For instance, in row 4, 1 + 6 + 1 = 4 + 4 = 23. In general, for any row n ≥ 1, we have
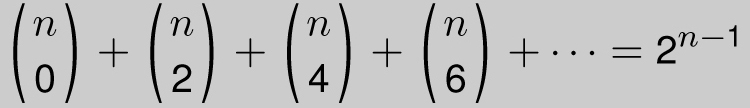

Why? The left side counts those ice cream cups that have an even number of scoops (when there are n possible flavors and all scoops must be different flavors). But we can also create such a cup by freely choosing flavors 1 through n − 1. We have 2 choices for the first flavor (yes or no), 2 choices for the second flavor, . . . , and 2 choices for the (n − 1)st flavor. But there is just one choice for the last flavor if we want the total number of flavors to be even. Hence the number of even-sized cups is 2n−1.
When we write Pascal’s triangle as a right triangle, more patterns emerge. The first column (column 0) consists of all 1s, the second column (column 1) are the positive integers 1, 2, 3, 4, and so on. Column 2, beginning 1, 3, 6, 10, 15 . . . , should also look familiar. These are the triangular numbers that we saw in Chapter 1. In general, the numbers in column 2 can also be expressed as
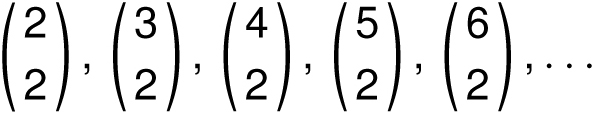
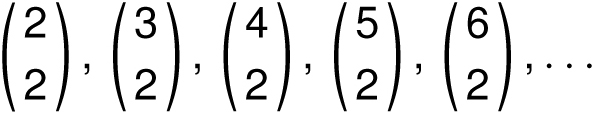
and column k consists of the numbers 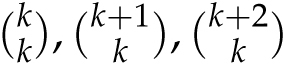
![]() , and so on.
, and so on.
Now look at what happens when you add the first few (or many) numbers of any column. For instance, if we add the first 5 numbers of column 2 (see next page), we get 1 + 3 + 6 + 10 + 15 = 35, which happens to be the number diagonally down from it. In other words:
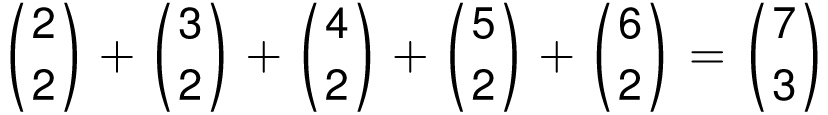
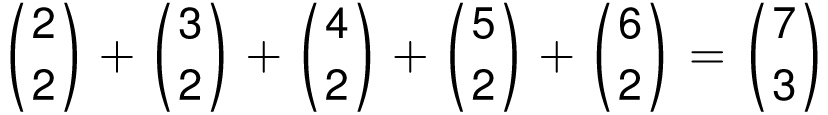
This is an example of the hockey stick identity because the pattern formed in Pascal’s triangle resembles a hockey stick, with a long column of numbers, next to another number jutting out from it. To understand why this pattern works, imagine we have a hockey team with 7 players, each with a different number on their jersey: 1, 2, 3, 4, 5, 6, 7. How
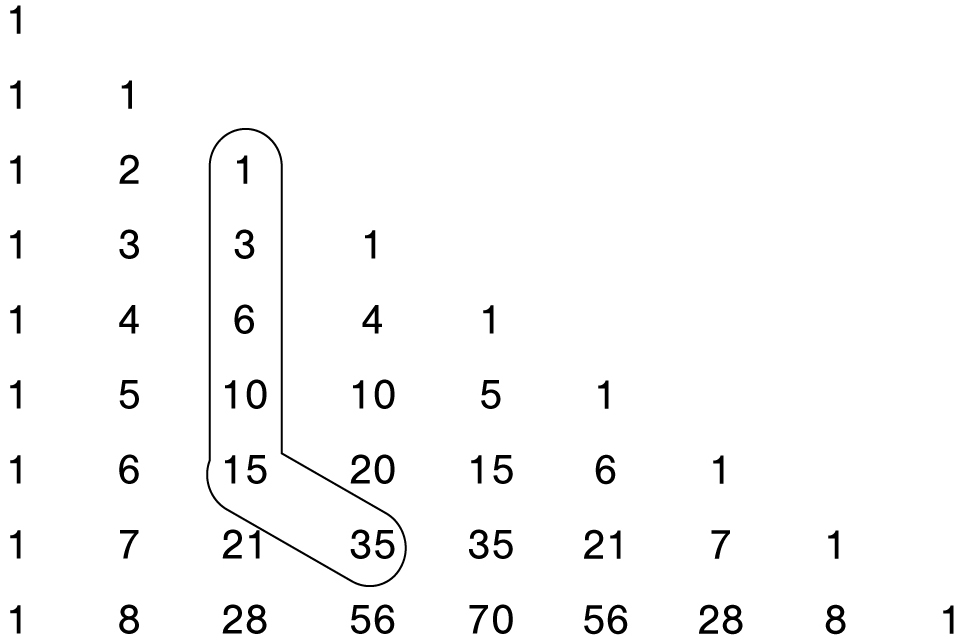

Pascal’s right triangle displays a “hockey stick” pattern
many ways can I choose 3 of these players for a practice session? Since order is not important, there are 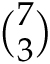
![]() ways this can be done. Now let’s answer that same question by breaking it into cases. How many of these ways include player 7? Equivalently, this asks: How many have 7 as the largest jersey number? Since 7 is included, there are
ways this can be done. Now let’s answer that same question by breaking it into cases. How many of these ways include player 7? Equivalently, this asks: How many have 7 as the largest jersey number? Since 7 is included, there are 
![]() ways to pick the other two players. Next, how many of these ways have 6 as the largest jersey number? Here, 6 must be chosen, and 7 must not be chosen, so there are
ways to pick the other two players. Next, how many of these ways have 6 as the largest jersey number? Here, 6 must be chosen, and 7 must not be chosen, so there are 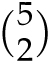
![]() ways to pick the other two players. Likewise, there are
ways to pick the other two players. Likewise, there are 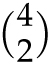
![]() ways for 5 to be the largest number,
ways for 5 to be the largest number, 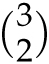
![]() ways for 4 to be the largest number, and
ways for 4 to be the largest number, and 
![]() way for 3 to be the largest number. Since the largest of the three numbers must be 3, 4, 5, 6, or 7, we have counted all of the possibilities, so the three members can be chosen in
way for 3 to be the largest number. Since the largest of the three numbers must be 3, 4, 5, 6, or 7, we have counted all of the possibilities, so the three members can be chosen in 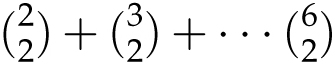
![]() ways, as described by the left side of the previous equation. More generally, this argument shows that
ways, as described by the left side of the previous equation. More generally, this argument shows that
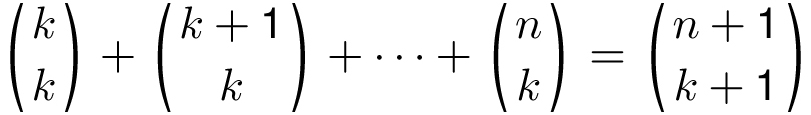
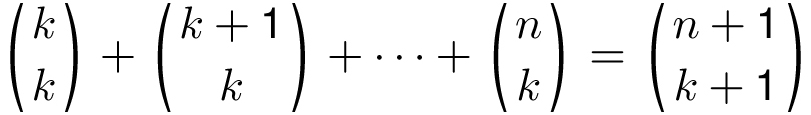
Let’s apply this formula to resolve an important problem that you probably think about every year during the holiday season. According to the popular song “The Twelve Days of Christmas,” on the first day your true love gives you 1 gift (a partridge). On the second day you get 3 gifts (1 partridge and 2 turtledoves). On the third day you get 6 gifts (1 partridge, 2 turtledoves, 3 French hens), and so on. The question is: After the 12th day, how many gifts do you receive in total?


After the 12th day of Christmas, how many gifts did my true love give to me?
On the nth day of Christmas, the number of gifts you receive is
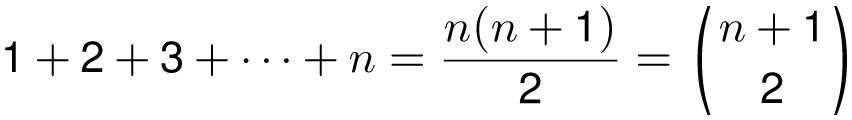
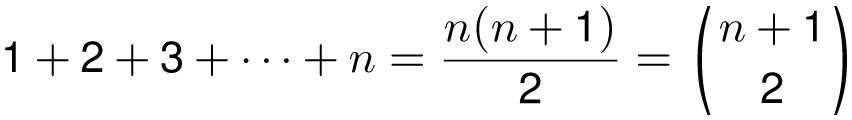
(This comes from our handy formula for triangular numbers or from the hockey stick identity when k = 1.) So on the first day you get 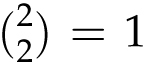
![]() gift; on the second day you get
gift; on the second day you get 
![]() gifts, and so on up through the 12th day, when you receive
gifts, and so on up through the 12th day, when you receive 
![]() gifts. Applying the hockey stick identity, it follows that the total number of gifts will be
gifts. Applying the hockey stick identity, it follows that the total number of gifts will be
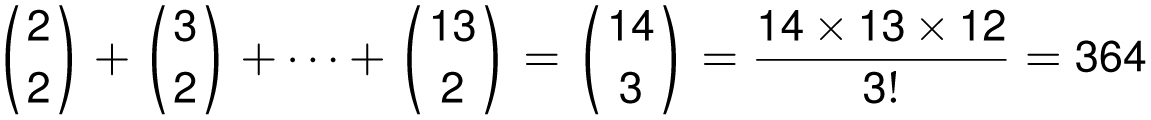
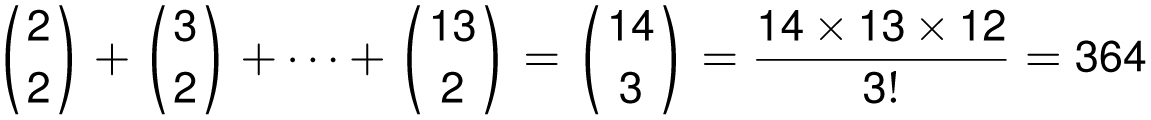
Thus, if you spread these gifts out over the next year, you could enjoy a new gift practically every day (perhaps taking one day off for your birthday)!
Let’s celebrate our answer to the last problem with a festive song I call “The nth Day of Christmas.”
On the nth day of Christmas, my true love gave to me
n novel knick-knacks
n − 1 thing or other
n − 2 et cetera
![]()
5 (plus 10) other things!
Counting all the gifts
Through day n,
What’s the total sum?
It’s precisely 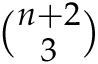
![]() .
.
Now here is one of the oddest patterns in Pascal’s triangle. If you look at the triangle, where we have circled each of the odd numbers, you will see triangles within the triangle.
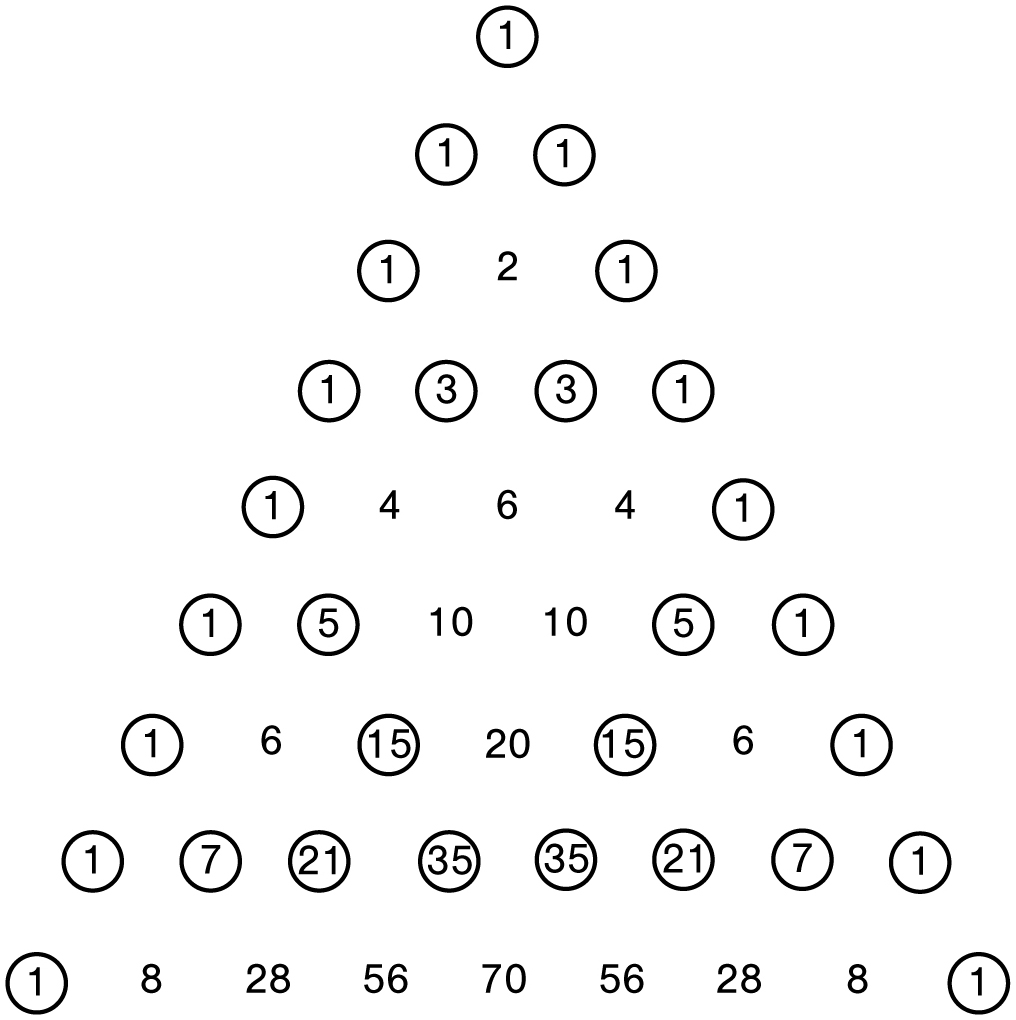

Odd numbers in Pascal’s triangle
Now let’s take a longer view of the triangle with 16 rows, where we replace each odd number with 1 and each even number with 0. Notice that underneath each pair of 0s and each pair of 1s, you get 0. This reflects the fact that you get an even total when you add two even numbers together or two odd numbers together.
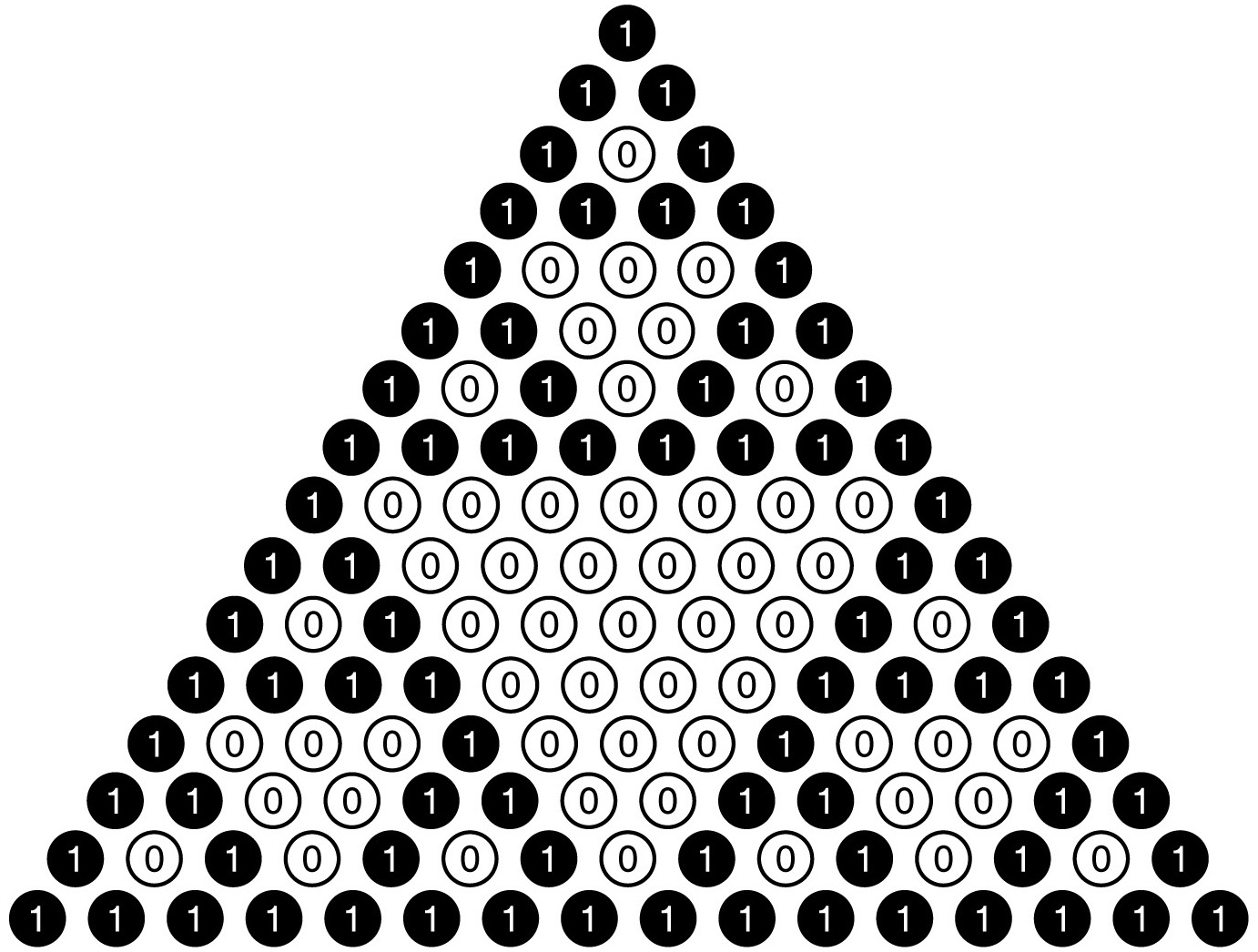

A longer view of the odd numbers
We have an even longer view of the triangle on the next page, consisting of the first 256 rows, where we have replaced each odd number with a black square and each even number with a white square.
This figure is an approximation of the fractal image known as the Sierpinski triangle. It’s just one of the many hidden treasures inside Pascal’s triangle. Here’s another surprise. How many odd numbers are in each row of Pascal’s triangle? Looking at rows 1 through 8 (excluding row 0), we count 2, 2, 4, 2, 4, 4, 8, 2, and so on. No obvious pattern jumps out, although it appears that the answer is always a power of 2. In fact, powers of 2 play an important role here. For example, notice that the rows with exactly 2 odd numbers are rows 1, 2, 4, and 8, which are powers of 2. For the general pattern, we exploit the fact that every


Pascal meets Sierpinski
whole number greater than or equal to zero can be obtained in a unique way by summing distinct powers of 2. For example:
1 |
= 1 |
2 |
= 2 |
3 |
= 2 + 1 |
4 |
= 4 |
5 |
= 4 + 1 |
6 |
= 4 + 2 |
7 |
= 4 + 2 + 1 |
8 |
= 8 |
We have 2 odd numbers in rows 1, 2, 4, and 8 (which are powers of 2). We have 4 odd numbers in rows 3, 5, and 6 (which are the sum of 2 powers of 2), and we have 8 odd numbers in row 7 (which is the sum of 3 powers of 2). Here is the surprising and beautiful rule. If n is the sum of p different powers of 2, then the number of odd numbers in row n is 2p. So, for example, how many odd numbers are in row 83? Since 83 = 64 + 16 + 2 + 1, the sum of 4 powers of 2, then row 83 will have 24 = 16 odd numbers!
Aside
We won’t prove the fact here, but in case you’re curious, 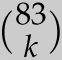
![]() is odd whenever
is odd whenever
k = 64a + 16b + 2c + d
where a, b, c, d can be 0 or 1. Specifically, k must be equal to one of these numbers:
0, 1, 2, 3, 16, 17, 18, 19, 64, 65, 66, 69, 80, 81, 82, 83
We end this chapter with one last pattern. We have seen what happens when we add along the rows of Pascal’s triangle (powers of 2) and the columns of Pascal’s triangle (hockey stick). But what happens when we add the diagonals?
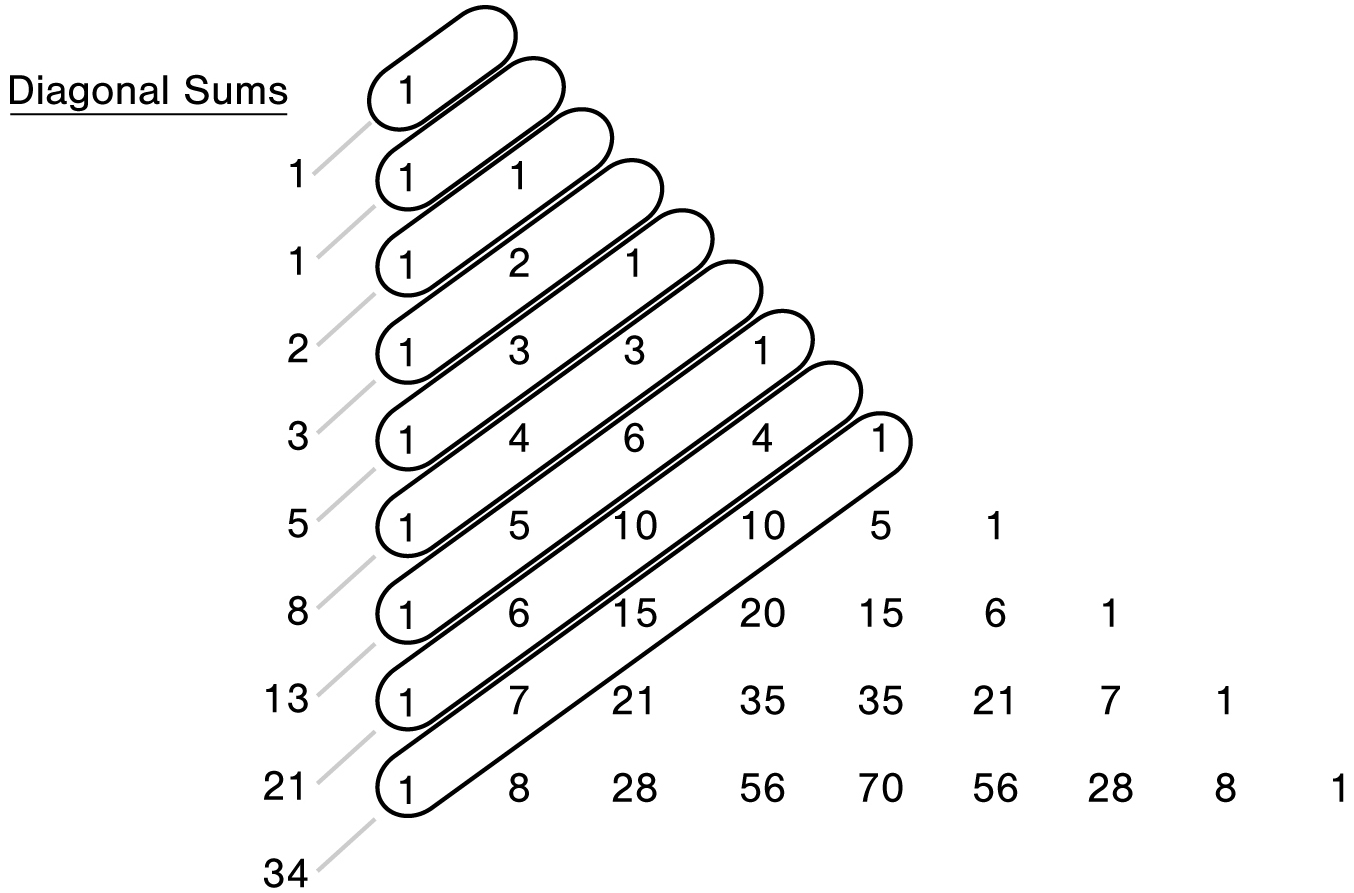

Pascal meets Fibonacci
When we add the diagonals, as illustrated above, we get the following totals:
1, 1, 2, 3, 5, 8, 13, 21, 34
These are the fabulous Fibonacci numbers, and they will be the subject of our next chapter.