How Big Waves Behave
If you have ever been at sea during a gale, you will never forget the awesome power of the great wind-driven waves. They rise majestically, foaming and spitting spume. They sweep by, pitching you into the deep troughs. Each one seems taller than the next, and each one threatens to overwhelm your puny ship.
Mariners often face such conditions in a voyage. From time immemorial, they have wanted reliable predictions of the waves they were likely to encounter. An accurate forecast could warn them to avoid the center of a storm. It could mean the difference between surviving and capsizing.
Oceanographers have worked hard to satisfy this demand, but it was not until the mid-twentieth century that they were able to provide some relief. To reach the final goal of a reliable forecast, they first had to learn how to measure storm waves and to describe them mathematically. And they had to understand how big waves differ in behavior from the very weak waves described by Airy. In this chapter we follow a few threads of their research.
Take a look at the stormy sea in figure 1.5. Waves seem to be arriving from several directions, with different heights and wavelengths. In a few moments the scene will change dramatically. How could anyone describe such a scene quantitatively?
Oceanographers have devised a practical approach to this challenge. They take a census of the waves—that is, sort them according to their wavelengths, directions, and heights. But they don’t attempt to track individual storm waves; that would be well-nigh impossible. Instead they describe the sea statistically. Their idea is to measure the heights of waves at one or more fixed positions in the sea as a function of time and then analyze the data to produce a so-called wave energy spectrum. A spectrum is a graph that shows how energy is distributed among waves of different periods or wavelengths. It can be compared with a predictive theory if one is available.
A rainbow is probably the most familiar example of a spectrum. When sunlight passes through a veil of water droplets, we see the colors of the rainbow spread out in a spectrum. Each color (that is, wavelength) has a definite amount of energy (brightness). We could measure the energy at each color with a photocell, record the results, and plot them in a graph. This would be the quantitative spectrum of sunlight. If we repeated the procedure with, say, fluorescent light, we’d learn that it contains a different mixture of wavelengths and therefore a different spectrum.
We can understand the concept more easily if we look at a specific example. Let’s imagine an oceanographer (let’s call her Dr. O) who wants to measure the energy spectrum of ocean waves. She will measure the heights of waves at a fixed location in the sea by measuring the pressure beneath them, using a pressure sensor. The higher the wave, the larger is the pressure under the crest. She will record the data for some length of time and then use a mathematical tool, devised by the French physicist Joseph Fourier (whom we met earlier), to calculate the energy spectrum of the waves.
Let’s imagine that Dr. O attaches an underwater pressure sensor on the leg of one of those stationary offshore oil rigs. The sensor measures the varying pressure under waves as they pass by. A simple calculation then converts the water pressure to a wave height. A record of the varying heights might look like the solid dark curve in figure 3.2.
Now it is very likely that in a stormy sea, several waves are overlapping at the leg of the oil rig at any instant. A few seconds later a different combination of waves may overlap at the leg. That is why the record looks so jagged. Dr. O wants to sort all the waves that are present in the sea according to their periods and determine their individual amplitudes. Then she can determine the energy each wave carries, since it is proportional to the square of the wave’s amplitude. And from these data she can plot a graph of energy versus period (or frequency, the inverse of period). This will be her desired spectrum of the stormy ocean. But how can she accomplish this task?
Joseph Fourier, that famous French mathematician and physicist, will come to her rescue. As I described in chapter 3, Fourier proved that any curve or surface, with few exceptions, could be represented as a sum of sine and cosine waves of different wavelengths and amplitudes. Moreover, he showed exactly how this could be done mathematically. The different sine and cosine waves are chosen to overlap constructively at some places and destructively elsewhere. In this way the peaks and depressions in any given curve or surface can be fitted, more and more accurately, by adding more and more trigonometric waves.
Following Fourier’s idea, we may view the ocean surface as made up of overlapping sine and cosine waves with a wide range of periods, each moving with its own particular speed, amplitude, and direction. Each sine wave carries an amount of wave energy that is proportional to the square of its amplitude. Our oceanographer wants to know how much energy is carried by waves of different wavelengths or periods.
This may seem like a daunting task, and to simplify the problem Dr. O has limited herself to sampling the heights of waves that pass by one point in space, the leg of the oil rig. If her observations extend over several hours, she can safely assume that every wave with a shorter period than this observation time will appear at her detector and will be recorded. That is the assumption she has to make to obtain a statistical description of the sea.
We’ll skip the details of the Fourier analysis of this raw data; Dr. O gives this task to her graduate students to undertake. For the present it’s enough to say that with the use of Fourier’s method, the slow undulations in Dr. O’s digital record (fig. 3.2) can be fitted with long-period sine and cosine waves, and the rapid variations with shorter and shorter–period sine and cosine waves. For each trigonometric wave Dr. O introduces, she can find the total energy present in the sea in waves with a definite period.
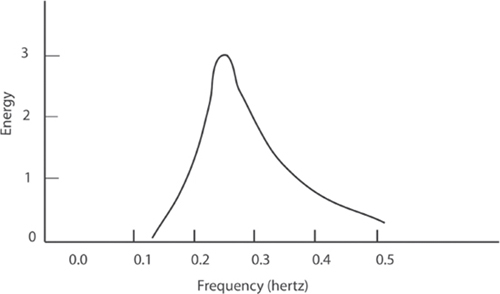
Figure 4.1 shows the spectrum she might find—the amount of energy as a function of frequency, which equals 1 divided by the period. Most of the energy is concentrated in a narrow range of frequencies, typically between 0.1 and 0.4 cycles per second (hertz) or periods of 10 and 2.5 seconds.
The spectrum may change during a long storm. In fact, if Dr. O carried out the calculation with only the first half of her digital record, repeated it for the second half, and compared the results, she might very well see how much the spectrum varies in time.
But Dr. O is looking only at one spot and so cannot tell what direction these waves are going. As noted earlier, we can consider the surface of a stormy sea to be a mixture of sine and cosine waves of different periods, but these will be running in many directions away from the center of a storm. If we could take a snapshot of, say, a square kilometer of the sea and could measure the instantaneous height of the sea at every point, we could apply Monsieur Fourier’s method. We could decompose the surface into sine and cosine waves, along the north-south and east-west directions. With this information we could derive the instantaneous energy spectrum with a good deal of certainty. And the spectrum obtained in this way would certainly be more reliable than the spectrum Dr. O could obtain from a single point in space. In addition, Dr. O could determine how the spectrum varies in different directions. We will see in a later chapter how radar satellites allow us now to take such snapshots and deliver high-quality spectra.
Fig. 4.1 A spectrum shows the distribution of energy among water waves of different frequencies.
Oceanographers have determined that the spectra of swells change more slowly than the spectra of waves in the middle of the stormy area. Swells, you will recall, are the trains of long-wavelength waves that propagate away from a storm center. Walter Munk, one of the founders of physical oceanography, used this property in a classic study of the propagation of swells.
As a young man Munk was pointed by his father toward a career in banking. After working in a bank for three years, he rebelled. He quit a job he hated, enrolled at the California Institute of Technology, and obtained a bachelor’s degree in physics in 1939. His summer job at the Scripps Institution of Oceanography (La Jolla, California) changed his life: he decided on a career in oceanography. Armed with a doctorate in geophysics from the University of California at Los Angeles, he found a job at Scripps in 1947 as an assistant professor of geophysics.
In 1959, Munk and three colleagues from Scripps set up a triangular array of three pressure gauges at a depth of 100m, 3km off San Clemente Island, California. Even at these depths, their sensitive sensors could detect the changes in pressure due to the heights of passing waves.
Munk and his associates recorded the variations of pressure continuously for several months. Every day, they computed the energy spectrum of the waves that arrived at each station in the array. The low-frequency (long-period) waves arrived first because their speed is higher, as we learned earlier. The higher-frequency waves arrived later and carried much more energy. From the lag of the higher-frequency waves and from their phase speeds (calculated with Airy’s theory), Munk could estimate the distance of a storm along a great circle of the earth. One of these turned out to be a staggering 12,000km, or 7,500 miles.
From the difference in times of arrival at the three stations in the triangle, the scientists could also determine the direction of the incoming swell. The distance and direction of this source of the storm noted above pointed to the Southern Ocean, between New Zealand and Antarctica. From the details of the data, Munk could also estimate the wind speed that produced the swell. When he compared his deductions with real weather maps, he found good agreement in most cases.
Munk was amazed at how little a swell decayed as it propagated long distances. To find out just how a swell decays, he decided to set up another experiment. In 1963, with the support of the U.S. Navy, he established six recording stations on a great circle from New Zealand to Alaska. Each station measured pressure variations at various depths. Five stations were near islands. The sixth station was that remarkable ship, FLIP, which could be flooded to cause the vessel to rest vertically in the sea. In this position the ship provided a very stable platform from which Munk could measure pressure variations in the water.
Munk learned that the swell decayed very little after it had traveled a distance from the edge of a storm equal to the storm’s diameter. The swell also decayed by spreading sideways, not because of the resistance of the air above it, as most oceanographers believed at the time. Apparently a swell is finally absorbed at the boundaries of the ocean, presumably as surf.
Walter Munk is a remarkable man. In a career spanning 72 years, his research interests have covered a very wide range. They include the rotation of the earth, wind-driven circulation in ocean basins, the tides, sonic tomography of the ocean, and ocean swells. In the early 1940s, Munk and Harald Sverdrup practically invented the science of forecasting wave and surf heights, as we will see in a later chapter.
Munk helped to make the Scripps Institution into the world-class center of ocean research it is today. Munk has received a dozen prestigious awards for his many contributions to science, including the National Medal of Science (1977). In 2012 he received the Crafoord Prize by the Swedish Academy of Sciences. It’s the nearest thing to a Nobel Prize.
At age 94, Munk married a younger woman. The San Diego Union-Tribune of March 23, 2012, quoted him as quipping, “When I came to La Jolla, the saying was that the community consisted of the newly-wed and the nearly dead. I now qualify on both counts.”
Not all waves are simple swells. Water waves are rather complicated once one begins to examine them closely. The pioneers of wave theory—men like Lagrange, Laplace, Cauchy, and Kelvin—understood this very well. The wave equations they had to deal with include some nasty “nonlinear” features, such as a product of velocity and the gradient of velocity. That meant that each point on a wave profile could have a different forward speed. The wave profile would evolve in time, which would require horrendous calculations to follow.
To obtain a wave with a stable profile that could be readily modeled mathematically, it was necessary to limit the wave height to a tiny fraction of the wavelength. Only then could one ignore the troublesome nonlinear features. The resulting “linear” theory of weak (low-amplitude) waves, summarized by Airy, has turned out to be very useful, despite its limitations, in getting a rough estimate of the behavior of realistic waves.
But to understand the behavior of real storm waves, which are dangerous and therefore more important to mariners, mathematical physicists have had to develop new theories of waves with heights comparable to, say, a tenth of their wavelengths. These waves turn out to have some unexpected and puzzling features, particularly the ability to exchange energy when they collide. At the same time, oceanographers have had to develop techniques for measuring the chaotic waves one sees in a stormy sea. This dual approach of crafting theory and experiment in parallel has paid off magnificently.
The theory of realistic water waves was launched in 1847 with the publication of a brief technical report by John Scott Russell, a British engineer. Russell had made a startling discovery in 1834 while working on the optimum shape of canal boats. He was watching a boat being pulled slowly on a canal by a team of horses. At some point the boat stopped abruptly, and a large “solitary heap of water” rolled ahead at high speed. Russell chased this wave on horseback. He reported later that the heap was about 1 foot high and 30 feet long and moved at about 9mph. He was most impressed to see that this solitary wave preserved its smooth, rounded shape for a distance of 2 miles.
Fascinated by this unique wave, Russell carried out experiments in a wave tank at home to investigate others like it. He named these waves “waves of transition.” He found that the speed of such solitary waves increases as their height increases, unlike the weak waves Airy described.
His experimental results were first ignored and then contested by the leading theorists of the time because they seemed to conflict with known physics. Airy, for example, calculated that different parts of a tall wave travel at different speeds. The speed of a chosen point on the wave profile depended on the elevation of the point above the undisturbed water level. So, for example, the crest moves faster than the trough. Therefore, Airy concluded that a big wave cannot propagate without a severe change of shape. The slope will become steeper at the front face of the crest and flatter at the back face. The wave will ultimately curl over and collapse. Russell, he concluded, must be mistaken.
Sir George Gabriel Stokes picked up the problem upon reading Russell’s report. Stokes (1819–1903) was a physicist and mathematician whose research at Cambridge University covered many different fields over a period of 50 years. He was a contemporary of two other Cambridge luminaries, James Clerk Maxwell and Lord Kelvin.
Stokes graduated in 1841 from Pembroke College with the highest honors in mathematics. He was elected to a fellowship, and in 1849 he was appointed as Lucasian professor of mathematics at Cambridge. Stokes was renowned for his extraordinary combination of mathematical power and experimental skill, which gave him the ability to find solutions to seemingly intractable problems. He was interested in all aspects of wave dynamics, including water, light, and sound waves.
In 1847, Stokes decided to try to explain John Russell’s wave. He searched for a mathematical solution to the full nonlinear wave equation that would describe a gravity wave of finite height that could propagate without a change of shape in shallow water. He eventually determined that the best solution has the shape of a trochoid, the curve traced in space by a point on the rim of a rolling wheel. Stokes’s wave has a sharper peak and a broader trough than a sine wave of the same wavelength. If the wavelength of a Stokes wave is sufficiently large, each crest appears to be a single pulse, a solitary wave like the one Russell observed.
A Stokes wave has some novel properties. Its speed is larger than that of a small-amplitude wave of the same wavelength. And, in agreement with Russell’s experiments, the wave speed increases as the wave grows in height. Also, the height of a Stokes wave has a limit: the wave will become unstable and break, even in deep water, if its height exceeds 14% of its wavelength. Here is a possible clue to the origin of breaking waves at sea, the so-called whitecaps.
Stokes also predicted that the blobs of water do not move in closed circles under a trochoidal wave. In one oscillation a blob is carried forward by a small amount in the direction of the wave’s propagation, an effect called Stokes drift. Real waves display this behavior. A swimmer resting in the swell soon becomes aware of slowly drifting toward the beach. (In chapter 2, I purposely ignored this small, persistent drift.)
A Stokes wave somehow avoids dissolving into its component sines and cosines as it travels with constant speed. At first sight this seems to be unnatural. As Airy commented, we should expect each wavelength in a composite wave form to travel at its characteristic phase speed. This is the “normal” wavelength dispersion effect. Therefore, he argued, a compound wave form should disintegrate after traveling a while. This is true for a wave group that is composed of small-amplitude sinusoidal waves.
However, as Russell learned from his experiments, tall waves are subject to a new phenomenon: amplitude dispersion. That is, the higher the wave, the faster it travels. In addition, a tall wave is subject to the usual wavelength dispersion: the longer the wavelength, the faster the speed of the wave. Stokes managed to exactly balance these two types of dispersion so as to ensure a stable profile. But complex things are rarely perfect: in later work, Stokes waves were shown to be unstable after they have traveled a sufficient distance.
Stokes’s theory was the first step toward describing waves whose heights are small but not infinitesimal, compared with their wavelengths. Real ocean waves are not pure sinusoids; they are much closer in profile to a Stokes wave. His theory also laid the foundation for the study of so-called solitons, waves with a large single peak that propagates without change of shape. As we will see, solitons have become very trendy because they appear as pulses in light, in plasmas, in sound, and possibly as rogue waves in the ocean. They represent an extreme form of a finite wave, and a lot of recent research is devoted toward understanding their properties.
Strictly speaking, Stokes was not the first to describe tall waves mathematically. That distinction properly belongs to Franz Joseph von Gerstner, a Bohemian physicist and railroad engineer, who published his results in 1803, long before Stokes. Gerstner adopted a form of the wave equation invented by Lagrange, which is easier to solve in some circumstances than Euler’s wave equation. Gerstner was able to obtain “exact” solutions, which are compact formulas without the string of correction terms that Stokes employed.
Gerstner’s solutions are waves that can travel without a change of shape in deep water. They are extreme examples of Stokes’s shallow-water trochoidal waves. Their crests are sharp pointed cusps, and their troughs are very flat. And yet the orbits of blobs under the surface are circles, just like the orbits of very weak Airy waves.
A Gerstner wave with a long wavelength begins to look a lot like the solitary wave that Russell reported, a single peak traveling swiftly with a finite height. However, Gerstner’s result remained buried in the literature until William J. M. Rankine rediscovered it in 1863. Even then, it was dismissed as having limited applicability to real waves because rather peculiar forces would be needed to set the wave in motion.
Diederik Korteweg and Gustav de Vries, two Dutch mathematicians, made the next important advance in the study of waves with finite heights. Korteweg, a professor of mathematics and physics at the University of Amsterdam, had a long-standing interest in wave motion, beginning with his doctoral thesis. In it he solved the problem of how a beating heart creates waves in elastic arteries.
In 1895 Korteweg and his student de Vries discovered a form of Euler’s wave equation that could be solved exactly and that yielded a family of shallow-water waves with finite heights. They are trochoids with even sharper crests and broader troughs than Gerstner’s waves. These Korteweg–de Vries (KdV) waves propagate without change of shape, and the long-wavelength versions resemble Russell’s solitary wave closely. However, they were considered exotic and were rediscovered only after solitary waves became interesting to physicists.
Solitary waves began to show up in a variety of physical situations during the 1960s, and the KdV waves proved useful in modeling them. For example, physicists working at Princeton University discovered solitary waves in the plasmas they were experimenting with. Plasma, you may recall, is a kind of gas composed of free electrons and electrically charged ions. It results from heating a substance to very high temperature.
In 1965 Norman Zabusky and Martin Kruskal, two plasma physicists, carried out pioneering numerical simulations in order to interpret their plasma waves. They discovered that KdV solutions matched the experimental solitary waves nicely and renamed the waves “solitons,” a species we encountered above and will encounter again. Moreover, they found that KdV waves do not change shape when they collide; they merely exchange positions. As we will see, this result conflicts with observations of ocean waves in storms.
Physicists have continued to search for a mathematical theory that accurately predicts the behavior of ocean waves, sometimes reaching into very disparate fields. Recently, they have successfully modified a wave equation that is well known in atomic and nuclear physics. These developments have proven useful in understanding the formation of rogue waves, so I will take a moment now to describe them in a general way.
In 1927, Joseph Davisson and Lester Germer demonstrated that electrons (usually thought of as particles) could be made to produce interference and diffraction patterns, just like waves. The idea that a particle could behave like a wave, or that an extended object like a wave could represent a localized particle, was revolutionary and called for an explanation.
In response, Erwin Schrödinger, an Austrian physicist, introduced his now-famous wave equation for atomic particles that same year. The equation governs the evolution of a wave that represents the probability that a particle is located near some chosen point in space. In the strange world of quantum physics, particle positions are not determined, even conceptually, until they are measured. However, the Schrödinger wave yields the probability of several independent measurements of position.
Schrödinger used his probability wave equation to predict the energy levels of the hydrogen atom, a theoretical advance of the highest importance. He went on to predict the energy levels of a pair of rotating atoms and the splitting of atomic energy levels in a strong electric field. These results matched experiments closely and established the Schrödinger equation as the basic tool in quantum physics. In recognition for this achievement, Schrödinger shared the Nobel Prize in physics with Paul Dirac in 1933.
Then in the 1960s physicists were struck by a possible analogy between a soliton in water waves (that is, a localized particle-like structure in a wave system) and an electron (that is, a single particle whose position is determined by a probability wave). They tinkered with the Schrödinger wave equation, added some new factors, and by 1979 applied this nonlinear version to model soli-tons, not only in water waves but also in light waves and plasma waves.
Meanwhile, Vladimir E. Zakharov, a world-class Soviet theoretician, derived another nonlinear wave equation that was suitable for plasma. In 1968 he demonstrated that his equation also governs the envelope of a group of steep water waves and that the envelope can shrink to form a set of steep narrow solitons.
So at this point, we had two parallel theories for the origin of solitons: the Schrödinger equation and the Zakharov equation. Which was closer to the truth? In 1999 Lev Shemer and his colleagues at Tel Aviv University decided to put them to an experimental test. Both theories performed quite well, but the Zakharov model was somewhat better. We will return to these models of solitons in the chapter on rogue waves.
Waves with very small heights relative to their wavelengths can collide and just pass through each other with no exchange of energy. (We saw this on the beach when two pebbles were dropped into a pool.) In effect, weak waves preserve their identities in a collision and separate without damage.
But tall waves (with heights a few percent of their wavelengths) are different. To begin with, they are no longer sinusoidal in shape. As the Webers discovered with their wave tank, tall waves have sharper cusps and broader troughs than sine waves. Moreover, when tall waves overlap, they can exchange energy and change shape. More importantly, they can spawn new waves that have quite different wavelengths. These effects are examples of nonlinear behavior, and they greatly complicate the task of predicting the steady-state spectrum of ocean waves.
In 1960 Owen Phillips, whom we first met in chapter 3, took the first step in analyzing how tall waves exchange energy. Phillips studied the collision of two deep-water wave trains of arbitrary wavelengths and directions. He set up an equation to describe the time history of the sine and cosine waves that represent the instantaneous shapes of the interacting waves. He found an approximate solution, such that weak secondary waves with new wavelengths are generated in the collision. These secondary waves could not grow at the expense of the primary waves because their speeds were mismatched.
However, tertiary waves with a different set of wavelengths were also spawned in the collision. And they could interact with the primary waves, growing indefinitely at a constant rate. As a result, the original wave trains decayed into these “sidebands.” Perhaps it is not surprising that a collision of two trains should result in a train wreck! But Phillips’s result was quite unexpected, an indication that tall waves interact nonlinearly. That is, they generate new waves with different wavelengths, and these new waves can drain energy from their parent waves.
In the ocean, where deep-water waves of all wavelengths could interact, Phillips could envision the continuous decay of waves by the growth of their sidebands. And then the process would repeat: the sidebands would develop sidebands and decay as well. Would the wave system settle to an equilibrium state? If so, what would it look like? This was a question that only new observations could answer.
Seven years after Phillips published his theory of colliding wave trains, a similar effect was observed in a laboratory experiment. Thomas Brooke Benjamin and his student James E. Feir were generating deepwater waves in a long tank at Cambridge University. They were using an oscillating paddle at one end of the tank to launch a train of moderately steep waves with a chosen period. The individual waves in the train would start out with well-defined profiles and an apparently constant frequency. But about halfway down the length of the tank, the wave train disintegrated. What went wrong?
The experimenters racked their brains to explain this odd result. Eventually, they traced the cause of the collapse to a slight imperfection of the paddle. It had introduced secondary frequencies in the wave train. These secondary waves had slightly larger and slightly smaller frequencies compared with the primary wave. In effect, the initial wave train was accidentally being frequency-modulated. The experimenters were able to show how energy was transferred from the primary wave to these sidebands and how they grew in amplitude explosively. This Benjamin-Feir instability was an example of wave nonlinearity: the possibility of energy transfers among finite waves. We will see that this instability has been invoked to explain extreme waves, the notorious rogues.
Brooke Benjamin was one of those rare scientists who combine mathematical ability with deep physical intuition. He contributed to the solution of many difficult problems in hydrodynamics, such as the supersonic collapse of air bubbles in water, the similarities between sea breezes and avalanches, and the mechanism through which vortices on aircraft wings could turn into shock waves.
A story is told that he was invited to dinner at Prime Minister Margaret Thatcher’s apartments at 10 Downing Street in London. While mingling with the guests, he met the prime minister’s husband, Denis, who asked who he was. He replied that he was a professor at Oxford University. “I should keep that quiet around here,” Thatcher murmured. Benjamin recalled that Margaret had been the dean of an Oxford college and had had some serious clashes with the equally strong-minded Oxford faculty.
Phillips’s analysis of two colliding wave trains was correct as far as it went, but it was not the whole story. In 1962 Klaus Hasselmann, a young researcher at the University of Hamburg, completed a doctoral thesis in which he showed how tall waves in the open ocean could exchange energy in a collision, but only under certain subtle restrictions. Moreover, he claimed that these exchanges could be just as important in changing the relative strengths of waves as the wind’s energy input.
As we will see, Hasselmann has played a prominent role in physical oceanography for the past 40 years. He debuted as a theorist in the 1960s. In the 1970s he organized a major observational campaign to measure wave spectra at sea, which I describe in the next chapter. In part, this campaign was intended to test Hasselmann’s theory of wave interactions. Then in the 1980s he helped to develop a practical wave forecasting procedure, based on observations by radar-equipped satellites.
In his seminal 1962 paper Hasselmann predicted that tall gravity waves moving in independent directions could exchange energy only in groups of four (a “quadruplet”) and only if the members of the quadruplet were related by direction, wavelength, and frequency. So, for example, the sum of the frequencies of one pair must equal the sum of frequencies of the other pair. This type of interaction was not merely academic, Hasselmann claimed. In fact, the transfer of energy among waves could be a central factor in the evolution of a wind-driven sea.
Hasselmann showed how to calculate the change in energy of a chosen wavelength resulting from interactions with all other wavelengths. Hasselmann’s math was elegant, but his formal solution was so complicated that it could not be calculated in a reasonable time with the computers that were available in the 1960s. Therefore, his solution was not suited for real-time forecasting. Over the next two decades, Hasselmann and his collaborators continued to search for approximate solutions that could be calculated quickly. He succeeded eventually.
Enough of theory for a while. Let’s move on to observations of real waves in a real ocean.