4 Universe from bit

Paul Davies
“I refute it thus!” Samuel Johnson famously dismissed Bishop George Berkeley’s argument for the unreality of matter by kicking a large stone (Boswell, 1823). In the light of modern physics, however, Johnson’s simple reasoning evaporates. Apparently solid matter is revealed, on closer inspection, to be almost all empty space, and the particles of which matter is composed are themselves ghostly patterns of quantum energy, mere excitations of invisible quantum fields, or possibly vibrating loops of string living in a ten-dimensional space–time (Greene, 1999). The history of physics is one of successive abstractions from daily experience and common sense, into a counterintuitive realm of mathematical forms and relationships, with a link to the stark sense data of human observation that is long and often tortuous. Yet at the end of the day, science is empirical, and our finest theories must be grounded, somehow, “in reality.” But where is reality? Is it in acts of observation of the world made by human and possibly non-human observers? In records stored in computer or laboratory notebooks? In some objective world “out there”? Or in a more abstract location?

4.1 The ground of reality

When a physicist performs an experiment, he or she interrogates nature and receives a response that, ultimately, is in the form of discrete bits of information (think of “yes” or “no” binary answers to specific questions), the discreteness implied by the underlying quantum nature of the universe (Zeilinger, 2004). Does reality then lie in the string of bits that come back from the set of all observations and experiments – a dry sequence of ones and zeros? Do these observations merely transfer really-existing bits of information from an external world reality to the minds of observers, or are the bits of information created by the very act of observation/experiment? And – the question to which this entire discussion is directed – are bits of “classical” information the only sort of information that count in the reality game, or does an altogether different form of information underpin reality? In short, where is the ontological ground on which our impression of a really-existing universe rests?
In the well-known parable of the tower of turtles, the search for the ultimate source of existence seems to lead to an infinite regress. Terminating the tower in a “levitating superturtle” requires either a leap of faith – accepting the bottom level as an unexplained brute fact – or some mental gymnastics, such as positing a necessary being, the non-existence of which is a logical impossibility. Classical Christian theology opted for the latter, with God cast in the role of that necessary being, upholding a contingent universe. Unfortunately, the concept of a necessary being is fraught with philosophical and theological difficulties, not least of which is the fact that such a being does not bear any obvious resemblance to traditional notions of God (Ward, 1982). Nor is it clear that a necessary being is necessarily unique (there could be many necessary gods), or necessarily good, or able to create a universe (or set of universes) that is not itself already necessary (thus rendering the underpinning redundant). But if the universe is contingent, another problem arises: can a necessary being’s nature, and hence choices, be contingent? In other words, can a necessary being freely choose to create something? (As opposed to necessarily making such-and-such a universe.) As a result of this philosophical quagmire, most theologians have abandoned the idea that God exists necessarily.
Science evaded all these complications by resting content to accept the physical universe itself, at each instant of time, as the basement level of reality, without the need for a god (necessary or otherwise) to underpin it. The latter view was well exemplified by British philosopher Bertrand Russell in a BBC radio debate with Fr Frederick Copleston (Russell, 1957). Russell expressed it bluntly: “I should say that the universe is just there, and that’s all.”
Sometime during the twentieth century, a major transition was made. The theory of relativity undermined the notion of absolute time and the shared reality of the state of the entire universe at each instant. Quantum mechanics then demolished the concept of an external state of reality in which all meaningful physical variables could be assigned well-defined values at all times. So a subtle shift occurred, at least among theoretical physicists, in which the ground of reality first became transferred to the laws of physics themselves, and then to their mathematical surrogates, such as Lagrangians, Hilbert spaces, etc. The logical conclusion of going down that path is to treat the physical universe as if it simply is mathematics. Many of my theoretical physicist colleagues do indeed regard ultimate reality as vested in the subset of mathematics that describes physical law. For them, (this subset of) mathematics is the ground of being. When, three centuries earlier, Galileo had proclaimed, “The great book of Nature can be read only by those who know the language in which it was written, and this language is mathematics” (Drake, 1957), he supposed that the mathematical laws were grounded in a deeper level – a level guaranteed and upheld by God. But today, the mathematical laws of physics are regarded by most scientists as free-floating – the levitating superturtle to which I referred above.
At this point, physics encounters its own conundrum of necessity versus contingency, as famously captured by Einstein’s informal remark about whether God had any choice in his creation. What he meant by this was, could the laws of physics have been otherwise (that is, different mathematical relationships), or do they have to be as they are, of necessity? The problem of course is that if the laws could have been different, one can ask why they are as they are, and – loosely speaking – where these particular laws have “come from.” To use a metaphor, it is as if mathematics is a wonderful warehouse richly stocked with forms and relationships, and Mother Nature passes through with a shopping trolley, judiciously selecting a handy differential equation here and an attractive symmetry group there, to use as laws for a physical universe.
The problem of the origin of the laws of physics is an acute one for physicists. Einstein’s suggestion that they may turn out necessarily to possess the form that they do has little support. It is sometimes said that a truly unified theory of physics might be so tightly constrained logically that its mathematical formulation is unique. But this claim is readily refuted. It is easy to construct artificial universe models, albeit impoverished ones bearing only a superficial resemblance to the real thing, which are nevertheless mathematically and logically self-consistent. For example, many papers are written in which four space–time dimensions are replaced by two, for ease of calculation. These simplified “universes” represent possible realities, but not the “actual” reality (Davies, 2006).
Given that the universe could be otherwise, in vastly many different ways, what is it that determines the way the universe actually is? Expressed differently, given the apparently limitless number of entities that can exist, who or what gets to decide what actually exists? The universe contains certain things: stars, planets, atoms, living organisms … Why do those things exist rather than others? Why not pulsating green jelly, or interwoven chains, or fractal hyperspheres? The same issue arises for the laws of physics. Why does gravity obey an inverse square law rather than an inverse cubed law? Why are there two varieties of electric charge rather than four, and three “flavors” of neutrino rather than seven? Even if we had a unified theory that connected all these facts, we would still be left with the puzzle of why that theory is “the chosen one.” Stephen Hawking has expressed this imponderable more eloquently: “What is it that breathes fire into the equations and makes a universe for them to describe?” (Hawking, 1988). Who, or what, promotes the “merely possible” to the “actually existing”?
There are two circumstances in which the problem of the “fire-breathing actualizer” – the mechanism to dignify a subset of the possible with the status of becoming “real” – is circumvented. The first circumstance is that nothing exists. However, we can rule that out on the basis of observation. The second is that everything exists, that is, everything that can exist does exist. Then no procedure is needed to select the actually existing things and separate them from the infinite set of the merely-possible-but-in-fact-non-existent things. Is this credible? Well, we cannot observe everything, and absence of evidence is not the same as evidence of absence. We cannot be sure that some particular thing we might imagine does not exist somewhere, perhaps beyond the reach of our most powerful instruments, or in some parallel universe.
Max Tegmark has proposed that, indeed, everything that can exist does exist, somewhere within an infinite stack of parallel worlds. “If the universe is inherently mathematical, then why was only one of the many mathematical structures singled out to describe a universe?” he challenges. “A fundamental asymmetry appears to be built into the heart of reality” (Tegmark, 2003). Tegmark’s suggestion is one of many so-called multiverse models, according to which the universe we observe is but an infinitesimal fragment amid a vast, possibly infinite, ensemble of universes. In most variants of this theory, the laws of physics differ from one universe to another. That is, the laws are not absolute and universal, but more like “local by-laws” (Rees, 2001).
A knee-jerk reaction to Tegmark’s version of the multiverse is that it flagrantly violates Occam’s razor. But Tegmark points out that everything can actually be simpler than something. That is, the whole can often be defined more economically than any of its parts. (The set of all integers, for example, is easily described, whereas a subset of integers consisting of, say, prime numbers, selected or not by a random coin toss, is not.) However, the notion of “everything” runs into formal conceptual problems when infinite sets are involved, and Tegmark’s proposal is very ill defined, perhaps to the point of meaninglessness. In any case, very few scientists or philosophers would subscribe to Tegmark’s extreme view. Even those who believe in some sort of multiverse usually stop short of supposing that literally everything exists.
The orthodox position seems to be that the actually-existing (as opposed to possible but non-existent) laws should simply be accepted as a brute fact, with no deeper explanation at all. Sean Carroll has expressed support for this position, in addressing the question, why those laws of physics? “That’s just how things are,” replies Carroll. “There is a chain of explanations concerning things that happen in the universe, which ultimately reaches to the fundamental laws of nature and stops” (Carroll, 2007). In other words, the laws of physics are “off limits” to science. We must just accept them as “given” and get on with the job of applying them.

4.2 Hidden assumptions about the laws of physics

The orthodox view of the nature of the laws of physics contains a long list of tacitly assumed properties. The laws are regarded, for example, as immutable, eternal, infinitely precise mathematical relationships that transcend the physical universe, and were imprinted on it at the moment of its birth from “outside,” like a maker’s mark, and have remained unchanging ever since – “cast in tablets of stone from everlasting to everlasting” was the poetic way that Wheeler put it (Wheeler, 1989). In addition, it is assumed that the physical world is affected by the laws, but the laws are completely impervious to what happens in the universe. No matter how extreme a physical state may be in terms of energy or violence, the laws change not a jot. It is not hard to discover where this picture of physical laws comes from: it is inherited directly from monotheism, which asserts that a rational being designed the universe according to a set of perfect laws. And the asymmetry between immutable laws and contingent states mirrors the asymmetry between God and nature: the universe depends utterly on God for its existence, whereas God’s existence does not depend on the universe.
Historians of science are well aware that Newton and his contemporaries believed that in doing science they were uncovering the divine plan for the universe in the form of its underlying mathematical order. This was explicitly stated by René Descartes:
[I]t is God who has established the laws of nature, as a King establishes laws in his kingdom … You will be told that if God has established these truths, he could also change them as a King changes his laws. To which it must be replied: yes, if his will can change. But I understand them as eternal and immutable. And I judge the same of God.
(Descartes, 1630)
The same conception was expressed by Spinoza:
Now, as nothing is necessarily true save only by Divine decree, it is plain that the universal laws of nature are decrees of God following from the necessity and perfection of the Divine nature … nature, therefore, always observes laws and rules which involves eternal necessity and truth, although they may not all be known to us, and therefore she keeps a fixed and immutable order.
(de Spinoza, 1670)
Clearly, then, the orthodox concept of laws of physics derives directly from theology. It is remarkable that this view has remained largely unchallenged after 300 years of secular science. Indeed, the “theological model” of the laws of physics is so ingrained in scientific thinking that it is taken for granted. The hidden assumptions behind the concept of physical laws, and their theological provenance, are simply ignored by almost all except historians of science and theologians. From the scientific standpoint, however, this uncritical acceptance of the theological model of laws leaves a lot to be desired. For a start, how do we know the laws are immutable and unchanging? Time-dependent laws have been considered occasionally (see, for example, Smolin, 2008), as well as observational tests carried out to look for evidence that some of the so-called fundamental constants of physics may in fact have changed slowly over cosmological time scales (Barrow, 2002). Particle physics suggests that the laws we observe today may actually be only effective laws, valid at relatively low energy, emergent from the big bang as the universe cooled from Planck temperatures. String theory suggests a mathematical landscape of different low-energy laws, with the possibility of different regimes in different cosmic patches, or universes – a variant on the multiverse theory (Susskind, 2005).
But even in these examples, there are fixed higher-level meta-laws that determine the pattern of lawfulness (Davies, 2006). Thus in the popular variant of the multiverse theory, called eternal inflation, there are many big bangs scattered through space and time, each “nucleating” via quantum tunneling, and thereby giving birth to a universe. As a universe cools from the violence of its origin, it inherits a set of laws, perhaps to some extent randomly (that is, as frozen accidents). To make this model work, there has to be a universe-generating mechanism operating in the overall multiverse (and in the case cited, it is based on quantum field theory and general relativity) and a set of general laws (like a string theory Lagrangian) from which a lucky dip of low-energy effective laws within each universe is available. Clearly this meta-law structure of the multiverse merely shifts the problem of the origin of the laws up a level.
Another strong influence on the orthodox concept of physical law is Platonism. Plato located numbers and geometrical structures in an abstract realm of ideal forms. This Platonic heaven contains, for example, perfect circles – as opposed to the circles we encounter in the real world, which are always flawed approximations of the ideal. Many mathematicians are Platonists, believing that mathematical objects have real existence, even though they are not situated in the physical universe. Theoretical physicists are steeped in the Platonic tradition, so they also find it natural to locate the mathematical laws of physics in a Platonic realm. The fusion of Platonism and monotheism created the powerful orthodox scientific concept of the laws of physics as ideal, perfect, infinitely precise, immutable, eternal, state-immune, unchanging mathematical forms and relationships that transcend the physical universe and reside in an abstract Platonic heaven beyond space and time.
It seems to me that after three centuries we should consider the possibility that the classical theological/Platonic model of laws is an idealization with little experimental or observational justification. Which leads naturally to the question: can we have a theory of laws? Instead of accepting the laws of physics as a levitating superturtle at the bottom of the stack – an unexplained brute fact – might we push beyond at least one step, and try to account for why the laws are as they are, to show that there are reasons for why they have the form that they do? To think creatively about this, it is necessary to jettison all the above-listed hidden assumptions. For example, we must allow that the asymmetry between laws and states may be incorrect, and reflect on what the consequences might be if the laws depend (at least to some extent) on what happens in the universe: that is, to the actual physical states. Might laws and states co-evolve, in such a way that “our world” is some sort of attractor in the product space of laws and states?
To illustrate a possible agenda along these lines, I want to concentrate on one aspect of the standard theological model of laws that is most vulnerable to falsification: namely, the assumption of infinite precision (Davies, 2006). The laws of physics are normally cast as differential equations, which embed the concepts of real numbers, and of infinite and infinitesimal quantities, as well as continuity of physical variables, such as those of space and time. This assumption extends even to string theory, where the link with the world of space, time, and matter is long and tenuous in the extreme. As any experiment or observation can be conducted to finite accuracy only, to assume infinitely precise laws is obviously a wholly unjustified extrapolation – a leap of faith. To the extent that it may be a technical convenience, that is all right. But as I shall show, there are circumstances where the extrapolation may lead us astray in a testable manner.
To focus the issue, consider Laplace’s famous statement about a computational demon. Laplace pointed out that the states of a closed deterministic system, such as a finite collection of particles subject to the laws of Newtonian mechanics, are completely fixed once the initial conditions are specified:
We may regard the present state of the universe as the effect of its past and the cause of its future. An intellect which at any given moment knew all of the forces that animate nature and the mutual positions of the beings that compose it, if this intellect were vast enough to submit the data to analysis, could condense into a single formula the movement of the greatest bodies of the universe and that of the lightest atom; for such an intellect nothing could be uncertain and the future just like the past would be present before its eyes.
(Laplace, 1825)
If Laplace’s argument is taken seriously, then everything that happens in the universe, including Laplace’s decision to write the above words and my decision to write this book chapter, are preordained. The necessary information is already contained in the state of the universe at any previous time. Laplace’s statement represents the pinnacle of Newtonian clockwork mechanics, with its embedded assumption of infinitely precise theological laws – I would say the pinnacle of absurdity. It is the starting point for my challenge to the orthodox concept of physical law.1

4.3 It from bit

The basis of the challenge, which builds on the work of John Wheeler (1979, 1983, 1989, 1994) and Rolf Landauer (1967, 1986), sprang originally from the theory of information and computation. The traditional relationship between mathematics, physics, and information may be expressed symbolically as follows:
Mathematics Physics Information
According to this orthodox view, mathematical relationships are the most basic aspects of existence. The physical world is an expression of a subset of mathematical relationships, whereas information is a secondary, or derived, concept that characterizes certain specific states of matter (such as a switch being either on or off, or an electron spin being up or down). However, an alternative view is gaining in popularity: a view in which information is regarded as the primary entity from which physical reality is built. It is popular among scientists and mathematicians who work on the foundations of computing, and physicists who work in the theory of quantum computation. Importantly, it is not merely a technical change in perspective, but represents a radical shift in world view, well captured by Wheeler’s pithy slogan “It from bit” (Wheeler and Ford, 1998). The variant I wish to explore here is to place information at the base of the explanatory scheme, thus:
Information Laws of physics Matter
After all, the laws of physics are informational statements: they tell us something about the way the physical world operates. This shift in perspective requires a shift in the foundational question I posed concerning the origin of the laws of physics; we may now ask about the origin and nature of the information content of the universe, and I refer the reader to Seth Lloyd’s essay in Chapter 5 of this volume for one perspective on that question. Here I wish to address a more basic aspect of the problem, which is whether the information content of the universe is finite or infinite.
In the standard model of cosmology, in which there is a single universe that began with a big bang (representing the origin of space and time), the universe contains a finite amount of information. To see why, first note that the universe began 13.7 billion years ago, according to the latest astronomical evidence. The region of space accessible to our observations is defined by the maximum distance that light has traveled since the big bang: namely, 13.7 billion light-years. Because the speed of light is a fundamental limit, no information can travel faster than light, so the volume of space delimited by the reach of light defines a sort of horizon in space beyond which we cannot see, or be influenced by in terms of causal physical effects. Expressed differently, we cannot access any information beyond the horizon at this time. The horizon does expand with time t (like t2), so that, in the future, the causally connected region of our universe will contain more information. In the past, it contained less. The technical term for the light horizon is “particle horizon,” because it separates particles of matter we can see (in principle) from those we cannot see because there has not yet been enough time since the cosmic origin for the light from them to reach us on Earth. It is likely that there is another type of horizon, technically termed an “event horizon.” It arises because the rate of expansion of the universe seems to be accelerating, implying (very crudely speaking) that some galaxies we now see flying away from us are speeding up, and will eventually recede so fast that their light will never again reach us. They will disappear across the event horizon for good. At some stage in the next few billion years, the event horizon effects will come to dominate over the particle horizon effects. By an odd coincidence, the radii of the particle and event horizons are roughly the same at the current epoch, and given the incompletely formulated nature of what I shall propose, either or both horizons may be regarded as the basis of the discussion (so I simply use the generic word “horizon” from now on).
A well-defined question is: how much information is there within the volume of space limited by the horizon? Information is quantified in bits, or binary digits, exemplified by a coin toss. The coin is either heads or tails, and determining which amounts to acquiring precisely one bit of information. So how many bits are there in the causally connected horizon region of our universe at this present epoch? The answer was worked out by Seth Lloyd (2002, 2006) using quantum mechanics. This is key: quantum mechanics says that the states of matter are fundamentally discrete rather than continuous, so they form a countable set. It is then possible to work out (approximately) how many bits of information any given volume of the universe contains by virtue of quantum discreteness. The answer is 10122 bits for the region within the horizon at this time. This number has a neat physical interpretation. 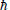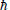It is the area of the horizon divided by the smallest area permitted by quantum discreteness, the so-called Planck area, 4πG/c3, which is roughly 10−65 cm2. So the cosmic bit count is a dimensionless ratio, and a fundamental parameter of the universe.
Lloyd’s number is not new in physical theory. It is roughly N3/2, where N is the so-called Eddington–Dirac number: the ratio of electromagnetic to gravitational force between an electron and a proton. It is also the current age of the universe expressed in atomic units. Both Arthur Eddington (1931) and Paul Dirac (1937) attempted to build fundamental theories of physics using this number as the starting point. Neither attained any long-term success, so we must be careful to learn that lesson of history. However, Eddington and Dirac did not have the benefit of our better understanding of the relationship between gravitation and the concept of entropy. That understanding stemmed from important work done in the 1960s and 1970s on the physics of black holes. By 1970 it was obvious that black holes possess fundamental thermodynamic properties, and that the event horizon area of a black hole – roughly, the surface area of its boundary – plays the role of entropy. In standard thermodynamics, as applied to heat engines, say, entropy is a measure of the degree of disorder in a system, or, alternatively, the negative of the amount of useful energy that may be extracted to perform work. In the early 1970s, Jacob Bekenstein discovered that if quantum mechanics were applied to black holes, a specific expression could be given for its entropy (Bekenstein, 1973). This work was firmed up by Stephen Hawking (1975), who discovered that black holes are not perfectly black after all, but glow with heat radiation. The temperature of the radiation is inversely proportional to the mass M of the black hole, so that small black holes are hotter than large ones. The corresponding Bekenstein–Hawking entropy of an uncharged, non-rotating black hole is
S = 4πkGM2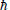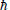/c3 = ¼kA (4.1)
where A is its area in Planck units, and k is Boltzmann’s constant, which converts units of energy to units of temperature. Significantly, in the black hole case entropy is a function of the boundary area, as opposed to volume. By contrast, the entropy of two masses of gas in identical thermodynamic states is the sum of the two volumes of gas.
I now come to the link with information. It has been known for many decades that entropy can been regarded as a measure of ignorance (Szilard, 1929, 1964). For example, if we know all the molecules of a mass of gas are confined to the corner of a box, the gas is ascribed a low entropy. Conversely, when the gas is distributed throughout the volume and its molecules are thoroughly shuffled and distributed chaotically, the entropy is high. Ignorance is the flip side of information, so we may deduce a mathematical relationship between entropy and information I. As given by Shannon (1948), that relationship is
S = −I (4.2)
One may think of the entropy of a gas as the information concerning the positions and motions of its molecules over which we have lost cognizance. In a similar vein, when matter falls into a black hole, we lose track of that too, because the black hole surface is an event horizon through which light cannot pass from the inside to the outside (which is why the hole is black). The Bekenstein–Hawking formula (4.1) relates the total information swallowed by a black hole to the surface area of its event horizon. The formula shows that the information of the black hole is simply one-quarter of the horizon area in Planck units.
The association of entropy and information with horizon area may be extended to all event horizons, not just those surrounding black holes; for example, the cosmological event horizon, which I discussed above (Davies and Davis, 2003; Gibbons and Hawking, 1977). Bekenstein proposed generalizing equation 4.1 to obtain a universal bound on entropy (or information content) for any physical system (Bekenstein, 1981). The black hole saturates the Bekenstein bound, and represents the maximum amount of information that can be packed into the volume encompassed by the horizon. A similar statement may be postulated for the cosmological horizon (where so-called de Sitter space saturates the bound).
The link between information (loss) and area seems to be a very deep property of the universe, and has been elevated to the status of a fundamental principle by Gerhard ’t Hooft (1993) and Leonard Susskind (1995), who proposed a so-called holographic principle, according to which the information content of a volume of space (any volume, not just a black hole) is captured by the information that resides on an enveloping surface that bounds that volume. (The use of the term “holographic” is an analogy based on the fact that a hologram is a three-dimensional image generated by shining a laser on a two-dimensional plate.) The holographic principle implies that the total information content of a region of space cannot exceed one-quarter of the surface area (in Planck units) that confines it (other variants of the holographic principle have been proposed, with different definitions of the enveloping area), and that this limit is attained in the case of the cosmological event horizon. If the holographic principle is applied to the state of the universe today, one recovers Lloyd’s cosmic information bound of 10122 bits.

4.4 What does the finite information content of the universe tell us about “reality”?

The fact that (in the standard cosmological model at least) the information content of the universe is finite would seem to be a very important foundational fact about the universe. What are its implications? For a start, it means that nothing in the universe (as defined by the bounding horizon) can be specified or described by more than 10122 bits of information. By “nothing” I refer to actually-existing physical structures or states. The bound does not apply, for example, to merely hypothetical specifications, such as all possible hands of cards, or all possible combinations of amino acids making up a protein (>10130) because there is no claim that all such combinations might be physically present in the universe. Thus the universe could not contain a hotel with 10130 rooms, for example. In fact, the universe contains only about 1090 particles in total (including photons but not gravitons), and the finite information bound says they could not be confined to the “corner of a box” very much smaller than the universe, to borrow from the example of classical thermodynamics, because we would then know their locations to a better-than-permitted level of description. Note that the informational properties of the quantum universe differ fundamentally in this respect from the classical universe of Laplace’s demon. Laplace assumed that the state of the universe at one instant could be specified to infinite precision; that is, the position and velocity of each particle could be ascribed a set of six real numbers. (It is easily shown that even tiny imprecisions lead to exponentially growing errors in the demon’s prediction.) But almost all real numbers require an infinite amount of information to specify them.
The above-mentioned whimsical example (a hotel) refers to a classical state. How about a quantum state? After all, the information bound is quantum mechanical in nature. Consider a series of photon beam splitters labeled i, each of which permits a photon to traverse it (or be destroyed) with a certain probability pi. Each encounter between a given photon and a beam splitter reduces the probability that the photon survives to exit the entire assemblage of beam splitters. After N such encounters, there is a probability P(N) = p1p2p3 … pN that the photon will have traversed the entire series. This becomes an exponentially small number as N rises. For example, if pi = ½ for all i and N>400, we find 2−N<10–122. Can the universe contain such a small number? Of course it can in a sense: I just wrote it down! But how can we test if the prediction for the photon’s penetration probability is correct? That is, how do we know quantum mechanics accurately describes this experimental set-up? We would have to perform >10122 experiments to verify it, and that is certainly not only impossible for us, it is impossible even in principle for a Laplace-type demon. Now consider that the pi are not all exactly ½, but numbers chosen randomly from the interval [0, 1]. Then for almost all of the set {pi} the total probability P(N) could not be accommodated in the universe. If a demon chose to write out the answer using every bit of information contained in the universe – every particle, say – the demon would run out of bits before the number could be expressed. Actually, the information would be very likely to be exhausted even for a single beam splitter, given that the real number p1 could almost always be expressed only by stipulating an infinite number of digits: for example 0.37652583 …
The question then arises, is the number P(N) in some sense unknowable, not just in practice, but in principle? Expressed differently, could a demon even know that number? And if not – if the number is fundamentally unknowable – does that signal a fundamental limit in the level of precision at which quantum mechanics may be applied even in principle? The immediate answer to the latter question is no, because a probability is not an actuality; it is merely a relative weighing of actualities, and in that respect it possesses the same status as the number of possible combinations of amino acids. The demon (or for that matter a laboratory technician) can merely look to see whether or not the photon has survived, and the answer requires only one bit of information (“yes” or “no”) to express it. But there is a subtlety buried here. Quantum mechanics generally cannot predict actualities, only probabilities. What it can predict – in principle with perfect accuracy – are wave-function amplitudes, from which the probabilities can be computed. In the example of the beam splitter, the wave function is a superposition of amplitudes, and the number of branches of the wave function, or components summed in the superposition, is 2N. For N>400, this number alone exceeds the information-carrying capacity of the universe, never mind the information required to specify the amplitudes of each component of the superposition.
So my question now is, can the quantum state (the superposition of amplitudes that make up the wave function) be contained in the universe? The standard answer is yes. After all, what would prevent us from assembling 400 random beam splitters and sending in a photon? It is true that we can create such a state, but can we specify, or describe it? Presumably not – not even the demon can do that. Which brings me to the crux of the matter. Is the quantum state in any sense real, given that it is in principle unknowable from within the universe? Or is it merely a Platonic fiction, useful (as is the concept of infinity) for doing calculations, its fictional nature safely buried beneath very much larger experimental and initial condition errors? Given that a full specification or description of the beam-splitter experiment requires more information than the universe contains, my question becomes the following: is information something that really exists, independently of observers, or is it merely our description of what can in principle become known to an agent or observer? If the latter is the case – if information is merely a description of what we know about the physical world – then there is no reason why Mother Nature should care about the cosmic information bound, and no reason that the bound should affect fundamental physics. A Platonic Mother Nature can be all-knowing. And according to the orthodox view of laws, in which the bedrock of physical reality is vested in perfect laws of physics inhabiting the Platonic domain, Mother Nature can indeed compute to arbitrary precision with the unlimited quantity of information at her disposal. But if information is “real” – if, so to speak, it occupies the ontological basement (as I propose) – then the bound on the information content of the universe is a fundamental limitation on all of nature, and not just on states of the world that humans perceive.
A scientist who advocated precisely this position was Rolf Landauer, who adopted the view that “the universe computes in the universe,” and not in a Platonic heaven, a point of view motivated by his insistence that “information is physical.” Landauer was quick to spot the momentous consequences of this shift in perspective:
The calculative process, just like the measurement process, is subject to some limitations. A sensible theory of physics must respect these limitations, and should not invoke calculative routines that in fact cannot be carried out.
(Landauer, 1967)
In other words, in a universe limited in resources and time – for example, a universe subject to the cosmic information bound – concepts such as real numbers, infinitely precise parameter values, differentiable functions, and the unitary evolution of a wave function are a fiction: a useful fiction to be sure, but a fiction nevertheless. Consider the case of Laplace’s demon, and the key phrase, “if this intellect were vast enough to submit the data to analysis.” If Mother Nature – in effect, Laplace’s demon – inhabits the Platonic realm of perfect, infinitely precise mathematics, then the finite information bound of the universe matters not at all, because the Platonic Mother Nature is, to paraphrase Laplace, certainly “vast enough,” because she is omniscient and possesses infinite intellect, and can therefore submit an infinity of bits of data to analysis. She can indeed “carry out” the “calculative processes” to which Landauer refers. But if information is physical, if it is ontologically real and physically fundamental, then there are no Platonic demons, no godlike transcendent Mother Nature computing with real numbers; indeed, no real numbers. There is only the hardware of the real physical universe doing its own calculation itself, in the manner that Lloyd describes in Chapter 5 of this book. Expressed differently, the laws of physics are inherent in and emergent with the universe, not transcendent of it.
Landauer made his original comments as part of a general analysis; his ideas pre-dated the holographic principle and the finite information bound on the universe. But the existence of this bound projects Landauer’s point beyond mere philosophy and places a real restriction on the nature of physical law. For example, one could not justify the application of the laws of physics in situations employing calculations that involve numbers greater than about 10122, and if one did, then one might expect to encounter departures between theory and experiment. For most purposes, the information bound is such a large number that the consequences of the shift I am proposing are negligible. Consider the law of conservation of electric charge, for example. The law has been tested to about only one part in 1012. If it were to fail at the 10122 bit level of accuracy, the implications are hardly significant.
Nevertheless there are situations in theoretical physics in which very large numbers do crop up. One obvious class of cases is where exponentiation occurs. Consider, for example, statistical mechanics, in which Poincaré’s recurrence times are predicted to be of the order exp(10N) Planck times (chosen to make the number dimensionless) and N is the number of particles in the system. Imposing a bound of 10122 implies that the recurrence time prediction is reliable only for recurrence times of about 1060 years. Again, this is so long we would be unlikely to notice any departure between theory and observation.
A more striking and potentially practical application of the same principle is quantum computation. Quantum computers hold out the promise of possessing exponentially greater power than classical computers, because of the phenomena of quantum superposition and entanglement. The latter refers to the fact that two quantum systems, even when physically separated, are still linked in a subtle way. The arithmetic of the linkage reveals that there are exponentially more possible states of entangled quantum systems than their separate components contain. Thus an n-component system (for example, n atoms) possesses 2n states, or 2n components of the wave function describing the system. The fundamentally exponential character of the quantum realm has been eloquently addressed by Scott Aaronson (2005), using the pithy question: “Is the universe a polynomial or exponential place?” to discuss what he calls “the ultimate Secret of Secrets.” He goes on to say:
For almost a century, quantum mechanics was like a Kabbalistic secret that God revealed to Bohr, Bohr revealed to the physicists, and the physicists revealed (clearly) to no one. So long as the lasers and transistors worked, the rest of us shrugged at all the talk of complementarity and wave–particle duality, taking for granted that we’d never understand, or need to understand, what such things actually meant. But today – largely because of quantum computing – the Schrödinger’s cat is out of the bag, and all of us are being forced to confront the exponential Beast that lurks inside our current picture of the world. And as you’d expect, not everyone is happy about that, just as the physicists themselves weren’t all happy when they first had to confront it in the 1920s.
(Aaronson, 2005)
The question I now ask is whether Aaronson’s “exponential Beast” is compatible with a Laplace-type demon located within the real universe and subject to its finite resources and age – a Laplacian demiurge would be a more accurate description. Let me call this Beast “Landauer’s demon.” Suppose it is required to predict the behavior of a quantum computer subject to the above discussed cosmological information bound. The key to quantum computation lies with the exponential character of quantum states, so here we have the crucial exponentiation at work that is vulnerable to the cosmic information bound. To be specific, a quantum state with more components than about n = 400 particles is described by a wave function with more components than Lloyd’s 10122 bits of information contained in the entire universe. A generic wave function of this state of 400-particles could not be expressed in terms of bits of information, even in principle. Even if the entire universe were commandeered as a data display, it would not be big enough to accommodate the specification of that quantum state. So a generic 400-particle quantum state cannot be described, let alone its evolution predicted, even by a Landauer demon. It could, however, be predicted with a truly god-like transcendent Platonic demon with infinite resources and patience at its disposal.
The conclusion is stark. If the cosmic information bound is set at 10122 bits, and if information is ontologically real, then the laws of physics have intrinsically finite accuracy. For the most part, that limitation of the laws will have negligible consequences, but in cases of exponentiation, like quantum entanglement, they make a big difference, a difference that could potentially be observed. Creating a state of 400 entangled quantum particles is routinely touted by physicists working on building a quantum computer (their target is 10 000 entangled particles). I predict a breakdown of the unitary evolution of the wave function at that point, and possibly the emergence of new phenomena. To quote Wittgenstein (1921): “Whereof one cannot speak, thereof one must remain silent.” We cannot – should not – pronounce on, or predict, the state, or dynamical evolution, of a generic quantum system with more than about 400 entangled particles, because there are not enough words in the entire universe to describe that state!
The orthodox position on the accuracy of predictions is that the laws of physics themselves are infinitely precise, but the concept of a perfectly isolated physical system and precisely known initial conditions are an idealization. In practice, so the argument goes, there will inevitably be errors, which will normally be enormously greater than one part in 10122. In the case of quantum computation, these errors are tackled using error-correcting procedures and redundancy. The position I am advocating is that the finite information bound on the universe limits the accuracy of the laws themselves, rendering them irreducibly “fuzzy.” This is a type of unavoidable cosmological noise, which no amount of error correction can remove. It would manifest itself as a breakdown in the unitary evolution of the wave function. What I am suggesting here seems to be close to the concept of unavoidable intrinsic decoherence proposed by Milburn (1991, 2006). Some clarification of these issues may emerge from the further study of the recent discovery that the entropy of quantum entanglement of a harmonic lattice also scales like area rather than volume (Cramer and Eisert, 2006), which would seem to offer support for the application of the holographic principle to entangled states. It would be good to know how general the entanglement–area relationship might be.
Finally, I should point out that the information bound (1) was derived using quantum field theory, but that same bound applies to quantum field theory. Ideally one should derive the bound using a self-consistent treatment. If one adopts the philosophy that information is primary and ontological, then such a self-consistency argument should be incorporated in a larger program directed at unifying mathematics and physics. If, following Landauer, one accepts that mathematics is meaningful only if it is the product of real computational processes (rather than existing independently in a Platonic realm) then there is a self-consistent loop: the laws of physics determine what can be computed, which in turn determines the informational basis of those same laws of physics. Paul Benioff (2002) has considered a scheme in which mathematics and the laws of physics co-emerge from a deeper principle of mutual self-consistency, thus addressing Wigner’s famous question of why mathematics is so “unreasonably effective” in describing the physical world (Wigner, 1960). I have discussed these deeper matters elsewhere (Davies, 2006).

4.5 Conclusion

Let me finish with a personal anecdote. A vivid memory from my high-school years was learning how to calculate the gravitational potential energy of a point mass by integrating the (negative) work done transporting the particle radially inwards from infinity to the Earth’s surface. I raised my hand and asked how a particle can actually be transported from infinity. The answer I received is that this mode of analysis is a device designed to make the calculation simple, and that the error involved in taking infinity as the starting point rather than some finite but very great distance is negligible. And so indeed it is. But this little exchange set me thinking about the use of mathematics as a device versus the actual mathematical nature of physical laws. I wanted to know whether the “real” potential energy of gravitation – the one based on the laws that Mother Nature herself uses – is the one that takes infinity as the starting point, or somewhere closer. In other words, although we human beings could never, even in principle, carry out the physical process involved in computing the exact potential energy, maybe nature somehow “knows” the answer without actually doing the experiment. That is, the exact answer is there, “embedded” in the laws of physics, and the business about infinity is a problem only for humans (and perhaps only for the likes of troublesome students such as the young Paul Davies).
The flip side of infinity is the use of infinitesimal intervals, which form the basis for the calculus. In view of the fact that all the fundamental laws of physics are expressed as differential equations, the status of infinitesimals is crucial. Again the question arises as to whether they are artifacts of human mathematics, or correspond to reality. A philosopher might express it by the question, What is the ontological status of infinitesimal intervals? This question is closely related to the use of real numbers and the property of continuity. Can an interval of space or time be subdivided without limit?
Over the years there have been many speculations by physicists that space–time may not in fact be continuous and differentiable, and that the application of real numbers and differentiation might be merely a convenient idealization. Most of these ideas remained restricted to small groups of devotees. The serious challenge came, however, not from physicists but computer scientists. Digital computers cannot, by their very nature, handle infinite and infinitesimal quantities because they manipulate discrete bits using Boolean algebra. This is in contrast to analog computers such as slide rules. The study of the performance of digital computers, which began with Turing, matured into an entire discipline in its own right in the decades after 1950. In recent years, theoretical physics and the theory of computation have been brought together, raising many deep conceptual issues that are as yet unresolved. The most basic of these is the following: Is the universe itself some sort of computer, and if so what? Analog, digital, quantum, or something else?
Lloyd advocates that the universe computes itself, but it does so quantum mechanically – the universe is a quantum computer (see Chapter 5 of this volume). We can envisage a corresponding quantum Landauer demon, able to observe all the branches of the wave function – in effect, all possible worlds, rather than a single actual world (this is precisely the ontology adopted in the Everett many-universes interpretation of quantum mechanics) (Everett, 1957). If that ontology is correct, if the ground of being is vested in the quantum wave function rather than the informational bits that emerge via measurement and observation, then the information bound on the universe is exponentially greater, and nothing would “go wrong” to an entangled state of 400 particles. Whether reality does lie in a quantum realm, to which human beings have no access, or whether it lies in the realm of real bits and real observations, could therefore be put to the test with a sufficiently complex quantum system. If the quantum computation optimists are right, it maybe that within a few years a new discipline will emerge: experimental ontology.

References

Aaronson, S. (2005). Are quantum states exponentially long vectors? Proceedings of the Oberwolfach Meeting on Complexity Theory, arXiv: quant-ph/0507242v1, accessed 8 March 2010 (http://arxiv.org/abs/quant-ph/0507242).
Barrow, J. D. (2002). The Constants of Nature. New York and London: Random House.
Bekenstein, J. D. (1973). Black holes and entropy. Physical Review D, 8: 2333–2346.
Bekenstein, J. D. (1981). Universal upper bound on the entropy-to-energy ratio for bounded systems. Physical Review D, 23: 287–298.
Benioff, P. (2002). Towards a coherent theory of physics and mathematics. Foundations of Physics, 32: 989–1029.
Boswell, J. (1823). The Life of Samuel Johnson, vol. 1. London: J. Richardson & Co.
Carroll, S. (2007). Edge: The Third Culture. Accessed 8 March 2010 (www.edge.org/discourse/science_faith.html).
Cramer, M., and Eisert, J. (2006). Correlations, spectral gap and entanglement in harmonic quantum systems on generic lattices. New Journal of Physics, 8: 71.
Davies, P. C. W., and Davis, T. M. (2003). How far can the generalized second law be generalized? Foundations of Physics, 32: 1877–1889.
Davies, P. (2006). The Goldilocks Enigma: Why Is the Universe Just Right for Life? London: Allen Lane, The Penguin Press.
Descartes, R. (1630). Letter to Mersenne, 15 April 1630. In Descartes’ Philosophical Letters, trans. and ed. A. Kenny (1970). Oxford: Clarendon Press.
de Spinoza, B. (1670). Theological–Political Treatise, 2nd ed, trans. S. Shirley. Indianapolis, IN: Hackett Publishing, 75.
Dirac, P. A. M. (1937). The cosmological constants. Nature, 139: 323.
Drake, S. (1957). Discoveries and Opinions of Galileo. New York: Doubleday-Anchor.
Eddington, A. S. (1931). Preliminary note on the masses of the electron, the proton, and the universe. Mathematical Proceedings of the Cambridge Philosophical Society, 27: 15–19.
Everett, H. (1957). Relative state formulation of quantum mechanics. Reviews of Modern Physics, 29: 454–462.
Gibbons, G. W., and Hawking, S. W. (1977). Cosmological event horizons, thermodynamics, and particle creation. Physical Review D, 15: 2738–2751.
Greene, B. (1999). The Elegant Universe. New York: Norton.
Hawking, S. W. (1975). Particle creation by black holes. Communications in Mathematical Physics, 43: 199–220.
Hawking, S. (1988). A Brief History of Time. New York: Bantam.
Landauer, R. (1986). Computation and physics: Wheeler’s meaning circuit? Foundations of Physics, 16(6): 551–564.
Laplace, P. (1825). Philosophical Essays on Probabilities. Trans. F. L. Emory and F. W. Truscott (1985). New York: Dover.
Lloyd, S. (2002). Computational capacity of the universe. Physical Review Letters, 88: 237901.
Lloyd, S. (2006). The Computational Universe. New York: Random House.
Milburn, G. (1991). Intrinsic decoherence in quantum mechanics. Physical Review A, 44: 5401–5406.
Milburn, G. (2006). Quantum computation by communication. New Journal of Physics, 8: 30.
Rees, M. (2001). Our Cosmic Habitat. Princeton: Princeton University Press.
Russell, B. (1957). Why I Am Not A Christian. New York: Touchstone.
Shannon, C. E. (1948). A mathematical theory of communication. Bell System Technical Journal, 27: 379–423, 623–656.
Smolin, L. (2008). On the reality of time and the evolution of laws. Online video lecture and PDF, accessed 8 March 2010 (http://pirsa.org/08100049/).
Susskind, L. (1995). The world as a hologram. Journal of Mathematical Physics, 36: 6377.
Susskind, L. (2005). The Cosmic Landscape: String Theory and the Illusion of Intelligent Design. New York: Little, Brown.
Szilard, L. (1929). Uber die Entropieverminderung in einem thermodynamischen System bei eingriffen intelligenter Wesen. Zeitschrift für Physik, 53: 840–856.
Szilard, L. (1964). On the decrease of entropy in a thermodynamic system by the intervention of intelligent beings. Behavioral Science, 9(4): 301–310.
Tegmark, M. (2003). Parallel universes. Scientific American, May 31, 2003.
Ward, K. (1982). Rational Theology and the Creativity of God. New York: Pilgrim Press.
Wheeler, J. A. (1979). Frontiers of time. In Problems in the Foundations of Physics, ed. G. Toraldo di Francia. Amsterdam: North-Holland, 395–497.
Wheeler, J. A. (1983). On recognizing ‘law without law’. American Journal of Physics, 51: 398–404.
Wheeler, J. A. (1989). Information, physics, quantum: The search for links. Proceedings of the Third International Symposium on the Foundations of Quantum Mechanics (Tokyo), 354.
Wheeler, J. A. (1994). At Home in the Universe. New York: AIP Press.
Wheeler, J. A., and Ford, K. (1998). It from bit. In Geons, Black Holes & Quantum Foam: A Life in Physics. New York: Norton.
Wigner, E. P. (1960). The unreasonable effectiveness of mathematics in the natural sciences. Communications in Pure and Applied Mathematics, 13(1): 1–14.
Wittgenstein, L. (1921). Tractatus Logico-Philosophicus, trans. D. Pears and B. McGuinness (1961). London: Routledge.
Zeilinger, A. (2004). Why the quantum? It from bit? A participatory universe? Three far-reaching, visionary questions from John Archibald Wheeler and how they inspired a quantum experimentalist. In Science and Ultimate Reality: Quantum Theory, Cosmology, and Complexity, eds Barrow J. D., Davies P. C. W., and C. L. Harper. Cambridge: Cambridge University Press, 201–220.
      Information and the Nature of Reality: From Physics to Metaphysics, eds. Paul Davies and Niels Henrik Gregersen. Published by Cambridge University Press © P. Davies and N. Gregersen 2010.
1 Although orthodox Newtonian mechanics assumes infinitely precise laws, Newton himself was more circumspect. He considered that the solar system might require an occasional divine prod to maintain its stability, a suggestion that incurred the derision of some of his contemporaries. Later Laplace would famously remark to Napoleon that he “had no need of this [divine prodding] hypothesis.”