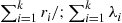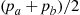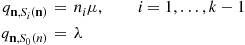
(b) Follows from the hint about using the lack of memory property and the fact that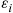 
, the minimum of 
independent exponentials with rate 
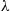, is exponential with rate 
.
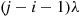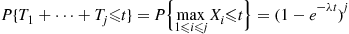
(d) With all probabilities conditional on 
,
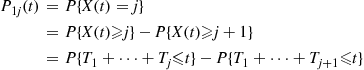
(e) The sum of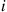 
independent geometrics, each having parameter 
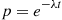, is a negative binomial with parameters 
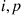. The result follows since starting with an initial population of 
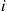is equivalent to having 
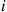independent Yule processes, each starting with a single individual.
2: an acceptable molecule is attached
1: an unacceptable molecule is attached.
Then, this is a birth and death process with balance equations
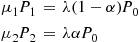
Since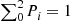 
, we get
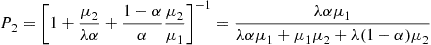
where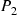 
is the percentage of time the site is occupied by an acceptable molecule. The percentage of time the site is occupied by an unacceptable molecule is
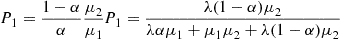
19. There are four states. Let state 0 mean that no machines are down, state 1 that machine 1 is down and 2 is up, state 2 that machine 1 is up and 2 is down, and state 3 that both machines are down. The balance equations are as follows:
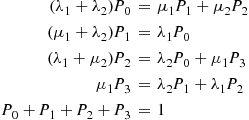
The equations are easily solved and the proportion of time machine 2 is down is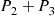 
.
24. We will let the state be the number of taxis waiting. Then, we get a birth and death process with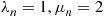 
. This is an 
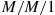. Therefore:
(a) Average number of taxis waiting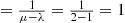 
.
(b) The proportion of arriving customers that gets taxis is the proportion of arriving customers that find at least one taxi waiting. The rate of arrival of such customers is 
. The proportion of such arrivals is therefore
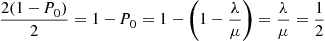
28. Let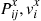 
denote the parameters of the 
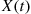and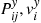 
of the 
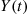process; and let the limiting probabilities be 
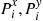, respectively. By independence we have that for the Markov chain 
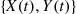its parameters are
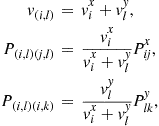
and
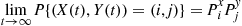
Hence, we need to show that
(That is, the rate from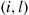 
to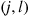 
equals the rate from 
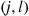to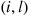 
.) But this follows from the fact that the rate from 
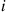to 
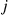in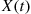 
equals the rate from 
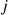to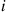 
; that is,
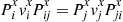
The analysis is similar in looking at pairs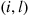 
and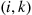 
.
33. Suppose first that the waiting room is of infinite size. Let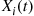 
denote the number of customers at server 
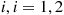. Then since each of the 
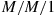processes 
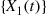is time reversible, it follows from Exercise 28 that the vector process 
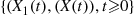is a time reversible Markov chain. Now the process of interest is just the truncation of this vector process to the set of states 
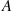where
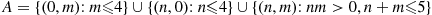
Hence, the probability that there are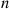 
with server 1 and 
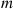with server 2 is
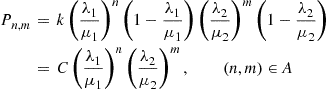
The constant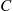 
is determined from
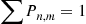
where the sum is over all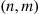 
in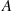 
.
(a) The state is 
if there ar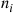e 
type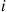 
patients in the hospital, for all 
.
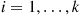(b) It is a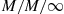 
birth and death process, and thus time reversible.
(c) Because 
are independent processes for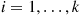 
, the vector process is a time reversible continuous time Markov chain.
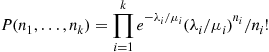
(e) As a truncation of a time reversible continuous time Markov chain, it has stationary probabilites
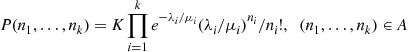
where 
, and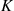 
is such that
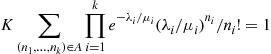
(f) With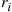 
equal to the rate at which type 
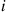patients are admitted,
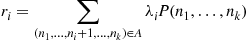
(a) The state is the set of idle servers.
(b) For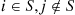 
, the infinitesimal rates of the chain are
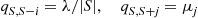
where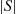 
is the number of elements in 
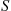. The time reversibility equations are
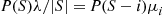
which has a solution
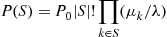
where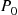 
, the probability there are no idle servers, is found from
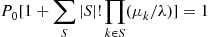
where the preceding sum is over all nonempty subsets of 
.
(a) The state is 
if 
is the set of idle servers, with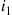 
having been idle the longest, 
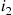the second longest, and so on.
(c) For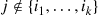 
, the infinitesimal rates of the chain are
The time reversibility equations are
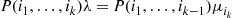
giving the solution
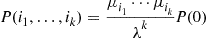
where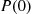 
is the probability there are no idle servers.
40. The time reversible equations are
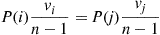
yielding the solution
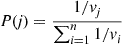
Hence, the chain is time reversible with long run proportions given by the preceding.
41. Show in Example 6.22 that the limiting probabilities satisfy Equations (6.33), (6.34), and (6.35).
42. Because the stationary departure process from an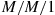 
queue is a Poisson process it follows that the number of customers with server 
is the stationary probability of an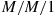 
system.
43. We make the conjecture that the reverse chain is a system of same type, except that the Poisson arrivals at rate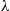 
arrive at server 
, then go to server 
, then to server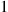 
, and then depart the system. Let 
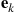be the 3-vector with 
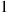in position 
and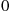 
elsewhere. With the state being 
when that there are 
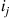customers at server 
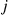for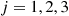 
, the instantaneous transition rates of the chain are
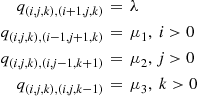
whereas the conjectured instantaneous rates for the reversed chain are
The conjecture is correct if we can find probabilities 
that satisfy the reverse time equations when the preceding are the instantaneous rates for the reversed chain, and it is easy to check that
satisfy.
(a) The matrix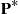 
can be written as
and so 
can be obtained by taking the 
element of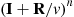 
, which gives the result when 
.
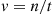(b) Uniformization shows that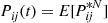 
, where 
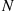is independent of the Markov chain with transition probabilities 
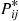and is Poisson distributed with mean 
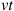. Since a Poisson random variable with mean 
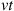has standard deviation 
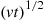, it follows that for large values of 
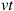it should be near 
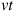. (For instance, a Poisson random variable with mean 
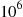has standard deviation 
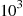and thus will, with high probability, be within 3000 of 
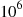.) Hence, since for fixed 
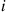and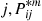 
should not vary much for values of 
about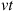 
where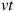 
is large, it follows that, for large 
,
Chapter 7
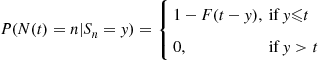
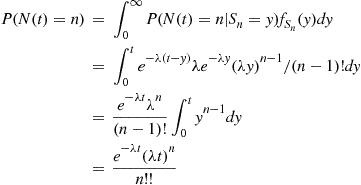
(a) Consider a Poisson process having rate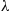 
and say that an event of the renewal process occurs whenever one of the events numbered 
of the Poisson process occurs. Then
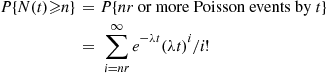
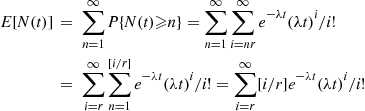
(a) The number of replaced machines by time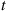 
constitutes a renewal process. The time between replacements equals 
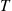, if the lifetime of new machine is 
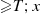, if the lifetime of new machine is 
. Hence,
and the result follows by Proposition 7.1.
(b) The number of machines that have failed in use by time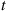 
constitutes a renewal process. The mean time between in-use failures, 
, can be calculated by conditioning on the lifetime of the initial machine as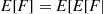 
lifetime of initial machine]]. Now
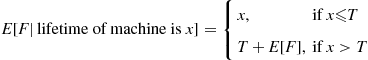
Hence,
or
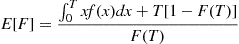
and the result follows from Proposition 7.1.
13. With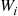 
equal to your winnings in game 
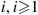, and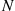 
the number of games played, Wald’s equation yields
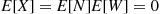
With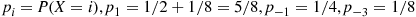 
, verifying that 
.
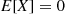18. We can imagine that a renewal corresponds to a machine failure, and each time a new machine is put in use its life distribution will be exponential with rate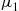 
with probability 
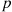, and exponential with rate 
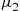otherwise. Hence, if our state is the index of the exponential life distribution of the machine presently in use, then this is a two-state continuous-time Markov chain with intensity rates
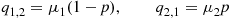
Hence,
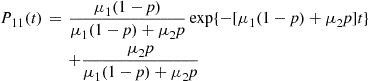
with similar expressions for the other transition probabilities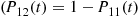 
, and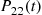 
is the same with 
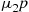and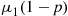 
switching places). Conditioning on the initial machine now gives
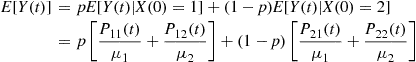
Finally, we can obtain 
from
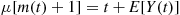
where
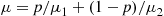
is the mean interarrival time.
(a) Let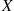 
denote the length of time that J keeps a car. Let 
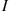equal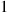 
if there is a breakdown by time 
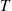and equal 
otherwise. Then
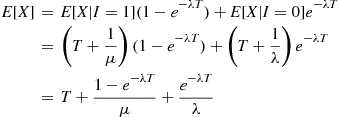
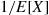is the rate that J buys a new car.
(b) Let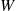 
equal to the total cost involved with purchasing a car. Then, with 
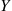equal to the time of the first breakdown
J’s long run average cost is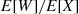 
.
(a) Say that a new cycle begins each time A wins a point. With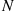 
equal to the number of points in a cycle
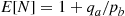
where the preceding used that, starting with 
serving, the number of points played until A wins a point is geometric with parameter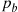 
. Hence, by renewal reward, the proportion of points won by A is 
.
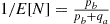(c)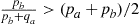 
is equivalent to 
.
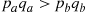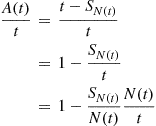
The result follows since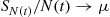 
(by the strong law of large numbers) and 
.
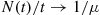(a) We can view this as an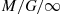 
system where a satellite launching corresponds to an arrival and 
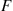is the service distribution. Hence,
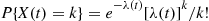
where 
.
(b) By viewing the system as an alternating renewal process that is on when there is at least one satellite orbiting, we obtain
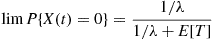
where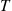 
, the on time in a cycle, is the quantity of interest. From part (a)
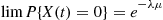
where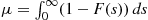 
is the mean time that a satellite orbits. Hence,
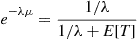
so