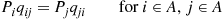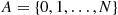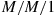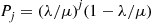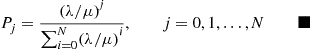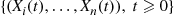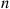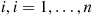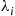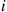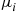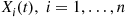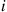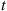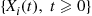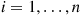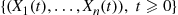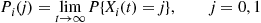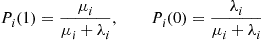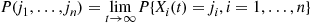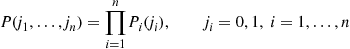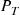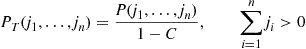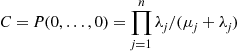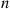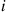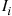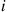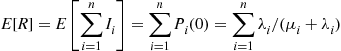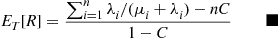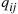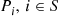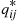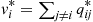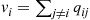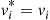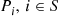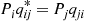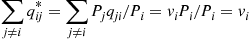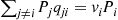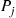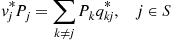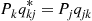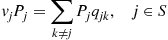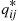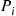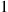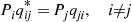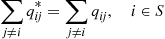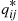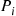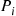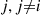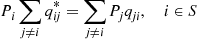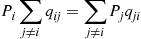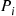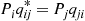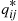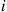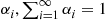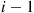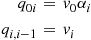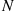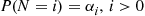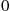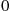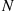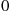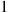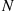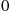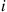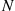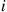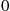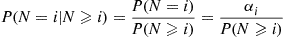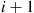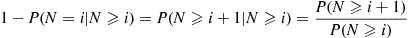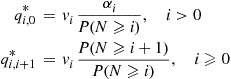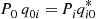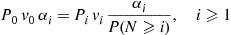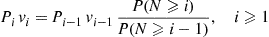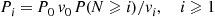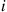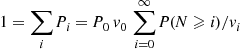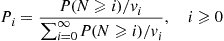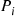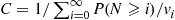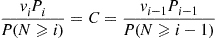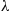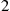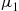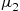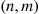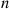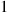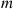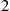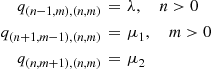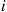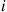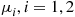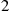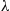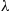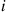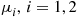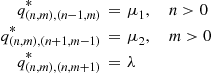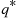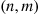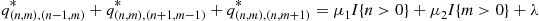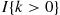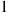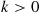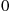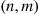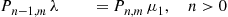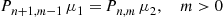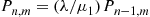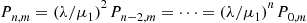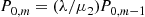6.7 The Reversed Chain
Consider an ergodic continuous-time Markov chain whose state space is S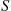 and which has instantaneous transition rates qij
and which has instantaneous transition rates qij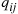 and limiting probabilities Pi,i∈S
and limiting probabilities Pi,i∈S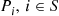 , and suppose that this chain that has been in operation for a long (in theory, an infinite) time. Then, it follows from results in the previous section that the process of states going backwards in time is also a continuous time Markov chain, having instantaneous transition rates qij∗
, and suppose that this chain that has been in operation for a long (in theory, an infinite) time. Then, it follows from results in the previous section that the process of states going backwards in time is also a continuous time Markov chain, having instantaneous transition rates qij∗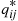 that satisfy
that satisfy
Piqij∗=Pjqji,i≠j
The reverse chain is a very useful concept even in cases where it differs from the forward chain (that is, even in cases where the chain is not time reversible).
To begin, note that the amount of time the reverse chain spends in state i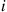 during a visit is exponential with rate vi∗≡∑j≠iqij∗
during a visit is exponential with rate vi∗≡∑j≠iqij∗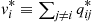 . Because the amount of time the process spends in a state i
. Because the amount of time the process spends in a state i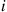 during a visit will be the same whether the chain is observed in the usual (forward) or in the reverse direction of time, it follows that the distribution of the time that the reverse chain spends in state i
during a visit will be the same whether the chain is observed in the usual (forward) or in the reverse direction of time, it follows that the distribution of the time that the reverse chain spends in state i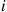 during a visit should be the same as the distribution of the time that the forward chain spends in that state during a visit. That is, we should have that
during a visit should be the same as the distribution of the time that the forward chain spends in that state during a visit. That is, we should have that
vi∗=vi
Moreover, because the proportion of time that the chain spends in state i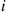 would be the same whether one was observing the chain in the usual (forward) direction of time or in the reverse direction, the two chains should intuitively have the same limiting probabilities.
would be the same whether one was observing the chain in the usual (forward) direction of time or in the reverse direction, the two chains should intuitively have the same limiting probabilities.
Proposition 6.10
Let a continuous-time Markov chain have instantaneous transition rates qij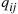 and limiting probabilities Pi,i∈S
and limiting probabilities Pi,i∈S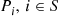 , and let qij∗
, and let qij∗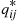 be the instantaneous rates of the reversed chain. Then, with vi∗=∑j≠iqij∗
be the instantaneous rates of the reversed chain. Then, with vi∗=∑j≠iqij∗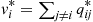 and vi=∑j≠iqij
and vi=∑j≠iqij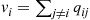
vi∗=vi
Moreover Pi,i∈S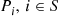 , are also the limiting probabilities of the reversed chain.
, are also the limiting probabilities of the reversed chain.
Proof
Using that Piqij∗=Pjqji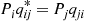 we see that
we see that
∑j≠iqij∗=∑j≠iPjqji/Pi=viPi/Pi=vi
where the preceding used (from (6.18)) that ∑j≠iPjqji=viPi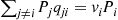 .
.
That the reversed chain has the same limiting probabilities as does the forward chain can be formally proven by showing that the Pj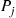 satisfy the balance equations of the reversed chain:
satisfy the balance equations of the reversed chain:
vj∗Pj=∑k≠jPkqkj∗,j∈S
Now, because vj∗=vj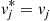 and Pkqkj∗=Pjqjk
and Pkqkj∗=Pjqjk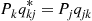 , the preceding equations are equivalent to
, the preceding equations are equivalent to
vjPj=∑k≠jPjqjk,j∈S
which are just the balance equations for the forward chain, which are known to be satisfied by the Pj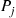 . ■
. ■
That the long-run proportions for the reverse chain are the same as for the forward chain makes it easy to understand why
Piqij∗=Pjqji,i≠j
Because Pi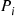 is the proportion of time the reverse chain spends in state i
is the proportion of time the reverse chain spends in state i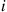 and qij∗
and qij∗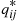 is the rate, when in i
is the rate, when in i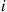 , that it makes a transition into state j
, that it makes a transition into state j , it follows that Piqij∗
, it follows that Piqij∗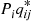 is the rate at which the reversed chain makes transitions from i
is the rate at which the reversed chain makes transitions from i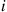 to j
to j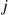 . Similarly, Pjqji
. Similarly, Pjqji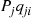 is the rate at which the forward chain makes transitions from j
is the rate at which the forward chain makes transitions from j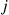 to i
to i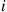 . Because every transition from j
. Because every transition from j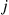 to i
to i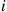 in the (forward) Markov chain would be seen as a transition from i
in the (forward) Markov chain would be seen as a transition from i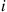 to j
to j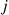 by someone looking backwards in time, it is evident that Piqij∗=Pjqji
by someone looking backwards in time, it is evident that Piqij∗=Pjqji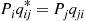 .
.
The following proposition shows that if one can find a solution of the “reverse chain equations” then the solution is unique and yields the limiting probabilities.
Proposition 6.11
Let qij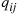 be the transition rates of an irreducible continuous time Markov chain. If one can find values qij∗
be the transition rates of an irreducible continuous time Markov chain. If one can find values qij∗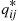 and a collection of positive values Pi
and a collection of positive values Pi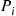 that sum to 1
that sum to 1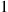 , such that
, such that
Piqij∗=Pjqji,i≠j (6.29)
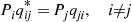 (6.29)
(6.29)
and
∑j≠iqij∗=∑j≠iqij,i∈S (6.30)
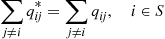 (6.30)
(6.30)
then qij∗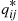 are the transition rates of the reversed chain and Pi
are the transition rates of the reversed chain and Pi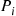 are the limiting probabilities (for both chains).
are the limiting probabilities (for both chains).
Proof
We show that the Pi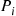 are the limiting probabilities by showing that they satisfy the balance Equations (6.18). To show this, sum (6.29) over all j,j≠i
are the limiting probabilities by showing that they satisfy the balance Equations (6.18). To show this, sum (6.29) over all j,j≠i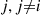 , to obtain
, to obtain
Pi∑j≠iqij∗=∑j≠iPjqji,i∈S
Using (6.30) now shows that
Pi∑j≠iqij=∑j≠iPjqji
Because ∑iPi=1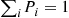 we see that the Pi
we see that the Pi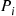 satisfy the balance equations and are thus the limiting probabilities. Because Piqij∗=Pjqji
satisfy the balance equations and are thus the limiting probabilities. Because Piqij∗=Pjqji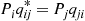 it also follows that qij∗
it also follows that qij∗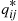 are the transition rates of the reversed chain. ■
are the transition rates of the reversed chain. ■
Suppose now that the structure of the continuous time Markov chain enables us to make a guess as to the transition rates of the reversed chain. Assuming that this guess satisfies Equation (6.30) of Proposition 6.11, we can then verify the correctness of our guess by seeing whether there are probabilities that satisfy Equations (6.29). If there are such probabilities, our guess is correct and we have also found the limiting probabilities; if there are not, our guess is incorrect.
Example 6.21
Consider a continuous-time Markov chain whose states are the nonnegative integers. Suppose that a transition out of state 0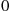 goes to state i
goes to state i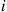 with probability αi,∑i=1∞αi=1
with probability αi,∑i=1∞αi=1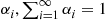 ; whereas a transition out of state i>0
; whereas a transition out of state i>0 always goes to state i-1
always goes to state i-1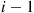 . That is, the instantaneous transition rates of this chain are, for i>0
. That is, the instantaneous transition rates of this chain are, for i>0
q0i=v0αiqi,i-1=vi
Let N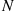 be a random variable having the distribution of the next state from state 0
be a random variable having the distribution of the next state from state 0 ; that is, P(N=i)=αi,i>0
; that is, P(N=i)=αi,i>0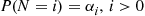 . Also, say that a cycle begins each time the chain goes to state 0
. Also, say that a cycle begins each time the chain goes to state 0 . Because the forward chain goes from 0
. Because the forward chain goes from 0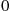 to N
to N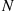 and then continually moves one step closer to 0
and then continually moves one step closer to 0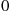 until reaching that state, it follows that the states in the reverse chain would continually increase by 1
until reaching that state, it follows that the states in the reverse chain would continually increase by 1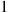 until it reaches N
until it reaches N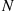 at which point it goes back to state 0
at which point it goes back to state 0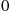 (see Figure 6.2).
(see Figure 6.2).
Now, if the chain is currently in state i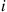 then the value of N
then the value of N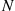 for that cycle must be at least i
for that cycle must be at least i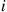 . Hence, the next state of the reversed chain will be 0
. Hence, the next state of the reversed chain will be 0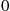 with probability
with probability
P(N=i∣N⩾i)=P(N=i)P(N⩾i)=αiP(N⩾i)
and will be i+1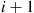 with probability
with probability
1-P(N=i∣N⩾i)=P(N⩾i+1∣N⩾i)=P(N⩾i+1)P(N⩾i)
Because the reversed chain spends the same time in a state during each visit as does the forward chain, it thus appears that the transition rates of the reversed chain are
qi,0∗=viαiP(N⩾i),i>0qi,i+1∗=viP(N⩾i+1)P(N⩾i),i⩾0
Based on the preceding guess, the reversed time equations P0q0i=Piqi0∗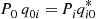 and Piqi,i-1=Pi-1qi-1,i∗
and Piqi,i-1=Pi-1qi-1,i∗ become
become
P0v0αi=PiviαiP(N⩾i),i⩾1 (6.31)
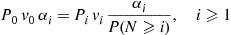 (6.31)
(6.31)
and
Pivi=Pi-1vi-1P(N⩾i)P(N⩾i-1),i⩾1 (6.32)
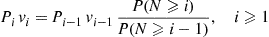 (6.32)
(6.32)
The set of Equations (6.31) gives
Pi=P0v0P(N⩾i)/vi,i⩾1
As the preceding equation is also valid when i=0 (since P(N⩾0)=1
(since P(N⩾0)=1 ), we obtain upon summing over all i
), we obtain upon summing over all i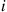 that
that
1=∑iPi=P0v0∑i=0∞P(N⩾i)/vi
Thus,
Pi=P(N⩾i)/vi∑i=0∞P(N⩾i)/vi,i⩾0
To show that the set of Equations (6.32) is also satisfied by the preceding values of Pi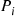 , note that, with C=1/∑i=0∞P(N⩾i)/vi
, note that, with C=1/∑i=0∞P(N⩾i)/vi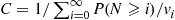 ,
,
viPiP(N⩾i)=C=vi-1Pi-1P(N⩾i-1)
which immediately shows that Equations (6.32) are also satisfied. Because we chose the transition rates of the reversed chain to be such that it spent as much time in state i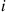 during a visit as does the forward chain, there is no need to check Condition (6.30) of Proposition 6.11, and so the stationary probabilities are as given. ■
during a visit as does the forward chain, there is no need to check Condition (6.30) of Proposition 6.11, and so the stationary probabilities are as given. ■
Example 6.22
A Sequential Queueing System
Consider a two-server queueing system in which customers arrive at server 1 in accordance with a Poisson process with rate λ
in accordance with a Poisson process with rate λ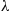 . An arrival at server 1
. An arrival at server 1 either enters service if server 1
either enters service if server 1 is free or joins the queue if server 1
is free or joins the queue if server 1 is busy. After completion of service at server 1
is busy. After completion of service at server 1 the customer moves over to server 2
the customer moves over to server 2 , where it either enters service if server 2
, where it either enters service if server 2 is free or join its queue otherwise. After completion of service at server 2
is free or join its queue otherwise. After completion of service at server 2 a customer departs the system. The service times at servers 1
a customer departs the system. The service times at servers 1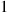 and 2
and 2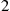 are exponential with rates μ1
are exponential with rates μ1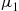 and μ2
and μ2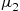 respectively. All service times are independent and are also independent of the arrival process.
respectively. All service times are independent and are also independent of the arrival process.
The preceding model can be analyzed as a continuous-time Markov chain whose state is (n,m)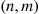 if there are currently n
if there are currently n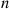 customers with server 1
customers with server 1 and m
and m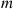 with server 2
with server 2 . The instantaneous transition rates of this chain are
. The instantaneous transition rates of this chain are
q(n-1,m),(n,m)=λ,n>0q(n+1,m-1),(n,m)=μ1,m>0q(n,m+1),(n,m)=μ2
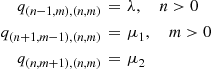
To find the limiting probabilities, let us first consider the chain going backwards in time. Because in real time the total number in the system decreases at moments when customers depart server 2 , looking backwards the total number in the system will at those moments increase by having an added customer at server 2
, looking backwards the total number in the system will at those moments increase by having an added customer at server 2 . Similarly while in real time the number will increase when a customer arrives at server 1
. Similarly while in real time the number will increase when a customer arrives at server 1 , in the reverse process at that moment there will be a decrease in the number at server 1
, in the reverse process at that moment there will be a decrease in the number at server 1 . Because the times spent in service at server i
. Because the times spent in service at server i will be the same whether looking in forward or in reverse time, it appears that the reverse process is a two-server system in which customers arrive first at server 2
will be the same whether looking in forward or in reverse time, it appears that the reverse process is a two-server system in which customers arrive first at server 2 , then go to server 1
, then go to server 1 , and then depart the system, with their service times at server i
, and then depart the system, with their service times at server i being exponential with rate μi,i=1,2
being exponential with rate μi,i=1,2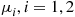 . Now the arrival rate to server 2
. Now the arrival rate to server 2 in the reverse process is equal to the departure rate from the system in the forward process and this must equal the arrival rate λ
in the reverse process is equal to the departure rate from the system in the forward process and this must equal the arrival rate λ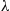 of the forward process. (If the departure rate of the forward process was less than the arrival rate, then the queue size would build to infinity and there would not be any limiting probabilities.) Although it is not clear that the arrival process of customers to server 2
of the forward process. (If the departure rate of the forward process was less than the arrival rate, then the queue size would build to infinity and there would not be any limiting probabilities.) Although it is not clear that the arrival process of customers to server 2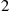 in the reverse process is a Poisson process, let us guess that this is the case and then use Proposition 6.11 to determine whether our guess is correct.
in the reverse process is a Poisson process, let us guess that this is the case and then use Proposition 6.11 to determine whether our guess is correct.
So, let us guess that the reverse process is a sequential queue where customers arrive at server 2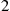 according to a Poisson process with rate λ
according to a Poisson process with rate λ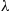 , and after receiving service at server 2
, and after receiving service at server 2 move over to server 1
move over to server 1 , and after receiving service at server 1
, and after receiving service at server 1 depart the system. In addition, the service times at server i
depart the system. In addition, the service times at server i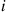 are exponential with rate μi,i=1,2
are exponential with rate μi,i=1,2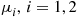 . Now, if this were true then the transition rates of the reverse chain would be
. Now, if this were true then the transition rates of the reverse chain would be
q(n,m),(n-1,m)∗=μ1,n>0q(n,m),(n+1,m-1)∗=μ2,m>0q(n,m),(n,m+1)∗=λ
The rate at which a chain with transition rates q∗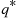 departs from state (n,m)
departs from state (n,m)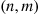 is
is
q(n,m),(n-1,m)∗+q(n,m),(n+1,m-1)∗+q(n,m),(n,m+1)∗=μ1I{n>0}+μ2I{m>0}+λ
where I{k>0}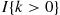 is equal to 1
is equal to 1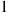 when k>0
when k>0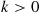 and is equal to 0
and is equal to 0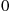 otherwise. As the preceding is also the rate at which the forward process departs from state (n,m)
otherwise. As the preceding is also the rate at which the forward process departs from state (n,m)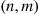 , the Condition (6.30) of Proposition 6.11 is satisfied.
, the Condition (6.30) of Proposition 6.11 is satisfied.
Using the preceding conjectured reverse time transition rates, the reverse time equations would be
Pn-1,mλ=Pn,mμ1,n>0 (6.33)
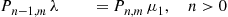 (6.33)
(6.33)
Pn+1,m-1μ1=Pn,mμ2,m>0 (6.34)
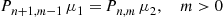 (6.34)
(6.34)
Pn,m+1μ2=Pn,mλ (6.35)
 (6.35)
(6.35)
Writing (6.33) as Pn,m=(λ/μ1)Pn-1,m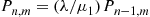 and iterating, yields that
and iterating, yields that
Pn,m=(λ/μ1)2Pn-2,m=⋯=(λ/μ1)nP0,m
Letting n=0,m=m-1 in Equation (6.35) shows that P0,m=(λ/μ2)P0,m-1
in Equation (6.35) shows that P0,m=(λ/μ2)P0,m-1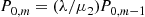 , which yields upon iteration that
, which yields upon iteration that
P0,m=(λ/μ2)2P0,m-2=⋯=(λ/μ2)mP0,0
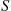 and which has instantaneous transition rates
and which has instantaneous transition rates 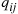 and limiting probabilities
and limiting probabilities 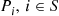 , and suppose that this chain that has been in operation for a long (in theory, an infinite) time. Then, it follows from results in the previous section that the process of states going backwards in time is also a continuous time Markov chain, having instantaneous transition rates
, and suppose that this chain that has been in operation for a long (in theory, an infinite) time. Then, it follows from results in the previous section that the process of states going backwards in time is also a continuous time Markov chain, having instantaneous transition rates 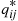 that satisfy
that satisfy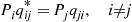
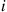 during a visit is exponential with rate
during a visit is exponential with rate 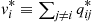 . Because the amount of time the process spends in a state
. Because the amount of time the process spends in a state 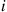 during a visit will be the same whether the chain is observed in the usual (forward) or in the reverse direction of time, it follows that the distribution of the time that the reverse chain spends in state
during a visit will be the same whether the chain is observed in the usual (forward) or in the reverse direction of time, it follows that the distribution of the time that the reverse chain spends in state 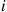 during a visit should be the same as the distribution of the time that the forward chain spends in that state during a visit. That is, we should have that
during a visit should be the same as the distribution of the time that the forward chain spends in that state during a visit. That is, we should have that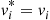
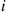 would be the same whether one was observing the chain in the usual (forward) direction of time or in the reverse direction, the two chains should intuitively have the same limiting probabilities.
would be the same whether one was observing the chain in the usual (forward) direction of time or in the reverse direction, the two chains should intuitively have the same limiting probabilities.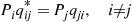
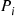 is the proportion of time the reverse chain spends in state
is the proportion of time the reverse chain spends in state 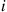 and
and 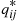 is the rate, when in
is the rate, when in 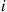 , that it makes a transition into state
, that it makes a transition into state  , it follows that
, it follows that 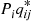 is the rate at which the reversed chain makes transitions from
is the rate at which the reversed chain makes transitions from 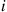 to
to 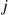 . Similarly,
. Similarly, 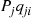 is the rate at which the forward chain makes transitions from
is the rate at which the forward chain makes transitions from 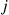 to
to 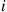 . Because every transition from
. Because every transition from 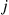 to
to 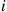 in the (forward) Markov chain would be seen as a transition from
in the (forward) Markov chain would be seen as a transition from 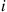 to
to 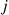 by someone looking backwards in time, it is evident that
by someone looking backwards in time, it is evident that 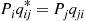 .
.