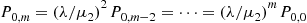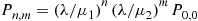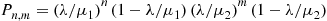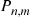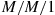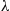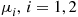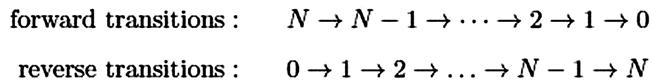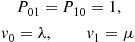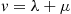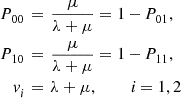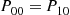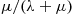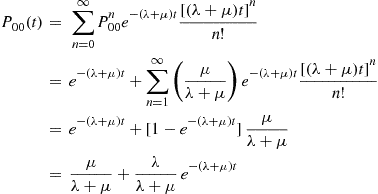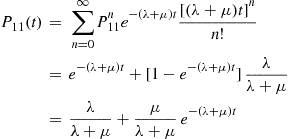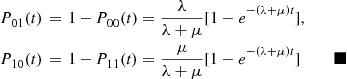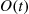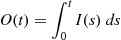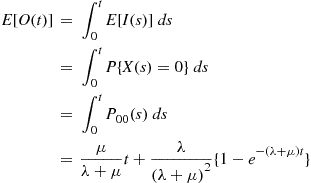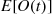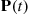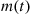6.8 Uniformization
Consider a continuous-time Markov chain in which the mean time spent in a state is the same for all states. That is, suppose that  , for all states
, for all states 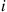 . In this case since the amount of time spent in each state during a visit is exponentially distributed with rate
. In this case since the amount of time spent in each state during a visit is exponentially distributed with rate  , it follows that if we let
, it follows that if we let 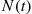 denote the number of state transitions by time
denote the number of state transitions by time 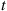 , then
, then 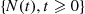 will be a Poisson process with rate
will be a Poisson process with rate  .
.
To compute the transition probabilities 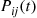 , we can condition on
, we can condition on 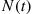 :
:
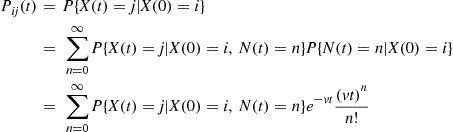
Now, the fact that there have been 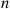 transitions by time
transitions by time 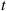 tells us something about the amount of time spent in each of the first
tells us something about the amount of time spent in each of the first 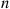 states visited, but since the distribution of time spent in each state is the same for all states, it follows that knowing that
states visited, but since the distribution of time spent in each state is the same for all states, it follows that knowing that  gives us no information about which states were visited. Hence,
gives us no information about which states were visited. Hence,
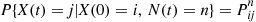
where 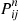 is just the
is just the 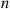 -stage transition probability associated with the discrete-time Markov chain with transition probabilities
-stage transition probability associated with the discrete-time Markov chain with transition probabilities 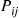 ; and so when
; and so when 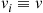
 (6.36)
(6.36)Equation (6.36) is often useful from a computational point of view since it enables us to approximate 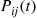 by taking a partial sum and then computing (by matrix multiplication of the transition probability matrix) the relevant
by taking a partial sum and then computing (by matrix multiplication of the transition probability matrix) the relevant 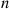 stage probabilities
stage probabilities 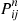 .
.
Whereas the applicability of Equation (6.36) would appear to be quite limited since it supposes that 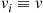 , it turns out that most Markov chains can be put in that form by the trick of allowing fictitious transitions from a state to itself. To see how this works, consider any Markov chain for which the
, it turns out that most Markov chains can be put in that form by the trick of allowing fictitious transitions from a state to itself. To see how this works, consider any Markov chain for which the 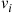 are bounded, and let
are bounded, and let  be any number such that
be any number such that
 (6.37)
(6.37)
When in state 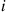 , the process actually leaves at rate
, the process actually leaves at rate 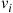 ; but this is equivalent to supposing that transitions occur at rate
; but this is equivalent to supposing that transitions occur at rate  , but only the fraction
, but only the fraction  of transitions are real ones (and thus real transitions occur at rate
of transitions are real ones (and thus real transitions occur at rate 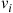 ) and the remaining fraction
) and the remaining fraction 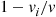 are fictitious transitions that leave the process in state
are fictitious transitions that leave the process in state 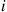 . In other words, any Markov chain satisfying Condition (6.37) can be thought of as being a process that spends an exponential amount of time with rate
. In other words, any Markov chain satisfying Condition (6.37) can be thought of as being a process that spends an exponential amount of time with rate  in state
in state 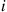 and then makes a transition to
and then makes a transition to 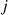 with probability
with probability 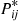 , where
, where
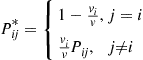 (6.38)
(6.38)
Hence, from Equation (6.36) we have that the transition probabilities can be computed by
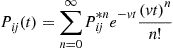
where 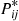 are the
are the 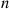 -stage transition probabilities corresponding to Equation (6.38). This technique of uniformizing the rate in which a transition occurs from each state by introducing transitions from a state to itself is known as uniformization.
-stage transition probabilities corresponding to Equation (6.38). This technique of uniformizing the rate in which a transition occurs from each state by introducing transitions from a state to itself is known as uniformization.
6.9 Computing the Transition Probabilities
For any pair of states 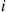 and
and  , let
, let
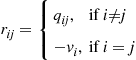
Using this notation, we can rewrite the Kolmogorov backward equations
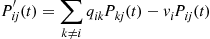
and the forward equations

as follows:
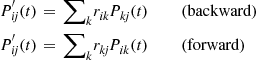
This representation is especially revealing when we introduce matrix notation. Define the matrices 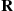 and
and 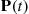 ,
, 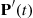 by letting the element in row
by letting the element in row 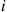 , column
, column 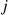 of these matrices be, respectively,
of these matrices be, respectively, 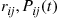 , and
, and 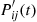 . Since the backward equations say that the element in row
. Since the backward equations say that the element in row 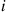 , column
, column 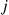 of the matrix
of the matrix 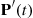 can be obtained by multiplying the
can be obtained by multiplying the  th row of the matrix
th row of the matrix 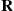 by the
by the 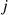 th column of the matrix
th column of the matrix  , it is equivalent to the matrix equation
, it is equivalent to the matrix equation
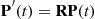 (6.39)
(6.39)Similarly, the forward equations can be written as
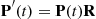 (6.40)
(6.40)Now, just as the solution of the scalar differential equation
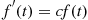
(or, equivalent, 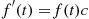 ) is
) is

it can be shown that the solution of the matrix differential Equations (6.39) and (6.40) is given by
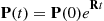
Since 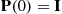 (the identity matrix), this yields that
(the identity matrix), this yields that
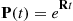 (6.41)
(6.41)
where the matrix 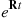 is defined by
is defined by
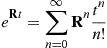 (6.42)
(6.42)
with 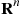 being the (matrix) multiplication of
being the (matrix) multiplication of  by itself
by itself 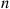 times.
times.
The direct use of Equation (6.42) to compute 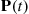 turns out to be very inefficient for two reasons. First, since the matrix
turns out to be very inefficient for two reasons. First, since the matrix 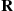 contains both positive and negative elements (remember the off-diagonal elements are the
contains both positive and negative elements (remember the off-diagonal elements are the 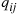 while the
while the 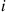 th diagonal element is
th diagonal element is 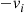 ), there is the problem of computer round-off error when we compute the powers of
), there is the problem of computer round-off error when we compute the powers of 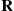 . Second, we often have to compute many of the terms in the infinite sum (6.42) to arrive at a good approximation. However, there are certain indirect ways that we can utilize the relation in (6.41) to efficiently approximate the matrix
. Second, we often have to compute many of the terms in the infinite sum (6.42) to arrive at a good approximation. However, there are certain indirect ways that we can utilize the relation in (6.41) to efficiently approximate the matrix 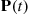 . We now present two of these methods.
. We now present two of these methods.
Approximation Method 1 Rather than using Equation (6.42) to compute 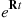 , we can use the matrix equivalent of the identity
, we can use the matrix equivalent of the identity
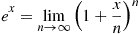
which states that
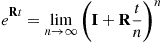
Thus, if we let 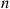 be a power of 2, say,
be a power of 2, say, 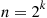 , then we can approximate
, then we can approximate  by raising the matrix
by raising the matrix 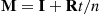 to the
to the 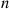 th power, which can be accomplished by
th power, which can be accomplished by 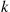 matrix multiplications (by first multiplying
matrix multiplications (by first multiplying 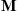 by itself to obtain
by itself to obtain 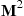 and then multiplying that by itself to obtain
and then multiplying that by itself to obtain 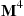 and so on). In addition, since only the diagonal elements of
and so on). In addition, since only the diagonal elements of 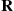 are negative (and the diagonal elements of the identity matrix
are negative (and the diagonal elements of the identity matrix  are equal to 1), by choosing
are equal to 1), by choosing 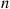 large enough we can guarantee that the matrix
large enough we can guarantee that the matrix 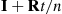 has all nonnegative elements.
has all nonnegative elements.
Approximation Method 2 A second approach to approximating  uses the identity
uses the identity
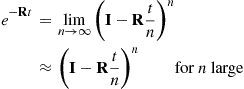
and thus

Hence, if we again choose 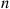 to be a large power of 2, say,
to be a large power of 2, say,  , we can approximate
, we can approximate  by first computing the inverse of the matrix
by first computing the inverse of the matrix  and then raising that matrix to the
and then raising that matrix to the 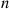 th power (by utilizing
th power (by utilizing 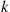 matrix multiplications). It can be shown that the matrix
matrix multiplications). It can be shown that the matrix 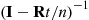 will have only nonnegative elements.
will have only nonnegative elements.
Exercises
1. A population of organisms consists of both male and female members. In a small colony any particular male is likely to mate with any particular female in any time interval of length 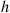 , with probability
, with probability  . Each mating immediately produces one offspring, equally likely to be male or female. Let
. Each mating immediately produces one offspring, equally likely to be male or female. Let 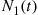 and
and 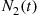 denote the number of males and females in the population at
denote the number of males and females in the population at 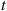 . Derive the parameters of the continuous-time Markov chain
. Derive the parameters of the continuous-time Markov chain 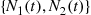 , i.e., the
, i.e., the 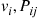 of Section 6.2.
of Section 6.2.
*2. Suppose that a one-celled organism can be in one of two states—either 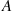 or
or 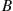 . An individual in state
. An individual in state  will change to state
will change to state  at an exponential rate
at an exponential rate 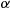 ; an individual in state
; an individual in state 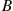 divides into two new individuals of type
divides into two new individuals of type  at an exponential rate
at an exponential rate 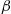 . Define an appropriate continuous-time Markov chain for a population of such organisms and determine the appropriate parameters for this model.
. Define an appropriate continuous-time Markov chain for a population of such organisms and determine the appropriate parameters for this model.
3. Consider two machines that are maintained by a single repairman. Machine 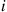 functions for an exponential time with rate
functions for an exponential time with rate 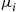 before breaking down,
before breaking down, 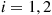 . The repair times (for either machine) are exponential with rate
. The repair times (for either machine) are exponential with rate 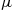 . Can we analyze this as a birth and death process? If so, what are the parameters? If not, how can we analyze it?
. Can we analyze this as a birth and death process? If so, what are the parameters? If not, how can we analyze it?
*4. Potential customers arrive at a single-server station in accordance with a Poisson process with rate 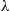 . However, if the arrival finds
. However, if the arrival finds 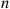 customers already in the station, then he will enter the system with probability
customers already in the station, then he will enter the system with probability 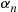 . Assuming an exponential service rate
. Assuming an exponential service rate 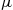 , set this up as a birth and death process and determine the birth and death rates.
, set this up as a birth and death process and determine the birth and death rates.
5. There are  individuals in a population, some of whom have a certain infection that spreads as follows. Contacts between two members of this population occur in accordance with a Poisson process having rate
individuals in a population, some of whom have a certain infection that spreads as follows. Contacts between two members of this population occur in accordance with a Poisson process having rate  . When a contact occurs, it is equally likely to involve any of the
. When a contact occurs, it is equally likely to involve any of the 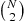 pairs of individuals in the population. If a contact involves an infected and a noninfected individual, then with probability
pairs of individuals in the population. If a contact involves an infected and a noninfected individual, then with probability  the noninfected individual becomes infected. Once infected, an individual remains infected throughout. Let
the noninfected individual becomes infected. Once infected, an individual remains infected throughout. Let  denote the number of infected members of the population at time
denote the number of infected members of the population at time  .
.
(a) Is  a continuous-time Markov chain?
a continuous-time Markov chain?
(c) Starting with a single infected individual, what is the expected time until all members are infected?
6. Consider a birth and death process with birth rates 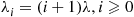 , and death rates
, and death rates  .
.
(a) Determine the expected time to go from state 0 to state 4.
(b) Determine the expected time to go from state 2 to state 5.
(c) Determine the variances in parts (a) and (b).
*7. Individuals join a club in accordance with a Poisson process with rate 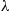 . Each new member must pass through
. Each new member must pass through 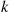 consecutive stages to become a full member of the club. The time it takes to pass through each stage is exponentially distributed with rate
consecutive stages to become a full member of the club. The time it takes to pass through each stage is exponentially distributed with rate  . Let
. Let  denote the number of club members at time
denote the number of club members at time  who have passed through exactly
who have passed through exactly 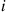 stages,
stages,  . Also, let
. Also, let  .
.
(a) Is 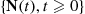 a continuous-time Markov chain?
a continuous-time Markov chain?
(b) If so, give the infinitesimal transition rates. That is, for any state  give the possible next states along with their infinitesimal rates.
give the possible next states along with their infinitesimal rates.
8. Consider two machines, both of which have an exponential lifetime with mean 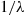 . There is a single repairman that can service machines at an exponential rate
. There is a single repairman that can service machines at an exponential rate  . Set up the Kolmogorov backward equations; you need not solve them.
. Set up the Kolmogorov backward equations; you need not solve them.
9. The birth and death process with parameters 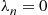 and
and 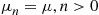 is called a pure death process. Find
is called a pure death process. Find  .
.
10. Consider two machines. Machine  operates for an exponential time with rate
operates for an exponential time with rate  and then fails; its repair time is exponential with rate
and then fails; its repair time is exponential with rate 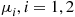 . The machines act independently of each other. Define a four-state continuous-time Markov chain that jointly describes the condition of the two machines. Use the assumed independence to compute the transition probabilities for this chain and then verify that these transition probabilities satisfy the forward and backward equations.
. The machines act independently of each other. Define a four-state continuous-time Markov chain that jointly describes the condition of the two machines. Use the assumed independence to compute the transition probabilities for this chain and then verify that these transition probabilities satisfy the forward and backward equations.
*11. Consider a Yule process starting with a single individual—that is, suppose 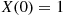 . Let
. Let  denote the time it takes the process to go from a population of size
denote the time it takes the process to go from a population of size 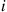 to one of size
to one of size 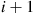 .
.
(a) Argue that  , are independent exponentials with respective rates
, are independent exponentials with respective rates  .
.
(b) Let  denote independent exponential random variables each having rate
denote independent exponential random variables each having rate  , and interpret
, and interpret  as the lifetime of component
as the lifetime of component 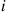 . Argue that
. Argue that  can be expressed as
can be expressed as

where 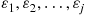 are independent exponentials with respective rates
are independent exponentials with respective rates 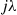 ,
, 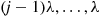 .
.
Hint: Interpret 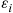 as the time between the
as the time between the 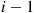 and the
and the 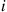 th failure.
th failure.
(c) Using (a) and (b) argue that


and hence, given 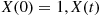 has a geometric distribution with parameter
has a geometric distribution with parameter 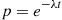 .
.
12. Each individual in a biological population is assumed to give birth at an exponential rate 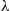 , and to die at an exponential rate
, and to die at an exponential rate 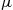 . In addition, there is an exponential rate of increase
. In addition, there is an exponential rate of increase 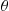 due to immigration. However, immigration is not allowed when the population size is
due to immigration. However, immigration is not allowed when the population size is 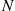 or larger.
or larger.
(a) Set this up as a birth and death model.
(b) If 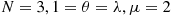 , determine the proportion of time that immigration is restricted.
, determine the proportion of time that immigration is restricted.
13. A small barbershop, operated by a single barber, has room for at most two customers. Potential customers arrive at a Poisson rate of three per hour, and the successive service times are independent exponential random variables with mean 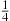 hour.
hour.
(a) What is the average number of customers in the shop?
(b) What is the proportion of potential customers that enter the shop?
(c) If the barber could work twice as fast, how much more business would he do?
14. Potential customers arrive at a full-service, one-pump gas station at a Poisson rate of 20 cars per hour. However, customers will only enter the station for gas if there are no more than two cars (including the one currently being attended to) at the pump. Suppose the amount of time required to service a car is exponentially distributed with a mean of five minutes.
(a) What fraction of the attendant’s time will be spent servicing cars?
(b) What fraction of potential customers are lost?
15. A service center consists of two servers, each working at an exponential rate of two services per hour. If customers arrive at a Poisson rate of three per hour, then, assuming a system capacity of at most three customers,
(a) what fraction of potential customers enter the system?
(b) what would the value of part (a) be if there was only a single server, and his rate was twice as fast (that is,  )?
)?
*16. The following problem arises in molecular biology. The surface of a bacterium consists of several sites at which foreign molecules—some acceptable and some not—become attached. We consider a particular site and assume that molecules arrive at the site according to a Poisson process with parameter 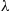 . Among these molecules a proportion
. Among these molecules a proportion 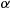 is acceptable. Unacceptable molecules stay at the site for a length of time that is exponentially distributed with parameter
is acceptable. Unacceptable molecules stay at the site for a length of time that is exponentially distributed with parameter  , whereas an acceptable molecule remains at the site for an exponential time with rate
, whereas an acceptable molecule remains at the site for an exponential time with rate 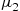 . An arriving molecule will become attached only if the site is free of other molecules. What percentage of time is the site occupied with an acceptable (unacceptable) molecule?
. An arriving molecule will become attached only if the site is free of other molecules. What percentage of time is the site occupied with an acceptable (unacceptable) molecule?
17. Each time a machine is repaired it remains up for an exponentially distributed time with rate  . It then fails, and its failure is either of two types. If it is a type 1 failure, then the time to repair the machine is exponential with rate
. It then fails, and its failure is either of two types. If it is a type 1 failure, then the time to repair the machine is exponential with rate 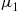 ; if it is a type 2 failure, then the repair time is exponential with rate
; if it is a type 2 failure, then the repair time is exponential with rate 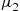 . Each failure is, independently of the time it took the machine to fail, a type 1 failure with probability
. Each failure is, independently of the time it took the machine to fail, a type 1 failure with probability 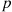 and a type 2 failure with probability
and a type 2 failure with probability  . What proportion of time is the machine down due to a type 1 failure? What proportion of time is it down due to a type 2 failure? What proportion of time is it up?
. What proportion of time is the machine down due to a type 1 failure? What proportion of time is it down due to a type 2 failure? What proportion of time is it up?
18. After being repaired, a machine functions for an exponential time with rate 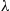 and then fails. Upon failure, a repair process begins. The repair process proceeds sequentially through
and then fails. Upon failure, a repair process begins. The repair process proceeds sequentially through  distinct phases. First a phase 1 repair must be performed, then a phase 2, and so on. The times to complete these phases are independent, with phase
distinct phases. First a phase 1 repair must be performed, then a phase 2, and so on. The times to complete these phases are independent, with phase  taking an exponential time with rate
taking an exponential time with rate 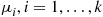 .
.
(a) What proportion of time is the machine undergoing a phase 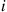 repair?
repair?
(b) What proportion of time is the machine working?
*19. A single repairperson looks after both machines 1 and 2. Each time it is repaired, machine 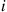 stays up for an exponential time with rate
stays up for an exponential time with rate 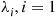 , 2. When machine
, 2. When machine  fails, it requires an exponentially distributed amount of work with rate
fails, it requires an exponentially distributed amount of work with rate 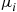 to complete its repair. The repairperson will always service machine 1 when it is down. For instance, if machine 1 fails while 2 is being repaired, then the repairperson will immediately stop work on machine 2 and start on 1. What proportion of time is machine 2 down?
to complete its repair. The repairperson will always service machine 1 when it is down. For instance, if machine 1 fails while 2 is being repaired, then the repairperson will immediately stop work on machine 2 and start on 1. What proportion of time is machine 2 down?
20. There are two machines, one of which is used as a spare. A working machine will function for an exponential time with rate  and will then fail. Upon failure, it is immediately replaced by the other machine if that one is in working order, and it goes to the repair facility. The repair facility consists of a single person who takes an exponential time with rate
and will then fail. Upon failure, it is immediately replaced by the other machine if that one is in working order, and it goes to the repair facility. The repair facility consists of a single person who takes an exponential time with rate 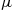 to repair a failed machine. At the repair facility, the newly failed machine enters service if the repairperson is free. If the repairperson is busy, it waits until the other machine is fixed; at that time, the newly repaired machine is put in service and repair begins on the other one. Starting with both machines in working condition, find
to repair a failed machine. At the repair facility, the newly failed machine enters service if the repairperson is free. If the repairperson is busy, it waits until the other machine is fixed; at that time, the newly repaired machine is put in service and repair begins on the other one. Starting with both machines in working condition, find
(b) the variance of the time until both are in the repair facility.
(c) In the long run, what proportion of time is there a working machine?
21. Suppose that when both machines are down in Exercise 20 a second repairperson is called in to work on the newly failed one. Suppose all repair times remain exponential with rate  . Now find the proportion of time at least one machine is working, and compare your answer with the one obtained in Exercise 20.
. Now find the proportion of time at least one machine is working, and compare your answer with the one obtained in Exercise 20.
22. Customers arrive at a single-server queue in accordance with a Poisson process having rate  . However, an arrival that finds
. However, an arrival that finds  customers already in the system will only join the system with probability
customers already in the system will only join the system with probability 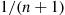 . That is, with probability
. That is, with probability 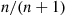 such an arrival will not join the system. Show that the limiting distribution of the number of customers in the system is Poisson with mean
such an arrival will not join the system. Show that the limiting distribution of the number of customers in the system is Poisson with mean 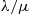 .
.
23. A job shop consists of three machines and two repairmen. The amount of time a machine works before breaking down is exponentially distributed with mean 10. If the amount of time it takes a single repairman to fix a machine is exponentially distributed with mean 8, then
(a) what is the average number of machines not in use?
(b) what proportion of time are both repairmen busy?
*24. Consider a taxi station where taxis and customers arrive in accordance with Poisson processes with respective rates of one and two per minute. A taxi will wait no matter how many other taxis are present. However, an arriving customer that does not find a taxi waiting leaves. Find
(a) the average number of taxis waiting, and
(b) the proportion of arriving customers that get taxis.
25. Customers arrive at a service station, manned by a single server who serves at an exponential rate  , at a Poisson rate
, at a Poisson rate  . After completion of service the customer then joins a second system where the server serves at an exponential rate
. After completion of service the customer then joins a second system where the server serves at an exponential rate 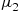 . Such a system is called a tandem or sequential queueing system. Assuming that
. Such a system is called a tandem or sequential queueing system. Assuming that 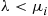 ,
, 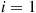 , 2, determine the limiting probabilities.
, 2, determine the limiting probabilities.
Hint: Try a solution of the form 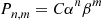 , and determine
, and determine  .
.
26. Consider an ergodic 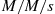 queue in steady state (that is, after a long time) and argue that the number presently in the system is independent of the sequence of past departure times. That is, for instance, knowing that there have been departures 2, 3, 5, and 10 time units ago does not affect the distribution of the number presently in the system.
queue in steady state (that is, after a long time) and argue that the number presently in the system is independent of the sequence of past departure times. That is, for instance, knowing that there have been departures 2, 3, 5, and 10 time units ago does not affect the distribution of the number presently in the system.
27. In the  queue if you allow the service rate to depend on the number in the system (but in such a way so that it is ergodic), what can you say about the output process? What can you say when the service rate
queue if you allow the service rate to depend on the number in the system (but in such a way so that it is ergodic), what can you say about the output process? What can you say when the service rate 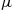 remains unchanged but
remains unchanged but 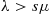 ?
?
*28. If  and
and 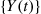 are independent continuous-time Markov chains, both of which are time reversible, show that the process
are independent continuous-time Markov chains, both of which are time reversible, show that the process 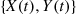 is also a time reversible Markov chain.
is also a time reversible Markov chain.
29. Consider a set of  machines and a single repair facility to service these machines. Suppose that when machine
machines and a single repair facility to service these machines. Suppose that when machine  , fails it requires an exponentially distributed amount of work with rate
, fails it requires an exponentially distributed amount of work with rate 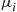 to repair it. The repair facility divides its efforts equally among all failed machines in the sense that whenever there are
to repair it. The repair facility divides its efforts equally among all failed machines in the sense that whenever there are 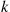 failed machines each one receives work at a rate of
failed machines each one receives work at a rate of  per unit time. If there are a total of
per unit time. If there are a total of  working machines, including machine
working machines, including machine  , then
, then  fails at an instantaneous rate
fails at an instantaneous rate 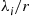 .
.
(a) Define an appropriate state space so as to be able to analyze the preceding system as a continuous-time Markov chain.
(b) Give the instantaneous transition rates (that is, give the  ).
).
(c) Write the time reversibility equations.
(d) Find the limiting probabilities and show that the process is time reversible.
30. Consider a graph with nodes  and the
and the 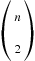 arcs
arcs 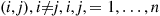 . (See Section 3.6.2 for appropriate definitions.) Suppose that a particle moves along this graph as follows: Events occur along the arcs
. (See Section 3.6.2 for appropriate definitions.) Suppose that a particle moves along this graph as follows: Events occur along the arcs 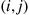 according to independent Poisson processes with rates
according to independent Poisson processes with rates 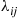 . An event along arc
. An event along arc  causes that arc to become excited. If the particle is at node
causes that arc to become excited. If the particle is at node 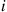 at the moment that
at the moment that 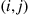 becomes excited, it instantaneously moves to node
becomes excited, it instantaneously moves to node 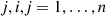 . Let
. Let 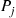 denote the proportion of time that the particle is at node
denote the proportion of time that the particle is at node 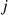 . Show that
. Show that

31. A total of 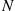 customers move about among
customers move about among  servers in the following manner. When a customer is served by server
servers in the following manner. When a customer is served by server 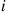 , he then goes over to server
, he then goes over to server 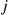 ,
,  , with probability
, with probability  . If the server he goes to is free, then the customer enters service; otherwise he joins the queue. The service times are all independent, with the service times at server
. If the server he goes to is free, then the customer enters service; otherwise he joins the queue. The service times are all independent, with the service times at server  being exponential with rate
being exponential with rate 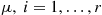 . Let the state at any time be the vector
. Let the state at any time be the vector  , where
, where  is the number of customers presently at server
is the number of customers presently at server  .
.
(a) Argue that if  is the state at time
is the state at time  , then
, then  is a continuous-time Markov chain.
is a continuous-time Markov chain.
(b) Give the infinitesimal rates of this chain.
(c) Show that this chain is time reversible, and find the limiting probabilities.
32. Customers arrive at a two-server station in accordance with a Poisson process having rate 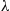 . Upon arriving, they join a single queue. Whenever a server completes a service, the person first in line enters service. The service times of server
. Upon arriving, they join a single queue. Whenever a server completes a service, the person first in line enters service. The service times of server 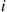 are exponential with rate
are exponential with rate 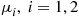 , where
, where  . An arrival finding both servers free is equally likely to go to either one. Define an appropriate continuous-time Markov chain for this model, show it is time reversible, and find the limiting probabilities.
. An arrival finding both servers free is equally likely to go to either one. Define an appropriate continuous-time Markov chain for this model, show it is time reversible, and find the limiting probabilities.
*33. Consider two 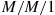 queues with respective parameters
queues with respective parameters 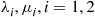 . Suppose they share a common waiting room that can hold at most three customers. That is, whenever an arrival finds her server busy and three customers in the waiting room, she goes away. Find the limiting probability that there will be
. Suppose they share a common waiting room that can hold at most three customers. That is, whenever an arrival finds her server busy and three customers in the waiting room, she goes away. Find the limiting probability that there will be 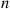 queue 1 customers and
queue 1 customers and  queue 2 customers in the system.
queue 2 customers in the system.
Hint: Use the results of Exercise 28 together with the concept of truncation.
34. Four workers share an office that contains four telephones. At any time, each worker is either “working” or “on the phone.” Each “working” period of worker 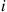 lasts for an exponentially distributed time with rate
lasts for an exponentially distributed time with rate 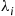 , and each “on the phone” period lasts for an exponentially distributed time with rate
, and each “on the phone” period lasts for an exponentially distributed time with rate 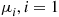 , 2, 3, 4.
, 2, 3, 4.
(a) What proportion of time are all workers “working”?
Let 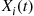 equal 1 if worker
equal 1 if worker 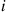 is working at time
is working at time 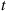 , and let it be 0 otherwise.
, and let it be 0 otherwise.
Let 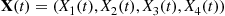 .
.
(b) Argue that  is a continuous-time Markov chain and give its infinitesimal rates.
is a continuous-time Markov chain and give its infinitesimal rates.
(c) Is  time reversible? Why or why not?
time reversible? Why or why not?
Suppose now that one of the phones has broken down. Suppose that a worker who is about to use a phone but finds them all being used begins a new “working” period.
(d) What proportion of time are all workers “working”?
35. Consider a time reversible continuous-time Markov chain having infinitesimal transition rates 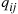 and limiting probabilities
and limiting probabilities 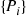 . Let
. Let  denote a set of states for this chain, and consider a new continuous-time Markov chain with transition rates
denote a set of states for this chain, and consider a new continuous-time Markov chain with transition rates  given by
given by
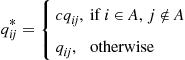
where  is an arbitrary positive number. Show that this chain remains time reversible, and find its limiting probabilities.
is an arbitrary positive number. Show that this chain remains time reversible, and find its limiting probabilities.
36. Consider a system of 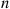 components such that the working times of component
components such that the working times of component 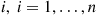 , are exponentially distributed with rate
, are exponentially distributed with rate 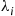 . When a component fails, however, the repair rate of component
. When a component fails, however, the repair rate of component 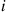 depends on how many other components are down. Specifically, suppose that the instantaneous repair rate of component
depends on how many other components are down. Specifically, suppose that the instantaneous repair rate of component 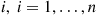 , when there are a total of
, when there are a total of 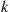 failed components, is
failed components, is  .
.
(a) Explain how we can analyze the preceding as a continuous-time Markov chain. Define the states and give the parameters of the chain.
(b) Show that, in steady state, the chain is time reversible and compute the limiting probabilities.
37. A hospital accepts 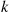 different types of patients, where type
different types of patients, where type 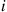 patients arrive according to a Poisson proccess with rate
patients arrive according to a Poisson proccess with rate 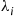 , with these
, with these 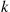 Poisson processes being independent. Type
Poisson processes being independent. Type 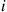 patients spend an exponentially distributed length of time with rate
patients spend an exponentially distributed length of time with rate 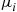 in the hospital,
in the hospital,  . Suppose that each type
. Suppose that each type 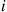 patient in the hospital requires
patient in the hospital requires 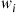 units of resources, and that the hospital will not accept a new patient if it would result in the total of all patient’s resource needs exceeding the amount
units of resources, and that the hospital will not accept a new patient if it would result in the total of all patient’s resource needs exceeding the amount 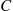 . Consequently, it is possible to have
. Consequently, it is possible to have 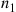 type
type 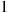 patients,
patients,  type
type  patients,
patients, , and
, and  type
type 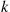 patients in the hospital at the same time if and only if
patients in the hospital at the same time if and only if
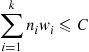
(a) Define a continuous-time Markov chain to analyze the preceding. For parts (b), (c), and (d) suppose that  .
.
(b) If 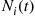 is the number of type
is the number of type  customers in the system at time
customers in the system at time 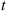 , what type of process is
, what type of process is  ? Is it time reversible?
? Is it time reversible?
(c) What can be said about the vector process 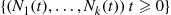 ?
?
(d) What are the limiting probabilities of the process of part (c). For the remaining parts assume that 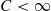 .
.
(e) Find the limiting probabilities for the Markov chain of part (a).
(f) At what rate are type  patients admitted?
patients admitted?
(g) What fraction of patients are admitted?
38. Consider an  server system where the service times of server
server system where the service times of server 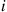 are exponentially distributed with rate
are exponentially distributed with rate 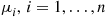 . Suppose customers arrive in accordance with a Poisson process with rate
. Suppose customers arrive in accordance with a Poisson process with rate  , and that an arrival who finds all servers busy does not enter but goes elsewhere. Suppose that an arriving customer who finds at least one idle server is served by a randomly chosen one of that group; that is, an arrival finding
, and that an arrival who finds all servers busy does not enter but goes elsewhere. Suppose that an arriving customer who finds at least one idle server is served by a randomly chosen one of that group; that is, an arrival finding 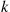 idle servers is equally likely to be served by any of these
idle servers is equally likely to be served by any of these 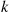 .
.
(a) Define states so as to analyze the preceding as a continuous-time Markov chain.
(b) Show that this chain is time reversible.
(c) Find the limiting probabilities.
39. Suppose in Exercise 38 that an entering customer is served by the server who has been idle the shortest amount of time.
(a) Define states so as to analyze this model as a continuous-time Markov chain.
(b) Show that this chain is time reversible.
(c) Find the limiting probabilities.
40. Consider a continuous-time Markov chain with states  , which spends an exponential time with rate
, which spends an exponential time with rate 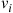 in state
in state 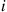 during each visit to that state and is then equally likely to go to any of the other
during each visit to that state and is then equally likely to go to any of the other 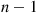 states.
states.
(a) Is this chain time reversible?
(b) Find the long-run proportions of time it spends in each state.
41. Show in Example 6.22 that the limiting probabilities satisfy Equations (6.33), (6.34), and (6.35).
42. In Example 6.22 explain why we would have known before analyzing Example 6.22 that the limiting probability there are  customers with server
customers with server 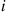 is
is 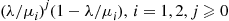 . (What we would not have known was that the number of customers at the two servers would, in steady state, be independent.)
. (What we would not have known was that the number of customers at the two servers would, in steady state, be independent.)
43. Consider a sequential queueing model with three servers, where customers arrive at server 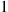 in accordance with a Poisson process with rate
in accordance with a Poisson process with rate  . After completion at server
. After completion at server  the customer then moves to server
the customer then moves to server 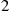 ; after a service completion at server
; after a service completion at server  the customer moves to server
the customer moves to server 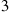 ; after a service completion at server
; after a service completion at server  the customer departs the system. Assuming that the service times at server
the customer departs the system. Assuming that the service times at server 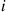 are exponential with rate
are exponential with rate 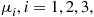 find the limiting probabilities of this system by guessing at the reverse chain and then verifying that your guess is correct.
find the limiting probabilities of this system by guessing at the reverse chain and then verifying that your guess is correct.
44. For the continuous-time Markov chain of Exercise 3 present a uniformized version.
45. In Example 6.20, we computed 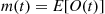 , the expected occupation time in state 0 by time
, the expected occupation time in state 0 by time 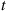 for the two-state continuous-time Markov chain starting in state 0. Another way of obtaining this quantity is by deriving a differential equation for it.
for the two-state continuous-time Markov chain starting in state 0. Another way of obtaining this quantity is by deriving a differential equation for it.

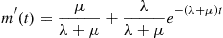
46. Let 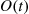 be the occupation time for state 0 in the two-state continuous-time Markov chain. Find
be the occupation time for state 0 in the two-state continuous-time Markov chain. Find 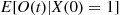 .
.
47. Consider the two-state continuous-time Markov chain. Starting in state 0, find 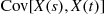 .
.
48. Let 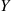 denote an exponential random variable with rate
denote an exponential random variable with rate  that is independent of the continuous-time Markov chain
that is independent of the continuous-time Markov chain 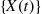 and let
and let
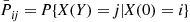

where 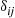 is 1 when
is 1 when 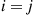 and 0 when
and 0 when 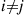 .
.
(b) Show that the solution of the preceding set of equations is given by

where  is the matrix of elements
is the matrix of elements 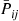 ,
,  is the identity matrix, and
is the identity matrix, and 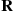 the matrix specified in Section 6.9.
the matrix specified in Section 6.9.
(c) Suppose now that  are independent exponentials with rate
are independent exponentials with rate 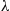 that are independent of
that are independent of 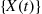 . Show that
. Show that

is equal to the element in row 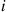 , column
, column 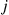 of the matrix
of the matrix  .
.
(d) Explain the relationship of the preceding to Approximation 2 of Section 6.9.
(a) Show that Approximation 1 of Section 6.9 is equivalent to uniformizing the continuous-time Markov chain with a value  such that
such that 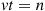 and then approximating
and then approximating 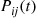 by
by 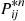 .
.
(b) Explain why the preceding should make a good approximation.
Hint: What is the standard deviation of a Poisson random variable with mean  ?
?