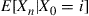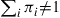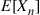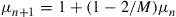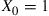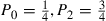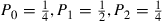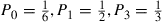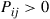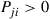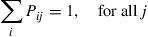
If such a chain is irreducible and aperiodic and consists of  states
states  , show that the long-run proportions are given by
, show that the long-run proportions are given by
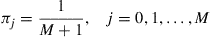
*21. A DNA nucleotide has any of four values. A standard model for a mutational change of the nucleotide at a specific location is a Markov chain model that supposes that in going from period to period the nucleotide does not change with probability 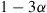 , and if it does change then it is equally likely to change to any of the other three values, for some
, and if it does change then it is equally likely to change to any of the other three values, for some 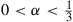 .
.
(a) Show that 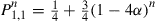 .
.
(b) What is the long-run proportion of time the chain is in each state?
22. Let  be the sum of
be the sum of  independent rolls of a fair die. Find
independent rolls of a fair die. Find
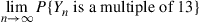
Hint: Define an appropriate Markov chain and apply the results of Exercise 20.
23. In a good weather year the number of storms is Poisson distributed with mean 1; in a bad year it is Poisson distributed with mean 3. Suppose that any year’s weather conditions depends on past years only through the previous year’s condition. Suppose that a good year is equally likely to be followed by either a good or a bad year, and that a bad year is twice as likely to be followed by a bad year as by a good year. Suppose that last year—call it year 0—was a good year.
(a) Find the expected total number of storms in the next two years (that is, in years 1 and 2).
(b) Find the probability there are no storms in year 3.
(c) Find the long-run average number of storms per year.
24. Consider three urns, one colored red, one white, and one blue. The red urn contains 1 red and 4 blue balls; the white urn contains 3 white balls, 2 red balls, and 2 blue balls; the blue urn contains 4 white balls, 3 red balls, and 2 blue balls. At the initial stage, a ball is randomly selected from the red urn and then returned to that urn. At every subsequent stage, a ball is randomly selected from the urn whose color is the same as that of the ball previously selected and is then returned to that urn. In the long run, what proportion of the selected balls are red? What proportion are white? What proportion are blue?
25. Each morning an individual leaves his house and goes for a run. He is equally likely to leave either from his front or back door. Upon leaving the house, he chooses a pair of running shoes (or goes running barefoot if there are no shoes at the door from which he departed). On his return he is equally likely to enter, and leave his running shoes, either by the front or back door. If he owns a total of 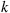 pairs of running shoes, what proportion of the time does he run barefooted?
pairs of running shoes, what proportion of the time does he run barefooted?
26. Consider the following approach to shuffling a deck of  cards. Starting with any initial ordering of the cards, one of the numbers
cards. Starting with any initial ordering of the cards, one of the numbers  is randomly chosen in such a manner that each one is equally likely to be selected. If number
is randomly chosen in such a manner that each one is equally likely to be selected. If number 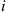 is chosen, then we take the card that is in position
is chosen, then we take the card that is in position  and put it on top of the deck—that is, we put that card in position 1. We then repeatedly perform the same operation. Show that, in the limit, the deck is perfectly shuffled in the sense that the resultant ordering is equally likely to be any of the
and put it on top of the deck—that is, we put that card in position 1. We then repeatedly perform the same operation. Show that, in the limit, the deck is perfectly shuffled in the sense that the resultant ordering is equally likely to be any of the  possible orderings.
possible orderings.
*27. Each individual in a population of size 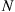 is, in each period, either active or inactive. If an individual is active in a period then, independent of all else, that individual will be active in the next period with probability
is, in each period, either active or inactive. If an individual is active in a period then, independent of all else, that individual will be active in the next period with probability 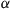 . Similarly, if an individual is inactive in a period then, independent of all else, that individual will be inactive in the next period with probability
. Similarly, if an individual is inactive in a period then, independent of all else, that individual will be inactive in the next period with probability  . Let
. Let 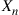 denote the number of individuals that are active in period
denote the number of individuals that are active in period 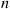 .
.
(a) Argue that 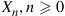 is a Markov chain.
is a Markov chain.
(c) Derive an expression for its transition probabilities.
(d) Find the long-run proportion of time that exactly 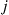 people are active.
people are active.
Hint for (d): Consider first the case where 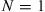 .
.
28. Every time that the team wins a game, it wins its next game with probability 0.8; every time it loses a game, it wins its next game with probability 0.3. If the team wins a game, then it has dinner together with probability 0.7, whereas if the team loses then it has dinner together with probability 0.2. What proportion of games result in a team dinner?
29. An organization has 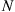 employees where
employees where 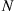 is a large number. Each employee has one of three possible job classifications and changes classifications (independently) according to a Markov chain with transition probabilities
is a large number. Each employee has one of three possible job classifications and changes classifications (independently) according to a Markov chain with transition probabilities

What percentage of employees are in each classification?
30. Three out of every four trucks on the road are followed by a car, while only one out of every five cars is followed by a truck. What fraction of vehicles on the road are trucks?
31. A certain town never has two sunny days in a row. Each day is classified as being either sunny, cloudy (but dry), or rainy. If it is sunny one day, then it is equally likely to be either cloudy or rainy the next day. If it is rainy or cloudy one day, then there is one chance in two that it will be the same the next day, and if it changes then it is equally likely to be either of the other two possibilities. In the long run, what proportion of days are sunny? What proportion are cloudy?
*32. Each of two switches is either on or off during a day. On day 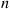 , each switch will independently be on with probability
, each switch will independently be on with probability
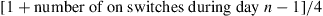
For instance, if both switches are on during day 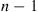 , then each will independently be on during day
, then each will independently be on during day 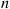 with probability
with probability 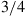 . What fraction of days are both switches on? What fraction are both off?
. What fraction of days are both switches on? What fraction are both off?
33. A professor continually gives exams to her students. She can give three possible types of exams, and her class is graded as either having done well or badly. Let 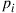 denote the probability that the class does well on a type
denote the probability that the class does well on a type 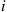 exam, and suppose that
exam, and suppose that 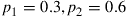 , and
, and 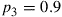 . If the class does well on an exam, then the next exam is equally likely to be any of the three types. If the class does badly, then the next exam is always type 1. What proportion of exams are type
. If the class does well on an exam, then the next exam is equally likely to be any of the three types. If the class does badly, then the next exam is always type 1. What proportion of exams are type 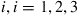 ?
?
34. A flea moves around the vertices of a triangle in the following manner: Whenever it is at vertex 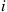 it moves to its clockwise neighbor vertex with probability
it moves to its clockwise neighbor vertex with probability 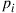 and to the counterclockwise neighbor with probability
and to the counterclockwise neighbor with probability 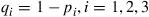 .
.
(a) Find the proportion of time that the flea is at each of the vertices.
(b) How often does the flea make a counterclockwise move that is then followed by five consecutive clockwise moves?
35. Consider a Markov chain with states 0, 1, 2, 3, 4. Suppose 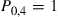 ; and suppose that when the chain is in state
; and suppose that when the chain is in state 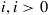 , the next state is equally likely to be any of the states
, the next state is equally likely to be any of the states  . Find the limiting probabilities of this Markov chain.
. Find the limiting probabilities of this Markov chain.
36. The state of a process changes daily according to a two-state Markov chain. If the process is in state 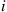 during one day, then it is in state
during one day, then it is in state 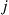 the following day with probability
the following day with probability 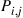 , where
, where
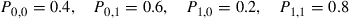
Every day a message is sent. If the state of the Markov chain that day is 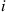 then the message sent is “good” with probability
then the message sent is “good” with probability 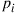 and is “bad” with probability
and is “bad” with probability 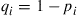 ,
, 
(a) If the process is in state 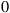 on Monday, what is the probability that a good message is sent on Tuesday?
on Monday, what is the probability that a good message is sent on Tuesday?
(b) If the process is in state 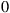 on Monday, what is the probability that a good message is sent on Friday?
on Monday, what is the probability that a good message is sent on Friday?
(c) In the long run, what proportion of messages are good?
(d) Let 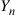 equal
equal  if a good message is sent on day
if a good message is sent on day 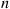 and let it equal
and let it equal 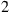 otherwise. Is
otherwise. Is 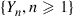 a Markov chain? If so, give its transition probability matrix. If not, briefly explain why not.
a Markov chain? If so, give its transition probability matrix. If not, briefly explain why not.
37. Show that the stationary probabilities for the Markov chain having transition probabilities 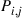 are also the stationary probabilities for the Markov chain whose transition probabilities
are also the stationary probabilities for the Markov chain whose transition probabilities 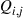 are given by
are given by
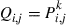
for any specified positive integer 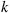 .
.
38. Capa plays either one or two chess games every day, with the number of games that she plays on successive days being a Markov chain with transition probabilities

Capa wins each game with probability  . Suppose she plays two games on Monday.
. Suppose she plays two games on Monday.
(a) What is the probability that she wins all the games she plays on Tuesday?
(b) What is the expected number of games that she plays on Wednesday?
(c) In the long run, on what proportion of days does Capa win all her games.
39. Consider the one-dimensional symmetric random walk of Example 4.18, which was shown in that example to be recurrent. Let 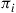 denote the long-run proportion of time that the chain is in state
denote the long-run proportion of time that the chain is in state 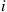 .
.
(a) Argue that 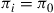 for all
for all 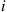 .
.
(c) Conclude that this Markov chain is null recurrent, and thus all 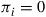 .
.
40. A particle moves on 12 points situated on a circle. At each step it is equally likely to move one step in the clockwise or in the counterclockwise direction. Find the mean number of steps for the particle to return to its starting position.
*41. Consider a Markov chain with states equal to the nonnegative integers, and suppose its transition probabilities satisfy 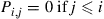 . Assume
. Assume 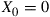 , and let
, and let 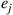 be the probability that the Markov chain is ever in state
be the probability that the Markov chain is ever in state 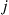 . (Note that
. (Note that 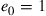 because
because 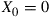 .) Argue that for
.) Argue that for 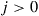
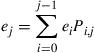
If 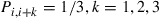 , find
, find 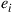 for
for  .
.
42. Let  be a set of states, and let
be a set of states, and let 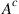 be the remaining states.
be the remaining states.
(a) What is the interpretation of
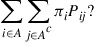
(b) What is the interpretation of
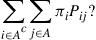
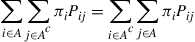
43. Each day, one of 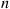 possible elements is requested, the
possible elements is requested, the  th one with probability
th one with probability 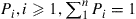 . These elements are at all times arranged in an ordered list that is revised as follows: The element selected is moved to the front of the list with the relative positions of all the other elements remaining unchanged. Define the state at any time to be the list ordering at that time and note that there are
. These elements are at all times arranged in an ordered list that is revised as follows: The element selected is moved to the front of the list with the relative positions of all the other elements remaining unchanged. Define the state at any time to be the list ordering at that time and note that there are 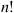 possible states.
possible states.
(a) Argue that the preceding is a Markov chain.
(b) For any state  (which is a permutation of
(which is a permutation of  ), let
), let 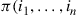 ) denote the limiting probability. In order for the state to be
) denote the limiting probability. In order for the state to be  , it is necessary for the last request to be for
, it is necessary for the last request to be for 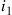 , the last non-
, the last non- request for
request for 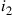 , the last non-
, the last non-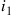 or
or 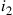 request for
request for 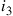 , and so on. Hence, it appears intuitive that
, and so on. Hence, it appears intuitive that
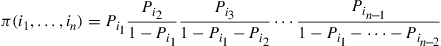
Verify when 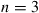 that the preceding are indeed the limiting probabilities.
that the preceding are indeed the limiting probabilities.
44. Suppose that a population consists of a fixed number, say, 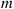 , of genes in any generation. Each gene is one of two possible genetic types. If exactly
, of genes in any generation. Each gene is one of two possible genetic types. If exactly 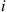 (of the
(of the 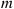 ) genes of any generation are of type 1, then the next generation will have
) genes of any generation are of type 1, then the next generation will have 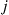 type 1 (and
type 1 (and 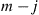 type 2) genes with probability
type 2) genes with probability
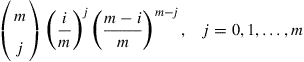
Let 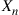 denote the number of type 1 genes in the
denote the number of type 1 genes in the 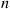 th generation, and assume that
th generation, and assume that 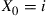 .
.
(b) What is the probability that eventually all the genes will be type 1?
45. Consider an irreducible finite Markov chain with states  .
.
(a) Starting in state 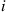 , what is the probability the process will ever visit state
, what is the probability the process will ever visit state 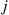 ? Explain!
? Explain!
(b) Let 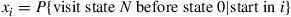 . Compute a set of linear equations that the
. Compute a set of linear equations that the 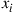 satisfy,
satisfy,  .
.
(c) If 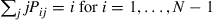 , show that
, show that 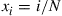 is a solution to the equations in part (b).
is a solution to the equations in part (b).
46. An individual possesses  umbrellas that he employs in going from his home to office, and vice versa. If he is at home (the office) at the beginning (end) of a day and it is raining, then he will take an umbrella with him to the office (home), provided there is one to be taken. If it is not raining, then he never takes an umbrella. Assume that, independent of the past, it rains at the beginning (end) of a day with probability
umbrellas that he employs in going from his home to office, and vice versa. If he is at home (the office) at the beginning (end) of a day and it is raining, then he will take an umbrella with him to the office (home), provided there is one to be taken. If it is not raining, then he never takes an umbrella. Assume that, independent of the past, it rains at the beginning (end) of a day with probability 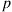 .
.
(a) Define a Markov chain with  states, which will help us to determine the proportion of time that our man gets wet. (Note: He gets wet if it is raining, and all umbrellas are at his other location.)
states, which will help us to determine the proportion of time that our man gets wet. (Note: He gets wet if it is raining, and all umbrellas are at his other location.)
(b) Show that the limiting probabilities are given by
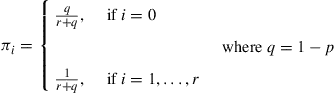
(c) What fraction of time does our man get wet?
(d) When 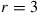 , what value of
, what value of 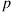 maximizes the fraction of time he gets wet
maximizes the fraction of time he gets wet
*47. Let 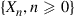 denote an ergodic Markov chain with limiting probabilities
denote an ergodic Markov chain with limiting probabilities 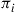 . Define the process
. Define the process 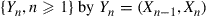 . That is,
. That is, 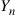 keeps track of the last two states of the original chain. Is
keeps track of the last two states of the original chain. Is 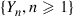 a Markov chain? If so, determine its transition probabilities and find
a Markov chain? If so, determine its transition probabilities and find

48. Consider a Markov chain in steady state. Say that a 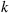 length run of zeroes ends at time
length run of zeroes ends at time 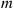 if
if
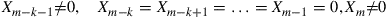
Show that the probability of this event is 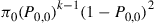 , where
, where 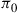 is the limiting probability of state 0.
is the limiting probability of state 0.
49. Let 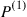 and
and 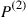 denote transition probability matrices for ergodic Markov chains having the same state space. Let
denote transition probability matrices for ergodic Markov chains having the same state space. Let 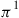 and
and 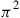 denote the stationary (limiting) probability vectors for the two chains. Consider a process defined as follows:
denote the stationary (limiting) probability vectors for the two chains. Consider a process defined as follows:
(a) 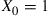 . A coin is then flipped and if it comes up heads, then the remaining states
. A coin is then flipped and if it comes up heads, then the remaining states  are obtained from the transition probability matrix
are obtained from the transition probability matrix 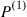 and if tails from the matrix
and if tails from the matrix 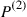 . Is
. Is 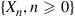 a Markov chain? If
a Markov chain? If 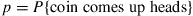 , what is
, what is 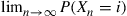 ?
?
(b) 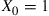 . At each stage the coin is flipped and if it comes up heads, then the next state is chosen according to
. At each stage the coin is flipped and if it comes up heads, then the next state is chosen according to 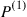 and if tails comes up, then it is chosen according to
and if tails comes up, then it is chosen according to 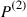 . In this case do the successive states constitute a Markov chain? If so, determine the transition probabilities. Show by a counterexample that the limiting probabilities are not the same as in part (a).
. In this case do the successive states constitute a Markov chain? If so, determine the transition probabilities. Show by a counterexample that the limiting probabilities are not the same as in part (a).
50. In Exercise 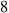 , if today’s flip lands heads, what is the expected number of additional flips needed until the pattern
, if today’s flip lands heads, what is the expected number of additional flips needed until the pattern 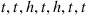 occurs?
occurs?
51. In Example 4.3, Gary is in a cheerful mood today. Find the expected number of days until he has been glum for three consecutive days.
52. A taxi driver provides service in two zones of a city. Fares picked up in zone 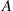 will have destinations in zone
will have destinations in zone 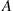 with probability 0.6 or in zone
with probability 0.6 or in zone  with probability 0.4. Fares picked up in zone
with probability 0.4. Fares picked up in zone 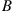 will have destinations in zone
will have destinations in zone 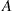 with probability 0.3 or in zone
with probability 0.3 or in zone 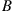 with probability 0.7. The driver’s expected profit for a trip entirely in zone
with probability 0.7. The driver’s expected profit for a trip entirely in zone 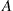 is
is 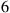 ; for a trip entirely in zone
; for a trip entirely in zone 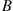 is
is 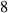 ; and for a trip that involves both zones is 12. Find the taxi driver’s average profit per trip.
; and for a trip that involves both zones is 12. Find the taxi driver’s average profit per trip.
53. Find the average premium received per policyholder of the insurance company of Example 4.27 if 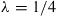 for one-third of its clients, and
for one-third of its clients, and 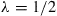 for two-thirds of its clients.
for two-thirds of its clients.
54. Consider the Ehrenfest urn model in which 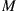 molecules are distributed between two urns, and at each time point one of the molecules is chosen at random and is then removed from its urn and placed in the other one. Let
molecules are distributed between two urns, and at each time point one of the molecules is chosen at random and is then removed from its urn and placed in the other one. Let 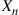 denote the number of molecules in urn 1 after the
denote the number of molecules in urn 1 after the 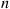 th switch and let
th switch and let 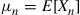 . Show that
. Show that
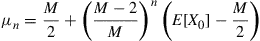
55. Consider a population of individuals each of whom possesses two genes that can be either type 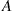 or type
or type  . Suppose that in outward appearance type
. Suppose that in outward appearance type 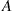 is dominant and type
is dominant and type 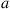 is recessive. (That is, an individual will have only the outward characteristics of the recessive gene if its pair is
is recessive. (That is, an individual will have only the outward characteristics of the recessive gene if its pair is 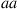 .) Suppose that the population has stabilized, and the percentages of individuals having respective gene pairs
.) Suppose that the population has stabilized, and the percentages of individuals having respective gene pairs 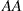 ,
, 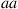 , and
, and 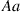 are
are 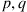 , and
, and  . Call an individual dominant or recessive depending on the outward characteristics it exhibits. Let
. Call an individual dominant or recessive depending on the outward characteristics it exhibits. Let  denote the probability that an offspring of two dominant parents will be recessive; and let
denote the probability that an offspring of two dominant parents will be recessive; and let 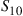 denote the probability that the offspring of one dominant and one recessive parent will be recessive. Compute
denote the probability that the offspring of one dominant and one recessive parent will be recessive. Compute 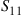 and
and 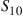 to show that
to show that  . (The quantities
. (The quantities 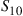 and
and 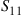 are known in the genetics literature as Snyder’s ratios.)
are known in the genetics literature as Snyder’s ratios.)
56. Suppose that on each play of the game a gambler either wins 1 with probability 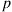 or loses 1 with probability
or loses 1 with probability 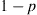 . The gambler continues betting until she or he is either up
. The gambler continues betting until she or he is either up 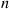 or down
or down 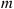 . What is the probability that the gambler quits a winner?
. What is the probability that the gambler quits a winner?
57. A particle moves among 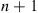 vertices that are situated on a circle in the following manner. At each step it moves one step either in the clockwise direction with probability
vertices that are situated on a circle in the following manner. At each step it moves one step either in the clockwise direction with probability 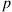 or the counterclockwise direction with probability
or the counterclockwise direction with probability 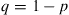 . Starting at a specified state, call it state 0, let
. Starting at a specified state, call it state 0, let 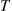 be the time of the first return to state 0. Find the probability that all states have been visited by time
be the time of the first return to state 0. Find the probability that all states have been visited by time 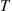 .
.
Hint: Condition on the initial transition and then use results from the gambler’s ruin problem.
58. In the gambler’s ruin problem of Section 4.5.1, suppose the gambler’s fortune is presently 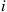 , and suppose that we know that the gambler’s fortune will eventually reach
, and suppose that we know that the gambler’s fortune will eventually reach 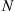 (before it goes to 0). Given this information, show that the probability he wins the next gamble is
(before it goes to 0). Given this information, show that the probability he wins the next gamble is
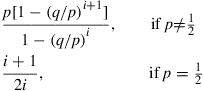
Hint: The probability we want is
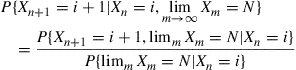
59. For the gambler’s ruin model of Section 4.5.1, let 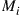 denote the mean number of games that must be played until the gambler either goes broke or reaches a fortune of
denote the mean number of games that must be played until the gambler either goes broke or reaches a fortune of 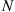 , given that he starts with
, given that he starts with 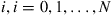 . Show that
. Show that 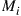 satisfies
satisfies
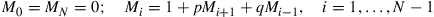
Solve these equations to obtain
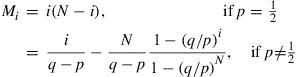
60. The following is the transition probability matrix of a Markov chain with states 
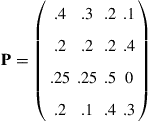
(a) find the probability that state 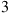 is entered before state
is entered before state 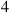 ;
;
(b) find the mean number of transitions until either state 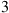 or state
or state 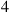 is entered.
is entered.
61. Suppose in the gambler’s ruin problem that the probability of winning a bet depends on the gambler’s present fortune. Specifically, suppose that  is the probability that the gambler wins a bet when his or her fortune is
is the probability that the gambler wins a bet when his or her fortune is 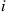 . Given that the gambler’s initial fortune is
. Given that the gambler’s initial fortune is 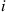 , let
, let 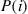 denote the probability that the gambler’s fortune reaches
denote the probability that the gambler’s fortune reaches 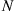 before 0.
before 0.
(a) Derive a formula that relates 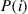 to
to  and
and 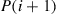 .
.
(b) Using the same approach as in the gambler’s ruin problem, solve the equation of part (a) for 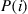 .
.
(c) Suppose that 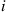 balls are initially in urn 1 and
balls are initially in urn 1 and  are in urn 2, and suppose that at each stage one of the
are in urn 2, and suppose that at each stage one of the 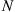 balls is randomly chosen, taken from whichever urn it is in, and placed in the other urn. Find the probability that the first urn becomes empty before the second.
balls is randomly chosen, taken from whichever urn it is in, and placed in the other urn. Find the probability that the first urn becomes empty before the second.
*62. Consider the particle from Exercise 57. What is the expected number of steps the particle takes to return to the starting position? What is the probability that all other positions are visited before the particle returns to its starting state?
63. For the Markov chain with states 1, 2, 3, 4 whose transition probability matrix 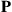 is as specified below find
is as specified below find 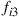 and
and 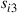 for
for 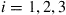 .
.

64. Consider a branching process having  . Show that if
. Show that if 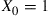 , then the expected number of individuals that ever exist in this population is given by
, then the expected number of individuals that ever exist in this population is given by 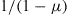 . What if
. What if 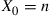 ?
?
65. In a branching process having 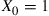 and
and 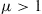 , prove that
, prove that 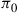 is the smallest positive number satisfying Equation (4.20).
is the smallest positive number satisfying Equation (4.20).
Hint: Let 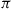 be any solution of
be any solution of 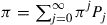 . Show by mathematical induction that
. Show by mathematical induction that 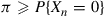 for all
for all 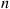 , and let
, and let 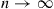 . In using the induction argue that
. In using the induction argue that
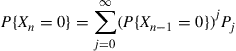
66. For a branching process, calculate 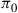 when
when
67. At all times, an urn contains 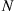 balls—some white balls and some black balls. At each stage, a coin having probability
balls—some white balls and some black balls. At each stage, a coin having probability  , of landing heads is flipped. If heads appears, then a ball is chosen at random from the urn and is replaced by a white ball; if tails appears, then a ball is chosen from the urn and is replaced by a black ball. Let
, of landing heads is flipped. If heads appears, then a ball is chosen at random from the urn and is replaced by a white ball; if tails appears, then a ball is chosen from the urn and is replaced by a black ball. Let  denote the number of white balls in the urn after the
denote the number of white balls in the urn after the 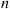 th stage.
th stage.
(a) Is 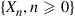 a Markov chain? If so, explain why.
a Markov chain? If so, explain why.
(b) What are its classes? What are their periods? Are they transient or recurrent?
(c) Compute the transition probabilities 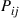 .
.
(d) Let 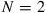 . Find the proportion of time in each state.
. Find the proportion of time in each state.
(e) Based on your answer in part (d) and your intuition, guess the answer for the limiting probability in the general case.
(f) Prove your guess in part (e) either by showing that Theorem 4.1 is satisfied or by using the results of Example 4.35.
(g) If 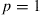 , what is the expected time until there are only white balls in the urn if initially there are
, what is the expected time until there are only white balls in the urn if initially there are 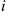 white and
white and  black?
black?
(a) Show that the limiting probabilities of the reversed Markov chain are the same as for the forward chain by showing that they satisfy the equations
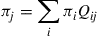
(b) Give an intuitive explanation for the result of part (a).
69. 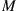 balls are initially distributed among
balls are initially distributed among  urns. At each stage one of the balls is selected at random, taken from whichever urn it is in, and then placed, at random, in one of the other
urns. At each stage one of the balls is selected at random, taken from whichever urn it is in, and then placed, at random, in one of the other  urns. Consider the Markov chain whose state at any time is the vector
urns. Consider the Markov chain whose state at any time is the vector  where
where 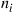 denotes the number of balls in urn
denotes the number of balls in urn 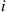 . Guess at the limiting probabilities for this Markov chain and then verify your guess and show at the same time that the Markov chain is time reversible.
. Guess at the limiting probabilities for this Markov chain and then verify your guess and show at the same time that the Markov chain is time reversible.
70. A total of 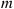 white and
white and 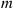 black balls are distributed among two urns, with each urn containing
black balls are distributed among two urns, with each urn containing 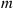 balls. At each stage, a ball is randomly selected from each urn and the two selected balls are interchanged. Let
balls. At each stage, a ball is randomly selected from each urn and the two selected balls are interchanged. Let 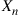 denote the number of black balls in urn 1 after the
denote the number of black balls in urn 1 after the 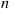 th interchange.
th interchange.
(a) Give the transition probabilities of the Markov chain  .
.
(b) Without any computations, what do you think are the limiting probabilities of this chain?
(c) Find the limiting probabilities and show that the stationary chain is time reversible.
71. It follows from Theorem 4.2 that for a time reversible Markov chain
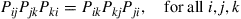
It turns out that if the state space is finite and 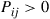 for all
for all 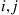 , then the preceding is also a sufficient condition for time reversibility. (That is, in this case, we need only check Equation (4.26) for paths from
, then the preceding is also a sufficient condition for time reversibility. (That is, in this case, we need only check Equation (4.26) for paths from 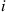 to
to 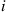 that have only two intermediate states.) Prove this.
that have only two intermediate states.) Prove this.
Hint: Fix 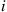 and show that the equations
and show that the equations
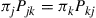
are satisfied by 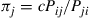 , where
, where  is chosen so that
is chosen so that 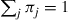 .
.
72. For a time reversible Markov chain, argue that the rate at which transitions from 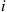 to
to 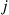 to
to 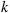 occur must equal the rate at which transitions from
occur must equal the rate at which transitions from 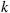 to
to 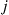 to
to 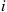 occur.
occur.
73. Show that the Markov chain of Exercise 31 is time reversible.
74. A group of 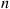 processors is arranged in an ordered list. When a job arrives, the first processor in line attempts it; if it is unsuccessful, then the next in line tries it; if it too is unsuccessful, then the next in line tries it, and so on. When the job is successfully processed or after all processors have been unsuccessful, the job leaves the system. At this point we are allowed to reorder the processors, and a new job appears. Suppose that we use the one-closer reordering rule, which moves the processor that was successful one closer to the front of the line by interchanging its position with the one in front of it. If all processors were unsuccessful (or if the processor in the first position was successful), then the ordering remains the same. Suppose that each time processor
processors is arranged in an ordered list. When a job arrives, the first processor in line attempts it; if it is unsuccessful, then the next in line tries it; if it too is unsuccessful, then the next in line tries it, and so on. When the job is successfully processed or after all processors have been unsuccessful, the job leaves the system. At this point we are allowed to reorder the processors, and a new job appears. Suppose that we use the one-closer reordering rule, which moves the processor that was successful one closer to the front of the line by interchanging its position with the one in front of it. If all processors were unsuccessful (or if the processor in the first position was successful), then the ordering remains the same. Suppose that each time processor 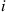 attempts a job then, independently of anything else, it is successful with probability
attempts a job then, independently of anything else, it is successful with probability  .
.
(a) Define an appropriate Markov chain to analyze this model.
(b) Show that this Markov chain is time reversible.
(c) Find the long-run probabilities.
75. A Markov chain is said to be a tree process if
(ii) for every pair of states 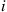 and
and 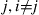 , there is a unique sequence of distinct states
, there is a unique sequence of distinct states 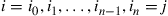 such that
such that
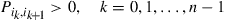
In other words, a Markov chain is a tree process if for every pair of distinct states  and
and 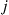 there is a unique way for the process to go from
there is a unique way for the process to go from 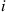 to
to 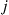 without reentering a state (and this path is the reverse of the unique path from
without reentering a state (and this path is the reverse of the unique path from 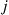 to
to 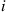 ). Argue that an ergodic tree process is time reversible.
). Argue that an ergodic tree process is time reversible.
76. On a chessboard compute the expected number of plays it takes a knight, starting in one of the four corners of the chessboard, to return to its initial position if we assume that at each play it is equally likely to choose any of its legal moves. (No other pieces are on the board.)
Hint: Make use of Example 4.36.
77. In a Markov decision problem, another criterion often used, different than the expected average return per unit time, is that of the expected discounted return. In this criterion we choose a number 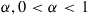 , and try to choose a policy so as to maximize
, and try to choose a policy so as to maximize 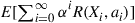 (that is, rewards at time
(that is, rewards at time 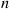 are discounted at rate
are discounted at rate 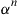 ). Suppose that the initial state is chosen according to the probabilities
). Suppose that the initial state is chosen according to the probabilities 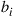 . That is,
. That is,
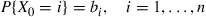
For a given policy 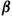 let
let 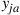 denote the expected discounted time that the process is in state
denote the expected discounted time that the process is in state 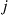 and action
and action 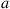 is chosen. That is,
is chosen. That is,
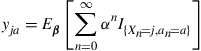
where for any event 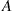 the indicator variable
the indicator variable 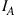 is defined by
is defined by
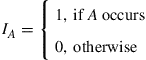
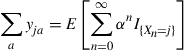
or, in other words, 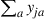 is the expected discounted time in state
is the expected discounted time in state 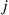 under
under 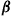 .
.

Hint: For the second equation, use the identity
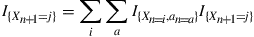
Take expectations of the preceding to obtain
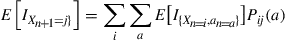
(c) Let 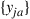 be a set of numbers satisfying
be a set of numbers satisfying
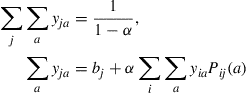 (4.38)
(4.38)Argue that 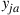 can be interpreted as the expected discounted time that the process is in state
can be interpreted as the expected discounted time that the process is in state 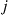 and action
and action 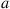 is chosen when the initial state is chosen according to the probabilities
is chosen when the initial state is chosen according to the probabilities 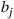 and the policy
and the policy 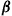 , given by
, given by
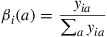
is employed.
Hint: Derive a set of equations for the expected discounted times when policy 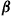 is used and show that they are equivalent to Equation (4.38).
is used and show that they are equivalent to Equation (4.38).
(d) Argue that an optimal policy with respect to the expected discounted return criterion can be obtained by first solving the linear program
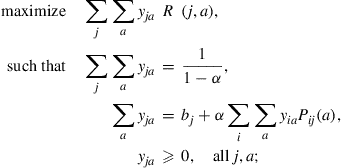
and then defining the policy 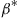 by
by
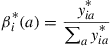
where the 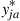 are the solutions of the linear program.
are the solutions of the linear program.
78. For the Markov chain of Exercise  , suppose that
, suppose that 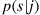 is the probability that signal
is the probability that signal  is emitted when the underlying Markov chain state is
is emitted when the underlying Markov chain state is 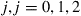 .
.
(a) What proportion of emissions are signal  ?
?
(b) What proportion of those times in which signal  is emitted is 0 the underlying state?
is emitted is 0 the underlying state?
79. In Example 4.43, what is the probability that the first 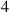 items produced are all acceptable?
items produced are all acceptable?